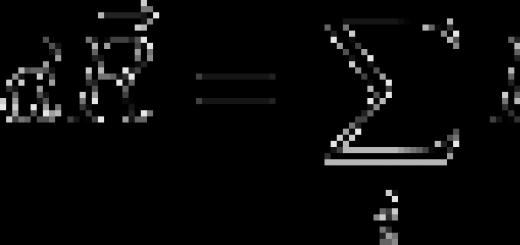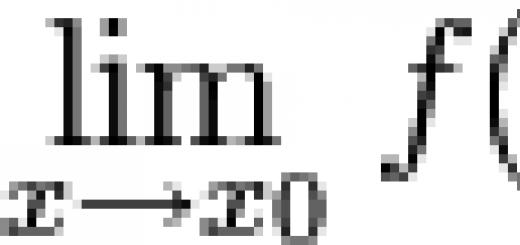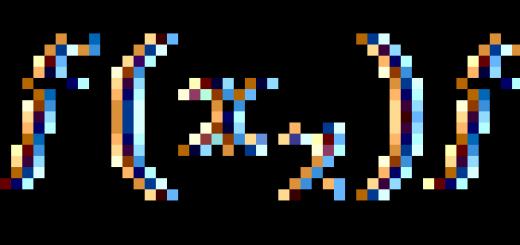في البداية ، نشأ الجيب وجيب التمام بسبب الحاجة إلى حساب الكميات في المثلثات القائمة. وقد لوحظ أنه إذا كانت قيمة درجة قياس الزوايا فيها مثلث قائملا تتغير ، فإن نسبة العرض إلى الارتفاع ، بغض النظر عن مدى تغير هذه الجوانب في الطول ، تظل دائمًا كما هي.

هذه هي الطريقة التي تم بها تقديم مفاهيم الجيب وجيب التمام. جيب الزاوية الحادة في المثلث القائم هو نسبة الضلع المقابلة إلى الوتر ، وجيب التمام هو نسبة الضلع المجاورة إلى الوتر.

نظريات الجيب والجيب

ولكن لا يمكن استخدام جيب التمام والجيب ليس فقط في المثلثات القائمة. لإيجاد قيمة زاوية منفرجة أو حادة ، أي جانب أي مثلث ، يكفي تطبيق نظرية جيب التمام والجيب.

نظرية جيب التمام بسيطة للغاية: "مربع ضلع المثلث يساوي المجموعمربعات الضلعين الآخرين مطروحًا منه ضعف حاصل ضرب هذين الضلعين بجيب تمام الزاوية بينهما.

هناك تفسيران لنظرية الجيب: صغير وممتد. وبحسب الصغير: "في المثلث تكون الزوايا متناسبة مع الضلعين المتقابلين". غالبًا ما يتم تمديد هذه النظرية بسبب خاصية الدائرة المحصورة حول المثلث: "في المثلث ، تكون الزوايا متناسبة مع الأضلاع المتقابلة ، ونسبتها تساوي قطر الدائرة المحددة".

المشتقات

المشتق هو أداة رياضية توضح مدى سرعة تغير الوظيفة فيما يتعلق بالتغيير في حجتها. تستخدم المشتقات في الهندسة وفي عدد من التخصصات الفنية.

عند حل المشكلات ، تحتاج إلى معرفة القيم الجدولية لمشتقات الدوال المثلثية: الجيب وجيب التمام. مشتق الجيب هو جيب التمام ، ومشتق الجيب هو الجيب ، ولكن بعلامة الطرح.

التطبيق في الرياضيات

في كثير من الأحيان ، يتم استخدام الجيب وجيب التمام في حل المثلثات القائمة اليمنى والمشاكل المتعلقة بها.

تنعكس راحة الجيب وجيب التمام أيضًا في التكنولوجيا. كان من السهل تقييم الزوايا والجوانب باستخدام نظريتي جيب التمام والجيب ، حيث تم تقسيم الأشكال والأشياء المعقدة إلى مثلثات "بسيطة". أمضى المهندسون ، الذين غالبًا ما يتعاملون مع حسابات نسب العرض إلى الارتفاع ومقاييس الدرجات ، الكثير من الوقت والجهد في حساب جيب التمام وجيب الزوايا غير الجدولية.

ثم جاءت جداول Bradis للإنقاذ ، حيث تحتوي على آلاف قيم الجيب وجيب التمام والظل والظل من زوايا مختلفة. في الوقت السوفياتيأجبر بعض المعلمين عنابرهم على حفظ صفحات جداول Bradys.

راديان - القيمة الزاوية للقوس بطول يساوي نصف القطر أو 57.295779513 درجة.

الدرجة (في الهندسة) - 1/360 جزء من دائرة أو 1/90 جزء زاوية مستقيمة.

π = 3.141592653589793238462 ... (القيمة التقريبية للبي).

في هذه المقالة سوف نوضح كيف تعريفات الجيب وجيب التمام والظل والظل للزاوية والرقم في علم المثلثات. هنا سنتحدث عن التدوين ، ونعطي أمثلة على التسجيلات ، ونعطي الرسوم التوضيحية. في الختام ، نرسم توازيًا بين تعريفات الجيب وجيب التمام والظل والظل في علم المثلثات والهندسة.

التنقل في الصفحة.

تعريف الجيب وجيب التمام والظل والظل

دعنا نتبع كيف يتم تشكيل مفهوم الجيب وجيب التمام والظل والظل دورة مدرسيةالرياضيات. في دروس الهندسة ، يتم إعطاء تعريف الجيب وجيب التمام والظل والظل للزاوية الحادة في المثلث القائم. ودُرس علم المثلثات لاحقًا ، والذي يشير إلى الجيب وجيب التمام والظل والظل لزاوية الدوران والرقم. نعطي كل هذه التعاريف ونعطي أمثلة ونعطي التعليقات اللازمة.

الزاوية الحادة في مثلث قائم الزاوية

من مجرى الهندسة ، تُعرف تعريفات الجيب وجيب التمام والظل والظل لزاوية حادة في مثلث قائم الزاوية. يتم إعطاؤهم كنسبة أضلاع مثلث قائم الزاوية. نقدم صيغهم.

تعريف.

جيب الزاوية الحادة في مثلث قائم الزاويةهي نسبة الضلع المقابلة إلى الوتر.

تعريف.

جيب التمام لزاوية حادة في مثلث قائم الزاويةهي نسبة الضلع المجاورة إلى الوتر.

تعريف.

ظل زاوية حادة في مثلث قائم الزاويةهي نسبة الساق المقابلة للساق المجاورة.

تعريف.

ظل التمام لزاوية حادة في مثلث قائم الزاويةهي نسبة الساق المجاورة إلى الرجل الأخرى.

كما تم تقديم تدوين الجيب وجيب التمام والظل والظل هناك - sin و cos و tg و ctg على التوالي.

على سبيل المثال ، إذا كان ABC مثلثًا قائمًا بزاوية قائمة C ، فإن جيب الزاوية A حاد يساوي النسبةالضلع المقابل BC للوتر AB ، أي sin∠A = BC / AB.

تسمح لك هذه التعريفات بحساب قيم الجيب وجيب التمام والظل والظل للزاوية الحادة من الأطوال المعروفة لأضلاع المثلث القائم ، وكذلك من القيم المعروفة للجيب وجيب التمام ، tangent و cotangent وطول أحد الجانبين ، أوجد أطوال الأضلاع الأخرى. على سبيل المثال ، إذا علمنا أن الضلع AC في المثلث القائم يساوي 3 والوتر AB يساوي 7 ، فيمكننا حساب جيب تمام الزاوية الحادة A بالتعريف: cos∠A = AC / AB = 3/7.

زاوية الدوران

في علم المثلثات ، بدأوا في النظر إلى الزاوية على نطاق أوسع - يقدمون مفهوم زاوية الدوران. لا تقتصر زاوية الدوران ، بخلاف الزاوية الحادة ، على الإطارات من 0 إلى 90 درجة ، ويمكن التعبير عن زاوية الدوران بالدرجات (وبالراديان) بأي رقم حقيقي من −∞ إلى + ∞.

في ضوء ذلك ، فإن تعريفات الجيب وجيب التمام والظل والظل لم تعد زاوية حادة ، ولكنها زاوية ذات حجم تعسفي - زاوية الدوران. يتم إعطاؤهم من خلال إحداثيات x و y للنقطة A 1 ، والتي تمر فيها ما يسمى بالنقطة الأولية A (1 ، 0) بعد أن تدور بزاوية α حول النقطة O - بداية نظام إحداثيات ديكارتي مستطيل ومركز دائرة الوحدة.

تعريف.

جيب زاوية الدورانα هو إحداثي النقطة A 1 ، أي sinα = y.

تعريف.

جيب تمام زاوية الدورانتسمى α حدود النقطة A 1 ، أي cosα = x.

تعريف.

ظل زاوية الدورانα هي نسبة إحداثي النقطة A 1 إلى إحداثياتها ، أي tgα = y / x.

تعريف.

ظل التمام لزاوية الدورانα هي نسبة إحداثيات النقطة A 1 إلى إحداثيتها ، أي ctgα = x / y.

يتم تحديد الجيب وجيب التمام لأي زاوية α ، حيث يمكننا دائمًا تحديد الإحداثي السيني وتنسيق النقطة ، والتي يتم الحصول عليها عن طريق تدوير نقطة البداية بالزاوية α. وظل التمام وظل التمام غير معرّفين لأي زاوية. لم يتم تعريف الظل لمثل هذه الزوايا α حيث تنتقل النقطة الأولية إلى نقطة بصفر حدودي (0 ، 1) أو (0 ، −1) ، وهذا يحدث عند الزوايا 90 درجة + 180 درجة ك ، k∈Z (π / 2 + π ك راد). في الواقع ، عند زوايا الدوران هذه ، فإن التعبير tgα = y / x لا معنى له ، لأنه يحتوي على قسمة على صفر. بالنسبة إلى ظل التمام ، لم يتم تعريفه لهذه الزوايا α حيث تنتقل نقطة البداية إلى نقطة ذات إحداثيات صفرية (1 ، 0) أو (−1 ، 0) ، وهذا هو الحال بالنسبة للزوايا 180 ° ك ، ك ∈Z (π ك راد).

لذلك ، يتم تحديد الجيب وجيب التمام لأي زوايا دوران ، ويتم تحديد الظل لجميع الزوايا باستثناء 90 درجة + 180 درجة ك ، k∈Z (π / 2 + ك راد) ، وتظل التمام لجميع الزوايا باستثناء 180 ° · ك ، كوز (π · ك راد).

تظهر الرموز التي نعرفها بالفعل في التعاريف sin و cos و tg و ctg ، كما أنها تُستخدم للإشارة إلى الجيب وجيب التمام والظل والظل التمام لزاوية الدوران (في بعض الأحيان يمكنك العثور على التدوين tan و cot المتوافق مع المماس و ظل التمام). لذلك يمكن كتابة جيب زاوية الدوران البالغة 30 درجة كـ sin30 ° ، والسجلات tg (24 ° 17 ′) و ctgα تتوافق مع ظل زاوية الدوران 24 درجة 17 دقيقة وظل التمام لزاوية الدوران α . تذكر أنه عند كتابة قياس الراديان لزاوية ، غالبًا ما يتم حذف الرمز "rad". على سبيل المثال ، عادةً ما يُرمز لجيب زاوية دوران مقدارها ثلاثة راديات إلى cos3 π.

في ختام هذه الفقرة ، تجدر الإشارة إلى أنه عند الحديث عن الجيب وجيب التمام والظل والظل لزاوية الدوران ، غالبًا ما يتم حذف عبارة "زاوية الدوران" أو كلمة "الدوران". هذا هو ، بدلاً من عبارة "جيب الزاوية ألفا" ، عادة ما يتم استخدام عبارة "جيب زاوية ألفا" ، أو حتى أقصر - "جيب ألفا". الأمر نفسه ينطبق على جيب التمام ، والظل ، وظل التمام.

لنفترض أيضًا أن تعريفات الجيب وجيب التمام والظل والظل لزاوية حادة في مثلث قائم الزاوية تتوافق مع التعريفات المقدمة للتو للجيب وجيب التمام والظل والظل لزاوية دوران تتراوح من 0 إلى 90 درجات. سوف ندعم هذا.

أعداد

تعريف.

الجيب وجيب التمام والظل والظل لعدد t هو رقم يساوي الجيب وجيب التمام والظل وظل التمام لزاوية الدوران في t راديان ، على التوالي.

على سبيل المثال ، جيب تمام 8 π هو ، حسب التعريف ، عددًا يساوي جيب تمام الزاوية 8 π راد. وجيب الزاوية يساوي 8 π rad يساوي واحد، إذن ، جيب تمام الرقم 8 π يساوي 1.

هناك نهج آخر لتعريف الجيب وجيب التمام والظل وظل التمام لرقم. وهو يتألف من حقيقة أن كل رقم حقيقي t يتم تعيين نقطة له من دائرة الوحدة المتمركزة في أصل نظام الإحداثيات المستطيلة ، ويتم تحديد الجيب وجيب التمام والظل والظل من خلال إحداثيات هذه النقطة. دعونا نتناول هذا بمزيد من التفصيل.

دعونا نوضح كيف يتم إنشاء المراسلات بين الأرقام الحقيقية ونقاط الدائرة:

• الرقم 0 يتم تعيين نقطة البداية A (1 ، 0) ؛
• يرتبط الرقم الموجب t بنقطة على دائرة الوحدة ، والتي سنصل إليها إذا تحركنا حول الدائرة من نقطة البداية في اتجاه عكس اتجاه عقارب الساعة وسرنا في مسار طوله t ؛
• رقم سالب t مرتبط بنقطة على دائرة الوحدة ، والتي سنصل إليها إذا تحركنا حول الدائرة من نقطة البداية في اتجاه عقارب الساعة وسرنا في مسار طول | t | .

الآن دعنا ننتقل إلى تعريفات الجيب وجيب التمام والظل والظل للعدد t. لنفترض أن الرقم t يتوافق مع نقطة من الدائرة A 1 (x ، y) (على سبيل المثال ، الرقم & pi / 2 ؛ يتوافق مع النقطة A 1 (0 ، 1)).

تعريف.

جيب الرقم t هو إحداثي نقطة دائرة الوحدة المقابلة للرقم t ، أي sint = y.

تعريف.

جيب التمام لعددتسمى t حدودي نقطة دائرة الوحدة المقابلة للرقم t ، أي التكلفة = x.

تعريف.

ظل رقم t هي نسبة الإحداثي إلى إحداثيات نقطة دائرة الوحدة المقابلة للرقم t ، أي ، tgt = y / x. في صيغة أخرى مكافئة ، ظل العدد t هو نسبة جيب هذا الرقم إلى جيب التمام ، أي tgt = sint / cost.

تعريف.

ظل التمام لرقم t هي نسبة الإحداثي إلى إحداثيات نقطة دائرة الوحدة المقابلة للرقم t ، أي ctgt = x / y. صيغة أخرى هي كما يلي: ظل الرقم t هو نسبة جيب التمام للرقم t إلى جيب الرقم t: ctgt = cost / sint.

نلاحظ هنا أن التعريفات المقدمة للتو تتفق مع التعريف الوارد في بداية هذا القسم الفرعي. في الواقع ، تتطابق نقطة دائرة الوحدة المقابلة للرقم t مع النقطة التي تم الحصول عليها من خلال تدوير نقطة البداية بزاوية t راديان.

يجدر أيضًا توضيح هذه النقطة. لنفترض أن لدينا إدخال sin3. كيف نفهم ما إذا كان جيب الرقم 3 أو جيب الزاوية لزاوية الدوران 3 راديان موضع تساؤل؟ عادة ما يكون هذا واضحًا من السياق ، وإلا فلن يكون مهمًا على الأرجح.

الدوال المثلثية للحجة الزاوية والرقمية

وفقًا للتعريفات الواردة في الفقرة السابقة ، تتوافق كل زاوية دوران α مع قيمة محددة جيدًا لـ sinα ، وكذلك قيمة cosα. بالإضافة إلى ذلك ، تتوافق جميع زوايا الدوران بخلاف 90 درجة + 180 درجة ك ، k∈Z (π / 2 + π ك راد) مع القيم tgα ، وغير 180 درجة ك ، k∈Z (π ك راد) هي قيم ctgα. لذلك فإن sinα و cosα و tgα و ctgα هي وظائف للزاوية α. بمعنى آخر ، هذه هي وظائف الحجة الزاوية.

وبالمثل ، يمكننا التحدث عن الدوال الجيب وجيب التمام والظل والظل لسعة عددية. في الواقع ، كل رقم حقيقي t يتوافق مع قيمة محددة جيدًا من sint ، بالإضافة إلى التكلفة. بالإضافة إلى ذلك ، تتوافق جميع الأرقام بخلاف π / 2 + π · k و k∈Z مع القيم tgt والأرقام π · k و k∈Z تتوافق مع القيم ctgt.

تسمى وظائف الجيب وجيب التمام والظل والظل الدوال المثلثية الأساسية.

يتضح عادة من السياق أننا نتعامل مع الدوال المثلثية للحجة الزاوية أو الحجة العددية. خلافًا لذلك ، يمكننا اعتبار المتغير المستقل مقياسًا للزاوية (وسيطة الزاوية) ووسيطة رقمية.

ومع ذلك ، فإن المدرسة تدرس بشكل أساسي وظائف رقمية، أي الدوال التي تكون وسيطاتها وقيم وظائفها المقابلة عبارة عن أرقام. لذلك ، إذا نحن نتكلمفيما يتعلق بالدوال تحديدًا ، من المناسب اعتبار الدوال المثلثية كوظائف للحجج العددية.

ربط التعاريف من علم الهندسة وعلم المثلثات

إذا أخذنا في الاعتبار زاوية الدوران α من 0 إلى 90 درجة ، فإن البيانات في سياق علم المثلثات لتعريف الجيب وجيب التمام والظل والظل لزاوية الدوران تتوافق تمامًا مع تعريفات الجيب وجيب التمام ، ظل وظل التمام لزاوية حادة في مثلث قائم الزاوية ، والتي يتم تقديمها في دورة الهندسة. دعنا ندعم هذا.

ارسم نظام إحداثيات ديكارتي مستطيل الشكل Oxy دائرة الوحدة. لاحظ نقطة البداية أ (1 ، 0). دعونا نديرها بزاوية α تتراوح من 0 إلى 90 درجة ، ونحصل على النقطة A 1 (x ، y). لنقم بإسقاط العمود العمودي A 1 H من النقطة A 1 إلى محور الثور.

من السهل أن نرى أنه في المثلث القائم الزاوية A 1 OH تساوي زاوية الدوران α ، وطول الساق OH المجاورة لهذه الزاوية يساوي حدودي النقطة A 1 ، أي | OH | = x ، طول الضلع A 1 H المقابل للزاوية يساوي إحداثي النقطة A 1 ، أي | A 1 H | = y ، وطول الوتر OA 1 يساوي واحدًا ، لأنه نصف قطر دائرة الوحدة. بعد ذلك ، حسب التعريف الهندسي ، فإن جيب الزاوية الحادة α في مثلث قائم الزاوية A 1 OH تساوي نسبة الساق المقابلة إلى الوتر ، أي sinα = | A 1 H | / | OA 1 | = ص / 1 = ص. وبحسب تعريف علم المثلثات ، فإن جيب الزاوية لزاوية الدوران α يساوي إحداثي النقطة A 1 ، أي sinα = y. يوضح هذا أن تعريف جيب الزاوية الحادة في مثلث قائم الزاوية يعادل تعريف جيب الزاوية لزاوية الدوران α لـ α من 0 إلى 90 درجة.

وبالمثل ، يمكن إثبات أن تعريفات جيب التمام والظل والظل للزاوية الحادة α تتوافق مع تعريفات جيب التمام والظل والظل لزاوية الدوران α.

فهرس.

1. الهندسة. 7-9 درجات: دراسات. للتعليم العام المؤسسات / [L. S. Atanasyan ، V. F. Butuzov ، S. B. Kadomtsev وآخرون]. - الطبعة العشرون. م: التربية والتعليم 2010. - 384 ص: مريض. - ردمك 978-5-09-023915-8.
2. بوجوريلوف أ.الهندسة: Proc. لـ7-9 خلايا. تعليم عام المؤسسات / أ ف بوغوريلوف. - الطبعة الثانية - م: التنوير 2001. - 224 ص: م. - ردمك 5-09-010803-X.
3. الجبر و وظائف الابتدائية : درس تعليميلطلاب الصف التاسع المدرسة الثانوية/ إ. س. كوشيتكوف ، إ. س. كوشيتكوفا ؛ حرره دكتور في العلوم الفيزيائية والرياضية O.N. Golovin. - 4th ed. موسكو: التعليم ، 1969.
4. الجبر:بروك. لـ 9 خلايا. متوسط المدرسة / Yu. ماكاريشيف ، إن جي مينديوك ، كي آي نيشكوف ، إس بي سوفوروفا ؛ إد. S.A Telyakovsky. - M: Enlightenment، 1990. - 272 p: Ill.- ISBN 5-09-002727-7
5. الجبروبداية التحليل: Proc. لـ 10-11 خلية. تعليم عام المؤسسات / A. N. Kolmogorov ، A. M. Abramov ، Yu. P. Dudnitsyn وآخرون ؛ إد. أ.ن.كولموغوروفا. - الطبعة 14. - م: التنوير ، 2004. - 384 ص: مريض - ISBN 5-09-013651-3.
6. مردكوفيتش أ.الجبر وبدايات التحليل. الصف 10. في 2 ص الفصل 1: برنامج تعليمي ل المؤسسات التعليمية(مستوى الملف الشخصي) / A.G Mordkovich، P. V. Semenov. - الطبعة الرابعة ، إضافة. - م: Mnemosyne، 2007. - 424 ص: مريض. ردمك 978-5-346-00792-0.
7. الجبروبداية التحليل الرياضي. الصف العاشر: كتاب مدرسي. للتعليم العام المؤسسات: الأساسية والملف الشخصي. المستويات / [Yu. M. Kolyagin، M. V. Tkacheva، N. E. Fedorova، M.I Shabunin]؛ إد. A. B. Zhizhchenko. - الطبعة الثالثة. - أولا: التعليم ، 2010. - 368 ص: إلينوي - ISBN 978-5-09-022771-1.
8. باشماكوف م.الجبر وبداية التحليل: Proc. لـ 10-11 خلية. متوسط المدرسة - الطبعة الثالثة. - م: التنوير ، 1993. - 351 ص: مريض. - ردمك 5-09-004617-4.
9. جوسيف ف.أ ، مردكوفيتش أ.الرياضيات (دليل للمتقدمين للمدارس الفنية): Proc. بدل. - م ؛ أعلى المدرسة ، 1984. - 351 ص. ، مريض.

كيف تجد الجيب؟

تساعد دراسة الهندسة على تنمية التفكير. يجب تضمين هذا العنصر في التعليم. في الحياة ، يمكن أن تكون معرفة هذا الموضوع مفيدة - على سبيل المثال ، عند التخطيط لشقة.

من التاريخ

كجزء من دورة الهندسة ، تمت دراسة علم المثلثات أيضًا ، والذي يستكشف الدوال المثلثية. في علم المثلثات ، ندرس الجيب وجيب التمام والظل والظل لزاوية.

لكن في الوقت الحالي ، لنبدأ بأبسط جيب. دعنا نلقي نظرة فاحصة على المفهوم الأول - جيب الزاوية في الهندسة. ما هو الجيب وكيفية العثور عليه؟

مفهوم "جيب الزاوية" والجيوب الأنفية

جيب الزاوية هو النسبة بين قيم الضلع المقابل والوتر في المثلث القائم. هذه دالة مثلثية مباشرة ، مكتوبة كـ "sin (x)" ، حيث (x) هي زاوية المثلث.

على الرسم البياني ، يُشار إلى جيب الزاوية بخصائصه الخاصة. يشبه الجيب الجيبي خطًا متموجًا مستمرًا يقع ضمن حدود معينة على مستوى الإحداثيات. الوظيفة فردية ، وبالتالي فهي متماثلة بالنسبة إلى 0 على مستوى الإحداثيات (تترك أصل الإحداثيات).

يقع مجال هذه الوظيفة في النطاق من -1 إلى +1 على نظام الإحداثيات الديكارتية. فترة دالة جيب الزاوية هي 2 Pi. هذا يعني أن كل 2 Pi يتكرر النمط وأن الموجة الجيبية تمر بدورة كاملة.

المعادلة الجيبية

• الخطيئة س = أ / ج
• حيث a هي الساق المقابلة لزاوية المثلث
• ج - وتر المثلث القائم

خصائص جيب الزاوية

1. الخطيئة (س) = - الخطيئة (س). توضح هذه الميزة أن الوظيفة متماثلة ، وإذا تم وضع القيمتين x و (-x) جانبًا على نظام الإحداثيات في كلا الاتجاهين ، فستكون إحداثيات هذه النقاط معاكسة. سيكونون مسافة متساويةمن بعضهما البعض.
2. ميزة أخرى لهذه الوظيفة هي أن الرسم البياني للوظيفة يزيد على المقطع [- P / 2 + 2 Pn] ؛ [P / 2 + 2Pn] ، حيث n هو أي عدد صحيح. سيُلاحظ انخفاض في الرسم البياني لجيب الزاوية على المقطع: [P / 2 + 2 Pn] ؛ [3P / 2 + 2Pn].
3. sin (x)> 0 عندما تكون x في النطاق (2Pn، P + 2Pn)
4. (خ)< 0, когда х находится в диапазоне (-П+2Пn, 2Пn)

يتم تحديد قيم جيب الزاوية بواسطة جداول خاصة. تم إنشاء هذه الجداول لتسهيل عملية حساب الصيغ والمعادلات المعقدة. إنه سهل الاستخدام ويحتوي على قيم ليس فقط وظائف الخطيئة(x) ، ولكن أيضًا قيم الوظائف الأخرى.

علاوة على ذلك ، يتم تضمين جدول القيم القياسية لهذه الوظائف في دراسة الذاكرة الإلزامية ، مثل جدول الضرب. هذا ينطبق بشكل خاص على الفصول ذات التحيز المادي والرياضي. في الجدول يمكنك رؤية قيم الزوايا الرئيسية المستخدمة في حساب المثلثات: 0 ، 15 ، 30 ، 45 ، 60 ، 75 ، 90 ، 120 ، 135 ، 150 ، 180 ، 270 ، 360 درجة.

يوجد أيضًا جدول يحدد قيم الدوال المثلثية للزوايا غير القياسية. باستخدام جداول مختلفة ، يمكنك بسهولة حساب الجيب وجيب التمام والظل والظل لبعض الزوايا.

تتكون المعادلات من الدوال المثلثية. حل هذه المعادلات سهل إذا كنت تعرف متطابقات مثلثية بسيطة واختزال وظائف ، على سبيل المثال ، مثل الخطيئة (P / 2 + x) \ u003d cos (x) وغيرها. كما تم تجميع جدول منفصل لمثل هذه القوالب.

كيفية إيجاد جيب الزاوية

عندما تكون المهمة هي إيجاد جيب الزاوية ، وبحسب الشرط لدينا فقط جيب التمام أو الظل أو ظل التمام للزاوية ، يمكننا بسهولة حساب ما نحتاج إليه باستخدام المتطابقات المثلثية.

• الخطيئة 2 س + كوس 2 س = 1

من هذه المعادلة ، يمكننا إيجاد كل من الجيب وجيب التمام ، اعتمادًا على القيمة غير المعروفة. سننجح المعادلة المثلثيةمع واحد غير معروف:

• sin 2 x = 1 - cos 2 x
• sin x = ± √ 1 - cos 2 x
• ctg 2 x + 1 = 1 / sin 2 x

من هذه المعادلة ، يمكنك إيجاد قيمة الجيب ، مع معرفة قيمة ظل التمام للزاوية. للتبسيط ، استبدل sin 2 x = y ، وستحصل على معادلة بسيطة. على سبيل المثال ، قيمة ظل التمام هي 1 ، ثم:

• 1 + 1 = 1 / ص
• 2 = 1 / ص
• 2 ص = 1
• ص = 1/2

الآن نقوم بالاستبدال العكسي للاعب:

• الخطيئة 2 س = ½
• الخطيئة س = 1 / √2

نظرًا لأننا أخذنا قيمة ظل التمام للزاوية القياسية (45 0) ، يمكن التحقق من القيم التي تم الحصول عليها مقابل الجدول.

إذا كانت لديك قيمة ظل ، لكنك تحتاج إلى إيجاد الجيب ، فستساعدك هوية مثلثية أخرى:

• tg x * ctg x = 1

إنه يتبع هذا:

• ctg x = 1 / tg x

لإيجاد جيب الزاوية غير القياسي ، على سبيل المثال ، 240 0 ، تحتاج إلى استخدام صيغ تقليل الزاوية. نعلم أن π تقابل 180 0 بالنسبة لنا. وبالتالي ، سوف نعبر عن مساواتنا باستخدام الزوايا القياسية عن طريق التوسع.

• 240 0 = 180 0 + 60 0

علينا إيجاد ما يلي: sin (180 0 + 60 0). في علم المثلثات ، توجد صيغ اختزال مفيدة في هذه الحالة. هذه هي الصيغة:

• الخطيئة (π + س) = - الخطيئة (س)

إذن ، جيب الزاوية 240 درجة هو:

• الخطيئة (180 0 + 60 0) = - الخطيئة (60 0) = - √3 / 2

في حالتنا ، x = 60 ، و P على التوالي ، 180 درجة. وجدنا القيمة (-3 / 2) من جدول قيم وظائف الزوايا القياسية.

بهذه الطريقة ، يمكن أن تتحلل الزوايا غير القياسية ، على سبيل المثال: 210 = 180 + 30.

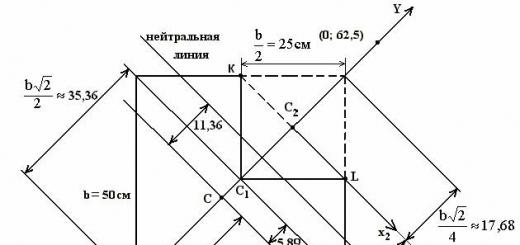
كما ترى ، هذه الدائرة مبنية في نظام الإحداثيات الديكارتية. نصف قطر الدائرة يساوي واحدًا ، بينما يقع مركز الدائرة عند نقطة الأصل ، والموضع الأولي لمتجه نصف القطر ثابتًا على طول الاتجاه الموجب للمحور (في مثالنا ، هذا هو نصف القطر).

تتوافق كل نقطة في الدائرة مع رقمين: التنسيق على طول المحور والإحداثيات على طول المحور. ما هي هذه الأرقام الإحداثيّة؟ وبشكل عام ، ما علاقتهم بالموضوع المطروح؟ للقيام بذلك ، تذكر معلومات المثلث القائم الزاوية. في الشكل أعلاه ، يمكنك أن ترى مثلثين قائمين كاملين. خذ بعين الاعتبار المثلث. إنه مستطيل لأنه عمودي على المحور.

ماذا يساوي المثلث؟ هذا صحيح. بالإضافة إلى ذلك ، نعلم أن هذا هو نصف قطر دائرة الوحدة ، وبالتالي ،. عوّض بهذه القيمة في صيغة جيب التمام. إليك ما يحدث:

وماذا يساوي المثلث؟ حسنا بالطبع، ! عوض بقيمة نصف القطر في هذه الصيغة واحصل على:

لذا ، هل يمكن أن تخبرني ما هي إحداثيات النقطة التي تنتمي إلى الدائرة؟ حسنًا ، مستحيل؟ وإذا أدركت ذلك وهل هي مجرد أرقام؟ ما هو التنسيق الذي يتوافق معه؟ حسنًا ، بالطبع ، التنسيق! ما هو التنسيق الذي يتوافق معه؟ هذا صحيح ، قم بالتنسيق! وهكذا ، فإن النقطة.

وماذا بعد ذلك متساوون و؟ هذا صحيح ، دعنا نستخدم التعريفات المناسبة لـ tangent و cotangent ونحصل على ذلك ، a.

ماذا لو كانت الزاوية أكبر؟ هنا على سبيل المثال كما في هذه الصورة:

ما الذي تغير في هذا المثال؟ دعونا نفهم ذلك. للقيام بذلك ، ننتقل مرة أخرى إلى مثلث قائم الزاوية. ضع في اعتبارك مثلث قائم الزاوية: زاوية (كمجاورة لزاوية). ما هي قيمة الجيب وجيب التمام والظل وظل التمام لزاوية؟ هذا صحيح ، نحن نلتزم بالتعريفات المقابلة للوظائف المثلثية:

حسنًا ، كما ترى ، لا تزال قيمة جيب الزاوية تتوافق مع الإحداثي ؛ قيمة جيب التمام للزاوية - الإحداثي ؛ وقيم الظل والظل للنسب المقابلة. وبالتالي ، فإن هذه العلاقات قابلة للتطبيق على أي دوران لمتجه نصف القطر.

لقد سبق أن ذكرنا أن الموضع الأولي لمتجه نصف القطر يقع على طول الاتجاه الإيجابي للمحور. حتى الآن قمنا بتدوير هذا المتجه عكس اتجاه عقارب الساعة ، ولكن ماذا يحدث إذا قمنا بتدويره في اتجاه عقارب الساعة؟ لا شيء غير عادي ، ستحصل أيضًا على زاوية بحجم معين ، لكنها ستكون سالبة فقط. وهكذا ، عند تدوير متجه نصف القطر عكس اتجاه عقارب الساعة ، نحصل على زوايا موجبة ، وعند الدوران في اتجاه عقارب الساعة - نفي.

لذلك ، نعلم أن الثورة الكاملة لمتجه نصف القطر حول الدائرة تساوي أو. هل من الممكن تدوير متجه نصف القطر بواسطة أم بجانبه؟ حسنا بالطبع يمكنك! لذلك ، في الحالة الأولى ، يقوم متجه نصف القطر بعمل ثورة كاملة ويتوقف عند الموضع أو.

في الحالة الثانية ، أي ، يقوم متجه نصف القطر بثلاث دورات كاملة ويتوقف عند الموضع أو.

وبالتالي ، من الأمثلة المذكورة أعلاه ، يمكننا أن نستنتج أن الزوايا التي تختلف في أو (أين يوجد أي عدد صحيح) تتوافق مع نفس موضع متجه نصف القطر.

يوضح الشكل أدناه زاوية. نفس الصورة تتوافق مع الزاوية ، وهكذا. يمكن أن تستمر هذه القائمة إلى أجل غير مسمى. يمكن كتابة كل هذه الزوايا بالصيغة العامة أو (أين يوجد أي عدد صحيح)

الآن ، بعد معرفة تعريفات الدوال المثلثية الأساسية واستخدام دائرة الوحدة ، حاول الإجابة عن القيم التي تساويها:

إليك دائرة الوحدة لمساعدتك:

أي صعوبات؟ ثم دعونا نكتشف ذلك. لذلك نحن نعلم أن:

من هنا نحدد إحداثيات النقاط المقابلة لقياسات معينة للزاوية. حسنًا ، لنبدأ بالترتيب: الزاوية عند تتوافق مع نقطة ذات إحداثيات ، لذلك:

غير موجود؛

علاوة على ذلك ، بالالتزام بالمنطق نفسه ، نجد أن الزوايا تتوافق مع النقاط ذات الإحداثيات ، على التوالي. بمعرفة ذلك ، من السهل تحديد قيم الدوال المثلثية في النقاط المقابلة. جربها بنفسك أولاً ، ثم تحقق من الإجابات.

الإجابات:

غير موجود

غير موجود

غير موجود

غير موجود

وهكذا يمكننا عمل الجدول التالي:

ليست هناك حاجة لتذكر كل هذه القيم. يكفي تذكر المراسلات بين إحداثيات النقاط على دائرة الوحدة وقيم الدوال المثلثية:

لكن قيم الدوال المثلثية للزوايا في ، والمذكورة في الجدول أدناه ، يجب تذكرها:

لا تخافوا ، الآن سنعرض أحد الأمثلة إلى حد ما حفظ بسيط للقيم المقابلة:

لاستخدام هذه الطريقة ، من الضروري تذكر قيم الجيب لجميع مقاييس الزاوية () ، بالإضافة إلى قيمة ظل الزاوية في. من خلال معرفة هذه القيم ، من السهل جدًا استعادة الجدول بأكمله - يتم نقل قيم جيب التمام وفقًا للأسهم ، أي:

بمعرفة هذا ، يمكنك استعادة قيم. سيتطابق البسط "" ويتطابق المقام "". يتم نقل قيم ظل التمام وفقًا للأسهم الموضحة في الشكل. إذا فهمت هذا وتذكرت الرسم التخطيطي بالسهام ، فسيكون ذلك كافيًا لتذكر القيمة بأكملها من الجدول.

إحداثيات نقطة على دائرة

هل من الممكن إيجاد نقطة (إحداثياتها) على دائرة ، معرفة إحداثيات مركز الدائرة ونصف قطرها وزاوية الدوران?

حسنا بالطبع يمكنك! دعونا نخرج الصيغة العامة لإيجاد إحداثيات نقطة.

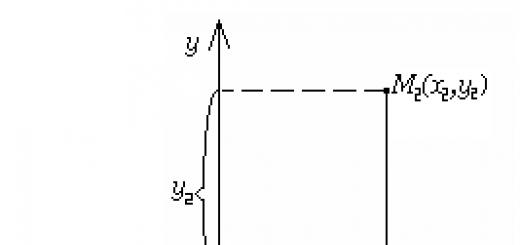
هنا ، على سبيل المثال ، لدينا مثل هذه الدائرة:

نعلم أن النقطة هي مركز الدائرة. نصف قطر الدائرة متساوي. من الضروري إيجاد إحداثيات النقطة التي تم الحصول عليها عن طريق تدوير النقطة بالدرجات.

كما يتضح من الشكل ، فإن تنسيق النقطة يتوافق مع طول المقطع. يتوافق طول المقطع مع إحداثيات مركز الدائرة ، أي أنه يساوي. يمكن التعبير عن طول المقطع باستخدام تعريف جيب التمام:

ثم لدينا هذا بالنسبة للنقطة الإحداثي.

بنفس المنطق ، نجد قيمة إحداثي ص للنقطة. هكذا،

حتى في نظرة عامةيتم تحديد إحداثيات النقاط بواسطة الصيغ:

إحداثيات مركز الدائرة ،

دائرة نصف قطرها

زاوية دوران متجه نصف القطر.

كما ترى ، بالنسبة لدائرة الوحدة التي ندرسها ، يتم تقليل هذه الصيغ بشكل كبير ، نظرًا لأن إحداثيات المركز تساوي صفرًا ونصف القطر يساوي واحدًا:

حسنًا ، لنجرب هذه الصيغ للتذوق ، ونتدرب على إيجاد النقاط على الدائرة؟

1. أوجد إحداثيات نقطة على دائرة الوحدة التي تم الحصول عليها عن طريق تشغيل نقطة.

2. أوجد إحداثيات نقطة على دائرة الوحدة التي تم الحصول عليها بتدوير نقطة على.

3. أوجد إحداثيات نقطة على دائرة الوحدة التي تم الحصول عليها عن طريق تشغيل نقطة.

4. نقطة - مركز الدائرة. نصف قطر الدائرة متساوي. من الضروري إيجاد إحداثيات النقطة التي تم الحصول عليها بتدوير متجه نصف القطر الأولي بمقدار.

5. نقطة - مركز الدائرة. نصف قطر الدائرة متساوي. من الضروري إيجاد إحداثيات النقطة التي تم الحصول عليها بتدوير متجه نصف القطر الأولي بمقدار.

هل تواجه مشكلة في العثور على إحداثيات نقطة في دائرة؟

قم بحل هذه الأمثلة الخمسة (أو افهم الحل جيدًا) وسوف تتعلم كيفية العثور عليها!

1.

ويمكن أن نرى أن. ونعرف ما يتوافق مع الانعطاف الكامل لنقطة البداية. وبالتالي ، ستكون النقطة المرغوبة في نفس الموضع عند التحول إلى. بمعرفة هذا نجد الإحداثيات المرغوبة للنقطة:

2. الدائرة عبارة عن وحدة مركزها نقطة ، مما يعني أنه يمكننا استخدام صيغ مبسطة:

ويمكن أن نرى أن. نحن نعلم ما يتوافق مع دورتين كاملتين لنقطة البداية. وبالتالي ، ستكون النقطة المرغوبة في نفس الموضع عند التحول إلى. بمعرفة هذا نجد الإحداثيات المرغوبة للنقطة:

الجيب وجيب التمام هما قيمتان جدوليتان. نتذكر قيمهم ونحصل على:

وبالتالي ، فإن النقطة المطلوبة لها إحداثيات.

3. الدائرة عبارة عن وحدة مركزها نقطة ، مما يعني أنه يمكننا استخدام صيغ مبسطة:

ويمكن أن نرى أن. دعنا نصور المثال المدروس في الشكل:

يجعل نصف القطر زوايا مع المحور تساوي و. معرفة أن قيم جدول جيب التمام والجيب متساوية ، وبعد تحديد أن جيب التمام هنا يأخذ معنى سلبيوالجيب موجب لدينا:

أكثر أمثلة مماثلةالفهم عند دراسة الصيغ لتقليل الدوال المثلثية في الموضوع.

وبالتالي ، فإن النقطة المطلوبة لها إحداثيات.

4.

زاوية دوران متجه نصف القطر (حسب الشرط)

لتحديد علامات الجيب وجيب التمام المقابلة ، نقوم ببناء دائرة وحدة وزاوية:

كما ترى ، القيمة ، أي موجبة ، والقيمة أي سالبة. بمعرفة القيم الجدولية للوظائف المثلثية المقابلة ، نحصل على ما يلي:

دعنا نعوض بالقيم التي تم الحصول عليها في الصيغة الخاصة بنا ونوجد الإحداثيات:

وبالتالي ، فإن النقطة المطلوبة لها إحداثيات.

5. لحل هذه المشكلة ، نستخدم الصيغ بشكل عام ، أين

إحداثيات مركز الدائرة (في مثالنا ،

نصف قطر الدائرة (حسب الشرط)

زاوية دوران متجه نصف القطر (حسب الشرط).

عوّض بكل القيم في الصيغة واحصل على:

و- قيم الجدول. نتذكرها ونستبدلها بالصيغة:

وبالتالي ، فإن النقطة المطلوبة لها إحداثيات.

ملخص وصيغة أساسية

جيب الزاوية هو نسبة الضلع المقابل (البعيد) إلى الوتر.

جيب تمام الزاوية هو نسبة الضلع المجاورة (القريبة) إلى الوتر.

ظل الزاوية هو نسبة الضلع المقابلة (البعيدة) إلى المجاورة (القريبة).

ظل التمام لزاوية هو نسبة الضلع المجاورة (القريبة) إلى الضلع المقابل (البعيد).

علم المثلثات - القسم العلوم الرياضيةالتي تدرس الدوال المثلثية واستخدامها في الهندسة. بدأ تطوير علم المثلثات في أيام اليونان القديمة. خلال العصور الوسطى ، قدم علماء من الشرق الأوسط والهند مساهمة مهمة في تطوير هذا العلم.

هذه المقالة مخصصة للمفاهيم والتعريفات الأساسية لعلم المثلثات. يناقش تعريفات الدوال المثلثية الرئيسية: الجيب وجيب التمام والظل والظل. يتم شرح وتوضيح معناها في سياق الهندسة.

في البداية ، تم التعبير عن تعريفات الدوال المثلثية ، التي تكون حجتها زاوية ، من خلال نسبة أضلاع المثلث القائم.

تعريفات الدوال المثلثية

جيب الزاوية (sin α) هو نسبة الضلع المقابلة لهذه الزاوية على الوتر.

جيب تمام الزاوية (cos α) هو نسبة الضلع المجاورة إلى الوتر.

ظل الزاوية (t g α) هو نسبة الساق المقابلة إلى المجاورة.

ظل التمام للزاوية (ct g α) هو نسبة الساق المجاورة إلى الأخرى.

يتم إعطاء هذه التعريفات لزاوية حادة للمثلث القائم!

دعونا نعطي توضيحا.

في المثلث ABC بالزاوية القائمة C ، جيب الزاوية A يساوي نسبة الضلع BC إلى الوتر AB.

تجعل تعريفات الجيب وجيب التمام والظل والظل من الممكن حساب قيم هذه الوظائف من الأطوال المعروفة لأضلاع المثلث.

من المهم أن تتذكر!

نطاق قيم الجيب وجيب التمام: من -1 إلى 1. بمعنى آخر ، يأخذ الجيب وجيب التمام قيمًا من -1 إلى 1. نطاق قيم الظل وجيب التمام هو خط الأرقام بالكامل ، أي هذه يمكن أن تأخذ الوظائف أي قيمة.

التعريفات الواردة أعلاه تشير إلى الزوايا الحادة. في علم المثلثات ، يتم تقديم مفهوم زاوية الدوران ، والتي لا تقتصر قيمتها ، على عكس الزاوية الحادة ، على إطارات من 0 إلى 90 درجة. يتم التعبير عن زاوية الدوران بالدرجات أو بالراديان بأي رقم حقيقي من - ∞ إلى + ∞.

في هذا السياق ، يمكن للمرء تحديد الجيب وجيب التمام والظل والظل لزاوية مقدار تعسفي. تخيل دائرة وحدة متمركزة في أصل نظام الإحداثيات الديكارتية.

نقطة البداية أ ذات الإحداثيات (1 ، 0) تدور حول مركز دائرة الوحدة بزاوية ما α وتنتقل إلى النقطة أ 1. يتم تقديم التعريف من خلال إحداثيات النقطة A 1 (x ، y).

جيب الزاوية لزاوية الدوران

جيب الزاوية α هو إحداثي النقطة A 1 (x، y). sinα = ذ

جيب التمام (كوس) لزاوية الدوران

جيب تمام زاوية الدوران α هو حدود النقطة A 1 (x، y). كوس α = س

الظل (tg) لزاوية الدوران

ظل زاوية الدوران α هو نسبة إحداثي النقطة A 1 (x، y) إلى الحد الفاصل لها. t g α = y x

ظل التمام (ctg) لزاوية الدوران

ظل التمام لزاوية الدوران α هو نسبة الحد الأقصى للنقطة A 1 (س ، ص) إلى إحداثيتها. ج t ز α = س ص

يتم تحديد الجيب وجيب التمام لأي زاوية دوران. هذا أمر منطقي ، لأنه يمكن تحديد إحداثيات النقطة والإحداثيات بعد الدوران بأي زاوية. يختلف الوضع مع الظل والظل. لا يتم تعريف الظل عندما تنتقل النقطة بعد الدوران إلى النقطة التي لا تحتوي على حد أقصى (0 ، 1) و (0 ، - 1). في مثل هذه الحالات ، فإن التعبير عن الظل t g α = y x ببساطة لا معنى له ، لأنه يحتوي على قسمة على صفر. الوضع مشابه مع ظل التمام. الفرق هو أن ظل التمام لم يتم تعريفه في الحالات التي يختفي فيها إحداثيات النقطة.

من المهم أن تتذكر!

يتم تعريف الجيب وجيب التمام لأي زوايا α.

يتم تحديد الظل لجميع الزوايا باستثناء α = 90 ° + 180 ° k، k ∈ Z (α = π 2 + π k، k ∈ Z)

يتم تعريف ظل التمام لجميع الزوايا باستثناء α = 180 ° k، k ∈ Z (α = π k، k ∈ Z)

عند حل الأمثلة العملية ، لا تقل "جيب زاوية الدوران α". تم حذف الكلمات "زاوية الدوران" ببساطة ، مما يعني أنه من الواضح بالفعل من السياق ما هو على المحك.

أعداد

ماذا عن تعريف الجيب وجيب التمام والظل والظل لعدد ، وليس زاوية الدوران؟

الجيب وجيب التمام والظل والظل لعدد

الجيب وجيب التمام والظل والظل لعدد ريسمى الرقم ، والذي يساوي على التوالي الجيب وجيب التمام والظل والظل في رراديان.

على سبيل المثال ، جيب 10 π يساوي جيب زاوية الدوران 10 π راد.

هناك نهج آخر لتعريف الجيب وجيب التمام والظل وظل التمام لرقم. دعونا ننظر في الأمر بمزيد من التفصيل.

أي رقم حقيقي ريتم وضع نقطة على دائرة الوحدة بالتوافق مع المركز في أصل نظام الإحداثيات الديكارتية المستطيل. يتم تعريف الجيب وجيب التمام والظل والظل من حيث إحداثيات هذه النقطة.

نقطة البداية على الدائرة هي النقطة أ ذات الإحداثيات (1 ، 0).

رقم موجب، عدد إيجابي ر

عدد السلبي ريتوافق مع النقطة التي ستتحرك إليها نقطة البداية إذا تحركت عكس اتجاه عقارب الساعة حول الدائرة ومرت المسار t.

الآن وقد تم إنشاء الاتصال بين الرقم والنقطة على الدائرة ، ننتقل إلى تعريف الجيب وجيب التمام والظل والظل.

الجيب (الخطيئة) للرقم ت

جيب رقم ر- إحداثيات نقطة دائرة الوحدة المقابلة للرقم ر. الخطيئة ر = ذ

جيب التمام (كوس) من ر

جيب التمام لعدد ر- حدود نقطة دائرة الوحدة المقابلة للرقم ر. كوس تي = س

الظل (tg) من t

ظل رقم ر- نسبة الإحداثي إلى إحداثيات نقطة دائرة الوحدة المقابلة للرقم ر. t g t = y x = sin t cos t

تتوافق التعريفات الأخيرة مع التعريف الوارد في بداية هذا القسم ولا تتعارض معه. أشر إلى دائرة مقابلة لرقم ر، يتزامن مع النقطة التي تمر إليها نقطة البداية بعد الالتفاف عبر الزاوية رراديان.

الدوال المثلثية للحجة الزاوية والرقمية

تتوافق كل قيمة للزاوية α مع قيمة معينة لجيب وجيب التمام لهذه الزاوية. تمامًا مثل جميع الزوايا α بخلاف α = 90 ° + 180 ° · k ، فإن k ∈ Z (α = π 2 + π · k، k ∈ Z) يتوافق مع قيمة معينة للماس. يتم تعريف ظل التمام ، كما هو مذكور أعلاه ، لجميع α ، باستثناء α = 180 ° k ، k ∈ Z (α = π k ، k ∈ Z).

يمكننا القول أن sin α و cos α و t g α و c t g α هي دوال للزاوية ألفا أو وظائف للوسيطة الزاوية.

وبالمثل ، يمكن للمرء أن يتحدث عن الجيب وجيب التمام والظل والظل كوظائف في حجة عددية. كل رقم حقيقي ريتوافق مع قيمة محددة لجيب أو جيب التمام لرقم ر. جميع الأرقام ما عدا π 2 + π · k ، k ∈ Z ، تتوافق مع قيمة الظل. يتم تعريف ظل التمام بالمثل لجميع الأرقام باستثناء π · k، k ∈ Z.

الوظائف الأساسية لعلم المثلثات

الجيب وجيب التمام والظل والظل هي الدوال المثلثية الأساسية.

من السياق ، يكون من الواضح عادةً أي حجة للدالة المثلثية ( حجة الزاويةأو حجة رقمية) نتعامل معها.

دعنا نعود إلى البيانات في بداية التعريفات والزاوية ألفا ، التي تقع في النطاق من 0 إلى 90 درجة. تتوافق تمامًا مع التعريفات المثلثية للجيب وجيب التمام والظل والظل التعاريف الهندسية، من خلال نسب أضلاع المثلث القائم الزاوية. دعونا نظهر ذلك.

خذ دائرة وحدة متمركزة على نظام إحداثيات ديكارتي مستطيل. دعنا ندير نقطة البداية أ (1 ، 0) بزاوية تصل إلى 90 درجة ونرسم من النقطة الناتجة أ 1 (س ، ص) عموديًا على المحور س. في المثلث الأيمن الناتج ، تكون الزاوية A 1 O H مساوية لزاوية الدوران α ، وطول الضلع O H يساوي حدود النقطة A 1 (x ، y). طول الضلع المقابل للزاوية يساوي إحداثي النقطة A 1 (x، y) ، وطول الوتر يساوي واحدًا ، لأنه نصف قطر دائرة الوحدة.

وفقًا للتعريف الهندسي ، فإن جيب الزاوية α يساوي نسبة الساق المقابلة إلى الوتر.

الخطيئة α \ u003d A 1 H O A 1 \ u003d y 1 \ u003d y

هذا يعني أن تعريف جيب الزاوية الحادة في مثلث قائم الزاوية من خلال نسبة العرض إلى الارتفاع يكافئ تعريف جيب زاوية الدوران α ، مع وجود ألفا في النطاق من 0 إلى 90 درجة.

وبالمثل ، يمكن إظهار تطابق التعاريف لجيب التمام والظل والظل.

إذا لاحظت وجود خطأ في النص ، فيرجى تمييزه والضغط على Ctrl + Enter