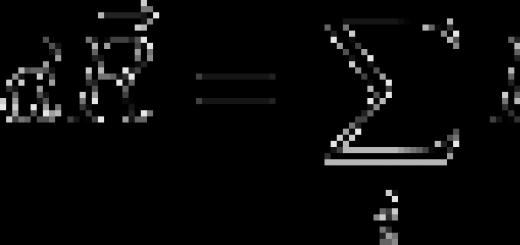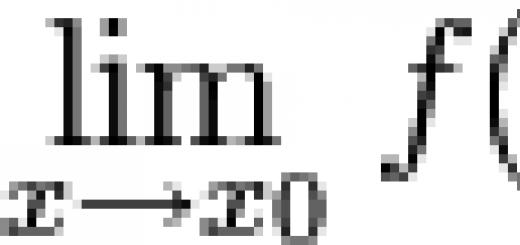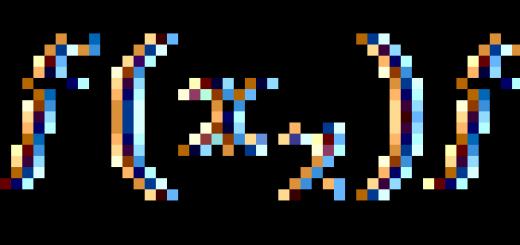من المستحيل تمامًا حل المشكلات الفيزيائية أو الأمثلة في الرياضيات دون معرفة المشتقات وطرق حسابها. يعتبر المشتق من أهم مفاهيم التحليل الرياضي. قررنا تكريس مقال اليوم لهذا الموضوع الأساسي. ما هو المشتق ، ما هو معناه الفيزيائي والهندسي ، كيف نحسب مشتق دالة؟ يمكن دمج كل هذه الأسئلة في سؤال واحد: كيف نفهم المشتق؟
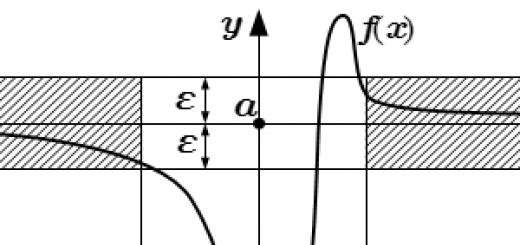
المعنى الهندسي والمادي للمشتق
يجب ألا تكون هناك وظيفة و (خ) ، في بعض الفترات (أ ، ب) . النقطتان x و x0 تنتمي إلى هذه الفترة. عندما تتغير x ، تتغير الوظيفة نفسها. تغيير الحجة - اختلاف قيمها x-x0 . هذا الاختلاف مكتوب كـ دلتا س ويسمى زيادة الوسيطة. تغيير أو زيادة دالة هو الفرق بين قيم الدالة عند نقطتين. تعريف مشتق:
مشتق دالة عند نقطة ما هو حد نسبة الزيادة في الدالة عند نقطة معينة إلى زيادة الوسيطة عندما تميل الأخيرة إلى الصفر.
وإلا يمكن كتابتها على النحو التالي:

ما الهدف من إيجاد مثل هذا الحد؟ لكن اي واحدة:
مشتق دالة عند نقطة ما يساوي ظل الزاوية بين محور OX وظل الرسم البياني للدالة عند نقطة معينة.

المعنى الماديالمشتق: المشتق الزمني للمسار يساوي سرعة الحركة المستقيمة.
في الواقع ، منذ أيام الدراسة ، يعلم الجميع أن السرعة مسار خاص. س = و (ر) و الوقت ر . متوسط السرعةلبعض الوقت:

لمعرفة سرعة الحركة في وقت واحد t0 تحتاج إلى حساب الحد:

القاعدة الأولى: أخرج الثابت
يمكن إخراج الثابت من علامة المشتق. علاوة على ذلك ، يجب أن يتم ذلك. عند حل الأمثلة في الرياضيات ، كقاعدة عامة - إذا كنت تستطيع تبسيط التعبير ، فتأكد من التبسيط .
مثال. دعنا نحسب المشتق:

القاعدة الثانية: مشتق مجموع الوظائف
مشتق مجموع وظيفتين يساوي مجموع مشتقات هاتين الدالتين. وينطبق الشيء نفسه على مشتق فرق الوظائف.

لن نعطي دليلًا على هذه النظرية ، بل سننظر في مثال عملي.
أوجد مشتق دالة:


القاعدة الثالثة: مشتق حاصل ضرب التوابع
يتم حساب مشتق منتج وظيفتين قابلتين للتفاضل بواسطة الصيغة:

مثال: أوجد مشتق دالة:

المحلول: 
من المهم هنا أن نقول عن حساب مشتقات الوظائف المعقدة. مشتق دالة معقدة يساوي منتج مشتق هذه الدالة فيما يتعلق بالحجة الوسيطة بمشتق الوسيطة فيما يتعلق بالمتغير المستقل.
في المثال أعلاه ، نواجه التعبير:

في هذه الحالة ، الوسيطة الوسيطة هي 8x أس الخامس. من أجل حساب مشتق مثل هذا التعبير ، نأخذ أولاً في الاعتبار مشتق الوظيفة الخارجية فيما يتعلق بالحجة الوسيطة ، ثم نضرب في مشتق الوسيطة نفسها فيما يتعلق بالمتغير المستقل.
القاعدة الرابعة: مشتق حاصل قسمة وظيفتين
صيغة لتحديد مشتق حاصل قسمة وظيفتين:



حاولنا الحديث عن مشتقات الدمى من الصفر. هذا الموضوع ليس بالبساطة التي يبدو عليها ، لذا كن حذرًا: غالبًا ما تكون هناك عيوب في الأمثلة ، لذا كن حذرًا عند حساب المشتقات.
مع أي سؤال حول هذا الموضوع وموضوعات أخرى ، يمكنك الاتصال بخدمة الطلاب. في وقت قصير ، سنساعدك في حل أصعب الضوابط والتعامل مع المهام ، حتى لو لم تتعامل مع حساب المشتقات من قبل.
فيما يلي جدول ملخص للراحة والوضوح عند دراسة الموضوع.
|
مستمرص = ج دالة الطاقة y = x p (س ع) "= ص س ص - 1 |
دالة أسيةص = س (أ س) "= أ س ل ن أ على وجه الخصوص ، متىأ = هـلدينا ص = ه س (هـ) "= هـ س |
|
دالة لوغاريتمية (log a x) "= 1 x ln a على وجه الخصوص ، متىأ = هـلدينا ص = تسجيل س (ln x) "= 1 x |
الدوال المثلثية (sin x) "= cos x (cos x)" = - sin x (t g x) "= 1 cos 2 x (c t g x)" = - 1 sin 2 x |
|
الدوال المثلثية العكسية (a r c sin x) "= 1 1 - x 2 (a r c cos x)" = - 1 1 - x 2 (a r c t g x) "= 1 1 + x 2 (a r c c t g x)" = - 1 1 + x 2 |
الدوال الزائدية (s h x) "= c h x (c h x)" = s h x (t h x) "= 1 c h 2 x (c t h x)" = - 1 s h 2 x |
دعونا نحلل كيف تم الحصول على صيغ الجدول المحدد ، أو بعبارة أخرى ، سنثبت اشتقاق الصيغ للمشتقات لكل نوع من الوظائف.
مشتق ثابت
إثبات 1من أجل إخراج هذه الصيغة، نأخذ تعريف مشتق دالة عند نقطة ما كأساس. نستخدم x 0 = x حيث xيأخذ قيمة أي رقم حقيقي ، أو بعبارة أخرى ، xهو أي رقم من مجال الوظيفة f (x) = C. لنكتب حد نسبة زيادة الدالة إلى زيادة الوسيطة كـ ∆ x → 0:
lim ∆ x → 0 ∆ f (x) ∆ x = lim ∆ x → 0 C - C ∆ x = lim ∆ x → 0 0 ∆ x = 0
يرجى ملاحظة أن التعبير 0 ∆ x يقع تحت علامة النهاية. لا يتعلق الأمر بارتياب "صفر مقسومًا على صفر" ، لأن البسط لا يحتوي على قيمة متناهية الصغر ، ولكنه يحتوي على صفر. بمعنى آخر ، زيادة دالة ثابتة تساوي دائمًا صفرًا.
إذن ، مشتق الدالة الثابتة f (x) = C يساوي صفرًا في مجال التعريف بأكمله.
مثال 1
إعطاء وظائف ثابتة:
و 1 (س) = 3 ، و 2 (س) = أ ، أ ∈ ص ، و 3 (س) = 4. 13 7 22 ، و 4 (س) = 0 ، و 5 (س) = - 8 7
المحلول
دعونا نصف الظروف المعطاة. في الدالة الأولى نرى مشتق العدد الطبيعي 3. في المثال التالي ، عليك أن تأخذ مشتق لكن، أين لكن- أي رقم حقيقي. المثال الثالث يعطينا مشتق العدد غير النسبي 4. 13 7 22، الرابع - مشتق الصفر (صفر عدد صحيح). أخيرًا ، في الحالة الخامسة لدينا المشتق جزء منطقي - 8 7 .
إجابه:المشتقات ضبط الوظائفهو صفر لأي حقيقي x(على كامل مجال التعريف)
f 1 "(x) = (3)" = 0، f 2 "(x) = (a)" = 0، a ∈ R، f 3 "(x) = 4. 13 7 22" = 0، f 4 "(س) = 0" = 0 ، و 5 "(س) = - 8 7" = 0
مشتق دالة القدرة
هيا بنا نمضي قدما ل وظيفة الطاقةوصيغة مشتقها ، والتي لها الشكل: (x p) "= p x p - 1 ، حيث الأس صهو أي رقم حقيقي.
إثبات 2
نقدم إثبات الصيغة عندما يكون الأس عدد طبيعي: ص = 1 ، 2 ، 3 ، ...
مرة أخرى ، نعتمد على تعريف المشتق. لنكتب حد نسبة زيادة دالة القوة إلى زيادة الوسيطة:
(x p) "= lim ∆ x → 0 = ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p - x p ∆ x
لتبسيط التعبير في البسط ، نستخدم صيغة نيوتن ذات الحدين:
(x + ∆ x) p - x p = C p 0 + x p + C p 1 x p - 1 ∆ x + C p 2 x p - 2 (∆ x) 2 +. . . + + C pp - 1 x (∆ x) p - 1 + C pp (x) p - xp = = C p 1 xp - 1 ∆ x + C p 2 xp - 2 (∆ x) 2 +. . . + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p
في هذا الطريق:
(xp) "= lim ∆ x → 0 ∆ (xp) ∆ x = lim ∆ x → 0 (x + ∆ x) p - xp ∆ x = = lim ∆ x → 0 (C p 1 xp - 1 ∆ x + C p 2 xp - 2 (∆ x) 2 +. + C pp - 1 x (∆ x) p - 1 + C pp (∆ x) p) ∆ x = = lim ∆ x → 0 (C p 1 xp - 1 + C p 2 xp - 2 x +. + C pp - 1 x (∆ x) p - 2 + C pp (x) p - 1) = = C p 1 xp - 1 + 0 + 0 +.. + 0 = p! 1! (ص - 1)! xp - 1 = p xp - 1
لذلك ، أثبتنا صيغة مشتقة دالة أس عندما يكون الأس عددًا طبيعيًا.
إثبات 3
لإثبات القضية متى ص-أي رقم حقيقي غير الصفر ، نستخدم المشتق اللوغاريتمي (هنا يجب أن نفهم الفرق من مشتق الدالة اللوغاريتمية). للحصول على فهم أكثر اكتمالاً ، من المستحسن دراسة مشتق الوظيفة اللوغاريتمية والتعامل بالإضافة إلى ذلك مع مشتق دالة معينة ضمنيًا ومشتق دالة معقدة.
النظر في حالتين: متى xإيجابية ومتى xسلبية.
لذا x> 0. ثم: x p> 0. نأخذ لوغاريتم المساواة y \ u003d x p إلى القاعدة e ونطبق خاصية اللوغاريتم:
y = x p ln y = ln x p ln y = p ln x
في هذه المرحلة ، تم الحصول على وظيفة محددة ضمنيًا. دعنا نحدد مشتقها:
(ln y) "= (p ln x) 1 y y" = p 1 x ⇒ y "= p y x = p x p x = p x p - 1
الآن نحن ننظر في القضية متى س-رقم سالب.
إذا كان المؤشر صتأكل رقم زوجي، ثم يتم تعريف دالة الطاقة أيضًا لـ x< 0 , причем является четной: y (x) = - y ((- x) p) " = - p · (- x) p - 1 · (- x) " = = p · (- x) p - 1 = p · x p - 1
ثم إكس بي< 0 и возможно составить доказательство, используя логарифмическую производную.
إذا صهو رقم فردي ، ثم يتم تعريف دالة الطاقة لـ x< 0 , причем является нечетной: y (x) = - y (- x) = - (- x) p . Тогда x p < 0 , а значит логарифмическую производную задействовать нельзя. В такой ситуации возможно взять за основу доказательства правила дифференцирования и правило нахождения производной сложной функции:
y "(x) \ u003d (- (- x) p)" \ u003d - ((- x) p) "\ u003d - p (- x) p - 1 (- x)" = \ u003d p (- x) ) ص - 1 = ص إكس بي - 1
الانتقال الأخير ممكن لأنه إذا صهو رقم فردي ، إذن ص - 1إما عدد زوجي أو صفر (ل p = 1) ، لذلك ، لسالب xالمساواة (- س) ص - 1 = س ص - 1 صحيحة.
لذا ، فقد أثبتنا صيغة مشتقة دالة أس لأي قيمة p حقيقية.
مثال 2
وظائف معينة:
و 1 (س) = 1 × 2 3 ، و 2 (س) = س 2-1 4 ، و 3 (س) = 1 × سجل 7 12
حدد مشتقاتها.
المحلول
نقوم بتحويل جزء من الدوال المعينة إلى شكل جدولي y = x p ، بناءً على خصائص الدرجة ، ثم نستخدم الصيغة:
f 1 (x) \ u003d 1 x 2 3 \ u003d x - 2 3 ⇒ f 1 "(x) \ u003d - 2 3 x - 2 3-1 \ u003d - 2 3 x - 5 3 f 2" (x) \ u003d x 2-1 4 = 2-1 4 x 2-1 4-1 = 2-1 4 x 2-5 4 f 3 (x) = 1 x log 7 12 = x - log 7 12 ⇒ f 3 " (x) = - السجل 7 12 x - السجل 7 12-1 = - السجل 7 12 x - السجل 7 12 - السجل 7 7 = - السجل 7 12 x - السجل 7 84
مشتق من الدالة الأسية
إثبات 4نشتق صيغة المشتق بناءً على التعريف:
(فأس) "= lim ∆ x → 0 ax + x - ax ∆ x = lim ∆ x → 0 ax (a ∆ x - 1) ∆ x = ax lim ∆ x → 0 a ∆ x - 1 ∆ x = 0 0
لدينا عدم اليقين. لتوسيعه ، نكتب متغيرًا جديدًا z = a ∆ x - 1 (z → 0 as ∆ x → 0). في هذه الحالة a ∆ x = z + 1 ⇒ ∆ x = log a (z + 1) = ln (z + 1) ln a. بالنسبة للانتقال الأخير ، يتم استخدام صيغة الانتقال إلى أساس جديد للوغاريتم.
لنقم باستبدال الحد الأصلي:
(فأس) "= ax lim ∆ x → 0 a ∆ x - 1 ∆ x = ax ln a lim ∆ x → 0 1 1 z ln (z + 1) = ax ln a lim ∆ x → 0 1 ln (z + 1) 1 z = ax ln a 1 ln lim ∆ x → 0 (z + 1) 1 z
تذكر الحد الثاني الرائع ثم نحصل على صيغة المشتق دالة أسية:
(a x) "= a x ln a 1 ln lim z → 0 (z + 1) 1 z = a x ln a 1 ln e = a x ln a
مثال 3
يتم إعطاء الوظائف الأسية:
و 1 (س) = 2 3 س ، و 2 (س) = 5 3 س ، و 3 (س) = 1 (هـ) س
علينا إيجاد مشتقاتهم.
المحلول
نستخدم صيغة مشتق الدالة الأسية وخصائص اللوغاريتم:
f 1 "(x) = 2 3 x" = 2 3 x ln 2 3 = 2 3 x (ln 2 - ln 3) f 2 "(x) = 5 3 x" = 5 3 x ln 5 1 3 = 1 3 5 3 x ln 5 f 3 "(x) = 1 (e) x" = 1 ex "= 1 ex ln 1 e = 1 ex ln e - 1 = - 1 ex
مشتق من دالة لوغاريتمية
إثبات 5نقدم إثبات صيغة مشتق الدالة اللوغاريتمية لأي xفي مجال التعريف وأي القيم المسموح بهاقواعد اللوغاريتم. بناءً على تعريف المشتق ، نحصل على:
(log ax) "= lim ∆ x → 0 log a (x + ∆ x) - log ax ∆ x = lim ∆ x → 0 log ax + ∆ xx ∆ x = = lim ∆ x → 0 1 ∆ x log a 1 + ∆ xx = lim ∆ x → 0 log a 1 + ∆ xx 1 ∆ x = = lim ∆ x → 0 log a 1 + ∆ xx 1 ∆ x xx = lim ∆ x → 0 1 x log a 1 + xxx ∆ x = = 1 x log a lim ∆ x → 0 1 + ∆ xxx ∆ x = 1 x log ae = 1 x ln e ln a = 1 x ln a
يمكن أن نرى من سلسلة المساواة المحددة أن التحولات قد بُنيت على أساس خاصية اللوغاريتم. المساواة lim ∆ x → 0 1 + ∆ x x x ∆ x = e صحيحة وفقًا للحد الثاني الملحوظ.
مثال 4
يتم إعطاء الوظائف اللوغاريتمية:
و 1 (س) = السجل سجل 3 س ، و 2 (س) = تسجيل س
من الضروري حساب مشتقاتها.
المحلول
دعنا نطبق الصيغة المشتقة:
f 1 "(x) = (log ln 3 x)" = 1 x ln (ln 3) ؛ f 2 "(x) \ u003d (ln x)" \ u003d 1 x ln e \ u003d 1 x
إذن ، مشتق اللوغاريتم الطبيعي يساوي واحدًا على x.
مشتقات التوابع المثلثية
إثبات 6نستخدم البعض الصيغ المثلثيةوأول حد رائع لاشتقاق صيغة مشتقة دالة مثلثية.
وفقًا لتعريف مشتق دالة الجيب ، نحصل على:
(sin x) "= lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x
ستسمح لنا صيغة اختلاف الجيب بتنفيذ الإجراءات التالية:
(sin x) "= lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x = = lim ∆ x → 0 2 sin x + ∆ x - x 2 cos x + x + x 2 x = = lim ∆ x → 0 sin ∆ x 2 cos x + x 2 ∆ x 2 = = cos x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2
أخيرًا ، نستخدم الحد الرائع الأول:
sin "x = cos x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = cos x
إذن ، مشتق الدالة الخطيئة xإرادة كوس x.
سنثبت أيضًا صيغة مشتق جيب التمام بنفس الطريقة:
cos "x = lim ∆ x → 0 cos (x + ∆ x) - cos x ∆ x = = lim ∆ x → 0-2 sin x + ∆ x - x 2 sin x + x + x 2 ∆ x = = - lim ∆ x → 0 sin ∆ x 2 sin x + x 2 ∆ x 2 = = - sin x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = - sin x
أولئك. المشتق وظائف جيب التمامسيكون x - الخطيئة x.
نشتق معادلات مشتقات الظل والظل بناءً على قواعد التفاضل:
tg "x = sin x cos x" = sin "x cos x - sin x cos" x cos 2 x = = cos x cos x - sin x (- sin x) cos 2 x = sin 2 x + cos 2 x cos 2 x = 1 cos 2 xctg "x = cos x sin x" = cos "x sin x - cos x sin" x sin 2 x = = - sin x sin x - cos x cos x sin 2 x = - sin 2 x + cos 2 x sin 2 x = - 1 sin 2 x
مشتقات الدوال المثلثية العكسية
يقدم القسم الخاص بمشتق الدوال العكسية معلومات شاملة عن إثبات الصيغ الخاصة بمشتقات قوس القوس ، قوس القوس ، قوس ظل الزاوية ، قوس التمام ، لذلك لن نكرر المادة هنا.
مشتقات الدوال الزائدية
إثبات 7يمكننا اشتقاق صيغ لمشتقات الجيب الزائدي وجيب التمام والظل والظل باستخدام قاعدة التفاضل وصيغة مشتق الدالة الأسية:
sh "x = ex - e - x 2" = 1 2 ex "- e - x" == 1 2 ex - - e - x = ex + e - x 2 = chxch "x = ex + e - x 2" = 1 2 ex "+ e - x" == 1 2 ex + - e - x = ex - e - x 2 = shxth "x = shxchx" = sh "x chx - shx ch" xch 2 x = ch 2 x - sh 2 xch 2 x = 1 ch 2 xcth "x = chxshx" = ch "x shx - chx sh" xsh 2 x = sh 2 x - ch 2 xsh 2 x = - 1 sh 2 x
إذا لاحظت وجود خطأ في النص ، فيرجى تمييزه والضغط على Ctrl + Enter
من المستحيل تمامًا حل المشكلات الفيزيائية أو الأمثلة في الرياضيات دون معرفة المشتقات وطرق حسابها. يعتبر المشتق من أهم مفاهيم التحليل الرياضي. قررنا تكريس مقال اليوم لهذا الموضوع الأساسي. ما هو المشتق ، ما هو معناه الفيزيائي والهندسي ، كيف نحسب مشتق دالة؟ يمكن دمج كل هذه الأسئلة في سؤال واحد: كيف نفهم المشتق؟
المعنى الهندسي والمادي للمشتق
يجب ألا تكون هناك وظيفة و (خ) ، في بعض الفترات (أ ، ب) . النقطتان x و x0 تنتمي إلى هذه الفترة. عندما تتغير x ، تتغير الوظيفة نفسها. تغيير الحجة - اختلاف قيمها x-x0 . هذا الاختلاف مكتوب كـ دلتا س ويسمى زيادة الوسيطة. تغيير أو زيادة دالة هو الفرق بين قيم الدالة عند نقطتين. تعريف مشتق:
مشتق دالة عند نقطة ما هو حد نسبة الزيادة في الدالة عند نقطة معينة إلى زيادة الوسيطة عندما تميل الأخيرة إلى الصفر.
وإلا يمكن كتابتها على النحو التالي:

ما الهدف من إيجاد مثل هذا الحد؟ لكن اي واحدة:
مشتق دالة عند نقطة ما يساوي ظل الزاوية بين محور OX وظل الرسم البياني للدالة عند نقطة معينة.

المعنى المادي للمشتق: المشتق الزمني للمسار يساوي سرعة الحركة المستقيمة.
في الواقع ، منذ أيام الدراسة ، يعلم الجميع أن السرعة مسار خاص. س = و (ر) و الوقت ر . متوسط السرعة خلال فترة زمنية معينة:

لمعرفة سرعة الحركة في وقت واحد t0 تحتاج إلى حساب الحد:

القاعدة الأولى: أخرج الثابت
يمكن إخراج الثابت من علامة المشتق. علاوة على ذلك ، يجب أن يتم ذلك. عند حل الأمثلة في الرياضيات ، كقاعدة عامة - إذا كنت تستطيع تبسيط التعبير ، فتأكد من التبسيط .
مثال. دعنا نحسب المشتق:

القاعدة الثانية: مشتق مجموع الوظائف
مشتق مجموع وظيفتين يساوي مجموع مشتقات هاتين الدالتين. وينطبق الشيء نفسه على مشتق فرق الوظائف.

لن نعطي دليلًا على هذه النظرية ، بل سننظر في مثال عملي.
أوجد مشتق دالة:


القاعدة الثالثة: مشتق حاصل ضرب التوابع
يتم حساب مشتق منتج وظيفتين قابلتين للتفاضل بواسطة الصيغة:

مثال: أوجد مشتق دالة:

المحلول: 
من المهم هنا أن نقول عن حساب مشتقات الوظائف المعقدة. مشتق دالة معقدة يساوي منتج مشتق هذه الدالة فيما يتعلق بالحجة الوسيطة بمشتق الوسيطة فيما يتعلق بالمتغير المستقل.
في المثال أعلاه ، نواجه التعبير:

في هذه الحالة ، الوسيطة الوسيطة هي 8x أس الخامس. من أجل حساب مشتق مثل هذا التعبير ، نأخذ أولاً في الاعتبار مشتق الوظيفة الخارجية فيما يتعلق بالحجة الوسيطة ، ثم نضرب في مشتق الوسيطة نفسها فيما يتعلق بالمتغير المستقل.
القاعدة الرابعة: مشتق حاصل قسمة وظيفتين
صيغة لتحديد مشتق حاصل قسمة وظيفتين:



حاولنا الحديث عن مشتقات الدمى من الصفر. هذا الموضوع ليس بالبساطة التي يبدو عليها ، لذا كن حذرًا: غالبًا ما تكون هناك عيوب في الأمثلة ، لذا كن حذرًا عند حساب المشتقات.
مع أي سؤال حول هذا الموضوع وموضوعات أخرى ، يمكنك الاتصال بخدمة الطلاب. في وقت قصير ، سنساعدك في حل أصعب الضوابط والتعامل مع المهام ، حتى لو لم تتعامل مع حساب المشتقات من قبل.
من السهل جدًا تذكرها.
حسنًا ، دعنا لا نذهب بعيدًا ، دعنا نفكر على الفور وظيفة عكسية. ما هو معكوس الدالة الأسية؟ اللوغاريتم:
في حالتنا ، الأساس هو رقم:
مثل هذا اللوغاريتم (أي اللوغاريتم ذو الأساس) يسمى اللوغاريتم "الطبيعي" ، ونستخدم تدوينًا خاصًا له: نكتب بدلاً من ذلك.
ما يساوي؟ بالطبع بكل تأكيد، .
مشتق اللوغاريتم الطبيعي بسيط جدًا أيضًا:
أمثلة:
- العثور على مشتق من وظيفة.
- ما هو مشتق الوظيفة؟
الإجابات: عارض و اللوغاريتم الطبيعي- الوظائف بسيطة بشكل فريد من حيث المشتق. سيكون للدوال الأسية واللوغاريتمية مع أي قاعدة أخرى مشتق مختلف ، سنقوم بتحليله لاحقًا ، بعد أن ننتقل إلى قواعد التفاضل.
قواعد التمايز
ما هي القواعد؟ مصطلح جديد مرة أخرى؟! ...
التفاضلهي عملية إيجاد المشتق.
فقط وكل شيء. ما هي الكلمة الأخرى لهذه العملية؟ ليس proizvodnovanie ... يسمى التفاضل في الرياضيات بزيادة الوظيفة في. يأتي هذا المصطلح من الاختلاف اللاتيني - الاختلاف. هنا.
عند اشتقاق كل هذه القواعد ، سنستخدم وظيفتين ، على سبيل المثال ، و. سنحتاج أيضًا إلى صيغ لزياداتها:
هناك 5 قواعد في المجموع.
يتم إخراج الثابت من علامة المشتق.
إذا - رقم ثابت (ثابت) ، إذن.
من الواضح أن هذه القاعدة تعمل أيضًا مع الاختلاف:.
دعنا نثبت ذلك. اسمحوا ، أو أسهل.
أمثلة.
أوجد مشتقات الدوال:
- عند النقطة
- عند النقطة
- عند النقطة
- في هذه النقطة.
حلول:
- (المشتق هو نفسه في جميع النقاط ، لأنه كذلك دالة خطية، تذكر؟)؛
مشتق من المنتج
كل شيء متشابه هنا: نقدم وظيفة جديدة ونجد زيادتها:
المشتق:
أمثلة:
- البحث عن مشتقات الوظائف و ؛
- أوجد مشتق دالة عند نقطة.
حلول:
مشتق من الدالة الأسية
الآن معرفتك كافية لتتعلم كيفية العثور على مشتق أي دالة أسية ، وليس فقط الأس (هل نسيت ما هو عليه حتى الآن؟).
إذن أين يوجد عدد.
نحن نعلم بالفعل مشتق الدالة ، لذلك دعونا نحاول نقل الدالة إلى أساس جديد:
لهذا نستخدم قاعدة بسيطة:. ثم:
حسنًا ، لقد نجحت. حاول الآن إيجاد المشتقة ، ولا تنس أن هذه الدالة معقدة.
حدث؟
هنا ، تحقق من نفسك:
تبين أن الصيغة تشبه إلى حد بعيد مشتق الأس: كما كانت ، لا تزال ، ظهر عامل فقط ، وهو مجرد رقم ، ولكن ليس متغيرًا.
أمثلة:
أوجد مشتقات الدوال:
الإجابات:
هذا مجرد رقم لا يمكن حسابه بدون آلة حاسبة ، أي أنه لا يمكن كتابته بصيغة أبسط. لذلك ، في الإجابة يتم تركها بهذا الشكل.
لاحظ أن هنا حاصل قسمة وظيفتين ، لذلك نطبق قاعدة التفاضل المناسبة:
في هذا المثال ، نتاج وظيفتين:
مشتق من دالة لوغاريتمية
هذا مشابه: أنت تعرف بالفعل مشتق اللوغاريتم الطبيعي:
لذلك ، لإيجاد تعسفي من اللوغاريتم بأساس مختلف ، على سبيل المثال:
علينا إحضار هذا اللوغاريتم إلى الأساس. كيف تغير قاعدة اللوغاريتم؟ أتمنى أن تتذكر هذه الصيغة:
الآن فقط بدلاً من أن نكتب:
تبين أن المقام مجرد ثابت (رقم ثابت ، بدون متغير). المشتق بسيط للغاية:
مشتقات الأسي و الدوال اللوغاريتميةيكاد لا يحدث أبدًا في الامتحان ، ولكن معرفتهم لن تكون زائدة عن الحاجة.
مشتق دالة معقدة.
ماذا حدث " وظيفة معقدة"؟ لا ، هذا ليس لوغاريتمًا ، وليس ظلًا قوسيًا. قد يكون من الصعب فهم هذه الوظائف (على الرغم من أنه إذا كان اللوغاريتم يبدو صعبًا بالنسبة لك ، فاقرأ موضوع "اللوغاريتمات" وسيعمل كل شيء) ، ولكن من حيث الرياضيات ، فإن كلمة "معقد" لا تعني "صعبة".
تخيل ناقلًا صغيرًا: شخصان يجلسان ويقومان ببعض الأعمال باستخدام بعض الأشياء. على سبيل المثال ، يلف الأول شريط شوكولاتة في غلاف ، والثاني يربطه بشريط. اتضح مثل هذا الكائن المركب: شريط شوكولاتة ملفوف ومربوط بشريط. لأكل لوح شوكولاتة ، عليك القيام بالخطوات المعاكسة بترتيب عكسي.
دعنا ننشئ خط أنابيب رياضيًا مشابهًا: أولاً سنجد جيب التمام لرقم ، ثم سنقوم بتربيع الرقم الناتج. لذا ، أعطونا رقمًا (شوكولاتة) ، أجد جيب التمام (غلاف) ، ثم قم بتربيع ما حصلت عليه (اربطه بشريط). ماذا حدث؟ دور. هذا مثال على دالة معقدة: عندما ، من أجل إيجاد قيمتها ، نقوم بتنفيذ الإجراء الأول مباشرة مع المتغير ، ثم إجراء آخر آخر مع ما حدث كنتيجة للأول.
بعبارات أخرى، الوظيفة المعقدة هي دالة تمثل حجة دالة أخرى: .
على سبيل المثال لدينا.
قد نقوم بنفس الخطوات بترتيب عكسي: أولاً أنت تربيع ، ثم أبحث عن جيب التمام للعدد الناتج :. من السهل تخمين أن النتيجة ستكون مختلفة دائمًا. ميزة مهمة للوظائف المعقدة: عندما يتغير ترتيب الإجراءات ، تتغير الوظيفة.
المثال الثاني: (same). .
سيتم استدعاء الإجراء الأخير الذي نقوم به وظيفة "خارجية"، والإجراء الذي تم تنفيذه أولاً - على التوالي وظيفة "داخلية"(هذه أسماء غير رسمية ، أستخدمها فقط لشرح المادة بلغة بسيطة).
حاول أن تحدد بنفسك أي وظيفة خارجية وأيها داخلية:
الإجابات:الفصل بين الوظائف الداخلية والخارجية مشابه جدًا للمتغيرات المتغيرة: على سبيل المثال ، في الوظيفة
- ما هو الإجراء الذي سنتخذه أولاً؟ أولًا نحسب الجيب ، وعندها فقط نرفعها إلى مكعب. إذن فهي وظيفة داخلية وليست خارجية.
والوظيفة الأصلية هي تكوينها:. - داخلي: ؛ خارجي: .
فحص: . - داخلي: ؛ خارجي: .
فحص: . - داخلي: ؛ خارجي: .
فحص: . - داخلي: ؛ خارجي: .
فحص: .
نغير المتغيرات ونحصل على دالة.
حسنًا ، الآن سنستخرج الشوكولاتة - ابحث عن المشتق. يتم عكس الإجراء دائمًا: أولاً ، نبحث عن مشتقة الدالة الخارجية ، ثم نضرب النتيجة في مشتق الدالة الداخلية. بالنسبة للمثال الأصلي ، يبدو كالتالي:
مثال آخر:
لذا ، دعنا أخيرًا نصيغ القاعدة الرسمية:
خوارزمية لإيجاد مشتق دالة معقدة:
يبدو أنه بسيط ، أليس كذلك؟
دعنا نتحقق من الأمثلة:
حلول:
1) داخلي: ؛
خارجي: ؛
2) داخلي: ؛
(فقط لا تحاول التقليل الآن! لا شيء مأخوذ من تحت جيب التمام ، تذكر؟)
3) داخلي: ؛
خارجي: ؛
من الواضح على الفور أن هناك وظيفة معقدة من ثلاثة مستويات هنا: بعد كل شيء ، هذه بالفعل وظيفة معقدة في حد ذاتها ، وما زلنا نستخرج الجذر منها ، أي أننا نقوم بالإجراء الثالث (ضع الشوكولاتة في غلاف وشريط في حقيبة). ولكن لا يوجد سبب للخوف: على أي حال ، سوف "نفك" هذه الوظيفة بنفس الترتيب المعتاد: من النهاية.
وهذا يعني أننا نفرق الجذر أولاً ، ثم جيب التمام ، وبعد ذلك فقط المقدار الموجود بين قوسين. ثم نضربها كلها.
في مثل هذه الحالات ، من الملائم ترقيم الإجراءات. أي دعونا نتخيل ما نعرفه. بأي ترتيب سنقوم بتنفيذ الإجراءات لحساب قيمة هذا التعبير؟ لنلقي نظرة على مثال:
كلما تم تنفيذ الإجراء لاحقًا ، كلما كانت الوظيفة المقابلة "خارجية". تسلسل الإجراءات - كما كان من قبل:
هنا يكون التعشيش بشكل عام من 4 مستويات. دعونا نحدد مسار العمل.
1. التعبير الراديكالي. .
2. الجذر. .
3. الجيوب الأنفية. .
4. مربع. .
5. تجميعها جميعًا:
المشتق. باختصار حول الرئيسي
مشتق وظيفي- نسبة زيادة الدالة إلى زيادة الوسيطة مع زيادة متناهية في الصغر للوسيطة:
المشتقات الأساسية:
قواعد التمايز:
يتم إخراج الثابت من علامة المشتق:
مشتق من المجموع:
منتج مشتق:
مشتق من حاصل القسمة:
مشتق دالة معقدة:
خوارزمية لإيجاد مشتق دالة معقدة:
- نحدد الوظيفة "الداخلية" ، ونجد مشتقها.
- نحدد الوظيفة "الخارجية" ، ونجد مشتقها.
- نضرب نتائج النقطتين الأولى والثانية.
المشتق الأول
المشتق الأول
(المشتق الأول)معدل نمو قيمة الوظيفة عندما تنمو حجتها في مرحلة ما ، إذا تم تحديد الوظيفة نفسها في هذه المرحلة. على الرسم البياني ، يوضح المشتق الأول للدالة زاوية ميلها. إذا ص = و (س) ،مشتقها الأول عند نقطة ما × 0هو الحد الذي f (x0 + а) –f (x0) / аكما لكنيميل إلى قيمة متناهية الصغر. يمكن الإشارة إلى المشتق الأول dy / dxأو y´ (x).دور ص (س)له قيمة ثابتة عند النقطة x0 ،إذا dy / dxفي هذه النقطة × 0يساوي صفر. يعتبر المشتق الأول الذي يساوي الصفر شرطًا ضروريًا ولكنه غير كافٍ للوظيفة للوصول إلى الحد الأقصى أو الحد الأدنى عند نقطة معينة.
اقتصاد. قاموس. - م: "INFRA-M" دار النشر "Ves Mir". J. بلاك. هيئة التحرير العامة: دكتور في الاقتصاد Osadchaya I.M.. 2000 .
القاموس الاقتصادي. 2000 .
شاهد ما هو "FIRST DERIVATIVE" في القواميس الأخرى:
- (مشتق) المعدل الذي تزداد فيه قيمة الوظيفة عند زيادة وسيطتها في نقطة ما ، إذا تم تعريف الوظيفة نفسها في تلك النقطة. على الرسم البياني ، يوضح المشتق الأول للدالة زاوية ميلها. إذا كان y \ u003d f (x) ، مشتقها الأول عند النقطة ... ... القاموس الاقتصادي
هذا المصطلح له معاني أخرى ، انظر المشتق. توضيح لمفهوم مشتق مشتق ... ويكيبيديا
المشتق هو المفهوم الأساسي لحساب التفاضل ، والذي يميز معدل تغير الوظيفة. يتم تعريفه على أنه حد نسبة زيادة دالة إلى زيادة وسيطتها عندما تميل زيادة الوسيطة إلى الصفر ، إذا كان هذا الحد ... ... ويكيبيديا
مشكلة الحدود نوع خاص؛ هو إيجاد المنطقة D المتغيرات x = (x1، ...، x n). الحلول المعادلة التفاضلية(1) من الترتيب الزوجي 2m في مجموعة القيممن جميع مشتقات الترتيب التي لا تزيد عن م على الحدود S للمجال D (أو جزء منه) ... موسوعة رياضية
- (المشتق الثاني) المشتق الأول من المشتق الأول للدالة. المشتق الأول يقيس ميل الوظيفة ؛ يقيس المشتق الثاني كيف يتغير الميل مع زيادة السعة. المشتق الثاني من y = f (x) ... ... القاموس الاقتصادي
هذه المقالة أو القسم يحتاج إلى مراجعة. يرجى تحسين المقال وفقًا لقواعد كتابة المقالات. فراكشنال برو ... ويكيبيديا
- (اشتقاق جزئي متقاطع) تأثير تغيير وسيطة واحدة لدالة من متغيرين أو أكثر على مشتق هذه الوظيفة ، مع مراعاة وسيطة أخرى. إذا كانت y \ u003d f (x، z) ، فإن مشتقها ، أو المشتق الأول للدالة y بالنسبة إلى الوسيطة x ، هو ... ... القاموس الاقتصادي
سرعة النقطة التناظرية- المشتق الأول من حركة النقطة على طول الإحداثي المعمم للآلية ...
التناظرية للسرعة الزاوية للارتباط- المشتق الأول لزاوية دوران الرابط فيما يتعلق بالإحداثيات المعممة للآلية ... القاموس التوضيحي للمصطلحات البوليتكنيك
السرعة العامة للآلية- المشتق الأول للإحداثيات المعممة للآلية فيما يتعلق بالوقت ... القاموس التوضيحي للمصطلحات البوليتكنيك
كتب
- مجموعة من المشاكل في الهندسة التفاضلية والطوبولوجيا Mishchenko A.S.
- مقالاتي العلمية الكتاب 3. طريقة مصفوفة الكثافة في نظريات الكم لليزر ، ذرة عشوائية ، بونداريف بوريس فلاديميروفيتش. يتناول هذا الكتاب المقالات العلمية المنشورة التي يتم فيها تقديم نظريات كمومية جديدة لليزر ، وذرة عشوائية ، ومذبذب كمي مخمد بطريقة مصفوفات الكثافة. ...