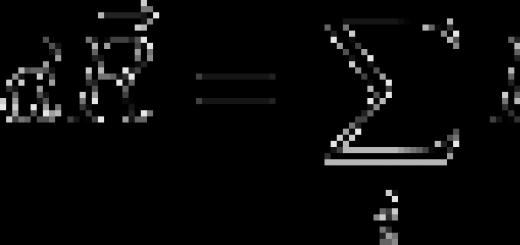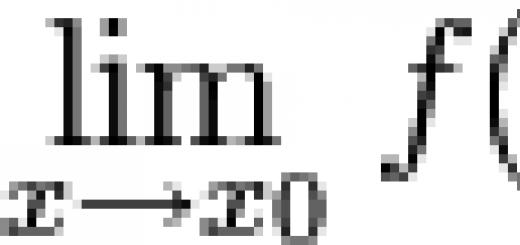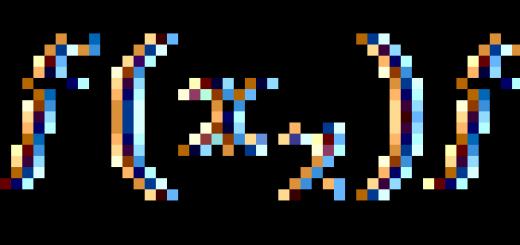تحديد مشتق دالة هو العملية العكسية لتكامل دالة. بالنسبة للوظائف الأولية ، ليس من الصعب حساب المشتق ؛ يكفي استخدام جدول المشتقات. إذا احتجنا أوجد المشتقمن وظيفة معقدة ، فإن التمايز سيكون أكثر صعوبة ، ويتطلب مزيدًا من العناية والوقت. من السهل جدًا ارتكاب خطأ إملائي أو خطأ بسيط ، مما يؤدي إلى الإجابة الخاطئة النهائية. لذلك ، من المهم دائمًا أن تكون قادرًا على التحقق من قرارك. يمكنك القيام بذلك باستخدام هذه الآلة الحاسبة عبر الإنترنت ، والتي تتيح لك العثور على مشتقات أي وظائف عبر الإنترنت مع حل مفصل مجانًا ، دون التسجيل في الموقع. إيجاد مشتق دالة (التمايز) هو نسبة زيادة الدالة إلى زيادة الوسيطة (عدديًا ، المشتق يساوي ظل منحدر المماس للرسم البياني للدالة). إذا كان من الضروري حساب مشتق دالة في نقطة معينة ، ثم في الاستجابة المستلمة ، بدلاً من الوسيطة xتأطير له قيمة عدديةوحساب التعبير. في حل مشتق عبر الإنترنتتحتاج إلى إدخال دالة في الحقل المقابل: في هذه الحالة ، يجب أن تكون الوسيطة متغيرًا x، لأن التمايز يسير على طوله بالضبط. لحساب المشتق الثاني ، تحتاج إلى اشتقاق الإجابة المستلمة.

عملية إيجاد المشتق تسمى التفاضل.

نتيجة لحل مشاكل إيجاد مشتقات لأبسط الوظائف (وليست بسيطة جدًا) من خلال تعريف المشتق على أنه حد نسبة الزيادة إلى الزيادة في الوسيطة ، ظهر جدول للمشتقات وقواعد محددة بدقة للتفاضل . كان إسحاق نيوتن (1643-1727) وجوتفريد فيلهلم ليبنيز (1646-1716) أول من عمل في مجال إيجاد المشتقات.

لذلك ، في عصرنا ، من أجل العثور على مشتق أي دالة ، ليس من الضروري حساب الحد المذكور أعلاه لنسبة زيادة الوظيفة إلى زيادة الوسيطة ، ولكن تحتاج فقط إلى استخدام الجدول المشتقات وقواعد التفاضل. الخوارزمية التالية مناسبة لإيجاد المشتق.

لإيجاد المشتق، فأنت بحاجة إلى تعبير تحت علامة السكتة الدماغية تحطيم الوظائف البسيطةوتحديد ما هي الإجراءات (المنتج ، المجموع ، الحاصل)ترتبط هذه الوظائف. علاوة على ذلك ، نجد مشتقات الدوال الأولية في جدول المشتقات ، والصيغ الخاصة بمشتقات المنتج ، والجمع والحاصل - في قواعد التفاضل. يتم إعطاء جدول المشتقات وقواعد التفاضل بعد المثالين الأولين.

مثال 1أوجد مشتق دالة

قرار. من قواعد التفاضل نجد أن مشتق مجموع الوظائف هو مجموع مشتقات الوظائف ، أي

من جدول المشتقات ، نجد أن مشتق "X" يساوي واحدًا ، ومشتق جيب التمام هو جيب التمام. نعوض بهذه القيم في مجموع المشتقات ونجد المشتق الذي تتطلبه حالة المشكلة:

مثال 2أوجد مشتق دالة

قرار. اشتق كمشتق من المجموع ، حيث يمكن إخراج المصطلح الثاني بعامل ثابت من علامة المشتق:

إذا كانت لا تزال هناك أسئلة حول مصدر شيء ما ، فإنها ، كقاعدة عامة ، تصبح واضحة بعد قراءة جدول المشتقات وأبسط قواعد الاشتقاق. نحن نذهب إليهم الآن.

جدول مشتقات وظائف بسيطة

1. مشتق ثابت (رقم). أي رقم (1 ، 2 ، 5 ، 200 ...) موجود في تعبير الدالة. دائما صفر. من المهم جدًا تذكر هذا ، لأنه مطلوب في كثير من الأحيان
2. مشتق المتغير المستقل. في أغلب الأحيان "x". دائما يساوي واحد. من المهم أيضًا تذكر هذا
3. مشتق من الدرجة. عند حل المشكلات ، تحتاج إلى تحويل الجذور غير التربيعية إلى أس.
4. مشتق من متغير أس -1
5. مشتق الجذر التربيعي
6. مشتق الجيب
7. مشتق جيب التمام
8. مشتق الظل
9. مشتق ظل التمام
10. مشتق القوسين
11. مشتق قوس جيب التمام
12. مشتق قوس الظل
13. مشتق من معكوس الظل
14. مشتق من اللوغاريتم الطبيعي
15. مشتق من دالة لوغاريتمية
16. مشتق من الأس
17. مشتق دالة أسية

قواعد التمايز

1. مشتق من المجموع أو الفرق
2. مشتق من المنتج
2 أ. مشتق من تعبير مضروب بعامل ثابت
3. مشتق من حاصل القسمة
4. مشتق دالة معقدة

قاعدة 1إذا كان يعمل

قابلة للتفاضل عند نقطة ما ، ثم الوظائف في نفس النقطة

و

هؤلاء. مشتق المجموع الجبري للوظائف هو مجموع جبريمشتقات هذه الوظائف.

عاقبة. إذا اختلفت دالتان قابلتان للتفاضل بواسطة ثابت ، فإن مشتقاتهما تكون كذلك، بمعنى آخر.

القاعدة 2إذا كان يعمل

قابلة للتفاضل في مرحلة ما ، فإن منتجها قابل للتفاضل أيضًا في نفس النقطة

و

هؤلاء. مشتق حاصل ضرب وظيفتين يساوي مجموع حاصل ضرب كل من هاتين الدالتين ومشتق الآخر.

النتيجة 1. يمكن إخراج العامل الثابت من علامة المشتق:

النتيجة 2. مشتق ناتج العديد من الوظائف القابلة للتفاضل يساوي مجموع حاصل ضرب مشتق كل من العوامل وكل العوامل الأخرى.

على سبيل المثال ، لثلاثة مضاعفات:

المادة 3إذا كان يعمل

قابلة للتفاضل في مرحلة ما و , ثم عند هذه النقطة يكون حاصل قسمةها أيضًا قابلاً للاشتقاق.u / v و

هؤلاء. مشتق خارج قسمة وظيفتين يساوي كسر ، بسطه هو الفرق بين حاصل ضرب المقام ومشتق البسط والبسط ومشتق المقام ، والمقام هو مربع البسط السابق .

أين تبحث في الصفحات الأخرى

عند العثور على مشتق المنتج وحاصل القسمة في مشاكل حقيقية ، من الضروري دائمًا تطبيق عدة قواعد تفاضل في وقت واحد ، لذلك توجد المزيد من الأمثلة على هذه المشتقات في المقالة."مشتق المنتج والحاصل".

تعليق.يجب ألا تخلط بين ثابت (أي رقم) كمصطلح في المجموع وكعامل ثابت! في حالة المصطلح ، فإن مشتقه يساوي صفرًا ، وفي حالة وجود عامل ثابت ، يتم استبعاده من علامة المشتقات. هذا هو خطأ نموذجي، والتي تحدث في المرحلة الأولى من دراسة المشتقات ، ولكن كحل للعديد من الأمثلة المكونة من جزئين ، لم يعد الطالب العادي يرتكب هذا الخطأ.

وإذا كان لديك مصطلح عند التفريق بين منتج أو حاصل قسمة ش"الخامس، حيث ش- رقم ، على سبيل المثال ، 2 أو 5 ، أي ثابت ، ثم مشتق هذا الرقم سيكون مساويًا للصفر ، وبالتالي ، فإن المصطلح بأكمله سيكون مساويًا للصفر (يتم تحليل هذه الحالة في المثال 10) .

خطأ شائع آخر هو الحل الميكانيكي لمشتق دالة معقدة كمشتق لدالة بسيطة. لذا مشتق دالة معقدةمكرسة لمقال منفصل. لكن في البداية سوف نتعلم إيجاد مشتقات وظائف بسيطة.

على طول الطريق ، لا يمكنك الاستغناء عن تحولات التعبيرات. للقيام بذلك ، قد تحتاج إلى فتح كتيبات النوافذ الجديدة أفعال ذات قوى وجذورو الأفعال مع الكسور .

إذا كنت تبحث عن حلول للمشتقات ذات القوى والجذور ، أي عندما تبدو الوظيفة ، ثم اتبع الدرس "مشتق مجموع الكسور ذات القوى والجذور".

إذا كان لديك مهمة مثل ، فأنت في الدرس "مشتقات الدوال المثلثية البسيطة".

أمثلة خطوة بخطوة - كيفية إيجاد المشتق

مثال 3أوجد مشتق دالة

قرار. نحدد أجزاء تعبير الدالة: يمثل التعبير بأكمله المنتج ، وعوامله عبارة عن مجاميع ، وفي الثانية يحتوي أحد المصطلحات على عامل ثابت. نطبق قاعدة تمايز المنتج: مشتق حاصل ضرب وظيفتين يساوي مجموع حاصل ضرب كل من هاتين الدالتين ومشتق الآخر:

بعد ذلك ، نطبق قاعدة اشتقاق المجموع: مشتق مجموع الدوال الجبري يساوي المجموع الجبري لمشتقات هذه الدوال. في حالتنا ، في كل مجموع ، الحد الثاني بعلامة ناقص. في كل مجموع ، نرى متغيرًا مستقلاً ، مشتقه يساوي واحدًا ، وثابتًا (رقمًا) مشتقه يساوي صفرًا. إذن ، "x" تتحول إلى واحد ، وسالب 5 - إلى صفر. في التعبير الثاني ، يتم ضرب "x" في 2 ، لذلك نضرب اثنين في نفس وحدة مشتق "x". نحصل على القيم التالية للمشتقات:

نستبدل المشتقات الموجودة في مجموع المنتجات ونحصل على مشتق الوظيفة بأكملها التي تتطلبها حالة المشكلة:

ويمكنك التحقق من حل المسألة على المشتق في.

مثال 4أوجد مشتق دالة

قرار. مطلوب منا إيجاد مشتق خارج القسمة. نطبق صيغة اشتقاق خارج القسمة: مشتق خارج قسمة دالتين يساوي كسرًا يكون بسطه هو الفرق بين حاصل ضرب المقام ومشتق البسط ومشتق المقام ، و المقام هو مربع البسط السابق. نحن نحصل:

لقد وجدنا بالفعل مشتق العوامل في البسط في المثال 2. دعونا لا ننسى أيضًا أن حاصل الضرب ، وهو العامل الثاني في البسط ، مأخوذ بعلامة ناقص في المثال الحالي:

إذا كنت تبحث عن حلول لمثل هذه المشاكل التي تحتاج فيها إلى إيجاد مشتق دالة ، حيث توجد كومة مستمرة من الجذور والدرجات ، مثل ، على سبيل المثال ، ثم مرحبًا بك في الفصل "مشتق مجموع الكسور ذات القوى والجذور" .

إذا كنت بحاجة إلى معرفة المزيد حول مشتقات الجيب وجيب التمام والظل وغيرها الدوال المثلثية، أي عندما تبدو الوظيفة ، ثم لديك درس "مشتقات الدوال المثلثية البسيطة" .

مثال 5أوجد مشتق دالة

قرار. في هذه الدالة ، نرى منتجًا ، أحد عوامله هو الجذر التربيعي للمتغير المستقل ، والذي تعرفنا على مشتقه في جدول المشتقات. وفقًا لقاعدة تمايز المنتج والقيمة الجدولية لمشتق الجذر التربيعي ، نحصل على:

يمكنك التحقق من حل مسألة المشتقات على مشتق حاسبة على الانترنت .

مثال 6أوجد مشتق دالة

قرار. في هذه الدالة ، نرى حاصل القسمة الذي يكون المقسوم عليه هو الجذر التربيعي للمتغير المستقل. وفقًا لقاعدة اشتقاق حاصل القسمة ، التي كررناها وطبقناها في المثال 4 ، والقيمة المجدولة لمشتق الجذر التربيعي ، نحصل على:

للتخلص من الكسر في البسط ، اضرب البسط والمقام في.

التاريخ: 05/10/2015

كيف تجد المشتق؟

قواعد التمايز.

للعثور على مشتق من أي دالة ، تحتاج إلى إتقان ثلاثة مفاهيم فقط:

2. قواعد التفاضل.

3. مشتق دالة معقدة.

إنه بهذا الترتيب. إنه تلميح.)

بالطبع ، سيكون من الجيد أن يكون لديك فكرة عن المشتق بشكل عام). حول ماهية المشتق وكيفية التعامل مع جدول المشتقات - يمكن الوصول إليه في الدرس السابق. هنا سنتعامل مع قواعد التفاضل.

التفاضل هو عملية إيجاد مشتق. لا يوجد شيء وراء هذا المصطلح. هؤلاء. التعبيرات "أوجد مشتق دالة"و "وظيفة التفريق"- نفس الشئ.

تعبير "قواعد التمايز"يشير إلى إيجاد المشتق من العمليات الحسابية.يساعد هذا الفهم كثيرًا في تجنب ظهور العصيدة في الرأس.

دعونا نركز ونتذكر كل شيء ، كل شيء ، كل شيء عمليات حسابية. هناك أربعة منهم). الجمع (المجموع) والطرح (الفرق) والضرب (حاصل الضرب) والقسمة (حاصل القسمة). ها هي قواعد التفاضل:

تظهر اللوحة خمسةالقواعد على أربعةعمليات حسابية. لم أخطئ في التقدير.) إنها فقط أن القاعدة 4 هي نتيجة أولية للقاعدة 3. لكنها شائعة جدًا لدرجة أنه من المنطقي كتابتها (وتذكرها!) كصيغة مستقلة.

تحت التدوين يوو الخامسبعض الوظائف (على الإطلاق!) ضمنية يو (س)و الخامس (خ).

لنلقِ نظرة على بعض الأمثلة. أولا ، أبسطها.

أوجد مشتق الدالة y = sinx - x 2

لدينا هنا فرقوظيفتين أساسيتين. نطبق القاعدة 2. سنفترض أن sinx دالة يو، و x 2 دالة الخامس.لدينا كل الحق في أن نكتب:

y "= (sinx - x 2)" = (sinx) "- (x 2)"

أفضل بالفعل ، أليس كذلك؟) يبقى إيجاد مشتقات الجيب ومربع x. يوجد جدول مشتق لهذا. نبحث فقط في الجدول عن الوظائف التي نحتاجها ( sinxو x2) ، انظر إلى مشتقاتهم واكتب الإجابة:

y "= (sinx)" - (x 2) "= cosx - 2x

هذا كل ما في الامر. تعمل القاعدة 1 الخاصة بالتفريق بين المجموع بنفس الطريقة تمامًا.

ماذا لو كان لدينا مصطلحات متعددة؟ لا بأس.) نقسم الدالة إلى حدود ونبحث عن مشتق كل حد ، بغض النظر عن الحدود الأخرى. علي سبيل المثال:

أوجد مشتق الدالة y = sinx - x 2 + cosx - x +3

لا تتردد في الكتابة:

y "= (sinx)" - (x 2) "+ (cosx)" - (x) "+ (3)"

في نهاية الدرس ، سأقدم نصائح حول جعل الحياة أسهل عند التفريق.)

نصائح عملية:

1. قبل الاشتقاق ، نتطلع إلى معرفة ما إذا كان من الممكن تبسيط الوظيفة الأصلية.

2. في الأمثلة المشوشة ، نرسم الحل بالتفصيل ، بكل الأقواس والحدود.

3. عند اشتقاق الكسور ذات العدد الثابت في المقام ، فإننا نحول القسمة إلى عملية ضرب ونستخدم القاعدة 4.

إذا اتبعنا التعريف ، فإن مشتق الدالة عند نقطة ما هو حد نسبة الزيادة للدالة Δ ذلزيادة الحجة Δ x:

يبدو أن كل شيء واضح. لكن حاول أن تحسب بهذه الصيغة ، على سبيل المثال ، مشتق الدالة F(x) = x 2 + (2x+ 3) · ه xالخطيئة x. إذا كنت تفعل كل شيء بحكم التعريف ، فبعد بضع صفحات من العمليات الحسابية سوف تغفو ببساطة. لذلك ، هناك طرق أبسط وأكثر فعالية.

بادئ ذي بدء ، نلاحظ أنه يمكن تمييز ما يسمى بالوظائف الأولية من مجموعة متنوعة من الوظائف. إنه نسبي تعابير بسيطة، التي تم حساب مشتقاتها وإدخالها في الجدول منذ فترة طويلة. من السهل تذكر مثل هذه الوظائف ، جنبًا إلى جنب مع مشتقاتها.

مشتقات الدوال الابتدائية

الوظائف الابتدائية هي كل شيء مدرج أدناه. يجب معرفة مشتقات هذه الوظائف عن ظهر قلب. علاوة على ذلك ، ليس من الصعب حفظها - وهذا هو سبب كونها ابتدائية.

إذن ، مشتقات الدوال الأولية:

اسم	وظيفة	المشتق
ثابت	F(x) = ج, ج ∈ ص	0 (نعم ، نعم ، صفر!)
درجة مع الأس المنطقي	F(x) = x ن	ن · x ن − 1
التجويف	F(x) = الخطيئة x	كوس x
جيب التمام	F(x) = كوس x	- خطيئة x(ناقص شرط)
الظل	F(x) = tg x	1 / كوس 2 x
ظل التمام	F(x) = ctg x	- 1 / الخطيئة 2 x
اللوغاريتم الطبيعي	F(x) = تسجيل الدخول x	1/x
اللوغاريتم التعسفي	F(x) = تسجيل الدخول أ x	1/(x ln أ)
دالة أسية	F(x) = ه x	ه x(لا شيء تغير)

إذا تم ضرب دالة أولية بثابت تعسفي ، فيمكن أيضًا حساب مشتق الوظيفة الجديدة بسهولة:

(ج · F)’ = ج · F ’.

بشكل عام ، يمكن إخراج الثوابت من علامة المشتق. علي سبيل المثال:

(2x 3) '= 2 ( x 3) '= 2 3 x 2 = 6x 2 .

من الواضح أنه يمكن إضافة الوظائف الأولية إلى بعضها البعض ، ومضاعفتها ، وتقسيمها ، وغير ذلك الكثير. هذه هي الطريقة التي ستظهر بها الوظائف الجديدة ، لم تعد أساسية جدًا ، ولكنها أيضًا قابلة للتمييز وفقًا لقواعد معينة. تتم مناقشة هذه القواعد أدناه.

مشتق المجموع والفرق

دع الوظائف F(x) و ز(x) ، التي نعرف مشتقاتها. على سبيل المثال ، يمكنك أن تأخذ الوظائف الأولية التي تمت مناقشتها أعلاه. ثم يمكنك إيجاد مشتق مجموع واختلاف هذه الدوال:

1. (F + ز)’ = F ’ + ز ’
2. (F − ز)’ = F ’ − ز ’

لذا ، فإن مشتق مجموع (فرق) وظيفتين يساوي مجموع (فرق) المشتقات. قد يكون هناك المزيد من الشروط. علي سبيل المثال، ( F + ز + ح)’ = F ’ + ز ’ + ح ’.

بالمعنى الدقيق للكلمة ، لا يوجد مفهوم "الطرح" في الجبر. هناك مفهوم "العنصر السلبي". لذلك ، فإن الاختلاف F − زيمكن إعادة كتابتها كمجموع F+ (1) ز، وبعد ذلك تبقى صيغة واحدة فقط - مشتق المجموع.

F(x) = x 2 + sinx ؛ ز(x) = x 4 + 2x 2 − 3.

وظيفة F(x) هو مجموع وظيفتين أساسيتين ، لذلك:

F ’(x) = (x 2+ خطيئة x)’ = (x 2) '+ (خطيئة x)’ = 2x+ كوسكس.

نحن نجادل بالمثل من أجل الوظيفة ز(x). يوجد فقط ثلاثة مصطلحات (من وجهة نظر الجبر):

ز ’(x) = (x 4 + 2x 2 − 3)’ = (x 4 + 2x 2 + (−3))’ = (x 4)’ + (2x 2)’ + (−3)’ = 4x 3 + 4x + 0 = 4x · ( x 2 + 1).

إجابه:
F ’(x) = 2x+ كوسكس.
ز ’(x) = 4x · ( x 2 + 1).

مشتق من المنتج

الرياضيات علم منطقي ، لذلك يعتقد الكثير من الناس أنه إذا كان مشتق المجموع يساوي مجموع المشتقات ، فإن مشتق المنتج إضراب\ u003e يساوي حاصل ضرب المشتقات. لكنك أنت التين! يتم حساب مشتق المنتج باستخدام صيغة مختلفة تمامًا. وهي:

(F · ز) ’ = F ’ · ز + F · ز ’

الصيغة بسيطة ، لكنها غالبًا ما تُنسى. وليس فقط تلاميذ المدارس ، ولكن أيضًا الطلاب. النتيجة هي حل المشاكل بشكل غير صحيح.

مهمة. أوجد مشتقات الدوال: F(x) = x 3 كوسكس ز(x) = (x 2 + 7x- 7) · ه x .

وظيفة F(x) هو نتاج وظيفتين أساسيتين ، لذلك كل شيء بسيط:

F ’(x) = (x 3 كوس x)’ = (x 3) 'كوس x + x 3 (كوس x)’ = 3x 2 كوس x + x 3 (−sin x) = x 2 (3cos x − xالخطيئة x)

وظيفة ز(x) المضاعف الأول أكثر تعقيدًا بعض الشيء ، لكن المخطط العام لا يتغير من هذا. من الواضح أن المضاعف الأول للدالة ز(x) هي كثيرة الحدود ومشتقاتها هي مشتق المجموع. نملك:

ز ’(x) = ((x 2 + 7x- 7) · ه x)’ = (x 2 + 7x- 7) '· ه x + (x 2 + 7x- 7) ( ه x)’ = (2x+ 7) · ه x + (x 2 + 7x- 7) · ه x = ه x(2 x + 7 + x 2 + 7x −7) = (x 2 + 9x) · ه x = x(x+ 9) · ه x .

إجابه:
F ’(x) = x 2 (3cos x − xالخطيئة x);
ز ’(x) = x(x+ 9) · ه x .

لاحظ أنه في الخطوة الأخيرة ، تم تحليل المشتق إلى عوامل. بشكل رسمي ، هذا ليس ضروريًا ، لكن معظم المشتقات لا تحسب من تلقاء نفسها ، ولكن لاستكشاف الوظيفة. هذا يعني أن المشتقة ستعادل صفرًا ، وسيتم اكتشاف علاماتها ، وهكذا. في مثل هذه الحالة ، من الأفضل أن يتحلل التعبير إلى عوامل.

إذا كان هناك نوعان من الوظائف F(x) و ز(x)، و ز(x) ≠ 0 في المجموعة التي تهمنا ، يمكننا تحديد وظيفة جديدة ح(x) = F(x)/ز(x). لمثل هذه الوظيفة ، يمكنك أيضًا العثور على المشتق:

ليس ضعيفا ، أليس كذلك؟ من أين أتى الطرح؟ لماذا ز 2؟ لكن مثل هذا! هذه واحدة من أكثر الصيغ تعقيدًا - لا يمكنك اكتشافها بدون زجاجة. لذلك ، من الأفضل دراستها بأمثلة محددة.

مهمة. أوجد مشتقات الدوال:

توجد دوال أولية في البسط والمقام لكل كسر ، لذلك كل ما نحتاجه هو صيغة مشتق خارج القسمة:

حسب التقاليد ، نقوم بتحويل البسط إلى عوامل - وهذا سوف يبسط الإجابة بشكل كبير:

ليس بالضرورة أن تكون الدالة المعقدة صيغة طولها نصف كيلومتر. على سبيل المثال ، يكفي أن تأخذ الوظيفة F(x) = الخطيئة xواستبدل المتغير x، يقول على x 2 + ln x. اتضح F(x) = الخطيئة ( x 2 + ln x) - هذا ما هو عليه وظيفة معقدة. لديها أيضًا مشتق ، لكن لن يجدي العثور عليها وفقًا للقواعد التي تمت مناقشتها أعلاه.

كيف تكون؟ في مثل هذه الحالات ، يساعد استبدال المتغير وصيغة مشتق دالة معقدة على:

F ’(x) = F ’(ر) · ر'، لو xلقد بدل بواسطة ر(x).

كقاعدة عامة ، يكون الموقف مع فهم هذه الصيغة أكثر حزنًا من مشتق حاصل القسمة. لذلك ، من الأفضل أيضًا شرحها بأمثلة محددة باستخدام وصف مفصلكل خطوة.

مهمة. أوجد مشتقات الدوال: F(x) = ه 2x + 3 ; ز(x) = الخطيئة ( x 2 + ln x)

لاحظ أنه إذا كان في الوظيفة F(x) بدلاً من التعبير 2 x+ 3 سيكون سهلاً x، ثم ستعمل دالة ابتدائية F(x) = ه x. لذلك ، نجري استبدالًا: دعنا 2 x + 3 = ر, F(x) = F(ر) = ه ر. نبحث عن مشتق دالة معقدة بالصيغة:

F ’(x) = F ’(ر) · ر ’ = (ه ر)’ · ر ’ = ه ر · ر ’

والآن - الاهتمام! إجراء تبديل عكسي: ر = 2x+ 3. نحصل على:

F ’(x) = ه ر · ر ’ = ه 2x+ 3 (2 x + 3)’ = ه 2x+ 3 2 = 2 ه 2x + 3

الآن دعونا نلقي نظرة على الوظيفة ز(x). من الواضح أنه يجب استبداله. x 2 + ln x = ر. نملك:

ز ’(x) = ز ’(ر) · ر'= (الخطيئة ر)’ · ر'= كوس ر · ر ’

الاستبدال العكسي: ر = x 2 + ln x. ثم:

ز ’(x) = كوس ( x 2 + ln x) · ( x 2 + ln x) '= كوس ( x 2 + ln x) · (2 x + 1/x).

هذا كل شئ! كما يتضح من التعبير الأخير ، تم اختزال المشكلة برمتها لحساب مشتق المجموع.

إجابه:
F ’(x) = 2 ه 2x + 3 ;
ز ’(x) = (2x + 1/x) كوس ( x 2 + ln x).

في كثير من الأحيان في دروسي ، بدلاً من مصطلح "مشتق" ، أستخدم كلمة "ضربة". على سبيل المثال ، ضربة من المجموع يساوي المجموعحدود. هل هذا أوضح؟ حسنا هذا جيد.

وبالتالي ، فإن حساب المشتق يتلخص في التخلص من هذه السكتات الدماغية وفقًا للقواعد التي تمت مناقشتها أعلاه. كمثال أخير ، دعنا نعود إلى القوة المشتقة ذات الأس المنطقي:

(x ن)’ = ن · x ن − 1

قلة يعرفون ذلك في الدور نقد يكون عددًا كسريًا. على سبيل المثال ، الجذر هو x 0.5 ولكن ماذا لو كان هناك شيء خادع تحت الجذر؟ مرة أخرى ، ستظهر وظيفة معقدة - إنهم يحبون إعطاء مثل هذه الإنشاءات مراقبة العملوالامتحانات.

مهمة. أوجد مشتق دالة:

أولًا ، دعنا نعيد كتابة الجذر في صورة قوة ذات أس كسري:

F(x) = (x 2 + 8x − 7) 0,5 .

الآن نقوم بإجراء استبدال: let x 2 + 8x − 7 = ر. نجد المشتق بالصيغة:

F ’(x) = F ’(ر) · ر ’ = (ر 0.5) ' ر'= 0.5 ر−0.5 ر ’.

نجري استبدال عكسي: ر = x 2 + 8x- 7. لدينا:

F ’(x) = 0.5 ( x 2 + 8x- 7) −0.5 ( x 2 + 8x- 7) '= 0.5 (2 x+8) ( x 2 + 8x − 7) −0,5 .

أخيرًا ، عد إلى الجذور:

من السهل جدًا تذكرها.

حسنًا ، دعنا لا نذهب بعيدًا ، دعنا نفكر على الفور وظيفة عكسية. ما هو معكوس الدالة الأسية؟ اللوغاريتم:

في حالتنا ، الأساس هو رقم:

مثل هذا اللوغاريتم (أي اللوغاريتم ذو الأساس) يسمى اللوغاريتم "الطبيعي" ، ونستخدم تدوينًا خاصًا له: نكتب بدلاً من ذلك.

ما يساوي؟ بالتاكيد، .

مشتق اللوغاريتم الطبيعي بسيط جدًا أيضًا:

أمثلة:

1. العثور على مشتق من وظيفة.
2. ما هو مشتق الوظيفة؟

الإجابات: عارض و اللوغاريتم الطبيعي- الوظائف بسيطة بشكل فريد من حيث المشتق. سيكون للدوال الأسية واللوغاريتمية مع أي قاعدة أخرى مشتق مختلف ، سنقوم بتحليله لاحقًا ، بعد أن ننتقل إلى قواعد التفاضل.

قواعد التمايز

ما هي القواعد؟ مصطلح جديد مرة أخرى؟! ...

التفاضلهي عملية إيجاد المشتق.

فقط وكل شيء. ما هي الكلمة الأخرى لهذه العملية؟ ليس proizvodnovanie ... يسمى التفاضل في الرياضيات بزيادة الوظيفة في. يأتي هذا المصطلح من الاختلاف اللاتيني - الاختلاف. هنا.

عند اشتقاق كل هذه القواعد ، سنستخدم وظيفتين ، على سبيل المثال ، و. سنحتاج أيضًا إلى صيغ لزياداتها:

هناك 5 قواعد في المجموع.

يتم إخراج الثابت من علامة المشتق.

إذا كان بعض رقم ثابت(ثابت) ، إذن.

من الواضح أن هذه القاعدة تعمل أيضًا مع الاختلاف:.

دعنا نثبت ذلك. اسمحوا ، أو أسهل.

أمثلة.

أوجد مشتقات الدوال:

1. عند النقطة
2. عند النقطة
3. عند النقطة
4. في هذه النقطة.

حلول:

1. (المشتق هو نفسه في جميع النقاط ، لأنه كذلك دالة خطية، يتذكر؟)؛

مشتق من المنتج

كل شيء متشابه هنا: نقدم وظيفة جديدة ونجد زيادتها:

المشتق:

أمثلة:

1. البحث عن مشتقات الوظائف و ؛
2. أوجد مشتق دالة عند نقطة.

حلول:

مشتق من الدالة الأسية

الآن معرفتك كافية لتتعلم كيفية العثور على مشتق أي دالة أسية ، وليس فقط الأس (هل نسيت ما هو عليه حتى الآن؟).

إذن أين يوجد عدد.

نحن نعلم بالفعل مشتق الدالة ، لذلك دعونا نحاول نقل الدالة إلى أساس جديد:

لهذا نستخدم قاعدة بسيطة:. ثم:

حسنًا ، لقد نجحت. حاول الآن إيجاد المشتقة ، ولا تنس أن هذه الدالة معقدة.

حدث؟

هنا ، تحقق من نفسك:

تبين أن الصيغة تشبه إلى حد بعيد مشتق الأس: كما كانت ، لا تزال ، ظهر عامل فقط ، وهو مجرد رقم ، ولكن ليس متغيرًا.

أمثلة:
أوجد مشتقات الدوال:

الإجابات:

هذا مجرد رقم لا يمكن حسابه بدون آلة حاسبة ، أي أنه لا يمكن كتابته بصيغة أبسط. لذلك ، في الإجابة يتم تركها بهذا الشكل.

لاحظ أن هنا حاصل قسمة وظيفتين ، لذلك نطبق قاعدة التفاضل المناسبة:

في هذا المثال ، نتاج وظيفتين:

مشتق من دالة لوغاريتمية

هذا مشابه: أنت تعرف بالفعل مشتق اللوغاريتم الطبيعي:

لذلك ، لإيجاد تعسفي من اللوغاريتم بأساس مختلف ، على سبيل المثال:

علينا إحضار هذا اللوغاريتم إلى الأساس. كيف تغير قاعدة اللوغاريتم؟ أتمنى أن تتذكر هذه الصيغة:

الآن فقط بدلاً من أن نكتب:

تبين أن المقام مجرد ثابت (رقم ثابت ، بدون متغير). المشتق بسيط للغاية:

مشتقات الأسي و الدوال اللوغاريتميةيكاد لا يحدث أبدًا في الامتحان ، ولكن معرفتهم لن تكون زائدة عن الحاجة.

مشتق دالة معقدة.

ما هي "وظيفة معقدة"؟ لا ، هذا ليس لوغاريتمًا ، وليس ظلًا قوسيًا. قد يكون من الصعب فهم هذه الوظائف (على الرغم من أنه إذا كان اللوغاريتم يبدو صعبًا بالنسبة لك ، فاقرأ موضوع "اللوغاريتمات" وسيعمل كل شيء) ، ولكن من حيث الرياضيات ، فإن كلمة "معقد" لا تعني "صعبة".

تخيل ناقلًا صغيرًا: شخصان يجلسان ويقومان ببعض الأعمال باستخدام بعض الأشياء. على سبيل المثال ، يلف الأول شريط شوكولاتة في غلاف ، والثاني يربطه بشريط. اتضح مثل هذا الكائن المركب: شريط شوكولاتة ملفوف ومربوط بشريط. لأكل لوح شوكولاتة ، عليك القيام بالخطوات المعاكسة بترتيب عكسي.

دعنا ننشئ خط أنابيب رياضيًا مشابهًا: أولاً سنجد جيب التمام لرقم ، ثم سنقوم بتربيع الرقم الناتج. لذا ، أعطونا رقمًا (شوكولاتة) ، أجد جيب التمام (غلاف) ، ثم قم بتربيع ما حصلت عليه (اربطه بشريط). ماذا حدث؟ وظيفة. هذا مثال على دالة معقدة: عندما ، من أجل إيجاد قيمتها ، نقوم بتنفيذ الإجراء الأول مباشرة مع المتغير ، ثم إجراء آخر آخر مع ما حدث كنتيجة للأول.

بعبارات أخرى، الوظيفة المعقدة هي دالة تمثل حجة دالة أخرى: .

على سبيل المثال لدينا.

قد نقوم بنفس الإجراءات بترتيب عكسي: أولاً ، تربّع ، ثم أبحث عن جيب التمام للعدد الناتج :. من السهل تخمين أن النتيجة ستكون مختلفة دائمًا. ميزة مهمة للوظائف المعقدة: عندما يتغير ترتيب الإجراءات ، تتغير الوظيفة.

المثال الثاني: (same). .

سيتم استدعاء الإجراء الأخير الذي نقوم به وظيفة "خارجية"، والإجراء الذي تم تنفيذه أولاً - على التوالي وظيفة "داخلية"(هذه أسماء غير رسمية ، أستخدمها فقط لشرح المادة بلغة بسيطة).

حاول أن تحدد بنفسك أي وظيفة خارجية وأيها داخلية:

الإجابات:الفصل بين الوظائف الداخلية والخارجية مشابه جدًا للمتغيرات المتغيرة: على سبيل المثال ، في الوظيفة

1. ما هو الإجراء الذي سنتخذه أولا؟ أولًا نحسب الجيب ، وعندها فقط نرفعها إلى مكعب. إذن فهي وظيفة داخلية وليست خارجية.
   والوظيفة الأصلية هي تكوينها:.
2. داخلي: ؛ خارجي: .
   فحص: .
3. داخلي: ؛ خارجي: .
   فحص: .
4. داخلي: ؛ خارجي: .
   فحص: .
5. داخلي: ؛ خارجي: .
   فحص: .

نغير المتغيرات ونحصل على دالة.

حسنًا ، الآن سنستخرج الشوكولاتة - ابحث عن المشتق. يتم عكس الإجراء دائمًا: أولاً نبحث عن مشتق الدالة الخارجية ، ثم نضرب النتيجة في مشتق الدالة الداخلية. بالنسبة للمثال الأصلي ، يبدو كالتالي:

مثال آخر:

لذا ، دعنا أخيرًا نصيغ القاعدة الرسمية:

خوارزمية لإيجاد مشتق دالة معقدة:

يبدو أنه بسيط ، أليس كذلك؟

دعنا نتحقق من الأمثلة:

حلول:

1) داخلي: ؛

خارجي: ؛

2) داخلي: ؛

(فقط لا تحاول التقليل الآن! لا شيء مأخوذ من تحت جيب التمام ، تذكر؟)

3) داخلي: ؛

خارجي: ؛

من الواضح على الفور أن هناك وظيفة معقدة من ثلاثة مستويات هنا: بعد كل شيء ، هذه بالفعل وظيفة معقدة في حد ذاتها ، وما زلنا نستخرج الجذر منها ، أي أننا نقوم بالإجراء الثالث (ضع الشوكولاتة في غلاف وشريط في حقيبة). ولكن لا يوجد سبب للخوف: على أي حال ، سوف "نفك" هذه الوظيفة بنفس الترتيب المعتاد: من النهاية.

وهذا يعني أننا نفرق الجذر أولاً ، ثم جيب التمام ، وبعد ذلك فقط المقدار الموجود بين قوسين. ثم نضربها كلها.

في مثل هذه الحالات ، من الملائم ترقيم الإجراءات. أي دعونا نتخيل ما نعرفه. في أي ترتيب سنقوم بتنفيذ الإجراءات لحساب قيمة هذا التعبير؟ لنلقي نظرة على مثال:

كلما تم تنفيذ الإجراء لاحقًا ، كلما كانت الوظيفة المقابلة "خارجية". تسلسل الإجراءات - كما كان من قبل:

هنا يكون التعشيش بشكل عام من 4 مستويات. دعونا نحدد مسار العمل.

1. التعبير الراديكالي. .

2. الجذر. .

3. الجيوب الأنفية. .

4. مربع. .

5. تجميعها جميعًا:

المشتق. باختصار حول الرئيسي

مشتق وظيفي- نسبة زيادة الدالة إلى زيادة الوسيطة مع زيادة متناهية في الصغر للوسيطة:

المشتقات الأساسية:

قواعد التمايز:

يتم إخراج الثابت من علامة المشتق:

مشتق من المجموع:

منتج مشتق:

مشتق من حاصل القسمة:

مشتق دالة معقدة:

خوارزمية لإيجاد مشتق دالة معقدة:

1. نحدد الوظيفة "الداخلية" ، ونجد مشتقها.
2. نحدد الوظيفة "الخارجية" ، ونجد مشتقها.
3. نضرب نتائج النقطتين الأولى والثانية.