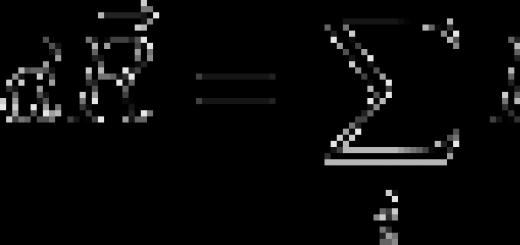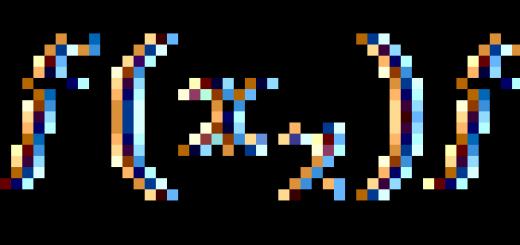Systemlösung lineare Gleichungen Gaußsche Methode. Angenommen, wir müssen eine Lösung für das System finden n lineare Gleichungen mit n unbekannte Variablen
die Determinante der Hauptmatrix davon von Null verschieden ist.
Die Essenz der Gauß-Methode besteht im sukzessiven Ausschluss unbekannter Variablen: erstens, die x 1 aus allen Gleichungen des Systems, beginnend mit der zweiten, dann x2 aller Gleichungen, beginnend mit der dritten, und so weiter, bis nur noch die unbekannte Variable in der letzten Gleichung übrig bleibt x n. Ein solcher Prozess der Transformation der Gleichungen des Systems zur sukzessiven Eliminierung unbekannter Variablen wird als bezeichnet direkte Gauss-Methode. Nach Abschluss der Vorwärtsbewegung der Gauß-Methode finden wir aus der letzten Gleichung x n, wobei dieser Wert aus der vorletzten Gleichung berechnet wird xn-1, und so weiter, aus der ersten Gleichung wird gefunden x 1. Der Prozess der Berechnung unbekannter Variablen beim Übergang von der letzten Gleichung des Systems zur ersten wird aufgerufen Reverse-Gauß-Methode.
Lassen Sie uns kurz den Algorithmus zum Eliminieren unbekannter Variablen beschreiben.
Wir nehmen das an, da wir dies immer erreichen können, indem wir die Gleichungen des Systems umstellen. Eliminiere die unbekannte Variable x 1 aus allen Gleichungen des Systems, beginnend mit der zweiten. Dazu addieren Sie die erste Gleichung multipliziert mit zur zweiten Gleichung des Systems, addieren die erste multipliziert mit zur dritten Gleichung und so weiter bis n-te addiere die erste Gleichung, multipliziert mit . Das Gleichungssystem nimmt nach solchen Transformationen die Form an 
wo ein  .
.
Wir würden zum gleichen Ergebnis kommen, wenn wir ausdrücken würden x 1 durch andere unbekannte Variablen in der ersten Gleichung des Systems und der resultierende Ausdruck wurde in alle anderen Gleichungen eingesetzt. Also die Variable x 1 von allen Gleichungen ausgeschlossen, beginnend mit der zweiten.
Als nächstes gehen wir ähnlich vor, aber nur mit einem Teil des resultierenden Systems, der in der Abbildung markiert ist 
Dazu addieren Sie die zweite multipliziert mit zur dritten Gleichung des Systems, addieren die zweite multipliziert mit zur vierten Gleichung und so weiter bis n-te addiere die zweite Gleichung, multipliziert mit . Das Gleichungssystem nimmt nach solchen Transformationen die Form an 
wo ein  . Also die Variable x2 von allen Gleichungen ausgeschlossen, beginnend mit der dritten.
. Also die Variable x2 von allen Gleichungen ausgeschlossen, beginnend mit der dritten.
Als nächstes fahren wir mit der Eliminierung des Unbekannten fort x 3, während wir mit dem in der Abbildung markierten Teil des Systems ähnlich verfahren 
Wir setzen also den direkten Weg der Gauß-Methode fort, bis das System die Form annimmt 
Von diesem Moment an beginnen wir den umgekehrten Weg der Gauß-Methode: Wir rechnen x n aus der letzten Gleichung als , unter Verwendung des erhaltenen Werts x n finden xn-1 aus der vorletzten Gleichung, und so weiter, finden wir x 1 aus der ersten Gleichung.
Beispiel.
Lineares Gleichungssystem lösen  Gaußsche Methode.
Gaußsche Methode.
In diesem Artikel wird die Methode als Lösungsweg betrachtet.Die Methode ist analytisch, das heißt, Sie können einen Lösungsalgorithmus hineinschreiben Gesamtansicht, und ersetzen Sie dort dann Werte aus bestimmten Beispielen. Anders als bei der Matrixmethode oder den Cramerschen Formeln kann man beim Lösen eines linearen Gleichungssystems mit der Gauß-Methode auch mit solchen arbeiten, die unendlich viele Lösungen haben. Oder sie haben es gar nicht.
Was bedeutet Gauß?
Zuerst müssen Sie unser Gleichungssystem in Es sieht so aus. Das System wird übernommen:
Die Koeffizienten werden in Form einer Tabelle und rechts in einer separaten Spalte geschrieben - freie Mitglieder. Die Spalte mit freien Elementen ist der Einfachheit halber getrennt.Die Matrix, die diese Spalte enthält, wird als erweitert bezeichnet.

Weiterhin muss die Hauptmatrix mit Koeffizienten auf die obere Dreiecksform reduziert werden. Dies ist der Hauptpunkt bei der Lösung des Systems durch das Gauß-Verfahren. Einfach ausgedrückt sollte die Matrix nach bestimmten Manipulationen so aussehen, sodass in ihrem unteren linken Teil nur Nullen stehen:

Wenn Sie die neue Matrix dann wieder als Gleichungssystem schreiben, werden Sie feststellen, dass die letzte Zeile bereits den Wert einer der Wurzeln enthält, die dann in die obige Gleichung eingesetzt wird, eine andere Wurzel gefunden wird und so weiter.
Dies ist eine allgemeinste Beschreibung der Lösung durch das Gauß-Verfahren. Und was passiert, wenn das System plötzlich keine Lösung hat? Oder gibt es davon unendlich viele? Um diese und viele weitere Fragen zu beantworten, müssen alle Elemente, die in der Lösung nach der Gauß-Methode verwendet werden, separat betrachtet werden.
Matrizen, ihre Eigenschaften
Es gibt keine versteckte Bedeutung in der Matrix. Es ist nur eine praktische Möglichkeit, Daten für spätere Operationen aufzuzeichnen. Auch Schulkinder sollten keine Angst vor ihnen haben.
Die Matrix ist immer rechteckig, weil es bequemer ist. Auch bei der Gauß-Methode, bei der alles auf den Aufbau einer Matrix hinausläuft dreieckig, erscheint ein Rechteck im Eintrag, nur mit Nullen an den Stellen, an denen keine Zahlen stehen. Nullen können weggelassen werden, sind aber impliziert.
Die Matrix hat eine Größe. Seine "Breite" ist die Anzahl der Zeilen (m), seine "Länge" ist die Anzahl der Spalten (n). Dann wird die Größe der Matrix A (normalerweise werden lateinische Großbuchstaben für ihre Bezeichnung verwendet) als A m × n bezeichnet. Wenn m=n, dann ist diese Matrix quadratisch und m=n ist ihre Ordnung. Dementsprechend kann jedes Element der Matrix A durch die Nummer seiner Zeile und Spalte bezeichnet werden: a xy ; x - Zeilennummer, Änderungen , y - Spaltennummer, Änderungen .
B ist nicht der Hauptpunkt der Lösung. Im Prinzip können alle Operationen direkt mit den Gleichungen selbst durchgeführt werden, aber die Notation wird sich als viel umständlicher herausstellen, und es wird viel einfacher sein, sich darin zu verwirren.
Bestimmend
Die Matrix hat auch eine Determinante. Dies ist eine sehr wichtige Funktion. Es lohnt sich nicht, ihre Bedeutung jetzt herauszufinden, Sie können einfach zeigen, wie sie berechnet wird, und dann sagen, welche Eigenschaften der Matrix sie bestimmt. Der einfachste Weg, die Determinante zu finden, ist durch Diagonalen. In die Matrix werden imaginäre Diagonalen eingezeichnet; Die auf jedem von ihnen befindlichen Elemente werden multipliziert und dann die resultierenden Produkte addiert: Diagonalen mit einer Neigung nach rechts - mit einem "Plus" -Zeichen, mit einer Neigung nach links - mit einem "Minus" -Zeichen.

Es ist äußerst wichtig zu beachten, dass die Determinante nur für eine quadratische Matrix berechnet werden kann. Für eine rechteckige Matrix können Sie Folgendes tun: Wählen Sie die kleinste der Anzahl der Zeilen und der Anzahl der Spalten (es sei k) und markieren Sie dann zufällig k Spalten und k Zeilen in der Matrix. Die Elemente, die sich am Schnittpunkt der ausgewählten Spalten und Zeilen befinden, bilden eine neue quadratische Matrix. Wenn die Determinante einer solchen Matrix eine andere Zahl als Null ist, wird sie als Basisminor der ursprünglichen rechteckigen Matrix bezeichnet.
Bevor Sie mit der Lösung des Gleichungssystems nach der Gauß-Methode fortfahren, schadet es nicht, die Determinante zu berechnen. Wenn es sich herausstellt, dass es Null ist, können wir sofort sagen, dass die Matrix entweder unendlich viele Lösungen hat oder gar keine. In solch einem traurigen Fall müssen Sie weiter gehen und den Rang der Matrix herausfinden.
Systemklassifizierung
Es gibt so etwas wie den Rang einer Matrix. Dies ist die maximale Ordnung ihrer Determinante, die sich von Null unterscheidet (wenn wir uns an die Basis-Minor erinnern, können wir sagen, dass der Rang einer Matrix die Ordnung der Basis-Minor ist).
Je nachdem, wie es mit dem Rang steht, kann SLAE unterteilt werden in:
- Gemeinsam. Bei Bei gemeinsamen Systemen stimmt der Rang der Hauptmatrix (nur aus Koeffizienten bestehend) mit dem Rang der erweiterten Matrix (mit einer Spalte freier Mitglieder) überein. Solche Systeme haben eine Lösung, aber nicht unbedingt eine, daher werden gemeinsame Systeme zusätzlich unterteilt in:
- - sicher- eine einzigartige Lösung zu haben. In bestimmten Systemen sind der Rang der Matrix und die Anzahl der Unbekannten (oder die Anzahl der Spalten, was dasselbe ist) gleich;
- - unbestimmt - mit unendlich vielen Lösungen. Der Rang der Matrizen für solche Systeme ist kleiner als die Anzahl der Unbekannten.
- Unvereinbar. Bei Bei solchen Systemen stimmen die Ränge der Haupt- und erweiterten Matrizen nicht überein. Inkompatible Systeme haben keine Lösung.
Das Gauß-Verfahren ist insofern gut, als es erlaubt, entweder einen eindeutigen Beweis für die Inkonsistenz des Systems zu erhalten (ohne die Determinanten großer Matrizen zu berechnen) oder eine allgemeine Lösung für ein System mit unendlich vielen Lösungen.
Elementare Transformationen
Bevor Sie direkt zur Lösung des Systems übergehen, ist es möglich, es für Berechnungen weniger umständlich und bequemer zu machen. Dies wird durch elementare Transformationen erreicht – derart, dass ihre Implementierung die endgültige Antwort in keiner Weise ändert. Es sollte beachtet werden, dass einige der obigen elementaren Transformationen nur für Matrizen gelten, deren Quelle genau die SLAE war. Hier ist eine Liste dieser Transformationen:
- String-Permutation. Es ist offensichtlich, dass eine Änderung der Reihenfolge der Gleichungen im Systemdatensatz die Lösung in keiner Weise beeinflusst. Folglich ist es auch möglich, Zeilen in der Matrix dieses Systems zu vertauschen, nicht zu vergessen natürlich die Spalte der freien Elemente.
- Multiplizieren aller Elemente einer Zeichenfolge mit einem Faktor. Sehr hilfreich! Es kann zum Kürzen verwendet werden große Zahlen in der Matrix oder entfernen Sie Nullen. Der Lösungssatz ändert sich wie üblich nicht und es wird bequemer, weitere Operationen durchzuführen. Die Hauptsache ist, dass der Koeffizient nicht gleich Null ist.
- Löschen Sie Zeilen mit proportionalen Koeffizienten. Dies folgt teilweise aus dem vorherigen Absatz. Wenn zwei oder mehr Zeilen in der Matrix proportionale Koeffizienten haben, werden beim Multiplizieren / Dividieren einer der Zeilen mit dem Proportionalitätskoeffizienten zwei (oder wieder mehr) absolut identische Zeilen erhalten, und Sie können die zusätzlichen entfernen und nur übrig lassen ein.
- Entfernen der Nulllinie. Wenn im Laufe von Transformationen irgendwo ein String entsteht, in dem alle Elemente, einschließlich des freien Elements, Null sind, dann kann ein solcher String Null genannt und aus der Matrix geworfen werden.
- Zu den Elementen einer Zeile werden die Elemente einer anderen (in den entsprechenden Spalten) addiert, multipliziert mit einem bestimmten Koeffizienten. Die obskurste und wichtigste Transformation von allen. Es lohnt sich, näher darauf einzugehen.
Addieren einer Zeichenfolge multipliziert mit einem Faktor
Zum leichteren Verständnis lohnt es sich, diesen Prozess Schritt für Schritt zu zerlegen. Aus der Matrix werden zwei Zeilen entnommen:
a 11 a 12 ... a 1n | b1
a 21 a 22 ... a 2n | b 2
Angenommen, Sie müssen den ersten zum zweiten addieren, multipliziert mit dem Koeffizienten "-2".
a" 21 \u003d a 21 + -2 × a 11
a" 22 \u003d a 22 + -2 × a 12
a" 2n \u003d a 2n + -2 × a 1n
Dann wird in der Matrix die zweite Zeile durch eine neue ersetzt und die erste bleibt unverändert.
a 11 a 12 ... a 1n | b1
a" 21 a" 22 ... a" 2n | b 2
Es sei darauf hingewiesen, dass der Multiplikationsfaktor so gewählt werden kann, dass durch die Addition zweier Strings eines der Elemente des neuen Strings gleich Null ist. Daher ist es möglich, eine Gleichung im System zu erhalten, bei der es eine weniger Unbekannte gibt. Und wenn Sie zwei solcher Gleichungen erhalten, kann die Operation erneut durchgeführt werden und Sie erhalten eine Gleichung, die bereits zwei Unbekannte weniger enthält. Und wenn wir jedes Mal einen Koeffizienten für alle Zeilen, die niedriger als der ursprüngliche sind, auf Null stellen, können wir wie Schritte bis zum Ende der Matrix gehen und eine Gleichung mit einer Unbekannten erhalten. Dies wird als Lösen des Systems mit der Gaußschen Methode bezeichnet.
Im Allgemeinen
Lass es ein System geben. Es hat m Gleichungen und n unbekannte Wurzeln. Du kannst es so aufschreiben:

Die Hauptmatrix wird aus den Koeffizienten des Systems zusammengestellt. Der erweiterten Matrix wird eine Spalte mit freien Mitgliedern hinzugefügt und der Einfachheit halber durch einen Balken getrennt.
- die erste Zeile der Matrix wird mit dem Koeffizienten k = (-a 21 / a 11) multipliziert;
- die erste modifizierte Reihe und die zweite Reihe der Matrix werden hinzugefügt;
- anstelle der zweiten Zeile wird das Ergebnis der Addition aus dem vorherigen Absatz in die Matrix eingefügt;
- jetzt ist der erste Koeffizient in der neuen zweiten Zeile a 11 × (-a 21 /a 11) + a 21 = -a 21 + a 21 = 0.
Jetzt wird die gleiche Reihe von Transformationen durchgeführt, nur die erste und dritte Zeile sind beteiligt. Dementsprechend wird in jedem Schritt des Algorithmus das Element a 21 durch a 31 ersetzt. Dann wiederholt sich alles für a 41 , ... a m1 . Das Ergebnis ist eine Matrix, bei der das erste Element in den Zeilen gleich Null ist. Jetzt müssen wir die Zeile Nummer eins vergessen und denselben Algorithmus ab der zweiten Zeile ausführen:
- Koeffizient k \u003d (-a 32 / a 22);
- die zweite modifizierte Zeile wird der "aktuellen" Zeile hinzugefügt;
- das Ergebnis der Addition wird in der dritten, vierten usw. Zeile eingesetzt, während die erste und die zweite unverändert bleiben;
- in den Zeilen der Matrix sind die ersten beiden Elemente bereits gleich Null.
Der Algorithmus muss wiederholt werden, bis der Koeffizient k = (-a m,m-1 /a mm) erscheint. Dies bedeutet, dass im das letzte Mal der Algorithmus wurde nur für die untere Gleichung durchgeführt. Jetzt sieht die Matrix wie ein Dreieck aus oder hat eine Stufenform. Die untere Zeile enthält die Gleichheit a mn × x n = b m . Der Koeffizient und der freie Term sind bekannt und die Wurzel wird durch sie ausgedrückt: x n = b m /a mn. Die resultierende Wurzel wird in die oberste Reihe eingesetzt, um x n-1 = (b m-1 - a m-1,n ×(b m /a mn))÷a m-1,n-1 zu finden. Und so weiter analog: In jeder nächsten Zeile gibt es eine neue Wurzel, und wenn Sie die "Spitze" des Systems erreicht haben, können Sie viele Lösungen finden. Es wird das einzige sein.
Wenn es keine Lösungen gibt
Wenn in einer der Matrixzeilen alle Elemente außer dem freien Term gleich Null sind, dann sieht die dieser Zeile entsprechende Gleichung so aus: 0 = b. Es hat keine Lösung. Und da eine solche Gleichung im System enthalten ist, ist die Lösungsmenge des gesamten Systems leer, dh entartet.
Wenn es unendlich viele Lösungen gibt
Es kann sich herausstellen, dass es in der reduzierten Dreiecksmatrix keine Zeilen mit einem Element - dem Koeffizienten der Gleichung - und einem - einem freien Element gibt. Es gibt nur Strings, die umgeschrieben wie eine Gleichung mit zwei oder mehr Variablen aussehen würden. Das bedeutet, dass das System unendlich viele Lösungen hat. In diesem Fall kann die Antwort in Form einer allgemeinen Lösung gegeben werden. Wie kann man das machen?
Alle Variablen in der Matrix sind in grundlegende und freie Variablen unterteilt. Einfach - das sind diejenigen, die "am Rand" der Zeilen in der abgestuften Matrix stehen. Der Rest ist kostenlos. In der allgemeinen Lösung werden die Basisvariablen in Bezug auf die freien geschrieben.
Der Einfachheit halber wird die Matrix zunächst wieder in ein Gleichungssystem umgeschrieben. Bei der letzten, wo genau nur eine Grundvariable übrig geblieben ist, bleibt sie auf der einen Seite und alles andere wird auf die andere übertragen. Dies geschieht für jede Gleichung mit einer Basisvariablen. Dann wird in den restlichen Gleichungen, wo möglich, anstelle der Basisvariable der dafür erhaltene Ausdruck eingesetzt. Wenn das Ergebnis wieder ein Ausdruck ist, der nur eine Basisvariable enthält, wird es von dort aus erneut ausgedrückt und so weiter, bis jede Basisvariable als Ausdruck mit freien Variablen geschrieben ist. Das ist es gemeinsame Entscheidung SLAU.
Sie können auch die Grundlösung des Systems finden - geben Sie den freien Variablen beliebige Werte und berechnen Sie dann für diesen speziellen Fall die Werte der Grundvariablen. Es gibt unendlich viele spezielle Lösungen.
Lösung mit konkreten Beispielen
Hier ist das Gleichungssystem.

Der Einfachheit halber ist es besser, die Matrix sofort zu erstellen

Es ist bekannt, dass beim Lösen nach der Gauß-Methode die der ersten Zeile entsprechende Gleichung am Ende der Transformationen unverändert bleibt. Daher ist es rentabler, wenn das obere linke Element der Matrix das kleinste ist - dann werden die ersten Elemente der verbleibenden Zeilen nach den Operationen zu Null. Dies bedeutet, dass es in der kompilierten Matrix vorteilhaft ist, die zweite Zeile anstelle der ersten Zeile zu platzieren.
zweite Zeile: k = (-a 21 / a 11) = (-3/1) = -3
a" 21 \u003d a 21 + k × a 11 \u003d 3 + (-3) × 1 \u003d 0
a" 22 \u003d a 22 + k × a 12 \u003d -1 + (-3) × 2 \u003d -7
a" 23 = a 23 + k×a 13 = 1 + (-3)×4 = -11
b "2 \u003d b 2 + k × b 1 \u003d 12 + (-3) × 12 \u003d -24
dritte Zeile: k = (-a 3 1 /a 11) = (-5/1) = -5
a" 3 1 = a 3 1 + k×a 11 = 5 + (-5)×1 = 0
a" 3 2 = a 3 2 + k×a 12 = 1 + (-5)×2 = -9
a" 3 3 = a 33 + k×a 13 = 2 + (-5)×4 = -18
b "3 \u003d b 3 + k × b 1 \u003d 3 + (-5) × 12 \u003d -57
Um jetzt nicht verwirrt zu werden, ist es notwendig, die Matrix mit den Zwischenergebnissen der Transformationen aufzuschreiben.

Es ist offensichtlich, dass eine solche Matrix mit Hilfe einiger Operationen für die Wahrnehmung bequemer gemacht werden kann. Sie können beispielsweise alle "Minuszeichen" aus der zweiten Zeile entfernen, indem Sie jedes Element mit "-1" multiplizieren.
Es ist auch erwähnenswert, dass in der dritten Reihe alle Elemente Vielfache von drei sind. Dann können Sie die Zeichenfolge um diese Zahl kürzen, indem Sie jedes Element mit "-1/3" multiplizieren (minus - gleichzeitig entfernen negative Werte).

Sieht viel schöner aus. Jetzt müssen wir die erste Zeile in Ruhe lassen und mit der zweiten und dritten arbeiten. Die Aufgabe besteht darin, die zweite Zeile zur dritten Zeile zu addieren, multipliziert mit einem solchen Faktor, dass das Element a 32 gleich Null wird.
k = (-a 32 / a 22) = (-3/7) = -3/7 gemeinsamer Bruchteil, und entscheiden Sie erst dann, wenn Antworten eingegangen sind, ob aufgerundet und in eine andere Form von Aufzeichnungen übersetzt werden soll)
a" 32 = a 32 + k × a 22 = 3 + (-3/7) × 7 = 3 + (-3) = 0
a" 33 \u003d a 33 + k × a 23 \u003d 6 + (-3/7) × 11 \u003d -9/7
b "3 \u003d b 3 + k × b 2 \u003d 19 + (-3/7) × 24 \u003d -61/7
Die Matrix wird erneut mit neuen Werten beschrieben.
| 1 | 2 | 4 | 12 |
| 0 | 7 | 11 | 24 |
| 0 | 0 | -9/7 | -61/7 |
Wie Sie sehen können, hat die resultierende Matrix bereits eine Stufenform. Daher sind weitere Transformationen des Systems durch das Gauß-Verfahren nicht erforderlich. Was hier getan werden kann, ist, den Gesamtkoeffizienten "-1/7" aus der dritten Zeile zu entfernen.

Jetzt ist alles schön. Der Punkt ist klein - schreiben Sie die Matrix erneut in Form eines Gleichungssystems und berechnen Sie die Wurzeln
x + 2y + 4z = 12(1)
7y + 11z = 24 (2)
Der Algorithmus, mit dem nun die Nullstellen gefunden werden, wird im Gauss-Verfahren Rückwärtsbewegung genannt. Gleichung (3) enthält den Wert von z:
y = (24 - 11 × (61/9))/7 = -65/9
Und die erste Gleichung ermöglicht es Ihnen, x zu finden:
x = (12 - 4z - 2y)/1 = 12 - 4x(61/9) - 2x(-65/9) = -6/9 = -2/3
Wir haben das Recht, ein solches System gemeinsam und sogar endgültig zu nennen, das heißt, eine einzigartige Lösung zu haben. Die Antwort wird in folgender Form geschrieben:
x 1 \u003d -2/3, y \u003d -65/9, z \u003d 61/9.
Ein Beispiel für ein unbestimmtes System
Die Variante, ein bestimmtes System mit der Gauß-Methode zu lösen, wurde analysiert, jetzt muss der Fall betrachtet werden, dass das System unbestimmt ist, dh unendlich viele Lösungen dafür gefunden werden können.
x 1 + x 2 + x 3 + x 4 + x 5 = 7 (1)
3x 1 + 2x 2 + x 3 + x 4 - 3x 5 = -2 (2)
x 2 + 2x 3 + 2x 4 + 6x 5 = 23 (3)
5x 1 + 4x 2 + 3x 3 + 3x 4 - x 5 = 12 (4)
Das bloße Erscheinungsbild des Systems ist bereits alarmierend, da die Anzahl der Unbekannten n = 5 beträgt und der Rang der Matrix des Systems bereits genau kleiner als diese Zahl ist, da die Anzahl der Zeilen also m = 4 beträgt größte Bestellung Determinantenquadrat - 4. Das bedeutet, dass es unendlich viele Lösungen gibt und wir nach ihrer allgemeinen Form suchen müssen. Das Gauß-Verfahren für lineare Gleichungen macht es möglich.
Zunächst wird wie üblich die Augmented Matrix kompiliert.

Zweite Zeile: Koeffizient k = (-a 21 / a 11) = -3. In der dritten Zeile befindet sich das erste Element vor den Transformationen, Sie müssen also nichts anfassen, Sie müssen es so lassen, wie es ist. Vierte Zeile: k = (-a 4 1 /a 11) = -5
Indem wir die Elemente der ersten Reihe nacheinander mit jedem ihrer Koeffizienten multiplizieren und zu den gewünschten Reihen addieren, erhalten wir eine Matrix der folgenden Form:

Wie Sie sehen können, bestehen die zweite, dritte und vierte Reihe aus Elementen, die zueinander proportional sind. Die zweite und die vierte sind im Allgemeinen gleich, also kann eine von ihnen sofort entfernt und der Rest mit dem Koeffizienten "-1" multipliziert werden und die Zeilennummer 3 erhalten. Und wieder eine von zwei identischen Zeilen belassen.
Es stellte sich eine solche Matrix heraus. Das System wurde noch nicht aufgeschrieben, hier müssen die Grundvariablen bestimmt werden - die bei den Koeffizienten a 11 \u003d 1 und a 22 \u003d 1 stehen und frei sind - der Rest.

Die zweite Gleichung hat nur eine Basisvariable – x 2 . Daher kann es von dort aus ausgedrückt werden, indem die Variablen x 3 , x 4 , x 5 geschrieben werden, die frei sind.
Wir setzen den resultierenden Ausdruck in die erste Gleichung ein.
Es stellte sich eine Gleichung heraus, in der die einzige Basisvariable x 1 ist. Machen wir damit dasselbe wie mit x 2 .
Alle Grundvariablen, von denen es zwei gibt, werden in Form von drei freien ausgedrückt, jetzt können Sie die Antwort in allgemeiner Form schreiben.

Sie können auch eine der speziellen Lösungen des Systems angeben. Für solche Fälle werden in der Regel Nullen als Werte für freie Variablen gewählt. Dann wird die Antwort lauten:
16, 23, 0, 0, 0.
Ein Beispiel für ein inkompatibles System
Die Lösung inkonsistenter Gleichungssysteme nach dem Gauß-Verfahren ist am schnellsten. Sie endet, sobald auf einer der Stufen eine Gleichung erhalten wird, die keine Lösung hat. Das heißt, die Phase mit der Berechnung der Wurzeln, die ziemlich lang und langweilig ist, verschwindet. Es wird folgendes System betrachtet:
x + y - z = 0 (1)
2x - y - z = -2 (2)
4x + y - 3z = 5 (3)
Wie gewohnt wird die Matrix zusammengestellt:
| 1 | 1 | -1 | 0 |
| 2 | -1 | -1 | -2 |
| 4 | 1 | -3 | 5 |
Und es wird auf eine Stufenform reduziert:
k1 \u003d -2k2 \u003d -4
| 1 | 1 | -1 | 0 |
| 0 | -3 | 1 | -2 |
| 0 | 0 | 0 | 7 |
Nach der ersten Transformation enthält die dritte Zeile eine Gleichung der Form
keine Lösung haben. Daher ist das System inkonsistent, und die Antwort ist die leere Menge.
Vor- und Nachteile der Methode
Wenn Sie sich für eine Methode entscheiden, um SLAE auf Papier mit einem Stift zu lösen, dann sieht die Methode, die in diesem Artikel betrachtet wurde, am attraktivsten aus. Bei elementaren Transformationen ist es viel schwieriger, verwirrt zu werden, als wenn Sie manuell nach der Determinante oder einer kniffligen inversen Matrix suchen müssen. Wenn Sie jedoch Programme zum Arbeiten mit Daten dieser Art verwenden, z. B. Tabellenkalkulationen, stellt sich heraus, dass solche Programme bereits Algorithmen zur Berechnung der Hauptparameter von Matrizen enthalten - Determinante, Minderjährige, Inverse usw. Und wenn Sie sicher sind, dass die Maschine diese Werte selbst berechnet und keinen Fehler macht, ist es sinnvoller, die Matrixmethode oder die Formeln von Cramer zu verwenden, da ihre Anwendung mit der Berechnung von Determinanten und inversen Matrizen beginnt und endet.
Anwendung
Da die Gaußsche Lösung ein Algorithmus ist und die Matrix tatsächlich ein zweidimensionales Array ist, kann sie beim Programmieren verwendet werden. Aber da sich der Artikel als Leitfaden „für Dummies“ positioniert, sollte gesagt werden, dass der einfachste Ort, um die Methode in Tabellenkalkulationen, zum Beispiel Excel, hineinzuschieben. Auch hier wird jede SLAE, die in Form einer Matrix in eine Tabelle eingegeben wird, von Excel als zweidimensionales Array betrachtet. Und für Operationen mit ihnen gibt es viele nette Befehle: Addition (man kann nur Matrizen gleicher Größe addieren!), Multiplikation mit einer Zahl, Matrizenmultiplikation (auch mit gewissen Einschränkungen), Finden der inversen und transponierten Matrizen und vor allem , Berechnung der Determinante. Wenn diese zeitraubende Aufgabe durch einen einzigen Befehl ersetzt wird, ist es viel schneller, den Rang einer Matrix zu bestimmen und damit ihre Kompatibilität oder Inkonsistenz festzustellen.
Die Gauß-Methode wurde von dem berühmten deutschen Mathematiker Carl Friedrich Gauß (1777 - 1855) vorgeschlagen und ist eine der universellsten Methoden zur Lösung von SLAE. Das Wesen dieser Methode liegt darin, dass durch sukzessives Eliminieren von Unbekannten das gegebene System in ein dem gegebenen äquivalentes Stufensystem (insbesondere Dreieckssystem) umgewandelt wird. Bei der praktischen Lösung des Problems wird die erweiterte Matrix des Systems mit Hilfe elementarer Transformationen über ihre Zeilen auf eine Stufenform reduziert. Dann werden alle Unbekannten nacheinander gefunden, beginnend von unten nach oben.
Das Prinzip der Gauß-Methode
Das Gaußsche Verfahren umfasst direkte (Reduzieren der erweiterten Matrix auf eine abgestufte Form, dh Erhalten von Nullen unter der Hauptdiagonalen) und umgekehrte (Erhalten von Nullen über der Hauptdiagonalen der erweiterten Matrix) Bewegungen. Die Vorwärtsbewegung wird als Gauß-Methode bezeichnet, die Rückwärtsbewegung als Gauß-Jordan-Methode, die sich von der ersten nur in der Reihenfolge des Ausschlusses von Variablen unterscheidet.
Das Gauß-Verfahren ist ideal zum Lösen von Systemen, die mehr als drei lineare Gleichungen enthalten, zum Lösen von Gleichungssystemen, die nicht quadratisch sind (was nicht über das Cramer-Verfahren und das Matrix-Verfahren gesagt werden kann). Das heißt, die Gauß-Methode ist die universellste Methode, um eine Lösung für ein beliebiges lineares Gleichungssystem zu finden; sie funktioniert in dem Fall, wenn das System unendlich viele Lösungen hat oder inkonsistent ist.
Beispiele zum Lösen von Gleichungssystemen
Beispiel
Die Aufgabe. Lösen Sie SLAE nach der Gauß-Methode.
Lösung. Wir schreiben die erweiterte Matrix des Systems und bringen diese Matrix durch elementare Transformationen über ihre Zeilen in eine Stufenform (Vorwärtsbewegung) und führen dann die umgekehrte Bewegung der Gauß-Methode durch (wir machen Nullen über der Hauptdiagonalen). Ändern Sie zunächst die erste und zweite Zeile so, dass das Element gleich 1 ist (wir tun dies, um die Berechnungen zu vereinfachen):

Teilen Sie alle Elemente der dritten Reihe durch zwei (oder, was dasselbe ist, multiplizieren Sie mit):


Von der dritten Zeile subtrahieren wir die zweite, multipliziert mit 3:

Multiplizieren wir die dritte Zeile mit , erhalten wir:

Führen wir nun den umgekehrten Ablauf des Gauß-Verfahrens (Gassou-Jordan-Verfahren) durch, dh wir setzen Nullen über der Hauptdiagonalen. Beginnen wir mit den Elementen der dritten Spalte. Es ist notwendig, das Element zurückzusetzen, dazu subtrahieren wir die dritte von der zweiten Zeile.
Carl Friedrich Gauß, der größte Mathematiker, zögerte lange und wählte zwischen Philosophie und Mathematik. Vielleicht war es gerade eine solche Denkweise, die es ihm ermöglichte, in der Weltwissenschaft so merklich „abzusteigen“. Insbesondere durch die Schaffung der "Gauß-Methode" ...
Seit fast 4 Jahren beschäftigen sich die Artikel dieser Seite mit schulische Ausbildung, hauptsächlich von der Seite der Philosophie, die Prinzipien des (Miss-)Verstehens, in die Köpfe der Kinder eingeführt. Es wird Zeit für mehr Einzelheiten, Beispiele und Methoden ... Ich glaube, dass dies die Herangehensweise an das Vertraute, Verwirrende und Verwirrende ist wichtig Lebensbereiche liefert die besten Ergebnisse.
Wir Menschen sind so eingerichtet, dass es egal ist, wie viel Sie reden abstraktes Denken, aber Verständnis immer geschieht durch Beispiele. Wenn es keine Beispiele gibt, dann ist es unmöglich, die Prinzipien zu erfassen ... Wie unmöglich ist es, auf der Spitze eines Berges zu sein, ohne seinen gesamten Hang vom Fuß aus zu durchqueren.
Dasselbe gilt für die Schule: vorerst lebendige Geschichten nicht genug, wir betrachten es weiterhin instinktiv als einen Ort, an dem Kinder verstehen lernen.
Zum Beispiel das Lehren der Gauß-Methode...
Gauss-Methode in der 5. Klasse der Schule
Ich werde gleich reservieren: Die Gauss-Methode hat noch viel mehr zu bieten Breite Anwendung, zum Beispiel beim Lösen Systeme linearer Gleichungen. Worüber wir sprechen werden, findet in der 5. Klasse statt. Das Anfang, nachdem Sie das verstanden haben, ist es viel einfacher, mehr "erweiterte Optionen" zu verstehen. In diesem Artikel sprechen wir darüber Methode (Methode) von Gauß beim Finden der Summe einer Reihe
Hier ist ein Beispiel, das ich aus der Schule mitgebracht habe jüngerer Sohn Besuch der 5. Klasse des Moskauer Gymnasiums.
Schuldemonstration der Gauß-Methode
Mathelehrer verwendet Interaktives Whiteboard (moderne Methoden Training) zeigte den Kindern eine Präsentation der Geschichte der "Entstehung der Methode" durch den kleinen Gauss.
Der Schullehrer hat den kleinen Carl ausgepeitscht (eine veraltete Methode, die jetzt nicht mehr in Schulen verwendet wird), weil er,
anstatt Zahlen von 1 bis 100 nacheinander zu addieren, um ihre Summe zu finden bemerkte dass sich Zahlenpaare mit gleichem Abstand von den Rändern einer arithmetischen Folge zu derselben Zahl addieren. zum Beispiel 100 und 1, 99 und 2. Nachdem der kleine Gauss die Anzahl solcher Paare gezählt hatte, löste er fast sofort das vom Lehrer vorgeschlagene Problem. Dafür wurde er vor einem erstaunten Publikum hingerichtet. An den Rest zu denken war respektlos.
Was hat der kleine Gauss gemacht entwickelt Zahlensinn? Bemerkte einige Funktion Zahlenreihe mit konstanter Schrittweite (arithmetische Progression). UND genau das machte ihn später zu einem großen Wissenschaftler, bemerken können, besitzen Gefühl, Instinkt des Verstehens.
Das ist der Wert der Mathematik, der sich entwickelt Fähigkeit zu sehen allgemein im besonderen - abstraktes Denken. Daher die meisten Eltern und Arbeitgeber halten Mathematik instinktiv für eine wichtige Disziplin ...
„Mathematik sollte später gelehrt werden, damit es den Verstand in Ordnung bringt.
M. W. Lomonossow".
Die Anhänger derjenigen, die zukünftige Genies auspeitschten, verwandelten die Methode jedoch in etwas Gegenteiliges. Wie sagte mein Vorgesetzter vor 35 Jahren: „Sie haben die Frage gelernt.“ Oder, wie mein jüngster Sohn gestern über die Gauß-Methode sagte: "Vielleicht lohnt es sich nicht, daraus eine große Wissenschaft zu machen, oder?"
Die Folgen der Kreativität der „Wissenschaftler“ zeigen sich im Niveau der aktuellen Schulmathematik, dem Niveau ihres Unterrichts und dem mehrheitlichen Verständnis der „Königin der Wissenschaften“.
Aber machen wir weiter...
Methoden zur Erläuterung der Gauß-Methode in der 5. Klasse der Schule
Ein Mathematiklehrer an einem Moskauer Gymnasium, der die Gauß-Methode auf Vilenkins Art erklärte, erschwerte die Aufgabe.
Was ist, wenn die Differenz (Stufe) einer arithmetischen Folge nicht eins, sondern eine andere Zahl ist? Zum Beispiel 20.
Die Aufgabe, die er den Fünftklässlern gab:
20+40+60+80+ ... +460+480+500
Bevor wir uns mit der Gymnastikmethode vertraut machen, schauen wir uns das Web an: Wie machen es Schullehrer - Mathelehrer? ..
Gauss-Methode: Erklärung Nr. 1
Ein bekannter Tutor führt auf seinem YOUTUBE-Kanal folgende Begründung an:
„Schreiben wir die Zahlen von 1 bis 100 so:
zuerst eine Zahlenreihe von 1 bis 50, und streng darunter eine weitere Zahlenreihe von 50 bis 100, aber in umgekehrter Reihenfolge.
1, 2, 3, ... 48, 49, 50
100, 99, 98 ... 53, 52, 51
„Bitte beachte: Die Summe jedes Zahlenpaares aus der oberen und unteren Reihe ist gleich und gleich 101! Zählen wir die Anzahl der Paare, es ist 50 und multiplizieren die Summe eines Paares mit der Anzahl der Paare! Voila: The Antwort ist fertig!".
„Wenn du es nicht verstehen konntest, reg dich nicht auf!“, wiederholte der Lehrer während der Erklärung dreimal. "Sie werden diese Methode in der 9. Klasse bestehen!"
Gauss-Methode: Erklärung Nr. 2
Ein anderer, weniger bekannter Tutor (nach der Anzahl der Aufrufe zu urteilen) verwendet mehr wissenschaftliche Herangehensweise, bietet einen Lösungsalgorithmus von 5 Punkten, die nacheinander ausgeführt werden müssen.
Für Uneingeweihte: 5 ist eine der Fibonacci-Zahlen, die traditionell als magisch angesehen werden. Die 5-Stufen-Methode ist immer wissenschaftlicher als beispielsweise die 6-Stufen-Methode. ... Und das ist kaum ein Zufall, höchstwahrscheinlich ist der Autor ein versteckter Anhänger der Fibonacci-Theorie
Dana arithmetische Progression: 4, 10, 16 ... 244, 250, 256 .
Algorithmus zum Ermitteln der Summe von Zahlen in einer Reihe mit der Gauß-Methode:
4, 10, 16 ... 244, 250, 256
256, 250, 244 ... 16, 10, 4
Gleichzeitig müssen Sie sich daran erinnern plus eine Regel : Eins muss zum resultierenden Quotienten addiert werden: Andernfalls erhalten wir ein Ergebnis, das um eins kleiner ist als die wahre Anzahl von Paaren: 42 + 1 = 43.
Das ist die gesuchte Summe der arithmetischen Folge von 4 bis 256 mit einer Differenz von 6!
Gauss-Methode: Erklärung in der 5. Klasse des Moskauer Gymnasiums
Und so war es erforderlich, das Problem zu lösen, die Summe einer Reihe zu finden:
20+40+60+ ... +460+480+500
in der 5. Klasse des Moskauer Gymnasiums Vilenkins Lehrbuch (laut meinem Sohn).
Nach dem Zeigen der Präsentation zeigte der Mathematiklehrer ein paar Gaußsche Beispiele und gab der Klasse die Aufgabe, die Summe der Zahlen in einer Reihe mit einer Schrittweite von 20 zu finden.
Dazu war Folgendes erforderlich:
Wie Sie sehen können, ist es kompakter und effektive Technik: Die Zahl 3 ist auch ein Mitglied der Fibonacci-Folge

Meine Anmerkungen zur Schulversion der Gauß-Methode
Der große Mathematiker hätte sich bestimmt für die Philosophie entschieden, wenn er vorhergesehen hätte, was seine Anhänger aus seiner „Methode“ machen würden. Deutschlehrer der Karl mit Stöcken geprügelt hat. Er hätte die Symbolik und die dialektische Spirale und die unsterbliche Dummheit der "Lehrer" gesehen versucht, die Harmonie des lebendigen mathematischen Denkens mit der Algebra des Missverständnisses zu messen ....
Übrigens, wissen Sie. dass unser Bildungssystem in der deutschen Schule des 18. und 19. Jahrhunderts verwurzelt ist?
Aber Gauß entschied sich für Mathematik.
Was ist die Essenz seiner Methode?
IN Vereinfachung. IN Beobachtung und Erfassung einfache Zahlenmuster. IN trockene Schularithmetik in verwandeln interessante und lustige Aktivität , aktiviert den Wunsch, im Gehirn weiterzumachen, und blockiert nicht die teure geistige Aktivität.
Ist es möglich, die Summe der Zahlen einer arithmetischen Folge mit einer der oben genannten "Modifikationen des Gauß-Verfahrens" zu berechnen? sofort? Laut den „Algorithmen“ hätte der kleine Karl Spanking garantiert vermieden, eine Abneigung gegen Mathematik kultiviert und seine kreativen Impulse im Keim erstickt.
Warum riet der Tutor den Fünftklässlern so eindringlich, „keine Angst vor Missverständnissen“ der Methode zu haben, und überzeugte sie davon, dass sie „solche“ Probleme schon in der 9. Klasse lösen würden? Psychologisch ungebildete Aktion. Es war eine gute Idee, dies zu beachten: "Mach's gut bereits in der 5. Klasse kann man löse Probleme, die du erst in 4 Jahren bestehen wirst! Was seid ihr für gute Kerle!"
Um die Gaußsche Methode anzuwenden, ist Stufe 3 der Klasse ausreichend wenn normale Kinder bereits wissen, wie man 2-3-stellige Zahlen addiert, multipliziert und dividiert. Probleme ergeben sich aus der Unfähigkeit erwachsener Lehrer, die "nicht hineingehen", um die einfachsten Dinge in einer normalen menschlichen Sprache zu erklären, nicht nur in Mathematik ... Sie sind nicht in der Lage, Mathematik zu interessieren und sogar die "Fähigen" vollständig zu entmutigen.
Oder, wie mein Sohn kommentierte, „eine große Wissenschaft daraus machen“.
Gauß-Methode, meine Erläuterungen
Meine Frau und ich haben unserem Kind diese "Methode" anscheinend schon vor der Schule erklärt ...
Einfachheit statt Komplexität oder ein Frage-Antwort-Spiel
„Schau, hier sind die Zahlen von 1 bis 100. Was siehst du?“
Es geht nicht darum, was das Kind sieht. Der Trick besteht darin, ihn aussehen zu lassen.
"Wie kannst du sie zusammensetzen?" Der Sohn hat gemerkt, dass solche Fragen nicht „einfach so“ gestellt werden und man die Frage „irgendwie anders, anders als sonst“ betrachten muss.
Es spielt keine Rolle, ob das Kind die Lösung sofort sieht, es ist unwahrscheinlich. Es ist wichtig, dass er keine Angst mehr zu haben, oder wie ich sage: "die Aufgabe verschoben". Dies ist der Beginn des Weges zum Verstehen
"Was ist einfacher: zum Beispiel 5 und 6 oder 5 und 95 addieren?" Eine Leitfrage... Aber schließlich läuft jedes Training darauf hinaus, eine Person zu einer "Antwort" zu "leiten" - in irgendeiner Weise, die für sie akzeptabel ist.
In diesem Stadium gibt es möglicherweise bereits Vermutungen darüber, wie man Berechnungen "einsparen" kann.
Wir haben nur angedeutet: Die "frontale, lineare" Zählweise ist nicht die einzig mögliche. Hat das Kind diese abgeschnitten, dann erfindet es später noch viele weitere solcher Methoden, weil es interessant ist!!! Und er wird definitiv ein "Missverständnis" der Mathematik vermeiden, wird keinen Ekel dafür empfinden. Er hat gewonnen!
Wenn Baby entdeckt dass das Addieren von Zahlenpaaren, die zusammen Hundert ergeben, eine unbedeutende Aufgabe ist "Arithmetische Progression mit Differenz 1"- für ein Kind eine ziemlich öde und uninteressante Sache - plötzlich hat ihm das Leben geschenkt . Aus Chaos wurde Ordnung, und diese begeistert immer wieder: so sind wir!
Eine kurze Frage: Warum sollten sie nach der Einsicht eines Kindes wieder in das Gerüst trockener Algorithmen getrieben werden, die in diesem Fall auch funktional unbrauchbar sind?!
Warum dumm umschreiben Sequenznummern in einem Notizbuch: damit auch der Tüchtige keine einzige Chance auf Verständnis hätte? Statistisch natürlich, aber die Massenerziehung konzentriert sich auf "Statistiken" ...
Wo ist die Null geblieben?
Und doch ist das Addieren von Zahlen, die zusammen 100 ergeben, für den Verstand viel akzeptabler als das Geben von 101 ...
Die "Schul-Gauß-Methode" verlangt genau das: gedankenlos faltenäquidistant von der Mitte des Verlaufs eines Zahlenpaares, Trotzdem.
Was ist, wenn du schaust?
Dennoch ist die Null die größte Erfindung der Menschheit, die mehr als 2.000 Jahre alt ist. Und Mathelehrer ignorieren ihn weiterhin.
Es ist viel einfacher, eine Zahlenreihe, die bei 1 beginnt, in eine Reihe umzuwandeln, die bei 0 beginnt. Die Summe ändert sich nicht, oder? Sie müssen aufhören, "in Lehrbüchern zu denken" und anfangen zu suchen ... Und um zu sehen, dass Paare mit der Summe 101 vollständig durch Paare mit der Summe 100 ersetzt werden können!
0 + 100, 1 + 99, 2 + 98 ... 49 + 51
Wie schafft man die „Regel plus 1“ ab?
Um ehrlich zu sein, habe ich zum ersten Mal von diesem YouTube-Tutor von einer solchen Regel gehört ...
Was mache ich noch, wenn ich die Anzahl der Mitglieder einer Serie ermitteln muss?
Blick auf die Reihenfolge:
1, 2, 3, .. 8, 9, 10
und wenn völlig müde, dann auf einer einfacheren Reihe:
1, 2, 3, 4, 5
und ich schätze: wenn du eins von 5 abziehst, bekommst du 4, aber ich bin ganz klar sehen 5 Zahlen! Daher müssen Sie eine hinzufügen! Zahlensinn entwickelt in Grundschule, schlägt vor: Auch wenn es ein ganzes Google an Mitgliedern der Serie gibt (10 hoch hundert), bleibt das Muster gleich.
Scheiß auf die Regeln? ...
Damit Sie in ein paar - drei Jahren den ganzen Raum zwischen Stirn und Hinterkopf ausfüllen und aufhören zu denken? Wie wäre es, Brot und Butter zu verdienen? Schließlich bewegen wir uns in geraden Reihen in die Ära der Digitalwirtschaft!
Mehr zur Schulmethode von Gauß: "warum daraus Wissenschaft machen? .."
Nicht umsonst habe ich einen Screenshot aus dem Notizbuch meines Sohnes gepostet...
"Was gab es in der Lektion?"
"Nun, ich habe sofort gezählt, meine Hand gehoben, aber sie hat nicht gefragt. Deshalb habe ich, während die anderen gezählt haben, angefangen, DZ auf Russisch zu machen, um keine Zeit zu verlieren. Dann, als die anderen mit dem Schreiben fertig waren (?? ?), sie hat mich an die Tafel gerufen. Ich habe die Antwort gesagt."
„Richtig, zeig mir, wie du es gelöst hast“, sagte der Lehrer. Ich zeigte. Sie sagte: "Falsch, du musst zählen, wie ich es gezeigt habe!"
"Es ist gut, dass ich keine Zwei gemacht habe. Und ich habe mich gezwungen, den "Entscheidungsprozess" auf ihre eigene Weise in ein Notizbuch zu schreiben. Warum eine große Wissenschaft daraus machen? .. "
Das Hauptverbrechen eines Mathelehrers
kaum danach dieser Fall Carl Gauß empfand eine hohe Wertschätzung für den Schullehrer der Mathematik. Aber wenn er wüsste wie Anhänger dieses Lehrers pervertiere das Wesen der Methode... würde er vor Empörung und durch brüllen die Weltorganisation Geistige Eigentumsrechte WIPO hat ein Verbot der Verwendung seines ehrlichen Namens in Schulbüchern erreicht! ..
Worin der Hauptfehler des schulischen Ansatzes? Oder, wie ich es ausdrücke, das Verbrechen von Schulmathematiklehrern an Kindern?
Algorithmus missverstanden
Was machen Schulmethodiker, von denen die allermeisten nicht denken können?
Erstellen Sie Methoden und Algorithmen (siehe). Das eine Abwehrreaktion, die Lehrer vor Kritik schützt ("Alles wird nach ... gemacht") und Kinder vor Verständnis schützt. Und damit - aus dem Wunsch, Lehrer zu kritisieren!(Die zweite Ableitung der bürokratischen "Weisheit", eine wissenschaftliche Herangehensweise an das Problem). Wer die Bedeutung nicht versteht, wird eher sein eigenes Missverständnis beschuldigen und nicht die Dummheit des Schulsystems.
Was passiert: Eltern geben den Kindern die Schuld, und Lehrer ... das gleiche gilt für Kinder, die "Mathematik nicht verstehen! ..
Bist du versiert?
Was hat der kleine Carl gemacht?
Absolut unkonventionell an eine Vorlagenaufgabe herangegangen. Das ist die Quintessenz seines Ansatzes. Das in der schule sollte vor allem gelehrt werden, nicht mit lehrbüchern, sondern mit dem kopf zu denken. Natürlich gibt es auch eine instrumentale Komponente, die verwendet werden kann ... auf der Suche nach einfacher u wirksame Methoden Konten.
Gauss-Verfahren nach Vilenkin
In der Schule lehren sie, dass es die Gauß-Methode ist
was, wenn die Anzahl der Elemente in der Zeile ungerade ist, wie in der Aufgabe, die dem Sohn übertragen wurde? ..
Der "Trick" ist das in diesem Fall Sie sollten die "zusätzliche" Nummer der Serie finden und zur Summe der Paare addieren. In unserem Beispiel ist diese Zahl 260.
Wie entdecken? Alle Zahlenpaare in ein Notizbuch umschreiben!(Deshalb hat der Lehrer die Kinder diesen dummen Job machen lassen und versucht, "Kreativität" mit der Gaußschen Methode zu lehren ... Und deshalb ist eine solche "Methode" praktisch nicht auf große Datenreihen anwendbar, und deshalb ist es keine Gaußsche Methode).
Ein bisschen Kreativität im Schulalltag...
Der Sohn handelte anders.
(20 + 500, 40 + 480 ...).
0+500, 20+480, 40+460 ...
Einfach richtig?
Aber in der Praxis wird es noch einfacher, was es Ihnen ermöglicht, 2-3 Minuten für die Fernerkundung auf Russisch herauszuarbeiten, während der Rest "zählt". Darüber hinaus behält es die Anzahl der Schritte der Methodik bei: 5, was es nicht erlaubt, den Ansatz als unwissenschaftlich zu kritisieren.
Offensichtlich ist dieser Ansatz im Stil der Methode einfacher, schneller und vielseitiger. Aber ... der Lehrer hat nicht nur nicht gelobt, sondern mich auch gezwungen, es "richtig" umzuschreiben (siehe Screenshot). Das heißt, sie unternahm einen verzweifelten Versuch, den kreativen Impuls und die Fähigkeit, Mathematik zu verstehen, im Keim zu ersticken! Offenbar, um später als Nachhilfelehrerin angestellt zu werden ... Sie hat den Falschen angegriffen ...
Alles, was ich so lang und mühsam beschrieben habe, kann einem normalen Kind in maximal einer halben Stunde erklärt werden. Zusammen mit Beispielen.
Und damit er es nie vergisst.
Und es wird Schritt zum Verstehen...nicht nur Mathematik.
Geben Sie es zu: Wie oft in Ihrem Leben haben Sie nach der Gauß-Methode addiert? Und ich nie!
Aber Instinkt des Verstehens, die sich während des Studiums mathematischer Methoden in der Schule entwickelt (oder erlischt) ... Oh! ... Das ist wirklich eine unersetzliche Sache!
Vor allem im Zeitalter der universellen Digitalisierung, in die wir unter strenger Führung von Partei und Regierung stillschweigend eingetreten sind.
Ein paar Worte zur Verteidigung der Lehrer...
Es ist unfair und falsch, die gesamte Verantwortung für diesen Unterrichtsstil allein den Schullehrern zuzuschieben. Das System ist in Betrieb.
Etwas Lehrer verstehen die Absurdität dessen, was passiert, aber was tun? Schulgesetz, Landesbildungsstandards, Methoden, Unterrichtskarten... Alles soll „nach und auf der Grundlage“ gemacht und alles dokumentiert werden. Schritt zur Seite - stand in der Schlange für die Entlassung. Seien wir keine Heuchler: Das Gehalt der Moskauer Lehrer ist sehr gut ... Wenn sie gefeuert werden, wohin sollen sie gehen? ...
Deshalb diese Seite nicht um Bildung. Er ist ungefähr individuelle Erziehung, nur möglicher Weg raus aus der Masse Generation Z ...
Definition und Beschreibung der Gauß-Methode
Die Gaußsche Transformationsmethode (auch als Methode der sequentiellen Eliminierung unbekannter Variablen aus einer Gleichung oder Matrix bekannt) zum Lösen von linearen Gleichungssystemen ist eine klassische Methode zum Lösen eines Systems algebraische Gleichungen(SLAU). Diese klassische Methode wird auch verwendet, um Probleme wie das Erhalten inverser Matrizen und das Bestimmen des Rangs einer Matrix zu lösen.
Die Transformation nach der Gauß-Methode besteht darin, kleine (elementare) sukzessive Änderungen im System linearer algebraischer Gleichungen vorzunehmen, die zur Eliminierung von Variablen von oben nach unten führen, wobei ein neues dreieckiges Gleichungssystem gebildet wird, das äquivalent ist zu das Original.
Bestimmung 1
Dieser Teil der Lösung wird als Vorwärtsbewegung der Gaußschen Lösung bezeichnet, da der gesamte Prozess von oben nach unten durchgeführt wird.
Nachdem das ursprüngliche Gleichungssystem in ein dreieckiges System gebracht wurde, werden alle Variablen des Systems von unten nach oben gefunden (d. h. die ersten gefundenen Variablen befinden sich genau auf den letzten Zeilen des Systems oder der Matrix). Dieser Teil der Lösung wird auch als umgekehrte Gauß-Lösung bezeichnet. Sein Algorithmus besteht aus folgendem: Zuerst werden die Variablen berechnet, die dem unteren Rand des Gleichungssystems oder einer Matrix am nächsten sind, dann werden die erhaltenen Werte oben ersetzt und somit eine andere Variable gefunden, und so weiter.
Beschreibung des Algorithmus der Gauß-Methode
Die Abfolge der Aktionen zur allgemeinen Lösung des Gleichungssystems nach dem Gauß-Verfahren besteht darin, die Matrix basierend auf dem SLAE abwechselnd mit den Vorwärts- und Rückwärtsstrichen zu beaufschlagen. Das ursprüngliche Gleichungssystem habe die folgende Form:
$\begin(cases) a_(11) \cdot x_1 +...+ a_(1n) \cdot x_n = b_1 \\ ... \\ a_(m1) \cdot x_1 + a_(mn) \cdot x_n = b_m \end(cases)$
Um SLAE nach der Gaußschen Methode zu lösen, ist es notwendig, das anfängliche Gleichungssystem in Form einer Matrix aufzuschreiben:
$A = \begin(pmatrix) a_(11) & … & a_(1n) \\ \vdots & … & \vdots \\ a_(m1) & … & a_(mn) \end(pmatrix)$, $b =\begin(pmatrix) b_1 \\ \vdots \\ b_m \end(pmatrix)$
Die Matrix $A$ wird als Hauptmatrix bezeichnet und stellt die Koeffizienten der Variablen dar, die der Reihe nach geschrieben sind, und $b$ wird als Spalte ihrer freien Elemente bezeichnet. Die durch die Zeile geschriebene Matrix $A$ mit einer Spalte freier Terme heißt erweiterte Matrix:
$A = \begin(array)(ccc|c) a_(11) & … & a_(1n) & b_1 \\ \vdots & … & \vdots & ...\\ a_(m1) & … & a_( mn) & b_m \end(array)$
Nun ist es notwendig, es durch elementare Transformationen über das Gleichungssystem (oder über die Matrix, wie es bequemer ist) auf die folgende Form zu bringen:
$\begin(cases) α_(1j_(1)) \cdot x_(j_(1)) + α_(1j_(2)) \cdot x_(j_(2))...+ α_(1j_(r)) \cdot x_(j_(r)) +... α_(1j_(n)) \cdot x_(j_(n)) = β_1 \\ α_(2j_(2)) \cdot x_(j_(2)). ..+ α_(2j_(r)) \cdot x_(j_(r)) +... α_(2j_(n)) \cdot x_(j_(n)) = β_2 \\ ...\\ α_( rj_(r)) \cdot x_(j_(r)) +... α_(rj_(n)) \cdot x_(j_(n)) = β_r \\ 0 = β_(r+1) \\ … \ \ 0 = β_m \end(cases)$ (1)
Die aus den Koeffizienten des transformierten Gleichungssystems (1) erhaltene Matrix wird Stufenmatrix genannt, so sehen Stufenmatrizen üblicherweise aus:
$A = \begin(array)(ccc|c) a_(11) & a_(12) & a_(13) & b_1 \\ 0 & a_(22) & a_(23) & b_2\\ 0 & 0 & a_(33) & b_3 \end(array)$
Diese Matrizen sind durch die folgenden Eigenschaften gekennzeichnet:
- Alle seine Null-Zeilen kommen nach Nicht-Null-Zeilen
- Wenn eine Zeile der Matrix mit dem Index $k$ ungleich Null ist, dann gibt es in der vorherigen Zeile derselben Matrix weniger Nullen als in dieser Zeile mit dem Index $k$.
Nach dem Erhalten der Schrittmatrix ist es notwendig, die erhaltenen Variablen in die verbleibenden Gleichungen einzusetzen (beginnend am Ende) und die verbleibenden Werte der Variablen zu erhalten.
Grundregeln und erlaubte Transformationen bei der Anwendung der Gauß-Methode
Bei der Vereinfachung einer Matrix oder eines Gleichungssystems mit dieser Methode sollten nur elementare Transformationen verwendet werden.
Solche Transformationen sind Operationen, die auf eine Matrix oder ein Gleichungssystem angewendet werden können, ohne deren Bedeutung zu ändern:
- Stellenweise Permutation mehrerer Zeilen,
- Hinzufügen oder Subtrahieren von einer Zeile der Matrix einer anderen Zeile davon,
- Multiplizieren oder Dividieren einer Zeichenfolge mit einer Konstanten ungleich Null,
- eine Linie, die nur aus Nullen besteht, die bei der Berechnung und Vereinfachung des Systems erhalten wurde, muss gelöscht werden,
- Sie müssen auch unnötige Proportionallinien entfernen und für das System die einzige mit Koeffizienten auswählen, die für weitere Berechnungen geeigneter und bequemer sind.
Alle elementaren Transformationen sind umkehrbar.
Analyse der drei Hauptfälle, die beim Lösen linearer Gleichungen mit der Methode der einfachen Gaußschen Transformationen auftreten
Bei der Anwendung der Gauß-Methode zur Lösung von Systemen treten drei Fälle auf:
- Wenn das System inkonsistent ist, das heißt, es hat keine Lösungen
- Das Gleichungssystem hat eine Lösung, und die einzige, und die Anzahl der Zeilen und Spalten ungleich Null in der Matrix ist gleich.
- Das System hat eine bestimmte Anzahl oder Menge möglicher Lösungen, und die Anzahl der Zeilen darin ist kleiner als die Anzahl der Spalten.
Lösungsergebnis mit inkonsistentem System
Für diese Variante ist es typisch, beim Lösen der Matrixgleichung nach der Gauß-Methode eine Linie mit der Unmöglichkeit zu erhalten, die Gleichheit zu erfüllen. Wenn also mindestens eine falsche Gleichheit auftritt, haben das resultierende und das ursprüngliche System keine Lösungen, unabhängig von den anderen Gleichungen, die sie enthalten. Ein Beispiel für eine inkonsistente Matrix:
$\begin(array)(ccc|c) 2 & -1 & 3 & 0 \\ 1 & 0 & 2 & 0\\ 0 & 0 & 0 & 1 \end(array)$
In der letzten Zeile erschien eine nicht erfüllte Gleichheit: $0 \cdot x_(31) + 0 \cdot x_(32) + 0 \cdot x_(33) = 1$.
Ein Gleichungssystem, das nur eine Lösung hat
Die Daten des Systems nach Reduktion auf eine Stufenmatrix und Streichung von Zeilen mit Nullen haben in der Hauptmatrix die gleiche Zeilen- und Spaltenzahl. Hier das einfachste Beispiel so ein System:
$\begin(cases) x_1 - x_2 = -5 \\ 2 \cdot x_1 + x_2 = -7 \end(cases)$
Schreiben wir es in Form einer Matrix:
$\begin(array)(cc|c) 1 & -1 & -5 \\ 2 & 1 & -7 \end(array)$
Um die erste Zelle der zweiten Zeile auf Null zu bringen, multiplizieren wir die obere Zeile mit $-2$ und subtrahieren sie von der unteren Zeile der Matrix und lassen die obere Zeile in ihrer ursprünglichen Form, als Ergebnis haben wir Folgendes :
$\begin(array)(cc|c) 1 & -1 & -5 \\ 0 & 3 & 10 \end(array)$
Dieses Beispiel kann als System geschrieben werden:
$\begin(cases) x_1 - x_2 = -5 \\ 3 \cdot x_2 = 10 \end(cases)$
Der folgende Wert von $x$ ergibt sich aus der unteren Gleichung: $x_2 = 3 \frac(1)(3)$. Setzen wir diesen Wert in die obere Gleichung ein: $x_1 – 3 \frac(1)(3)$, erhalten wir $x_1 = 1 \frac(2)(3)$.
Ein System mit vielen Lösungsmöglichkeiten
Dieses System zeichnet sich durch eine geringere Anzahl signifikanter Zeilen als die Anzahl der darin enthaltenen Spalten aus (die Zeilen der Hauptmatrix werden berücksichtigt).
Variablen in einem solchen System werden in zwei Typen unterteilt: einfach und frei. Bei der Transformation eines solchen Systems müssen die darin enthaltenen Hauptvariablen im linken Bereich vor dem „=“-Zeichen belassen und die restlichen Variablen auf die rechte Seite der Gleichheit übertragen werden.
Ein solches System hat nur eine bestimmte allgemeine Lösung.
Analysieren wir das folgende Gleichungssystem:
$\begin(cases) 2y_1 + 3y_2 + x_4 = 1 \\ 5y_3 - 4y_4 = 1 \end(cases)$
Schreiben wir es in Form einer Matrix:
$\begin(array)(cccc|c) 2 & 3 & 0 & 1 & 1 \\ 0 & 0 & 5 & 4 & 1 \\ \end(array)$
Unsere Aufgabe ist es, eine allgemeine Lösung für das System zu finden. Für diese Matrix sind die Basisvariablen $y_1$ und $y_3$ (für $y_1$ - da es an erster Stelle steht, und im Fall von $y_3$ - es befindet sich nach Nullen).
Als Basisvariablen wählen wir genau die, die in der Zeile an erster Stelle ungleich Null sind.
Die verbleibenden Variablen werden als frei bezeichnet, durch sie müssen wir die grundlegenden ausdrücken.
Mit dem sogenannten Reverse Move zerlegen wir das System von unten nach oben, dazu drücken wir zunächst $y_3$ aus der untersten Zeile des Systems aus:
$5y_3 – 4y_4 = 1$
$5y_3 = 4y_4 + 1$
$y_3 = \frac(4/5)y_4 + \frac(1)(5)$.
Nun setzen wir das ausgedrückte $y_3$ in die obere Gleichung des Systems $2y_1 + 3y_2 + y_4 = 1$ ein: $2y_1 + 3y_2 - (\frac(4)(5)y_4 + \frac(1)(5)) + y_4 = 1$
Wir drücken $y_1$ durch die freien Variablen $y_2$ und $y_4$ aus:
$2y_1 + 3y_2 - \frac(4)(5)y_4 - \frac(1)(5) + y_4 = 1$
$2y_1 = 1 - 3y_2 + \frac(4)(5)y_4 + \frac(1)(5) - y_4$
$2y_1 = -3y_2 - \frac(1)(5)y_4 + \frac(6)(5)$
$y_1 = -1,5x_2 – 0,1y_4 + 0,6$
Die Lösung ist fertig.
Beispiel 1
Lösen Sie den Sumpf mit der Gaußschen Methode. Beispiele. Ein Beispiel für die Lösung eines linearen Gleichungssystems, das durch eine 3-mal-3-Matrix mit der Gauß-Methode gegeben ist
$\begin(cases) 4x_1 + 2x_2 - x_3 = 1 \\ 5x_1 + 3x_2 - 2x^3 = 2\\ 3x_1 + 2x_2 - 3x_3 = 0 \end(cases)$
Wir schreiben unser System in Form einer erweiterten Matrix:
$\begin(array)(ccc|c) 4 & 2 & -1 & 1 \\ 5 & 3 & -2 & 2 \\ 3 & 2 & -3 & 0\\ \end(array)$
Jetzt müssen wir der Einfachheit halber die Matrix so transformieren, dass sich $1$ in der oberen Ecke der letzten Spalte befindet.
Fügen Sie dazu die Zeile aus der Mitte multipliziert mit $-1$ zur 1. Zeile hinzu und schreiben Sie die mittlere Zeile selbst so, wie sie ist:
$\begin(array)(ccc|c) -1 & -1 & 1 & -1 \\ 5 & 3 & -2 & 2 \\ 3 & 2 & -3 & 0\\ \end(array)$
$\begin(array)(ccc|c) -1 & -1 & 1 & -1 \\ 0 & -2 & 3 & -3 \\ 0 & -1 & 0 & -3\\ \end(array) $
Multiplizieren Sie die oberste und die letzte Reihe mit $-1$ und tauschen Sie die letzte und die mittlere Reihe aus:
$\begin(array)(ccc|c) 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & -2 & 3 & -3\\ \end(array)$
$\begin(array)(ccc|c) 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 3 & 3\\ \end(array)$
Und teilen Sie die letzte Zeile durch $3$:
$\begin(array)(ccc|c) 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 1\\ \end(array)$
Wir erhalten das folgende Gleichungssystem, das dem ursprünglichen entspricht:
$\begin(cases) x_1 + x_2 – x_3 = 1\\ x_2 = 3 \\ x_3 = 1 \end(cases)$
Aus der oberen Gleichung drücken wir $x_1$ aus:
$x1 = 1 + x_3 - x_2 = 1 + 1 - 3 = -1$.
Beispiel 2
Ein Beispiel für die Lösung eines Systems, das mit einer 4-mal-4-Matrix unter Verwendung der Gauß-Methode definiert ist
$\begin(array)(cccc|c) 2 & 5 & 4 & 1 & 20 \\ 1 & 3 & 2 & 1 & 11 \\ 2 & 10 & 9 & 7 & 40\\ 3 & 8 & 9 & 2 & 37 \\ \end(array)$.
Am Anfang tauschen wir die oberen Zeilen danach aus, um $1$ in der oberen linken Ecke zu erhalten:
$\begin(array)(cccc|c) 1 & 3 & 2 & 1 & 11 \\ 2 & 5 & 4 & 1 & 20 \\ 2 & 10 & 9 & 7 & 40\\ 3 & 8 & 9 & 2 & 37 \\ \end(array)$.
Jetzt multiplizieren wir die oberste Zeile mit $-2$ und addieren zur 2. und zur 3. Zeile. Zur 4. fügen wir die 1. Zeile hinzu, multipliziert mit $-3$:
$\begin(array)(cccc|c) 1 & 3 & 2 & 1 & 11 \\ 0 & -1 & 0 & -1 & -2 \\ 0 & 4 & 5 & 5 & 18\\ 0 & - 1 & 3 & -1 & 4 \\ \end(array)$
Jetzt fügen wir zu Zeile 3 Zeile 2 multipliziert mit $4$ hinzu, und zu Zeile 4 fügen wir Zeile 2 multipliziert mit $-1$ hinzu.
$\begin(array)(cccc|c) 1 & 3 & 2 & 1 & 11 \\ 0 & -1 & 0 & -1 & -2 \\ 0 & 0 & 5 & 1 & 10\\ 0 & 0 & 3 & 0 & 6 \\ \end(array)$
Multipliziere Zeile 2 mit $-1$, dividiere Zeile 4 durch $3$ und ersetze Zeile 3.
$\begin(array)(cccc|c) 1 & 3 & 2 & 1 & 11 \\ 0 & 1 & 0 & 1 & 2 \\ 0 & 0 & 1 & 0 & 2\\ 0 & 0 & 5 & 1 & 10 \\ \end(array)$
Jetzt addieren wir zur letzten Zeile die vorletzte, multipliziert mit $-5$.
$\begin(array)(cccc|c) 1 & 3 & 2 & 1 & 11 \\ 0 & 1 & 0 & 1 & 2 \\ 0 & 0 & 1 & 0 & 2\\ 0 & 0 & 0 & 1 & 0 \\ \end(array)$
Wir lösen das resultierende Gleichungssystem:
$\begin(cases) m = 0 \\ g = 2\\ y + m = 2\ \ x + 3y + 2g + m = 11\end(cases)$