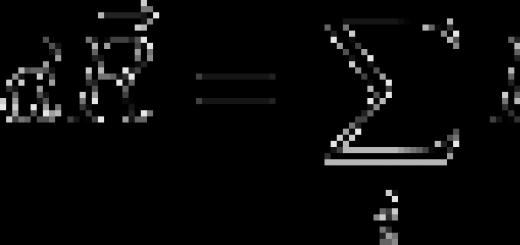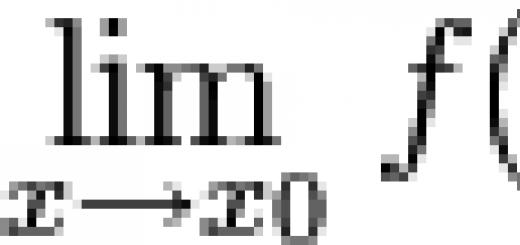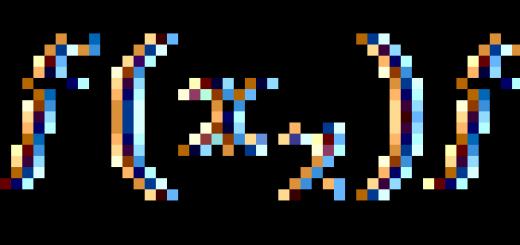Berechnung von Stäben bei exzentrischer Druck-Zug-Beanspruchung

Beispiel 1

Gusseisen kurz Die Stange wird durch eine Längskraft zusammengedrückt F= 600 kN an der Stelle aufgebracht BEIM.

Erforderlich:

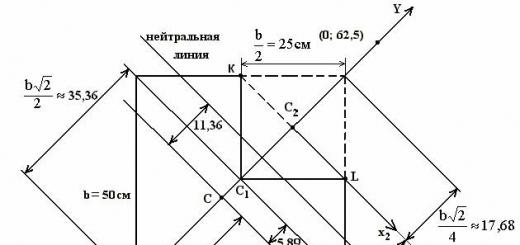
1. Bestimmen Sie die Position der neutralen Linie;

2. Berechnen Sie die größten Zug- und größten Druckspannungen.

Entscheidung.

1. Zeichnen Sie den Schnitt maßstabsgetreu.

2. Bestimmen Sie die Position der Hauptmittelachsen. Der Schnitt hat eine Symmetrieachse, also die Achse Y können wir Ihnen gleich zeigen.

3. Bestimmen Sie die Position des Schwerpunkts der Figur (die Figur besteht aus zwei Quadraten). Wir wählen ein beliebiges Hilfskoordinatensystem.

x 1 C 1 J– Hilfskoordinatensystem;

bestimme die Koordinaten der Punkte Mit 1 und Mit 2 im System x 1 C 1 J.

SONDERN 1 , SONDERN 2 ist die Fläche des ersten bzw. zweiten Quadrats.

A \u003d A 1 - A 2 ist die Fläche der ganzen Figur.

SONDERN 1 = b 2 \u003d 2500 cm 2

Mit (X c = 0; beim c = -5,89) - die Position des Schwerpunkts im Hilfskoordinatensystem x 1 C 1 J.

Achse X senkrecht zur Achse zeichnen Y durch einen Punkt Mit.

Da ist der Schnitt also symmetrisch XC Y ist das wichtigste zentrale Koordinatensystem.

4. Bestimmen Sie die zentralen Hauptträgheitsmomente und die Quadrate der Hauptradien des Abschnitts.

wo a 1 \u003d 5,89 cm - Abstand zwischen den Achsen X und X 1 ;

a 2 \u003d 5,89 + 17,68 \u003d 23,57 - Abstand zwischen den Achsen X und X 2 .

5. Bestimmen Sie die Koordinaten des Punktes BEIM(Kraftangriffspunkte) im zentralen Hauptkoordinatensystem x mit Su mit.

6. Bestimmen Sie die Position der neutralen Linie.

,

wo X N, beim N - Koordinaten der Punkte der neutralen Linie.

Bei dieser Aufgabe

Die neutrale Linie verläuft durch den Punkt ( X N=0;beim N = 11,36) parallel zur Achse X mit.

7. Bei dieser Aufgabe wirkt eine Druckkraft auf den Stab, sodass die Normalspannungen an jedem Punkt des Querschnitts durch die Formel bestimmt werden

wo x, y sind die Koordinaten des Punktes, an dem die Spannungen berechnet werden.

8. An der Stelle werden die größten Druckspannungen erreicht BEIM. Dies ist der Punkt, der am weitesten von der neutralen Linie im Kompressionsbereich entfernt ist.

An den Stellen werden die größten Zugspannungen erreicht Zu und Lj K = beim L = 23,57 cm.

Antworten: ,

Beispiel 2

Erstellen Sie einen Abschnittskern.

Entscheidung.

1. Bestimmen Sie die Art der Kontur des Schnittkerns.

2. Wir bestimmen die Anzahl der Eckpunkte des innerhalb der Kontur erhaltenen Polygons (dh die Anzahl der Grenztangenten zum Querschnitt der Stange). 6 Grenztangenten - 6 Eckpunkte.

3. Bestimmen Sie die Position der Hauptmittelachsen. Der Schnitt hat eine horizontale Symmetrieachse, also die Achse " X Wir können sofort zeigen. XOY 0 - Hilfskoordinatensystem (Achse " Y 0 "wir geben willkürlich aus).

Der Abschnitt besteht aus zwei einfachen Formen (Rechteck und Quadrat). Bestimmen Sie die Koordinaten der Schwerpunkte Mit 1 und Mit 2 in einem beliebigen Koordinatensystem XOY 0 .

Der Schwerpunkt des Rechtecks.

Der Schwerpunkt des Quadrats.

Die Fläche des Rechtecks.

Quadratischer Bereich.

(als Mit 1 und Mit 2 liegen auf der Achse).

Der Schwerpunkt des gesamten Abschnitts im Koordinatensystem XOY 0 hat Koordinaten Mit(0,015; 0). (Wir werden in der Zeichnung zeigen).

Achse Y senkrecht zur Achse zeichnen Y 0 durch den Schwerpunkt Mit.

Da der Schnitt symmetrisch ist, bilden die Symmetrieachse und die dazu senkrechte Achse, die durch den Schwerpunkt verläuft, das zentrale Hauptkoordinatensystem.

X, Y sind die zentralen Hauptachsen des Abschnitts.

4. Wir bestimmen die geometrischen Eigenschaften des Abschnitts relativ zu den Hauptmittelachsen.

Wir berechnen die wichtigsten zentralen Trägheitsmomente J x und J y .

Zentrale Hauptträgheitsmomente eines Rechtecks.

Zentrale Hauptträgheitsmomente eines Quadrats.

(Hier wurden Formeln verwendet, um die Trägheitsmomente um parallele Achsen zu bestimmen. Axiale Trägheitsmomente eines ebenen Schnitts um beliebige Achsen X 1 und beim 1 parallel zu den Mittelachsen X und beim, bestimmt durch die Formeln

;

wo a,b– Achsabstand X und X 1 , beim und beim 1 , SONDERN- Querschnittsfläche. das wird akzeptiert x, y– Mittelachsen, d. h. durch den Schwerpunkt verlaufende Achsen Mit flacher Abschnitt).

Berechnen Sie die Quadrate der Hauptträgheitsradien

5. Bestimmen Sie die Eckpunkte des Kerns des Abschnitts.

Lassen Sie die Position der neutralen Linie bekannt sein. Es ist erforderlich, die Koordinaten des Kraftangriffspunktes zu bestimmen.

1. Betrachten Sie die Position des Neutralleiters 1 - 1.

Verwenden Sie die Eigenschaft der neutralen Linie. Da die neutrale Linie 1-1 parallel zur Achse verläuft Y, dann der Angriffspunkt der Kraft ich 1 liegt auf der Achse X, also beim F=0.

X N - Abszisse des Punktes der neutralen Linie 1 - 1 (Entfernung vom Punkt Mit zum Neutralleiter 1 - 1).

2. Betrachten Sie die Position der neutralen Linie 2 - 2.

Nehmen Sie zwei Punkte der neutralen Linie 2 - 2 (es ist besser, Punkte zu wählen, an denen Sie die Koordinaten leicht berechnen können)

BEIM(-0,615; 0,3) und D(-0,015; 0,6)

Ersetzen Sie die Koordinaten der Punkte BEIM und D in die neutrale Liniengleichung.

(1)

(2)

Lösen wir das Gleichungssystem (1) - (2)

Aus der ersten Gleichung

(3)

(3) durch (2) ersetzen

3. Betrachten Sie die Position der neutralen Linie 3 - 3.

Verwenden Sie die Eigenschaft der neutralen Linie. Da die neutrale Linie 3 - 3 parallel zur Achse verläuft X, dann der Angriffspunkt der Kraft ich 3 liegt auf der Achse Y, also X F =0.

beim N - Ordinate des Punktes der neutralen Linie 3 - 3 (Entfernung vom Punkt Mit zum Neutralleiter 3 - 3).

4. Betrachten Sie die Position der neutralen Linie 4 - 4.

Verwenden Sie die Eigenschaft der neutralen Linie. Da die neutrale Linie 4 - 4 parallel zur Achse verläuft Y, dann der Angriffspunkt der Kraft ich 4 liegt auf der Achse X, also beim F = 0.

Beispiel3 .

Ein starrer Stab wird mit zwei Kräften belastet - Zug und Druck (Abb. 1). Der Stab besteht aus einem spröden Material mit den Eigenschaften und . Der Querschnitt des Stabes ist symmetrisch und hat die Form und Abmessungen entsprechend Abb. 2.

Erforderlich:

1) Finden Sie die zulässige Belastung der Stange aus dem Festigkeitszustand, wenn das Verhältnis von Druck- und Zugkräften ist

2) Bauen Sie den Kern des Abschnitts auf.

Abb.1Abb.2

Entscheidung.

Die Position der zentralen Hauptträgheitsachsen und die Trägheitsmomente um diese Achsen eines bestimmten Abschnitts wurden früher gefunden (siehe Abschnitt "Geometrische Eigenschaften von flachen Abschnitten"). Lassen Sie uns die inneren Kräfte in einem beliebigen Abschnitt der Stange finden:

Um die Position gefährlicher Punkte zu bestimmen, konstruieren wir eine neutrale Linie. Neutrale Liniengleichung in diesem Problem hat die Form

Von hier aus finden wir die Segmente, die durch die neutrale Linie auf den Achsen und abgeschnitten sind. Wenn, dann

und wenn, dann

Die neutrale Linie ist in Abb. 1 dargestellt. 3.

Abb. 3

Zeichnen Sie Tangenten an die Kontur des Abschnitts, parallel zur neutralen Linie. Punkt 1 und 1 sind gefährlich ¢ (siehe Abb. 3), die am weitesten von der neutralen Linie entfernt ist. Bei einem spröden Material ist die Stelle mit den höchsten Zugspannungen gefährlicher, d.h. Punkt 1. Ermitteln Sie die Spannung an diesem Punkt, indem Sie sie in die Formel einsetzen Punkt 1 Koordinaten:

Festigkeitszustand unter Punkt 1. Or

Hier finden Sie den zulässigen Belastungswert (vergessen Sie nicht, die Maßeinheiten richtig zu ersetzen. Multiplikator vorher F p hat in diesem Beispiel die Dimension cm -2).

Abschließend ist darauf hinzuweisen, dass bei Punkt 1 ¢ , der in diesem Beispiel weiter von der neutralen Achse entfernt ist als der Punkt 1, und in dem Druckspannungen wirken, ist auch die Festigkeitsbedingung erfüllt, d.h.

Lassen Sie uns nun den Kernel des Abschnitts erstellen. Wir platzieren die Stangen an den äußeren Eckpunkten des Abschnitts. Angesichts der Symmetrie des Abschnitts reicht es aus, die Stangen an drei Punkten zu platzieren: 1, 2 und 3 (siehe Abb. 3). Einsetzen in Formeln ; die Koordinaten der Pole finden wir die Segmente abgeschnitten durch neutrale Linien auf den Achsen und . Wenn sich der Pol an Punkt 1 befindet, dann seine Koordinaten und

Die neutrale Linie 1–1, die dem Pol an Punkt 1 entspricht, ist in Abb. 1 dargestellt. 3. Auf ähnliche Weise bauen wir die neutralen Linien 2-2 und 3-3, die den Polen 2 und 3 entsprechen. Achten Sie beim Bau einer neutralen Linie darauf, dass sie im entgegengesetzten Quadranten zu dem verläuft, in dem sich der Pol befindet. Der schraffierte Bereich in Abb. 3 ist der Kern des Abschnitts. Zur Steuerung in Abb. 3 zeigt die Trägheitsellipse. Der Kern des Abschnitts muss innerhalb der Trägheitsellipse liegen, ohne sie irgendwo zu kreuzen.

Beispiel 4

Ein Stab mit asymmetrischem Querschnitt wird durch eine punktuell aufgebrachte Kraft zusammengedrückt SONDERN (Abb. 1). Der Querschnitt hat die in Abb. 1 gezeigte Form und Abmessungen. 2. Das Material der Stange ist spröde.

Erforderlich:

1) Finden Sie die zulässige Last, die die Festigkeitsbedingung erfüllt;

2) Bauen Sie den Kern des Abschnitts auf.

Entscheidung.

Zunächst müssen die Trägheitsmomente und Trägheitsradien des Querschnitts relativ zu den Hauptmittelachsen bestimmt werden. Dieser Teil der Lösung des Problems ist im Abschnitt "Geometrische Eigenschaften von Flachprofilen" angegeben. Auf Abb. 1 zeigt die zentralen Hauptträgheitsachsen des Abschnitts , , dessen Position früher gefunden wurde. Im System der zentralen Achsen Ja,Z(Abb. 2) Koordinaten des Kraftangriffspunktes SONDERN , . Berechnen Sie die Koordinaten des Punktes SONDERN im System der Hauptmittelachsen gemäß den Formeln

.

Abb.1Abb.2

Um die Position gefährlicher Punkte zu bestimmen, konstruieren wir eine neutrale Linie mit den Formeln ; . Trägheitsradien, früher gefunden.

Lassen Sie uns diese Segmente entlang der Hauptachsen legen und eine neutrale Linie durch die erhaltenen Punkte ziehen (siehe Abb. 3).

Abb. 3

Gefahrenstellen, d.h. die am weitesten von der neutralen Achse entfernten Punkte sind die Punkte 1 und 3 (siehe Abb. 3). Am Punkt 1 wirkt die größte Zugspannung. Den Festigkeitszustand schreiben wir an dieser Stelle mit der Formel :

Setzen wir die Koordinaten des gefährlichen Punktes 1 in den Hauptachsen in die Festigkeitsbedingung ein und berechnen sie mit den Formeln

oder durch Aufmaß nach maßstäblicher Zeichnung, Dann können Sie aus dem Festigkeitszustand unter Punkt 1 den zulässigen Belastungswert ermitteln:

.

Für den gefundenen Wert der zulässigen Belastung ist darauf zu achten, dass die Festigkeitsbedingung auch am Punkt 3 erfüllt ist, der weiter von der Neutrallinie entfernt ist und in dem die Druckspannung wirkt. Um die Spannung am Punkt 3 zu bestimmen, setzen wir die Koordinaten dieses Punktes in die Formel ein

.

Diese Spannung sollte nicht überschreiten. Wenn der Festigkeitszustand an der Stelle mit den höchsten Druckspannungen nicht erfüllt ist, muss aus dem Festigkeitszustand an dieser Stelle der Wert der zulässigen Belastung wieder ermittelt werden.

Abschließend konstruieren wir den Kern des Abschnitts. Wir platzieren die Stangen an den äußeren Eckpunkten des Abschnitts, d.h. an den Punkten 1, 2, 3, 4, 5 (siehe Abb. 3). Punkt 4, der sich auf der Kontur des Kreisquadranten befindet, wurde wie folgt erhalten. Schneiden wir den inneren Eckpunkt ab, ziehen wir eine Tangente an die Schnittkontur (gestrichelte Linie in Abb. 3). Punkt 4 ist der Punkt, an dem diese Linie den Quadranten des Kreises berührt. Wir finden nacheinander die Position der neutralen Linien, die den Polen an den angegebenen Punkten entsprechen, und finden die Segmente, die von den neutralen Linien auf den Achsen , abgeschnitten sind, gemäß den Formeln ; .Zum Beispiel, wenn der Pol an Punkt 1 ist, dann ersetzen Sie in ; Koordinaten von Punkt 1 (), finden

Da sie viel größer ist, bedeutet dies, dass die neutrale Linie 1–1 praktisch parallel zur Achse ist. Wir zeichnen das Segment auf einer Skala entlang der Achse und zeichnen eine gerade Linie 1–1 parallel zur Achse (siehe Abb. 3). In ähnlicher Weise bauen wir neutrale Linien, die den an anderen Punkten befindlichen Polen entsprechen. Der Kern des Abschnitts (schattierter Bereich) ist in Abb. 1 dargestellt. 3. Beachten Sie, dass die Kontur des Kerns des Abschnitts zwischen den neutralen Linien 4–4 und 5–5 entlang einer Kurve umrissen ist, da der Übergang des Pols von Punkt 4 zu Punkt 5 erfolgt nicht geradlinig. Auf Abb. 3 zeigt auch die Trägheitsellipse des Abschnitts, der früher gebaut wurde.

Beispiel 5

Auf einem Balken mit einem bestimmten Querschnitt an einem Punkt D am oberen Ende gibt es eine Längsdruckkraft R=300 kN (siehe Abbildung). Es ist erforderlich, die Position der Nulllinie zu finden, die größten (Zug- und Druck-) Spannungen zu bestimmen und den Kern des Abschnitts zu konstruieren.

Entscheidung:

1. Ermitteln der Lage der Hauptträgheitsmittelachsen und Bestimmen der Querschnittsfläche

Da der Querschnitt des Balkens (Abb. 1) zwei Symmetrieachsen hat und diese immer durch den Schwerpunkt des Abschnitts verlaufen und die Hauptachsen sind, dann die Hauptmittelachsen des Abschnitts X mit und beim c fällt mit diesen Symmetrieachsen zusammen.

Schwerpunkt des Abschnitts Mit In diesem Fall ist eine Bestimmung nicht erforderlich, da sie mit dem geometrischen Mittelpunkt des Abschnitts zusammenfällt.

Die Querschnittsfläche des Balkens ist gleich:

2. Bestimmung der zentralen Hauptträgheitsmomente und der Hauptträgheitsradien

Die Trägheitsmomente werden durch die Formeln bestimmt:

Wir berechnen die Quadrate der Hauptträgheitsradien:

3. Bestimmen der Position der Nulllinie

Die von der Nulllinie auf den Hauptträgheitsmittelachsen abgeschnittenen Segmente werden durch die Formeln bestimmt:

wo x S= 2,3 cm und y r\u003d 2 cm - Koordinaten des Kraftangriffspunkts R(Punkt P Abb.11). Legen Sie die Segmente beiseite bzw. auf die Achsen x s und uns und durch Ziehen einer geraden Linie durch ihre Enden erhalten wir eine Null-Schnittlinie, auf der die Normalspannungen gleich Null sind (). In Fig. 1 ist diese Linie mit n-n gekennzeichnet.

4. Ermittlung der höchsten Druck- und Zugspannungen und Erstellung eines Spannungsdiagramms

Punkt D , dessen Koordinaten X D = 5,25 cm und beim D\u003d 5 cm, am weitesten von der Nulllinie in der komprimierten Zone des Abschnitts entfernt, daher treten darin die größten Druckspannungen auf und werden durch die Formel bestimmt

Die größten Zugspannungen treten am Punkt K auf, der Koordinaten hat x k= -5,25 cm, bei k= -5 cm.

Basierend auf den erhaltenen Werten erstellen wir ein Diagramm der Normalspannungen (siehe Abb. 11).

5. Konstruktion des Abschnittskerns

Um den Kern des Abschnitts zu konstruieren, berücksichtigen Sie, dass der Abschnitt symmetrisch ist, zwei Positionen der Tangente an die Kontur des Abschnitts I-I und II-II (siehe Abb. 1).

Durch die Tangente I -I abgeschnittene Segmente auf den Koordinatenachsen sind gleich:

Die Koordinaten des Randpunktes 1 des Querschnittskerns werden durch die Formeln bestimmt:

Tangente II-II schneidet Segmente ab = 5,25 cm, = ¥ .

Grenzpunktkoordinaten 2 :

Die Koordinaten der Randpunkte der zweiten Hälfte des Querschnittskerns dürfen nicht bestimmt werden, da der Querschnitt des Balkens symmetrisch ist. Berücksichtigt man dabei für die Tangenten III-III und IV-IV die Koordinaten der Randpunkte 3 und 4 wird sein:

= 0; = 15,2× 10 -3 m;

=23,0× 10 -3 m = 0.

Wenn wir die Punkte 1, 2, 3 und 4 in Reihe mit geraden Linien verbinden, erhalten wir den Kern des Abschnitts (Abb. 1).

Beispiel 6

Bestimmen Sie in dem in der Abbildung angegebenen Abschnitt, der zu einer exzentrisch komprimierten Säule gehört, die gefährlichsten Punkte und die Spannungen in ihnen. Druckkraft F= 200 kN = 20 t punktuell aufgebracht EIN.

Entscheidung.

Da die X- und Y-Achsen die Symmetrieachsen sind, sind sie die Hauptmittelachsen.

Die gefährlichsten Punkte werden die Punkte sein, an denen maximal normal Spannung, und dies sind die Punkte, die am weitesten von der Nulllinie entfernt sind. Daher müssen wir zuerst die Position der Nulllinie bestimmen. Wir schreiben die Gleichung der Nulllinie.

In unserem Fall sind die Koordinaten des Kraftangriffspunktes wie folgt (siehe Abb.):

= - 90 mm = - 0,09 m;

= - 60 mm = - 0,06 m.

Die Quadrate der Trägheitsradien und sind wie folgt definiert:

hier und - axiale Trägheitsmomente um die Hauptmittelachsen X und Y.

Ermittlung axialer Trägheitsmomente. Für unseren Abschnitt haben wir:

M4;

M4 .

Die Fläche des gesamten Abschnitts ist gleich:

M2,

und dann die Quadrate der Trägheitsradien:

m2;

m 2.

Mit den Formeln bestimmen wir die Segmente, die die Nulllinie auf den Achsen abschneidet X und Y:

m;

m.

Legen wir diese Segmente auf den Koordinatenachsen beiseite, erhalten wir die Punkte, an denen die Nulllinie die Koordinatenachsen schneidet. Wir ziehen eine gerade Linie durch diese Punkte (siehe Abb.). Wir sehen, dass die am weitesten entfernten Punkte - dies ist Punkt B im Bereich negativer Spannungen und Punkt D im Bereich positiver Spannungen.

Lassen Sie uns die Spannungen an diesen Punkten bestimmen:

;

Anhand der Zeichnung (siehe Abb.) erhalten wir:

= - 0,12 m; = - 0,03 m.

= –5,39× 10 4 kN / m 2 \u003d - 53,9 MPa.

;

0,12m; = 0,03 m.

1,86× 10 4 kN / m 2 \u003d 18,6 MPa.

Beispiel 7

Gusseisen kurzein Stab, dessen Querschnitt in der Figur gezeigt ist, wird durch eine Längskraft zusammengedrückt F, an der Stelle angewendet SONDERN.

Erforderlich:

1) Berechnen Sie die größten Zug- und größten Druckspannungen im Querschnitt, indem Sie die Größe dieser Spannungen durch ausdrücken F und Querschnittsabmessungen; a= 40 mm, b= 60mm;

2) Finden Sie die zulässige Last F bei gegebenen Querschnittsabmessungen und zulässigen Spannungen für Gusseisen für Druck = 100 MPa und für Zug = 30 MPa.

Entscheidung.

Es wurde oben erwähnt, dass die geometrischen Eigenschaften in den Berechnungsformeln relativ zu den Hauptmittelachsen genommen werden, also werden wir den Schwerpunkt des Abschnitts bestimmen. Achse X ist eine Symmetrieachse und geht daher durch den Schwerpunkt, also müssen wir nur ihre Position auf dieser Achse finden. Lassen Sie uns den Abschnitt in zwei Komponenten (1 und 2) teilen und Hilfsachsen auswählen. Mit 1 und Mit 2 in diesen Achsen.

Werde haben Mit 1 (0,0); Mit 2 (0,04; 0), dann:

m;

Also in Achsen xy 1 hat der Schwerpunkt des gesamten Abschnitts Koordinaten Mit (0,0133; 0). Wir zeichnen eine Achse durch den Schwerpunkt des Abschnitts Y senkrecht zur Achse X. X-Achse und Y und werden die zentralen Hauptachsen des Abschnitts sein.

Lassen Sie uns die Position der Nulllinie bestimmen.

Kraftanwendungspunktkoordinaten (points SONDERN) wird wie folgt sein: \u003d (0,02–0,0133) + 0,04 \u003d 0,0467 m; = 0,06 m;

m 4,

m 4,

wo = 0,0133 m;

m 2.

m 2, m2;

und erhalten Sie die von der neutralen Achse abgeschnittenen Segmente auf den Hauptträgheitsachsen X bzw. Y:

Auf der Achse beiseite legen X, und auf der Achse Y und ziehen Sie eine Nulllinie durch die erhaltenen Punkte (siehe Abb.). Wir sehen, dass die am weitesten entfernten Punkte des Abschnitts von der Nulllinie entfernt sind - das ist der Punkt SONDERN in der komprimierten Zone und Punkt BEIM im erweiterten Bereich. Die Koordinaten dieser Punkte lauten wie folgt: SONDERN(0,0467; 0,06); BEIM(-0,0333; -0,12). Lassen Sie uns die Spannungen an diesen Punkten bestimmen und sie in Form von ausdrücken F.

Punktspannung SONDERN darf die zulässige Druckspannung nicht überschreiten , und die Spannung an dem Punkt BEIM darf die zulässige Zugspannung nicht überschreiten, d.h. Bedingungen müssen erfüllt sein:

, ,

oder

(a),

(b).

Von einem):

aus (b):

Um gleichzeitig die Festigkeitsbedingung sowohl in der gestreckten als auch in der komprimierten Zone der Säule zu erfüllen, müssen wir die kleinere der beiden empfangenen als zulässige Last nehmen, d.h. = 103 kN.

Beispiel 8

Gusseisen kurz Ein in der Figur gezeigter Stab mit rechteckigem Querschnitt wird durch eine Längskraft zusammengedrückt F, an der Stelle angewendet SONDERN.

Erforderlich:

1) Berechnen Sie die größten Zug- und größten Druckspannungen im Querschnitt, indem Sie die Größe dieser Spannungen durch ausdrücken F und Querschnittsabmessungen;

2) Finden Sie die zulässige Last F bei gegebenen Querschnittsabmessungen und zulässigen Spannungen für Gusseisen unter Druck und zugfest .

Entscheidung.

Lassen Sie uns die Position der Nulllinie bestimmen. Dazu verwenden wir die Formeln

Die Koordinaten des Kraftangriffspunkts (Punkt A) sind wie folgt:

Die Quadrate der Trägheitsradien werden durch die Formeln bestimmt:

Bestimmen Sie die Segmente, die die Nulllinie auf den Achsen abschneidet X und beim.

Auf der Achse beiseite legen X – X 0 und auf der Achse beim – beim 0 und ziehe eine Nulllinie durch die erhaltenen Punkte n – n(siehe Abb.). Wir sehen, dass die am weitesten entfernten Punkte des Abschnitts Punkt A im komprimierten Bereich und Punkt B im gestreckten Bereich sind. Die Koordinaten dieser Punkte lauten wie folgt: A (0,04; 0,06), B (–0,04; –0,06). Lassen Sie uns die Größe der Spannung an diesen Punkten bestimmen, indem wir sie durch die Kraft ausdrücken F:

Die Spannung am Punkt A sollte die zulässige Druckspannung nicht überschreiten, und die Spannung am Punkt B sollte die zulässige Zugspannung nicht überschreiten, d.h. die Bedingung muss erfüllt sein

Aus dem ersten Ausdruck, dem Wert F

Die Last ist die kleinste der beiden gefundenen, d.h. = 567 kn.

Beispiel 9

Ein kurzer Gusseisenstab mit dem in Abb. a, wird durch eine Längskraft zusammengedrückt P, an der Stelle angewendet EIN. Bestimmen Sie die größten Zug- und größten Druckspannungen im Stabquerschnitt und geben Sie sie in Kraft an P und Querschnittsabmessungen, cm, cm Finden Sie die zulässige Belastung bei gegebenen zulässigen Spannungen für das Material für Druck kN / cm 2 und für Zug kN / cm 2.

Entscheidung.

Auf die Stange wirkende Kraft P Zusätzlich zur Kompression biegt es die Stange relativ zu den Hauptmittelachsen x und j. Die Biegemomente sind jeweils gleich:

wobei cm und cm die Koordinaten des Kraftangriffspunktes sind P(Punktkoordinaten EIN).

Normalspannungen irgendwann mit Koordinaten x und jirgendein Querschnitt des Stabes werden durch die Formel bestimmt

,

wo F ist die Fläche und und sind die Trägheitsradien des Querschnitts.

1. Bestimmen Sie die geometrischen Eigenschaften des Stabquerschnitts.

Die Querschnittsfläche der Stange beträgt:

Die wichtigsten zentralen Trägheitsmomente werden wie folgt bestimmt.

Trägheitsmoment berechnen Gesamt Abschnitt um die Achse x, teilen Sie die ganze Figur in ein Rechteck mit Breite und Höhe und zwei Rechtecke mit Breite und Höhe, so dass die Achse x stand im Mittelpunkt all dieser drei Figuren. Dann

.

Zur Berechnung des Trägheitsmoments des gesamten Abschnitts um die Achse j Lassen Sie uns die ganze Figur ein wenig anders aufteilen: ein Rechteck mit Breite und Höhe und zwei Rechtecke mit Breite und Höhe, so dass jetzt die Achse j stand im Mittelpunkt all dieser drei Figuren. Werden

.

Die Quadrate der Trägheitsradien sind:

; .

2. Bestimmen Sie die Position der Nulllinie.

Die Segmente und , abgeschnitten durch die Nulllinie von den Koordinatenachsen, sind gleich:

cm ; cm.

Nulllinie anzeigen N-N in Abb. b. Die Nulllinie teilt den Querschnitt in zwei Bereiche, von denen einer auf Zug und der andere auf Druck steht. Abbildung 1, b gestreckt Querschnittsfläche des Stabes von uns schattiert.

3. Berechnen Sie das Größte dehnen Stromspannung.

Es tritt an den Punkten auf 6 und 7 , also an den Punkten, die am weitesten von der Nulllinie entfernt sind. Der Wert dieser Spannung wird beispielsweise für einen Punkt berechnet 6 gleich:

4. Berechnen Sie das Größte komprimierend Stromspannung.

Es tritt an den Punkten auf 2 und 3 , auch am weitesten von der Nulllinie entfernt. Der Wert dieser Spannung wird beispielsweise für einen Punkt berechnet 2 , gleich:

5. Bestimmen Sie die zulässige Belastung aus dem Zustand der Zugfestigkeit:

kN/cm2; kN.

6. Bestimmen Sie die zulässige Belastung aus dem Zustand der Druckfestigkeit:

kN/cm2; kN.

der beiden in den Absätzen 6 und 7 gefundenen Werte:

Beispiel 10

Eine kurze Säule, deren Querschnitt in Fig. 1 gezeigt ist, wird durch eine Längskraft zusammengedrückt F= 200 kN an der Stelle angewendet Zu. Abschnittsabmessungen a= 40cm b= 16cm Geschätzte Zugfestigkeit des Materials Rt = 3 MPa, für Kompression R mit = 30 MPa .

Erforderlich:

1. Suchen Sie die Position der Nulllinie.

2. Berechnen Sie die größten Druck- und Zugspannungen und erstellen Sie ein Spannungsdiagramm. Geben Sie eine Schlussfolgerung über die Stärke der Säule.

3. Bestimmen Sie die Bemessungstragfähigkeit (Auslegungslast) F max für vorgegebene Querschnittsgrößen.

4. Konstruieren Sie den Kern des Abschnitts.

Abb.1

Entscheidung.

1. Bestimmung der Koordinaten des Schwerpunkts des Abschnitts.

Der Querschnitt der Säule hat eine Symmetrieachse Xs, daher liegt der Schwerpunkt auf dieser Achse und die Koordinate zu finden x s relativ zur Nebenachse Y o (siehe Abb. 1) teilen wir den komplexen Abschnitt in drei Rechtecke

2. Geometrische Eigenschaften des Abschnitts.

Zur Berechnung der wichtigsten zentralen Trägheitsmomente verwenden wir die Beziehung zwischen den Trägheitsmomenten bei Parallelverschiebung der Achsen.

Bestimmen Sie die Quadrate der Trägheitsradien

Koordinaten des Kraftangriffspunkts F

3. Position der Nulllinie

Gefunden Segmente, die auf den von uns gezeichneten Koordinatenachsen abgeschnitten sind Nulllinie (siehe Abb. 2).

4. Bestimmung der höchsten Druck- und Zugspannungen. Diagramm .

Die am weitesten von der Nulllinie entfernten Punkte: BEIM(-60; 16)undD(60; -32). Betont diese gefährlichen Punkte mit Koordinaten X Dan , j Dan darf den entsprechenden Bemessungswiderstand nicht überschreiten

.

Zugspannung

Druckspannung

Die Festigkeit der Säule ist gewährleistet.

Nach den Ergebnissen der Spannungsberechnung und in Abb. 2 gebautes Diagramm .

5. Berechnung der berechneten Tragfähigkeit der Stütze Fmax .

Da bei einem gegebenen Wert der Druckkraft die Festigkeit des Stützenmaterials deutlich unterausgenutzt wird, finden wir den Maximalwert der äußeren Belastung durch Gleichsetzen der Maximalspannungen s t und s c errechneter Widerstand.

Wählen Sie schließlich einen kleineren Wert Fmax = 425,8 kN, Versehen von sowohl gestreckten als auch komprimierten Querschnittszonen mit Festigkeit.

Abb.2

6. Konstruktion des Abschnittskerns.

Um den Umriss des Kerns des Abschnitts zu erhalten, ist es notwendig, alle möglichen Positionen der Tangenten an die Kontur des Abschnitts zu berücksichtigen und unter der Annahme, dass diese Tangenten Nulllinien sind, die Koordinaten der Randpunkte des Kerns relativ zu berechnen die Hauptmittelachsen des Abschnitts. Wenn wir diese Punkte verbinden, erhalten wir den Umriss des Kerns des Abschnitts.

Tangente 1-1: ja = 32 cm,

.

Tangente 2-2: , .

Tangente 3-3: , .

Tangente 4-4: ; ;

; ;

;

.

Tangente 5-5: ; .

Tangente 6-6: ; ;

Beispiel 11 .

Am Punkt P Angewendete Druckkraft der rechteckigen Säule P(siehe Abb.). Bestimmen Sie die maximalen und minimalen Normalspannungen.

Entscheidung.

Die Normalspannung unter exzentrischer Kompression wird durch die Formel bestimmt:

Bei unserer Aufgabe

Trägheitsmoment, Fläche ,

Somit

Auf der neutralen Linie. Also ihre Gleichung

Die Punkte, die am weitesten von der neutralen Achse entfernt sind, sind die Punkte EIN und B:

am Punkt EIN und

am Punkt B und

Wenn das Material Zug und Druck unterschiedlich widersteht, sollten zwei Festigkeitsgleichungen aufgestellt werden:

Beispiel 12.

Ermitteln Sie die zulässige Belastung für den in der Abbildung gezeigten Träger, wenn die Bemessungswiderstände des Trägermaterials für Zug und Druck gleich sind Radm,t= 20 MPa; Radm, mit= 100 MPa.

Entscheidung. Wir schreiben die Festigkeitsbedingung für die am stärksten beanspruchten Punkte eines beliebigen Balkenabschnitts, da alle Abschnitte gleich gefährlich sind:

Lassen Sie uns diese Bedingungen unter Berücksichtigung dessen umschreiben

und dann

und

Von hier aus ermitteln wir die Werte der zulässigen Belastungen.

Exzentrischer Zug (Druck) wird durch eine Kraft verursacht, die parallel zur Balkenachse verläuft, aber nicht mit ihr zusammenfällt (Abb. 9.4).

Die Projektion des Kraftangriffspunkts auf den Querschnitt wird als Pol oder Kraftpunkt bezeichnet, und die durch den Pol und die Mitte des Querschnitts verlaufende Gerade wird als Kraftlinie bezeichnet.

Exzentrischer Zug (Druck) lässt sich auf Axialzug (Druck) und Schrägbiegung reduzieren, wenn die Kraft P auf den Profilschwerpunkt übertragen wird. Also die Kraft P, markiert in Abb. 9.4 mit einem Strich G verursacht eine axiale Spannung des Balkens, und ein mit zwei Strichen markiertes Kräftepaar verursacht eine schräge Biegung.

Basierend auf dem Prinzip der Unabhängigkeit der Wirkung von Spannungskräften an den Punkten des Querschnitts während exzentrischer Spannung (Kompression) werden sie durch die Formel bestimmt

In dieser Formel sind die Normalkraft, Biegemomente sowie die Koordinaten des Schnittpunktes, an dem die Spannung ermittelt wird, mit ihrem Vorzeichen zu ersetzen. Für Biegemomente nehmen wir die gleiche Vorzeichenregel wie bei Schrägbiegung und betrachten die Normalkraft als positiv, wenn sie Spannung verursacht.

Werden die Koordinaten des Pols mit bezeichnet, so nimmt das Moment Formel (9.5) die Form an

Aus dieser Gleichung ist ersichtlich, dass die Enden der Spannungsvektoren an den Schnittpunkten in der Ebene liegen. Die Schnittlinie der Spannungsebene mit der Querschnittsebene ist eine neutrale Linie, deren Gleichung gefunden wird, indem die rechte Seite der Gleichung (9.6) mit Null gleichgesetzt wird. Nach Reduktion um P erhalten wir

Die neutrale Linie bei außermittigem Zug (Druck) geht also nicht durch den Schwerpunkt des Profils und steht nicht senkrecht auf der Wirkungsebene des Biegemoments. Die neutrale Linie schneidet Segmente auf den Koordinatenachsen ab

Die Trägheitsmomente stellen wir als Produkt aus der Querschnittsfläche und dem Quadrat des entsprechenden Trägheitsradius dar

Dann können Ausdrücke (9.8) wie folgt geschrieben werden:

Aus den Formeln (9.8) ist ersichtlich, dass der Pol und die neutrale Linie immer auf gegenüberliegenden Seiten des Schwerpunkts des Abschnitts liegen und die Position der neutralen Linie durch die Koordinaten des Pols bestimmt wird.

Wenn sich die Stange dem Schwerpunkt des Abschnitts entlang der Kraftlinie nähert, bewegt sich die neutrale Linie von der Mitte weg und bleibt parallel zu ihrer ursprünglichen Richtung. In der Grenze bei tritt die neutrale Linie ins Unendliche zurück. In diesem Fall wird der Balken mittig gespannt (komprimiert).

Auf der Kraftlinie finden Sie immer eine solche Position des Pols, in der die neutrale Linie die Kontur des Abschnitts berührt, ohne sie irgendwo zu kreuzen. Wenn wir alle möglichen neutralen Linien so zeichnen, dass sie die Kontur des Abschnitts berühren, ohne ihn irgendwo zu kreuzen, und die ihnen entsprechenden Pole finden, stellt sich heraus, dass sich die Pole auf einer geschlossenen Linie befinden, die für jeden ganz spezifisch ist Sektion. Der von dieser Linie begrenzte Bereich wird als Kern des Abschnitts bezeichnet. Bei einem kreisförmigen Querschnitt ist der Kern beispielsweise ein Kreis mit einem Durchmesser, der viermal kleiner ist als der Querschnittsdurchmesser, und bei rechteckigen und I-Querschnitten hat der Kern die Form eines Parallelogramms (Abb. 9.5).

Aus der eigentlichen Konstruktion des Kerns des Abschnitts folgt, dass, solange sich der Pol innerhalb des Kerns befindet, die neutrale Linie die Kontur des Abschnitts nicht schneidet und die Spannungen im gesamten Abschnitt das gleiche Vorzeichen haben. Befindet sich der Pol jedoch außerhalb des Kerns, kreuzt die neutrale Linie die Kontur des Abschnitts, und es wirken dann Spannungen unterschiedlichen Vorzeichens im Abschnitt. Dieser Umstand muss bei der Berechnung der außermittigen Stauchung von Zahnstangen aus spröden Werkstoffen berücksichtigt werden. Da spröde Materialien Zugbelastungen schlecht wahrnehmen, ist es wünschenswert, äußere Kräfte auf die Zahnstange so aufzubringen, dass im gesamten Abschnitt nur Druckspannungen wirken. Dazu muss der Angriffspunkt der Resultierenden äußerer Kräfte, die die Zahnstange zusammendrücken, innerhalb des Profilkerns liegen.

Die Festigkeitsberechnung bei außermittigem Zug und Druck erfolgt wie bei Schrägbiegung – entsprechend der Beanspruchung an der gefährlichen Stelle des Querschnitts. Gefährlich ist der Punkt des Abschnitts, der am weitesten von seiner neutralen Linie entfernt ist. In Fällen, in denen an dieser Stelle jedoch eine Druckspannung anliegt und das Strebenmaterial spröde ist, kann die Stelle, an der die Zugspannung am größten ist, gefährlich werden.

Das Spannungsdiagramm wird auf einer Achse senkrecht zur Neutrallinie des Schnitts aufgebaut und durch eine Gerade begrenzt (siehe Abb. 9.4).

Die Festigkeitsbedingung wird wie folgt geschrieben.

Stellen Sie sich einen geraden Stab vor, der am Ende mit parallel zur Achse gerichteten Kräften belastet wird Oh. Die Resultierende dieser Kräfte F an der Stelle angewendet MIT. Im lokalen rechtshändigen Koordinatensystem yOz, die mit den Hauptmittelachsen des Abschnitts zusammenfallen, die Koordinaten des Punktes Mit gleich a und b(Abb. 5.18).

Ersetzen wir die aufgebrachte Last durch ein statisch äquivalentes System von Kräften und Momenten. Dazu übertragen wir die resultierende Kraft F zum Schwerpunkt des Abschnitts Ö und die Stange mit zwei Biegemomenten belasten, die gleich dem Produkt der Kraft T^ auf ihre Arme in Bezug auf die Koordinatenachsen sind: Mff = Fa und Mz = Fb.

Beachten Sie, dass nach der Regel des rechtshändigen Koordinatensystems für den Punkt C, der im ersten Quadranten liegt, die Biegemomente formal wie folgt erhalten werden

Reis. 5.18.Gerader Stab, der am Ende mit parallel zur Achse gerichteten Kräften belastet wirdOh

Schlagzeichen: Meine \u003d Fa und M7 = -Fb. In diesem Fall verursachen im im ersten Viertel liegenden Elementarbereich beide Momente Zugspannungen.

Unter Ausnutzung des Prinzips der Unabhängigkeit der Krafteinwirkung ermitteln wir die Spannungen am aktuellen Punkt des Schnittes mit Koordinaten beim und z von jedem Leistungsfaktor separat. Die Gesamtspannung ergibt sich aus der Summierung aller drei Spannungskomponenten:

Lassen Sie uns die Position der neutralen Achse bestimmen. Dazu setzen wir gemäß Formel (5.69) den Wert der Normalspannung am aktuellen Punkt zu Null:

Als Ergebnis einfacher Transformationen erhalten wir die neutrale Liniengleichung

wo ich ja und i z - Hauptträgheitsradien bestimmt durch Formeln (3.14).

Bei exzentrischem Zug-Druck geht die neutrale Linie also nicht durch den Querschnittsschwerpunkt (Abb. 5.19), was durch das Vorhandensein eines von Null verschiedenen freien Gliedes in Gleichung (5.70) angedeutet wird.

Die maximalen Spannungen treten an den Stellen des Profils auf SONDERN und BEIM, am weitesten von der neutralen Linie entfernt. Lassen Sie uns die Beziehung zwischen den Koordinaten des Kraftangriffspunkts und der Position der neutralen Linie herstellen. Dazu bestimmen wir die Schnittpunkte der Koordinatenachsen durch diese Gerade:

Reis. 5.19.

Die resultierenden Formeln zeigen, dass die Koordinate des Kraftangriffspunktes a und die Koordinate des Schnittpunkts der neutralen Linie der Koordinatenachse Unze(Punkt r 0) haben entgegengesetzte Vorzeichen. Dasselbe gilt für die Mengen b und bei 0 . Somit liegen der Angriffspunkt der resultierenden Kraft und die neutrale Linie auf gegenüberliegenden Seiten des Ursprungs.

Gemäß den erhaltenen Formeln bewegt sich die neutrale Linie von der Mittelzone weg, wenn sich der Kraftangriffspunkt dem Schwerpunkt des Abschnitts nähert. Im Grenzfall (a = b = 0) kommen wir zum zentralen Zug-Druck-Fall.

Es ist von Interesse, die Zone der Krafteinleitung zu bestimmen, in der die Spannungen im Querschnitt das gleiche Vorzeichen haben. Insbesondere bei dehnungsarmen Materialien ist es sinnvoll, gerade in dieser Zone eine Druckkraft aufzubringen, damit in dem Abschnitt nur Druckspannungen wirken. Eine solche Zone um den Schwerpunkt des Abschnitts wird genannt Abschnitt Kern.

Wenn die Kraft im Kern des Abschnitts aufgebracht wird, schneidet die neutrale Linie den Abschnitt nicht. Wird entlang der Grenze des Profilkerns eine Kraft aufgebracht, berührt die neutrale Linie die Profilkontur. Mit Formel (5.71) kann der Kern des Abschnitts bestimmt werden.

Wenn wir die neutrale Linie als Tangente an die Schnittkontur darstellen und alle möglichen Positionen der Tangente und die diesen Positionen entsprechenden Kraftangriffspunkte berücksichtigen, dann umreißen die Kraftangriffspunkte den Kern der Sektion.

Reis. 5.20.

a - Ellipse; 6 - Rechteck

Viele Elemente von Gebäudestrukturen (Säulen, Gestelle, Stützen) stehen unter dem Einfluss von Druckkräften, die nicht im Schwerpunkt des Abschnitts aufgebracht werden. Auf Abb. 12.9 zeigt die Stütze, auf der der Deckenbalken ruht. Wie man sieht, wirkt die Kraft bezüglich der Stützenachse mit einer Exzentrizität e, und damit in einem beliebigen Abschnitt Ah Spalten zusammen mit Längskraft N = -R es gibt ein Biegemoment, dessen Größe gleich ist Betreff. Die exzentrische Spannung (Stauchung) einer Stange ist eine Verformungsart, bei der die Resultierende äußerer Kräfte entlang einer geraden Linie parallel zur Stangenachse wirkt. Im Folgenden werden hauptsächlich Probleme der exzentrischen Kompression betrachtet. Bei außermittiger Spannung ist bei allen angegebenen Berechnungsformeln das Vorzeichen vor der Kraft zu ändern R zum Gegenteil.

Ein Stab beliebigen Querschnitts (Abb. 12.10) sei am Ende mit einer außermittig aufgebrachten Druckkraft belastet R, parallel zur Achse gerichtet Oh. Positiv annehmen

Richtungen der Hauptträgheitsachsen des Profils OU und Unze damit der Kraftangriffspunkt R lag im ersten Viertel der Koordinatenachsen. Wir bezeichnen die Koordinaten des Kraftangriffspunktes R durch y r und z P -

Schnittgrößen in einem beliebigen Stababschnitt sind gleich

Die Minuszeichen der Biegemomente sind darauf zurückzuführen, dass diese Momente im ersten Viertel der Koordinatenachsen eine Stauchung bewirken. Die Werte der Schnittkräfte in diesem Beispiel ändern sich nicht über die Länge der Stange, und daher ist die Verteilung der Spannungen in Abschnitten, die ausreichend vom Ort der Belastung entfernt sind, gleich.

Durch Einsetzen von (12.11) in (12.1) erhalten wir die Formel für Normalspannungen unter exzentrischem Druck:

Diese Formel kann in die Form umgewandelt werden

wo ich, ich- Hauptträgheitsradien des Profils. Dabei

Setzen wir (12.12) o = 0 ein, erhalten wir die Gleichung Nulllinie:

Hier bei 0 und z 0 - Koordinaten der Punkte der Nulllinie (Abb. 12.11). Gleichung (12.14) ist die Gleichung einer Geraden, die nicht durch den Schwerpunkt des Querschnitts geht. Um eine Nulllinie zu zeichnen, finden wir die Punkte ihrer Schnittpunkte mit den Koordinatenachsen. Unter der Annahme in (12.14) sukzessive y 0 = 0 und z0= 0 finden wir

wo ein z und Andy- von der Nulllinie abgeschnittene Segmente auf den Koordinatenachsen (Abb. 12.11).

Lassen Sie uns die Merkmale der Position der Nulllinie unter exzentrischer Kompression feststellen.

• 1. Aus den Formeln (12.15) folgt, dass und bei und ein z haben jeweils entgegengesetzte Vorzeichen y r und z P - Die Nulllinie verläuft also durch die Viertel der Koordinatenachsen, die nicht den Kraftangriffspunkt enthalten (Abb. 12.12).
• 2. Wenn sich der Angriffspunkt der Kraft nähert R in gerader Linie zum Schwerpunkt des Abschnitts die Koordinaten dieses Punktes y r und z P Abnahme. Aus (12.15) folgt, dass in diesem Fall die Beträge der Längen der Segmente und bei und ein z zunehmen, d. h. die Nulllinie bewegt sich vom Schwerpunkt weg und bleibt parallel zu sich selbst (Abb. 12.13). In der Grenze bei Z P = y P = 0 (Kraft wirkt im Schwerpunkt) wird die Nulllinie ins Unendliche verschoben. In diesem Fall sind die Spannungen im Querschnitt konstant und gleich o = -P/F.
• 3. Wenn der Angriffspunkt der Kraft R auf einer der Hauptachsen liegt, ist die Nulllinie parallel zur anderen Achse. Tatsächlich setzt man (12.15) beispielsweise ein y r= 0, das bekommen wir und bei= das heißt, die Nulllinie schneidet die Achse nicht OU(Abb. 12.14).
• 4. Bewegt sich der Angriffspunkt der Kraft entlang einer Geraden, die nicht durch den Schwerpunkt geht, dann dreht sich die Nulllinie um einen bestimmten Punkt. Beweisen wir diese Eigenschaft. Angriffspunkte der Kräfte Rx und R 2, die auf den Koordinatenachsen liegen, entsprechen den achsenparallelen Nulllinien 1-1 und 2-2 (Abb. 12.15), die sich im Punkt schneiden D. Da dieser Punkt zu zwei Nulllinien gehört, ergeben sich die Spannungen an diesem Punkt aus gleichzeitig einwirkenden Kräften Rx und R2 wird gleich null sein. Da jede Kraft R3, deren Angriffspunkt auf einer geraden Linie liegt R ( R 2 , kann

in zwei parallele Komponenten zerlegen, die an den Punkten Pj und angelegt werden R 2, dann folgt daraus, dass die Spannungen an der Stelle liegen D von der Kraft R3 ebenfalls gleich Null sind. Somit entspricht die Nulllinie 3-3 der Stärke R3, geht durch einen Punkt D.

Mit anderen Worten, eine Reihe von Punkten R, auf einer Geraden gelegen R ( R 2 , entspricht einem Linienbündel, das durch einen Punkt verläuft D. Auch die umgekehrte Aussage gilt: Wenn sich die Nulllinie um einen bestimmten Punkt dreht, bewegt sich der Angriffspunkt der Kraft entlang einer Geraden, die nicht durch den Schwerpunkt geht.

Wenn die Nulllinie den Abschnitt kreuzt, dann teilt sie ihn in Druck- und Zugzonen. Wie beim Schrägbiegen folgt aus der Flachschnitthypothese, dass die Spannungen an den von der Nulllinie am weitesten entfernten Stellen ihre größten Werte erreichen. Die Art des Spannungsdiagramms in diesem Fall ist in Abb. 12.16, a.

Liegt die Nulllinie außerhalb des Schnitts, so haben die Spannungen an allen Stellen des Schnitts das gleiche Vorzeichen (Bild 12.16, b).

Beispiel 12.3. Lassen Sie uns ein Diagramm der Normalspannungen in einem beliebigen Abschnitt einer exzentrisch komprimierten rechteckigen Stütze mit Abmessungen erstellen b X h(Abb. 12.17). Die Quadrate der Trägheitsradien des Schnitts nach (12.22) sind

Die von der Nulllinie auf den Koordinatenachsen abgeschnittenen Segmente werden durch die Formeln (12.15) bestimmt:

Setzen Sie nacheinander in (12.12) die Koordinaten der Punkte C und des am weitesten von der Nulllinie entfernten Punktes ein BEIM(Abb. 12.18)

finden

Plot o ist in Abb. 1 gezeigt. 12.18. Die höchsten Druckspannungen im absoluten Wert sind viermal höher als die Spannungen, die bei einer zentralen Krafteinleitung auftreten würden. Außerdem traten im Querschnitt erhebliche Zugspannungen auf. Beachten Sie, dass aus (12.12) folgt, dass im Schwerpunkt (y = z\u003d 0) die Spannungen sind gleich o \u003d -P/F.

Beispiel 12.4. Mit Zugkraft belasteter Ausschnittstreifen R(Abb. 12.19, a). Vergleichen Sie die Spannungen im Schnitt lv, weit genug vom Ende und der Stelle des Schnitts entfernt, mit Spannungen im Abschnitt CD am Ausschnitt.

im Abschnitt AB(Abb. 12.19, b) Gewalt R verursacht zentrale Spannung und die Spannungen sind a = P/F = P/bh.

im Abschnitt CD(Abb. 12.19, in) Kraftlinie R nicht durch den Schwerpunkt des Abschnitts verläuft, und daher tritt eine exzentrische Spannung auf. Indem man das Vorzeichen in Formel (12.12) ins Gegenteil ändert und nimmt y r= 0 erhalten wir für diesen Abschnitt

Nehmen

Nulllinie im Schnitt CD parallel zur Achse OU und kreuzt die Achse Unze auf Distanz ein =-i 2 y /z P- b/ 12. An den Punkten des Abschnitts, die am weitesten von der Nulllinie entfernt sind C(z - -b/ 4) und D(z - b/ 4) Spannungen nach (12.16) sind gleich

Diagramme der Normalspannungen für Abschnitte LV und CD in Abb. gezeigt. 12.19, b, c.

Also trotz der Tatsache, dass der Querschnitt CD hat eine Fläche, die zweimal kleiner ist als der Querschnitt AB, Durch die außermittige Krafteinleitung erhöhen sich die Zugspannungen im geschwächten Bereich nicht um den Faktor zwei, sondern um den Faktor acht. Außerdem treten in diesem Abschnitt erhebliche Druckspannungen auf.

Es sollte beachtet werden, dass die obige Berechnung keine zusätzlichen lokalen Spannungen berücksichtigt, die nahe dem Punkt C aufgrund des Vorhandenseins einer Aussparung auftreten. Diese Spannungen sind abhängig vom Radius der Hinterschneidung (sie nehmen mit abnehmendem Radius zu) und können den gefundenen Wert deutlich überschreiten ein c = 8P/bh. In diesem Fall unterscheidet sich die Art des Spannungsdiagramms in der Nähe von Punkt C erheblich von der linearen. Die Definition lokaler Spannungen (Spannungskonzentration) wird in Kapitel 18 diskutiert.

Viele Baumaterialien (Beton, Mauerwerk usw.) widerstehen einer Dehnung nicht gut. Ihre Zugfestigkeit ist um ein Vielfaches geringer als die Druckfestigkeit. Daher ist das Auftreten von Zugspannungen in Strukturelementen aus solchen Materialien unerwünscht. Damit diese Bedingung erfüllt ist, muss die Nulllinie außerhalb des Schnitts liegen. Andernfalls kreuzt die Nulllinie den Abschnitt und es treten Zugspannungen darin auf. Ist die Nulllinie tangential zur Schnittkontur, so ist die entsprechende Position des Kraftangriffspunktes die Grenze. Gemäß Eigenschaft 2 der Nulllinie bewegt sich die Nulllinie davon weg, wenn sich der Kraftangriffspunkt dem Schwerpunkt des Abschnitts nähert. Der Ort der Grenzpunkte, die verschiedenen Tangenten an die Schnittkontur entsprechen, ist die Grenze Abschnitt Kerne. Der Kern des Profils ist ein konvexer Bereich um den Schwerpunkt herum, der folgende Eigenschaft hat: Liegt der Angriffspunkt der Kraft innerhalb oder am Rand dieses Bereichs, dann wirken an allen Stellen des Profils die Spannungen gleiches Zeichen. Der Kern des Schnitts ist eine konvexe Figur, da die Nulllinien die Hüllkurve der Schnittkontur berühren und nicht kreuzen müssen.

Durch den Punkt SONDERN(Abb. 12.20) Sie können unendlich viele Tangenten (Nulllinien) zeichnen; während nur tangential AC tangential zur Hüllkurve ist und ihr ein bestimmter Punkt der Schnittkernkontur entsprechen muss. Gleichzeitig ist es beispielsweise unmöglich, eine Tangente an das Segment zu ziehen AB Abschnittskontur, da sie den Abschnitt schneidet.

Bauen wir einen Schnittkern für ein Rechteck (Abb. 12.21). Für Tangente 1 - 1 a 7 - b/ 2; a= . Aus (12.15) ergibt sich für den dieser Tangente entsprechenden Punkt 1 z P \u003d -i 2 y / a 7 \u003d -b / 6; y r - 0. Für Tangente 2-2 und y - k / 2; a 7 \u003d ° °, und die Koordinaten von Punkt 2 sind gleich beimR- -h/6; z P - 0. Gemäß Eigenschaft 4 der Nulllinie liegen die Kraftangriffspunkte, die unterschiedlichen Tangenten an den unteren rechten Eckpunkt des Schnitts entsprechen, auf der Geraden 1-2. Die Lage der Punkte 3 und 4 wird aus den Symmetriebedingungen bestimmt. Somit ist der Schnittkern für ein Rechteck eine Raute mit Diagonalen b/3 und AUS.

Um einen Schnittkern für einen Kreis zu bilden, genügt es, eine Tangente zu zeichnen (Abb. 12.22). Dabei a = R; a= °o.

„U U ^^

Betrachtet man das für einen Kreis ich y - J y /F - R / 4, aus (12.15) erhalten wir

Der Schnittkern für einen Kreis ist also ein Kreis mit Radius R/4.

Auf Abb. 12.23, a, 6 Abschnittskerne für einen I-Träger und einen Kanal sind gezeigt. Das Vorhandensein von vier Eckpunkten des Querschnittskerns in jedem dieser Beispiele ist darauf zurückzuführen, dass die Einhüllende der Kontur sowohl für den I-Träger als auch für den Kanal ein Rechteck ist.

Zur Ermittlung der Schnittgrößen ersetzen wir in den Querschnitten des Trägers bei exzentrischem Zug (Druck) das gegebene Kräftesystem durch ein statisch äquivalentes System anderer Kräfte. Nach dem Saint-Venant-Prinzip führt ein solcher Austausch zu keinen Änderungen der Belastungs- und Verformungszustände der Trägerteile, die ausreichend weit vom Ort der Krafteinleitung entfernt sind.

Zunächst übertragen wir den Angriffspunkt der Kraft auf die Achse und wenden an diesem Punkt eine Kraft an, die gleich der Kraft, aber entgegengesetzt gerichtet ist (Abb. 3.2). Um eine Kraft auf der Achse zu hinterlassen, muss zu ihrer Wirkung die Wirkung eines mit zwei Linien markierten Kräftepaares oder eines Moments hinzugefügt werden. Als nächstes übertragen wir die Kraft auf den Schwerpunkt des Abschnitts und wenden an diesem Punkt eine Kraft an, die der Kraft entspricht, aber entgegengesetzt gerichtet ist (Abb. 3.2). Um die Kraft im Schwerpunkt zu belassen, muss ihrer Wirkung ein weiteres, mit Kreuzen markiertes Kräftepaar oder ein Moment hinzugefügt werden.

Die Wirkung einer exzentrisch auf das Profil aufgebrachten Kraft ist also gleichbedeutend mit der kombinierten Wirkung einer mittig aufgebrachten Kraft und zweier äußerer konzentrierter Momente u.

Mit der Schnittmethode lässt sich leicht feststellen, dass in allen Querschnitten eines exzentrisch gestreckten (gestauchten) Trägers folgende Schnittgrößen wirken: eine Längskraft und zwei Biegemomente und (Abb. 3.3).

Die Spannungen in den Balkenquerschnitten ermitteln wir nach dem Prinzip der Kraftwirkungsunabhängigkeit. Aus allen Schnittgrößen entstehen Normalspannungen in den Querschnitten. Spannungszeichen werden entsprechend der Art der Verformungen gesetzt: Plus - Zug, Minus - Kompression. Ordnen wir die Spannungsvorzeichen von jedem der Schnittgrößen an den Punkten, dem Schnittpunkt der Achsen und mit der Querschnittskontur an (Abb. 3.3). Von der Längskraft an allen Stellen sind die Schnitte gleich und positiv; ab dem Moment am Stresspunkt - Plus, am Punkt - Minus, an Punkten und, weil die Achse ist in diesem Fall die neutrale Linie; ab dem Moment am Stresspunkt - Plus, am Punkt - Minus, an Punkten und, weil die Achse ist in diesem Fall die neutrale Linie.

Die Gesamtspannung am Punkt mit den Koordinaten und ist gleich:

Der am stärksten belastete Punkt in einem Freiformabschnitt ist der Punkt, der am weitesten von der neutralen Linie entfernt ist. In diesem Zusammenhang sind Fragen im Zusammenhang mit der Bestimmung der Position der neutralen Linie von großer Bedeutung.

Bestimmung der Lage des Neutralleiters

Die Lage der neutralen Linie kann mit Formel (3.1) bestimmt werden, indem die Normalspannungen zu Null gesetzt werden

wobei und die Koordinaten eines Punktes sind, der auf der neutralen Linie liegt.

Der letzte Ausdruck kann mit den Formeln für die Trägheitsradien umgerechnet werden: und. Dann

Gleichung (3.2) zeigt, dass die Neutrallinie bei exzentrischem Zug (Druck) eine Gerade ist, die nicht durch den Ursprung (Schwerpunkt des Querschnitts) geht.

Ziehen wir diese Linie durch zwei Punkte, die auf den Koordinatenachsen liegen (Abb. 3.4). Lassen Sie Punkt 1 auf der Achse liegen, dann sind seine Koordinaten und, und Punkt 2 - auf der Achse, dann sind seine Koordinaten und (basierend auf Gleichung (3.2)).

Wenn die Koordinaten des Kraftangriffspunktes (Pol) positiv sind, dann sind die Koordinaten der Punkte 1 und 2 negativ und umgekehrt. Somit befinden sich der Pol und die neutrale Linie auf gegenüberliegenden Seiten des Ursprungs.

Durch die Bestimmung der Position der neutralen Linie können Sie gefährliche Stellen in der Strecke identifizieren, d.h. die Punkte, an denen die Normalspannungen die größten Werte annehmen. Konstruieren Sie dazu Tangenten an die Kontur des Schnitts, parallel zur neutralen Linie. Die Berührungspunkte und werden gefährlich sein (Abb. 3.4).

Die Festigkeitsbedingungen für Gefahrenstellen hängen von den Eigenschaften des Materials ab, aus dem der Träger hergestellt ist. Da ein spröder Werkstoff bei Zug und Druck unterschiedliche Eigenschaften hat – er widersteht Zug schlecht und gut Druck, gelten die Festigkeitsbedingungen für zwei Punkte: dort, wo die maximale Zugspannung (t.) und die maximale Druckspannung (t.) wirken (Abb. 3.4)

Für einen Kunststoff, der sowohl Zug als auch Druck gleichermaßen widersteht, wird eine Festigkeitsbedingung für den Querschnittspunkt aufgestellt, an dem die Normalspannungen betragsmäßig maximal sind. In unserem Fall ist ein solcher Punkt ein Punkt, an dem Betonungen gleichen Vorzeichens wirken.

Das Konzept der Kernsektion

Bei der Konstruktion einer neutralen Linie (Abb. 3.4) wurden die Koordinaten der Punkte 1 und 2 bestimmt, durch die sie gezogen wurde

Die Koordinaten der auf der neutralen Linie liegenden Punkte hängen von der Position des Kraftangriffspunktes (Pol) mit den Koordinaten ab. Wenn die Polkoordinaten kleiner werden, d.h. der Pol nähert sich dem Schwerpunkt des Abschnitts, dann nehmen sie zu, d.h. die neutrale Linie kann sich über den Schnitt hinaus erstrecken oder die Schnittkontur berühren. In diesem Fall treten im Schnitt Spannungen gleichen Vorzeichens auf.

Der Angriffsbereich von Längskräften, die in diesem Fall Spannungen gleichen Vorzeichens im Querschnitt hervorrufen, wird als bezeichnet Abschnitt Kernel.

Die Frage der Bestimmung des Profilkerns ist am relevantesten für Strukturelemente aus sprödem Material, die in exzentrischer Kompression arbeiten, um nur Druckspannungen im Querschnitt zu erhalten, weil sprödes Material widersteht Zugverformung nur schlecht. Dazu ist es notwendig, mehrere Positionen der neutralen Linie festzulegen, sie durch die Randpunkte der Kontur zu ziehen und die Koordinaten der entsprechenden Kraftangriffspunkte nach den aus (3.5) folgenden Formeln zu berechnen.

Die geometrische Lage der auf diese Weise berechneten Punkte bestimmt die Kontur des Kerns des Abschnitts. Auf Abb. 3.6 zeigt Beispiele eines Schnittkerns für gängige Formen.

Betrachten Sie ein Beispiel für Berechnungen für außermittige Zug-Kompression.

Beispiel 3.1. Ein Stahlband = 10 cm breit und = 1 cm dick, mittig gedehnt durch Kräfte = 70 kN, hat einen Schlitz = 3 cm breit (Abb. 3.6). Ermittlung der größten Normalspannungen im Querschnitt ohne Berücksichtigung von Spannungskonzentrationen. Wie breit wäre der Schlitz bei gleicher Zugkraft, wenn er in der Mitte der Streifenbreite liegen würde?

Entscheidung. Bei einem asymmetrischen Schlitz verschiebt sich der Schwerpunkt des geschwächten Abschnitts von der Wirkungslinie der Kraft nach rechts und es kommt zu einer außermittigen Spannung. Um die Position des Schwerpunkts () zu bestimmen, stellen wir den geschwächten Abschnitt als großes Rechteck mit Abmessungen (Abbildung I) dar, aus dem ein kleines Rechteck mit Abmessungen entfernt wird (Abbildung II). Für die ursprüngliche Achse nehmen wir die Achse.

Dabei treten im Querschnitt zwei Schnittgrößen auf: die Längskraft und das Biegemoment.

Um die Gefahrenstelle zu bestimmen, platzieren wir die Belastungszeichen an den seitlichen Seiten des Querschnitts (Abb. 3.6). Aus der Längskraft ergeben sich an allen Stellen des Profils positive (Zug-) Spannungen. Ab dem Biegemoment treten links der Achse Zugspannungen (Pluszeichen) und rechts Druckspannungen (Minuszeichen) auf.

Somit entstehen die maximalen Normalspannungen in den sog.

wo ist die Fläche des geschwächten Abschnitts gleich =7 cm 2;

Trägheitsmoment des geschwächten Abschnitts um die Hauptmittelachse

Abstand von der neutralen Linie () zum entferntesten Punkt (t.)

Als Ergebnis werden die maximalen Normalspannungen gleich sein

Bei symmetrischer Schlitzbreite tritt nur Zug auf