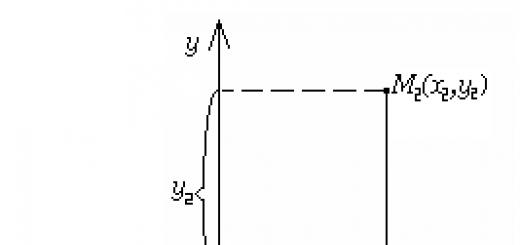
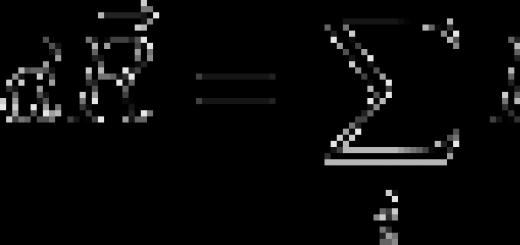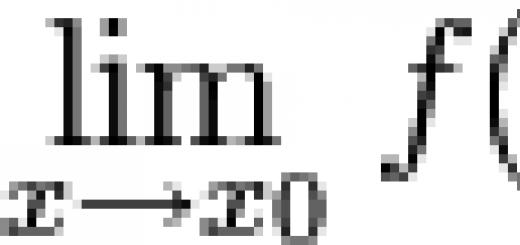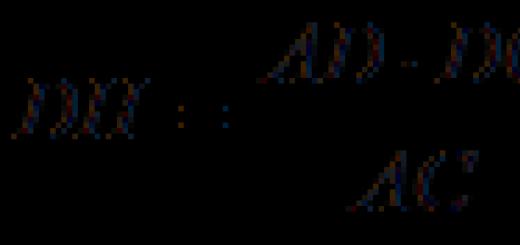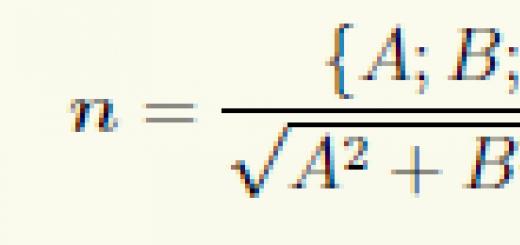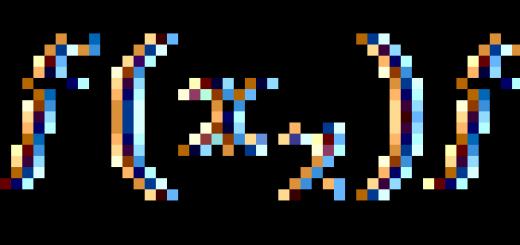Ihre Privatsphäre ist uns wichtig. Aus diesem Grund haben wir eine Datenschutzrichtlinie entwickelt, die beschreibt, wie wir Ihre Informationen verwenden und speichern. Bitte lesen Sie unsere Datenschutzerklärung und lassen Sie uns wissen, wenn Sie Fragen haben.

Erhebung und Verwendung personenbezogener Daten

Personenbezogene Daten sind Daten, mit denen eine bestimmte Person identifiziert oder kontaktiert werden kann.

Sie können jederzeit um die Angabe Ihrer persönlichen Daten gebeten werden, wenn Sie uns kontaktieren.

Im Folgenden finden Sie einige Beispiele für die Arten von personenbezogenen Daten, die wir möglicherweise erfassen, und wie wir diese Daten möglicherweise verwenden.

Welche personenbezogenen Daten wir erheben:

• Wenn Sie eine Bewerbung auf der Website einreichen, erfassen wir möglicherweise verschiedene Informationen, einschließlich Ihres Namens, Ihrer Telefonnummer, Ihrer E-Mail-Adresse usw.

Wie wir Ihre personenbezogenen Daten verwenden:

• Die von uns gesammelten personenbezogenen Daten ermöglichen es uns, Sie zu kontaktieren und Sie über einzigartige Angebote, Werbeaktionen und andere Veranstaltungen und bevorstehende Veranstaltungen zu informieren.
• Von Zeit zu Zeit können wir Ihre personenbezogenen Daten verwenden, um Ihnen wichtige Mitteilungen und Mitteilungen zu senden.
• Wir können personenbezogene Daten auch für interne Zwecke verwenden, z. B. zur Durchführung von Audits, Datenanalysen und verschiedenen Recherchen, um die von uns angebotenen Dienstleistungen zu verbessern und Ihnen Empfehlungen zu unseren Dienstleistungen zu geben.
• Wenn Sie an einer Verlosung, einem Wettbewerb oder einem ähnlichen Anreiz teilnehmen, können wir die von Ihnen bereitgestellten Informationen verwenden, um solche Programme zu verwalten.

Weitergabe an Dritte

Wir geben die von Ihnen erhaltenen Informationen nicht an Dritte weiter.

Ausnahmen:

• Für den Fall, dass es erforderlich ist - gemäß dem Gesetz, der gerichtlichen Anordnung, in Gerichtsverfahren und / oder aufgrund öffentlicher Anfragen oder Anfragen staatlicher Stellen im Hoheitsgebiet der Russischen Föderation - Ihre personenbezogenen Daten offenzulegen. Wir können auch Informationen über Sie offenlegen, wenn wir feststellen, dass eine solche Offenlegung für Sicherheits-, Strafverfolgungs- oder andere Zwecke von öffentlichem Interesse notwendig oder angemessen ist.
• Im Falle einer Umstrukturierung, Fusion oder eines Verkaufs können wir die von uns erfassten personenbezogenen Daten an den entsprechenden Drittnachfolger übertragen.

Schutz personenbezogener Daten

Wir treffen Vorkehrungen – einschließlich administrativer, technischer und physischer – zum Schutz Ihrer personenbezogenen Daten vor Verlust, Diebstahl und Missbrauch sowie vor unbefugtem Zugriff, Offenlegung, Änderung und Zerstörung.

Wahrung Ihrer Privatsphäre auf Unternehmensebene

Um sicherzustellen, dass Ihre persönlichen Daten sicher sind, kommunizieren wir Datenschutz- und Sicherheitspraktiken an unsere Mitarbeiter und setzen Datenschutzpraktiken strikt durch.

AUFGABEN C2 DES EINHEITLICHEN STAATsexamens Mathematik zum Ermitteln der Entfernung von einem Punkt zu einer Ebene

Kulikova Anastasia Jurjewna

Student im 5. Jahr, Fachbereich Mathematik. Analysis, Algebra und Geometrie EI KFU, Russische Föderation, Republik Tatarstan, Elabuga

Ganeeva Aigul Rifowna

wissenschaftlicher Betreuer, Ph.D. päd. Wissenschaften, außerordentlicher Professor, EI KFU, Russische Föderation, Republik Tatarstan, Elabuga

In den letzten Jahren sind Aufgaben zur Berechnung der Entfernung von einem Punkt zu einer Ebene in USE-Aufgaben in der Mathematik erschienen. In diesem Artikel werden am Beispiel eines Problems verschiedene Methoden zur Bestimmung der Entfernung von einem Punkt zu einer Ebene betrachtet. Um verschiedene Probleme zu lösen, können Sie die am besten geeignete Methode verwenden. Nachdem das Problem mit einer Methode gelöst wurde, kann eine andere Methode die Korrektheit des Ergebnisses überprüfen.

Definition. Der Abstand von einem Punkt zu einer Ebene, die diesen Punkt nicht enthält, ist die Länge des von diesem Punkt auf die gegebene Ebene fallenden Abschnitts der Senkrechten.

Eine Aufgabe. Gegeben sei ein rechteckiges Parallelepiped ABERBVONDA 1 B 1 C 1 D 1 mit Seiten AB=2, BC=4, AA 1=6. Finden Sie die Entfernung von einem Punkt D bis zum Flugzeug ACD 1 .

1 Weg. Verwenden Definition. Finde den Abstand r( D, ACD 1) von einem Punkt D bis zum Flugzeug ACD 1 (Abb. 1).

Abbildung 1. Erster Weg

Lass uns ausgeben DH⊥AC, also nach dem Satz über drei Senkrechte D 1 h⊥AC Und (DD 1 h)⊥AC. Lass uns ausgeben Direkte DT aufrecht D 1 h. Gerade DT liegt im Flugzeug DD 1 h, Folglich DT⊥AC. Folglich, DT⊥ACD 1.

ABERGleichstrom Finden Sie die Hypotenuse AC und Höhe DH

Aus einem rechtwinkligen Dreieck D 1 DH Finden Sie die Hypotenuse D 1 h und Höhe DT

Antworten: .

2-Wege.Volumenmethode (Verwendung einer Hilfspyramide). Ein Problem dieser Art kann auf das Problem der Berechnung der Höhe einer Pyramide reduziert werden, wobei die Höhe der Pyramide der gewünschte Abstand von einem Punkt zu einer Ebene ist. Beweisen Sie, dass diese Höhe der gewünschte Abstand ist; Finden Sie das Volumen dieser Pyramide auf zwei Arten und drücken Sie diese Höhe aus.

Beachten Sie, dass es bei dieser Methode nicht erforderlich ist, eine Senkrechte von einem bestimmten Punkt zu einer bestimmten Ebene zu konstruieren.

Ein Quader ist ein Quader, dessen Flächen alle Rechtecke sind.

AB=CD=2, BC=ANZEIGE=4, AA 1 =6.

Der gewünschte Abstand ist die Höhe h Pyramiden ACD 1 D, fiel von oben D auf dem Boden ACD 1 (Abb. 2).

Berechne das Volumen der Pyramide ACD 1 D zwei Wege.

Bei der ersten Berechnung gehen wir von ∆ aus ACD 1 dann

Bei der zweiten Berechnung gehen wir von ∆ aus ACD, dann

Gleichen Sie die rechten Seiten der letzten beiden Gleichheiten, erhalten wir

Abbildung 2. Der zweite Weg

Aus rechtwinkligen Dreiecken ACD, ADDIEREN 1 , CDD 1 Finden Sie die Hypotenusen mit dem Satz des Pythagoras

ACD

Berechnen Sie die Fläche eines Dreiecks ACD 1 unter Verwendung der Heron-Formel

Antworten: .

3 Wege. koordinieren methode.

Lassen Sie einen Punkt vergeben m(x 0 ,j 0 ,z 0) und Ebene α , gegeben durch die Gleichung Axt+durch+cz+D=0 im rechtwinkligen kartesischen Koordinatensystem. Entfernung vom Punkt m zur Ebene α kann nach folgender Formel berechnet werden:

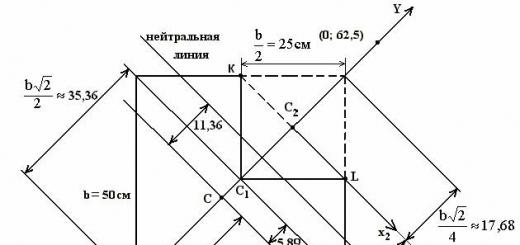
Führen wir ein Koordinatensystem ein (Abb. 3). Ursprung am Punkt IN;

Gerade AB- Achse x, gerade Sonne- Achse j, gerade BB 1 - Achse z.

Abbildung 3. Der dritte Weg

B(0,0,0), ABER(2,0,0), VON(0,4,0), D(2,4,0), D 1 (2,4,6).

Lassen einx+durch+ cz+ D=0 – Ebenengleichung ACD ein . Ersetzen Sie darin die Koordinaten der Punkte EIN, C, D 1 erhalten wir:

Ebenengleichung ACD 1 nimmt das Formular an

Antworten: .

4 Wege. Vektormethode.

Wir führen die Basis ein (Abb. 4) , .

Abbildung 4. Der vierte Weg

, Wettbewerb "Präsentation für den Unterricht"

Klasse: 11

Präsentation für den Unterricht

Zurück vorwärts

Aufmerksamkeit! Die Folienvorschau dient nur zu Informationszwecken und stellt möglicherweise nicht den vollen Umfang der Präsentation dar. Wenn Sie an dieser Arbeit interessiert sind, laden Sie bitte die Vollversion herunter.

Ziele:

• Verallgemeinerung und Systematisierung von Wissen und Fähigkeiten der Studierenden;
• Entwicklung von Fähigkeiten zum Analysieren, Vergleichen, Schlussfolgerungen ziehen.

Ausrüstung:

• Multimedia-Projektor;
• Computer;
• Aufgabenblätter

STUDIENPROZESS

I. Organisatorischer Moment

II. Die Phase der Wissensaktualisierung(Folie 2)

Wir wiederholen, wie die Entfernung von einem Punkt zu einer Ebene bestimmt wird

III. Vorlesung(Folien 3-15)

In der Lektion werden wir uns verschiedene Methoden ansehen, um die Entfernung von einem Punkt zu einer Ebene zu bestimmen.

Erste Methode: Schritt für Schritt rechnerisch

Abstand vom Punkt M zur Ebene α:
– ist gleich dem Abstand zur Ebene α von einem beliebigen Punkt P, der auf der Linie a liegt, die durch den Punkt M geht und parallel zur Ebene α ist;
– ist gleich dem Abstand zur Ebene α von einem beliebigen Punkt P, der auf der Ebene β liegt, die durch den Punkt M geht und parallel zur Ebene α ist.

Wir werden folgende Aufgaben lösen:

№1. Finden Sie im Würfel A ... D 1 die Entfernung vom Punkt C 1 zur Ebene AB 1 C.

Es bleibt der Wert der Länge des Segments O 1 N zu berechnen.

№2. Finden Sie in einem regelmäßigen sechseckigen Prisma A ... F 1, dessen Kanten alle gleich 1 sind, den Abstand von Punkt A zur Ebene DEA 1.

Nächste Methode: Volumenmethode.

Wenn das Volumen der Pyramide ABCM V ist, dann wird der Abstand vom Punkt M zur Ebene α, die ∆ABC enthält, durch die Formel ρ(M; α) = ρ(M; ABC) = berechnet
Bei der Lösung von Problemen verwenden wir die Gleichheit der Volumina einer Figur, die auf zwei verschiedene Arten ausgedrückt wird.

Lassen Sie uns das folgende Problem lösen:

№3. Die Kante AD der Pyramide DABC steht senkrecht auf der Ebene der Basis ABC. Finden Sie den Abstand von A zu der Ebene, die durch die Mittelpunkte der Kanten AB, AC und AD verläuft, wenn.

Beim Lösen von Problemen koordinieren methode der Abstand vom Punkt M zur Ebene α kann nach der Formel ρ(M; α) = berechnet werden , wobei M(x 0; y 0; z 0) und die Ebene durch die Gleichung ax + by + cz + d = 0 gegeben ist

Lassen Sie uns das folgende Problem lösen:

№4. Finden Sie im Einheitswürfel A…D 1 den Abstand vom Punkt A 1 zur Ebene BDC 1 .

Lassen Sie uns ein Koordinatensystem mit dem Ursprung im Punkt A einführen, die y-Achse verläuft entlang der Kante AB, die x-Achse - entlang der Kante AD, die z-Achse - entlang der Kante AA 1. Dann sind die Koordinaten der Punkte B (0; 1; 0) D (1; 0; 0;) C 1 (1; 1; 1)
Lassen Sie uns die Gleichung der Ebene aufstellen, die durch die Punkte B, D, C 1 verläuft.

Dann ist – dx – dy + dz + d = 0 x + y – z – 1= 0. Also ρ =

Die folgende Methode, die zur Lösung von Problemen dieser Art verwendet werden kann - Methode der Referenzaufgaben.

Die Anwendung dieser Methode besteht in der Anwendung bekannter Referenzprobleme, die als Theoreme formuliert sind.

Lassen Sie uns das folgende Problem lösen:

№5. Finden Sie in einem Einheitswürfel A ... D 1 den Abstand vom Punkt D 1 zur Ebene AB 1 C.

Betrachten Sie die Anwendung Vektormethode.

№6. Finden Sie in einem Einheitswürfel A ... D 1 den Abstand vom Punkt A 1 zur Ebene BDC 1.

Daher haben wir verschiedene Methoden in Betracht gezogen, die zur Lösung dieser Art von Problem verwendet werden können. Die Wahl der einen oder anderen Methode hängt von der konkreten Aufgabe und Ihren Vorlieben ab.

IV. Gruppenarbeit

Versuchen Sie, das Problem auf unterschiedliche Weise zu lösen.

№1. Die Kante des Würfels А…D 1 ist gleich . Finden Sie den Abstand vom Scheitelpunkt C zur Ebene BDC 1 .

№2. Finden Sie in einem regelmäßigen Tetraeder ABCD mit einer Kante den Abstand von Punkt A zur Ebene BDC

№3. Finden Sie in einem regelmäßigen dreieckigen Prisma ABCA 1 B 1 C 1, dessen Kanten alle gleich 1 sind, den Abstand von A zur Ebene BCA 1.

№4. Finden Sie in einer regelmäßigen viereckigen Pyramide SABCD, deren Kanten alle gleich 1 sind, den Abstand von A zur Ebene SCD.

V. Zusammenfassung der Lektion, Hausaufgaben, Reflexion

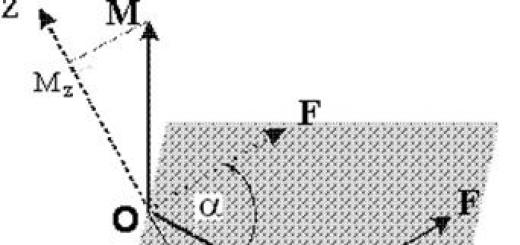
Betrachten Sie eine Ebene π und einen beliebigen Punkt M 0 im Raum. Entscheiden wir uns für das Flugzeug Einheitsnormalenvektor n s Anfang an einem Punkt M 1 ∈ π, und p(M 0 ,π) sei der Abstand vom Punkt M 0 zur Ebene π. Dann (Abb. 5.5)

p(M 0 ,π) = | pr n M 1 M 0 | = |nM 1 M 0 |, (5.8)

seit |n| = 1.

Wenn die Ebene π angegeben ist rechtwinkliges Koordinatensystem mit seiner allgemeinen Gleichung Ax + By + Cz + D = 0, dann ist sein Normalenvektor der Vektor mit den Koordinaten (A; B; C) und als Einheitsnormalenvektor können wir wählen

Seien (x 0 ; y 0 ; z 0) und (x 1 ; y 1 ; z 1) die Koordinaten der Punkte M 0 und M 1 . Dann ist die Gleichheit Ax 1 + By 1 + Cz 1 + D = 0 erfüllt, da der Punkt M 1 zur Ebene gehört, und Sie können die Koordinaten des Vektors M 1 M 0 finden: M 1 M 0 = (x 0 –x 1 ;y 0 –y 1;z 0 –z 1). Aufschreiben Skalarprodukt nM 1 M 0 in Koordinatenform und Transformation (5.8) erhalten wir

da Ax 1 + By 1 + Cz 1 = - D. Um also den Abstand von einem Punkt zu einer Ebene zu berechnen, müssen Sie die Koordinaten des Punktes in die allgemeine Gleichung der Ebene einsetzen und dann den Absolutwert von teilen das Ergebnis um einen Normierungsfaktor gleich der Länge des entsprechenden Normalenvektors.

In diesem Artikel geht es um die Bestimmung der Entfernung von einem Punkt zu einer Ebene. Analysieren wir die Koordinatenmethode, mit der wir die Entfernung von einem bestimmten Punkt im dreidimensionalen Raum ermitteln können. Betrachten Sie zur Konsolidierung Beispiele für mehrere Aufgaben.

Der Abstand von einem Punkt zu einer Ebene wird durch einen bekannten Abstand von einem Punkt zu einem Punkt gefunden, wobei einer davon gegeben ist und der andere eine Projektion auf eine gegebene Ebene ist.

Wenn ein Punkt M 1 mit einer Ebene χ im Raum gegeben ist, dann kann durch den Punkt eine senkrecht zur Ebene stehende Gerade gezogen werden. H 1 ist ein gemeinsamer Punkt ihres Schnittpunkts. Daraus ergibt sich, dass die Strecke M 1 H 1 eine Senkrechte ist, die vom Punkt M 1 zur Ebene χ gezogen wurde, wobei der Punkt H 1 die Basis der Senkrechten ist.

Bestimmung 1

Sie nennen den Abstand von einem bestimmten Punkt zur Basis der Senkrechten, die von einem bestimmten Punkt zu einer bestimmten Ebene gezogen wurde.

Die Definition kann in verschiedenen Formulierungen geschrieben werden.

Bestimmung 2

Abstand von Punkt zu Ebene wird die Länge der Senkrechten genannt, die von einem bestimmten Punkt zu einer bestimmten Ebene gezogen wird.

Der Abstand vom Punkt M 1 zur Ebene χ ist wie folgt definiert: Der Abstand vom Punkt M 1 zur Ebene χ ist der kleinste von einem gegebenen Punkt zu irgendeinem Punkt in der Ebene. Wenn sich der Punkt H 2 in der χ-Ebene befindet und nicht gleich dem Punkt H 2 ist, erhalten wir ein rechtwinkliges Dreieck der Form M 2 H 1 H 2 , die rechteckig ist, wo es ein Bein M 2 H 1, M 2 H 2 gibt - Hypotenuse. Daraus folgt also, dass M 1 H 1< M 1 H 2 . Тогда отрезок М 2 H 1 als geneigt betrachtet, die vom Punkt M 1 zur Ebene χ gezogen wird. Wir haben festgestellt, dass die von einem gegebenen Punkt zu einer Ebene gezogene Senkrechte kleiner ist als die von einem Punkt zu einer gegebenen Ebene gezogene Senkrechte. Betrachten Sie diesen Fall in der Abbildung unten.

Abstand von einem Punkt zu einer Ebene - Theorie, Beispiele, Lösungen

Es gibt eine Reihe geometrischer Probleme, deren Lösungen den Abstand von einem Punkt zu einer Ebene enthalten müssen. Die Möglichkeiten, dies zu erkennen, können unterschiedlich sein. Verwenden Sie zur Auflösung den Satz des Pythagoras oder die Ähnlichkeit von Dreiecken. Wenn es gemäß der Bedingung erforderlich ist, die Entfernung von einem Punkt zu einer Ebene zu berechnen, die in einem rechteckigen Koordinatensystem des dreidimensionalen Raums gegeben ist, lösen sie sie mit der Koordinatenmethode. Dieser Absatz befasst sich mit dieser Methode.

Gemäß der Bedingung des Problems haben wir, dass ein Punkt im dreidimensionalen Raum mit Koordinaten M 1 (x 1, y 1, z 1) mit der Ebene χ gegeben ist, es ist notwendig, die Entfernung von M 1 zu zu bestimmen die Ebene χ. Zur Lösung werden mehrere Lösungen verwendet.

Erster Weg

Dieses Verfahren basiert auf dem Finden des Abstands von einem Punkt zu einer Ebene unter Verwendung der Koordinaten des Punktes H 1 , die die Basis der Senkrechten von dem Punkt M 1 zu der Ebene χ sind. Als nächstes müssen Sie den Abstand zwischen M 1 und H 1 berechnen.

Um das Problem auf dem zweiten Weg zu lösen, wird die Normalengleichung einer gegebenen Ebene verwendet.

Zweiter Weg

Als Bedingung haben wir, dass H 1 die Basis der Senkrechten ist, die vom Punkt M 1 auf die Ebene χ abgesenkt wurde. Dann bestimmen wir die Koordinaten (x 2, y 2, z 2) des Punktes H 1. Der gewünschte Abstand von M 1 zur χ-Ebene wird durch die Formel M 1 H 1 \u003d (x 2 - x 1) 2 + (y 2 - y 1) 2 + (z 2 - z 1) 2 ermittelt, wobei M 1 (x 1, y 1 , z 1) und H 1 (x 2 , y 2 , z 2) . Zum Lösen müssen Sie die Koordinaten des Punktes H 1 kennen.

Wir haben, dass H 1 der Schnittpunkt der Ebene χ mit der Linie a ist, die durch den senkrecht zur Ebene χ liegenden Punkt M 1 verläuft. Daraus folgt, dass es notwendig ist, die Gleichung einer geraden Linie zu formulieren, die durch einen gegebenen Punkt senkrecht zu einer gegebenen Ebene verläuft. Dann können wir die Koordinaten des Punktes H 1 bestimmen. Es ist notwendig, die Koordinaten des Schnittpunkts der Linie und der Ebene zu berechnen.

Algorithmus zum Ermitteln des Abstands von einem Punkt mit den Koordinaten M 1 (x 1, y 1, z 1) zur χ-Ebene:

Bestimmung 3

• komponieren Sie die Gleichung einer geraden Linie a, die durch den Punkt M 1 und gleichzeitig geht
• senkrecht zur χ-Ebene;
• Finde und berechne die Koordinaten (x 2, y 2, z 2) des Punktes H 1, die Punkte sind
• Schnittpunkt der Geraden a mit der Ebene χ ;
• Berechnen Sie den Abstand von M 1 zu χ mit der Formel M 1 H 1 = (x 2 - x 1) 2 + (y 2 - y 1) 2 + z 2 - z 1 2.

Dritter Weg

In einem gegebenen rechtwinkligen Koordinatensystem O x y z gibt es eine Ebene χ, dann erhalten wir eine Normalgleichung der Ebene der Form cos α · x + cos β · y + cos γ · z - p = 0 . Daraus ergibt sich, dass der Abstand M 1 H 1 mit dem Punkt M 1 (x 1 , y 1 , z 1 ) zur Ebene χ gezogen wird, berechnet nach der Formel M 1 H 1 = cos α x + cos β y + cos γ z-p. Diese Formel ist gültig, da sie dank des Satzes aufgestellt ist.

Satz

Wenn ein Punkt M 1 (x 1 , y 1 , z 1) im dreidimensionalen Raum gegeben ist, mit einer Normalengleichung der χ-Ebene der Form cos α x + cos β y + cos γ z – p = 0, dann wird die Berechnung des Abstands vom Punkt zur Ebene M 1 H 1 aus der Formel M 1 H 1 = cos α · x + cos β · y + cos γ · z - p abgeleitet, da x = x 1 , y = y 1 , z = z 1 .

Nachweisen

Der Beweis des Satzes reduziert sich darauf, den Abstand zwischen einem Punkt und einer Geraden zu bestimmen. Daraus erhalten wir, dass der Abstand von M 1 zur χ-Ebene der Betrag der Differenz zwischen der numerischen Projektion des Radiusvektors M 1 mit dem Abstand vom Ursprung zur χ-Ebene ist. Dann erhalten wir den Ausdruck M 1 H 1 = n p n → O M → - p . Der Normalenvektor der Ebene χ hat die Form n → = cos α , cos β , cos γ , und seine Länge ist gleich eins, npn → OM → ist die numerische Projektion des Vektors OM → = (x 1 , y 1 , z 1) in der durch den Vektor n → bestimmten Richtung.

Wenden wir die Formel zur Berechnung von Skalarvektoren an. Dann erhalten wir einen Ausdruck zum Finden eines Vektors der Form n → , OM → = n → npn → OM → = 1 npn → OM → = npn → OM → , da n → = cos α , cos β , cos γ z und OM → = (x 1 , y 1 , z 1) . Die Koordinatenform der Notation hat die Form n →, OM → = cos α x 1 + cos β y 1 + cos γ z 1, dann M 1 H 1 = npn → OM → - p = cos α x 1 + cos β · y 1 + cos γ · z 1 - p . Der Satz ist bewiesen.

Daraus ergibt sich, dass der Abstand vom Punkt M 1 (x 1, y 1, z 1) zur Ebene χ durch Einsetzen in die linke Seite der Normalgleichung der Ebene cos α x + cos β y + cos berechnet wird γ z - p = 0 statt x, y, z Koordinaten x 1 , y 1 und z1 bezogen auf den Punkt M 1 , wobei der Absolutwert des erhaltenen Werts genommen wird.

Betrachten Sie Beispiele zum Ermitteln der Entfernung von einem Punkt mit Koordinaten zu einer bestimmten Ebene.

Beispiel 1

Berechnen Sie den Abstand vom Punkt mit den Koordinaten M 1 (5 , - 3 , 10) zur Ebene 2 x - y + 5 z - 3 = 0 .

Lösung

Lassen Sie uns das Problem auf zwei Arten lösen.

Die erste Methode beginnt mit der Berechnung des Richtungsvektors der Linie a . Als Bedingung haben wir, dass die gegebene Gleichung 2 x - y + 5 z - 3 \u003d 0 eine allgemeine Ebenengleichung ist und n → \u003d (2, - 1, 5) der Normalenvektor der gegebenen Ebene ist. Er wird als Richtungsvektor der Geraden a verwendet, die senkrecht auf der gegebenen Ebene steht. Sie sollten die kanonische Gleichung einer geraden Linie im Raum schreiben, die durch M 1 (5, - 3, 10) mit einem Richtungsvektor mit den Koordinaten 2, - 1, 5 verläuft.

Die Gleichung sieht folgendermaßen aus: x - 5 2 = y - (- 3) - 1 = z - 10 5 ⇔ x - 5 2 = y + 3 - 1 = z - 10 5 .

Schnittpunkte sollten definiert werden. Kombinieren Sie dazu die Gleichungen vorsichtig zu einem System für den Übergang von der kanonischen zu den Gleichungen zweier sich schneidender Linien. Nehmen wir diesen Punkt als H 1 . Das verstehen wir

x - 5 2 = y + 3 - 1 = z - 10 5 ⇔ - 1 (x - 5) = 2 (y + 3) 5 (x - 5) = 2 (z - 10) 5 ( y + 3) = - 1 (z - 10) ⇔ ⇔ x + 2 y + 1 = 0 5 x - 2 z - 5 = 0 5 y + z + 5 = 0 ⇔ x + 2 y + 1 = 0 5 x - 2 z - 5 = 0

Dann müssen Sie das System aktivieren

x + 2 y + 1 = 0 5 x - 2 z - 5 = 0 2 x - y + 5 z - 3 = 0 ⇔ x + 2 y = 1 5 x - 2 z = 5 2 x - y + 5 z = 3

Wenden wir uns der Regel zur Lösung des Systems nach Gauß zu:

1 2 0 - 1 5 0 - 2 5 2 - 1 5 3 ~ 1 2 0 - 1 0 - 10 - 2 10 0 - 5 5 5 ~ 1 2 0 - 1 0 - 10 - 2 10 0 0 6 0 ⇒ ⇒ z = 0 6 = 0 , y = - 1 10 10 + 2 z = - 1 , x = - 1 - 2 y = 1

Wir erhalten das H 1 (1, - 1, 0) .

Wir berechnen die Entfernung von einem bestimmten Punkt zu einer Ebene. Wir nehmen die Punkte M 1 (5, - 3, 10) und H 1 (1, - 1, 0) und erhalten

M 1 H 1 \u003d (1 - 5) 2 + (- 1 - (- 3)) 2 + (0 - 10) 2 \u003d 2 30

Die zweite Lösung besteht darin, zunächst die gegebene Gleichung 2 x - y + 5 z - 3 = 0 in Normalform zu bringen. Wir bestimmen den Normierungsfaktor und erhalten 1 2 2 + (- 1) 2 + 5 2 = 1 30 . Daraus leiten wir die Gleichung der Ebene 2 30 · x - 1 30 · y + 5 30 · z - 3 30 = 0 ab. Die linke Seite der Gleichung wird berechnet, indem x \u003d 5, y \u003d - 3, z \u003d 10 ersetzt wird, und Sie müssen den Abstand von M 1 (5, - 3, 10) bis 2 x - y + nehmen 5 z - 3 = 0 modulo. Wir erhalten den Ausdruck:

M 1 H 1 \u003d 2 30 5 - 1 30 - 3 + 5 30 10 - 3 30 \u003d 60 30 \u003d 2 30

Antwort: 2 30 .

Wenn die χ-Ebene durch eine der Methoden im Abschnitt Methoden zur Ebenendefinition gegeben ist, müssen Sie zuerst die Gleichung der χ-Ebene erhalten und die gewünschte Entfernung mit einer beliebigen Methode berechnen.

Beispiel 2

Punkte mit Koordinaten M 1 (5, –3, 10), A (0, 2, 1), B (2, 6, 1), C (4, 0, – 1) werden im dreidimensionalen Raum gesetzt. Berechne den Abstand von M 1 zur Ebene A B C.

Lösung

Zuerst müssen Sie die Gleichung der Ebene aufschreiben, die durch die gegebenen drei Punkte mit den Koordinaten M 1 (5, - 3, 10) , A (0 , 2 , 1) , B (2 , 6 , 1) , C ( 4 , 0 , - eins) .

x - 0 y - 2 z - 1 2 - 0 6 - 2 1 - 1 4 - 0 0 - 2 - 1 - 1 = 0 ⇔ xy - 2 z - 1 2 4 0 4 - 2 - 2 = 0 ⇔ ⇔ - 8x + 4y - 20z + 12 = 0 ⇔ 2x - y + 5z - 3 = 0

Daraus folgt, dass das Problem eine ähnliche Lösung wie das vorherige hat. Daher beträgt der Abstand vom Punkt M 1 zur Ebene A B C 2 30 .

Antwort: 2 30 .

Um den Abstand von einem bestimmten Punkt auf einer Ebene oder zu einer Ebene, zu der sie parallel sind, zu ermitteln, ist es bequemer, die Formel M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 - p anzuwenden . Daraus ergibt sich, dass die Normalgleichungen der Ebenen in mehreren Schritten erhalten werden.

Beispiel 3

Finden Sie den Abstand von einem gegebenen Punkt mit den Koordinaten M 1 (-3, 2, -7) zu der Koordinatenebene O x y z und der Ebene, die durch die Gleichung 2 y - 5 = 0 gegeben ist.

Lösung

Die Koordinatenebene O y z entspricht einer Gleichung der Form x = 0. Für die O y z-Ebene ist es normal. Daher ist es notwendig, die Werte x \u003d - 3 auf der linken Seite des Ausdrucks einzusetzen und den Absolutwert der Entfernung vom Punkt mit den Koordinaten M 1 (- 3, 2, - 7) zur Ebene zu nehmen . Wir erhalten den Wert gleich -3 = 3 .

Nach der Transformation nimmt die Normalgleichung der Ebene 2 y - 5 = 0 die Form y - 5 2 = 0 an. Dann können Sie den erforderlichen Abstand vom Punkt mit den Koordinaten M 1 (- 3 , 2 , - 7) zur Ebene 2 y - 5 = 0 finden. Durch Einsetzen und Rechnen erhalten wir 2 - 5 2 = 5 2 - 2.

Antworten: Der gewünschte Abstand von M 1 (–3, 2, –7) zu O y z hat einen Wert von 3 und zu 2 y – 5 = 0 hat einen Wert von 5 2 – 2 .

Wenn Sie einen Fehler im Text bemerken, markieren Sie ihn bitte und drücken Sie Strg+Enter