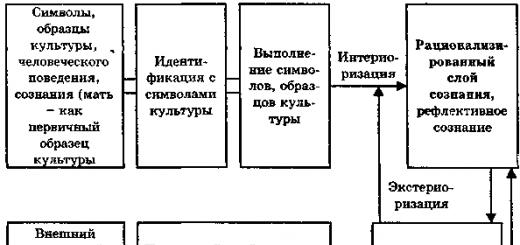
Funktion Gradient an einem Punkt heißt ein Vektor, dessen Koordinaten gleich den entsprechenden partiellen Ableitungen sind, und wird bezeichnet.

Betrachten wir den Einheitsvektor e=(), so ist nach Formel (3) die Richtungsableitung das Skalarprodukt aus der Steigung und dem Einheitsvektor, der die Richtung angibt. Es ist bekannt, dass das Skalarprodukt zweier Vektoren maximal ist, wenn sie die gleiche Richtung haben. Daher charakterisiert die Steigung der Funktion an einem bestimmten Punkt die Richtung und Größe des maximalen Wachstums der Funktion an diesem Punkt.

Satz . Ist die Funktion differenzierbar und am Punkt M 0 der Wert des Gradienten ungleich Null ist, dann ist der Gradient senkrecht zur Niveaulinie, die durch den gegebenen Punkt verläuft, und ist in Richtung der zunehmenden Funktion gerichtet, während

FAZIT: 1) Die Ableitung einer Funktion an einem Punkt entlang der Richtung, die durch den Gradienten dieser Funktion an dem angegebenen Punkt bestimmt wird, hat einen maximalen Wert im Vergleich zu der Ableitung an diesem Punkt entlang einer beliebigen anderen Richtung.

• 2) Der Wert der Ableitung der Funktion in der Richtung, die den Gradienten dieser Funktion an einem gegebenen Punkt bestimmt, ist gleich.
• 3) Wenn man den Gradienten der Funktion an jedem Punkt kennt, ist es möglich, ebene Linien mit einem gewissen Fehler zu erstellen. Beginnen wir beim Punkt M 0 . Lassen Sie uns an dieser Stelle einen Farbverlauf erstellen. Legen Sie die Richtung senkrecht zum Farbverlauf fest. Lassen Sie uns einen kleinen Teil der Levellinie bauen. Betrachten Sie einen engen Punkt M 1 , bauen Sie dort einen Gradienten auf und so weiter.

Konzept gerichtete Ableitung für Funktionen mit zwei und drei Variablen berücksichtigt. Um die Bedeutung einer gerichteten Ableitung zu verstehen, müssen wir Ableitungen per Definition vergleichen.

Somit,

Jetzt können wir die Ableitung in Richtung dieser Funktion durch ihre Formel finden:

Und jetzt - Hausaufgaben. Es gibt eine Funktion von nicht drei, sondern nur zwei Variablen, aber der Richtungsvektor wird auf etwas andere Weise angegeben. Du musst also wiederholen Vektoralgebra .

Beispiel 2 Finden Sie die Ableitung einer Funktion an einem Punkt M0 (1; 2) in Richtung des Vektors , wo M1 - Punkt mit Koordinaten (3; 0) .

Der Vektor, der die Richtung der Ableitung angibt, kann auch in einer solchen Form wie im folgenden Beispiel angegeben werden - in der Form Erweiterungen in Einheitsvektoren von Koordinatenachsen, aber das ist ein bekanntes Thema seit den Anfängen der Vektoralgebra.

Beispiel 3 Finden Sie die Ableitung einer Funktion am Punkt M0 (1; 1; 1) in Richtung des Vektors .

Entscheidung. Finden Sie die Richtungskosinusse des Vektors

Lassen Sie uns partielle Ableitungen von Funktionen an einem Punkt finden M0 :

Daher können wir die Ableitung in Richtung dieser Funktion durch ihre Formel finden:

.

Funktionsgradient

Gradientenfunktion mehrerer Variablen an einem Punkt M0 charakterisiert die Richtung des maximalen Wachstums dieser Funktion an dem Punkt M0 und die Größe dieses maximalen Wachstums.

Wie findet man den Gradienten?

Muss definiert werden Vektor, dessen Projektionen auf die Koordinatenachsen sind die Werte partielle Ableitungen, , dieser Funktion an der entsprechenden Stelle:

.

Das heißt, es sollte sein Darstellung eines Vektors durch die Einheitsvektoren der Koordinatenachsen, bei der die ihrer Achse entsprechende partielle Ableitung mit jedem Einheitsvektor multipliziert wird.

Gradient Funktionen ist eine Vektorgröße, deren Feststellung mit der Definition partieller Ableitungen der Funktion verbunden ist. Die Richtung des Gradienten gibt den Weg des schnellsten Wachstums der Funktion von einem Punkt des Skalarfelds zum anderen an.

Anweisung

1. Um das Problem des Gradienten einer Funktion zu lösen, werden Methoden der Differentialrechnung verwendet, nämlich das Finden partieller Ableitungen erster Ordnung in drei Variablen. Es wird angenommen, dass die Funktion selbst und alle ihre partiellen Ableitungen die Eigenschaft der Stetigkeit im Bereich der Funktion haben.

2. Ein Gradient ist ein Vektor, dessen Richtung die Richtung des schnellsten Anstiegs der Funktion F angibt. Dazu werden auf dem Graphen zwei Punkte M0 und M1 ausgewählt, die die Enden des Vektors darstellen. Der Wert des Gradienten ist gleich der Anstiegsrate der Funktion vom Punkt M0 zum Punkt M1.

3. Die Funktion ist an allen Punkten dieses Vektors differenzierbar, daher sind die Projektionen des Vektors auf die Koordinatenachsen alle seine partiellen Ableitungen. Dann sieht die Gradientenformel so aus: grad = (?F/?x) i + (?F/?y) j + (?F/?z) k, wobei i, j, k die Einheitsvektorkoordinaten sind. Mit anderen Worten, der Gradient einer Funktion ist ein Vektor, dessen Koordinaten seine partiellen Ableitungen grad F = (?F/?х, ?F/?y, ?F/?z) sind.

4. Beispiel 1. Gegeben sei die Funktion F = sin (x z?) / y. Es ist erforderlich, seinen Gradienten am Punkt (&agr;/6, 1/4, 1) zu finden.

5. Lösung Bestimmen Sie die partiellen Ableitungen in Bezug auf eine beliebige Variable: F'_x \u003d 1 / y cos (x z?) z?; F'_y \u003d sin (x z?) (-1) 1 / (y?); F '_z \u003d 1/y cos(x z?) 2 x z.

6. Ersetzen Sie die berühmten Punktkoordinaten: F'_x = 4 cos(?/6) = 2 ?3; F'_y = sin(?/6) (-1) 16 = -8; F'_z \u003d 4 cos (? / 6) 2? / 6 \u003d 2? /? 3.

7. Wenden Sie die Funktionsgradientenformel an: grad F = 2 ?3 i – 8 j + 2 ?/?3 k.

8. Beispiel 2. Finden Sie die Koordinaten des Gradienten der Funktion F = y arñtg (z / x) am Punkt (1, 2, 1).

9. Lösung F'_x \u003d 0 arctg (z / x) + y (arctg (z / x)) '_x \u003d y 1 / (1 + (z / x)?) (-z / x?) \u003d -y z / (x? (1 + (z/x)?)) = -1;F'_y = 1 arctg(z/x) = arctg 1 = ?/4;F'_z = 0 arctg(z/x ) + y (arctg(z/x))'_z = y 1/(1 + (z/x)?) 1/x = y/(x (1 + (z/x)?)) = 1.grad = (- 1, ?/4, 1).

Der skalare Feldgradient ist eine Vektorgröße. Um ihn zu finden, ist es daher erforderlich, alle Komponenten des entsprechenden Vektors basierend auf dem Wissen über die Aufteilung des Skalarfelds zu bestimmen.

Anweisung

1. Lesen Sie in einem Lehrbuch der höheren Mathematik nach, was der Gradient eines Skalarfeldes ist. Wie Sie wissen, hat diese Vektorgröße eine Richtung, die durch die maximale Zerfallsrate der Skalarfunktion gekennzeichnet ist. Eine solche Wahrnehmung einer gegebenen Vektorgröße wird durch einen Ausdruck zur Bestimmung ihrer Komponenten gerechtfertigt.

2. Denken Sie daran, dass jeder Vektor durch die Werte seiner Komponenten definiert ist. Vektorkomponenten sind eigentlich Projektionen dieses Vektors auf die eine oder andere Koordinatenachse. Wenn also der dreidimensionale Raum betrachtet wird, muss der Vektor drei Komponenten haben.

3. Schreiben Sie auf, wie die Komponenten eines Vektors, der der Gradient eines Feldes ist, bestimmt werden. Alle Koordinaten eines solchen Vektors sind gleich der Ableitung des Skalarpotentials in Bezug auf die Variable, deren Koordinaten berechnet werden. Das heißt, wenn Sie die „x“-Komponente des Feldgradientenvektors berechnen müssen, müssen Sie die Skalarfunktion in Bezug auf die Variable „x“ differenzieren. Beachten Sie, dass die Ableitung ein Quotient sein muss. Das bedeutet, dass beim Differenzieren die restlichen Variablen, die nicht daran teilnehmen, als Konstanten betrachtet werden müssen.

4. Schreiben Sie einen Ausdruck für das Skalarfeld. Wie Sie wissen, bedeutet dieser Begriff jeweils nur eine skalare Funktion mehrerer Variablen, die ebenfalls skalare Größen sind. Die Anzahl der Variablen einer Skalarfunktion ist durch die Dimension des Raums begrenzt.

5. Differenzieren Sie separat die Skalarfunktion in Bezug auf jede Variable. Als Ergebnis haben Sie drei neue Funktionen. Schreiben Sie eine beliebige Funktion in den Ausdruck für den Gradientenvektor des Skalarfelds. Jede der erhaltenen Funktionen ist wirklich ein Indikator für einen Einheitsvektor einer gegebenen Koordinate. Somit sollte der endgültige Gradientenvektor wie ein Polynom mit Exponenten als Ableitungen einer Funktion aussehen.

Wenn es um Probleme geht, die die Darstellung eines Gradienten betreffen, ist es üblicher, sich jeden als skalares Feld vorzustellen. Daher müssen wir die entsprechende Notation einführen.

Du wirst brauchen

• - Boom;
• - Griff.

Anweisung

1. Die Funktion sei durch drei Argumente u=f(x, y, z) gegeben. Die partielle Ableitung einer Funktion, beispielsweise nach x, ist definiert als die Ableitung nach diesem Argument, die man durch Festlegen der übrigen Argumente erhält. Die restlichen Argumente sind ähnlich. Die partielle Ableitungsnotation wird geschrieben als: df / dx \u003d u’x ...

2. Das Gesamtdifferential ist gleich du \u003d (df / dx) dx + (df / dy) dy + (df / dz) dz. Partielle Ableitungen können als Ableitungen in Richtung der Koordinatenachsen verstanden werden. Folglich stellt sich die Frage, die Ableitung nach der Richtung eines gegebenen Vektors s im Punkt M(x, y, z) zu finden (vergessen Sie nicht, dass die Richtung s einen Einheitsvektorort s^o angibt). In diesem Fall ist der Differentialvektor der Argumente (dx, dy, dz) = (dscos(alpha), dscos(beta), dscos(gamma)).

3. Betrachtet man die Form des Gesamtdifferentials du, kann man schließen, dass die Ableitung nach der Richtung s im Punkt M ist: (du/ds)|M=((df/dx)|M)cos(alpha) + ((df/dy) |M) cos(beta) +((df/dz)|M) cos(gamma). Wenn s= s(sx,sy,sz), dann Richtungskosinus (cos(alpha), cos(beta), cos(gamma)) werden berechnet (siehe Abb. 1a).

4. Die Definition der Richtungsableitung, die den Punkt M als Variable betrachtet, kann als Skalarprodukt umgeschrieben werden: (du/ds)=((df/dx, df/dy,df/dz), (cos(alpha) , cos(beta), cos(gamma)))=(grad u, s^o). Dieser Ausdruck ist für ein Skalarfeld objektiv. Betrachten wir eine einfache Funktion, dann ist gradf ein Vektor, dessen Koordinaten mit den partiellen Ableitungen f(x, y, z) zusammenfallen.gradf(x,y,z)=((df/dx, df/dy, df/ dz )=)=(df/dx)i+(df/dy)j +(df/dz)k. Dabei sind (i, j, k) die Einheitsvektoren der Koordinatenachsen in einem rechtwinkligen kartesischen Koordinatensystem.

5. Wenn wir den Differentialvektoroperator von Hamilton Nabla verwenden, dann kann gradf als Multiplikation dieses Operatorvektors mit dem Skalar f geschrieben werden (siehe Abb. 1b). Aus Sicht des Zusammenhangs von gradf mit der Richtungsableitung ist die Gleichheit (gradf, s^o)=0 zulässig, wenn diese Vektoren orthogonal sind. Folglich wird gradf oft als die Richtung der schnellsten Metamorphose eines Skalarfeldes definiert. Und vom Standpunkt der Differentialoperationen (gradf ist eine davon) wiederholen die Eigenschaften von gradf genau die Eigenschaften der Differentiation von Funktionen. Insbesondere wenn f=uv, dann gradf=(vgradu+ugradv).

Ähnliche Videos

Gradient Dies ist ein Werkzeug, das in Grafikeditoren die Silhouette mit einem sanften Übergang von einer Farbe zur anderen füllt. Gradient kann einer Silhouette das Ergebnis von Volumen verleihen, Beleuchtung, Lichtreflexionen auf der Oberfläche eines Objekts oder das Ergebnis eines Sonnenuntergangs im Hintergrund eines Fotos simulieren. Dieses Tool ist weit verbreitet, daher ist es für die Bearbeitung von Fotos oder die Erstellung von Illustrationen sehr wichtig, seine Verwendung zu erlernen.

Du wirst brauchen

• Computer, Grafikeditor Adobe Photoshop, Corel Draw, Paint.Net oder andere.

Anweisung

1. Öffnen Sie das Bild im Programm oder erstellen Sie ein neues. Erstellen Sie eine Silhouette oder wählen Sie den gewünschten Bereich auf dem Bild aus.

2. Aktivieren Sie das Verlaufswerkzeug in der Symbolleiste des Grafikeditors. Platzieren Sie den Mauszeiger auf einem Punkt innerhalb des ausgewählten Bereichs oder der Silhouette, wo die 1. Farbe des Farbverlaufs beginnt. Klicken und halten Sie die linke Maustaste. Bewegen Sie den Mauszeiger an den Punkt, an dem der Farbverlauf in die endgültige Farbe übergehen soll. Lassen Sie die linke Maustaste los. Die ausgewählte Silhouette wird mit einer Verlaufsfüllung gefüllt.

3. Gradient y Es ist möglich, Transparenz, Farben und deren Verhältnis an einem bestimmten Füllpunkt festzulegen. Öffnen Sie dazu das Verlaufsbearbeitungsfenster. Um das Bearbeitungsfenster in Photoshop zu öffnen, klicken Sie auf das Verlaufsbeispiel in der Optionenpalette.

4. In dem sich öffnenden Fenster werden die verfügbaren Farbverlaufsoptionen als Beispiele angezeigt. Um eine der Optionen zu bearbeiten, wählen Sie sie mit einem Mausklick aus.

5. Ein Beispiel für einen Farbverlauf wird unten im Fenster in Form einer breiten Skala mit Schiebereglern angezeigt. Die Schieberegler geben die Punkte an, an denen der Farbverlauf die angegebenen Sortierungen haben soll, und im Intervall zwischen den Schiebereglern geht die Farbe gleichmäßig von der am ersten Punkt festgelegten Farbe in die Farbe des 2. Punktes über.

6. Die Schieberegler am oberen Rand der Skala legen die Transparenz des Farbverlaufs fest. Um die Transparenz zu ändern, klicken Sie auf den gewünschten Schieberegler. Unterhalb der Skala erscheint ein Feld, in das Sie den gewünschten Transparenzgrad in Prozent eingeben.

7. Die Schieberegler am unteren Rand der Skala legen die Farben des Farbverlaufs fest. Wenn Sie auf eine davon klicken, können Sie die gewünschte Farbe bevorzugen.

8. Gradient kann mehrere Übergangsfarben haben. Um eine andere Farbe einzustellen, klicken Sie auf einen leeren Bereich am unteren Rand der Skala. Darauf erscheint ein weiterer Schieberegler. Stellen Sie die gewünschte Farbe dafür ein. Die Skala zeigt ein Beispiel für einen Gradienten mit einem weiteren Punkt. Sie können die Schieberegler verschieben, indem Sie sie mit Unterstützung der linken Maustaste halten, um die gewünschte Kombination zu erreichen.

9. Gradient Es gibt verschiedene Arten, die flachen Silhouetten Form verleihen können. Nehmen wir an, um einem Kreis die Form einer Kugel zu geben, wird ein radialer Verlauf angewendet, und um ihm die Form eines Kegels zu geben, wird ein konischer Verlauf angewendet. Ein Spiegelverlauf kann verwendet werden, um der Oberfläche die Illusion einer Wölbung zu verleihen, und ein Diamantverlauf kann verwendet werden, um Glanzlichter zu erzeugen.

Ähnliche Videos

Ähnliche Videos

Bestimmung 1

Wenn jedem Paar $(x,y)$ von Werten zweier unabhängiger Variablen aus irgendeinem Bereich ein bestimmter Wert von $z$ zugewiesen wird, dann heißt $z$ eine Funktion zweier Variablen $(x,y )$. Schreibweise: $z=f(x,y)$.

Betrachten Sie die Funktion $z=f(x,y)$, die in irgendeiner Domäne im Raum $Oxy$ definiert ist.

Somit,

Bestimmung 3

Wenn jedem Tripel $(x,y,z)$ von Werten dreier unabhängiger Variablen aus irgendeinem Bereich ein bestimmter Wert $w$ zugeordnet wird, dann heißt $w$ eine Funktion von drei Variablen $(x, y,z)$ in diesem Bereich.

Bezeichnung:$w=f(x,y,z)$.

Betrachten Sie die Funktion $w=f(x,y,z)$, die in irgendeiner Domäne im Raum $Oxyz$ definiert ist.

Für eine gegebene Funktion definieren wir einen Vektor, dessen Projektionen auf die Koordinatenachsen die Werte der partiellen Ableitungen der gegebenen Funktion an einem bestimmten Punkt sind $\frac(\partial z)(\partial x) ;\frac(\partial z)(\partiell y) $.

Bestimmung 4

Der Gradient einer gegebenen Funktion $w=f(x,y,z)$ ist ein Vektor $\overrightarrow(gradw) $ der folgenden Form:

Satz 3

Ein Gradientenfeld sei in einem Skalarfeld $w=f(x,y,z)$ definiert

\[\overrightarrow(gradw) =\frac(\partial w)(\partial x) \cdot \overrightarrow(i) +\frac(\partial w)(\partial y) \cdot \overrightarrow(j) +\frac (\partial w)(\partial z) \cdot \overrightarrow(k) .\]

Die Ableitung $\frac(\partial w)(\partial s) $ in Richtung des gegebenen Vektors $\overrightarrow(s) $ ist gleich der Projektion des Gradientenvektors $\overrightarrow(gradw) $ auf den gegebenen Vektor $\overrightarrow(s) $.

Beispiel 4

Entscheidung:

Der Ausdruck für den Gradienten wird durch die Formel gefunden

\[\overrightarrow(gradw) =\frac(\partial w)(\partial x) \cdot \overrightarrow(i) +\frac(\partial w)(\partial y) \cdot \overrightarrow(j) +\frac (\partial w)(\partial z) \cdot \overrightarrow(k) .\]

\[\frac(\partial w)(\partial x) =2x;\frac(\partial w)(\partial y) =4y;\frac(\partial w)(\partial z) =2.\]

Somit,

\[\overrightarrow(gradw) =2x\cdot \overrightarrow(i) +4y\cdot \overrightarrow(j) +2\cdot \overrightarrow(k) .\]

Beispiel 5

Bestimmen Sie den Gradienten einer gegebenen Funktion

am Punkt $M(1;2;1)$. Berechne $\left(|\overrightarrow(gradz) |\right)_(M) $.

Entscheidung:

Der Ausdruck für den Gradienten an einem bestimmten Punkt wird durch die Formel gefunden

\[\left(\overrightarrow(gradw) \right)_(M) =\left(\frac(\partial w)(\partial x) \right)_(M) \cdot \overrightarrow(i) +\left (\frac(\partial w)(\partial y) \right)_(M) \cdot \overrightarrow(j) +\left(\frac(\partial w)(\partial z) \right)_(M) \cdot \overrightarrow(k) .\]

Die partiellen Ableitungen haben die Form:

\[\frac(\partial w)(\partial x) =2x;\frac(\partial w)(\partial y) =4y;\frac(\partial w)(\partial z) =6z^(2) .\]

Ableitungen am Punkt $M(1;2)$:

\[\frac(\partial w)(\partial x) =2\cdot 1=2;\frac(\partial w)(\partial y) =4\cdot 2=8;\frac(\partial w)( \partial z) =6\cdot 1^(2) =6.\]

Somit,

\[\left(\overrightarrow(gradw) \right)_(M) =2\cdot \overrightarrow(i) +8\cdot \overrightarrow(j) +6\cdot \overrightarrow(k) \]

\[\left(|\overrightarrow(gradw) |\right)_(M) =\sqrt(2^(2) +8^(2) +6^(2) ) =\sqrt(4+64+36 ) =\sqrt(104) .\]

Lassen Sie uns einige auflisten Verlaufseigenschaften:

Die Ableitung einer gegebenen Funktion an einem gegebenen Punkt in Richtung eines Vektors $\overrightarrow(s)$ hat den größten Wert, wenn die Richtung des gegebenen Vektors $\overrightarrow(s)$ mit der Richtung des Gradienten übereinstimmt. In diesem Fall fällt dieser größte Wert der Ableitung mit der Länge des Gradientenvektors zusammen, d. h. $|\overrightarrow(gradw) |$.

Die Ableitung der gegebenen Funktion in Bezug auf die Richtung des Vektors, die senkrecht zum Gradientenvektor steht, d.h. $\overrightarrow(gradw) $ ist gleich 0. Da $\varphi =\frac(\pi )(2) $, dann ist $\cos \varphi =0$; also $\frac(\partial w)(\partial s) =|\overrightarrow(gradw) |\cdot \cos \varphi =0$.

Aus einem Schulmathematikkurs ist bekannt, dass ein Vektor auf einer Ebene eine gerichtete Strecke ist. Sein Anfang und sein Ende haben zwei Koordinaten. Die Vektorkoordinaten werden berechnet, indem die Startkoordinaten von den Endkoordinaten subtrahiert werden.

Das Konzept eines Vektors kann auch auf einen n-dimensionalen Raum erweitert werden (statt zwei Koordinaten gibt es n Koordinaten).

Gradient gradz Funktion z=f(x 1 , x 2 , ... x n) ist der Vektor der partiellen Ableitungen der Funktion an einem Punkt, d.h. Vektor mit Koordinaten.

Es kann bewiesen werden, dass die Steigung einer Funktion die Richtung des schnellsten Anstiegs des Niveaus der Funktion an einem Punkt charakterisiert.

Beispielsweise hat für die Funktion z \u003d 2x 1 + x 2 (siehe Abbildung 5.8) der Gradient an jedem Punkt Koordinaten (2; 1). Es kann auf verschiedene Weise auf einer Ebene aufgebaut werden, wobei jeder Punkt als Anfang des Vektors genommen wird. Beispielsweise können Sie Punkt (0; 0) mit Punkt (2; 1) oder Punkt (1; 0) mit Punkt (3; 1) oder Punkt (0; 3) mit Punkt (2; 4) verbinden. oder t .P. (siehe Abbildung 5.8). Alle auf diese Weise konstruierten Vektoren haben die Koordinaten (2 - 0; 1 - 0) = = (3 - 1; 1 - 0) = (2 - 0; 4 - 3) = (2; 1).

Abbildung 5.8 zeigt deutlich, dass das Niveau der Funktion in Richtung des Gradienten wächst, da die konstruierten Niveaulinien den Niveauwerten 4 > 3 > 2 entsprechen.

Abbildung 5.8 - Gradient der Funktion z \u003d 2x 1 + x 2

Betrachten wir ein weiteres Beispiel – die Funktion z= 1/(x 1 x 2). Die Steigung dieser Funktion wird nicht mehr an verschiedenen Stellen immer gleich sein, da ihre Koordinaten durch die Formeln (-1 / (x 1 2 x 2); -1 / (x 1 x 2 2)) bestimmt sind.

Abbildung 5.9 zeigt die Pegellinien der Funktion z= 1/(x 1 x 2) für die Ebenen 2 und 10 (die Linie 1/(x 1 x 2) = 2 ist gestrichelt dargestellt, die Linie 1/( x 1 x 2) = 10 ist durchgezogene Linie).

Abbildung 5.9 - Gradienten der Funktion z \u003d 1 / (x 1 x 2) an verschiedenen Punkten

Nehmen Sie zum Beispiel den Punkt (0,5; 1) und berechnen Sie den Gradienten an diesem Punkt: (-1 / (0,5 2 * 1); -1 / (0,5 * 1 2)) \u003d (-4; - 2) . Beachten Sie, dass der Punkt (0,5; 1) auf der Niveaulinie 1 / (x 1 x 2) \u003d 2 liegt, weil z \u003d f (0,5; 1) \u003d 1 / (0,5 * 1) \u003d 2. To Zeichnen Sie den Vektor (-4; -2) in Abbildung 5.9, verbinden Sie den Punkt (0,5; 1) mit dem Punkt (-3,5; -1), denn (-3,5 - 0,5; -1 - 1) = (-4; -2).

Nehmen wir einen anderen Punkt auf derselben Höhenlinie, zum Beispiel Punkt (1; 0,5) (z=f(1; 0,5) = 1/(0,5*1) = 2). Berechnen Sie den Gradienten an diesem Punkt (-1/(1 2 *0,5); -1/(1*0,5 2)) = (-2; -4). Um es in Abbildung 5.9 darzustellen, verbinden wir den Punkt (1; 0,5) mit dem Punkt (-1; -3,5), denn (-1 - 1; -3,5 - 0,5) = (-2; - 4).

Nehmen wir noch einen Punkt auf der gleichen Höhenlinie, aber nur jetzt in einem kraftschlüssigen Koordinatenviertel. Beispiel: Punkt (-0,5; -1) (z=f(-0,5; -1) = 1/((-1)*(-0,5)) = 2). Der Gradient an diesem Punkt ist (-1/((-0,5) 2 *(-1)); -1/((-0,5)*(-1) 2)) = (4; 2). Stellen wir es in Abbildung 5.9 dar, indem wir den Punkt (-0,5; -1) mit dem Punkt (3,5; 1) verbinden, denn (3,5 - (-0,5); 1 - (-1)) = (4 ; 2).

Zu beachten ist, dass in allen drei betrachteten Fällen der Gradient die Wachstumsrichtung des Funktionsniveaus zeigt (in Richtung der Niveaulinie 1/(x 1 x 2) = 10 > 2).

Es kann bewiesen werden, dass die Steigung immer senkrecht zur Nivellierlinie (Niveaufläche) steht, die durch den gegebenen Punkt verläuft.

Extrema einer Funktion mehrerer Variablen

Lassen Sie uns das Konzept definieren extrem für eine Funktion mit vielen Variablen.

Die Funktion vieler Variablen f(X) hat an der Stelle X (0) Maximum Minimum), wenn es eine solche Umgebung dieses Punktes gibt, dass für alle Punkte X aus dieser Umgebung die Ungleichungen f(X)f(X (0)) () gelten.

Sind diese Ungleichungen streng erfüllt, so spricht man vom Extremum stark, und wenn nicht, dann schwach.

Beachten Sie, dass das auf diese Weise definierte Extremum ist lokal Charakter, da diese Ungleichungen nur für eine gewisse Umgebung des Extremumpunktes gelten.

Eine notwendige Bedingung für ein lokales Extremum einer differenzierbaren Funktion z=f(x 1, . . ., x n) an einem Punkt ist die Nullgleichheit aller partiellen Ableitungen erster Ordnung an diesem Punkt:
.

Die Punkte, an denen diese Gleichheiten gelten, werden genannt stationär.

Anders lässt sich die notwendige Bedingung für ein Extremum wie folgt formulieren: Am Extremumpunkt ist die Steigung gleich Null. Es ist auch möglich, eine allgemeinere Aussage zu beweisen - am Extremumspunkt verschwinden die Ableitungen der Funktion in alle Richtungen.

Stationäre Punkte sollten zusätzlichen Studien unterzogen werden - ob ausreichende Bedingungen für die Existenz eines lokalen Extremums erfüllt sind. Bestimmen Sie dazu das Vorzeichen des Differentials zweiter Ordnung. Wenn es für alle, die nicht gleichzeitig gleich Null sind, immer negativ (positiv) ist, dann hat die Funktion ein Maximum (Minimum). Wenn es nicht nur bei Nullinkrementen verschwinden kann, dann bleibt die Frage nach dem Extremum offen. Wenn es sowohl positive als auch negative Werte annehmen kann, gibt es am stationären Punkt kein Extremum.

Im allgemeinen Fall ist die Bestimmung des Vorzeichens des Differentials ein ziemlich kompliziertes Problem, auf das wir hier nicht eingehen werden. Für eine Funktion von zwei Variablen kann man das beweisen, wenn sie an einem stationären Punkt ist
, dann gibt es ein Extremum. In diesem Fall stimmt das Vorzeichen des zweiten Differentials mit dem Vorzeichen überein
, d.h. Wenn
, dann ist dies das Maximum, und wenn
, dann ist dies das Minimum. Wenn ein
, dann gibt es an dieser Stelle kein Extremum, und wenn
, dann bleibt die Frage nach dem Extremum offen.

Beispiel 1. Finden Sie Extrema einer Funktion
.

Lassen Sie uns partielle Ableitungen durch die Methode der logarithmischen Differenzierung finden.

ln z = ln 2 + ln (x + y) + ln (1 + xy) – ln (1 + x 2) – ln (1 + y 2)

Ähnlich
.

Lassen Sie uns stationäre Punkte aus dem Gleichungssystem finden:

Somit werden vier stationäre Punkte (1; 1), (1; -1), (-1; 1) und (-1; -1) gefunden.

Finden wir partielle Ableitungen zweiter Ordnung:

ln (z x `) = ln 2 + ln (1 - x 2) -2ln (1 + x 2)

Ähnlich
;
.

Als
, Ausdruckszeichen
hängt nur davon ab
. Beachten Sie, dass bei diesen beiden Ableitungen der Nenner immer positiv ist, sodass Sie nur das Vorzeichen des Zählers oder sogar das Vorzeichen der Ausdrücke x (x 2 - 3) und y (y 2 - 3) berücksichtigen können. Lassen Sie es uns an jedem kritischen Punkt bestimmen und die Erfüllung der hinreichenden Extremumsbedingung überprüfen.

Für Punkt (1; 1) erhalten wir 1*(1 2 - 3) = -2< 0. Т.к. произведение двух отрицательных чисел
> 0 und
< 0, в точке (1; 1) можно найти максимум. Он равен
= 2*(1 + 1)*(1 +1*1)/((1 +1 2)*(1 +1 2)) = = 8/4 = 2.

Für Punkt (1; -1) erhalten wir 1*(1 2 - 3) = -2< 0 и (-1)*((-1) 2 – 3) = 2 >0. Weil das Produkt dieser Zahlen
< 0, в этой точке экстремума нет. Аналогично можно показать, что нет экстремума в точке (-1; 1).

Für den Punkt (-1; -1) erhalten wir (-1)*((-1) 2 - 3) = 2 > 0. Produkt zweier positiver Zahlen
> 0 und
> 0, am Punkt (-1; -1) findet man ein Minimum. Es ist gleich 2*((-1) + (-1))*(1 +(-1)*(-1))/((1 +(-1) 2)*(1 +(-1) 2) ) = -8/4 = = -2.

Finden global Das Maximum oder Minimum (der größte oder kleinste Wert der Funktion) ist etwas komplizierter als das lokale Extremum, da diese Werte nicht nur an stationären Punkten, sondern auch an der Grenze des Definitionsbereichs erreicht werden können. Es ist nicht immer einfach, das Verhalten einer Funktion an der Grenze dieses Bereichs zu untersuchen.