EGOROVA VICTORIA VALEREVNA

Mathematic teacher

highest qualification category

TOPIC: “IDENTITY TRANSFORMATION

LOGARITHMIC EXPRESSIONS"

Knowledge and skills that students should master after studying this lesson:

know the definition of the logarithm of a number, the basic logarithmic identity, the properties of logarithms;

be able to perform transformations of expressions containing logarithms, calculate logarithms.

Literature:

1. Alimov Sh.A., Kolyagin Yu.M., Sidorov Yu.V. and others. Algebra and the beginning of analysis: a textbook for grades 10-11 educational institutions. - M .: Education, 2001.

2. Kochagin V.V., Kochagina M.V., Intensive course of preparation for the exam. – M.: Eksmo, 2009.

3. A. G. Merzlyak, V. B. Polonsky, and M. S. Yakir, Algebraic simulator: A guide for schoolchildren and university entrants. – M.: Ileksa, 2005.

4. Gusev V.A., Mordkovich A.G. Maths: Reference materials: A book for students. - M .: Education, 2001.

Lesson plan:

During the classes:

1) Logarithm is a Greek word that consists of 2 words: “logos” - relation, “arithmos” - number. So the logarithm is the number that measures the ratio. A publication in 1614 reported that Napier had invented logarithms. Later, he compiled logarithmic tables, which are now known to us as the tables of Bradys. In less than a century, tables have spread throughout the world and have become an indispensable computing tool. In the future, they were, as it were, built into a convenient device that extremely speeds up the calculation process - a slide rule, which was used until the seventies of the twentieth century.

Attachment 1.

2) logarithm positive numberb by reason a, moreover greater than zero and not equal to one,is the exponent to which a number must be raiseda to get the numberb.

This equality expressing the definition of the logarithm is calledbasic logarithmic identity .

C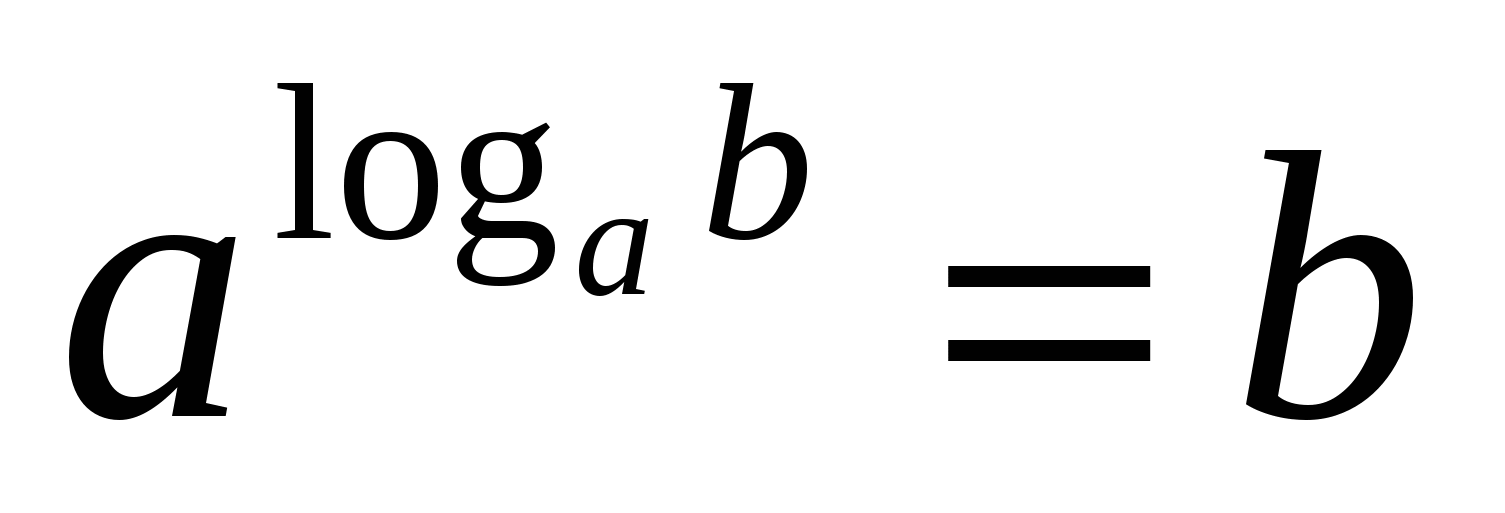

OR 1

P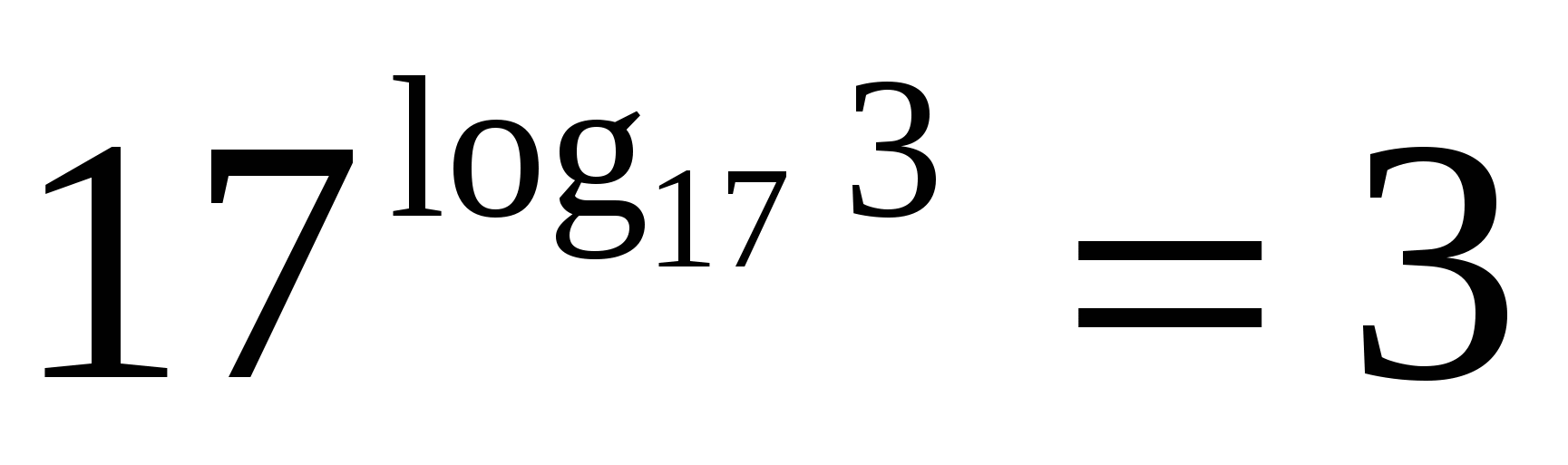

The base of the degree and the base of the logarithm are seventeen, which means that according to the basic logarithmic identity, the value of the expression is three.

We will work verbally:

SCH
ELCHOK

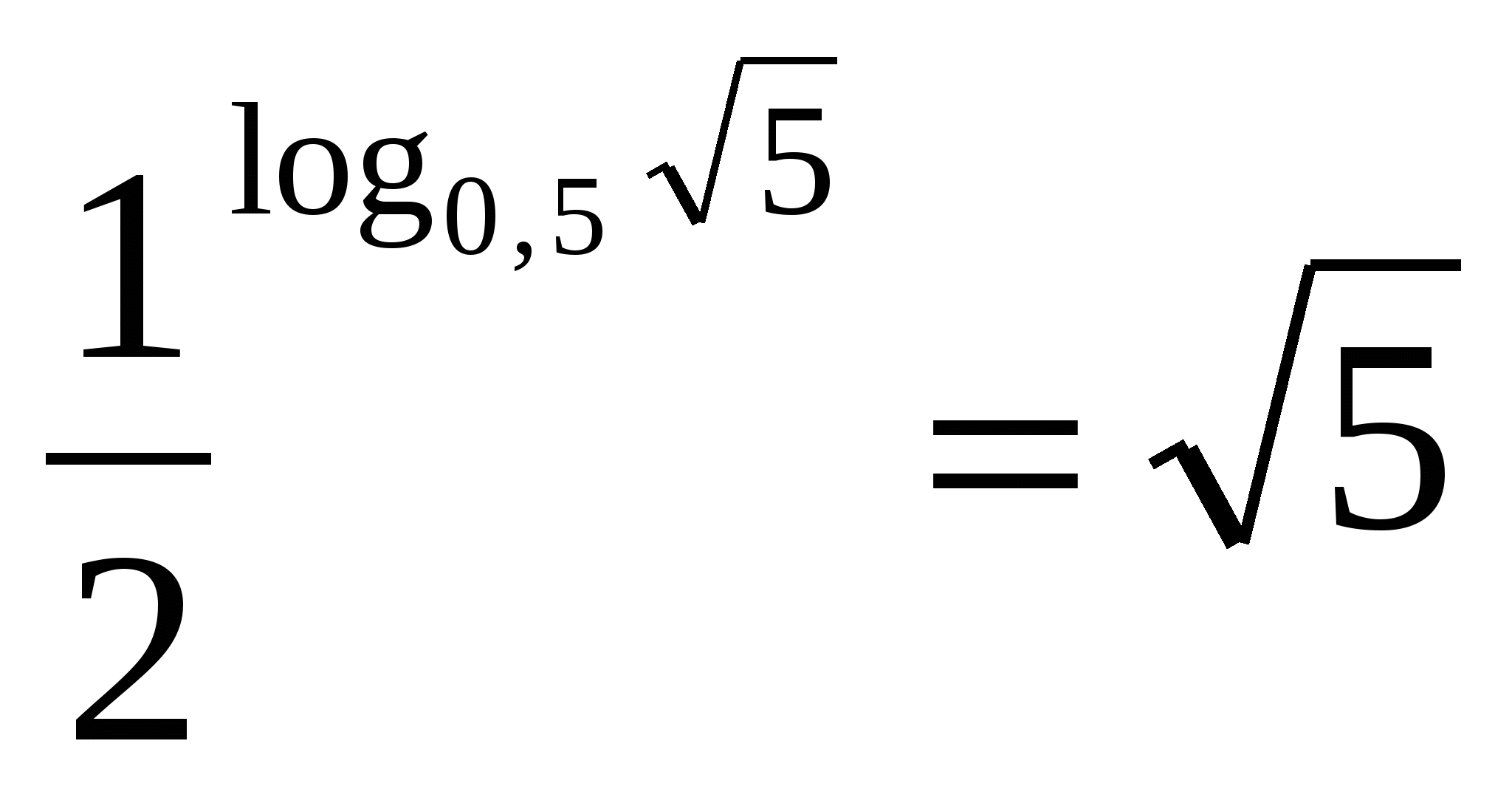
ABOUT the bottom second is zero point five tenths, so the expression is equal to the arithmetic square root of five.

P

appendix 2.

Equality means that

From the definition of the logarithm, the following important equalities are obtained:

For example:

P
appendix 3.

Let's move on to USE assignments:

Appendix 4

3
) There is a special notation and name for the base ten logarithm.decimal logarithm .

L
arithm to basee callednatural logarithm .

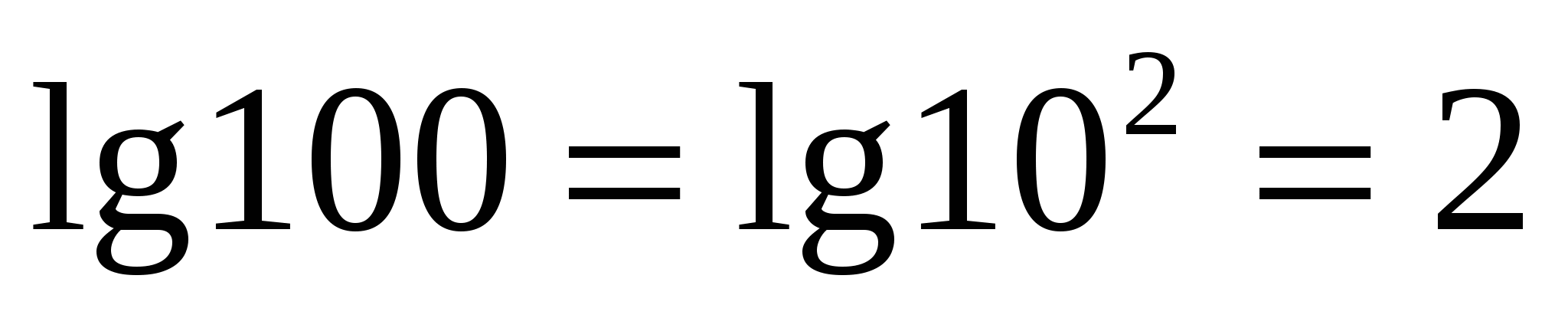
H
for example,

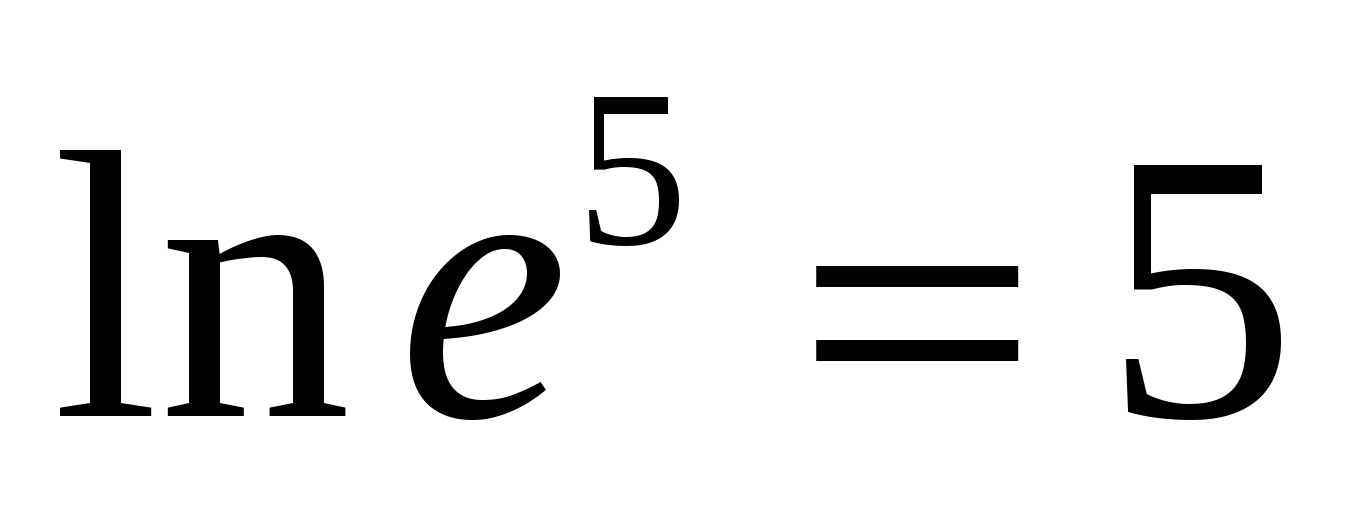
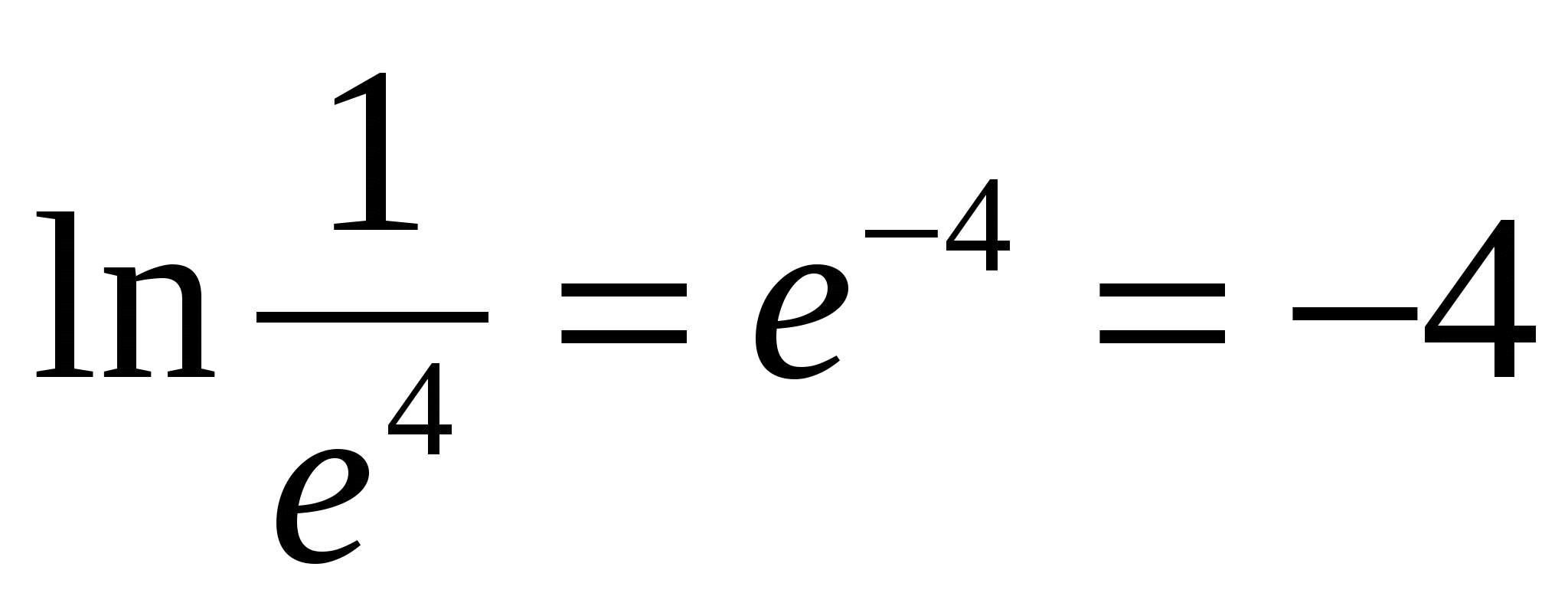
4) The following properties follow from the definition of the logarithm. All properties are formulated and proved only for positive values ​​of variables contained under logarithm signs.

Base logarithm of the product of two positive numbers but is equal to the sum logarithms of these numbers with the same base.

DER 2

For example,

W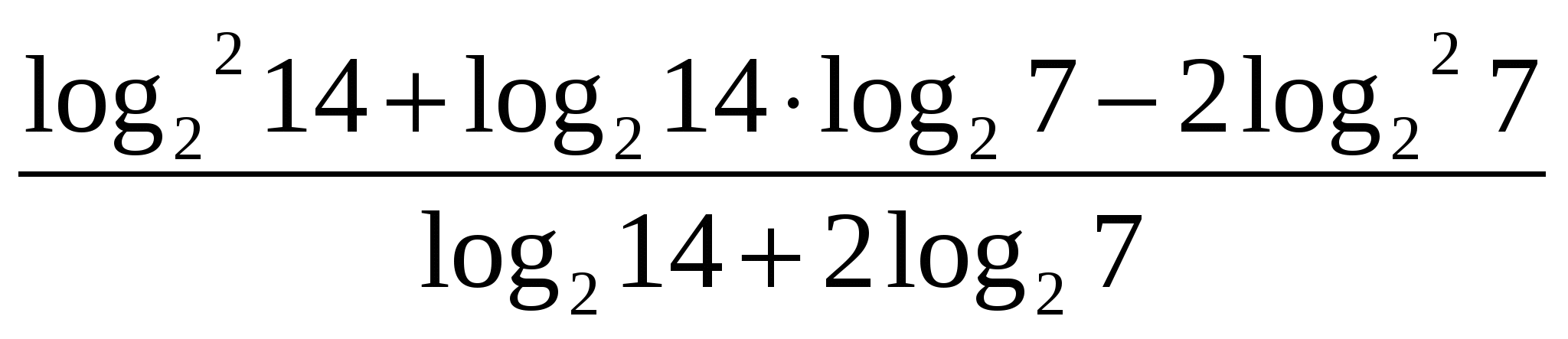
assignment 1.

Task 2. Simplify the expression

IN
Let's use the previous example. Let's replace

Note that the logarithm is squared, so the sum must also be squared. Using the formula for the square of the sum, open the brackets. We present similar terms.

5) The logarithm of the quotient is equal to the difference between the logarithms of the dividend and the divisor.

C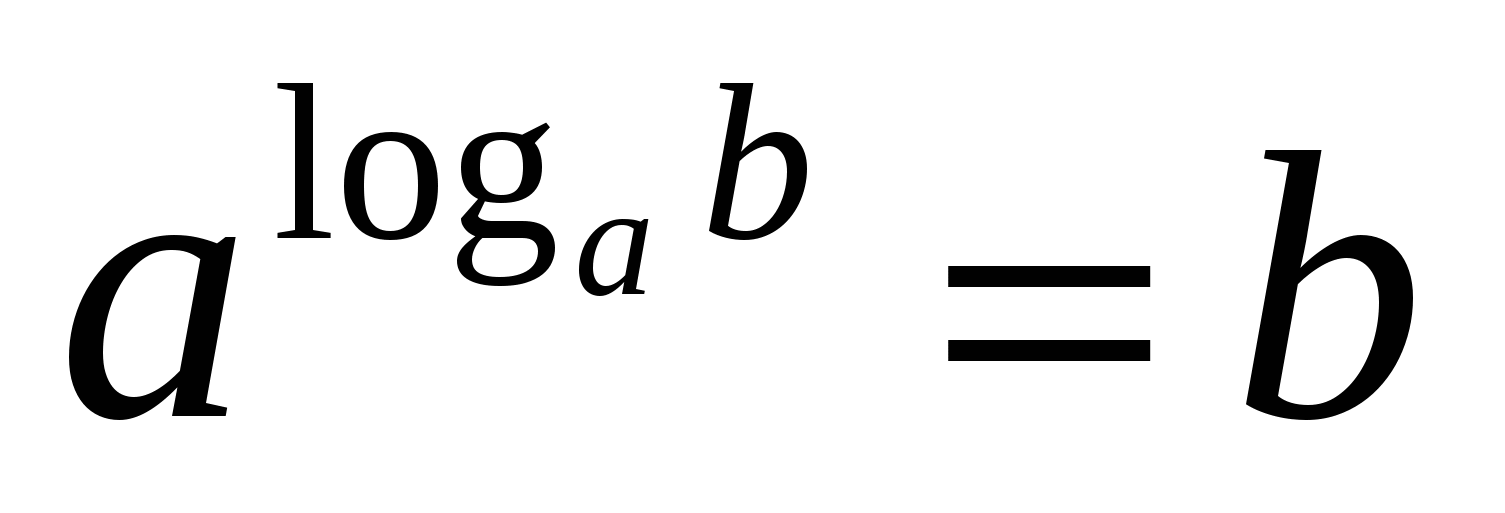

Pay attention to the base of the degree and the base of the logarithm - they are the same.

OR 3

R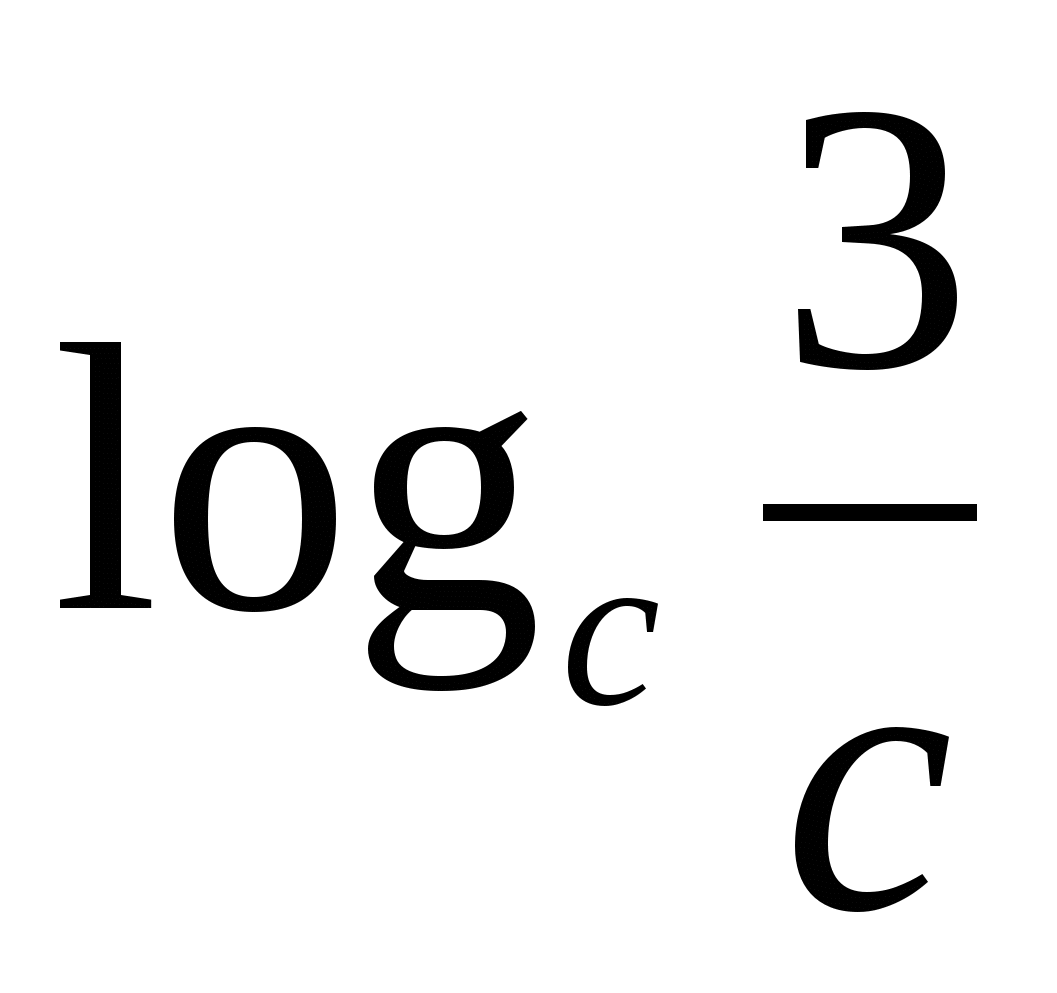

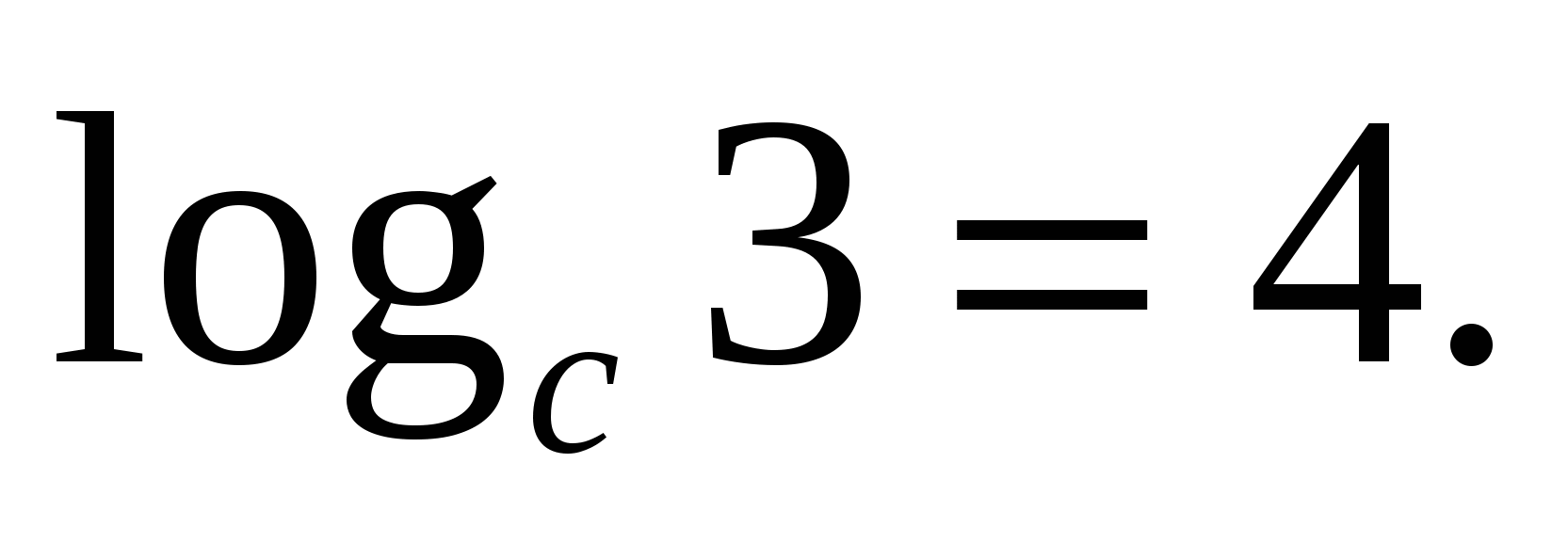Let's look at the application of this formula with an example:

W
assignment 1. Find the value of the expression if

Task 2. Find the value b by its logarithm

6) Logarithm of the degree to the basebut , is equal to the product of the exponent and the logarithm in the same base.

DER 4

For example,

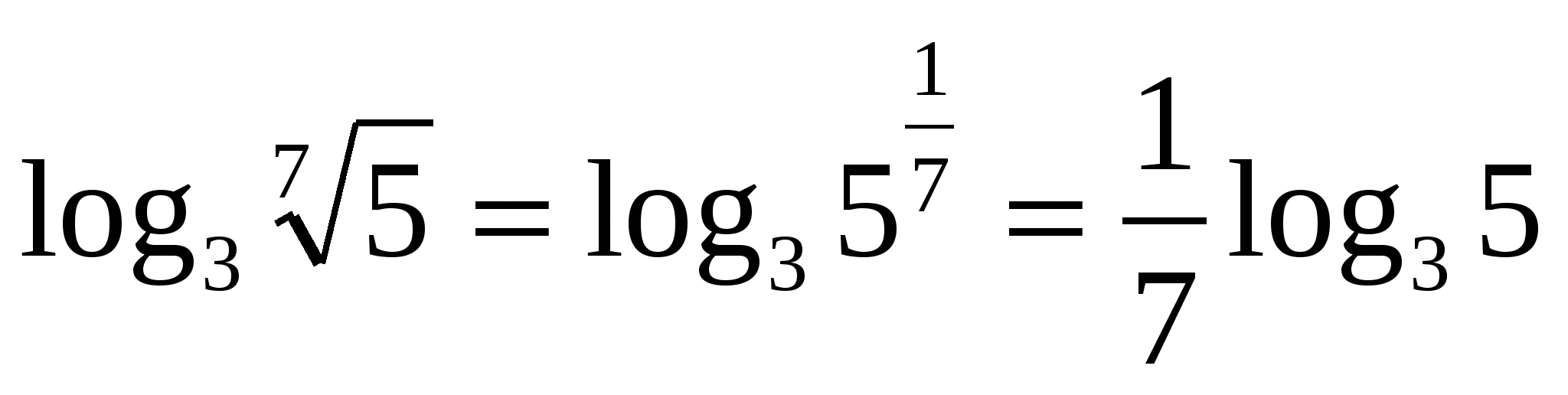
W
assignment 1. Calculate if

Let's simplify the expression

Formula

called formula for transition to a new basis.

W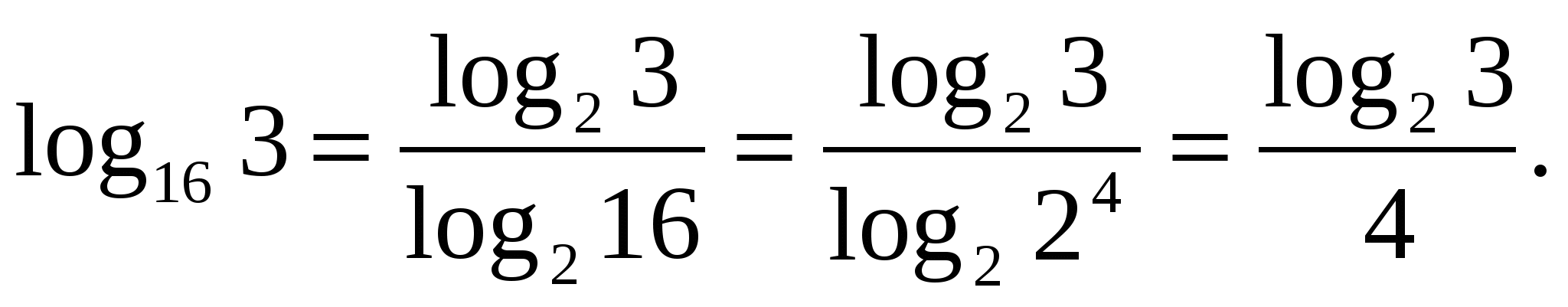

assignment 1. Express in terms of a logarithm with base 2.

Task 2. Calculate

CER 5

CER 6

For example,

W

assignment 1. Calculate

W
assignment 2. Calculate

9) You can start logarithmic transformations only if if you remember all the properties of logarithms. Having repeated them, we consider tasks for transformations logarithmic expressions on the other hand.

To convert the sum or difference of logarithmic expressions, sometimes it is enough to use the definition of the logarithm, and most often the properties of the logarithm of the product or quotient.

W
assignment 1. Calculate

Let's solve it in two ways.

1 way, using the definition of the logarithm:

Method 2 based on quotient logarithm property:

Task 2. Find the value of an expression

Let us first apply the formula the logarithm of the product, then the definition of the logarithm.

The basic logarithmic identity is used when converting expressions containing a logarithm in the exponent. The idea of ​​such operations is to obtain equal grounds powers and bases of the logarithm.

Sometimes it is necessary to transform the expression by the properties of the logarithm and by the properties of the degree, also one can easily move from one base to another using the transition formula. In other cases, multiple properties should be applied.

W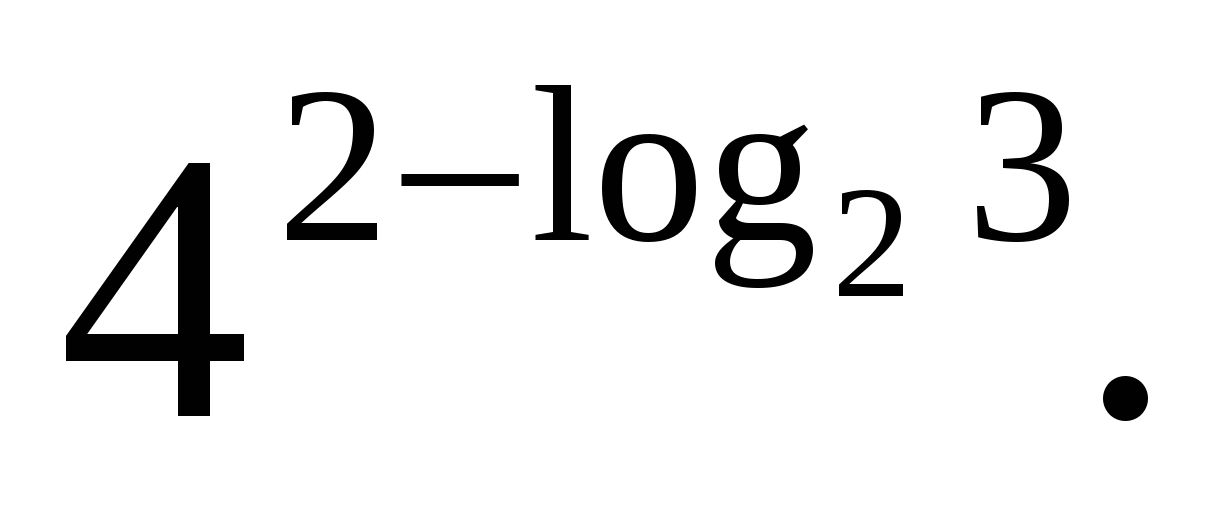
assignment 3. Calculate

W
assignment 4. Find the value of an expression

Task 5. Find the value of an expression

W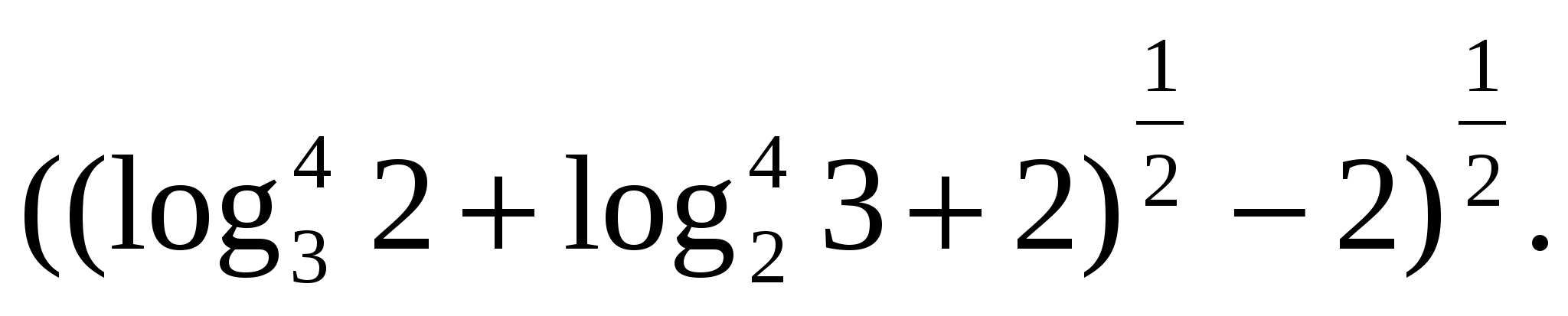
assignment 6. Express as a difference of logarithms

H
The greatest difficulty is the transformation of logarithmic expressions under the radical. In the process of transformations, one has to consider the modules of logarithmic expressions, for the disclosure of which it is necessary to compare irrational numbers or rational and irrational numbers. We will act consistently. Consider the expression under the inner radical.

Substitute in the original expression.

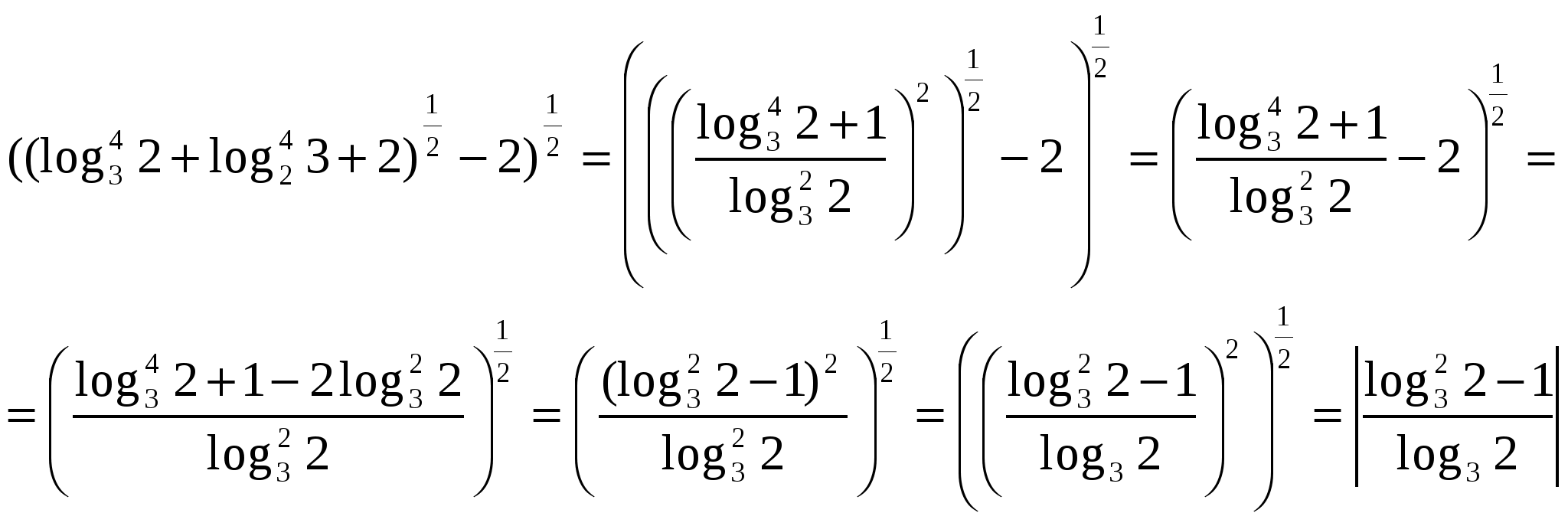It should be noted that the transformation of logarithmic expressions can also be encountered when solving equations and inequalities or studying functions, therefore, in an implicit form, they can also be present in the assignments of groups B and C.

10) Summing up. Questions:

The base 10 logarithm is called

basic logarithm

main logarithm

natural logarithm

decimal logarithm

2) What values ​​canx in expression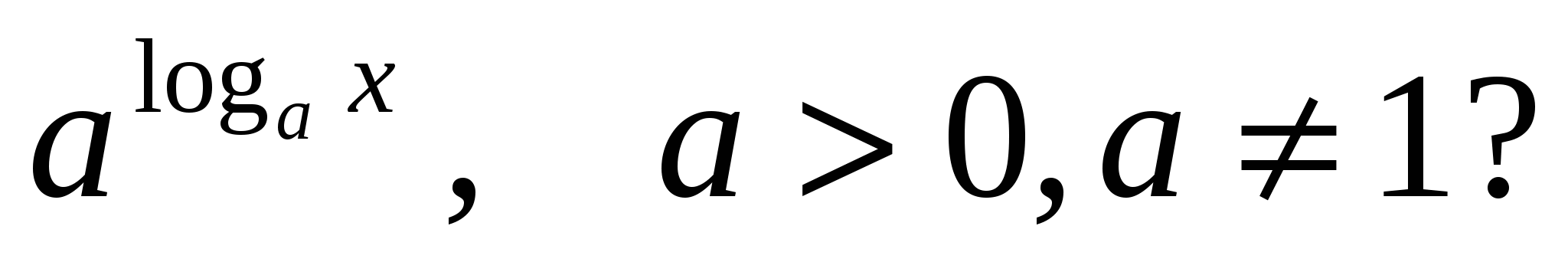

Value is not defined

5) Indicate the ratio that is true for allx ≠ 0 .

6) Specify the correct ratio for the formula for the transition to a new base.

7) Indicate the correct equality for

11) Control testing.

Maths. Thematic tests. Part II. Preparation for the Unified State Exam-2010. 10-11 grades. Ed. Lysenko F.F. - Rostov n / D .: Legion, 2009. - 176s.

Maths. USE-2009. Thematic tests. Part II (B4-B8, C1-C2) Ed. Lysenko F.F. - Rostov n / D: Legion, 2008 - 160 p.

The manual consists of tests on individual topics, which are traditional in the course of mathematics and therefore, as a rule, are included in the exam. They fully cover the groups of tasks of an increased and high level of complexity of the USE, except for text tasks and problems in geometry. One or more test suites are offered for each topic. Each set contains 10 tests, each test contains 8 tasks.

The purpose of this book is to work out tasks with a short and detailed answer. USE tests. It is necessary primarily for graduates who expect to receive USE good assessment, as well as for students of the 10th grade, who can consolidate the topics covered from the point of view of the USE. The proposed manual can be useful to all graduates preparing for the USE in mathematics, as well as teachers preparing students for the USE.

Format: djvu/zip (2009 , 176s.)

Size: 2.5 MB

Download / Download file 14

Format: pdf (2009 , 176s.)

Size: 8.6 MB

Download: 14 .12.2018, links removed at the request of the Legion publishing house (see note)

Format: djvu/zip (2008 , 160s.)

Size: 3 MB

Download / Download file 14 .12.2018, links removed at the request of the Legion publishing house (see note)

Format: pdf (2008 , 160s.)

Size: 9.9 MB

Download: 14 .12.2018, links removed at the request of the Legion publishing house (see note)

Training and metodology complex"Mathematics. USE-2010" ed. Lysenko F.F. and Kulabukhov S.Yu. includes tutorials:
1. Maths. Preparation for the Unified State Exam-2010.
2. Reshebnik. Maths. Preparation for the Unified State Exam-2010.
3. Maths. Thematic tests. Part I (basic level). Preparation for the Unified State Exam-2010. 10-11 grades.
4. Maths. Thematic tests. Part II. Preparation for the Unified State Exam-2010. 10-11 grades.
5. Maths. Thematic tests: geometry, word problems. Preparation for the Unified State Exam-2010. 10-11 grades.
6. Maths. Collection of USE tests 2001 - 2010.
7. Maths. Preparation for the Unified State Exam-2010. Training tests.
8. Pocket guide mathematics.

Table of contents
From authors 11
§ 1. Identity transformations of logarithmic expressions 13
Option number 1 13
Option number 2 13
Option number 3 14
Option number 4 14
Option number 5 15
Option number 6 15
Option number 7 16
Option number 8 16
Option number 9 17
Option number 10 17
§ 2. Identity transformations of expressions containing degree 18
Option number 1 18
Option number 2 19
Option number 3 19
Option number 4 20
Option number 5 21
Option number 6 21
Option number 7 22
Option number 8 23
Option number 9 23
Option number 10 24
§ 3. Identity transformations irrational expressions 25
Option number 1 25
Option number 2 25
Option number 3 26
Option number 4 26
Option number 5 27
Option number 6 28
Option number 7 28
Option number 8 29
Option number 9 30
Option number 10 30
§ 4. Systems of equations 31
Option number 1 31
Option number 2 32
Option number 3 33
Option number 4 33
Option number 5 34
Option number 6 35
Option number 7 36
Option number 8 37
Option number 9 38
Option number 10 39
§ five. geometric sense derivative 39
Option number 1 39
Option number 2 41
Option number 3 43
Option number 4 44
Option number 5 46
Option number 6 48
Option number 7 50
Option number 8 52
Option number 9 54
Option number 10 55
§ 6. Inequalities 56
Option number 1 g 56
Option number 2 57
Option number 3 58
Option number 4 58
Option number 5 59
Option number 6 60
Option number 7 60
Option number 8 61
Option number 9 62
Option number 10 63
§ 7. Irrational Equations 63
Option number 1 63
Option number 2 64
Option number 3 65
Option number 4 65
Option number 5 66
Option number 6 66
Option number 7 67
Option number 8 67
Option number 9 68
Option No. Yu 68
§ 8. Trigonometric Equations 69
Option number 1 69
Option number 2 69
Option number 3 70
Option number 4 70
Option number 5 71
Option number 6 72
Option number 7 72
Option number 8 73
Option number 9 74
Option number 10 74
§ 9. Logarithmic equations 75
Option number 1 75
Option number 2 75
Option number 3 76
Option number 4 76
Option number 5 77
Option number 6 77
Option number 7 78
Option No. 8 * 78
Option number 9 79
Option number 10 79
§ 10. Exponential Equations 80
Option number 1 80
Option number 2 80
Option number 3 81
Option number 4 81
Option number 5 82
Option number 6 82
Option number 7 83
Option number 8 83
Option number 9 84
Option number 10 84
§eleven. Periodicity, even and odd functions 85
Option number 1 85
Option number 2 86
Option number 3 87
Option number 4 89
Option number 5 90
Option number 6 91
Option number 7 92
Option number 8 93
Option number 9 94
Option number 10 95
§ 12. Zeros complex function. Limited function 97
Option number 1 97
Option number 2 97
Option number 3 98
Option number 4 98
Option number 5 99
Option number 6 99
Option number 7 100
Option number 8 100
Option number 9 101
Option number 10 101
§ 13. Domain of definition, set of values, monotonicity of functions 102
Option number 1 102
Option number 2 102
Option number 3 103
Option number 4 103
Option number 5 104
Option number 6 104
Option number 7 105
Option number 8 105
Option number 9 106
Option number 10 107
§ 14. Extrema of a function. The largest and smallest values ​​of the function 107
Option number 1 107
Option number 2 108
Option number 3 108
Option number 4 109
Option number 5 109
Option number 6 110
Option number 7 110
Option number 8 111
Option number 9 111
Option number 10 112
§ 15. Various techniques for solving logarithmic equations 113
Option number 1 113
Option number 2 113
Option number 3 114
Option number 4 114
Option number 5 115
Option number 6 115
Option number 7 116
Option number 8 116
Option number 9 117
Option number 10 117
§ 16. Various methods for solving trigonometric equations 118
Option number 1 118
Option number 2 118
Option number 3 118
Option number 4 119
Option number 5 119
Option number 6 120
Option number 7 120
Option number 8 121
Option number 9 121
Option number 10 122
§ 17. Various methods for solving irrational equations 123
Option number 1 123
Option number 2 123
Option number 3 124
Option number 4 124
Option number 5 125
Option number 6 125
Option number 7 125
Option number 8 126
Option number 9 126
Option No. 10 127
§ 18. Equations containing a variable under the modulo sign 127
Option number 1 127
Option number 2 128
Option number 3 128
Option number 4 129
Option number 5 129
Option number 6 130
Option number 7 130
Option number 8 131
Option number 9 131
Option number 10 131
§ 19. Various methods for solving exponential equations.132
Option number 1 132
Option number 2 133
Option number 3 133
Option number 4 134
Option number 5 134
Option number 6 135
Option number 7 135
Option number 8 135
Option number 9 136
Option number 10 136
§ 20. Various techniques for solving combined equations 137
Option number 1 137
Option number 2 137
Option number 3 138
Option number 4 138
Option number 5 139
Option number 6 139
Option number 7 140
Option number 8 140
Option number 9 141
Option number 10 141
§ 21. Equations with a parameter containing module 142
Option number 1 142
Option number 2 142
Option number 3 143
Option number 4 144
Option number 5 144
Option number 6 145
Option number 7 146
Option number 8 146
Option number 9 147
Option number 10 148
Answers 149
§ one. Identity transformations logarithmic expressions 149
§ 2. Identity transformations of expressions containing the degree 150
§ 3. Identity transformations of irrational expressions 150
§ 4. Systems of equations 151
§ 5. The geometric meaning of the derivative 151
§ 6. Inequalities 152
§ 7. Irrational equations 152
§ 8. Trigonometric equations 153
§ 9. Logarithmic equations 153
§ 10. Exponential Equations 154
§eleven. Periodicity, even and odd functions 154
§ 12. Zeros of a complex function. Limited function 155
§ 13. Domain of definition, set of values, monotonicity of functions 156
§ 14. Extrema of a function. The largest and smallest values ​​of the function 158
§ 15. Various tricks for solving logarithmic equations 159
§ 16. Various techniques for solving trigonometric equations 160
§ 17. Various tricks for solving irrational equations 164
§ 18. Equations containing a variable under the modulo sign 165
§ 19. Various techniques for solving exponential equations.166
§ 20. Various techniques for solving combined equations 167
§ 21. Equations with a parameter containing module 169
Literature 170

Problem B7 gives an expression that needs to be simplified. The result should be a regular number that can be written on the answer sheet. All expressions are conditionally divided into three types:

1. logarithmic,
2. Demonstration,
3. Combined.

Exponential and logarithmic expressions in their pure form are almost never found. However, knowing how they are calculated is essential.

In general, problem B7 is solved quite simply and is quite within the power of the average graduate. The lack of clear algorithms is compensated by its standard and uniformity. You can learn how to solve such problems simply by a large number workouts.

Logarithmic Expressions

The vast majority of B7 problems contain logarithms in one form or another. This topic is traditionally considered difficult, since its study, as a rule, falls on the 11th grade - the era of mass preparation for final exams. As a result, many graduates have a very vague idea about logarithms.

But in this task, no one requires deep theoretical knowledge. We will meet only the simplest expressions that require straightforward reasoning and may well be mastered independently. Below are the basic formulas you need to know to deal with logarithms:

In addition, one must be able to replace roots and fractions with degrees with rational indicator, otherwise in some expressions there will simply be nothing to take out from under the sign of the logarithm. Replacement formulas:

A task. Find expression values:
log 6 270 − log 6 7.5
log 5 775 − log 5 6.2

The first two expressions are converted as the difference of logarithms:
log 6 270 − log 6 7.5 = log 6 (270: 7.5) = log 6 36 = 2;
log 5 775 − log 5 6.2 = log 5 (775: 6.2) = log 5 125 = 3.

To calculate the third expression, you will have to select degrees - both in the base and in the argument. First, let's find the internal logarithm:

Then - external:

Constructions like log a log b x seem complicated and misunderstood to many. Meanwhile, this is just the logarithm of the logarithm, i.e. log a (log b x ). First, the inner logarithm is calculated (put log b x = c ), and then the outer one: log a c .

exponential expressions

We will call an exponential expression any construction of the form a k , where the numbers a and k are arbitrary constants, and a > 0. Methods for working with such expressions are quite simple and are considered in the 8th grade algebra lessons.

Below are the basic formulas that you must know. The application of these formulas in practice, as a rule, does not cause problems.

1. a n a m = a n + m ;
2. a n / a m = a n − m ;
3. (a n ) m = a n m ;
4. (a b) n = a n b n ;
5. (a : b ) n = a n : b n .

If a complex expression with powers is encountered, and it is not clear how to approach it, a universal technique is used - decomposition into prime factors. As a result big numbers in the bases of degrees are replaced by simple and understandable elements. Then it remains only to apply the above formulas - and the problem will be solved.

A task. Find expression values: 7 9 3 11: 21 8 , 24 7: 3 6: 16 5 , 30 6: 6 5: 25 2 .

Solution. We decompose all bases of powers into prime factors:
7 9 3 11: 21 8 = 7 9 3 11: (7 3) 8 = 7 9 3 11: (7 8 3 8) = 7 9 3 11: 7 8: 3 8 = 7 3 3 = 189.
24 7: 3 6: 16 5 = (3 2 3) 7: 3 6: (2 4) 5 = 3 7 2 21: 3 6: 2 20 = 3 2 = 6.
30 6: 6 5: 25 2 = (5 3 2) 6: (3 2) 5: (5 2) 2 = 5 6 3 6 2 6: 3 5: 2 5: 5 4 = 5 2 3 2 = 150.

Combined tasks

If you know the formulas, then all exponential and logarithmic expressions are solved literally in one line. However, in problem B7, powers and logarithms can be combined to form rather strong combinations.

Transnistrian State University

them. T.G. Shevchenko

Faculty of Physics and Mathematics

Department of Mathematical Analysis

and methods of teaching mathematics

COURSE WORK

"Identity Transformations

exponential and logarithmic

expressions"

Work completed:

student of ______ group

Faculty of Physics and Mathematics

_________________________

Checked work:

_________________________

Tiraspol, 2003

Introduction………………………………………………………………………2

Chapter 1

§one. Formation of skills for applying specific types of transformations………………………………………………………………………………….4

§2. Features of the organization of a knowledge system in the study of identical transformations.…….………………………….………..………….5

§3. Mathematics Program ……………………………………….11

Chapter 2

§one. Generalization of the concept of degree……………………………………..13

§2. The exponential function…………………………………………..15

§3. Logarithmic function………………………………………….16

Chapter 3. Identical transformations of exponential and logarithmic expressions in practice ............................................ ...................................19

Conclusion………………………………………………………………..24

List of used literature…………………………………….25
Introduction

In this term paper identical transformations of the exponential and logarithmic functions will be considered, the methodology for teaching them in the school course of algebra and the beginning of analysis will be considered.

The first chapter of this work describes the methodology for teaching identical transformations in the school course of mathematics, it also includes a program in mathematics in the course "Algebra and the beginning of analysis" with the study of exponential and logarithmic functions.

The second chapter deals directly with the exponential and logarithmic functions themselves, their main properties used in identical transformations.

The third chapter is the solution of examples and problems using the identical transformations of the exponential and logarithmic functions.

The study of various transformations of expressions and formulas takes up a significant part of the study time in the course of school mathematics. The simplest transformations based on properties arithmetic operations, are already produced in primary school and in grades IV-V. But the main burden on the formation of skills and abilities to perform transformations is borne by the course of school algebra. This is connected both with a sharp increase in the number and variety of transformations performed, and with the complication of activities to substantiate them and clarify the conditions of applicability, with the identification and study of generalized concepts of identity, identical transformation, equivalent transformation, logical consequence.

The culture of performing identical transformations develops in the same way as the culture of computing, based on a solid knowledge of the properties of operations on objects (numbers, vectors, polynomials, etc.) and algorithms for their implementation. It manifests itself not only in the ability to correctly justify transformations, but also in the ability to find the shortest path to the transition from the original analytical expression to the expression that best suits the purpose of the transformation, in the ability to track changes in the domain of definition of analytical expressions in a chain of identical transformations, in the speed and error-free execution of transformations. .

Security high culture calculations and identical transformations represents important issue teaching mathematics. However, this problem is still far from being solved satisfactorily. Proof of this is the statistical data of the organs public education, which annually state errors and irrational methods of calculations and transformations made by students of various classes when performing control works. This is confirmed by the opinions of higher educational institutions about the quality of mathematical knowledge and skills of applicants. One cannot but agree with the conclusions of public education authorities and universities that the level of culture of computing and identical transformations in high school is a consequence of formalism in the knowledge of students, the separation of theory from practice.

Identity transformations and teaching methods

in the school course of algebra and the beginning of analysis.

§one. Formation of application skills

specific types of transformations.

The system of methods and rules for carrying out transformations, used at the stage of the beginnings of algebra, has a very wide range of applications: it is used in the study of the entire course of mathematics. However, precisely because of its low specificity, this system needs additional transformations that take into account the peculiarities of the structure of the transformed expressions and the properties of newly introduced operations and functions. The development of the corresponding types of transformations begins with the introduction of abbreviated multiplication formulas. Then we consider the transformations associated with the exponentiation operation, with different classes elementary functions- exponential, power, logarithmic, trigonometric. Each of these types of transformations goes through a stage of study, in which attention is focused on the assimilation of their characteristic features.

With the accumulation of material, it becomes possible to single out the common features of all the transformations under consideration and, on this basis, introduce the concepts of identical and equivalent transformations.

It should be noted that the concept of an identical transformation is given in the school course of algebra not in full generality, but only in application to expressions. Transformations are divided into two classes: identical transformations are transformations of expressions, and equivalent transformations are transformations of formulas. In the case when there is a need to simplify one part of the formula, an expression is highlighted in this formula, which serves as an argument for the applied identical transformation. The corresponding predicate is considered unchanged.

As for the organization of an integral system of transformations (synthesis), its main goal is to form a flexible and powerful; apparatus suitable for use in solving a variety of learning tasks.

In the course of algebra and the beginning of analysis, an integral system of transformations, already formed in its main features, continues to be gradually improved. Some new types of transformations are also added to it, but they only enrich it, expand its capabilities, but do not change its structure. The methodology for studying these new transformations practically does not differ from that used in the course of algebra.

§2. Features of the organization of the task system

in the study of identical transformations.

The basic principle of organizing any system of tasks is to present them from simple to complex, taking into account the need for students to overcome feasible difficulties and create problem situations. The specified basic principle requires concretization in relation to the features of this educational material. To describe various systems of tasks in the methodology of mathematics, the concept of a cycle of exercises is used. The cycle of exercises is characterized by the combination in the sequence of exercises of several aspects of the study and methods of arranging the material. In relation to identical transformations, the idea of ​​a cycle can be given as follows.

The cycle of exercises is connected with the study of one identity, around which other identities are grouped, which are in a natural connection with it. The composition of the cycle, along with executive tasks, includes tasks that require recognition of the applicability of the considered identity. The identity under study is used to perform calculations on various numerical domains. The specificity of the identity is taken into account; in particular, turns of speech associated with it are organized.

The tasks in each cycle are divided into two groups. The first includes tasks performed during the initial acquaintance with identity. They serve educational material for several consecutive lessons, united by one topic. The second group of exercises relates the identity under study to various applications. This group does not form a compositional unity - the exercises here are scattered over various topics.

The described structure of the cycle refers to the stage of formation of skills for applying specific types of transformations. On the final stage- stage of synthesis cycles are modified. First, both groups of tasks are combined, forming an "unfolded" cycle, and the simplest ones in terms of wording or the complexity of the task are excluded from the first group. The remaining types of tasks become more difficult. Secondly, there is a merging of cycles related to different identities, due to which the role of actions to recognize the applicability of one or another identity increases.

We note the features of task cycles related to identities for elementary functions. These features are due to the fact that, firstly, the corresponding identities are studied in connection with the study of functional material and, secondly, they appear later than the identities of the first group and are studied using already formed skills for carrying out identical transformations.

Each newly introduced elementary function sharply expands the area of ​​numbers that can be designated and named individually. Therefore, the first group of tasks of the cycles should include tasks to establish a connection between these new numerical areas with the original area rational numbers. We give examples of such tasks.

Example 1 Calculate:

Next to each expression, there is an identity, in the cycles for which the proposed tasks may be present. The purpose of such tasks is to master the features of records, including symbols of new operations and functions, and to develop mathematical speech skills.

A significant part of the use of identity transformations associated with elementary functions falls on the solution of irrational and transcendental equations. The cycles related to the assimilation of identities include only the most simple equations, but already here it is advisable to carry out work on mastering the method of solving such equations: reducing it by replacing the unknown to algebraic equation.

The sequence of steps for this solution is as follows:

a) find a function for which given equation represent in the form ;

b) make a substitution and solve the equation;

c) solve each of the equations , where is the set of roots of the equation .

When using the described method, step b) is often performed implicitly, without introducing a notation for . In addition, students often choose from the various paths leading to finding an answer to choose the one that leads to the algebraic equation faster and easier.

Example 2. Solve the equation.

First way:

Second way:

but)

b)

It can be seen here that step a) is more difficult in the first method than in the second. The first way is “harder to start”, although the further course of the solution is much easier. On the other hand, the second method has advantages, consisting in greater ease, greater sophistication in teaching reduction to an algebraic equation.

For school course algebra tasks are typical, in which the transition to an algebraic equation is even easier than in this example. The main load of such tasks relates to the selection of step c) as an independent part of the solution process associated with the use of the properties of the elementary function under study.

Example 3. Solve the equation:

but) ; b) .

These equations are reduced to the equations: a) or ; b) or. Solving these equations requires knowledge of only the simplest facts about exponential function: its monotonicity, range of values. Like the previous example, equations a) and b) can be attributed to the first group of a cycle of exercises for solving quadratic exponential equations.

Thus, we come to the classification of tasks in cycles related to the solution of transcendental equations, including an exponential function:

1) equations that are reduced to equations of the form and have a simple answer, general in form: ;

2) equations that reduce to equations , where is an integer, or , where ;

3) equations that reduce to equations and require an explicit analysis of the form in which the number is written.

Similar tasks can be classified for other elementary functions.

A significant part of the identities studied in the courses on algebra and algebra and the beginnings of analysis are proved in them or at least explained. This side of the study of identities has great importance for both courses, since demonstrative reasoning in them is carried out with the greatest clarity and rigor precisely in relation to identities. Outside of this material, the evidence is usually less complete, it is not always distinguished from the composition of the applied means of justification.

The properties of arithmetic operations are used as a support on which the proofs of identities are built.

The educational impact of calculations and identical transformations can be directed to the development of logical thinking, if only students are systematically required to substantiate calculations and identical transformations, to the development of functional thinking, which is achieved in various ways. The importance of calculations and identical transformations in the development of will, memory, ingenuity, self-control, and creative initiative is quite obvious.

Requests for everyday, industrial computing practice require the formation of strong, automated skills of rational calculations and identical transformations in students. These skills are developed in the process of any computational work, however, special training exercises are needed in fast calculations and transformations.

So, if the lesson involves solving logarithmic equations using the basic logarithmic identity, then it is useful to include oral exercises in the lesson plan to simplify or calculate the values ​​of expressions: , , . The purpose of the exercises is always communicated to the students. During the exercise, it may be necessary to require students to justify individual transformations, actions, or solve the entire problem, even if this was not planned. Where possible various ways problem solving, it is desirable to always ask questions: “How was the problem solved?”, “Who solved the problem in a different way?”

The concepts of identity and identical transformation, they are explicitly introduced in the class VI algebra course. The very definition identical expressions cannot be practically used to prove the identity of two expressions, and to understand that the essence of identical transformations consists in applying to the expression the definitions and properties of those actions that are indicated in the expression, or in adding to it an expression that is identically equal to 0, or in multiplying it by expression, identical equal to one. But, even having mastered these provisions, students often do not understand why these transformations allow us to assert that the original and resulting expressions are identical, i.e. take the same values ​​for any systems (sets) of variable values.

It is also important to ensure that students understand well that such conclusions of identical transformations are consequences of the definitions and properties of the corresponding actions.

The apparatus of identical transformations, accumulated in previous years, is being expanded in the 6th grade. This extension begins with the introduction of an identity expressing the property of the product of powers with the same bases: , where , are integers.

§3. Mathematics Program. In the school course "Algebra and the Beginnings of Analysis", students systematically study exponential and logarithmic functions and their properties, identical transformations of logarithmic and exponential expressions and their application to solving the corresponding equations and inequalities, get acquainted with the basic concepts, statements. In the 11th grade, algebra lessons take 3 hours a week, for a total of 102 hours a year. To study exponential, logarithmic and power function The program takes 36 hours. The program includes consideration and study of the following issues: The concept of a degree with a rational indicator. Solution of irrational equations. An exponential function, its properties and graph. identical transformations of exponential expressions. Solution of exponential equations and inequalities. The logarithm of a number. Basic properties of logarithms. Logarithmic function, its properties and graph. Solution of logarithmic equations and inequalities. Derivative of exponential function. Number and natural logarithm. Derivative of a power function. The main purpose of the section on the study of exponential and logarithmic functions is to familiarize students with exponential, logarithmic and power functions; teach students to solve exponential and logarithmic equations and inequalities. The concepts of the root of the th degree and the degree with a rational exponent are a generalization of the concepts of the square root and the degree with an integer exponent. Students should pay attention to the fact that the properties of roots and degrees with a rational exponent considered here are similar to those properties that have been studied earlier. square roots and degrees with integer exponents. It is necessary to devote enough time to working out the properties of degrees and the formation of skills for identical transformations. The concept of degree with an irrational exponent is introduced on a visual-intuitive basis. This material plays an auxiliary role and is used when introducing the exponential function. The study of the properties of exponential, logarithmic and power functions is built in accordance with the accepted general scheme for studying functions. In this case, an overview of the properties is given depending on the parameter values. Demonstration and logarithmic inequalities are solved based on the studied properties of functions. characteristic feature course are the systematization and generalization of students' knowledge, the consolidation and development of the skills and abilities acquired in the algebra course, which is carried out both when studying new material and when conducting a generalizing repetition.
Chapter 2

§one. Generalization of the concept of degree.

Definition: The root of the th degree of pure is such a number, the th degree of which is equal to.

According to this definition, the root of the th degree of a number is a solution to the equation. The number of roots of this equation depends on and . Let's consider a function. As is known, on the interval this function increases for any and takes all values ​​from the interval . By the root theorem, the equation for any has a non-negative root, and moreover, only one. It is called the arithmetic root of the th degree of a number and denoted; the number is called the index of the root, and the number itself is called the radical expression. The sign is also called a radical.

Definition: The arithmetic root of the th degree of a number is called non-negative number, whose th degree is equal to .

For even, the function is even. It follows that if , then the equation , in addition to the root , also has a root . If , then there is only one root: ; if , then this equation has no roots, because even degree any number is non-negative.

For odd values, the function increases along the entire number line; its range is the set of all real numbers. Applying the root theorem, we find that the equation has one root for any and, in particular, for . This root for any value is denoted by .

For roots of odd degree, equality is true. Indeed, , i.e. number is the th root of . But such a root for odd is unique. Consequently, .

Remark 1: For any real

Recall the well-known properties of arithmetic roots of the th degree.

For any natural , integer and any non-negative integers and equalities are true:

1.

2.

3.

4.

Degree with a rational exponent.

The expression is defined for all and , except for the case when . Recall the properties of such powers.

For any numbers , and any integers and equalities are valid:

We also note that if , then for and for .. and

For students studying for the Unified State Examination, mathematics teachers at secondary school No. 26 in Yakutsk use a list of content questions (codifier) ​​of the school mathematics course, the assimilation of which is checked when passing the unified state exam in 2007. elective course in preparation for the Unified State Exam is based on repetition, systematization and deepening of knowledge acquired earlier. Classes are held in the form of free...