Consider a system of 3 equations with three unknowns

Using third-order determinants, the solution of such a system can be written in the same form as for a system of two equations, i.e.

(2.4)

if 0. Here

It is Cramer's rule solutions of the system of three linear equations with three unknowns.

Example 2.3. Solve a system of linear equations using Cramer's rule:

Decision . Finding the determinant of the main matrix of the system

Since 0, then to find a solution to the system, you can apply Cramer's rule, but first calculate three more determinants:

Examination:

Therefore, the solution is found correctly. 

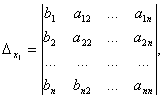
Cramer's rules derived for linear systems 2nd and 3rd order, suggest that the same rules can be formulated for linear systems of any order. Really takes place

Cramer's theorem. Quadratic system of linear equations with a non-zero determinant of the main matrix of the system (0) has one and only one solution, and this solution is calculated by the formulas

(2.5)

where  – main matrix determinant,  i – matrix determinant, derived from the main, replacementith column free members column.

Note that if =0, then Cramer's rule is not applicable. This means that the system either has no solutions at all, or has infinitely many solutions.

Having formulated Cramer's theorem, the question naturally arises of calculating higher-order determinants.

2.4. nth order determinants

Additional minor M ij element a ij is called the determinant obtained from the given by deleting i-th line and j-th column. Algebraic addition A ij element a ij is called the minor of this element, taken with the sign (–1) i + j, i.e. A ij = (–1) i + j M ij .

For example, let's find minors and algebraic complements of elements a 23 and a 31 determinants

We get



Using the concept of algebraic complement, we can formulate the determinant expansion theoremn-th order by row or column.

Theorem 2.1. Matrix determinantAis equal to the sum of the products of all elements of some row (or column) and their algebraic complements:

(2.6)

This theorem underlies one of the main methods for calculating determinants, the so-called. order reduction method. As a result of the expansion of the determinant n th order in any row or column, we get n determinants ( n–1)-th order. In order to have fewer such determinants, it is advisable to choose the row or column that has the most zeros. In practice, the expansion formula for the determinant is usually written as:

those. algebraic additions are written explicitly in terms of minors.

Examples 2.4. Calculate the determinants by first expanding them in any row or column. Usually in such cases, choose the column or row that has the most zeros. The selected row or column will be marked with an arrow.



2.5. Basic properties of determinants

Expanding the determinant in any row or column, we get n determinants ( n–1)-th order. Then each of these determinants ( n–1)-th order can also be decomposed into a sum of determinants ( n–2)th order. Continuing this process, one can reach the determinants of the 1st order, i.e. to the elements of the matrix whose determinant is being calculated. So, to calculate the 2nd order determinants, you will have to calculate the sum of two terms, for the 3rd order determinants - the sum of 6 terms, for the 4th order determinants - 24 terms. The number of terms will increase sharply as the order of the determinant increases. This means that the calculation of determinants of very high orders becomes a rather laborious task, beyond the power of even a computer. However, determinants can be calculated in another way, using the properties of determinants.

Property 1 . The determinant will not change if rows and columns are swapped in it, i.e. when transposing a matrix:

.

This property indicates the equality of rows and columns of the determinant. In other words, any statement about the columns of a determinant is true for its rows, and vice versa.

Property 2 . The determinant changes sign when two rows (columns) are interchanged.

Consequence . If the determinant has two identical rows (columns), then it is equal to zero.

Property 3 . The common factor of all elements in any row (column) can be taken out of the sign of the determinant.

For example,

Consequence . If all elements of some row (column) of the determinant are equal to zero, then the determinant itself is equal to zero.

Property 4 . The determinant will not change if the elements of one row (column) are added to the elements of another row (column) multiplied by some number.

For example,

Property 5 . The determinant of the matrix product is equal to the product of the matrix determinants:

Cramer's method is based on the use of determinants in solving systems of linear equations. This greatly speeds up the solution process.

Cramer's method can be used to solve a system of as many linear equations as there are unknowns in each equation. If the determinant of the system is not equal to zero, then Cramer's method can be used in the solution; if it is equal to zero, then it cannot. In addition, Cramer's method can be used to solve systems of linear equations that have a unique solution.

Definition. The determinant, composed of the coefficients of the unknowns, is called the determinant of the system and is denoted by (delta).

Determinants

are obtained by replacing the coefficients at the corresponding unknowns by free terms:

;

.

Cramer's theorem. If the determinant of the system is nonzero, then the system of linear equations has one single solution, and the unknown is equal to the ratio of the determinants. The denominator contains the determinant of the system, and the numerator contains the determinant obtained from the determinant of the system by replacing the coefficients with the unknown by free terms. This theorem holds for a system of linear equations of any order.

Example 1 Solve the system of linear equations:

According to Cramer's theorem we have:

So, the solution of system (2):

online calculator, decisive method Kramer.

Three cases in solving systems of linear equations

As appears from Cramer's theorems, when solving a system of linear equations, three cases may occur:

First case: the system of linear equations has a unique solution

(the system is consistent and definite)

Second case: the system of linear equations has an infinite number of solutions

(the system is consistent and indeterminate)

** ,

those. the coefficients of the unknowns and the free terms are proportional.

Third case: the system of linear equations has no solutions

(system inconsistent)

So the system m linear equations with n variables is called incompatible if it has no solutions, and joint if it has at least one solution. A joint system of equations that has only one solution is called certain, and more than one uncertain.

Examples of solving systems of linear equations by the Cramer method

Let the system

.

Based on Cramer's theorem

………….
,

where
-

system identifier. The remaining determinants are obtained by replacing the column with the coefficients of the corresponding variable (unknown) with free members:

Example 2

.

Therefore, the system is definite. To find its solution, we calculate the determinants

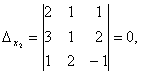
By Cramer's formulas we find:

So, (1; 0; -1) is the only solution to the system.

To check the solutions of systems of equations 3 X 3 and 4 X 4, you can use the online calculator, the Cramer solving method.

If there are no variables in the system of linear equations in one or more equations, then in the determinant the elements corresponding to them are equal to zero! This is the next example.

Example 3 Solve the system of linear equations by Cramer's method:

.

Decision. We find the determinant of the system:

Look carefully at the system of equations and at the determinant of the system and repeat the answer to the question in which cases one or more elements of the determinant are equal to zero. So, the determinant is not equal to zero, therefore, the system is definite. To find its solution, we calculate the determinants for the unknowns

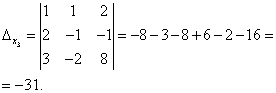
By Cramer's formulas we find:

So, the solution of the system is (2; -1; 1).

To check the solutions of systems of equations 3 X 3 and 4 X 4, you can use the online calculator, the Cramer solving method.

Top of page

We continue to solve systems using the Cramer method together

As already mentioned, if the determinant of the system is equal to zero, and the determinants for the unknowns are not equal to zero, the system is inconsistent, that is, it has no solutions. Let's illustrate with the following example.

Example 6 Solve the system of linear equations by Cramer's method:

Decision. We find the determinant of the system:

The determinant of the system is equal to zero, therefore, the system of linear equations is either inconsistent and definite, or inconsistent, that is, it has no solutions. To clarify, we calculate the determinants for the unknowns

The determinants for the unknowns are not equal to zero, therefore, the system is inconsistent, that is, it has no solutions.

To check the solutions of systems of equations 3 X 3 and 4 X 4, you can use the online calculator, the Cramer solving method.

In problems on systems of linear equations, there are also those where, in addition to the letters denoting variables, there are also other letters. These letters stand for some number, most often a real number. In practice, such equations and systems of equations lead to search problems common properties any phenomena or objects. That is, did you invent any new material or a device, and to describe its properties, which are common regardless of the size or number of copies, it is necessary to solve a system of linear equations, where instead of some coefficients for variables there are letters. You don't have to look far for examples.

The next example is for a similar problem, only the number of equations, variables, and letters denoting some real number increases.

Example 8 Solve the system of linear equations by Cramer's method:

Decision. We find the determinant of the system:

Finding determinants for unknowns

A system of linear equations is a set of several linear equations considered together.

The system can have any number of equations with any number of unknowns.

The solution of a system of equations is a set of unknown values ​​that satisfies all the equations of the system, that is, converts them into identities.

A system that has a solution is called compatible, otherwise it is called inconsistent.

Various methods are used to solve the system.

Let be
(the number of equations is equal to the number of unknowns).

Cramer method

Consider the solution of a system of three linear equations with three unknowns:

(7)

To find the unknown
Let's apply Cramer's formula:

(8)

where - the determinant of the system, the elements of which are the coefficients of the unknowns:

.

obtained by replacing the first column of the determinant column of free members:

.

Similarly:

;
.

Example 1 Solve the system using Cramer's formula:

.

Solution: Let's use formulas (8):

;

;

;

;

Answer:
.

For any system linear equations with unknowns can say:

Matrix solution

Consider the solution of system (7) of three linear equations with three unknowns in a matrix way.

Using the rules of matrix multiplication, this system of equations can be written as:
, where

.

Let the matrix non-degenerate, i.e.
. Multiplying both sides of the matrix equation on the left by the matrix
, the inverse of the matrix , we get:
.

Given that
, we have

(9)

Example 2 Solve the system in a matrix way:

.

Solution: Let's introduce matrices:

- from coefficients at unknown;

- column of free members.

Then the system can be written as a matrix equation:
.

We use formula (9). Let's find the inverse matrix
according to formula (6):

;

.

Hence,

Got:

.

Answer:
.

Sequential elimination of unknowns (Gauss method)

The main idea of ​​the method used is the successive elimination of unknowns. Let us explain the meaning of this method on a system of three equations with three unknowns:

.

Let's assume that
(if
, then we change the order of the equations, choosing as the first equation the one in which the coefficient at is not equal to zero).

First step: a) divide the equation
on the
; b) multiply the resulting equation by
and subtract from
; c) then multiply the result by
and subtract from
. As a result of the first step, we will have a system:

,

Second step: deal with the equation
and
just like with equations
.

As a result, the original system is transformed to the so-called stepwise form:

From the transformed system, all unknowns are determined sequentially without difficulty.

Comment. In practice, it is more convenient to reduce to a stepped form not the system of equations itself, but a matrix of coefficients, at unknowns, and free terms.

Example 3 Solve the system using the Gaussian method:

.

The transition from one matrix to another will be written using the equivalence sign ~.

~
~
~
~

~
.

Using the resulting matrix, we write out the transformed system:

.

Answer:
.

Note: If the system has a unique solution, then the stepwise system is reduced to a triangular one, that is, to one in which the last equation will contain one unknown. In the case of an indefinite system, that is, one in which the number of unknowns more number linearly independent equations, there will be no triangular system, since the last equation will contain more than one unknown (the system has an infinite number of solutions). When the system is inconsistent, then, after reducing it to a stepped form, it will contain at least one kind value
, that is, an equation in which all unknowns have zero coefficients, and the right side is nonzero (there is no solution system). The Gauss method is applicable to an arbitrary system of linear equations (for any
and ).

Existence theorem for a solution to a system of linear equations

When solving a system of linear equations by the Gaussian method, the answer to the question of whether a given system is consistent or inconsistent can be given only at the end of the calculations. However, it is often important to solve the question of the compatibility or inconsistency of a system of equations without finding the solutions themselves. The answer to this question is given by the following Kronecker-Capelli theorem.

Let the system
linear equations with unknown:

(10)

For system (10) to be consistent, it is necessary and sufficient that the rank of the system matrix

.

was equal to the rank of its augmented matrix

.

Moreover, if
, then system (10) has a unique solution; if
, then the system has an infinite number of solutions.

Consider a homogeneous system (all free terms are equal to zero) of linear equations:

.

This system is always consistent since it has a zero solution .

The following theorem gives conditions under which the system also has nonzero solutions.

Terema. In order for a homogeneous system of linear equations to have a zero solution, it is necessary and sufficient that its determinant was equal to zero:

.

Thus, if
, then the solution is unique. If a
, then there are an infinite number of other non-zero solutions. Let us indicate one of the methods for finding solutions for a homogeneous system of three linear equations with three unknowns in the case
.

It can be proved that if
, and the first and second equations are non-proportional (linearly independent), then the third equation is a consequence of the first two. The solution of a homogeneous system of three equations with three unknowns is reduced to the solution of two equations with three unknowns. The so-called free unknown appears, to which arbitrary values ​​can be assigned.

Example 4 Find all system solutions:

.

Decision. The determinant of this system

.

Therefore the system has zero solutions. It can be seen that the first two equations, for example, are not proportional, hence they are linearly independent. The third is a consequence of the first two (obtained by adding twice the second to the first equation). Rejecting it, we obtain a system of two equations with three unknowns:

.

Assuming, for example,
, we get

.

Solving a system of two linear equations, we express and through :
. Therefore, the solution of the system can be written as:
, where - arbitrary number.

Example 5 Find all system solutions:

.

Decision. It is easy to see that in this system there is only one independent equation (the other two are proportional to it). A system of three equations with three unknowns has been reduced to one equation with three unknowns. Two free unknowns appear. Finding, for example, from the first equation
for arbitrary and , we obtain solutions of this system. The general form of the solution can be written as and - arbitrary numbers.

Questions for self-examination

Formulate Cramer's rule for solving the system linear equations with unknown.

What is the essence of the matrix method for solving systems?

What is the Gauss method for solving a system of linear equations?

Formulate the Kronecker-Capelli theorem.

Formulate a necessary and sufficient condition for the existence of nonzero solutions of a homogeneous system of linear equations.

Examples for self-solving

Find all system solutions:

1.
; 2.
;

3.
; 4.
;

5.
; 6.
;

7.
; 8.
;

9.
; 10.
;

11.
; 12.
;

13.
; 14.
;

15.
.

Determine at what values and system of equations

a) has a unique solution;

b) has no solution;

c) has infinitely many solutions.

16.
; 17.
;

Find all solutions of the following homogeneous systems:

18.
; 19.
;

20.
; 21.
;

22.
; 23.
;

Answers to examples

1.
; 2.
; 3. Ǿ; 4. Ǿ;

5.
- arbitrary number.

6.
, where - arbitrary number.

7.
; 8.
; 9. Ǿ; 10. Ǿ;

11.
, where - arbitrary number.

12. , where and - arbitrary numbers.

13.
; 14.
where and - arbitrary numbers.

15. Ǿ; 16. a)
; b)
; in)
.

17. a)
; b)
; in)
;

18.
; 19.
; 20., where - arbitrary number.

21. , where - arbitrary number.

22. , where - arbitrary number.

23. , where and - arbitrary numbers.

Practical work

"Solution of systems of linear equations of the third order by Cramer's method"

Goals of the work:

expand the understanding of the methods for solving the SLE and work out the algorithm for solving the SLE by the Cramor method;

to develop the logical thinking of students, the ability to find rational solution tasks;

to educate students in the accuracy and culture of written mathematical speech when they make their decision.

Basic theoretical material.

Cramer's method. Application for systems of linear equations.

A system of N linear algebraic equations (SLAE) with unknowns is given, the coefficients of which are the elements of the matrix , and the free members are the numbers

The first index next to the coefficients indicates in which equation the coefficient is located, and the second - at which of the unknowns it is located.

If the matrix determinant is not equal to zero

then the system of linear algebraic equations has a unique solution. The solution of a system of linear algebraic equations is such an ordered set of numbers , which at turns each of the equations of the system into a correct equality. If the right sides of all equations of the system are equal to zero, then the system of equations is called homogeneous. In the case when some of them are nonzero, non-uniform If a system of linear algebraic equations has at least one solution, then it is called compatible, otherwise it is incompatible. If the solution of the system is unique, then the system of linear equations is called definite. In the case when the solution of the compatible system is not unique, the system of equations is called indefinite. Two systems of linear equations are called equivalent (or equivalent) if all solutions of one system are solutions of the second, and vice versa. Equivalent (or equivalent) systems are obtained using equivalent transformations.

Equivalent transformations of SLAE

1) rearrangement of equations;

2) multiplication (or division) of equations by a non-zero number;

3) adding to some equation another equation, multiplied by an arbitrary non-zero number.

The solution of SLAE can be found in different ways, for example, by Cramer's formulas (Cramer's method)

Cramer's theorem. If the determinant of a system of linear algebraic equations with unknowns is nonzero, then this system has a unique solution, which is found by the Cramer formulas: - determinants formed with the replacement of the -th column, a column of free members.

If , and at least one of is nonzero, then SLAE has no solutions. If , then the SLAE has many solutions.

A system of three linear equations with three unknowns is given. Solve the system by Cramer's method

Decision.

Find the determinant of the matrix of coefficients for unknowns

Since , then the given system of equations is consistent and has a unique solution. Let's calculate the determinants:

Using Cramer's formulas, we find the unknowns

So the only solution to the system.

A system of four linear algebraic equations is given. Solve the system by Cramer's method.

Let us find the determinant of the matrix of coefficients for the unknowns. To do this, we expand it by the first line.

Find the components of the determinant:

Substitute the found values ​​into the determinant

The determinant, therefore, the system of equations is consistent and has a unique solution. We calculate the determinants using Cramer's formulas:

Evaluation criteria:

The work is evaluated at "3" if: one of the systems is completely and correctly solved independently.

The work is evaluated at "4" if: any two systems are completely and correctly solved independently.

The work is evaluated at "5" if: three systems are completely and correctly solved independently.

Coursework: Determinants and systems of linear equations

1. Determinants of the second and third orders and their properties

1.1. The concept of a matrix and second-order determinant

Rectangular table of numbers

matrix. To designate a matrix, either double vertical

dashes or parentheses. For example:

1 7 9.2 1 7 9.2

28 20 18 28 20 18

6 11 2 -6 11 2

If the number of rows of a matrix is ​​the same as the number of columns, then the matrix is ​​called

square. The numbers that make up the matrix are called it elements.

Consider a square matrix consisting of four elements:

The second-order determinant corresponding to matrix (3.1) is the number

and denoted by the symbol

So by definition

The elements that make up the matrix of a given determinant are usually called

elements of this determinant.

The following statement is true: so that the determinant of the second

order was equal to zero, it is necessary and sufficient that the elements of its rows (or

respectively of its columns) were proportional.

To prove this assertion, it suffices to note that each of

proportions /

is equivalent to

And the last equality, by virtue of (3.2), is equivalent to the vanishing of the determinant.

1.2. System of two linear equations with two unknowns

Let us show how second-order determinants are used to study and

finding solutions to a system of two linear equations with two unknowns

(coefficients ,

and free members,

are assumed to be given). Recall that a pair of numbers

called

solution of system (3.3) if the substitution of these numbers in place

and in this system

turns both equations (3.3) into identities.

Multiplying the first equation of system (3.3) by -

And the second - on -and

then adding the resulting equalities, we get

Similarly, by multiplying equations (3.3) by - and, respectively, we obtain:

Let us introduce the following notation:

Using these notations and the expression for the second-order determinant

equations (3.4) and (3.5) can be rewritten as:

Determinant,

composed of the coefficients of the unknowns of system (3.3), it is customary to call

determinant of this system. Note that the determinants

and are obtained from

system qualifier

by replacing its first or, respectively, second column with free

There can be two cases: 1) system determinant

different from zero; 2) this determinant is equal to zero.

Consider first the case

0. From equations (3.7) we immediately obtain formulas for the unknowns,

called Cramer's formulas:

The resulting Cramer formulas (3.8) give a solution to system (3.7) and therefore prove

uniqueness of the solution of the original system (3.3). Indeed, system (3.7)

is a consequence of system (3.3), so any solution of system (3.3) (in

if it exists!) must also be a solution of system (3.7). So,

so far it has been proved that if the original system (3.3) exists for

0 solution, then this solution is uniquely determined by the Cramer formulas (3.8).

It is also easy to verify the existence of a solution, i.e., that what at

0 two numbers and

Defined by Cramer's formulas (3.8). being put in the place of the unknown in

equations (3.3) turn these equations into identities. (Let the reader

write expressions for determinants yourself

And to verify the validity of these identities.)

We arrive at the following conclusion: if the determinant

system (3.3) is different from zero, then there exists and, moreover, a unique solution to this

system defined by the Cramer formulas (3.8).

Consider now the case when the determinant

system is zero. May introduce themselves two subcases: Or maybe

one of the determinants

or , different from

zero; b) both determinants

and are equal to zero. (if

determinant and

one of two determinants

and are equal to zero, then

the other of these two determinants is equal to zero. Indeed, let

for example = 0

Then from these proportions we get that

In subcase a), at least one of the equalities (3.7) turns out to be impossible, i.e.,

system (3.7) has no solutions, and therefore has no solutions and the original system

(3.3) (a consequence of which is system (3.7)).

In subcase b), the original system (3.3) has an uncountable set of solutions. AT

in fact, from the equalities

0 and from the statement at the end of Sec. 1.1 we conclude that the second equation of the system

(3.3) is a consequence of the first one and can be discarded. But one equation with

two unknowns

has infinitely many solutions (at least one of the coefficients

Or different from

zero, and the unknown associated with it can be determined from equation (3.9)

through arbitrarily set value another unknown).

Thus, if the determinant

system (3.3) is equal to zero, then system (3.3) either has no solutions at all (in

if at least one of the determinants

or different from

zero) or has an infinite number of solutions (in the case when

0). In the last

case, two equations (3.3) can be replaced by one, and when solving it, one

the unknown is given arbitrarily.

Comment. When free members

and equal to zero,

linear system (3.3) is called homogeneous. Note that the same

the system always has the so-called trivial solution:

0, = 0 (these two

numbers turn both homogeneous equations into identities).

If the determinant of a homogeneous system

is different from zero, then this system has only a trivial solution. If

= 0, then the homogeneous system has an infinite number of solutions(insofar as

for a homogeneous system, the possibility of the absence of solutions is excluded). So

the way homogeneous system has a non-trivial solution if and only if

when the determinant is zero.