Let us demonstrate the possibilities of the Ostrogradsky-Gauss theorem using several examples.
Field of an infinite uniformly charged plane
The surface charge density on an arbitrary plane with area S is determined by the formula:
where dq is the charge concentrated on the area dS; dS is a physically infinitely small area of the surface.
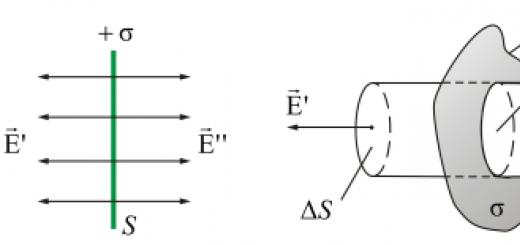
Let σ be the same at all points of the plane S. The charge q is positive. The tension at all points will have a direction perpendicular to the plane S(Fig. 2.11).
Obviously, at symmetrical points relative to the plane, the tension will be the same in magnitude and opposite in direction.
Imagine a cylinder with generators perpendicular to the plane and bases Δ S, located symmetrically with respect to the plane (Fig. 2.12).
 |
|||
| Rice. 2.11 | Rice. 2.12 | ||
We apply the Ostrogradsky-Gauss theorem. The flow F E through the side of the surface of the cylinder is zero, because For the base of the cylinder
The total flow through a closed surface (cylinder) will be equal to:
There is a charge inside the surface. Therefore, from the Ostrogradsky–Gauss theorem we obtain:
;
whence it can be seen that the field strength of the plane S is equal to:
| (2.5.1) |
The result obtained does not depend on the length of the cylinder. This means that at any distance from the plane
Field of two uniformly charged planes
Let two infinite planes be charged with opposite charges with the same density σ (Fig. 2.13).
The resulting field, as mentioned above, is found as a superposition of the fields created by each of the planes.
Then inside planes
| (2.5.2) |
Out of planes field strength
The result obtained is also valid for planes of finite dimensions, if the distance between the planes is much less than the linear dimensions of the planes (flat capacitor).
Between the plates of the capacitor acts the force of mutual attraction (per unit area of the plates):
where S is the area of the capacitor plates. Because , then
 .
|
(2.5.5) |
This is the formula for calculating pondermotor force.
The field of a charged infinitely long cylinder (thread)
Let the field be created by an infinite cylindrical surface of radius R, charged with a constant linear density, where dq is the charge concentrated on a segment of the cylinder (Fig. 2.14).
From considerations of symmetry it follows that E at any point will be directed along the radius, perpendicular to the axis of the cylinder.
Imagine around a cylinder (thread) coaxial closed surface ( cylinder within a cylinder) radius r and length l (the bases of the cylinders are perpendicular to the axis). For cylinder bases for lateral surface i.e. depends on distance r.
Therefore, the vector flux through the considered surface is equal to
When there will be a charge on the surface According to the Ostrogradsky-Gauss theorem, hence
 .
|
(2.5.6) |
If , since there are no charges inside a closed surface (Fig. 2.15).
If the radius of the cylinder R is reduced (at ), then a field with a very high strength can be obtained near the surface and, at , a filament can be obtained.
Field of two coaxial cylinders with the same linear density λ but different sign
There will be no field inside the smaller and outside the larger cylinder (Fig. 2.16).
In the gap between the cylinders, the field is determined in the same way as in the previous case:
This is true for an infinitely long cylinder, and for cylinders of finite length, if the gap between the cylinders is much less than the length of the cylinders (cylindrical capacitor).
The field of a charged hollow sphere
A hollow ball (or sphere) of radius R is charged with a positive charge with surface density σ. The field in this case will be centrally symmetrical - at any point it passes through the center of the ball. , and the lines of force are perpendicular to the surface at any point. Imagine around the ball - a sphere of radius r (Fig. 2.17).
Field potential
Field potential
Field potential
field potentials
Electric field potential point charge Q at a point:
The field of a charged infinitely long cylinder (thread)
Let the field be created by an infinite cylindrical surface of radius R, charged with a constant linear density , where d q- charge concentrated on a segment of the cylinder (Fig. 2.14).
It follows from symmetry considerations that E at any point will be directed along the radius, perpendicular to the axis of the cylinder.
Imagine around a cylinder (thread) coaxial closed surface ( cylinder within a cylinder) radius r and length l(the bases of the cylinders are perpendicular to the axis). For cylinder bases for lateral surface i.e. depends on distance r.
Therefore, the vector flux through the considered surface is equal to
When there will be a charge on the surface According to the Ostrogradsky-Gauss theorem, hence
 .
| (2.5.6) |
If , since there are no charges inside a closed surface (Fig. 2.15).
If we decrease the radius of the cylinder R(at ), then it is possible to obtain a field with a very high strength near the surface and, at , obtain a filament.
27. The potential of the field created by a uniformly charged infinite plane.
Field potential- this is the energy characteristic of the field, characterizes the potential energy that a positive unit charge would have, placed at a given point in the field.
The unit of electrical potential is the volt (V).
Field potential is equal to the ratio of the potential energy of the charge to this charge:
Field potential is the energy characteristic of the electric field and as a scalar quantity can take positive or negative values.
The physical meaning is the difference field potentials, since the work of the field forces on the movement of the charge is expressed through it.
The field of a uniformly charged infinite plane.
Let us introduce the concept of surface charge density >0, numerically equal to the charge per unit area:
Due to the homogeneity and isotropy of space, the field lines of the field of a uniformly charged infinite plane must be perpendicular to it and have a uniform density, which corresponds to the definition of field homogeneity E= const. As a "convenient" closed surface, we choose a straight cylinder, the lateral surface of which is parallel to the lines of force (everywhere on it is 0 and, therefore, the flux through it is 0), and the end surfaces of area S are parallel to the charged plane (so that everywhere on them 
1):
Uniform field flow E through both end surfaces perpendicular to it, S is simply E 2S, and the charge concentrated on the area S of the charged surface is equal to S:
Surface charge density on an arbitrary plane with an area S is determined by the formula:
where d q is the charge concentrated on the area d S; d S is a physically infinitesimal area of the surface.
Let σ at all points of the plane S is the same. Charge q- positive. The tension at all points will have a direction perpendicular to the plane S(Fig. 2.11).
Obviously, at points that are symmetrical with respect to the plane, the tension will be the same in magnitude and opposite in direction.
Imagine a cylinder with generators perpendicular to the plane and bases Δ S, located symmetrically with respect to the plane (Fig. 2.12).
 | |||
| Rice. 2.11 | Rice. 2.12 | ||
We apply the Ostrogradsky-Gauss theorem. Flow F E through the lateral part of the cylinder surface is zero, because . For cylinder base
The total flow through a closed surface (cylinder) will be equal to:
There is a charge inside the surface. Therefore, from the Ostrogradsky–Gauss theorem we obtain:
;
whence it can be seen that the field strength of the plane S is equal to:
 |
||||
| An electrostatic field has an important property: The work of the forces of an electrostatic field when moving a charge from one point of the field to another does not depend on the shape of the trajectory, but is determined only by the position of the starting and ending points and the magnitude of the charge. The gravitational field has a similar property, and there is nothing surprising in this, since the gravitational and Coulomb forces are described by the same ratios. The consequence of the independence of the work from the shape of the trajectory is the following statement: The work of the forces of the electrostatic field when moving the charge along any closed trajectory is equal to zero. Force fields with this property are called potential or conservative. On fig. 1.4.2 shows the lines of force of the Coulomb field of a point charge Q and two different test charge trajectories q from start point (1) to end point (2). On one of the trajectories, a small displacement is distinguished Work Δ A Coulomb forces on this displacement is equal to The result obtained does not depend on the shape of the trajectory. On trajectories I and II shown in Figs. 1.4.2, the work of the Coulomb forces is the same. If on one of the trajectories we change the direction of charge movement q to the opposite, then the work will change sign. This implies that the work of the Coulomb forces on a closed trajectory is equal to zero. If the electrostatic field is created by a set of point charges, then when moving the test charge q Job A the resulting field in accordance with the principle of superposition will consist of the work of the Coulomb fields of point charges: Since each term of the sum does not depend on the shape of the trajectory, then the total work A The resulting field is independent of the path and is determined only by the position of the start and end points. The potentiality property of the electrostatic field allows us to introduce the concept potential energy charge in an electric field. To do this, a certain point (0) is selected in space, and the potential energy of the charge q placed at this point is taken equal to zero. Potential charge energy q, placed at any point (1) of space, with respect to a fixed point (0) is equal to the work A 10 , which the electrostatic field will make when moving the charge q from point (1) to point (0):
(In electrostatics, energy is usually denoted by the letter W, since the letter E indicate the field strength.) Just as in mechanics, the potential energy is defined up to a constant value, depending on the choice of the reference point (0). Such ambiguity in the definition of potential energy does not lead to any misunderstanding, since it is not the potential energy itself that has physical meaning, but the difference in its values at two points in space. Your opinion is important to us! Was the published material helpful? Yes | Not
|
Zhidkevich V. I. The electric field of the plane // Physics: Problems of Laying Out. - 2009. - No. 6. - S. 19-23.
Problems in electrostatics can be divided into two groups: problems about point charges and problems about charged bodies, the dimensions of which cannot be ignored.
Solving problems of calculating electric fields and interactions of point charges is based on the application of Coulomb's law and does not cause any particular difficulties. More difficult is the determination of the field strength and the interaction of charged bodies of finite dimensions: spheres, cylinders, planes. When calculating the strength of electrostatic fields of various configurations, one should emphasize the importance of the superposition principle and use it when considering fields created not only by point charges, but also by charges distributed over the surface and volume. When considering the action of a field on a charge, the formula F=qE in the general case, it is valid for point charged bodies and only in a uniform field is applicable to bodies of any size and shape that carry a charge q.
The electric field of a capacitor is obtained by superimposing the two fields created by each plate.
In a flat capacitor, one plate can be considered as a body with a chargeq 1placed in an electric field of strength E 2, created by another plate.
Let's consider several tasks.
1. Infinite plane charged with surface density σ >0. Find the field strength E and potential ϕ on both sides of the plane, assuming the potential of the plane to be zero. Plot Dependency Plots E(x), ϕ (X). x-axis is perpendicular to the plane, the point x=0 lies on the plane.
Decision. The electric field of an infinite plane is uniform and symmetrical with respect to the plane. His tension Relationship between intensity and potential difference between two points of a homogeneous electrostatic field is expressed by the formula where x - distance between points, measured along the line of force. Then ϕ 2 = ϕ 1 -Ex. At x<0 при х>0 Dependences Е(х) and ϕ (x) are shown in Figure 1.
2. Two plane-parallel thin plates located at a small distance d from each other, uniformly charged with a charge of surface densityσ 1 and σ 2. Find the field strengths at the points lying between the plates and on the outside. Plot the tension dependence E(x) and potential ϕ (x), counting ϕ (0)=0. Consider cases where: a)σ 1 \u003d-σ 2; b) σ 1 = σ 2; c) σ 1 \u003d 3 σ 2 -
Decision. Since the distance between the plates is small, they can be considered as infinite planes.
The field strength of a positively charged plane is and directed from her; the field strength of a negatively charged plane is directed towards it.
According to the principle of superposition, the field at any considered point will be created by each of the charges separately.
a) The fields of two planes charged with equal and opposite charges (a flat capacitor) add up in the area between the planes and cancel each other out in the outer areas (Fig. 2, a).
At X<0
E=
0,
ϕ
=0; at 0
If the planes are of finite dimensions, then the field between the planes will not be strictly uniform, and the field outside the planes will not be exactly zero.
b) Fields of planes charged with charges equal in magnitude and sign (σ1 = σ2 ), compensate each other in the space between the planes and add up in the outer regions (Fig. 3, a). At x<0
при 0
Using the chart E(x) (Fig. 3, b), we construct a qualitative dependence graph ϕ (x) (Fig. 3, c).
c) If σ 1 = σ 2 , then, taking into account the directions of the fields and choosing the direction to the right as positive, we find:
The dependence of the tension E on the distance is shown in Figure 4.
3. On one of the plates of a flat capacitor with a capacity With there is a chargeq 1=+3q, and on the other q2 =+ q. Determine the potential difference between the plates of the capacitor.
Decision. 1st way. Let the area of the capacitor plate S, and the distance between them d. The field inside the capacitor is uniform, so the potential difference (voltage) across the capacitor can be determined by the formula U=E*d, where E is the field strength inside the capacitor.
where E 1, E 2 - field strength created by the capacitor plates.
Then 
2nd way. Add charge to each plate Then the plates are condensed satora will have charges + q and -q. The fields of identical charges of the plates inside the capacitor cancel each other out. The added charges did not change the field between the plates, and hence the potential difference by condenser. U= q/C .
4.
A thin metal plate with a charge + is introduced into the space between the plates of an uncharged flat capacitor. q. Determine the potential difference between the capacitor plates.
Decision. Since the capacitor is not charged, the electric field is created only by a plate that has a charge q (Fig. 5). This field is uniform, symmetrical with respect to the plate, and its intensityLet the potential of the metal plate be ϕ
. Then the potentials of the plates BUT and AT capacitors will be equal ϕ-
ϕ A
=
ϕ
El 1 ; ϕ A
=
ϕ-El 1
;
ϕ-
ϕ B
=
ϕ-El 2
;
ϕ B
=
ϕ-El 2
.
Potential difference between capacitor plates
If the plate is at the same distance from the capacitor plates, then the potential difference between the plates is zero.
5. Into a uniform electric field with strength E 0 a charged metal plate is placed perpendicular to the lines of force with a charge density on the surface of each side of the plate σ (Fig. 6). Determine the field strength E" inside and outside the plate and the surface charge densityσ 1 and σ 2 , which will appear on the left and right sides of the plate.
Decision. The field inside the plate is zero and is a superposition of three fields: the external field E 0, the field created by the charges on the left side of the plate and the field created by the charges on the right side of the plate. Hence,
where σ 1 and σ 2 - surface charge density on the left and right sides of the plate, which occurs after the plate is introduced into the field E 0 . The total charge of the plate will not change, soσ 1 + σ 2 =2 σ, whence σ 1 = σ- ε 0 E 0
, σ 2 = σ + ε 0 E 0
. The field outside the plate is a superposition of the field E 0 and the fields of the charged plate E. On the left of plates To the right of the plate
6. In a flat air capacitor, the field strength is E \u003d 10 4 V / m. Distance between plates d= 2 cm. What will be the potential difference if a metal sheet with a thickness ofd0\u003d 0.5 cm (Fig. 7)?
Decision. Since the electric field between the plates is uniform, then U=Ed, U=200 V.
If a metal sheet is marked between the plates, then a system of two series-connected capacitors is obtained with a distance between the platesd1 and d2. The capacitances of these capacitorsTheir total capacity
Since the capacitor is disconnected from the current source, the charge of the capacitor does not change when the metal sheet is introduced: q"=CU=C"U 1 ; where is the capacitance sator before introducing a metal sheet into it. We get:
U 1= 150 V.
7. On plates BUT and C, located parallel at a distance d= 8 cm apart, potentials maintained φ 1= 60 V and φ 2 =- 60 V respectively. A grounded plate was placed between them. D at a distance d 1 = 2 cm from plate A. How much has the field strength changed in sections AD and CD? Plot Dependency Plots ϕ (x) and E(x).
An infinite plane charged with a surface charge density: to calculate the strength of the electric field created by an infinite plane, we select a cylinder in space, the axis of which is perpendicular to the charged plane, and the bases are parallel to it and one of the bases passes through the field point of interest to us. According to the Gauss theorem, the flow of the electric field strength vector through a closed surface is:
Ф=, on the other hand it is: Ф=E
Equate the right parts of the equations:
We express = - through the surface charge density and find the electric field strength:
Find the electric field strength between oppositely charged plates with the same surface density:
(3)
Find the field outside the plates:
; ; 
(4)
Field strength of a charged sphere
(1)
Ф= (2) t. Gauss
for r< R
; , because (there are no charges inside the sphere)
For r = R
( ; ; 
) 
For r > R
The intensity of the field created by a ball charged uniformly throughout the volume
Volumetric charge density,
distributed over the ball:
For r< R
( ; Ф= ) 
For r = R
For r > R
THE WORK OF THE ELECTROSTATIC FIELD ON THE MOVEMENT OF THE CHARGE
electrostatic field- email stationary charge field.
Fel, acting on the charge, moves it, doing work.
In a uniform electric field, Fel = qE is a constant value
Field work (electronic force) does not depend on the shape of the trajectory and on a closed trajectory = zero.
If another point charge Q 0 moves along any trajectory (Fig. 1) in the electrostatic field of a point charge Q from point 1 to point 2, then the force applied to the charge does some work. The work of the force F on the elementary displacement dl is Since d l/cosα=dr, then  Work when moving charge Q 0 from point 1 to point 2 (1) does not depend on the trajectory of movement, but is determined only by the positions of the initial 1 and final 2 points. This means that the electrostatic field of a point charge is potential, and the electrostatic forces are conservative. From formula (1), it can be seen that the work that is done when an electric charge moves in an external electrostatic field along an arbitrary closed path L is equal to zero, i.e. (2) If we take a single point positive charge as a charge that is moved in an electrostatic field, then the elementary work of the field forces on the path dl is equal to Еdl = E l d l, where E l= Ecosα - the projection of the vector E on the direction of the elementary displacement. Then formula (2) can be represented as  (3) Integral  is called the circulation of the tension vector. This means that the circulation of the electrostatic field strength vector along any closed loop is equal to zero. A force field that has property (3) is called potential. From the equality to zero of the circulation of the vector E it follows that the lines of the electrostatic field cannot be closed, they necessarily begin and end on charges (on positive or negative) or go to infinity. Formula (3) is valid only for an electrostatic field. In what follows, it will be shown that condition (3) is not true in the case of a field of moving charges (for it, the circulation of the intensity vector is nonzero). |
The circulation theorem for an electrostatic field.
Since the electrostatic field is central, the forces acting on a charge in such a field are conservative. Since it represents the elementary work that the field forces produce on a unit charge, the work of conservative forces on a closed loop is equal to
Potential
The "charge - electrostatic field" or "charge - charge" system has potential energy, just as the "gravitational field - body" system has potential energy.
The physical scalar quantity characterizing the energy state of the field is called potential given point in the field. A charge q is placed in the field, it has a potential energy W. Potential is a characteristic of an electrostatic field.
Consider potential energy in mechanics. Potential energy is zero when the body is on the ground. And when the body is raised to a certain height, then the body is said to have potential energy.
Regarding potential energy in electricity, there is no zero level of potential energy. He is chosen at random. Therefore, the potential is a relative physical quantity.
The potential energy of a field is the work that an electrostatic force does when moving a charge from a given point in the field to a point with zero potential.
Let us consider a special case when an electrostatic field is created by an electric charge Q. To study the potential of such a field, there is no need to introduce a charge q into it. You can calculate the potential of any point of such a field, located at a distance r from the charge Q.
The dielectric constant of the medium has a known value (table), it characterizes the medium in which the field exists. For air, it is equal to one.
Potential difference
The work of the field to move the charge from one point to another is called the potential difference
This formula can be presented in a different form
Superposition principle
The potential of the field created by several charges is equal to the algebraic (taking into account the sign of the potential) sum of the potentials of the fields of each field separately
This is the energy of a system of fixed point charges, the energy of a solitary charged conductor and the energy of a charged capacitor.
If there is a system of two charged conductors (capacitor), then the total energy of the system is equal to the sum of the intrinsic potential energies of the conductors and the energy of their interaction:
Electrostatic field energy system of point charges is equal to: 
A uniformly charged plane.
The electric field strength generated by an infinite plane charged with a surface charge density can be calculated using the Gauss theorem.
It follows from the symmetry conditions that the vector E everywhere perpendicular to the plane. In addition, at points symmetric with respect to the plane, the vector E will be the same in magnitude and opposite in direction.
As a closed surface, we choose a cylinder, the axis of which is perpendicular to the plane, and the bases are located symmetrically relative to the plane, as shown in the figure.
Since the lines of tension are parallel to the generators of the lateral surface of the cylinder, the flow through the lateral surface is zero. Therefore, the flow of the vector E through the surface of the cylinder
,
where is the area of the base of the cylinder. The cylinder cuts out the charge from the plane. If the plane is in a homogeneous isotropic medium with relative permittivity , then
When the field strength does not depend on the distance between the planes, such a field is called homogeneous. dependency graph E (x) for a plane.
Potential difference between two points located at distances R 1 and R 2 from the charged plane is equal to
Example 2. Two uniformly charged planes.
Let's calculate the strength of the electric field created by two infinite planes. The electric charge is distributed uniformly with surface densities and . We find the field strength as a superposition of the field strengths of each of the planes. The electric field is different from zero only in the space between the planes and is equal to .
Potential difference between planes 
, where d- distance between planes.
The results obtained can be used for an approximate calculation of the fields created by flat plates of finite dimensions, if the distances between them are much less than their linear dimensions. Noticeable errors in such calculations appear when considering fields near the edges of the plates. dependency graph E (x) for two planes.
Example 3. A thin charged rod.
To calculate the strength of the electric field created by a very long rod charged with a linear charge density, we use the Gauss theorem.
At sufficiently large distances from the ends of the rod, the electric field lines are directed radially from the axis of the rod and lie in planes perpendicular to this axis. At all points equidistant from the axis of the rod, the numerical values of the strength are the same if the rod is in a homogeneous isotropic medium with a relative dielectric
permeability.
To calculate the field strength at an arbitrary point located at a distance r from the axis of the rod, draw a cylindrical surface through this point
(see picture). The radius of this cylinder is r, and its height h.
The fluxes of the tension vector through the upper and lower bases of the cylinder will be equal to zero, since the lines of force do not have components normal to the surfaces of these bases. At all points on the lateral surface of the cylinder
E= const.
Therefore, the total flow of the vector E through the surface of the cylinder will be equal to
,
By the Gauss theorem, the flow of the vector E is equal to the algebraic sum of electric charges located inside the surface (in this case, the cylinder) divided by the product of the electric constant and the relative permittivity of the medium
where is the charge of that part of the rod that is inside the cylinder. Therefore, the electric field strength
The potential difference of the electric field between two points located at distances R 1 and R 2 from the axis of the rod, we will find using the relationship between the strength and potential of the electric field. Since the field strength changes only in the radial direction, then
Example 4. Charged spherical surface.
The electric field created by a spherical surface, over which an electric charge with a surface density is uniformly distributed, has a centrally symmetric character.
The lines of tension are directed along the radii from the center of the sphere, and the modulus of the vector E only depends on the distance r from the center of the sphere. To calculate the field, we choose a closed spherical surface of radius r.
When r o
The field strength is zero, since there is no charge inside the sphere.
For r > R (outside the sphere), according to the Gauss theorem
,
where is the relative permittivity of the medium surrounding the sphere.
.
The intensity decreases according to the same law as the field strength of a point charge, i.e., according to the law.
When r o
For r > R (outside the sphere) 
.
dependency graph E (r) for the sphere.
Example 5. Volume-charged dielectric ball.
If a ball with a radius R from a homogeneous isotropic dielectric with a relative permeability is uniformly charged over the volume with a density , then the electric field it creates is also centrally symmetric.
As in the previous case, we choose a closed surface to calculate the vector flow E in the form of a concentric sphere, the radius of which r can vary from 0 to .
At r < R flow vector E through this surface will be determined by the charge
So that
At r < R(inside the ball) 
.
Inside the ball, the tension increases in direct proportion to the distance from the center of the ball. Outside the ball (at r > R) in a medium with permittivity , the flux vector E across the surface will be determined by the charge.
When r o >R o (outside the ball) 
.
At the "ball - environment" boundary, the electric field strength changes abruptly, the value of which depends on the ratio of the permittivities of the ball and the medium. dependency graph E (r) for ball().
Outside the ball ( r > R) the potential of the electric field varies according to the law
.
inside the ball ( r < R) the potential is described by the expression
In conclusion, we give expressions for calculating the field strengths of charged bodies of various shapes
| Potential difference | |
 | |
| Voltage- the difference between the values of the potential at the initial and final points of the trajectory. Voltage numerically equal to the work of the electrostatic field when moving a unit positive charge along the lines of force of this field. Potential difference (voltage) does not depend on the choice coordinate systems! | |
Unit of potential difference  The voltage is 1 V if, when a positive charge of 1 C moves along the lines of force, the field does work of 1 J. |
Conductor is a solid body in which there are “free electrons” moving within the body.
Metal conductors are generally neutral: they have an equal number of negative and positive charges. Positively charged are ions in the nodes of the crystal lattice, negative are electrons that freely move along the conductor. When the conductor is given an excess number of electrons, it is charged negatively, but if a certain amount of electrons is “taken away” from the conductor, it is charged positively.
Excess charge is distributed only over the outer surface of the conductor.
1 . The field strength at any point inside the conductor is zero.
2 . The vector on the surface of the conductor is directed along the normal to each point on the surface of the conductor.
From the fact that the surface of the conductor is equipotential, it follows that directly at this surface the field is directed along the normal to it at each point (the condition 2 ). If this were not the case, then under the action of the tangential component, the charges would move along the surface of the conductor. those. equilibrium of charges on a conductor would be impossible.
From 1 it follows that since
There are no excess charges inside the conductor.
Charges are distributed only on the surface of the conductor with a certain density s and are located in a very thin surface layer (its thickness is about one or two interatomic distances).
charge density- this is the amount of charge per unit length, area or volume, thus determining the linear, surface and volume charge densities, which are measured in the SI system: in Coulombs per meter [C/m], in Coulombs per square meter [C/m² ] and in Coulomb per cubic meter [C/m³], respectively. Unlike the density of matter, the charge density can have both positive and negative values, this is due to the fact that there are positive and negative charges.
General problem of electrostatics
tension vector,
according to the Gauss theorem 
- Poisson's equation.
In the case - there are no charges between the conductors, we get
- Laplace equation.
Let the boundary conditions on the surfaces of the conductors be known: the values 
; then this problem has a unique solution according to uniqueness theorem.
When solving the problem, the value is determined and then the field between the conductors is determined by the distribution of charges on the conductors (according to the intensity vector near the surface).
Consider an example. Find the tension in the empty cavity of the conductor.
The potential in the cavity satisfies the Laplace equation;
potential on the walls of the conductor.
The solution of the Laplace equation in this case is trivial, and by the uniqueness theorem there are no other solutions
, i.e. there is no field in the conductor cavity.
Poisson equation is an elliptic partial differential equation that, among other things, describes
the electrostatic field
a stationary temperature field,
The pressure field
· velocity potential field in hydrodynamics.
It is named after the famous French physicist and mathematician Simeon Denis Poisson.
This equation looks like:
where is the Laplace operator or Laplacian, and is a real or complex function on some manifold.
In a three-dimensional Cartesian coordinate system, the equation takes the form:
In the Cartesian coordinate system, the Laplace operator is written in the form and the Poisson equation takes the form:
If a f tends to zero, then the Poisson equation turns into the Laplace equation (the Laplace equation is a special case of the Poisson equation):
Poisson's equation can be solved using the Green's function; see, for example, the article screened Poisson equation. There are various methods for obtaining numerical solutions. For example, an iterative algorithm is used - the "relaxation method".
| We will consider a solitary conductor, i.e., a conductor significantly removed from other conductors, bodies and charges. Its potential, as you know, is directly proportional to the charge of the conductor. It is known from experience that different conductors, being equally charged, have different potentials. Therefore, for a solitary conductor, you can write the Value (1) is called the electrical capacity (or simply capacitance) of a solitary conductor. The capacitance of a solitary conductor is given by a charge, the communication of which to the conductor changes its potential by one. The capacitance of a solitary conductor depends on its size and shape, but does not depend on the material, shape and size of the cavities inside the conductor, as well as its state of aggregation. The reason for this is that excess charges are distributed on the outer surface of the conductor. The capacitance also does not depend on the charge of the conductor, nor on its potential. The unit of electrical capacity is farad (F): 1 F is the capacitance of such a solitary conductor, in which the potential changes by 1 V when a charge of 1 C is imparted to it. According to the formula for the potential of a point charge, the potential of a solitary ball of radius R, which is located in a homogeneous medium with a permittivity ε, is equal to Applying formula (1), we obtain that the capacitance of the ball (2) From this it follows that a solitary ball would have a capacity of 1 F, located in a vacuum and having a radius R=C/(4πε 0)≈9 10 6 km, which is approximately 1400 times greater than the radius of the Earth (electric capacity of the Earth C≈0.7 mF). Consequently, the farad is a rather large value, therefore, in practice, submultiple units are used - millifarad (mF), microfarad (μF), nanofarad (nF), picofarad (pF). It also follows from formula (2) that the unit of the electrical constant ε 0 is a farad per meter (F/m) (see (78.3)). |
Capacitor(from lat. condensare- “compact”, “thicken”) - a two-terminal network with a certain value of capacitance and low ohmic conductivity; a device for accumulating charge and energy of an electric field. The capacitor is a passive electronic component. Usually consists of two plate-shaped electrodes (called facings), separated by a dielectric, the thickness of which is small compared to the dimensions of the plates.
Capacity
The main characteristic of a capacitor is its capacity characterizing the ability of a capacitor to store an electric charge. The value of the nominal capacity appears in the designation of the capacitor, while the actual capacity can vary significantly depending on many factors. The actual capacitance of a capacitor determines its electrical properties. So, by definition of capacitance, the charge on the plate is proportional to the voltage between the plates ( q=CU). Typical capacitance values range from picofarads to thousands of microfarads. However, there are capacitors (ionistors) with a capacity of up to tens of farads.
Capacitance of a flat capacitor, consisting of two parallel metal plates with an area S each located at a distance d from each other, in the SI system is expressed by the formula: This formula is valid only when d much smaller than the linear dimensions of the plates.
To obtain large capacitances, capacitors are connected in parallel. In this case, the voltage between the plates of all capacitors is the same. Total battery capacity parallel connected capacitors is equal to the sum of the capacitances of all capacitors included in the battery.
If all capacitors connected in parallel have the same distance between the plates and the properties of the dielectric, then these capacitors can be represented as one large capacitor, divided into fragments of a smaller area.
When capacitors are connected in series, the charges of all capacitors are the same, since they are supplied from the power source only to the external electrodes, and on the internal electrodes they are obtained only due to the separation of charges that previously neutralized each other. Total battery capacity successively connected capacitors is
Or 
This capacitance is always less than the minimum capacitance of the capacitor included in the battery. However, when connected in series, the possibility of breakdown of capacitors is reduced, since each capacitor accounts for only a part of the potential difference of the voltage source.
If the area of the plates of all capacitors connected in series is the same, then these capacitors can be represented as one large capacitor, between the plates of which there is a stack of dielectric plates of all the capacitors that make it up.
[edit] Specific capacity
Capacitors are also characterized by specific capacitance - the ratio of capacitance to the volume (or mass) of the dielectric. The maximum value of the specific capacitance is achieved at the minimum thickness of the dielectric, however, this reduces its breakdown voltage.
Electrical circuits use a variety of ways to connect capacitors. Connection of capacitors can be made: successively, parallel and series-parallel(the latter is sometimes called a mixed capacitor connection). The existing types of connection of capacitors are shown in Figure 1.
Figure 1. Methods for connecting capacitors.
In a uniform electric field, the force acting on a charged particle is constant both in magnitude and in direction. Therefore, the motion of such a particle is completely analogous to the motion of a body in the earth's gravity field without taking into account air resistance. The trajectory of the particle in this case is flat, lies in the plane containing the vectors of the initial velocity of the particle and the electric field strength
The potential of the electrostatic field. A general expression relating potential to tension.
The potential φ at any point of the electrostatic field is a physical quantity determined by the potential energy of a single positive charge placed at this point. The potential of the field created by a point charge Q is
Potential - a physical quantity, which is determined by the work of moving a single positive electric charge when it is removed from a given point of the field to infinity. This work is numerically equal to the work done by external forces (against the forces of the electrostatic field) in moving a unit positive charge from infinity to a given point in the field.
The unit of potential is the volt (V): 1 V is equal to the potential of such a point in the field at which a charge of 1 C has a potential energy of 1 J (1 V = 1 J/C). Considering the dimension of the volt, it can be shown that the unit of electrostatic field strength introduced earlier is indeed 1 V/m: 1 N/Cl=1 N m/(Cl m)=1 J/(Cl m)=1 V/m.
From formulas (3) and (4) it follows that if the field is created by several charges, then the potential of the given field of the system of charges is equal to the algebraic sum of the potentials of the fields of all these charges:
The strength at any point of the electric field is equal to the potential gradient at this point, taken with the opposite sign. The minus sign indicates that the intensity E is directed in the direction of decreasing potential.
E = - grad phi = - N phi.
To establish a connection between the power characteristic of the electric field - the strength and its energy characteristic - the potential, consider the elementary work of the electric field forces on an infinitely small displacement of a point charge q: dA = q E dl, the same work is equal to the decrease in the potential energy of the charge q: dA = - dWп = - q dphi, where d phi is the change in the potential of the electric field over the travel length dl. Equating the right parts of the expressions, we get: E dl = -d phi or in the Cartesian coordinate system
Ex dx + Ey dy + Ez dz = -d fi
where Ex, Ey, Ez are the projections of the intensity vector on the axes of the coordinate system. Since the expression is a total differential, then for the projections of the intensity vector we have
The expression in brackets is the gradient of the phi potential.
Superposition principle as a fundamental property of fields. General expressions for the strength and potential of the field created at a point with a radius vector by a system of point charges located at points with coordinates. (See item 4)
If we consider the principle of superposition in the most general sense, then according to it, the sum of the impact of external forces acting on a particle will be the sum of the individual values of each of them. This principle applies to various linear systems, i.e. systems whose behavior can be described by linear relations. An example is a simple situation when a linear wave propagates in some particular medium, in which case its properties will be preserved even under the influence of disturbances arising from the wave itself. These properties are defined as a specific sum of the effects of each of the harmonic components.
The superposition principle can also take other formulations that are completely equivalent to the one given above:
· The interaction between two particles does not change when a third particle is introduced, which also interacts with the first two.
· The interaction energy of all particles in a many-particle system is simply the sum of the energies of pair interactions between all possible pairs of particles. There are no multiparticle interactions in the system.
· The equations describing the behavior of a multiparticle system are linear in the number of particles.
6 The circulation of the tension vector is the work that electric forces do when moving a single positive charge along a closed path L
Since the work of the electrostatic field forces in a closed loop is zero (the work of the potential field forces), therefore, the circulation of the electrostatic field strength in a closed loop is zero.
Field potential. The work of any electrostatic field when moving a charged body in it from one point to another also does not depend on the shape of the trajectory, as well as the work of a uniform field. On a closed trajectory, the work of the electrostatic field is always zero. Fields with this property are called potential fields. In particular, the electrostatic field of a point charge has a potential character.
The work of a potential field can be expressed in terms of a change in potential energy. The formula is valid for any electrostatic field.
7-11 If the lines of force of a uniform electric field of strength penetrate some area S, then the flux of the intensity vector (we used to call the number of lines of force through the area) will be determined by the formula:
where En is the product of the vector and the normal to the given area (Fig. 2.5).
Rice. 2.5
The total number of lines of force passing through the surface S is called the flow of the intensity vector FU through this surface.
In vector form, you can write - the scalar product of two vectors, where the vector .
Thus, the vector flow is a scalar, which, depending on the angle α, can be either positive or negative.
Consider the examples shown in Figures 2.6 and 2.7.
 | |||
| Rice. 2.6 | Rice. 2.7 | ||
For Figure 2.6, surface A1 is surrounded by a positive charge and the flow here is directed outward, i.e. The A2– surface is surrounded by a negative charge, and here it is directed inward. The total flow through surface A is zero.
For Figure 2.7, the flux will be non-zero if the total charge inside the surface is non-zero. For this configuration, the flux through surface A is negative (count the number of field lines).
Thus, the intensity vector flux depends on the charge. This is the meaning of the Ostrogradsky-Gauss theorem.
Gauss theorem
The experimentally established Coulomb's law and the principle of superposition make it possible to completely describe the electrostatic field of a given system of charges in vacuum. However, the properties of the electrostatic field can be expressed in a different, more general form, without resorting to the concept of the Coulomb field of a point charge.
Let us introduce a new physical quantity that characterizes the electric field - the flux Φ of the electric field strength vector. Let some sufficiently small area ΔS be located in the space where the electric field is created. The product of the vector module and the area ΔS and the cosine of the angle α between the vector and the normal to the site is called the elementary flux of the intensity vector through the site ΔS (Fig. 1.3.1):
Let us now consider some arbitrary closed surface S. If we divide this surface into small areas ΔSi, determine the elementary fluxes ΔΦi of the field through these small areas, and then sum them up, then as a result we get the flow Φ of the vector through the closed surface S (Fig. 1.3.2 ):
Gauss' theorem states:
The flow of the electrostatic field strength vector through an arbitrary closed surface is equal to the algebraic sum of the charges located inside this surface, divided by the electric constant ε0.
where R is the radius of the sphere. The flux Φ through the spherical surface will be equal to the product of E and the area of the sphere 4πR2. Hence,
Let us now surround the point charge with an arbitrary closed surface S and consider an auxiliary sphere of radius R0 (Fig. 1.3.3).
Consider a cone with a small solid angle ΔΩ at the vertex. This cone selects a small area ΔS0 on the sphere, and an area ΔS on the surface S. The elementary flows ΔΦ0 and ΔΦ through these areas are the same. Really,
In a similar way, one can show that if the closed surface S does not enclose a point charge q, then the flow Φ = 0. Such a case is shown in fig. 1.3.2. All lines of force of the electric field of a point charge penetrate the closed surface S through and through. There are no charges inside the surface S, therefore, in this region, the lines of force do not break and do not originate.
The generalization of the Gauss theorem to the case of an arbitrary distribution of charges follows from the principle of superposition. The field of any charge distribution can be represented as a vector sum of electric fields of point charges. The flow Φ of a system of charges through an arbitrary closed surface S will be the sum of the flows Φi of the electric fields of individual charges. If the charge qi turned out to be inside the surface S, then it makes a contribution to the flow equal to if this charge turned out to be outside the surface, then the contribution of its electric field to the flow will be equal to zero.
Thus, the Gauss theorem is proved.
Gauss's theorem is a consequence of Coulomb's law and the superposition principle. But if we accept the statement contained in this theorem as an initial axiom, then Coulomb's law will turn out to be its consequence. Therefore, Gauss's theorem is sometimes called an alternative formulation of Coulomb's law.
Using the Gauss theorem, in a number of cases it is easy to calculate the electric field strength around a charged body if the given charge distribution has some kind of symmetry and the general structure of the field can be guessed in advance.
An example is the problem of calculating the field of a thin-walled, hollow, uniformly charged long cylinder of radius R. This problem has axial symmetry. For reasons of symmetry, the electric field must be directed along the radius. Therefore, to apply the Gauss theorem, it is advisable to choose a closed surface S in the form of a coaxial cylinder of some radius r and length l, closed at both ends (Fig. 1.3.4).
For r ≥ R, the entire flow of the intensity vector will pass through the side surface of the cylinder, the area of which is equal to 2πrl, since the flow through both bases is zero. Applying the Gauss theorem gives:
This result does not depend on the radius R of the charged cylinder, so it is also applicable to the field of a long uniformly charged filament.
To determine the field strength inside a charged cylinder, it is necessary to construct a closed surface for the case r< R. В силу симметрии задачи поток вектора напряженности через боковую поверхность гауссова цилиндра должен быть и в этом случае равен Φ = E 2πrl. Согласно теореме Гаусса, этот поток пропорционален заряду, оказавшемуся внутри замкнутой поверхности. Этот заряд равен нулю. Отсюда следует, что электрическое поле внутри однородно заряженного длинного полого цилиндра равно нулю.
Similarly, Gauss's theorem can be applied to determine the electric field in a number of other cases where the charge distribution has some kind of symmetry, for example, symmetry about the center, plane or axis. In each of these cases, it is necessary to choose a closed Gaussian surface of an expedient form. For example, in the case of central symmetry, it is convenient to choose a Gaussian surface in the form of a sphere centered at a point of symmetry. With axial symmetry, a closed surface must be chosen in the form of a coaxial cylinder closed at both ends (as in the example discussed above). If the distribution of charges does not have any symmetry and the general structure of the electric field cannot be guessed, the application of the Gauss theorem cannot simplify the problem of determining the field strength.
Consider another example of a symmetrical distribution of charges - the definition of the field of a uniformly charged plane (Fig. 1.3.5).
In this case, it is advisable to choose the Gaussian surface S in the form of a cylinder of some length, closed at both ends. The axis of the cylinder is directed perpendicular to the charged plane, and its ends are located at the same distance from it. Due to symmetry, the field of a uniformly charged plane must be directed along the normal everywhere. Applying the Gauss theorem gives:
|
where σ is the surface charge density, i.e., the charge per unit area.
The resulting expression for the electric field of a uniformly charged plane is also applicable in the case of flat charged areas of a finite size. In this case, the distance from the point at which the field strength is determined to the charged area must be significantly less than the size of the area.
And schedules for 7 - 11
1. The intensity of the electrostatic field created by a uniformly charged spherical surface.
Let a spherical surface of radius R (Fig. 13.7) bear a uniformly distributed charge q, i.e. the surface charge density at any point on the sphere will be the same.
a. We enclose our spherical surface in a symmetric surface S with radius r>R. The intensity vector flux through the surface S will be equal to
According to the Gauss theorem
Hence
c. Let us draw through the point B, located inside the charged spherical surface, the sphere S with radius r 2. Electrostatic field of the ball. Let we have a ball of radius R, uniformly charged with bulk density. At any point A, lying outside the ball at a distance r from its center (r> R), its field is similar to the field of a point chargelocated at the center of the ball. Then outside the ball and on its surface (r=R) At point B, lying inside the ball at distances r from its center (r>R), the field is determined only by the charge enclosed inside the sphere of radius r. The intensity vector flow through this sphere is equal to on the other hand, according to the Gauss theorem According to the Gauss theorem From the last two expressions, we determine the field strength created by a uniformly charged thread: Let the plane have an infinite extent and the charge per unit area is equal to σ. From the laws of symmetry it follows that the field is directed everywhere perpendicular to the plane, and if there are no other external charges, then the fields on both sides of the plane should be the same. Let us limit a part of the charged plane to an imaginary cylindrical box, so that the box is cut in half and its generators are perpendicular, and two bases, each having an area S, are parallel to the charged plane (Figure 1.10). 12. Field of a uniformly charged sphere. Let the electric field be created by the charge Q, uniformly distributed over the surface of a sphere of radius R(Fig. 190). To calculate the field potential at an arbitrary point located at a distance r from the center of the sphere, it is necessary to calculate the work done by the field when moving a unit positive charge from a given point to infinity. Earlier we proved that the field strength of a uniformly charged sphere outside it is equivalent to the field of a point charge located at the center of the sphere. Therefore, outside the sphere, the potential of the field of the sphere will coincide with the potential of the field of a point charge φ
(r)=Q 4πε
0r . (1) In particular, on the surface of a sphere, the potential is equal to φ
0=Q 4πε
0R. There is no electrostatic field inside the sphere, so the work to move a charge from an arbitrary point inside the sphere to its surface is zero A= 0, therefore, the potential difference between these points is also equal to zero Δ φ
= -A= 0. Therefore, all points inside the sphere have the same potential, which coincides with the potential of its surface φ
0=Q 4πε
0R . So, the distribution of the field potential of a uniformly charged sphere has the form (Fig. 191) φ
(r)=⎧⎩⎨Q 4πε
0R, npu r<RQ 4πε
0r, npu r>R . (2) Please note that there is no field inside the sphere, and the potential is different from zero! This example is a vivid illustration of the fact that the potential is determined by the value of the field from a given point to infinity.
(13.10)
(13.11)
(13.13)
