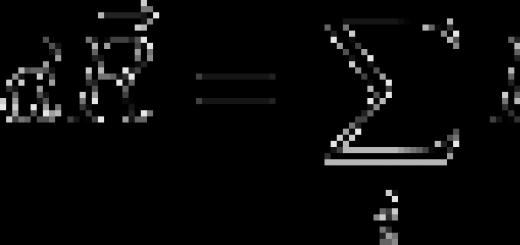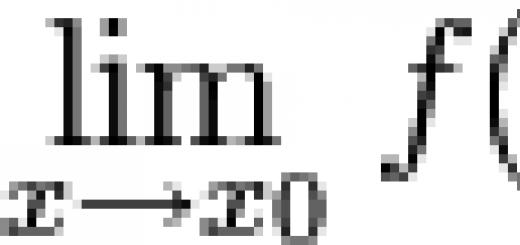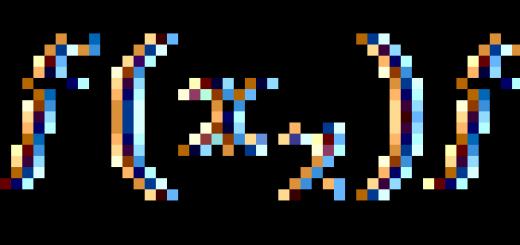Determining the derivative of a function is the inverse operation of integrating a function. For elementary functions, it is not difficult to calculate the derivative; it is enough to use the table of derivatives. If we need find the derivative from a complex function, then differentiation will be much more difficult, requiring more care and time. It is very easy to make a typo or a minor mistake, which will lead to the final wrong answer. Therefore, it is always important to be able to check your decision. You can do this with this online calculator, which allows you to find derivatives of any functions online with a detailed solution for free, without registering on the site. Finding the derivative of a function (differentiation) is the ratio of the increment of the function to the increment of the argument (numerically, the derivative is equal to the tangent of the slope of the tangent to the graph of the function). If it is necessary to calculate the derivative of a function at a specific point, then in the received response, instead of the argument x frame him numerical value and calculate the expression. At online derivative solution you need to enter a function in the corresponding field: in this case, the argument must be a variable x, since differentiation goes exactly along it. To calculate the second derivative, you need to differentiate the received answer.
The operation of finding a derivative is called differentiation.
As a result of solving problems of finding derivatives of the simplest (and not very simple) functions by defining the derivative as the limit of the ratio of the increment to the increment of the argument, a table of derivatives and precisely defined rules of differentiation appeared. Isaac Newton (1643-1727) and Gottfried Wilhelm Leibniz (1646-1716) were the first to work in the field of finding derivatives.
Therefore, in our time, in order to find the derivative of any function, it is not necessary to calculate the above-mentioned limit of the ratio of the increment of the function to the increment of the argument, but only need to use the table of derivatives and the rules of differentiation. The following algorithm is suitable for finding the derivative.
To find the derivative, you need an expression under the stroke sign break down simple functions and determine what actions (product, sum, quotient) these functions are related. Further, we find the derivatives of elementary functions in the table of derivatives, and the formulas for the derivatives of the product, sum and quotient - in the rules of differentiation. The table of derivatives and differentiation rules are given after the first two examples.
Example 1 Find the derivative of a function
Decision. From the rules of differentiation we find out that the derivative of the sum of functions is the sum of derivatives of functions, i.e.
From the table of derivatives, we find out that the derivative of "X" is equal to one, and the derivative of the sine is cosine. We substitute these values in the sum of derivatives and find the derivative required by the condition of the problem:
Example 2 Find the derivative of a function
Decision. Differentiate as a derivative of the sum, in which the second term with a constant factor, it can be taken out of the sign of the derivative:
![]()
If there are still questions about where something comes from, they, as a rule, become clear after reading the table of derivatives and the simplest rules of differentiation. We are going to them right now.
Table of derivatives of simple functions
| 1. Derivative of a constant (number). Any number (1, 2, 5, 200...) that is in the function expression. Always zero. This is very important to remember, as it is required very often | |
| 2. Derivative of the independent variable. Most often "x". Always equal to one. This is also important to remember | |
| 3. Derivative of degree. When solving problems, you need to convert non-square roots to a power. | |
| 4. Derivative of a variable to the power of -1 | |
| 5. Derivative square root | |
| 6. Sine derivative | |
| 7. Cosine derivative | |
| 8. Tangent derivative | |
| 9. Derivative of cotangent | |
| 10. Derivative of the arcsine | |
| 11. Derivative of arc cosine | |
| 12. Derivative of arc tangent | |
| 13. Derivative of the inverse tangent | |
| 14. Derivative of natural logarithm | |
| 15. Derivative of a logarithmic function | |
| 16. Derivative of the exponent | |
| 17. Derivative exponential function |
Differentiation rules
| 1. Derivative of the sum or difference | |
| 2. Derivative of a product | |
| 2a. Derivative of an expression multiplied by a constant factor | |
| 3. Derivative of the quotient | |
| 4. Derivative of a complex function |  |
Rule 1If functions
are differentiable at some point , then at the same point the functions
and
![]()
those. the derivative of the algebraic sum of functions is algebraic sum derivatives of these functions.
Consequence. If two differentiable functions differ by a constant, then their derivatives are, i.e.
Rule 2If functions
are differentiable at some point , then their product is also differentiable at the same point
and
![]()
those. the derivative of the product of two functions is equal to the sum of the products of each of these functions and the derivative of the other.
Consequence 1. The constant factor can be taken out of the sign of the derivative:
Consequence 2. The derivative of the product of several differentiable functions is equal to the sum of the products of the derivative of each of the factors and all the others.
For example, for three multipliers:
Rule 3If functions
differentiable at some point and , then at this point their quotient is also differentiable.u/v , and
![]()
those. the derivative of a quotient of two functions is equal to a fraction whose numerator is the difference between the products of the denominator and the derivative of the numerator and the numerator and the derivative of the denominator, and the denominator is the square of the former numerator.
Where to look on other pages
When finding the derivative of the product and the quotient in real problems, it is always necessary to apply several differentiation rules at once, so more examples on these derivatives are in the article."The derivative of a product and a quotient".
Comment. You should not confuse a constant (that is, a number) as a term in the sum and as a constant factor! In the case of a term, its derivative is equal to zero, and in the case of a constant factor, it is taken out of the sign of the derivatives. This is typical mistake, which occurs at the initial stage of the study of derivatives, but as the solution of several one-two-component examples is already made, the average student no longer makes this mistake.
And if, when differentiating a product or a quotient, you have a term u"v, wherein u- a number, for example, 2 or 5, that is, a constant, then the derivative of this number will be equal to zero and, therefore, the entire term will be equal to zero (such a case is analyzed in example 10).
Another common mistake is the mechanical solution of the derivative of a complex function as the derivative of a simple function. So derivative of a complex function devoted to a separate article. But first we will learn to find derivatives of simple functions.
Along the way, you can not do without transformations of expressions. To do this, you may need to open in new windows manuals Actions with powers and roots and Actions with fractions .
If you are looking for solutions to derivatives with powers and roots, that is, when the function looks like ![]() , then follow the lesson " Derivative of the sum of fractions with powers and roots".
, then follow the lesson " Derivative of the sum of fractions with powers and roots".
If you have a task like ![]() , then you are in the lesson "Derivatives of simple trigonometric functions".
, then you are in the lesson "Derivatives of simple trigonometric functions".
Step by step examples - how to find the derivative
Example 3 Find the derivative of a function
Decision. We determine the parts of the expression of the function: the entire expression represents the product, and its factors are sums, in the second of which one of the terms contains a constant factor. We apply the product differentiation rule: the derivative of the product of two functions is equal to the sum of the products of each of these functions and the derivative of the other:
![]()
Next, we apply the rule of differentiation of the sum: the derivative of the algebraic sum of functions is equal to the algebraic sum of the derivatives of these functions. In our case, in each sum, the second term with a minus sign. In each sum, we see both an independent variable, the derivative of which is equal to one, and a constant (number), the derivative of which is equal to zero. So, "x" turns into one, and minus 5 - into zero. In the second expression, "x" is multiplied by 2, so we multiply two by the same unit as the derivative of "x". We get the following values of derivatives:
We substitute the found derivatives into the sum of products and obtain the derivative of the entire function required by the condition of the problem:
![]()
And you can check the solution of the problem on the derivative on .
Example 4 Find the derivative of a function
Decision. We are required to find the derivative of the quotient. We apply the formula for differentiating a quotient: the derivative of a quotient of two functions is equal to a fraction whose numerator is the difference between the products of the denominator and the derivative of the numerator and the numerator and the derivative of the denominator, and the denominator is the square of the former numerator. We get:
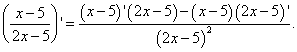
We have already found the derivative of the factors in the numerator in Example 2. Let's also not forget that the product, which is the second factor in the numerator, is taken with a minus sign in the current example:

If you are looking for solutions to such problems in which you need to find the derivative of a function, where there is a continuous pile of roots and degrees, such as, for example, ![]() then welcome to class "The derivative of the sum of fractions with powers and roots" .
then welcome to class "The derivative of the sum of fractions with powers and roots" .
If you need to learn more about derivatives of sines, cosines, tangents and others trigonometric functions, that is, when the function looks like ![]() , then you have a lesson "Derivatives of simple trigonometric functions" .
, then you have a lesson "Derivatives of simple trigonometric functions" .
Example 5 Find the derivative of a function
Decision. In this function, we see a product, one of the factors of which is the square root of the independent variable, with the derivative of which we familiarized ourselves in the table of derivatives. According to the product differentiation rule and the tabular value of the derivative of the square root, we get:

You can check the solution of the derivative problem on derivative calculator online .
Example 6 Find the derivative of a function
Decision. In this function, we see the quotient, the dividend of which is the square root of the independent variable. According to the rule of differentiation of the quotient, which we repeated and applied in example 4, and the tabular value of the derivative of the square root, we get:

To get rid of the fraction in the numerator, multiply the numerator and denominator by .
Date: 05/10/2015
How to find the derivative?
Differentiation rules.
To find the derivative of any function, you need to master only three concepts:
2. Rules of differentiation.
3. Derivative of a complex function.
It's in that order. It's a hint.)
Of course, it would be nice to have an idea about the derivative in general). About what a derivative is and how to work with a table of derivatives - it is accessible in the previous lesson. Here we will deal with the rules of differentiation.
Differentiation is the operation of finding a derivative. There is nothing more behind this term. Those. expressions "find the derivative of a function" and "differentiate function"- This is the same.
Expression "rules of differentiation" refers to finding the derivative from arithmetic operations. This understanding helps a lot to avoid porridge in the head.
Let's focus and remember everything, everything, everything arithmetic operations. There are four of them). Addition (sum), subtraction (difference), multiplication (product), and division (quotient). Here they are, the rules of differentiation:
The plate shows five rules on four arithmetic operations. I didn't miscalculate.) It's just that rule 4 is an elementary corollary of rule 3. But it's so popular that it makes sense to write it down (and remember!) as an independent formula.
Under the notation U and V some (absolutely any!) functions are implied U(x) and V(x).
Let's look at a few examples. First, the simplest ones.
Find the derivative of the function y=sinx - x 2
Here we have difference two elementary functions. We apply rule 2. We will assume that sinx is a function U, and x 2 is a function v. We have every right to write:
y" = (sinx - x 2)" = (sinx)"- (x 2)"
Already better, right?) It remains to find the derivatives of the sine and the square of x. There is a derivative table for this. We just look in the table for the functions we need ( sinx and x2), look at their derivatives and write down the answer:
y" = (sinx)" - (x 2)" = cosx - 2x
That's all there is to it. Rule 1 of differentiating the sum works in exactly the same way.
What if we have multiple terms? It's okay.) We break the function into terms and look for the derivative of each term, regardless of the others. For example:
Find the derivative of the function y=sinx - x 2 +cosx - x +3
Feel free to write:
y" = (sinx)" - (x 2)" + (cosx)" - (x)" + (3)"
At the end of the lesson, I will give tips on making life easier when differentiating.)
Practical Tips:
1. Before differentiation, we look to see if it is possible to simplify the original function.
2. In confused examples, we paint the solution in detail, with all brackets and strokes.
3. When differentiating fractions with a constant number in the denominator, we turn division into multiplication and use rule 4.
If we follow the definition, then the derivative of a function at a point is the limit of the increment ratio of the function Δ y to the increment of the argument Δ x:
Everything seems to be clear. But try to calculate by this formula, say, the derivative of the function f(x) = x 2 + (2x+ 3) · e x sin x. If you do everything by definition, then after a couple of pages of calculations you will simply fall asleep. Therefore, there are simpler and more effective ways.
To begin with, we note that the so-called elementary functions can be distinguished from the whole variety of functions. It's relative simple expressions, whose derivatives have long been calculated and entered in the table. Such functions are easy enough to remember, along with their derivatives.
Derivatives of elementary functions
Elementary functions are everything listed below. The derivatives of these functions must be known by heart. Moreover, it is not difficult to memorize them - that's why they are elementary.
So, the derivatives of elementary functions:
| Name | Function | Derivative |
| Constant | f(x) = C, C ∈ R | 0 (yes, yes, zero!) |
| Degree with rational exponent | f(x) = x n | n · x n − 1 |
| Sinus | f(x) = sin x | cos x |
| Cosine | f(x) = cos x | − sin x(minus sine) |
| Tangent | f(x) = tg x | 1/cos 2 x |
| Cotangent | f(x) = ctg x | − 1/sin2 x |
| natural logarithm | f(x) = log x | 1/x |
| Arbitrary logarithm | f(x) = log a x | 1/(x ln a) |
| Exponential function | f(x) = e x | e x(nothing changed) |
If an elementary function is multiplied by an arbitrary constant, then the derivative of the new function is also easily calculated:
(C · f)’ = C · f ’.
In general, constants can be taken out of the sign of the derivative. For example:
(2x 3)' = 2 ( x 3)' = 2 3 x 2 = 6x 2 .
Obviously, elementary functions can be added to each other, multiplied, divided, and much more. This is how new functions will appear, no longer very elementary, but also differentiable according to certain rules. These rules are discussed below.
Derivative of sum and difference
Let the functions f(x) and g(x), whose derivatives are known to us. For example, you can take the elementary functions discussed above. Then you can find the derivative of the sum and difference of these functions:
- (f + g)’ = f ’ + g ’
- (f − g)’ = f ’ − g ’
So, the derivative of the sum (difference) of two functions is equal to the sum (difference) of the derivatives. There may be more terms. For example, ( f + g + h)’ = f ’ + g ’ + h ’.
Strictly speaking, there is no concept of "subtraction" in algebra. There is a concept of "negative element". Therefore, the difference f − g can be rewritten as a sum f+ (−1) g, and then only one formula remains - the derivative of the sum.
f(x) = x 2 + sinx; g(x) = x 4 + 2x 2 − 3.
Function f(x) is the sum of two elementary functions, so:
f ’(x) = (x 2+ sin x)’ = (x 2)' + (sin x)’ = 2x+ cosx;
We argue similarly for the function g(x). Only there are already three terms (from the point of view of algebra):
g ’(x) = (x 4 + 2x 2 − 3)’ = (x 4 + 2x 2 + (−3))’ = (x 4)’ + (2x 2)’ + (−3)’ = 4x 3 + 4x + 0 = 4x · ( x 2 + 1).
Answer:
f ’(x) = 2x+ cosx;
g ’(x) = 4x · ( x
2 + 1).
Derivative of a product
Mathematics is a logical science, so many people believe that if the derivative of the sum is equal to the sum of the derivatives, then the derivative of the product strike"\u003e equal to the product of derivatives. But figs to you! The derivative of the product is calculated using a completely different formula. Namely:
(f · g) ’ = f ’ · g + f · g ’
The formula is simple, but often forgotten. And not only schoolchildren, but also students. The result is incorrectly solved problems.
Task. Find derivatives of functions: f(x) = x 3 cosx; g(x) = (x 2 + 7x− 7) · e x .
Function f(x) is a product of two elementary functions, so everything is simple:
f ’(x) = (x 3 cos x)’ = (x 3)' cos x + x 3 (cos x)’ = 3x 2 cos x + x 3 (−sin x) = x 2 (3cos x − x sin x)
Function g(x) the first multiplier is a little more complicated, but the general scheme does not change from this. Obviously, the first multiplier of the function g(x) is a polynomial, and its derivative is the derivative of the sum. We have:
g ’(x) = ((x 2 + 7x− 7) · e x)’ = (x 2 + 7x− 7)' · e x + (x 2 + 7x− 7) ( e x)’ = (2x+ 7) · e x + (x 2 + 7x− 7) · e x = e x(2 x + 7 + x 2 + 7x −7) = (x 2 + 9x) · e x = x(x+ 9) · e x .
Answer:
f ’(x) = x 2 (3cos x − x sin x);
g ’(x) = x(x+ 9) · e
x
.
Note that in the last step, the derivative is factorized. Formally, this is not necessary, but most derivatives are not calculated on their own, but to explore the function. This means that further the derivative will be equated to zero, its signs will be found out, and so on. For such a case, it is better to have an expression decomposed into factors.
If there are two functions f(x) and g(x), and g(x) ≠ 0 on the set of interest to us, we can define a new function h(x) = f(x)/g(x). For such a function, you can also find the derivative:
Not weak, right? Where did the minus come from? Why g 2? But like this! This is one of the most complex formulas - you can’t figure it out without a bottle. Therefore, it is better to study it with specific examples.
Task. Find derivatives of functions:
There are elementary functions in the numerator and denominator of each fraction, so all we need is the formula for the derivative of the quotient:
By tradition, we factor the numerator into factors - this will greatly simplify the answer:
A complex function is not necessarily a formula half a kilometer long. For example, it suffices to take the function f(x) = sin x and replace the variable x, say, on x 2+ln x. It turns out f(x) = sin ( x 2+ln x) - That's what it is complex function. She also has a derivative, but it will not work to find it according to the rules discussed above.
How to be? In such cases, the replacement of a variable and the formula for the derivative of a complex function help:
f ’(x) = f ’(t) · t', if x is replaced by t(x).
As a rule, the situation with the understanding of this formula is even more sad than with the derivative of the quotient. Therefore, it is also better to explain it with specific examples, with detailed description every step.
Task. Find derivatives of functions: f(x) = e 2x + 3 ; g(x) = sin ( x 2+ln x)
Note that if in the function f(x) instead of expression 2 x+ 3 will be easy x, then it will work elementary function f(x) = e x. Therefore, we make a substitution: let 2 x + 3 = t, f(x) = f(t) = e t. We are looking for the derivative of a complex function by the formula:
f ’(x) = f ’(t) · t ’ = (e t)’ · t ’ = e t · t ’
And now - attention! Performing a reverse substitution: t = 2x+ 3. We get:
f ’(x) = e t · t ’ = e 2x+ 3 (2 x + 3)’ = e 2x+ 3 2 = 2 e 2x + 3
Now let's look at the function g(x). Obviously needs to be replaced. x 2+ln x = t. We have:
g ’(x) = g ’(t) · t' = (sin t)’ · t' = cos t · t ’
Reverse replacement: t = x 2+ln x. Then:
g ’(x) = cos( x 2+ln x) · ( x 2+ln x)' = cos ( x 2+ln x) · (2 x + 1/x).
That's all! As can be seen from the last expression, the whole problem has been reduced to calculating the derivative of the sum.
Answer:
f ’(x) = 2 e
2x + 3 ;
g ’(x) = (2x + 1/x) cos( x 2+ln x).
Very often in my lessons, instead of the term “derivative”, I use the word “stroke”. For example, a stroke from the sum is equal to the sum strokes. Is that clearer? Well, that's good.
Thus, the calculation of the derivative comes down to getting rid of these very strokes according to the rules discussed above. As a final example, let's return to the derivative power with a rational exponent:
(x n)’ = n · x n − 1
Few know that in the role n may well be a fractional number. For example, the root is x 0.5 . But what if there is something tricky under the root? Again, a complex function will turn out - they like to give such constructions on control work and exams.
Task. Find the derivative of a function:
First, let's rewrite the root as a power with a rational exponent:
f(x) = (x 2 + 8x − 7) 0,5 .
Now we make a substitution: let x 2 + 8x − 7 = t. We find the derivative by the formula:
f ’(x) = f ’(t) · t ’ = (t 0.5)' t' = 0.5 t−0.5 t ’.
We make a reverse substitution: t = x 2 + 8x− 7. We have:
f ’(x) = 0.5 ( x 2 + 8x− 7) −0.5 ( x 2 + 8x− 7)' = 0.5 (2 x+ 8) ( x 2 + 8x − 7) −0,5 .
Finally, back to the roots:
It's very easy to remember.
Well, let's not go far, let's immediately consider inverse function. What is the inverse of the exponential function? Logarithm:
In our case, the base is a number:
Such a logarithm (that is, a logarithm with a base) is called “natural”, and we use a special notation for it: we write instead.
What is equal to? Of course, .
The derivative of the natural logarithm is also very simple:
Examples:
- Find the derivative of the function.
- What is the derivative of the function?
Answers: Exhibitor and natural logarithm- functions are uniquely simple in terms of the derivative. Exponential and logarithmic functions with any other base will have a different derivative, which we will analyze later, after we go through the rules of differentiation.
Differentiation rules
What rules? Another new term, again?!...
Differentiation is the process of finding the derivative.
Only and everything. What is another word for this process? Not proizvodnovanie... The differential of mathematics is called the very increment of the function at. This term comes from the Latin differentia - difference. Here.
When deriving all these rules, we will use two functions, for example, and. We will also need formulas for their increments:
There are 5 rules in total.
The constant is taken out of the sign of the derivative.
If - some constant number(constant), then.
Obviously, this rule also works for the difference: .
Let's prove it. Let, or easier.
Examples.
Find derivatives of functions:
- at the point;
- at the point;
- at the point;
- at the point.
Solutions:
- (the derivative is the same at all points, since it is linear function, remember?);
Derivative of a product
Everything is similar here: we introduce a new function and find its increment:
Derivative:
Examples:
- Find derivatives of functions and;
- Find the derivative of a function at a point.
Solutions:
Derivative of exponential function
Now your knowledge is enough to learn how to find the derivative of any exponential function, and not just the exponent (have you forgotten what it is yet?).
So where is some number.
We already know the derivative of the function, so let's try to bring our function to a new base:
For this we use simple rule: . Then:
Well, it worked. Now try to find the derivative, and don't forget that this function is complex.
Happened?
Here, check yourself:
The formula turned out to be very similar to the derivative of the exponent: as it was, it remains, only a factor appeared, which is just a number, but not a variable.
Examples:
Find derivatives of functions:
Answers:
This is just a number that cannot be calculated without a calculator, that is, it cannot be written in a simpler form. Therefore, in the answer it is left in this form.
Note that here is the quotient of two functions, so we apply the appropriate differentiation rule:
In this example, the product of two functions:
Derivative of a logarithmic function
Here it is similar: you already know the derivative of the natural logarithm:
Therefore, to find an arbitrary from the logarithm with a different base, for example, :
We need to bring this logarithm to the base. How do you change the base of a logarithm? I hope you remember this formula:
Only now instead of we will write:
The denominator turned out to be just a constant (a constant number, without a variable). The derivative is very simple:
Derivatives of exponential and logarithmic functions almost never occur in the exam, but it will not be superfluous to know them.
Derivative of a complex function.
What is a "complex function"? No, this is not a logarithm, and not an arc tangent. These functions can be difficult to understand (although if the logarithm seems difficult to you, read the topic "Logarithms" and everything will work out), but in terms of mathematics, the word "complex" does not mean "difficult".
Imagine a small conveyor: two people are sitting and doing some actions with some objects. For example, the first wraps a chocolate bar in a wrapper, and the second ties it with a ribbon. It turns out such a composite object: a chocolate bar wrapped and tied with a ribbon. To eat a chocolate bar, you need to do the opposite steps in reverse order.
Let's create a similar mathematical pipeline: first we will find the cosine of a number, and then we will square the resulting number. So, they give us a number (chocolate), I find its cosine (wrapper), and then you square what I got (tie it with a ribbon). What happened? Function. This is an example of a complex function: when, in order to find its value, we perform the first action directly with the variable, and then another second action with the result of the first.
In other words, A complex function is a function whose argument is another function: .
For our example, .
We may well do the same steps in reverse order: first you square, and then I look for the cosine of the resulting number:. It is easy to guess that the result will almost always be different. An important feature of complex functions: when the order of actions changes, the function changes.
Second example: (same). .
The last action we do will be called "external" function, and the action performed first - respectively "internal" function(these are informal names, I use them only to explain the material in simple language).
Try to determine for yourself which function is external and which is internal:
Answers: The separation of inner and outer functions is very similar to changing variables: for example, in the function
- What action will we take first? First we calculate the sine, and only then we raise it to a cube. So it's an internal function, not an external one.
And the original function is their composition: . - Internal: ; external: .
Examination: . - Internal: ; external: .
Examination: . - Internal: ; external: .
Examination: . - Internal: ; external: .
Examination: .
we change variables and get a function.
Well, now we will extract our chocolate - look for the derivative. The procedure is always reversed: first we look for the derivative of the outer function, then we multiply the result by the derivative of the inner function. For the original example, it looks like this:
Another example:
So, let's finally formulate the official rule:
Algorithm for finding the derivative of a complex function:
It seems to be simple, right?
Let's check with examples:
Solutions:
1) Internal: ;
External: ;
2) Internal: ;
(just don’t try to reduce by now! Nothing is taken out from under the cosine, remember?)
3) Internal: ;
External: ;
It is immediately clear that there is a three-level complex function here: after all, this is already a complex function in itself, and we still extract the root from it, that is, we perform the third action (put chocolate in a wrapper and with a ribbon in a briefcase). But there is no reason to be afraid: anyway, we will “unpack” this function in the same order as usual: from the end.
That is, first we differentiate the root, then the cosine, and only then the expression in brackets. And then we multiply it all.
In such cases, it is convenient to number the actions. That is, let's imagine what we know. In what order will we perform actions to calculate the value of this expression? Let's look at an example:
The later the action is performed, the more "external" the corresponding function will be. The sequence of actions - as before:
Here the nesting is generally 4-level. Let's determine the course of action.
1. Radical expression. .
2. Root. .
3. Sinus. .
4. Square. .
5. Putting it all together:
DERIVATIVE. BRIEFLY ABOUT THE MAIN
Function derivative- the ratio of the increment of the function to the increment of the argument with an infinitesimal increment of the argument:
Basic derivatives:
Differentiation rules:
The constant is taken out of the sign of the derivative:
Derivative of sum:
Derivative product:
Derivative of the quotient:
Derivative of a complex function:
Algorithm for finding the derivative of a complex function:
- We define the "internal" function, find its derivative.
- We define the "external" function, find its derivative.
- We multiply the results of the first and second points.