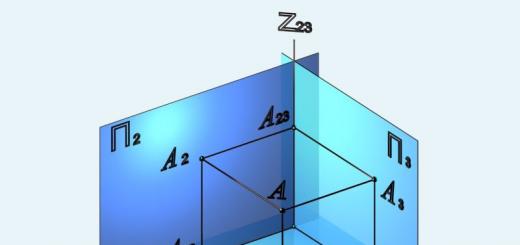
Consider some plane π and an arbitrary point M 0 in space. Let's choose for the plane unit normal vector n s start at some point M 1 ∈ π, and let p(M 0 ,π) be the distance from the point M 0 to the plane π. Then (Fig. 5.5)
p(M 0 ,π) = | pr n M 1 M 0 | = |nM 1 M 0 |, (5.8)
since |n| = 1.
If the plane π is given in rectangular coordinate system with its general equation Ax + By + Cz + D = 0, then its normal vector is the vector with coordinates (A; B; C) and as the unit normal vector we can choose
Let (x 0 ; y 0 ; z 0) and (x 1 ; y 1 ; z 1) be the coordinates of points M 0 and M 1 . Then the equality Ax 1 + By 1 + Cz 1 + D = 0 is satisfied, since the point M 1 belongs to the plane, and you can find the coordinates of the vector M 1 M 0 : M 1 M 0 = (x 0 -x 1 ; y 0 -y 1; z 0 -z 1). writing down scalar product nM 1 M 0 in coordinate form and transforming (5.8), we obtain
since Ax 1 + By 1 + Cz 1 = - D. So, to calculate the distance from a point to a plane, you need to substitute the coordinates of the point into the general equation of the plane, and then divide the absolute value of the result by a normalizing factor equal to the length of the corresponding normal vector.
, Competition "Presentation for the lesson"
Class: 11
Presentation for the lesson
Back forward
Attention! The slide preview is for informational purposes only and may not represent the full extent of the presentation. If you are interested in this work, please download the full version.
Goals:
- generalization and systematization of knowledge and skills of students;
- development of skills to analyze, compare, draw conclusions.
Equipment:
- multimedia projector;
- a computer;
- task sheets
STUDY PROCESS
I. Organizational moment
II. The stage of updating knowledge(slide 2)
We repeat how the distance from a point to a plane is determined
III. Lecture(slides 3-15)
In the lesson, we will look at various ways to find the distance from a point to a plane.
First method: step-by-step computational
Distance from point M to plane α:
is equal to the distance to the plane α from an arbitrary point P lying on the line a, which passes through the point M and is parallel to the plane α;
– is equal to the distance to the plane α from an arbitrary point P lying on the plane β, which passes through the point M and is parallel to the plane α.
We will solve the following tasks:
№1. In the cube A ... D 1 find the distance from the point C 1 to the plane AB 1 C.
It remains to calculate the value of the length of the segment O 1 N.
№2. In a regular hexagonal prism A ... F 1, all edges of which are equal to 1, find the distance from point A to the plane DEA 1.
Next method: volume method.
If the volume of the pyramid ABCM is V, then the distance from the point M to the plane α containing ∆ABC is calculated by the formula ρ(M; α) = ρ(M; ABC) =
When solving problems, we use the equality of the volumes of one figure, expressed in two different ways.
Let's solve the following problem:
№3. The edge AD of the pyramid DABC is perpendicular to the plane of the base ABC. Find the distance from A to the plane passing through the midpoints of the edges AB, AC and AD, if.
When solving problems coordinate method the distance from the point M to the plane α can be calculated by the formula ρ(M; α) = 
, where M(x 0; y 0; z 0), and the plane is given by the equation ax + by + cz + d = 0
Let's solve the following problem:
№4. In the unit cube A…D 1 find the distance from point A 1 to plane BDC 1 .
Let us introduce a coordinate system with the origin at point A, the y axis will pass along the edge AB, the x axis - along the edge AD, the z axis - along the edge AA 1. Then the coordinates of the points B (0; 1; 0) D (1; 0; 0;) C 1 (1; 1; 1)
Let us compose the equation of the plane passing through the points B, D, C 1 .
Then – dx – dy + dz + d = 0 x + y – z – 1= 0. Therefore, ρ = 
The following method, which can be used in solving problems of this type - method of reference tasks.
The application of this method consists in the application of well-known reference problems, which are formulated as theorems.
Let's solve the following problem:
№5. In a unit cube A ... D 1 find the distance from the point D 1 to the plane AB 1 C.
Consider Application vector method.
№6. In a unit cube A ... D 1 find the distance from point A 1 to the plane BDC 1.
So, we have considered various methods that can be used in solving this type of problem. The choice of one or another method depends on the specific task and your preferences.
IV. Group work
Try to solve the problem in different ways.
№1. The edge of the cube А…D 1 is equal to . Find the distance from vertex C to plane BDC 1 .
№2. In a regular tetrahedron ABCD with an edge, find the distance from point A to plane BDC
№3. In a regular triangular prism ABCA 1 B 1 C 1, all edges of which are equal to 1, find the distance from A to the plane BCA 1.
№4. In a regular quadrangular pyramid SABCD, all edges of which are equal to 1, find the distance from A to the plane SCD.
V. Lesson summary, homework, reflection
Let there be a plane 
. Let's draw a normal 
through the origin O. Let 
are the angles formed by the normal 
with coordinate axes. 
. Let be 
is the length of the normal segment 
before crossing the plane. Assuming that the direction cosines of the normal are known 
, we derive the equation of the plane 
.
Let be 
) is an arbitrary point of the plane. The unit normal vector has coordinates. Let's find the projection of the vector 
to normal.
Since the point M belongs to the plane, then
.
This is the equation for a given plane, called normal .
Distance from point to plane
Let a plane be given 
,M*
- a point in space d
is its distance from the plane.
Definition.
deviation
points M* from the plane is called the number ( +
d),
if M*
lies on the other side of the plane where the positive direction of the normal points 
, and number (- d) if the point is located on the other side of the plane:
.
Theorem.
Let the plane 
with unit normal 
given by the normal equation:
Let be M*
– point of space Deviation t. M* from the plane is given by the expression
Proof. projection t. 
* denote the normal Q.
Point Deviation M* from the plane is
.
Rule. To find deviation
t. M* from the plane, you need to substitute the coordinates t in the normal equation of the plane. M*
. The distance from a point to a plane is 
.
Reduction of the general equation of the plane to normal form
Let the same plane be given by two equations:
General Equation,
normal equation.
Since both equations define the same plane, their coefficients are proportional:
We square the first three equalities and add:
From here we find 
is the normalizing factor:
. (10)
Multiplying the general equation of the plane by the normalizing factor, we obtain the normal equation of the plane:
Examples of tasks on the topic "Plane".
Example 1 Compose the equation of the plane 
passing through a given point 
(2,1,-1) and parallel to the plane.
Decision. Normal to plane 
:
. Since the planes are parallel, the normal 
is also the normal to the desired plane 
. Using the equation of a plane passing through a given point (3), we obtain for the plane 
the equation:
Answer:
Example 2 The base of the perpendicular dropped from the origin to the plane 
, is a point 
. Find the equation of the plane 
.
Decision. Vector 
is the normal to the plane 
. Dot M 0
belongs to the plane. You can use the equation of a plane passing through a given point (3):
Answer:
Example 3 Build Plane 
passing through the points 
and perpendicular to the plane 
:.
Therefore, for some point M
(x,
y,
z) belonged to the plane 
, it is necessary that three vectors 
were coplanar:
=0.
It remains to open the determinant and bring the resulting expression to the form of the general equation (1).
Example 4 Plane 
given by the general equation:
Find point deviation 
from a given plane.
Decision. We bring the equation of the plane to normal form.
,
.
Substitute into the resulting normal equation the coordinates of the point M*.
.
Answer: 
.
Example 5 Whether the segment intersects the plane.
Decision. To cut AB crossed the plane, deviations 
and 
from the plane 
must have different signs:
.
Example 6 The intersection of three planes at one point.
.
The system has a unique solution, hence the three planes have one common point.
Example 7 Finding the bisectors of a dihedral angle formed by two given planes.
Let be 
and 
- deviation of some point 
from the first and second planes.
On one of the bisectoral planes (corresponding to the angle in which the origin of coordinates lies), these deviations are equal in magnitude and sign, and on the other, they are equal in magnitude and opposite in sign.
This is the equation of the first bisectoral plane.
This is the equation of the second bisectoral plane.
Example 8 Finding the Location of Two Data Points 
and 
relative to the dihedral angles formed by these planes.
Let be 
. Determine: in one, in adjacent or in vertical corners there are points 
and 
.
a). If a 
and 
lie on one side of 
and from 
, then they lie in the same dihedral angle.
b). If a 
and 
lie on one side of 
and different from 
, then they lie in adjacent corners.
in). If a 
and 
lie on opposite sides of 
and 
, then they lie in vertical angles.
Coordinate systems 3
Lines on plane 8
Lines of the first order. Straight lines on a plane. ten
Angle between lines 12
General equation of a straight line 13
Incomplete equation of the first degree 14
Equation of a straight line “in segments” 14
Joint study of equations of two lines 15
Normal to line 15
Angle between two straight lines 16
Canonical equation of a straight line 16
Parametric equations of a straight line 17
Normal (normalized) equation of a straight line 18
Distance from point to line 19
Line bundle equation 20
Examples of problems on the topic "straight line on a plane" 22
Cross product of vectors 24
Cross product properties 24
Geometric properties 24
Algebraic properties 25
Expression of the cross product in terms of the coordinates of factors 26
Mixed product of three vectors 28
The geometric meaning of the mixed product 28
Expressing the mixed product in terms of vector coordinates 29
Examples of problem solving
This article talks about determining the distance from a point to a plane. let's analyze the coordinate method, which will allow us to find the distance from a given point in three-dimensional space. To consolidate, consider examples of several tasks.
The distance from a point to a plane is found by means of a known distance from a point to a point, where one of them is given, and the other is a projection onto a given plane.
When a point M 1 with a plane χ is given in space, then a straight line perpendicular to the plane can be drawn through the point. H 1 is a common point of their intersection. From here we get that the segment M 1 H 1 is a perpendicular, which was drawn from the point M 1 to the plane χ, where the point H 1 is the base of the perpendicular.
Definition 1
They call the distance from a given point to the base of the perpendicular, which was drawn from a given point to a given plane.
The definition can be written in different formulations.
Definition 2
Distance from point to plane called the length of the perpendicular, which was drawn from a given point to a given plane.
The distance from the point M 1 to the plane χ is defined as follows: the distance from the point M 1 to the plane χ will be the smallest from a given point to any point in the plane. If the point H 2 is located in the χ plane and is not equal to the point H 2, then we get a right triangle of the form M 2 H 1 H 2 , which is rectangular, where there is a leg M 2 H 1, M 2 H 2 - hypotenuse. Hence, this implies that M 1 H 1< M 1 H 2 . Тогда отрезок М 2 H 1 is considered inclined, which is drawn from the point M 1 to the plane χ. We have that the perpendicular drawn from a given point to a plane is less than the inclined one drawn from a point to a given plane. Consider this case in the figure below.
Distance from a point to a plane - theory, examples, solutions
There are a number of geometric problems whose solutions must contain the distance from a point to a plane. Ways to detect this may be different. To resolve, use the Pythagorean theorem or the similarity of triangles. When, according to the condition, it is necessary to calculate the distance from a point to a plane, given in a rectangular coordinate system of three-dimensional space, they solve using the coordinate method. This paragraph deals with this method.
According to the condition of the problem, we have that a point in three-dimensional space with coordinates M 1 (x 1, y 1, z 1) with the plane χ is given, it is necessary to determine the distance from M 1 to the plane χ. Several solutions are used to solve.
First way
This method is based on finding the distance from a point to a plane using the coordinates of the point H 1, which are the base of the perpendicular from the point M 1 to the plane χ. Next, you need to calculate the distance between M 1 and H 1.
To solve the problem in the second way, the normal equation of a given plane is used.
Second way
By condition, we have that H 1 is the base of the perpendicular, which was lowered from the point M 1 to the plane χ. Then we determine the coordinates (x 2, y 2, z 2) of the point H 1. The desired distance from M 1 to the χ plane is found by the formula M 1 H 1 \u003d (x 2 - x 1) 2 + (y 2 - y 1) 2 + (z 2 - z 1) 2, where M 1 (x 1, y 1 , z 1) and H 1 (x 2 , y 2 , z 2) . To solve, you need to know the coordinates of the point H 1.
We have that H 1 is the point of intersection of the plane χ with the line a, which passes through the point M 1 located perpendicular to the plane χ. It follows that it is necessary to formulate the equation of a straight line passing through a given point perpendicular to a given plane. It is then that we can determine the coordinates of the point H 1 . It is necessary to calculate the coordinates of the point of intersection of the line and the plane.
Algorithm for finding the distance from a point with coordinates M 1 (x 1, y 1, z 1) to the χ plane:
Definition 3
- compose the equation of a straight line a passing through the point M 1 and at the same time
- perpendicular to the χ plane;
- find and calculate the coordinates (x 2, y 2, z 2) of the point H 1, which are points
- intersection of the line a with the plane χ ;
- calculate the distance from M 1 to χ using the formula M 1 H 1 = (x 2 - x 1) 2 + (y 2 - y 1) 2 + z 2 - z 1 2.
Third way
In a given rectangular coordinate system O x y z there is a plane χ, then we obtain a normal equation of the plane of the form cos α · x + cos β · y + cos γ · z - p = 0 . From here we get that the distance M 1 H 1 with the point M 1 (x 1 , y 1 , z 1) drawn to the plane χ, calculated by the formula M 1 H 1 = cos α x + cos β y + cos γ z-p. This formula is valid, since it is established thanks to the theorem.
Theorem
If a point M 1 (x 1 , y 1 , z 1) is given in three-dimensional space, having a normal equation of the χ plane of the form cos α x + cos β y + cos γ z - p = 0, then calculating the distance from the point to plane M 1 H 1 is derived from the formula M 1 H 1 = cos α · x + cos β · y + cos γ · z - p, since x = x 1 , y = y 1 , z = z 1 .
Proof
The proof of the theorem is reduced to finding the distance from a point to a line. From here we get that the distance from M 1 to the χ plane is the modulus of the difference between the numerical projection of the radius vector M 1 with the distance from the origin to the χ plane. Then we get the expression M 1 H 1 = n p n → O M → - p . The normal vector of the plane χ has the form n → = cos α , cos β , cos γ , and its length is equal to one, n p n → O M → is the numerical projection of the vector O M → = (x 1 , y 1 , z 1) in the direction determined by the vector n → .
Let's apply the formula for calculating scalar vectors. Then we obtain an expression for finding a vector of the form n → , O M → = n → n p n → O M → = 1 n p n → O M → = n p n → O M → , since n → = cos α , cos β , cos γ z and O M → = (x 1 , y 1 , z 1) . The coordinate form of the notation will take the form n →, O M → = cos α x 1 + cos β y 1 + cos γ z 1, then M 1 H 1 = n p n → O M → - p = cos α x 1 + cos β · y 1 + cos γ · z 1 - p . The theorem has been proven.
From here we get that the distance from the point M 1 (x 1, y 1, z 1) to the plane χ is calculated by substituting into the left side of the normal equation of the plane cos α x + cos β y + cos γ z - p = 0 instead of x, y, z coordinates x 1 , y 1 and z1 relating to the point M 1 , taking the absolute value of the obtained value.
Consider examples of finding the distance from a point with coordinates to a given plane.
Example 1
Calculate the distance from the point with coordinates M 1 (5 , - 3 , 10) to the plane 2 x - y + 5 z - 3 = 0 .
Decision
Let's solve the problem in two ways.
The first method will start by calculating the direction vector of the line a . By condition, we have that the given equation 2 x - y + 5 z - 3 \u003d 0 is a general plane equation, and n → \u003d (2, - 1, 5) is the normal vector of the given plane. It is used as a directing vector for the straight line a, which is perpendicular to the given plane. You should write the canonical equation of a straight line in space passing through M 1 (5, - 3, 10) with a direction vector with coordinates 2, - 1, 5.
The equation will look like x - 5 2 = y - (- 3) - 1 = z - 10 5 ⇔ x - 5 2 = y + 3 - 1 = z - 10 5 .
Intersection points should be defined. To do this, gently combine the equations into a system for the transition from the canonical to the equations of two intersecting lines. Let's take this point as H 1 . We get that
x - 5 2 = y + 3 - 1 = z - 10 5 ⇔ - 1 (x - 5) = 2 (y + 3) 5 (x - 5) = 2 (z - 10) 5 ( y + 3) = - 1 (z - 10) ⇔ ⇔ x + 2 y + 1 = 0 5 x - 2 z - 5 = 0 5 y + z + 5 = 0 ⇔ x + 2 y + 1 = 0 5 x - 2 z - 5 = 0
Then you need to enable the system
x + 2 y + 1 = 0 5 x - 2 z - 5 = 0 2 x - y + 5 z - 3 = 0 ⇔ x + 2 y = 1 5 x - 2 z = 5 2 x - y + 5 z = 3
Let us turn to the rule for solving the system according to Gauss:
1 2 0 - 1 5 0 - 2 5 2 - 1 5 3 ~ 1 2 0 - 1 0 - 10 - 2 10 0 - 5 5 5 ~ 1 2 0 - 1 0 - 10 - 2 10 0 0 6 0 ⇒ ⇒ z = 0 6 = 0 , y = - 1 10 10 + 2 z = - 1 , x = - 1 - 2 y = 1
We get that H 1 (1, - 1, 0) .
We calculate the distance from a given point to a plane. We take points M 1 (5, - 3, 10) and H 1 (1, - 1, 0) and get
M 1 H 1 \u003d (1 - 5) 2 + (- 1 - (- 3)) 2 + (0 - 10) 2 \u003d 2 30
The second solution is to first bring the given equation 2 x - y + 5 z - 3 = 0 to normal form. We determine the normalizing factor and get 1 2 2 + (- 1) 2 + 5 2 = 1 30 . From here we derive the equation of the plane 2 30 · x - 1 30 · y + 5 30 · z - 3 30 = 0 . The left side of the equation is calculated by substituting x \u003d 5, y \u003d - 3, z \u003d 10, and you need to take the distance from M 1 (5, - 3, 10) to 2 x - y + 5 z - 3 = 0 modulo. We get the expression:
M 1 H 1 \u003d 2 30 5 - 1 30 - 3 + 5 30 10 - 3 30 \u003d 60 30 \u003d 2 30
Answer: 2 30 .
When the χ plane is given by one of the methods of the plane definition methods section, then you first need to obtain the equation of the χ plane and calculate the desired distance using any method.
Example 2
Points with coordinates M 1 (5 , - 3 , 10) , A (0 , 2 , 1) , B (2 , 6 , 1) , C (4 , 0 , - 1) are set in three-dimensional space. Calculate the distance from M 1 to the plane A B C.
Decision
First you need to write down the equation of the plane passing through the given three points with coordinates M 1 (5, - 3, 10) , A (0 , 2 , 1) , B (2 , 6 , 1) , C (4 , 0 , - one) .
x - 0 y - 2 z - 1 2 - 0 6 - 2 1 - 1 4 - 0 0 - 2 - 1 - 1 = 0 ⇔ x y - 2 z - 1 2 4 0 4 - 2 - 2 = 0 ⇔ ⇔ - 8x + 4y - 20z + 12 = 0 ⇔ 2x - y + 5z - 3 = 0
It follows that the problem has a solution similar to the previous one. Hence, the distance from the point M 1 to the plane A B C is 2 30 .
Answer: 2 30 .
Finding the distance from a given point on a plane or to a plane to which they are parallel is more convenient by applying the formula M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 - p . From here we get that the normal equations of the planes are obtained in several steps.
Example 3
Find the distance from a given point with coordinates M 1 (- 3 , 2 , - 7) to the coordinate plane O x y z and the plane given by the equation 2 y - 5 = 0 .
Decision
The coordinate plane O y z corresponds to an equation of the form x = 0. For the O y z plane, it is normal. Therefore, it is necessary to substitute the values x \u003d - 3 into the left side of the expression and take the absolute value of the distance from the point with coordinates M 1 (- 3, 2, - 7) to the plane. We get the value equal to - 3 = 3 .
After the transformation, the normal equation of the plane 2 y - 5 = 0 will take the form y - 5 2 = 0 . Then you can find the required distance from the point with coordinates M 1 (- 3 , 2 , - 7) to the plane 2 y - 5 = 0 . Substituting and calculating, we get 2 - 5 2 = 5 2 - 2.
Answer: The desired distance from M 1 (- 3 , 2 , - 7) to O y z has a value of 3 , and to 2 y - 5 = 0 has a value of 5 2 - 2 .
If you notice a mistake in the text, please highlight it and press Ctrl+Enter
Finding the distance from a point to a plane is a common problem that arises when solving various problems of analytical geometry, for example, finding the distance between two intersecting lines or between a line and a plane parallel to it can be reduced to this problem.
Consider the plane $β$ and the point $M_0$ with coordinates $(x_0;y_0; z_0)$, which does not belong to the plane $β$.
Definition 1
The shortest distance between a point and a plane is the perpendicular dropped from the point $M_0$ to the plane $β$.
Figure 1. Distance from a point to a plane. Author24 - online exchange of student papers
Below is how to find the distance from a point to a plane using the coordinate method.
Derivation of the formula for the coordinate method of finding the distance from a point to a plane in space
The perpendicular from the point $M_0$, which intersects the plane $β$ at the point $M_1$ with coordinates $(x_1;y_1; z_1)$, lies on a straight line whose direction vector is the normal vector of the plane $β$. In this case, the length of the unit vector $n$ is equal to one. Accordingly, the distance from $β$ to the point $M_0$ will be:
$ρ= |\vec(n) \cdot \vec(M_1M_0)|\left(1\right)$, where $\vec(M_1M_0)$ is the normal vector of $β$ and $\vec(n)$ - unit normal vector of the considered plane.
In the case when the equation of the plane is given in the general form $Ax+ By + Cz + D=0$, the coordinates of the normal vector of the plane are the coefficients of the equation $\(A;B;C\)$, and the unit normal vector in this case has the coordinates , calculated according to the following equation:
$\vec(n)= \frac(\(A;B;C\))(\sqrt(A^2 + B^2 + C^2))\left(2\right)$.
Now we can find the coordinates of the normal vector $\vec(M_1M_0)$:
$\vec(M_0M_1)= \(x_0 - x_1;y_0-y_1;z_0-z_1\)\left(3\right)$.
We also express the coefficient $D$ using the coordinates of a point lying in the $β$ plane:
$D= Ax_1+By_1+Cz_1$
The coordinates of the unit normal vector from the equality $(2)$ can be substituted into the equation of the $β$ plane, then we have:
$ρ= \frac(|A(x_0 -x_1) + B(y_0-y_1)+C(z_0-z_1)|)(\sqrt(A^2+B^2+C^2))= \frac( |Ax_0+ By_0 + Cz_0-(Ax_1+By_1+Cz_1)|)(\sqrt(A^2+B^2+C^2)) = \frac(Ax_0+ By_0 + Cz_0 + D)(\sqrt(A^2 +B^2+C^2))\left(4\right)$
The equality $(4)$ is a formula for finding the distance from a point to a plane in space.
General algorithm for finding distance from point $M_0$ to plane
- If the equation of the plane is not given in a general form, first you need to bring it to a general one.
- After that, it is necessary to express the normal vector of the given plane from the general equation of the plane in terms of the point $M_0$ and the point belonging to the given plane, for this you need to use the equality $(3)$.
- The next stage is the search for the coordinates of the unit normal vector of the plane using the formula $(2)$.
- Finally, you can start searching for the distance from a point to a plane, this is done by calculating the scalar product of the vectors $\vec(n)$ and $\vec(M_1M_0)$.
