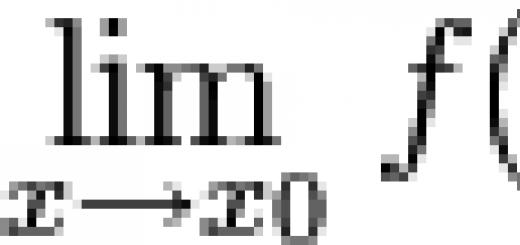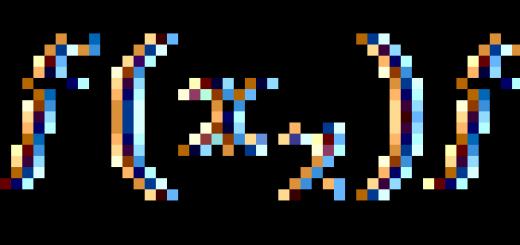Instruction

The direct calculation of limits is connected, first of all, with the limits of rational Qm(x)/Rn(x), where Q and R are polynomials. If the limit is calculated at x → a (a is a number), then uncertainty may arise, for example. To eliminate it, divide the numerator and denominator by (x-a). Repeat the operation until the uncertainty disappears. The division of polynomials is carried out in almost the same way as the division of numbers. It is based on the fact that division and multiplication are inverse operations. An example is shown in fig. one.

Application of the first remarkable limit. The formula for the first remarkable limit is shown in fig. 2a. To use it, bring your example expression to the appropriate form. This can always be done purely algebraically or by change of variable. The main thing - do not forget that if the sine is from kx, then the denominator is also kx. An example is shown in Fig. 2e. In addition, if we take into account that tgx=sinx/cosx, cos0=1, then, as a consequence, it appears (see Fig. 2b). arcsin(sinx)=x and arctg(tgx)=x. Therefore, there are two more consequences (Fig. 2c and 2d). A fairly wide range of methods has also emerged.

Application of the second remarkable limit (see Fig. 3a) Limits of this type are used to eliminate type uncertainties. To solve the corresponding problems, simply transform the condition to a structure corresponding to the type of limit. Remember that when raising to a power an expression that is already in a power, their exponents are multiplied. The corresponding example is shown in Fig. 2e. Apply the substitution α=1/x and get the consequence of the second remarkable limit (Fig. 2b). Having taken the logarithm in base a, both parts of this corollary, you will come to the second corollary, including when a = e (see Fig. 2c). Make the substitution a^x-1=y. Then x=log(a)(1+y). As x tends to zero, y also tends to zero. Therefore, a third consequence also arises (see Fig. 2d).

Application of equivalent infinitesimals. Infinitely small functions are equivalent as x → a if the limit of their ratio α(x)/γ(x) is equal to one. When calculating limits using such infinitesimals, simply write γ(x)=α(x)+o(α(x)). o(α(x)) is an infinitesimal of a higher order of smallness than α(x). For it lim(x→a)o(α(x))/α(x)=0. To clarify the equivalence, use the same wonderful limits. The method allows to significantly simplify the process of finding the limits, making it more transparent.

L'Hopital's rule

Definition 1

L'Hopital's rule: under certain conditions, the limit of the ratio of functions whose variable tends to $a$ is equal to the limit of the ratio of their derivatives, with $x$ also tending to $a$ :

$\mathop(\lim )\limits_(x\to a) \frac(f(x))(g(x)) =\mathop(\lim )\limits_(x\to a) \frac(f"( x))(g"(x)) $

L'Hopital's rule was discovered by the Swedish mathematician Johann Bernoulli, who then spoke about it in a letter to L'Hopital. Lopital published this rule in the first textbook on differential calculus in 1696 with his own authorship.

L'Hopital's rule applies to expressions reducible to uncertainties of the following form:

$\frac(0)(0) \begin(array)(ccc) () & () & (\frac(\infty )(\infty ) ) \end(array)$

Instead of zero in the first expression, there can be any infinitesimal value.

In the general case, L'Hospital's rule can be used if both the numerator and the denominator are both zero or infinity.

Conditions under which L'Hopital's rule can be applied:

• The condition is observed under which the limits of the functions $f(x)$ and $g(x)$ as $x$ tends to $a$ are equal and tend to zero or infinity: $\mathop(\lim )\limits_(x \to a) f(x)=\mathop(\lim )\limits_(x\to a) g(x)=0$ or $\mathop(\lim )\limits_(x\to a) f(x) =\mathop(\lim )\limits_(x\to a) g(x)=\infty $;
• It is possible to obtain derivatives of $f(x)$ and $g(x)$ in a neighborhood of $a$;
• The derivative of the function $g(x)$ is not zero $g"(x)\ne 0$ in a neighborhood of $a$;
• The limit of the ratio of the derivatives of the functions $f(x)$ and $g(x)$, written as $\mathop(\lim )\limits_(x\to a) \frac(f"(x))(g"( x)) $ exists.

Proof of L'Hospital's rule:

1. Let the functions $f(x)$ and $g(x)$ be given, and the limits are equal:
2. $\mathop(\lim )\limits_(x\to a+0) f(x)=\mathop(\lim )\limits_(x\to a+0) g(x)=0 $.
3. Let us extend the functions at the point $a$. For this point, the following condition will be true:
4. $\frac(f(x))(g(x)) =\frac(f(x)-f(a))(g(x)-g(a)) =\frac(f"(c)) (g"(c))$.
5. The value of $c$ depends on $x$, but if $x\to a+0$ then $c\to a$.
6. $\mathop(\lim )\limits_(x\to a+0) \frac(f(x))(g(x)) =\mathop(\lim )\limits_(c\to a+0) \frac (f"(c))(g"(c)) =\mathop(\lim )\limits_(x\to a+0) \frac(f"(c))(g"(c)) $.

Algorithm for calculating the solution using the L'Hopital rule

1. Checking the entire expression for uncertainty.
2. Checking all the conditions outlined above before further use of L'Hospital's rule.
3. Checking if the derivative of a function tends to $0$.
4. Retesting for uncertainty.

Example #1:

Find limit:

$\mathop(\lim )\limits_(x\to 0) \frac(x^(2) +5x)(3x) $

Solution:

• The limit of the function $f(x)$ is equal to the limit $g(x)$ and both of them are equal to zero: $\mathop(\lim )\limits_(x\to a) f(x)=\mathop(\lim )\limits_ (x\to 0) (x^(2) +5x)=0$; $\mathop(\lim )\limits_(x\to a) g(x)=\mathop(\lim )\limits_(x\to 0) (3x)=0$
• $g"(x)=3\ne 0$ in a neighborhood of $a$
• $\mathop(\lim )\limits_(x\to a) \frac(f"(x))(g"(x)) =\mathop(\lim )\limits_(x\to 0) \frac(2x +5)(3) $

$\mathop(\lim )\limits_(x\to 0) \frac(x^(2) +5x)(3x) =\left\langle \frac(0)(0) \right\rangle =\mathop( \lim )\limits_(x\to 0) \frac(\left(x^(2) +5x\right)")(\left(3x\right)") =\mathop(\lim )\limits_(x \to 0) \frac(2x+5)(3) =\frac(0+5)(3) =\frac(5)(3) $

Example #2:

Find limit:

$\mathop(\lim )\limits_(x\to \infty ) \frac(x^(3) -3x^(2) +2x)(x^(3) -x) $

Solution:

Let's check the conditions for the applicability of L'Hospital's rule:

• $\mathop(\lim )\limits_(x\to a) f(x)=\mathop(\lim )\limits_(x\to \infty ) (x^(3) -3x^(2) +2x) =\infty$; $\mathop(\lim )\limits_(x\to a) g(x)=\mathop(\lim )\limits_(x\to \infty ) (x^(3) -x)=\infty $
• $f(x)$ and $g(x)$ are differentiable in a neighborhood of $a$
• $g"(x)=6\ne 0$ in a neighborhood of $a$
• $\mathop(\lim )\limits_(x\to a) \frac(f"(x))(g"(x)) =\mathop(\lim )\limits_(x\to \infty ) \frac( 3x^(2) -6x+2)(3x^(2) -1) $

Let's write the derivative and find the limit of the function:

$\mathop(\lim )\limits_(x\to \infty ) \frac(x^(3) -3x^(2) +2x)(x^(3) -x) =\left\langle \frac( \infty )(\infty ) \right\rangle =\mathop(\lim )\limits_(x\to \infty ) \frac(\left(x^(3) -3x^(2) +2x\right)" )(\left(x^(3) -x\right)") =\mathop(\lim )\limits_(x\to \infty ) \frac(3x^(2) -6x+2)(3x^( 2)-1)=\left\langle \frac(\infty )(\infty )\right\rangle $

We repeat the calculation of the derivative until we get rid of the uncertainty:

$\mathop(\lim )\limits_(x\to \infty ) \frac(\left(3x^(2) -6x+2\right)")(\left(3x^(2) -1\right) ") =\mathop(\lim )\limits_(x\to \infty ) \frac(6x-6)(6x) =\left\langle \frac(\infty )(\infty ) \right\rangle =\mathop (\lim )\limits_(x\to \infty ) \frac(\left(6x-6\right)")(\left(6x\right)") =\frac(6)(6) =1$

Example #3:

Find limit:

$\mathop(\lim )\limits_(x\to 0) \frac(\sin 5x)(x) $

Solution:

$\mathop(\lim )\limits_(x\to 0) \frac(\sin 5x)(x) =\left\langle \frac(0)(0) \right\rangle =\mathop(\lim )\ limits_(x\to 0) \frac(\left(\sin 5x\right)")(\left(x\right)") =\mathop(\lim )\limits_(x\to 0) \frac(5 \cos 5x)(1) =5\mathop(\lim )\limits_(x\to 0) \cos 5x=5$

Example #4:

Find limit:

$\mathop(\lim )\limits_(x\to \infty ) (1+x^(2))^(1/x) $

Solution:

Let's log the function:

$\ln y=\frac(1)(x) \ln (1+x^(2))=\frac(\ln (1+x^(2)))(x) $

$\mathop(\lim )\limits_(x\to \infty ) \frac(\ln (1+x^(2)))(x) =\mathop(\lim )\limits_(x\to \infty ) \frac(\left[\ln (1+x^(2))\right]")(x") =\mathop(\lim )\limits_(x\to \infty ) \frac(\frac(2x) (1+x^(2) ) )(1) =0$

Since the function $ln(y)$ is continuous, we get:

$\mathop(\lim )\limits_(x\to \infty ) (\ln y)=\ln (\mathop(\lim )\limits_(x\to \infty ) y)$

Consequently,

$\ln (\mathop(\lim )\limits_(x\to \infty ) y)=0$

$\mathop(\lim )\limits_(x\to \infty ) y=1$

$\mathop(\lim )\limits_(x\to \infty ) (1+x^(2))^(1/x) =1$

Solution online function limits. Find the limit value of a function or functional sequence at a point, calculate limiting function value at infinity. determine the convergence of a number series and much more can be done thanks to our online service -. We allow you to find function limits online quickly and accurately. You yourself enter the function variable and the limit to which it aspires, our service does all the calculations for you, giving an accurate and simple answer. And for finding the limit online you can enter both numerical series and analytic functions containing constants in a literal expression. In this case, the found function limit will contain these constants as constant arguments in the expression. Our service solves any complex problems of finding limits online, it is enough to specify the function and the point at which it is necessary to calculate function limit. Computing limits online, you can use various methods and rules for solving them, while comparing the result with limit solution online on www.site, which will lead to the successful completion of the task - you will avoid your own mistakes and typos. Or you can completely trust us and use our result in your work, without spending extra effort and time on independent calculations of the function limit. We allow input of limit values ​​such as infinity. You must enter a common term of the numerical sequence and www.site will calculate the value limit online to plus or minus infinity.

One of the basic concepts of mathematical analysis is function limit And sequence limit at a point and at infinity, it is important to be able to correctly solve limits. With our service it will not be difficult. A decision is being made limits online within seconds, the answer is accurate and complete. The study of calculus begins with passage to the limit, limits are used in almost all sections of higher mathematics, so it is useful to have a server at hand for limit solutions online, which is matematikam.ru.

Application of L'Hospital's rule is necessary to calculate the limits when obtaining uncertainties of the form 0 0 and ∞ ∞ .

There are uncertainties of the form 0 · ∞ and ∞ - ∞ .

The most important part of L'Hopital's rule is to differentiate a function and find its derivative.

L'Hopital's rule

Definition 1

When lim x → x 0 f (x) g (x) = 0 0 or ∞ ∞ and the functions f (x) , g (x) are differentiable within the point x 0 , then lim x → x 0 f (x) g (x) = lim x → x 0 f " (x) g " (x) .

If the uncertainty is unresolved after applying the L'Hopital rule, then it must be applied again. For a complete understanding, consider a few examples.

Example 1

Perform calculations using L'Hopital's rule lim x → 0 sin 2 (3 x) x cos (x) .

Solution

To solve according to L'Hopital's rule, you first need to make a substitution. We get that lim x → 0 sin 2 (3 x) x cos (x) = sin 2 (3 0) 0 cos (0) = 0 0 .

Now you can proceed to the calculation of limits using the rule. We get that

lim x → 0 sin 2 (3 x) x cos (x) = 0 0 = lim x → 0 sin 2 (3 x) "x cos (x)" = lim x → 0 2 sin (3 x) ( sin (3 x)) "x" cos (x) + x (cos (x)) " = = lim x → 0 6 sin (3 x) cos (3 x) cos (x) - x sin ( x) = 6 sin (3 0) cos (3 0) cos (0) - 0 sin (0) = 0 1 = 0

Answer: lim x → 0 sin 2 (3 x) x cos (x) = 0 .

Example 2

Calculate the limit of the given function lim x → ∞ ln (x) x .

Solution

We make the statement infinity. We get that

lim x → ∞ log (x) x = log (∞) ∞ = ∞ ∞

The resulting uncertainty indicates that it is necessary to apply the L'Hopital rule. We have that

lim x → ∞ ln (x) x = ∞ ∞ = lim x → ∞ ln (x) " x " = lim x → ∞ 1 x 1 = 1 ∞ = 0

Answer: lim x → ∞ ln (x) x = 0

Example 3

Calculate the limit of the given function lim x → 0 + 0 (x 4 ln (x))

Solution

We make a substitution of the x value. we get that

lim x → 0 + 0 (x 4 ln (x)) = (0 + 0) 4 ln (0 + 0) = 0 (-∞)

The solution resulted in an uncertainty of the form zero multiplied by negative infinity. This indicates that it is necessary to refer to the table of uncertainties and make decisions for the choice of method for finding this limit. After the transformation, we apply L'Hopital's rule. We get that

lim x → 0 + 0 (x 4 ln (x)) = 0 (- ∞) = lim x → 0 + 0 ln (x) x - 4 = ln (0 + 0) (0 + 0) - 4 = -∞+∞

The approach to uncertainty suggests that it is necessary to re-apply this rule. We have that

lim x → 0 + 0 (x 4 ln (x)) = 0 (- ∞) = lim x → 0 + 0 ln (x) x - 4 = - ∞ + ∞ = = lim x → 0 + 0 (ln (x)) "(x - 4)" = lim x → 0 + 0 1 x - 4 - 5 = - 1 4 lim x → 0 + 0 1 x - 4 = - 1 4 1 (0 + 0) - 4 = = - 1 4 (0 + 0) 4 = 0

Answer: lim x → 0 + 0 (x 4 log (x)) = 0

Example 4

Calculate the limit of the function lim x → 0 c t g 2 (x) - 1 x 2 .

Solution

After substitution, we get

lim x → 0 c t g 2 (x) - 1 x 2 = ∞ - ∞

The presence of uncertainty indicates that L'Hopital's rule should be used. We get that

lim x → 0 ctg 2 (x) - 1 x 2 = ∞ - ∞ = lim x → 0 cos 2 (x) sin 2 (x) - 1 x 2 = = lim x → 0 x 2 cos 2 (x) - sin 2 (x) x 2 sin 2 (x) = lim x → 0 x cos x - sin xx cos x + sin xx 2 sin 2 (x) = = lim x → 0 x cos x - sin xx sin 2 (x ) x cos x + sin xx = lim x → 0 x cos x - sin xx sin 2 (x) cos x + sin xx = = lim x → 0 cos x + sin xx lim x → 0 x cos x - sin xx sin 2 (x) = 2 lim x → 0 x cos x - sin xx sin 2 (x) = = 2 0 cos (0) - sin (0) 0 sin 2 (0) = 0 0

For the last transition, the first remarkable limit was used. Then we come to the solution according to L'Hopital. We get that

2 lim x → 0 x cos x - sin xx sin 2 (x) = 0 0 = 2 lim x → 0 (x cos x - sin x) "(x sin 2 (x))" = = 2 lim x → 0 cos x - x sin x - cos x sin 2 (x) + 2 x sin x cos x = 2 lim x → 0 - x sin (x) + 2 x cos x = 0 0

Since the uncertainty has not gone away, one more application of L'Hopital's rule is necessary. We get the limit of the form

2 lim x → 0 - x sin (x) + 2 x cos x = 0 0 = 2 lim x → 0 - x "sin (x) + 2 x cos x" == 2 lim x → 0 1 cos x + 2 cos x - 2 x sin x = - 2 1 3 cos (0) - 2 0 sin (0) = - 2 3

Answer: lim x → 0 c t g 2 (x) - 1 x 2 = - 2 3

If you notice a mistake in the text, please highlight it and press Ctrl+Enter

A method for solving the limits using L'Hopital's rule is presented. Statements of the corresponding theorems are given. Examples of solving limits containing uncertainties ∞/∞, 0/0, 0 to the power of 0 and ∞ - ∞ using L'Hopital's rule are analyzed in detail.

Content

See also: Rules for calculating derivatives

Solution method

One of the most powerful methods for uncovering uncertainties and calculating the limits of functions is the use of L'Hospital's rule. It allows you to reveal the uncertainties of the form 0/0 or ∞/∞ at the endpoint or at infinity, which we will denote as x 0 . L'Hopital's rule is that we find the derivatives of the numerator and denominator of a fraction. If there is a limit , .
If, after differentiation, we again get uncertainty, then the process can be repeated, that is, apply the L'Hospital rule already to the limit. And so on, until the uncertainty is revealed.

For this rule to apply, there must be such a punctured neighborhood of the point x 0 , on which the functions in the numerator and denominator are differentiable and the function in the denominator and its derivative do not vanish.

The application of L'Hopital's rule consists of the following steps.
1) We bring the uncertainty to the form 0/0 or ∞/∞ . To do this, if necessary, we perform transformations and make a change of variable . As a result, we obtain the limit of the form .
2) We make sure that there is such a punctured neighborhood of the point x 0 , on which the functions in the numerator and denominator are differentiable and the denominator and its derivative do not vanish.
3) Find the derivatives of the numerator and denominator.
4) If there is a finite or infinite limit , then the problem is solved: .
5) If the limit does not exist, then this does not mean that the original limit does not exist. This means that this problem cannot be solved using L'Hospital's rule. You need to apply another method (see example below).
6) If uncertainty reappears in the limit, then L'Hopital's rule can also be applied to it, starting from point 2).

As stated above, the application of L'Hospital's rule can lead to a function whose limit does not exist. However, this does not mean that there is no original limit. Consider the following example.
.
We apply L'Hopital's rule. , .
However, there is no limit. Despite this, the original function has a limit:
.

L'Hopital's rule. Statements of the theorems

Here we present the formulations of the theorems on which the disclosure of uncertainties according to L'Hospital's rule is based.

Uncertainty disclosure theorem 0/0
Let the functions f and g have derivatives in a punctured (two-sided or one-sided) neighborhood of a finite or at infinity () point, and and are not equal to zero in this neighborhood. Let it go
.
,
then there is an equal limit
.

Uncertainty disclosure theorem ∞/∞
Let the functions f and g have derivatives in a punctured (two-sided or one-sided) neighborhood of a finite or at infinity () point, and not equal to zero in this neighborhood. Let it go
.
Then if there is a finite or infinite limit
,
then there is an equal limit
.
Here for a two-way neighborhood. For a one-sided neighborhood, , or .

Examples

Example 1

Show that the exponent grows faster than any power function, while the logarithm grows more slowly. That is, to show that
BUT) ;
B) ,
where .

Consider the limit A). At . This is the type uncertainty. For its disclosure, we apply the L'Hopital rule. Let be
.
We find derivatives. . Then
.
If , then the uncertainty disappears, because at . According to L'Hopital's rule,
.

If , then we apply L'Hopital's rule n times, where is the integer part of the number b.
;

.
Because , then . Although we are accustomed to reading from left to right, this series of equalities should be read from right to left as follows. Since there is a limit, then there is a limit equal to it. Since there is a limit, then there is a limit equal to it. And so on, until we reach the limit.

Now consider limit B):
. Let's make a change of variable. Then ; at ; .

Example 2

Find the limit using L'Hopital's rule:
.

This is an indeterminacy of the form 0/0 . We find by L'Hopital's rule.

.

Here, after the first application of the rule, we again got uncertainty. Therefore, L'Hopital's rule was applied a second time. This series of equalities should be read from right to left as follows. Since there is a limit, then there is a limit equal to it. Since there is a limit, then there is an initial limit equal to it.

Example 3

Calculate the limit using L'Hospital's rule.
.

Let's find the values ​​of the numerator and denominator at:
;

.
The numerator and denominator are zero. We have an uncertainty of the form 0/0 . For its disclosure, we apply the L'Hopital rule.

.

Example 4

Solve the limit using L'Hospital's rule.
.

Here we have an uncertainty of the form (+0) +0 . Let's transform it to the form +∞/+∞ . To do this, we perform transformations.
.

We find the limit in the exponent by applying L'Hopital's rule.
.

Since the exponent is a continuous function for all values ​​of the argument, then
.

Example 5

Find the limit using L'Hopital's rule:
.

Here we have an uncertainty of the form ∞ - ∞ . Reducing fractions to a common denominator, we bring it to an uncertainty of the form 0/0 :
.

We apply L'Hopital's rule.
;
;
.

Here we again have an indeterminacy of the form 0/0 . Let's apply L'Hopital's rule again.
;

;
.

Finally we have:

.
As with all limits calculated using L'Hospital's rule, you need to read from the end. Since there is a limit, then there is a limit equal to it. Since there is a limit, then there is an initial limit equal to it.

Note. Calculations can be simplified if we use the theorem on the replacement of functions by equivalents in the limit of the quotient. According to this theorem, if a function is a fraction or a product of factors, then the factors can be replaced by equivalent functions. Since at , then

.

References:
L.D. Kudryavtsev, A.D. Kutasov, V.I. Chekhlov, M.I. Shabunin. Collection of problems in mathematical analysis. Volume 1. Moscow, 2003.

See also: