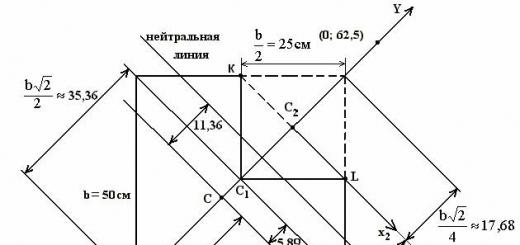
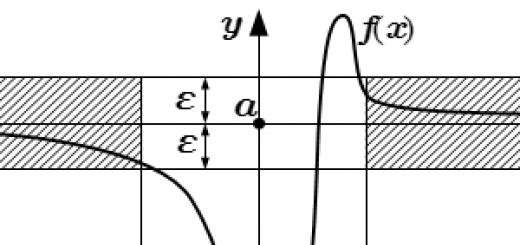
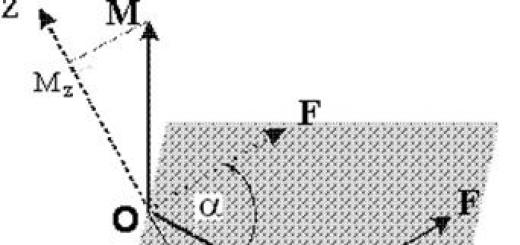
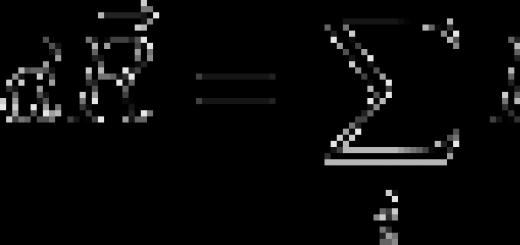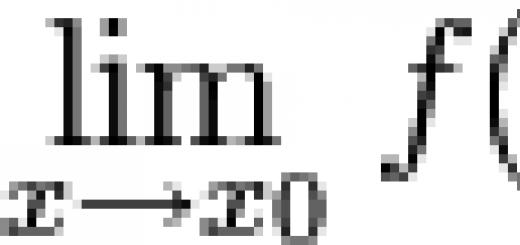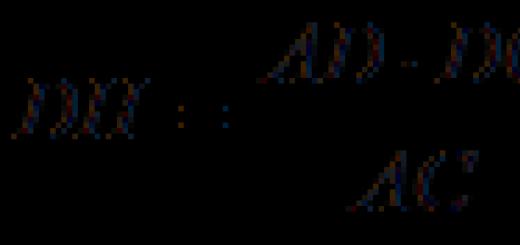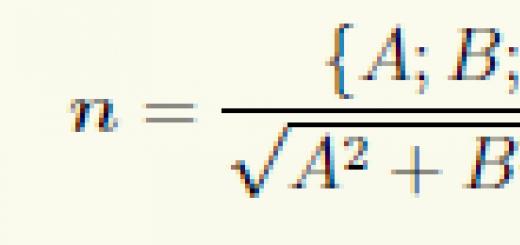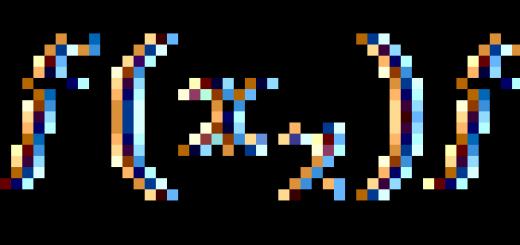Der Abstand zwischen schrägen Linien ist die Länge ihrer gemeinsamen Senkrechten (das Segment mit Enden auf diesen Linien und senkrecht zu jeder von ihnen). Schrittweises Rechenverfahren (Konstruktion einer gemeinsamen Senkrechten). b ρ Beispiel a

Konstruieren Sie eine Ebene, die eine der Geraden enthält und parallel zur anderen verläuft. Dann entspricht der gewünschte Abstand dem Abstand von einem Punkt der zweiten geraden Linie zur konstruierten Ebene (zu diesem Zeitpunkt können Sie verwenden koordinieren methode) Methode der parallelen Linien und Ebenen. Beispiel b ρ a α A B shah.ucoz.ru/load/egeh/egeh_s2/k oordinatnyj_metod_kljuchevye_za dachi/

Konstruieren Sie eine Ebene senkrecht zu einer der gegebenen Geraden und konstruieren Sie eine orthogonale Projektion der anderen Geraden auf diese Ebene. Orthogonale Entwurfsmethode. Beispiel b ρ a α A B L N S NE - Projektion b

Wenn AB und CD Kanten der dreieckigen Pyramide ABCD kreuzen, d der Abstand zwischen ihnen ist, α der Winkel zwischen AB und CD ist, V das Volumen der Pyramide ABCD ist, dann das Stützproblem. Beispiel B C A D Methoden zum Ermitteln des Winkels zwischen Geraden finden Sie unter:

Bestimmen Sie aus dem System die Koordinaten, dann finden Sie Let, dann ist die Bedingung erfüllt: Bestimmen Sie die Koordinaten der Richtungsvektoren und. Standard-Bild - Koordinatenmethode. Beispiel B C A D Hinweis: Um die Koordinaten der Punkte M und K aufzuzeichnen, verwenden Sie die Formel: M K

Finden Sie in einer regelmäßigen viereckigen Pyramide SABCD, deren Kanten alle gleich 1 sind, den Abstand zwischen den Linien BD und SA. Lösung: D. p.: OH lässt sich aus dem Dreieck AOS nach der Flächenmethode ermitteln. O A B C D S H OH - gemeinsame Senkrechte zu den Linien BD und AS Back

Finden Sie in einer regelmäßigen viereckigen Pyramide SABCD, deren Kanten alle gleich 1 sind, den Abstand zwischen den Linien BD und SA. Lösung: (halbe Diagonale des Einheitsquadrats) O A B C D S H Zurück

Rechts dreieckiges Prisma ABCA 1 C 1 B 1, dessen Kanten alle gleich 1 sind, finde den Abstand zwischen den Linien AA 1 und B 1 C. Lösung: BC C1C1 B1B1 HA A1A1 D. p .: (senkrecht zum Schnittpunkt senkrechter Ebenen gezogen ) Vom Dreieck ASN zurück

Finden Sie in einer regulären viereckigen Pyramide ABCDA 1 B 1 C 1 D 1 mit Basisseiten gleich 4 und 8 und einer Höhe gleich 6 den Abstand zwischen der Diagonale und BD 1 der Diagonale der größeren Basis AC. Lösung: B A C D A1A1 B1B1 C1C1 D1D1 O O1O1 D.p.: H (ist seine Projektion auf (BB 1 D 1)) Betrachte gleichschenkliges Trapez BB 1 D 1 D Zurück

Finden Sie in einer regulären viereckigen Pyramide ABCDA 1 B 1 C 1 D 1 mit Basisseiten gleich 4 und 8 und einer Höhe gleich 6 den Abstand zwischen der Diagonale und BD 1 der Diagonale der größeren Basis AC. Lösung: BD B1B1 D1D1 O Zurück K H Im Dreieck BD 1 K Die Dreiecke BD 1 K und BON sind in zwei Winkeln ähnlich Im Dreieck BHO

Finden Sie im Einheitswürfel ABCDA 1 B 1 C 1 D 1 den Abstand zwischen der Diagonalen des Würfels BD 1 und der Diagonalen der Fläche AB 1. Lösung: Betrachten Sie die Pyramide D 1 AB 1 B. Nehmen Sie AB 1 B als Basis , dann ist die Höhe BC. (Diagonale eines Einheitsquadrats) A C D D1D1 B1B1 C A1A1 B (Diagonale eines Einheitswürfels) Finden Sie den Winkel zwischen den Linien AB 1 und B 1 D 1. Sie können die Vektorkoordinatenmethode verwenden. zurück

Finden Sie im Einheitswürfel ABCDA 1 B 1 C 1 D 1 den Abstand zwischen der Diagonalen des Würfels BD 1 und der Diagonalen der Fläche AB 1. Lösung: Führen wir ein rechtwinkliges Koordinatensystem ein A C D D1D1 B1B1 C A1A1 B X Z Y Dann: Zurück

Finden Sie im Einheitswürfel ABCDA 1 B 1 C 1 D 1 den Abstand zwischen der Diagonalen des Würfels BD 1 und der Diagonalen der Fläche AB 1. Lösung: A C D D1D1 B1B1 C A1A1 B Zurück

Finden Sie im Einheitswürfel ABCDA 1 B 1 C 1 D 1 den Abstand zwischen der Diagonalen des Würfels AB 1 und der Diagonalen der Fläche A 1 C 1. Lösung: ACD D1D1 B1B1 C A1A1 B Wir führen ein rechtwinkliges Koordinatensystem ein Dann: Lassen Sie MK Dann: XZY Zurück und

Finden Sie im Einheitswürfel ABCDA 1 B 1 C 1 D 1 den Abstand zwischen der Diagonalen des Würfels AB 1 und der Diagonalen der Fläche A 1 C 1. Lösung: A C D D1D1 B1B1 C A1A1 B X Z Y M K Zurück

Finden Sie im Einheitswürfel ABCDA 1 B 1 C 1 D 1 den Abstand zwischen der Diagonalen des Würfels AB 1 und der Diagonalen der Fläche A 1 C 1. Lösung: Zurück

2) In einer regelmäßigen viereckigen Pyramide MABCD, deren Kanten alle gleich 1 sind, finde den Abstand zwischen den Linien MA und BC Übungsaufgaben Lösung 3) Die Seite der Basis ABC einer regelmäßigen dreieckigen Pyramide ABCD ist gleich der Höhe der Pyramide ist DO=6. Die Punkte A 1, C 1 sind die Mittelpunkte der Kanten AD bzw. CD. Finden Sie den Abstand zwischen den Linien BA 1 und AC 1. Lösung 1) Finden Sie den Abstand zwischen sich nicht schneidenden Diagonalen zweier benachbarter Flächen eines Würfels mit der Kantenlänge 1.

Lösung: Rückenprobleme 1) Finden Sie den Abstand zwischen sich nicht schneidenden Diagonalen zweier benachbarter Seiten eines Würfels mit der Kantenlänge 1. ACD D1D1 B1B1 C A1A1 BOO O1O1 H Wir konstruieren eine orthogonale Projektion der Linie AB 1 auf die Ebene (BB 1 D 1) D. p .: Finden Sie O 1 H finden Sie aus dem Dreieck B 1 OO 1

Lösung: A D B C M O N 2) Finden Sie in einer regelmäßigen viereckigen Pyramide MABCD, deren Kanten alle gleich 1 sind, den Abstand zwischen den Linien MA und BC. (Dreieck AMD ist gleichseitig) Finden Sie den Winkel zwischen den Linien AD und BC. Aufgaben der Streitkräfte || ANZEIGE => "> "> " title="(!LANG:Lösung: A D B C M O N 2) Finden Sie in einer regelmäßigen viereckigen Pyramide MABCD mit allen Kanten gleich 1 den Abstand zwischen den Linien MA und BC. (Dreieck AMD ist gleichseitig) Finden Sie den Winkel zwischen den Linien AD und BC. Aufgaben der Streitkräfte || ANZEIGE =>"> title="Lösung: A D B C M O N 2) Finden Sie in einer regelmäßigen viereckigen Pyramide MABCD, deren Kanten alle gleich 1 sind, den Abstand zwischen den Linien MA und BC. (Dreieck AMD ist gleichseitig) Finden Sie den Winkel zwischen den Linien AD und BC. Aufgaben der Streitkräfte || ANZEIGE =>"> !}

A B C D Lösung: A1A1 C1C1 3) Die Seite der Basis ABC der regelmäßigen Dreieckspyramide ABCD ist gleich, die Höhe der Pyramide ist DO=6. Die Punkte A 1, C 1 sind die Mittelpunkte der Kanten AD bzw. CD. Finden Sie den Abstand zwischen den Linien BA 1 und AC 1. Die Segmente AC 1 und BA 1 sind die Kanten der dreieckigen Pyramide C 1 ABA 1 (Stützproblem). 5) Das Volumen der Pyramide mit der Grundfläche VA 1 A? 4) Abstand vom Punkt C 1 zur Ebene (BDA) (Höhe der Pyramide)? 6) ρ(VA 1 ;AC 1)? 1) Die Längen der Rippen BA 1 und AC 1? 2) Der Sinus des Winkels zwischen den Geraden BA 1 und AC 1? 3) Die Fläche der Basis der Pyramide - VA 1 A? O Aufgaben

A 3) Die Seite der Basis ABC der regelmäßigen Dreieckspyramide ABCD ist gleich, die Höhe der Pyramide ist DO=6. Die Punkte A 1, C 1 sind die Mittelpunkte der Kanten AD bzw. CD. Finden Sie den Abstand zwischen den Linien BA 1 und AC 1. Lösung: O A D A1A1 X Z Y x CxC 1) Führen Sie ein rechtwinkliges Koordinatensystem ein Dann: xDxD Finden Sie die Koordinaten der Punkte C und D B X Y O C H (Dreiecksmitteleigenschaft) xDxD x CxC C B C1C1 Aufgaben

Die Seite der Grundfläche ABC der regelmäßigen Dreieckspyramide ABCD ist gleich groß, die Höhe der Pyramide ist DO=6. Die Punkte A 1, C 1 sind die Mittelpunkte der Kanten AD bzw. CD. Finden Sie den Abstand zwischen den Linien BA 1 und AC 1. Lösung: A B C D A1A1 C1C1 X Z Y (Mittelpunkte von CD und AD) Bestimmen Sie die Koordinaten der Richtungsvektoren Probleme

Die Seite der Grundfläche ABC der regelmäßigen Dreieckspyramide ABCD ist gleich groß, die Höhe der Pyramide ist DO=6. Die Punkte A 1, C 1 sind die Mittelpunkte der Kanten AD bzw. CD. Finden Sie den Abstand zwischen den Linien BA 1 und AC 1. Lösung: 4) Finden Sie den Abstand vom Punkt C 1 zur Ebene (BDA) (Höhe der Pyramide). Lassen Sie uns die Probleme der Gleichung der Ebene (EFP) ableiten

A B C D Lösung: A1A1 C1C1 3) Die Seite der Basis ABC der regelmäßigen Dreieckspyramide ABCD ist gleich, die Höhe der Pyramide ist DO=6. Die Punkte A 1, C 1 sind die Mittelpunkte der Kanten AD bzw. CD. Finden Sie den Abstand zwischen den Linien BA 1 und AC 1. 5) Finden Sie das Volumen der Pyramide mit der Basis BA 1 A? O Aufgaben

Bei der Erstellung der Präsentation wurde das Handbuch verwendet:

"Abstand zwischen schiefen Linien" - Theorem. Vorbereitende mündliche Aufgaben. Finden Sie den Abstand zwischen der Linie MN und der Ebene AA1D1D. Finden Sie den Abstand zwischen der Linie B1K und der Ebene DD1C1C. OK=OO1?OM/O1M =a/3 (nach Satz des Pythagoras O1M=3/2?2, OM=1/2?2). Die Diagonalebene AA1C1C ist senkrecht zur Linie BD. Die neuen Positionen der Punkte B und N sind die Punkte der Linien AD und BM, die am nächsten beieinander liegen.

"Lesson Speed ​​​​Time Distance" - Mathematisches Aufwärmen. Der Zweck der Lektion: den Schülern beizubringen, Probleme mit der Bewegung zu lösen. Distanz. Wie lange dauert es, 30 km mit einer konstanten Geschwindigkeit von 5 km/h zu laufen? Zusammenhang zwischen Geschwindigkeit, Zeit und Entfernung. Wie viele Menschen gingen in die Stadt? Ein Flugzeug fliegt die Strecke von Stadt A nach Stadt B in 1 Stunde und 20 Minuten.

"Geschwindigkeits-Zeit-Entfernungs-Mathematik" - Reduzieren Sie die Summe der Zahlen 5 und 65 um das Zweifache. Keine Ahnung, ging zum Mond. Reisen Sie durch die Seiten eines Märchenbuchs. Fiskultminutka. Einer ging um 8 Uhr und der andere um 10 Uhr. Zusammenfassend. Hat Laura recht? -Laura hat folgendes Problem gelöst: „500 km. Ein Auto wird in 10 Stunden vorbeifahren. Zeit. Der Schlüssel mit der Antwort „38“ öffnet das Buch:

"Dialog direkte Rede" - Was ist der Unterschied zwischen direkter Rede und Dialog? Zum Beispiel: L. N. Tolstoi sagte: „Wir alle brauchen einander auf der Welt.“ Grafiken der direkten Rede. A: "p." Aufgabe 3. Ersetzen Sie direkte Rede durch Dialog. Zum Beispiel: "P?" - aber. "P!" - aber. Zeigen Sie die richtigen Diagramme für die folgenden Sätze. Dialoggrafiken. Wie schreibt man direkte Rede und Dialog schriftlich?

"Sätze mit direkter Rede" - Petronius, antiker römischer Schriftsteller. Spiel "Finde den Fehler" (Check). Worte des Autors, die die direkte Rede einleiten: Ich tauchte wieder auf und ging zum Haus von Pater Gerasim. Ein Freund aus dem Dorf kam mich besuchen. Vorschläge mit direkter Rede. Kreative Aufgabe. In schriftlicher Form wird direkte Rede in Anführungszeichen gesetzt. Lesen!" rief Konstantin Georgiewitsch Paustowski.

"Distance and Scale" - Modell des Atoms in starker Vergrößerung. Auf einer Karte mit Maßstab beträgt der Abstand 5 cm.Wenn der Maßstab durch einen Bruch mit einem Zähler von 1 angegeben wird, dann. Maßstabsgetreues Modell eines Feuerwehrautos. Algorithmus zur Ermittlung der Entfernung am Boden: Auf der Autobahn beträgt die Streckenlänge 700 km. Beenden Sie den Satz: Die Entfernung zwischen zwei Städten beträgt 400 km.

ABSTAND ZWISCHEN RECHTEN IM RAUM Der Abstand zwischen zwei sich schneidenden Geraden im Raum ist die Länge der gemeinsamen Senkrechten zu diesen Geraden. Wenn eine der beiden sich schneidenden Geraden in einer Ebene liegt und die andere parallel zu dieser Ebene, dann ist der Abstand zwischen den gegebenen Geraden gleich dem Abstand zwischen der Geraden und der Ebene. Wenn zwei sich schneidende Geraden in parallelen Ebenen liegen, dann ist der Abstand zwischen diesen Geraden gleich dem Abstand zwischen ihnen parallele Ebenen.

Würfel 1 Finden Sie im Einheitswürfel A…D 1 den Abstand zwischen den Linien AA 1 und BC. Antwort 1.

Würfel 2 In dem Einheitswürfel A…D 1 finden Sie den Abstand zwischen den Linien AA 1 und CD. Antwort 1.

Würfel 3 Finde im Einheitswürfel A…D 1 den Abstand zwischen den Linien AA 1 und B 1 C 1. Antwort: 1.

Würfel 4 Finden Sie im Einheitswürfel A…D 1 den Abstand zwischen den Linien AA 1 und C 1 D 1. Antwort: 1.

Würfel 5 Finde im Einheitswürfel A…D 1 den Abstand zwischen den Linien AA 1 und BC 1. Antwort: 1.

Würfel 6 Finde im Einheitswürfel A…D 1 den Abstand zwischen den Linien AA 1 und B 1 C. Antwort: 1.

Würfel 7 Finden Sie im Einheitswürfel A…D 1 den Abstand zwischen den Linien AA 1 und CD 1. Antwort: 1.

Würfel 8 Finde im Einheitswürfel A…D 1 den Abstand zwischen den Linien AA 1 und DC 1. Antwort: 1.

Würfel 9 Finde im Einheitswürfel A…D 1 den Abstand zwischen den Linien AA 1 und CC 1. Antwort:

Würfel 10 In dem Einheitswürfel A…D 1 finden Sie den Abstand zwischen den Linien AA 1 und BD. Lösung. Sei O der Mittelpunkt von BD. Der gewünschte Abstand ist die Länge des Segments AO. Es ist gleich Antwort:

Würfel 11 Finden Sie im Einheitswürfel A…D 1 den Abstand zwischen den Linien AA 1 und B 1 D 1. Antwort:

Würfel 12 Finde im Einheitswürfel A…D 1 den Abstand zwischen den Linien AA 1 und BD 1. Lösung. Seien P, Q die Mittelpunkte von AA 1, BD 1. Der gewünschte Abstand ist die Länge des Segments PQ. Es ist gleich Antwort:

Würfel 13 Finden Sie im Einheitswürfel A…D 1 den Abstand zwischen den Linien AA 1 und BD 1. Antwort:

Würfel 14 Finde im Einheitswürfel A…D 1 den Abstand durch die Linien AB 1 und CD 1. Antwort: 1.

Würfel 15 Finde im Einheitswürfel A…D 1 den Abstand zwischen den Linien AB 1 und BC 1. Lösung. Der gewünschte Abstand ist gleich dem Abstand zwischen den parallelen Ebenen AB 1 D 1 und BDC 1. Die Diagonale A 1 C steht senkrecht auf diesen Ebenen und wird an den Schnittpunkten in drei gleiche Teile geteilt. Daher ist der gewünschte Abstand gleich der Länge des Segments EF und gleich Antwort:

Würfel 16 Finden Sie im Einheitswürfel A…D 1 den Abstand zwischen den Linien AB 1 und A 1 C 1. Die Lösung ist ähnlich wie die vorherige. Antworten:

Würfel 17 In dem Einheitswürfel A…D 1 finden Sie den Abstand zwischen den Linien AB 1 und BD. Die Lösung ist ähnlich wie die vorherige. Antworten:

Würfel 18 Finde im Einheitswürfel A…D 1 die Entfernung durch die Linien AB 1 und BD 1. Lösung. Die Diagonale BD 1 steht senkrecht auf der Ebene gleichseitiges Dreieck ACB 1 und schneidet sie im Mittelpunkt P des darin eingeschriebenen Kreises. Der gewünschte Abstand ist gleich dem Radius OP dieses Kreises. OP = Antwort:

Pyramide 1 Finden Sie im Einheitstetraeder ABCD den Abstand zwischen den Linien AD und BC. Lösung. Der gewünschte Abstand ist gleich der Länge des Segments EF, wobei E, F die Mittelpunkte der Kanten AD, GF sind. Im Dreieck DAG DA = 1, AG = DG = Antwort: Also EF =

Pyramide 2 In einer regulären Pyramide SABCD, deren Kanten alle gleich 1 sind, finden Sie den Abstand zwischen den Linien AB und CD. Antwort 1.

Pyramide 3 Finden Sie in einer regulären Pyramide SABCD, deren Kanten alle gleich 1 sind, den Abstand zwischen den Linien SA und BD. Lösung. Der gewünschte Abstand ist gleich der Höhe OH des Dreiecks SAO, wobei O der Mittelpunkt von BD ist. IN rechtwinkliges Dreieck SAO haben wir: SA = 1, AO = SO = Antwort: Also OH =

Pyramide 4 In einer regulären Pyramide SABCD, deren Kanten alle gleich 1 sind, finde den Abstand zwischen den Linien SA und BC. Lösung. Ebene SAD ist parallel zur Linie BC. Daher ist der gewünschte Abstand gleich dem Abstand zwischen der Linie BC und der Ebene SAD. Sie ist gleich der Höhe EH des Dreiecks SEF, wobei E, F die Mittelpunkte der Kanten BC, AD sind. Im Dreieck SEF haben wir: EF = 1, SE = SF = Höhe SO ist also EH = Antwort:

Pyramide 5 Ermitteln Sie in einer regulären 6. Pyramide SABCDEF mit Basiskanten gleich 1 den Abstand zwischen den Linien AB und DE. Antworten:

Pyramide 6 In der regulären 6. Pyramide SABCDEF, deren Seitenkanten 2 und die Basiskanten 1 sind, finden Sie den Abstand zwischen den Linien SA und BC. Lösung: Verlängere die Kanten BC und AF, bis sie sich im Punkt G schneiden. Die gemeinsame Senkrechte zu SA und BC ist die Höhe AH des Dreiecks ABG. Es ist gleich Antwort:

Pyramide 7 In der regulären 6. Pyramide SABCDEF, deren Seitenkanten 2 und die Basiskanten 1 sind, finden Sie den Abstand zwischen den Linien SA und BF. Lösung: Der gesuchte Abstand ist die Höhe GH des Dreiecks SAG, wobei G der Schnittpunkt von BF und AD ist. Im Dreieck SAG haben wir: SA = 2, AG = 0,5, Höhe SO ist gleich Ab hier finden wir GH = Antwort:

Pyramide 8 In der regulären 6. Pyramide SABCDEF, deren Seitenkanten 2 und die Basiskanten 1 sind, finden Sie den Abstand zwischen den Linien SA und CE. Lösung: Der gesuchte Abstand ist die Höhe GH des Dreiecks SAG, wobei G der Schnittpunkt von CE und AD ist. Im Dreieck SAG haben wir: SA = 2, AG = , die Höhe SO ist gleich Ab hier finden wir GH = Antwort:

Pyramide 9 In der regulären 6. Pyramide SABCDEF, deren Seitenkanten 2 und die Basiskanten 1 sind, finden Sie den Abstand zwischen den Linien SA und BD. Lösung: Linie BD ist parallel zur Ebene SAE. Der gewünschte Abstand ist gleich dem Abstand zwischen der Linie BD und dieser Ebene und ist gleich der Höhe PH des Dreiecks SPQ. In diesem Dreieck ist die Höhe SO, PQ = 1, SP = SQ = Ab hier finden wir PH = Antwort:

Pyramide 10 In der regulären 6. Pyramide SABCDEF, deren Seitenkanten 2 und die Basiskanten 1 sind, finden Sie den Abstand zwischen den Linien SA und BG, wobei G der Mittelpunkt der Kante SC ist. Lösung: Ziehe eine Linie durch den Punkt G parallel zu SA. Q bezeichne den Schnittpunkt mit der Linie AC. Der gesuchte Abstand ist gleich der Höhe QH des rechtwinkligen Dreiecks ASQ, in dem AS = 2, AQ = , SQ = Daraus ergibt sich QH = Antwort: .

Prisma 1 In einem regulären dreieckigen Prisma ABCA 1 B 1 C 1, dessen Kanten alle gleich 1 sind, finden Sie den Abstand zwischen den Linien: BC und B 1 C 1. Antwort: 1.

Prisma 2 In einem regulären dreieckigen Prisma ABCA 1 B 1 C 1, dessen Kanten alle gleich 1 sind, finden Sie den Abstand zwischen den Linien: AA 1 und BC. Antworten:

Prisma 3 In einem regulären dreieckigen Prisma ABCA 1 B 1 C 1, dessen Kanten alle gleich 1 sind, finden Sie den Abstand zwischen den Linien: AA 1 und BC 1. Antwort:

Prisma 4 In einem regulären dreieckigen Prisma ABCA 1 B 1 C 1, dessen Kanten alle gleich 1 sind, finden Sie den Abstand zwischen den Linien: AB und A 1 C 1. Antwort: 1.

Prisma 5 In einem regulären dreieckigen Prisma ABCA 1 B 1 C 1, dessen Kanten alle gleich 1 sind, finde den Abstand zwischen den Linien: AB und A 1 C. Lösung: Der gesuchte Abstand ist gleich dem Abstand zwischen der Linie AB und die Ebene A 1 B 1 C. Lassen Sie uns D und D 1 die Mittelpunkte der Kanten AB und A 1 B 1 bezeichnen. Zeichnen Sie in einem rechtwinkligen Dreieck CDD 1 eine Höhe DE von der Ecke D. Es wird die gewünschte Entfernung sein. Wir haben, DD 1 = 1, CD = Antwort: Also DE = , CD 1 = .

Prisma 6 In einem regulären dreieckigen Prisma ABCA 1 B 1 C 1, dessen Kanten alle gleich 1 sind, finden Sie den Abstand zwischen den Linien: AB 1 und BC 1. Lösung: Bauen wir das Prisma zu einem 4-Winkel-Prisma. Der gewünschte Abstand ist gleich dem Abstand zwischen den parallelen Ebenen AB 1 D 1 und BDC 1. Er ist gleich der Höhe OH des rechtwinkligen Dreiecks AOO 1, in dem die Antwort. Diese Höhe ist

Prisma 7 Finden Sie im richtigen 6. Prisma A…F 1, dessen Kanten gleich 1 sind, den Abstand zwischen den Linien: AB und A 1 B 1. Antwort: 1.

Prisma 8 Finden Sie im regulären 6. Prisma A…F 1, dessen Kanten gleich 1 sind, den Abstand zwischen den Linien: AB und B 1 C 1. Antwort: 1.

Prisma 9 Finden Sie im regulären 6. Prisma A…F 1, dessen Kanten gleich 1 sind, den Abstand zwischen den Linien: AB und C 1 D 1. Antwort: 1.

Prisma 10 Finden Sie im richtigen 6. Prisma A…F 1, dessen Kanten gleich 1 sind, den Abstand zwischen den Linien: AB und DE. Antworten: .

Prisma 11 Finden Sie im richtigen 6. Prisma A ... F 1, dessen Kanten gleich 1 sind, den Abstand zwischen den Linien: AB und D 1 E 1. Antwort: 2.

Prisma 12 Finden Sie im regulären 6. Prisma A…F 1, dessen Kanten gleich 1 sind, den Abstand zwischen den Linien: AA 1 und CC 1. Antwort: .

Prisma 13 Finden Sie im richtigen 6. Prisma A ... F 1, dessen Kanten gleich 1 sind, den Abstand zwischen den Linien: AA 1 und DD 1. Antwort: 2.

Prisma 14 Im regulären 6. Prisma A…F 1, dessen Kanten gleich 1 sind, finden Sie den Abstand zwischen den Linien: AA 1 und B 1 C 1. Lösung: Setzen wir die Seiten B 1 C 1 und A 1 F 1 fort bis sie schneiden sich im Punkt G. Das Dreieck A 1 B 1 G ist gleichseitig. Seine Höhe A 1 H ist die gewünschte gemeinsame Senkrechte. Seine Länge ist gleich. Antworten: .

Prisma 15 Bestimmen Sie im regulären 6. Prisma A…F 1, dessen Kanten gleich 1 sind, den Abstand zwischen den Geraden: AA 1 und C 1 D 1. Lösung: Die gesuchte gemeinsame Senkrechte ist die Strecke A 1 C 1. Ihre Länge ist gleich. Antworten: .

Prisma 16 Finden Sie im richtigen 6. Prisma A…F 1, dessen Kanten gleich 1 sind, den Abstand zwischen den Linien: AA 1 und BC 1. Lösung: Der gesuchte Abstand ist der Abstand zwischen den parallelen Ebenen ADD 1 und BCC 1. Es ist gleich. Antworten: .

Prisma 17 Finden Sie im regulären 6. Prisma A…F 1, dessen Kanten gleich 1 sind, den Abstand zwischen den Linien: AA 1 und CD 1. Lösung: Die gesuchte gemeinsame Senkrechte ist die Strecke AC. Seine Länge ist gleich. Antworten: .

Prisma 18 Im regulären 6. Prisma A…F 1, dessen Kanten gleich 1 sind, bestimme den Abstand zwischen den Geraden: AA 1 und DE 1. Lösung: Die gesuchte gemeinsame Senkrechte ist die Strecke A 1 E 1. Ihre Länge ist gleich . Antworten: .

Prisma 19 Finden Sie im regulären 6. Prisma A…F 1, dessen Kanten gleich 1 sind, den Abstand zwischen den Geraden: AA 1 und BD 1. Lösung: Die gesuchte gemeinsame Senkrechte ist die Strecke AB. Seine Länge ist 1. Antwort: 1.

Prisma 20 In einem regulären 6. Prisma A…F 1, dessen Kanten gleich 1 sind, finde den Abstand zwischen den Linien: AA 1 und CE 1. Lösung: Der gesuchte Abstand ist der Abstand zwischen der Linie AA 1 und der Ebene CEE 1 Es ist gleich. Antworten: .

Prisma 21 Finde im richtigen 6. Prisma A…F 1, dessen Kanten gleich 1 sind, den Abstand zwischen den Linien: AA 1 und BE 1. Lösung: Der gesuchte Abstand ist der Abstand zwischen der Linie AA 1 und der Ebene BEE 1 Es ist gleich. Antworten: .

Prisma 22 In einem regulären 6. Prisma A…F 1, dessen Kanten gleich 1 sind, finde den Abstand zwischen den Linien: AA 1 und CF 1. Lösung: Der gesuchte Abstand ist der Abstand zwischen der Linie AA 1 und der Ebene CFF 1 Es ist gleich. Antworten: .

Prisma 23 Bestimmen Sie im regulären 6. Prisma A…F 1, dessen Kanten gleich 1 sind, den Winkel zwischen den Linien: AB 1 und DE 1. Lösung: Der gesuchte Abstand ist der Abstand zwischen den parallelen Ebenen ABB 1 und DEE 1. Der Abstand zwischen ihnen ist gleich. Antworten: .

Prisma 24 Bestimmen Sie in einem regulären 6. Prisma A…F 1, dessen Kanten gleich 1 sind, den Winkel zwischen den Linien: AB 1 und CF 1. Lösung: Der gesuchte Abstand ist der Abstand zwischen der Linie AB 1 und der Ebene CFF 1 Es ist gleich. Antworten:

Prisma 25 Im regulären 6. Prisma A…F 1, dessen Kanten gleich 1 sind, finden Sie den Abstand zwischen den Linien: AB 1 und BC 1. Lösung: Seien O, O 1 die Mittelpunkte der Prismenflächen. Die Ebenen AB 1 O 1 und BC 1 O sind parallel. Die Ebene ACC 1 A 1 steht senkrecht auf diesen Ebenen. Der gesuchte Abstand d ist gleich dem Abstand zwischen den Linien AG 1 und GC 1. Im Parallelogramm AGC 1 G 1 haben wir AG = Antwort: ; AG 1 = Die zur Seite AA 1 gezeichnete Höhe ist gleich 1. Daher ist d= . .

Prisma 26 Finden Sie im regulären 6. Prisma A…F 1, dessen Kanten gleich 1 sind, den Abstand zwischen den Linien: AB 1 und BD 1. Lösung: Betrachten Sie die Ebene A 1 B 1 HG senkrecht zu BD 1. Die orthogonale Projektion auf diese Ebene verschiebt die Linie BD 1 zum Punkt H und die Linie AB 1 zur Linie GB 1. Daher ist der gewünschte Abstand d gleich dem Abstand vom Punkt H zur Linie GB 1. In einem rechtwinkligen Dreieck GHB 1 haben wir GH = 1; Antwort: B 1 H = . Daher ist d = .

Prisma 27 Finden Sie im regulären 6. Prisma A…F 1, dessen Kanten gleich 1 sind, den Abstand zwischen den Linien: AB 1 und BE 1. Lösung: Betrachten Sie die Ebene A 1 BDE 1, senkrecht zu AB 1. Die orthogonale Projektion auf diese Ebene verschiebt die Linie AB 1 zum Punkt G, und die Linie BE 1 bleibt an Ort und Stelle. Daher ist der gewünschte Abstand d gleich dem Abstand GH vom Punkt G zur Linie BE 1. In einem rechtwinkligen Dreieck A 1 BE 1 gilt A 1 B = ; EIN 1 E 1 =. Antwort: Daher ist d = .

In diesem Artikel wird am Beispiel der Lösung der Aufgabe C2 aus der Einheitlichen Staatsprüfung die Methode der Koordinatenfindung mit der Methode analysiert. Denken Sie daran, dass Linien schief sind, wenn sie nicht in derselben Ebene liegen. Insbesondere wenn eine Gerade in einer Ebene liegt und die zweite Gerade diese Ebene an einem Punkt schneidet, der nicht auf der ersten Geraden liegt, dann sind solche Geraden schief (siehe Abbildung).

Zur Findung Abstände zwischen sich schneidenden Linien notwendig:

1. Zeichnen Sie eine Ebene durch eine der schrägen Linien, die parallel zur anderen schrägen Linie ist.
2. Lassen Sie eine Senkrechte von einem beliebigen Punkt der zweiten Geraden auf die resultierende Ebene fallen. Die Länge dieser Senkrechten ist der gewünschte Abstand zwischen den Linien.

Analysieren wir diesen Algorithmus am Beispiel der Lösung der Aufgabe C2 aus der Einheitlichen Staatsprüfung Mathematik näher.

Abstand zwischen Linien im Raum

Eine Aufgabe. in einem einzigen Würfel ABCDA 1 B 1 C 1 D 1 Finden Sie den Abstand zwischen den Linien BA 1 und DB 1 .

Reis. 1. Zeichnen für die Aufgabe

Lösung. Durch den Mittelpunkt der Diagonalen des Würfels DB 1 (Punkt Ö) Zeichnen Sie eine Linie parallel zur Linie EIN 1 B. Schnittpunkte einer gegebenen Geraden mit Kanten BC Und EIN 1 D 1 bezeichnen jeweils n Und m. Gerade MN liegt im Flugzeug MNB 1 und parallel zur Linie EIN 1 B, die nicht in dieser Ebene liegt. Das bedeutet, dass die direkte EIN 1 B parallel zur Ebene MNB 1 auf der Grundlage der Parallelität einer geraden Linie und einer Ebene (Fig. 2).

Reis. 2. Der gewünschte Abstand zwischen den sich kreuzenden Linien ist gleich dem Abstand von jedem Punkt der ausgewählten Linie zur abgebildeten Ebene

Wir suchen nun die Entfernung von einem Punkt auf der Geraden EIN 1 B bis zum Flugzeug MNB ein . Dieser Abstand ist definitionsgemäß der gewünschte Abstand zwischen den Schräglinien.

Um diesen Abstand zu finden, verwenden wir die Koordinatenmethode. Wir führen ein rechtwinkliges kartesisches Koordinatensystem ein, so dass sein Ursprung mit dem Punkt B, der Achse, zusammenfällt x wurde entlang der Kante geführt BA, Achse Y- entlang der Rippe BC, Achse Z- entlang der Rippe BB 1 (Abb. 3).

Reis. 3. Wir wählen ein rechteckiges kartesisches Koordinatensystem wie in der Abbildung gezeigt

Wir finden die Gleichung der Ebene MNB 1 in diesem Koordinatensystem. Dazu bestimmen wir zunächst die Koordinaten der Punkte m, n Und B 1: Die resultierenden Koordinaten werden ersetzt allgemeine Gleichung Gerade und wir erhalten folgendes Gleichungssystem:

Aus der zweiten Gleichung des Systems erhalten wir aus der dritten und dann aus der ersten. Wir setzen die erhaltenen Werte in die allgemeine Gleichung der Geraden ein:

Beachten Sie, dass sonst das Flugzeug MNB 1 würde durch den Ursprung gehen. Wir dividieren beide Seiten dieser Gleichung durch und erhalten:

Der Abstand von einem Punkt zu einer Ebene wird durch die Formel bestimmt.