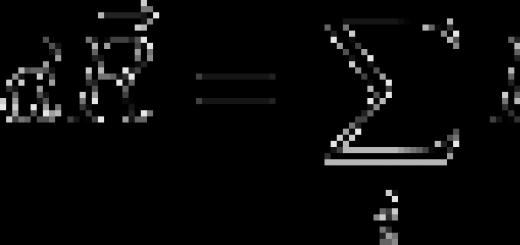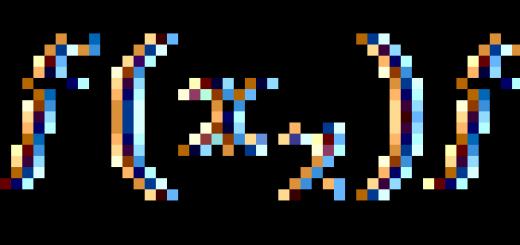На цьому уроці ми виведемо формулу суми членів кінцевої арифметичної прогресії та вирішимо деякі завдання із застосуванням цієї формули.

Тема: Прогресії

Форма суми членів кінцевої арифметичної прогресії

1. Вступ

Розглянемо завдання: знайти суму натуральних чиселвід 1 до 100 включно.

Дано: 1, 2, 3, …, 98, 99, 100.

Знайти: S100 = 1 +2 +3 … +98 + 99 + 100.

Рішення: S100=(1+100)+(2+99)+(3+98)+…+(50+51)=101+101+101+…+101=101 х 50=5050.

Відповідь: 5050.

Послідовність натуральних чисел 1, 2, 3, …, 98, 99, 100 є арифметичною прогресією: а1 = 1, d = 1.

Ми знайшли суму перших ста натуральних чисел, тобто суму перших n членів арифметичної прогресії.

Розглянуте рішення запропонував великий математик Карл Фрідріх Гаус, який жив у 19 столітті. Завдання було їм вирішено у віці 5 років.

Історична довідка:Йоганн Карл Фрідріх Гаус (1777 - 1855) - німецький математик, механік, фізик та астроном. Вважається одним із найбільших математиків усіх часів, «королем математиків». Лауреат медалі Коплі (1838), іноземний член Шведської (1821) та Російської (1824) Академій наук, англійського Королівського товариства. Згідно з легендою, шкільний вчитель математики, щоб зайняти дітей на довгий час, запропонував їм порахувати суму чисел від 1 до 100. Юний Гаус зауважив, що попарні суми з протилежних до однакових: 1+100=101, 2+99=101 і т.д. д., і миттєво одержав результат: 101x50=5050.

2. Висновок формули суми перших n членів арифметичної прогресії

Розглянемо аналогічне завдання довільної арифметичної прогресії.

Знайти: суму перших n членів арифметичної прогресії.

Покажемо, що всі вирази в дужках рівні між собою, а саме . Нехай d – різниця арифметичної прогресії. Тоді:

І т. д. Отже, ми можемо записати:

Звідки отримуємо формулу суми перших n членів арифметичної прогресії:

.

3. Розв'язання задач застосування формули суми перших n членів арифметичної прогресії

1. Розв'яжемо задачу про суму натуральних чисел від 1 до 100 за допомогою формули суми перших n членів арифметичної прогресії:

Рішення: а1 = 1, d = 1, n = 100.

Загальна формула:

.

У нашому випадку: .

Відповідь: 5050.

Загальна формула:

. Знайдемо за формулою n-го члена арифметичної прогресії: .

У нашому випадку: .

Щоб знайти, спочатку треба знайти.

Це можна зробити за загальною формулою .Спочатку застосуємо цю формулу для знаходження різниці арифметичної прогресії.

Т. е. . Значить.

Тепер можемо знайти.

Використовуючи формулу суми перших n членів арифметичної прогресії

, знайдемо .

4. Виведення другої формули суми перших n членів арифметичної прогресії

Отримаємо другу формулу для суми перших n членів арифметичної прогресії, а саме: доведемо, що .

Доказ:

У формулу суми перших n членів арифметичної прогресії підставимо вираз для , а саме . Отримаємо: , тобто. . Що і потрібно було довести.

Проаналізуємо отримані формули. Для обчислень за першою формулою треба знати перший член, останній член і n за другою формулою - треба знати перший член, різницю та n.

І насамкінець зауважимо, що у будь-якому разі Sn- це квадратична функціявід n, тому що .

5. Розв'язання задач застосування другої формули суми перших n членів арифметичної прогресії

Загальна формула:

.

У нашому випадку:.

Відповідь: 403.

2. Знайти суму всіх двоцифрових чисел, кратних 4.

(12; 16; 20; …; 96) - безліч чисел, що задовольняють умові задачі.

Отже, маємо арифметичну прогресію.

n знайдемо з формули для :.

Т. е. . Значить.

Використовуючи другу формулу суми перших n членів арифметичної прогресії

, знайдемо .

Потрібно знайти суму всіх членів з 10 по 25 включно.

Один із способів вирішення полягає в наступному:

Отже, .

6. Підсумок уроку

Отже, ми вивели формули суми членів кінцевої арифметичної прогресії. Використовували ці формули під час вирішення деяких завдань.

На наступному уроці ми познайомимося з характерною властивістю арифметичної прогресії.

1. Макарічев Ю. Н. та ін Алгебра 9 клас (підручник для середньої школи).-М: Просвітництво, 1992.

2. Макарічев Ю. Н., Міндюк Н. Г., Нешков, К. І. Алгебра для 9 класу з поглибл. вивч. математики.-М.: Мнемозіна, 2003.

3. Макарічев Ю. Н., Міндюк Н. Г. Додаткові розділи до шкільного підручника алгебри 9 класу.-М.: Просвітництво, 2002.

4. Галицький М. Л., Гольдман А. М., Звавіч Л. І. Збірник завдань з алгебри для 8-9 класів ( навчальний посібникдля учнів шкіл та класів з поглибл. вивч. математики).-М.: Просвітництво, 1996.

5. Мордкович А. Г. Алгебра 9 клас, підручник для загальноосвітніх закладів. - М: Менімозіна, 2002.

6. Мордкович А. Г., Мішутіна Т. Н., Тульчинська Є. Є. Алгебра 9 клас, задачник для загальноосвітніх установ. - М: Менімозіна, 2002.

7. Глейзер Г. І. Історія математики у школі. 7-8 класи (посібник для вчителів).-М: Просвітництво, 1983.

1. Розділ College. ru з математики.

2. Портал Природних Наук.

3. Exponenta. jw.org uk Освітній математичний сайт.

1. № 362, 371, 377, 382 (Макарич Ю. Н. та ін. Алгебра 9 клас).

2. № 12.96 (Галицький М. Л., Гольдман А. М., Звавіч Л. І. Збірник завдань з алгебри для 8-9 класів).

Сума арифметичної прогресії.

Сума арифметичної прогресії – штука проста. І за змістом, і за формулою. Але завдання на цю тему бувають усілякі. Від елементарних до цілком солідних.

Спочатку розберемося зі змістом та формулою суми. А потім і вирішуємо. На своє задоволення.) Сенс суми простий, як мукання. Щоб знайти суму арифметичної прогресії, треба просто акуратно скласти всі її члени. Якщо цих членів мало, можна складати без жодних формул. Але якщо багато, або дуже багато... додавання напружує.) У цьому випадку рятує формула.

Формула суми виглядає просто:

Розберемося, що за літери входять у формулу. Це багато чого прояснить.

S n - Сума арифметичної прогресії. Результат додавання всіхчленів, з першогопо останній.Це важливо. Складаються саме Усечлени поспіль, без перепусток та перескоків. І, саме, починаючи з першого.У завданнях типу знайти суму третього і восьмого членів, або суму членів з п'ятого по двадцятий - пряме застосування формули розчарує.)

a 1 - першийчлен прогресії. Тут все зрозуміло, це просто першеЧисло ряду.

a n- Останнійчлен прогресії. Остання кількістьряду. Не дуже звична назва, але, стосовно суми, дуже годиться. Далі самі побачите.

n - Номер останнього члена. Важливо розуміти, що у формулі цей номер збігається з кількістю членів, що складаються.

Визначимося з поняттям останньогочлена a n. Питання на засипку: який член буде останнім,якщо дана нескінченнаарифметична прогресія?)

Для впевненої відповіді слід розуміти елементарний сенс арифметичної прогресії та... уважно читати завдання!)

У завданні на пошук суми арифметичної прогресії завжди фігурує (прямо чи опосередковано) останній член, яким слід обмежитися.Інакше кінцевої, конкретної суми просто не існує.Для вирішення не має значення, яка задана прогресія: кінцева, або нескінченна. Не має значення, як вона задана: поруч чисел, або формулою n-го члена.

Найголовніше - розуміти, що формула працює з першого члена прогресії до члена з номером n.Власне, повна назва формули виглядає так: сума n перших членів арифметичної прогресії.Кількість цих перших членів, тобто. n, Визначається виключно завданням. У завданні вся ця цінна інформація часто зашифровується, так ... Але нічого, у прикладах нижче ми ці секрети розкриваємо.)

Приклади завдань у сумі арифметичної прогресії.

Насамперед, корисна інформація:

Основна складність у завданнях у сумі арифметичної прогресії полягає у правильному визначенні елементів формули.

Ці елементи укладачі завдань шифрують з безмежною фантазією.) Тут головне - не боятися. Розуміючи суть елементів, просто їх розшифрувати. Докладно розберемо кілька прикладів. Почнемо із завдання на основі реального ДІА.

1. Арифметична прогресія задана умовою: an = 2n-3,5. Знайдіть суму перших 10 її членів.

Гарне завдання. Легке.) Нам визначення суми за формулою чого треба знати? Перший член a 1, останній член a n, та номер останнього члена n.

Де взяти номер останнього члена n? Та там же, за умови! Там сказано: знайти суму перших 10 членів.Ну і з яким номером буде останній,десятий член?) Ви не повірите, його номер - десятий!) Отже, замість a nу формулу будемо підставляти a 10, а замість n- десятку. Повторюю, номер останнього члена збігається з кількістю членів.

Залишилось визначити a 1і a 10. Це легко вважається за формулою n-го члена, яка дана за умови завдання. Чи не знаєте, як це зробити? Завітайте на попередній урок, без цього - ніяк.

a 1= 2 · 1 - 3,5 = -1,5

a 10= 2 · 10 - 3,5 = 16,5

S n = S 10.

Ми з'ясували значення всіх елементів формули суми арифметичної прогресії. Залишається підставити їх, та порахувати:

Ось і всі справи. Відповідь: 75.

Ще завдання з урахуванням ГИА. Трохи складніше:

2. Дана арифметична прогресія (a n), різниця якої дорівнює 3,7; a 1 = 2,3. Знайти суму перших 15 її членів.

Відразу пишемо формулу суми:

Ця формулка дозволяє нам знайти значення будь-якого члена за номером. Шукаємо простою підстановкою:

a 15 = 2,3 + (15-1) · 3,7 = 54,1

Залишилося підставити всі елементи у формулу суми арифметичної прогресії та порахувати відповідь:

Відповідь: 423.

До речі, якщо у формулу суми замість a nпросто підставимо формулу n-го члена, отримаємо:

Наведемо подібні, отримаємо нову формулу суми членів арифметичної прогресії:

Як бачимо, тут не потрібно n-й член a n. У деяких завданнях ця формула чудово рятує, так... Можна цю формулу запам'ятати. А можна потрібний момент її просто вивести, як тут. Адже формулу суми і формулу n-го члена треба пам'ятати.)

Тепер завдання у вигляді короткого шифрування):

3. Знайти суму всіх позитивних двоцифрових чисел, кратних трьом.

Ось як! Ні тобі першого члена, ні останнього, ні прогресії взагалі... Як жити?

Прийде думати головою і витягати з умови всі елементи суми арифметичної прогресії. Що таке двоцифрові числа - знаємо. З двох циферок складаються.) Яке двозначне число буде першим? 10, треба думати.) А останнєдвоцифрове число? 99, зрозуміло! За ним уже тризначні підуть...

Кратні трьом... Гм... Це такі числа, що діляться на три націло, ось! Десятка не ділиться на три, 11 не ділиться... 12... ділиться! Так, дещо вимальовується. Вже можна записати ряд за умовою завдання:

12, 15, 18, 21, ... 96, 99.

Чи буде цей ряд арифметичною прогресією? Звичайно! Кожен член відрізняється від попереднього на трійку. Якщо члену додати 2, чи 4, скажімо, результат, тобто. нове число, що вже не поділиться націло на 3. До купи можна відразу і різницю арифметичної прогресії визначити: d=3.Стане в нагоді!)

Отже, можна сміливо записати деякі параметри прогресії:

А який буде номер nостаннього члена? Той, хто думає, що 99 - фатально помиляється... Номери - вони завжди йдуть підряд, а члени у нас - через трійку перескакують. Чи не збігаються вони.

Тут два шляхи вирішення. Один шлях – для надпрацьовитих. Можна розписати прогресію, весь ряд чисел, і порахувати кількість членів.) Другий шлях - для вдумливих. Потрібно згадати формулу n-го члена. Якщо формулу застосувати до нашого завдання, то отримаємо, що 99 - це тридцятий член прогресії. Тобто. n = 30.

Дивимося на формулу суми арифметичної прогресії:

Дивимося, і радіємо.) Ми витягли з умови завдання все необхідне розрахунку суми:

a 1= 12.

a 30= 99.

S n = S 30.

Залишається елементарна арифметика. Підставляємо числа у формулу та вважаємо:

Відповідь: 1665

Ще один тип популярних завдань:

4. Дана арифметична прогресія:

-21,5; -20; -18,5; -17; ...

Знайти суму членів із двадцятого по тридцять четвертий.

Дивимося на формулу суми і... засмучуємось.) Формула, нагадаю, вважає суму з першогочлена. А в завданні треба рахувати суму з двадцятого...Чи не спрацює формула.

Можна, звичайно, розписати всю прогресію до ряду, та поскладувати члени з 20 по 34. Але... якось тупо і довго виходить, правда?)

Є більш елегантне рішення. Розіб'ємо наш ряд на дві частини. Перша частина буде з першого члена до дев'ятнадцятого.Друга частина - з двадцятого до тридцять четвертого.Зрозуміло, що якщо ми порахуємо суму членів першої частини S 1-19, так складемо із сумою членів другої частини S 20-34, отримаємо суму прогресії з першого члена по тридцять четвертий S 1-34. Ось так:

S 1-19 + S 20-34 = S 1-34

Звідси видно, що знайти суму S 20-34можна простим відніманням

S 20-34 = S 1-34 - S 1-19

Обидві суми у правій частині вважаються з першогочлена, тобто. до них цілком застосовна стандартна формула суми. Приступаємо?

Витягуємо з умови завдання парметри прогресії:

d = 1,5.

a 1= -21,5.

Для розрахунку сум перших 19 та перших 34 членів нам потрібні будуть 19-й та 34-й члени. Вважаємо їх за формулою n-го члена, як у задачі 2:

a 19= -21,5 + (19-1) · 1,5 = 5,5

a 34= -21,5 + (34-1) · 1,5 = 28

Залишається нічого. Від суми 34 членів відібрати суму 19 членів:

S 20-34 = S 1-34 - S 1-19 = 110,5 - (-152) = 262,5

Відповідь: 262,5

Одне важливе зауваження! У вирішенні цього завдання є дуже корисна фішка. Замість прямого розрахунку того, що потрібно (S 20-34),ми порахували те, що, здавалося б, не потрібне - S 1-19 .А вже потім визначили і S 20-34відкинувши від повного результату непотрібне. Такий "фінт вухами" часто рятує в злих завданнях.)

У цьому уроці ми розглянули завдання, на вирішення яких досить розуміти сенс суми арифметичної прогресії. Ну і пару формул знати треба.

Практична порада:

При розв'язанні будь-якого завдання на суму арифметичної прогресії рекомендую відразу виписувати дві основні формули цієї теми.

Формулу n-го члена:

Ці формули одразу підкажуть, що потрібно шукати, у якому напрямку думати, щоб вирішити завдання. Допомагає.

А тепер – завдання для самостійного вирішення.

5. Знайти суму всіх двоцифрових чисел, які не діляться націло на три.

Круто?) Підказка прихована у зауваженні до завдання 4. Та й завдання 3 допоможе.

6. Арифметична прогресія задана умовою: a 1 = -5,5; an+1 = an+0,5. Знайдіть суму перших 24 її членів.

Незвично?) Це рекурентна формула. Про неї можна прочитати у попередньому уроці. Не ігноруйте посилання, такі завдання в ДПА часто зустрічаються.

7. Вася накопичив до Свята грошей. Цілих 4550 рублів! І вирішив подарувати найулюбленішій людині (собі) кілька днів щастя). Пожити гарно, ні в чому не відмовляючи. Витратити в перший день 500 рублів, а кожен наступний день витрачати на 50 рублів більше, ніж у попередній! Поки не скінчиться запас грошей. Скільки днів щастя вийшло у Васі?

Складно?) Допоможе додаткова формулаіз завдання 2.

Відповіді (безладно): 7, 3240, 6.

Якщо Вам подобається цей сайт...

До речі, у мене є ще кілька цікавих сайтів для Вас.)

Можна потренуватися у вирішенні прикладів та дізнатися свій рівень. Тестування з миттєвою перевіркою. Вчимося – з інтересом!)

можна познайомитися з функціями та похідними.

ЧИСЛОВІ НАСЛІДКИ VI

§ 144. Сума членів арифметичної прогресії

Розповідають, що одного разу вчитель початкової школи, Бажаючи зайняти клас на тривалий час самостійною роботою, дав дітям «важке» завдання - обчислити суму всіх натуральних чисел від 1 до 100:

1 + 2 + 3 + 4 + ... + 100.

Один із учнів моментально запропонував рішення. Ось воно.:

1+2 +3+... + 98 +99+ 100 = (1 + 100) + (2 + 99) + (3 + 98) + ... +(49 + 52)+ (50 + 51) =
= 101 + 101 + . . . + 101 + 101 = 101 50 = 5050.
50 разів

Це був Карл Гаусс, який згодом став одним із найзнаменитіших математиків світу.

*Подібний випадок з Гауссом дійсно мав місце. Однак тут він значно спрощений. Запропоновані вчителем числа були п'ятизначними та становили арифметичну прогресію із тризначною різницею.

Ідею такого рішення можна використовувати для знаходження суми членів будь-якої арифметичної прогресії.

Лемма.Сума двох членів кінцевої арифметичної прогресії, рівновіддалених від кінців, дорівнює сумі крайніх членів.

Наприклад, у кінцевій арифметичній прогресії

1, 2, 3.....98, 99, 100

члени 2 і 99, 3 і 98, 4 і 97 тощо є рівновіддаленими від кінців цієї прогресії. Тому їх суми 2 + 99, 3 + 98, 4 + 97 дорівнюють сумі крайніх членів 1 + 100.

Доказ леми. Нехай у кінцевій арифметичній прогресії

a 1 , a 2 , ..., a n - 1 , a n

два якихось члени однаково віддалені від кінців. Припустимо, що один із них є k -й член зліва, тобто a k , а інший - k -й член праворуч, тобто a n -k+ 1 . Тоді

a k + a n -k+ 1 =[a 1 + (k - 1)d ] + [a 1 + (п - k )d ] = 2a 1 + (n - 1)d .

Сума крайніх членів даної прогресії дорівнює

a 1 + a n = a 1 + [a 1 + (n - 1)d ] = 2a 1 + (n - 1)d .

Таким чином,

a k + a n -k+ 1 = a 1 + a n

що і потрібно було довести.

Використовуючи доведену лему, легко отримати загальну формулу для суми п членів будь-якої арифметичної прогресії.

S n = a 1 +a 2 + ...+ a n - 1 + a n

S n = a n + a n - 1 + ... + a 2 + a 1 .

Складаючи ці дві рівності почленно, отримуємо:

2S n = (a 1 +a n ) + (a 2 +a n - 1)+...+(a n - 1 +a 2) + (a n +a 1)

a 1 +a n = a 2 +a n - 1 = a 3 +a n - 2 =... .

2S n = n (a 1 +a n ),

Сума членів кінцевої арифметичної прогресії дорівнює добутку напівсуми крайніх членів число всіх членів.

Зокрема,

Вправи

971. Знайти суму всіх непарних трицифрових чисел.

972. Скільки ударів зроблять годинник протягом доби, якщо він відбиває лише число цілих годинників?

973. Чому дорівнює сума перших п чисел натурального ряду?

974. Вивести формулу довжини шляху, пройденого тілом за рівномірно прискореного руху:

де v 0 - початкова швидкість м/сек , а - прискорення в м/сек 2 , t - час руху в сік.

975. Знайти суму всіх нескоротних дробів із знаменником 3, укладених між цілими позитивними числами т і п (т< п ).

976. Робочий обслуговує 16 ткацьких верстатів, що працюють автоматично. Продуктивність кожного верстата а м/год. Робочий увімкнув перший верстат у 7 год, а кожен наступний на 5 хвпізніше попереднього. Дізнатися про вироблення в метрах за перші 2 годроботи.

977. Розв'язати рівняння:

а) 1+7+13+...+ х = 280;

б) ( х + 1) + (х + 4) + (х + 7) +...+ (х + 28) = 155

978. З 1 по 12 липня включно температура повітря щодня піднімалася в середньому на 1/2 градуси. Знаючи, що середня, температура за цей час дорівнювала 18 3 / 4 градуси, визначити, якою була температура повітря 1 липня.

979. Знайти арифметичну прогресію, яка має середню арифметичну п перших членів за будь-якого п і їх числу.

980. Знайти суму перших двадцяти членів арифметичної прогресії, у якій

a 6 + a 9 + a 12 + a 15 = 20.

Тип уроку:Вивчення нового матеріалу.

Цілі уроку:

• розширення та поглиблення уявлень учнів про завдання, які вирішуються з використанням арифметичної прогресії; організація пошукової діяльностіучнів під час виведення формули суми перших n членів арифметичної прогресії;
• розвиток умінь самостійно набувати нових знань, використовувати для досягнення поставленого завдання вже отримані знання;
• вироблення бажання та потреби узагальнювати отримані факти, розвиток самостійності.

Завдання:

• узагальнити та систематизувати наявні знання на тему “Арифметична прогресія”;
• вивести формули для обчислення суми n перших членів арифметичної прогресії;
• навчити застосовувати отримані формули під час вирішення різних завдань;
• звернути увагу учнів на порядок дій при знаходженні значення числового виразу.

Обладнання:

• картки із завданнями для роботи в групах та парах;
• оцінний лист;
• презентація"Арифметична прогресія".

I. Актуалізація опорних знань.

1. Самостійна роботау парах.

1-й варіант:

Дайте визначення арифметичної прогресії. Запишіть рекурентну формулу, за допомогою якої задається арифметична прогресія. Привіт приклад арифметичної прогресії та вкажіть її різницю.

2-й варіант:

Запишіть формулу n члена арифметичної прогресії. Знайдіть 100-й член арифметичної прогресії ( a n}: 2, 5, 8 …
У цей час двоє учнів на звороті дошки готують відповіді на ці ж питання.
Учні оцінюють роботу партнера, звіряючи з дошкою. (листочки з відповідями здають).

2. Ігровий момент.

Завдання 1.

Вчитель.Я задумала деяку арифметичну прогресію. Поставте мені тільки два питання, щоб після відповідей ви швидко змогли б назвати 7-й член цієї прогресії. (1, 3, 5, 7, 9, 11, 13, 15…)

Запитання учнів.

1. Чому дорівнює шостий член прогресії і чому дорівнює різниця?
2. Чому дорівнює восьмий член прогресії і чому дорівнює різниця?

Якщо питань більше не піде, то вчитель може стимулювати їх - "заборона" на d (різницю), тобто не дозволяється запитувати чому дорівнює різниця. Можна поставити запитання: чому дорівнює 6-й член прогресії і чому дорівнює 8-й член прогресії?

Завдання 2.

На дошці записано 20 чисел: 1, 4, 7 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58.

Вчитель стоїть спиною до дошки. Учні називають номер числа, а вчитель миттєво називає саме число. Поясніть, як це мені вдається?

Вчитель пам'ятає формулу n-го члена a n = 3n - 2і, підставляючи значення n, знаходить відповідні значення a n.

ІІ. Постановка навчальної задачі.

Пропоную вирішити старовинне завдання, що відноситься до II тисячоліття до нашої ери, знайдену в єгипетських папірусах.

Завдання:“Нехай тобі сказано: розділи 10 заходів ячменю між 10 людьми, різниця між кожною людиною та її сусідом дорівнює 1/8 міри”.

• Як це завдання пов'язані з темою арифметична прогресія? (Кожен наступний отримує на 1/8 міри більше, значить різницю d=1/8, 10 чоловік, отже n=10.)
• А що, на вашу думку, означає число 10 заходів? (Сума всіх членів прогресії.)
• Що ще необхідно знати, щоб було легко і просто поділити ячмінь згідно з умовою завдання? (Перший член прогресії.)

Завдання уроку- Отримання залежності суми членів прогресії від їх числа, першого члена і різниці, і перевірка того, чи правильно в давнину вирішували поставлене завдання.

Перш ніж зробити висновок формули, подивимося, як вирішували завдання давні єгиптяни.

А вирішували її так:

1) 10 заходів: 10 = 1 міра - середня частка;
2) 1 міра ∙ = 2 міри – подвоєна середнячастка.
Подвоєна середнячастка – це сума часток 5-го та 6-го чоловік.
3) 2 міри – 1/8 міри = 1 7/8 міри – подвоєна частка п'ятої особи.
4) 17/8: 2 = 5/16 - частка п'ятого; і так далі можна знайти частку кожної попередньої та наступної людини.

Отримаємо послідовність:

ІІІ. Вирішення поставленого завдання.

1. Робота у групах

Перша група:Знайти суму 20 послідовних натуральних чисел: S 20 =(20+1)∙10 =210.

У загальному вигляді

Друга група:Знайти суму натуральних чисел від 1 до 100 (Легенда про маленького Гауса).

S 100 = (1+100) ∙ 50 = 5050

Висновок:

ІІІ-я група:Знайти суму натуральних чисел від 1 до 21.

Рішення: 1+21=2+20=3+19=4+18…

Висновок:

IV-я група:Знайти суму натуральних чисел від 1 до 101.

Висновок:

Цей спосіб вирішення розглянутих завдань називається “Метод Гаусса”.

2. Кожна група представляє розв'язання задачі на дошці.

3. Узагальнення запропонованих рішень для довільної арифметичної прогресії:

a 1 , a 2 , a 3 ,…, a n-2 , a n-1 , a n .
S n =a 1 + a 2 + a 3 + a 4 +…+ a n-3 + an-2 + an-1 + an .

Знайдемо цю суму розмірковуючи аналогічно:

4. Вирішили ми поставлене завдання?(Так.)

IV. Первинне осмислення та застосування отриманих формул під час вирішення завдань.

1. Перевірка розв'язання старовинного завдання за формулою.

2. Застосування формули під час вирішення різних задач.

3. Вправи формування вміння застосування формули під час вирішення задач.

А) №613

Дано: ( а n) -арифметична прогресія;

(а n): 1, 2, 3, …, 1500

Знайти: S 1500

Рішення: , а 1 = 1, а 1500 = 1500

Б) Дано: ( а n) -арифметична прогресія;
(а n): 1, 2, 3, …
S n = 210

Знайти: n
Рішення:

V. Самостійна робота із взаємоперевіркою.

Денис вступив на роботу кур'єром. У перший місяць його зарплата склала 200 рублів, кожен наступний вона підвищувалася на 30 рублів. Скільки всього він заробив за рік?

Дано: ( а n) -арифметична прогресія;
а 1 = 200, d = 30, n = 12
Знайти: S 12
Рішення:

Відповідь: 4380 рублів отримав Денис протягом року.

VI. Інструктаж за домашнім завданням.

1. п. 4.3 - вивчити висновок формули.
2. №№ 585, 623 .
3. Скласти завдання, яке вирішувалося б з використанням формули суми n перших членів арифметичної прогресії.

VII. Підбиття підсумків уроку.

1. Оцінний лист

2. Продовжи речення

• Сьогодні на уроці я дізнався...
• Вивчені формули …
• Я вважаю що …

3. Чи зможеш знайти суму чисел від 1 до 500? Яким методом вирішуватимеш це завдання?

Список літератури.

1. Алгебра, 9 клас. Підручник для загальноосвітніх установ. За ред. Г.В. Дорофєєва.М.: "Освіта", 2009.

При вивченні алгебри в загальноосвітній школі(9 клас) однією з важливих тем є вивчення числових послідовностей, до яких відносяться прогресії – геометрична та арифметична. У цій статті розглянемо арифметичну прогресію та приклади з рішеннями.

Що являє собою арифметична прогресія?

Щоб це зрозуміти, необхідно дати визначення розглянутої прогресії, а також навести основні формули, які будуть використані при вирішенні завдань.

Арифметична чи алгебраїчна прогресія - це такий набір упорядкованих раціональних чисел, кожен член якого відрізняється від попереднього на певну постійну величину. Ця величина називається різницею. Тобто, знаючи будь-який член упорядкованого ряду чисел та різницю, можна відновити всю арифметичну прогресію.

Наведемо приклад. Наступна послідовність чисел буде арифметичною прогресією: 4, 8, 12, 16, ..., оскільки різниця в цьому випадку дорівнює 4 (8 - 4 = 12 - 8 = 16 - 12). А ось набір чисел 3, 5, 8, 12, 17 вже не можна віднести до виду прогресії, що розглядається, оскільки різниця для нього не є постійною величиною (5 - 3 ≠ 8 - 5 ≠ 12 - 8 ≠ 17 - 12).

Важливі формули

Наведемо тепер основні формули, які знадобляться вирішення завдань з використанням арифметичної прогресії. Позначимо символом a n n член послідовності, де n - ціле число. Різницю позначимо латинською літерою d. Тоді справедливі такі вирази:

1. Для визначення значення n-го члена підійде формула: n = (n-1) * d + a 1 .
2. Для визначення суми перших n доданків: S n = (a n +a 1) * n/2.

Щоб зрозуміти будь-які приклади арифметичної прогресії з рішенням у 9 класі, достатньо запам'ятати ці дві формули, оскільки на їх використанні будуються будь-які завдання типу, що розглядається. Також слід пам'ятати, що різниця прогресії визначається за формулою: d = a n - a n-1 .

Приклад №1: знаходження невідомого члена

Наведемо простий приклад арифметичної прогресії і формул, які необхідно використовувати для вирішення.

Нехай дана послідовність 10, 8, 6, 4, ..., необхідно знайти п'ять членів.

З умови завдання вже випливає, що перші 4 доданки відомі. П'яте можна визначити двома способами:

1. Обчислимо для початку різницю. Маємо: d = 8 – 10 = -2. Аналогічним чином можна було взяти будь-які два інших члени, що стоять поряд один з одним. Наприклад, d = 4 – 6 = -2. Оскільки відомо, що d = a n - a n-1 тоді d = a 5 - a 4 , звідки отримуємо: a 5 = a 4 + d. Підставляємо відомі значення: a 5 = 4+(-2) = 2.
2. Другий спосіб також вимагає знання різниці аналізованої прогресії, тому спочатку потрібно визначити її, як показано вище (d = -2). Знаючи, що перший член a 1 = 10, скористаємося формулою для числа n послідовності. Маємо: a n = (n – 1) * d + a 1 = (n – 1) * (-2) + 10 = 12 – 2 * n. Підставляючи останній вираз n = 5, отримуємо: a 5 = 12-2 * 5 = 2.

Як видно, обидва способи рішення привели до одного і того ж результату. Зазначимо, що у цьому прикладі різниця d прогресії є негативною величиною. Такі послідовності називаються спадними, оскільки кожен наступний член менший за попередній.

Приклад №2: різниця прогресії

Тепер ускладнимо трохи завдання, наведемо приклад, як

Відомо, що деякий 1-й член дорівнює 6, а 7-й член дорівнює 18. Необхідно знайти різницю і відновити цю послідовність до 7 члена.

Скористаємося формулою визначення невідомого члена: a n = (n - 1) * d + a 1 . Підставимо до неї відомі дані з умови, тобто числа a 1 і a 7 маємо: 18 = 6 + 6 * d. З цього виразу можна легко вирахувати різницю: d = (18 - 6) / 6 = 2. Таким чином, відповіли на першу частину завдання.

Щоб відновити послідовність до 7 члена, слід скористатися визначенням прогресу алгебри, тобто a 2 = a 1 + d, a 3 = a 2 + d і так далі. У результаті відновлюємо всю послідовність: a 1 = 6, a 2 = 6 + 2 = 8, a 3 = 8 + 2 = 10, a 4 = 10 + 2 = 12, a 5 = 12 + 2 = 14, a 6 = 14 + 2 = 16, а 7 = 18.

Приклад №3: складання прогресії

Ускладнимо ще сильніша умова завдання. Тепер необхідно відповісти на питання, як шукати арифметичну прогресію. Можна навести наступний приклад: дані два числа, наприклад, - 4 і 5. Необхідно скласти алгебраїчну прогресію так, щоб між цими містилося ще три члени.

Перш ніж починати вирішувати це завдання, необхідно зрозуміти, яке місце займатимуть задані числа у майбутній прогресії. Оскільки між ними будуть ще три члени, тоді a 1 = -4 і a 5 = 5. Встановивши це, переходимо до завдання, яке аналогічне попередньому. Знову для n-го члена скористаємося формулою, отримаємо: a 5 = a 1 + 4*d. Звідки: d = (a 5 – a 1)/4 = (5 – (-4)) / 4 = 2,25. Тут набули не ціле значення різниці, проте воно є раціональним числом, Тому формули для алгебраїчної прогресії залишаються тими самими.

Тепер додамо знайдену різницю до a 1 і відновимо члени прогресії. Отримуємо: a 1 = - 4, a 2 = - 4 + 2,25 = - 1,75, a 3 = -1,75 + 2,25 = 0,5, a 4 = 0,5 + 2,25 = 2,75, a 5 = 2,75 + 2,25 = 5, що збіглося з умовою задачі.

Приклад №4: перший член прогресії

Продовжимо наводити приклади арифметичної прогресії із рішенням. У всіх попередніх завданнях було відоме перше число прогресії алгебри. Тепер розглянемо завдання іншого типу: нехай дані два числа, де a 15 = 50 і a 43 = 37. Необхідно знайти, з якого числа починається ця послідовність.

Формули, якими користувалися досі, припускають знання a 1 і d. За умови завдання про ці числа нічого невідомо. Проте випишемо вирази для кожного члена, про який є інформація: a 15 = a 1 + 14 * d і a 43 = a 1 + 42 * d. Отримали два рівняння, у яких 2 невідомі величини (a 1 та d). Це означає, що завдання зводиться до розв'язання системи лінійних рівнянь.

Вказану систему найпростіше вирішити, якщо виразити в кожному рівнянні a 1 , а потім порівняти отримані вирази. Перше рівняння: a 1 = a 15 – 14*d = 50 – 14*d; друге рівняння: a 1 = a 43 - 42 * d = 37 - 42 * d. Прирівнюючи ці вирази, отримаємо: 50 – 14*d = 37 – 42*d, звідки різниця d = (37 – 50) / (42 – 14) = – 0,464 (наведено лише 3 знаки точності після коми).

Знаючи d, можна скористатися будь-яким із 2 наведених вище виразів для a 1 . Наприклад, першим: a 1 = 50 – 14 * d = 50 – 14 * (- 0,464) = 56,496.

Якщо виникають сумніви в отриманому результаті, можна його перевірити, наприклад, визначити член прогресії, який заданий в умові. Отримаємо: a 43 = a 1 + 42*d = 56,496 + 42*(-0,464) = 37,008. Невелика похибка пов'язані з тим, що з обчисленнях використовувалося округлення до тисячних часток.

Приклад №5: сума

Тепер розглянемо кілька прикладів із рішеннями на суму арифметичної прогресії.

Нехай дано числова прогресія наступного виду: 1, 2, 3, 4, ...,. Як розрахувати суму 100 цих чисел?

Завдяки розвитку комп'ютерних технологійможна це завдання вирішити, тобто послідовно скласти всі числа, що обчислювальна машина зробить відразу ж, як людина натисне клавішу Enter. Однак завдання можна вирішити в умі, якщо звернути увагу, що представлений ряд чисел є алгебраїчною прогресією, причому її різниця дорівнює 1. Застосовуючи формулу для суми, отримуємо: S n = n * (a 1 + an) / 2 = 100 * (1 + 100)/2 = 5050.

Цікаво відзначити, що це завдання носить назву "гаусової", оскільки в початку XVIIIстоліття знаменитий німецький ще у віці всього 10 років, зміг вирішити її в умі за кілька секунд. Хлопчик не знав формули для суми алгебраїчної прогресії, але він помітив, що якщо складати попарно числа, що знаходяться на краях послідовності, то завжди виходить один результат, тобто 1 + 100 = 2 + 99 = 3 + 98 = ..., а оскільки цих сум буде рівно 50 (100/2), то для отримання правильної відповіді достатньо помножити 50 на 101.

Приклад №6: сума членів від n до m

Ще одним типовим прикладом суми арифметичної прогресії є наступний: дано такий чисел ряд: 3, 7, 11, 15, ..., потрібно знайти, чому дорівнюватиме сума його членів з 8 по 14.

Завдання вирішується двома способами. Перший передбачає знаходження невідомих членів з 8 по 14, а потім їх послідовне підсумовування. Оскільки доданків небагато, такий спосіб не є досить трудомістким. Проте пропонується вирішити це завдання другим методом, який є більш універсальним.

Ідея полягає в отриманні формули для суми прогресу алгебри між членами m і n, де n > m - цілі числа. Випишемо для обох випадків два вирази для суми:

1. S m = m*(a m + a 1)/2.
2. S n = n*(a n + a 1)/2.

Оскільки n > m, то очевидно, що 2 сума включає першу. Останній висновок означає, що якщо взяти різницю між цими сумами, і додати до неї член a m (у разі взяття різниці він віднімається із суми S n), то отримаємо необхідну відповідь на завдання. Маємо: S mn = S n - S m + am = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am = a 1 * (n - m) / 2 + an * n/2+am* (1- m/2). У цей вираз необхідно підставити формули для a n і a m. Тоді отримаємо: S mn = a 1 * (n - m) / 2 + n * (a 1 + (n - 1) * d) / 2 + (a 1 + (m - 1) * d) * (1 - m / 2) = a 1 * (n - m + 1) + d * n * (n - 1) / 2 + d * (3 * m - m 2 - 2) / 2.

Отримана формула є дещо громіздкою, проте сума S mn залежить лише від n, m, a 1 та d. У нашому випадку a 1 = 3, d = 4, n = 14, m = 8. Підставляючи ці числа отримаємо: S mn = 301.

Як видно з наведених рішень, всі завдання ґрунтуються на знанні виразу для n-го члена та формули для суми набору перших доданків. Перед тим як розпочати вирішення будь-якого з цих завдань, рекомендується уважно прочитати умову, ясно зрозуміти, що потрібно знайти, і лише потім приступати до вирішення.

Ще одна порада полягає у прагненні до простоти, тобто якщо можна відповісти на питання, не застосовуючи складні математичні викладки, то необхідно чинити саме так, оскільки в цьому випадку ймовірність припуститися помилки менше. Наприклад, у прикладі арифметичної прогресії з рішенням №6 можна було б зупинитися на формулі S mn = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am і розбити загальне завдання на окремі підзадачі (у разі спочатку знайти члени an і am).

Якщо виникають сумніви в отриманому результаті, рекомендується перевіряти, як це було зроблено в деяких наведених прикладах. Як знаходити арифметичну прогресію, з'ясували. Якщо розібратися, це не так складно.