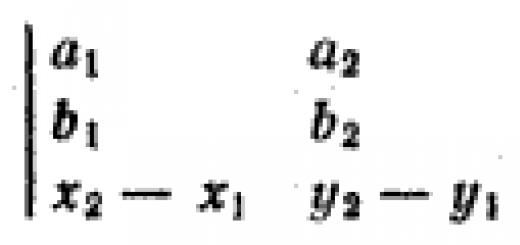Градієнтом функціїу точці називається вектор, координати якого рівні відповідним приватним похідним і позначається.

Якщо розглянути одиничний вектор e=(), то згідно з формулою (3) похідна за напрямом є скалярний добуток градієнта та одиничного вектора, що задає напрямок. Відомо, що скалярний добуток двох векторів максимально, якщо вони однаково спрямовані. Отже, градієнт функції у цій точці характеризує напрям і величину максимального зростання функції у цій точці.

Теорема . Якщо функція диференційована й у точці М 0 величина градієнта відмінна від нуля, то градієнт перпендикулярний лінії рівня, що проходить через дану точку і направлений у бік зростання функції при цьому

ВИСНОВОК: 1)Похідна функції у точці за напрямом, що визначається градієнтом цієї функції у зазначеній точці, має максимальне значення порівняно з похідною у цій точці за будь-яким іншим напрямком.

• 2) Значення похідної функції у напрямку, яке визначає градієнт цієї функції у цій точці, одно.
• 3) Знаючи градієнт функції у кожній точці, можна з деякою похибкою будувати лінії рівня. Почнемо з точки М0. Збудуємо градієнт у цій точці. Задамо напрямок, перпендикулярний градієнту. Побудуємо малу частину лінії рівня. Розглянемо близьку точку М 1 побудуємо градієнт у ній і так далі.

Концепція похідною за напрямом розглядається для функцій двох та трьох змінних. Щоб зрозуміти зміст похідної за напрямом, потрібно порівняти похідні за визначенням

Отже,

Тепер можемо знайти похідну за даною функцією за її формулою:

А зараз – домашнє завдання. У ньому дана функція не трьох, а лише двох змінних, але дещо інакше заданий напрямний вектор. Так що доведеться знову повторити векторну алгебру .

приклад 2.Знайти похідну функції у точці M0 (1; 2) за напрямом вектора , де M1 - точка з координатами (3; 0).

Вектор, що задає напрямок похідної, може бути дано і в такій формі, як у наступному прикладі - у вигляді розкладання по орт координатних осейале ця добре знайома тема з самого початку векторної алгебри.

приклад 3.Знайти похідну функції у точці M0 (1; 1; 1) за напрямом вектора.

Рішення. Знайдемо напрямні косинуси вектора

Знайдемо приватні похідні функції у точці M0 :

Отже, можемо визначити похідну за напрямом цієї функції за її формулою:

.

Градієнт функції

Градієнт функції кількох змінних у точці M0 характеризує напрямок максимального зростання цієї функції в точці M0 та величину цього максимального зростання.

Як знайти градієнт?

Потрібно визначити вектор, проекціями якого на осі координатє значення приватних похідних, , цієї функції у відповідній точці:

.

Тобто, має вийти подання вектора по ортам координатних осей, у якому кожен орт множиться відповідна його осі приватна похідна.

Градієнт функції- Векторна величина, знаходження якої пов'язане з визначенням приватних похідних функції. Напрямок градієнта вказує шлях якнайшвидшого зростання функції від однієї точки скалярного поля до іншої.

Інструкція

1. Для вирішення задачі на градієнт функції застосовуються способи диференціального обчислення, а саме знаходження приватних похідних першого порядку за трьома змінними. При цьому передбачається, що сама функція і всі її похідні приватні володіють властивістю безперервності в області визначення функції.

2. Градієнт – це вектор, напрямок якого вказує напрямок максимально стрімкого зростання функції F. Для цього на графіку вибираються дві точки M0 і M1, які є кінцями вектора. Розмір градієнта дорівнює швидкості зростання функції від точки M0 до точки M1.

3. Функція диференційована у всіх точках цього вектора, отже, проекціями вектора на координатних осях є всі її похідні. Тоді формула градієнта виглядає подальшим чином: grad = (? F /? x) i + (? F/? y) j + (? F/? z) k, де i, j, k - координати одиничного вектора. Інакше кажучи, градієнт функції – це вектор, координатами якого є її приватні похідні grad F = (?F/?х, ?F/?y, ?F/?z).

4. Приклад1.Нехай задана функція F = sin(х z?)/y. Потрібно виявити її градієнт у точці (?/6, 1/4, 1).

5. Рішення. Визначте приватні похідні за будь-якою змінною: F'_х = 1/y соs(х z?) z?; F'_y = sin(х z?) (-1) 1/(y?); 1/y соs(х z?) 2 х z.

6. Підставте знамениті значення координат точки: F'_x = 4 соs (? / 6) = 2? 3; F'_y = sin(?/6) (-1) 16 = -8; F'_z = 4 соs(?/6) 2?/6 = 2?/?3.

7. Застосуйте формулу градієнта функції: grad F = 2? 3 i - 8 j + 2? /? 3 k.

8. Приклад2. Виявіть координати градієнта функції F = y arctg (z/x) у точці (1, 2, 1).

9. Рішення. F'_х = 0 аrсtg (z/х) + y (аrсtg(z/х))'_х = y 1/(1 + (z/х)?) (-z/х?) = -y z/ (х? (1 + (z/х)?)) = -1; (аrсtg(z/х))'_z = y 1/(1 + (z/х)?) 1/х = y/(х (1 + (z/х)?)) = 1.grad = (- 1,? / 4, 1).

Градієнт скалярного поля є величиною векторної. Таким чином, для його знаходження потрібно визначити всі компоненти відповідного вектора, виходячи з знань про поділ скалярного поля.

Інструкція

1. Прочитайте у підручнику з вищої математики, що є градієнтом скалярного поля. Як відомо, дана векторна величина має напрямок, що характеризується максимальною швидкістю спаду скалярної функції. Такий толк даної векторної величини обґрунтовується виразом визначення її компонент.

2. Пам'ятайте, кожен вектор визначається величинами його компонент. Компоненти вектора є реально проекціями цього вектора ту чи іншу координатну вісь. Таким чином, якщо розглядається тривимірний простір, то вектор має мати три компоненти.

3. Запишіть, як визначаються компоненти вектора, який є градієнтом певного поля. Вся координат такого вектора дорівнює похідної скалярного потенціалу по змінній, координата якої розраховується. Тобто, якщо необхідно визначити "іксову" компоненту вектора градієнта поля, то потрібно продиференціювати скалярну функцію по змінній "ікс". Зверніть увагу, що похідна має бути приватною. Це означає, що з диференціюванні інші змінні, які у ньому, треба вважати константами.

4. Напишіть вираз для скалярного поля. Як відомо, цей термін має на увазі кожного лише скалярну функцію декількох змінних, що є також скалярними величинами. Число змінних скалярної функції обмежено розмірністю простору.

5. Продиференціюйте окремо скалярну функцію за будь-якою змінною. В результаті у вас вийде три нові функції. Впишіть будь-яку функцію для вектора градієнта скалярного поля. Кожна з отриманих функцій є показником при одиничному векторі даної координати. Таким чином, фінальний вектор градієнта має виглядати як багаточлен із показниками у вигляді похідних функції.

При розгляді питань, що включають уявлення градієнта, частіше кожного функції сприймають як скалярні поля. Отже слід запровадити відповідні позначення.

Вам знадобиться

• - Буман;
• - Ручка.

Інструкція

1. Нехай функція задається трьома аргументами u = f (x, y, z). Приватну похідну функції, наприклад, х, визначають як похідну з цього доводу, отриману при фіксуванні інших доводів. Для решти аргументів подібно. Позначення приватної похідної записується як: дf/дх = u’x …

2. Повний диференціал дорівнюватиме du=(дf/дх)dx+ (дf/дy)dy+(дf/дz)dz.Приватні похідні можна розуміти, як похідні за напрямами координатних осей. Відтак виникає питання про знаходження похідної за напрямом заданого вектора s у точці M(x, y, z) (не забувайте, що напрямок задає одиничний вектор-орт s^o). При цьому вектор-диференціал доводів (dx, dy, dz)=(дscos(альфа), дsсоs(бета), дsсоs(гама)).

3. Розглядаючи вид повного диференціала du, можна зробити результат, що похідна по напрямку s в точці М дорівнює: (д/дs) | M = ((дf / дх) | |M) соs(бета) +((дf/дz)|M) соs(гама).Якщо s= s(sx,sy,sz), то напрямні косинуси (соs(альфа), соs(бета), соs( гамма)) обчислюються (див. рис.1а).

4. Визначення похідної за напрямом, вважаючи точку М змінної, можна переписати у вигляді скалярного добутку: (дu/дs)=((дf/дх, дf/дy,дf/дz), (соs(альфа), соs(бета), соs (Гама))) = (grad u, s ^ ​​o). Цей вираз буде об'єктивним для скалярного поля. Якщо легко розглядається функція, то gradf - це вектор, що має координати, що збігаються з приватними похідними f(x, y, z). дz)=)=(дf/дх)i+(дf/дy)j +(дf/дz)k. Тут (i, j, k) – орти координатних осей у прямокутній декартовій системі координат.

5. Якщо використовувати диференціальний вектор-оператор Гамільтона набла, то gradf можна записати, як збільшення цього вектора-оператора на скаляр f (див. рис. 1б). З погляду зв'язку gradf c похідної за напрямом, рівність (gradf, s^o)=0 допустимо, якщо ці вектори ортогональні. Отже gradf найчастіше визначають, як напрямок найшвидшого метаморфози скалярного поля. А з погляду диференціальних операцій (gradf – одна з них), властивості gradf точно повторюють властивості диференціювання функцій. Зокрема, якщо f=uv, gradf=(vgradu+u gradv).

Відео на тему

Градієнтце інструмент, що у графічних редакторах виконує заливку силуету плавним переходом одного кольору в інший. Градієнтможе надати силуету результату обсягу, імітувати освітлення, відблиски світла лежить на поверхні предмета чи результат заходу на задньому плані фотографии. Цей інструмент має широке використання, тому для обробки фотографій або створення ілюстрацій дуже значно навчиться ним користуватися.

Вам знадобиться

• Комп'ютер, графічний редактор Adobe Photoshop, Corel Draw, Paint.Net чи інший.

Інструкція

1. Відкрийте у програмі зображення чи зробіть нове. Зробіть силует або виділіть потрібну область на зображенні.

2. Увімкніть інструмент градієнта на панелі інструментів графічного редактора. Розмістіть курсор мишки на точку всередині виділеної області чи силуету, у якій розпочинатиметься 1-й колір градієнта. Натисніть та утримуйте ліву клавішу мишки. Переміщайте курсор у точку, де градієнт повинен перейти в кінцевий колір. Відпустіть ліву клавішу мишки. Виділений силует заповнить заливку градієнтом.

3. Градієнту можна встановити прозорість, кольори та їх співвідношення в певній точці заливки. Для цього відкрийте вікно редагування градієнта. Щоб відкрити вікно редагування у Photoshop – натисніть на прикладі градієнта в панелі «Параметри».

4. У вікні у вигляді прикладів відображаються доступні варіанти градієнтної заливки. Щоб відредагувати один з варіантів, виберіть його клацанням мишки.

5. У нижній частині вікна відображається приклад градієнта у вигляді широкої шкали, де розташовані повзунки. Повзунки позначають точки, у яких градієнт повинен мати задані коляції, а інтервалі між повзунками колір рівномірно переходить із заданого у першій точці до кольору 2-ї точки.

6. Повзунки, які розташовані у верхній частині шкали, задають прозорість градієнта. Щоб змінити прозорість, клацніть по необхідному повзунку. Під шкалою з'явиться поле, у яке введіть необхідний рівень прозорості у відсотках.

7. Повзунки в нижній частині шкали задають кольори градієнта. Клікнувши по одному з них, ви зможете віддати перевагу потрібний колір.

8. Градієнтможе мати кілька кольорів переходу. Щоб задати ще один колір - клацніть по вільному місцю на нижній частині шкали. На ній з'явиться ще один повзунок. Встановіть для нього необхідний колір. Шкала відобразить приклад градієнта із ще однією точкою. Ви можете пересувати повзунки, утримуючи їх за допомогою лівої кнопки мишки, щоб досягти потрібного поєднання.

9. Градієнтбувають декілька типів, які можуть надати форму плоским силуетам. Скажімо, щоб надати колу форму кулі застосовується радіальний градієнт, а щоб надати форму конуса - конусоподібний. Щоб надати поверхні ілюзію опуклості можна користуватися дзеркальним градієнтом, а ромбовидний градієнт може використовуватися для створення відблисків.

Відео на тему

Відео на тему

Визначення 1

Якщо кожної пари $(x,y)$ значень двох незалежних змінних із певної області ставиться у відповідність певне значення $z$, то кажуть, що $z$ є функцією двох змінних $(x,y)$. Позначення: $ z = f (x, y) $.

Розглянемо функцію $z=f(x,y)$, яка визначена у певній області у просторі $Oxy$.

Отже,

Визначення 3

Якщо для кожної трійки $(x,y,z)$ значень трьох незалежних змінних з певної області ставиться у відповідність певне значення $w$, то кажуть, що $w$ є функцією трьох змінних $(x,y,z)$ цій галузі.

Позначення:$ w = f (x, y, z) $.

Розглянемо функцію $w=f(x,y,z)$, яка визначена у певній області у просторі $Oxyz$.

Для заданої функції визначимо вектор, для якого проекціями на осі координат є значення приватних похідних заданої функції в деякій точці $\frac(\partial z)(\partial x); \frac(\partial z)(\partial y) $.

Визначення 4

Градієнтом заданої функції $w=f(x,y,z)$ називається вектор $\overrightarrow(gradw) $ наступного виду:

Теорема 3

Нехай у деякому скалярному полі $w=f(x,y,z)$ визначено поле градієнтів

\[\overrightarrow(gradw) =\frac(\partial w)(\partial x) \cdot \overrightarrow(i) +\frac(\partial w)(\partial y) \cdot \overrightarrow(j) +\frac (\partial w)(\partial z) \cdot \overrightarrow(k) .\]

Похідна $\frac(\partial w)(\partial s) $ у напрямку заданого вектора $\overrightarrow(s) $ дорівнює проекції вектора градієнта $\overrightarrow(gradw) $ на заданий вектор $\overrightarrow(s) $.

Приклад 4

Рішення:

Вираз для градієнта знаходимо за формулою

\[\overrightarrow(gradw) =\frac(\partial w)(\partial x) \cdot \overrightarrow(i) +\frac(\partial w)(\partial y) \cdot \overrightarrow(j) +\frac (\partial w)(\partial z) \cdot \overrightarrow(k) .\]

\[\frac(\partial w)(\partial x) = 2x;\frac(\partial w)(\partial y) =4y;\frac(\partial w)(\partial z) =2.\]

Отже,

\[\overrightarrow(gradw) =2x\cdot \overrightarrow(i) +4y\cdot \overrightarrow(j) +2\cdot \overrightarrow(k) .\]

Приклад 5

Визначити градієнт заданої функції

у точці $ M (1; 2; 1) $. Обчислити $\left(|\overrightarrow(gradz) |\right)_(M) $.

Рішення:

Вираз для градієнта у заданій точці знаходимо за формулою

\[\left(\overrightarrow(gradw) \right)_(M) =\left(\frac(\partial w)(\partial x) \right)_(M) \cdot \overrightarrow(i) +\left (\frac(\partial w)(\partial y) \right)_(M) \cdot \overrightarrow(j) +\left(\frac(\partial w)(\partial z) \right)_(M) \cdot \overrightarrow(k) .\]

Приватні похідні мають вигляд:

\[\frac(\partial w)(\partial x) =2x;\frac(\partial w)(\partial y) =4y;\frac(\partial w)(\partial z) =6z^(2) .\]

Похідні у точці $M(1;2)$:

\[\frac(\partial w)(\partial x) =2\cdot 1=2;\frac(\partial w)(\partial y) =4\cdot 2=8;\frac(\partial w)( \partial z) = 6 \ cdot 1 ^ (2) = 6.

Отже,

\[\left(\overrightarrow(gradw) \right)_(M) =2\cdot \overrightarrow(i) +8\cdot \overrightarrow(j) +6\cdot \overrightarrow(k) \]

\[\left(|\overrightarrow(gradw) |\right)_(M) =\sqrt(2^(2) +8^(2) +6^(2) ) =\sqrt(4+64+36 ) = \ sqrt (104).

Перерахуємо деякі властивості градієнта:

Похідна заданої функції в заданій точці у напрямку деякого вектора $\overrightarrow(s) $ має найбільше значення, якщо напрямок даного вектора $\overrightarrow(s) $ збігається з напрямком градієнта. У цьому дане найбільше значення похідної збігається з довжиною вектора градієнта, тобто. $|\overrightarrow(gradw) |$.

Похідна заданої функції у напрямку вектора, який перпендикулярний до вектора градієнта, тобто. $ \ overrightarrow (gradw) $, дорівнює 0. Так як $ \ varphi = \ frac (\ pi ) (2) $, то $ \ cos \ varphi = 0 $; отже, $\frac(\partial w)(\partial s) =|\overrightarrow(gradw) |\cdot \cos \varphi =0$.

Зі шкільного курсу математики відомо, що вектор на площині є спрямованим відрізком. Його початок та кінець мають по дві координати. Координати вектора розраховуються шляхом віднімання координат координат координат координат початку.

Поняття вектора може бути поширене і на n-мірний простір (замість двох координат буде nкоординат).

Градієнтом gradzфункцииz=f(х 1 , х 2 , …х n) називається вектор приватних похідних функції у точці, тобто. вектор з координат.

Можна довести, що градієнт функції характеризує напрямок якнайшвидшого зростання рівня функції у точці.

Наприклад, для функції z = 2х 1 + х 2 (див. малюнок 5.8) градієнт у будь-якій точці матиме координати (2; 1). Побудувати його на площині можна різними способами, взявши як початок вектора будь-яку точку. Наприклад, можна з'єднати точку (0; 0) з точкою (2; 1), або точку (1; 0) з точкою (3; 1), або точку (0; 3) з точкою (2; 4), або т .п. (Див. малюнок 5.8). Всі побудовані таким чином вектори матимуть координати (2 – 0; 1 – 0) = = (3 – 1; 1 – 0) = (2 – 0; 4 – 3) = (2; 1).

З малюнка 5.8 добре видно, що рівень функції зростає у напрямку градієнта, оскільки побудовані лінії рівня відповідають значенням рівня 4>3>2.

Малюнок 5.8 - Градієнт функції z = 2x1 + x2

Розглянемо інший приклад - функцію z = 1/(х 1 х 2). Градієнт цієї функції вже завжди буде однаковим у різних точках, оскільки його координати визначаються формулами (-1/(х 1 2 х 2); -1/(х 1 х 2 2)).

На рис. лінією).

Малюнок 5.9 - Градієнти функції z = 1/(х 1 х 2) у різних точках

Візьмемо, наприклад, точку (0,5; 1) і обчислимо градієнт у цій точці: (-1/(0,5 2 *1); -1/(0,5*1 2)) = (-4; - 2). Зауважимо, що точка (0,5; 1) лежить лінії рівня 1/(х 1 х 2) = 2, боz=f(0,5; 1) = 1/(0,5*1) = 2. Щоб зобразити вектор (-4; -2) малюнку 5.9, з'єднаємо точку (0,5; 1) з точкою (-3,5; -1), бо (-3,5 – 0,5; -1 - 1) = (-4; -2).

Візьмемо іншу точку тієї ж лінії рівня, наприклад, точку (1; 0,5) (z=f(1; 0,5) = 1/(0,5*1) = 2). Обчислимо градієнт у цій точці (-1/(1 2 *0,5); -1/(1*0,5 2)) = (-2; -4). Щоб зобразити його на малюнку 5.9, з'єднаємо точку (1; 0,5) з точкою (-1; -3,5), бо (-1 - 1; -3,5 - 0,5) = (-2; - 4).

Візьмемо ще одну точку на тій самій лінії рівня, але тільки тепер у непозитивній координатній чверті. Наприклад, точку (-0,5; -1) (z=f(-0,5; -1) = 1/((-1)*(-0,5)) = 2). Градієнт у цій точці дорівнюватиме (-1/((-0,5) 2 *(-1)); -1/((-0,5)*(-1) 2)) = (4; 2). Зобразимо його малюнку 5.9, з'єднавши точку (-0,5; -1) з точкою (3,5; 1), бо (3,5 – (-0,5); 1 – (-1)) = (4 2).

Слід звернути увагу, що у всіх трьох розглянутих випадках градієнт показує напрямок зростання рівня функції (у бік лінії рівня 1/(х 1 х 2) = 10 > 2).

Можна довести, що градієнт завжди перпендикулярний лінії рівня (поверхні рівня), що проходить через цю точку.

Екстремуми функції багатьох змінних

Визначимо поняття екстремумудля багатьох змінних.

Функція багатьох змінних f(X) має у точці Х(0) максимум (мінімум),якщо знайдеться така околиця цієї точки, що для всіх точок Х з цієї околиці виконуються нерівності f(X)f(X(0)) ().

Якщо ці нерівності виконуються як суворі, то екстремум називається сильним, а якщо ні, то слабким.

Зауважимо, що певний таким чином екстремум носить локальнийхарактер, оскільки ці нерівності виконуються лише з деякою околиці точки екстремуму.

Необхідною умовою локального екстремуму диференційованої функції z=f(х 1 , . . ., х n) у точці є рівність нулю всіх похідних приватних першого порядку в цій точці:
.

Крапки, у яких виконуються ці рівності, називаються стаціонарними.

Інакше необхідну умову екстремуму можна сформулювати так: у точці екстремуму градієнт дорівнює нулю. Можна довести і загальне твердження - у точці екстремуму звертаються у нуль похідні функції у всіх напрямах.

Стаціонарні точки мають бути піддані додатковим дослідженням - чи достатні умови існування локального екстремуму. І тому визначають знак диференціалу другого порядку. Якщо за будь-яких , не рівних одночасно нулю, він завжди негативний (позитивний), то функція має максимум (мінімум). Якщо може звертатися в нуль не тільки при нульових збільшеннях, то питання про екстремум залишається відкритим. Якщо може набувати як позитивних, так і негативних значень, то екстремуму в стаціонарній точці немає.

У загальному випадку визначення знака диференціала є досить складною проблемою, яку тут розглядати не будемо. Для функції двох змінних можна довести, що якщо у стаціонарній точці
, то екстремум є. При цьому знак другого диференціалу збігається зі знаком
, тобто. якщо
, то це максимум, а якщо
, то це мінімум. Якщо
, то екстремуму в цій точці немає, а якщо
, то питання про екстремум залишається відкритим.

Приклад 1. Знайти екстремуми функції
.

Знайдемо приватні похідні методом логарифмічного диференціювання.

ln z = ln 2 + ln (x + y) + ln (1 + xy) - ln (1 + x 2) - ln (1 + y 2)

Аналогічно
.

Знайдемо стаціонарні точки із системи рівнянь:

Таким чином, знайдено чотири стаціонарні точки (1; 1), (1; -1), (-1; 1) та (-1; -1).

Знайдемо приватні похідні другого порядку:

ln (z x `) = ln 2 + ln (1 - x 2) -2ln (1 + x 2)

Аналогічно
;
.

Так як
, знак виразу
залежить тільки від
. Зазначимо, що в обох цих похідних знаменник завжди позитивний, тому можна розглядати тільки знак чисельника, або навіть знак виразів х (х 2 - 3) і y (y 2 - 3). Визначимо його у кожній критичній точці та перевіримо виконання достатньої умови екстремуму.

Для точки (1; 1) отримаємо 1 * (1 2 - 3) = -2< 0. Т.к. произведение двух отрицательных чисел
> 0, а
< 0, в точке (1; 1) можно найти максимум. Он равен
= 2*(1 + 1)*(1 +1*1)/((1 +1 2)*(1 +1 2)) = = 8/4 = 2.

Для точки (1; -1) отримаємо 1 * (1 2 - 3) = -2< 0 и (-1)*((-1) 2 – 3) = 2 >0. Т.к. добуток цих чисел
< 0, в этой точке экстремума нет. Аналогично можно показать, что нет экстремума в точке (-1; 1).

Для точки (-1; -1) отримаємо (-1) * ((-1) 2 - 3) = 2> 0. Т.к. добуток двох позитивних чисел
> 0, а
> 0, у точці (-1; -1) можна знайти мінімум. Він дорівнює 2*((-1) + (-1))*(1 +(-1)*(-1))/((1 +(-1) 2)*(1 +(-1) 2) ) = -8/4 = = -2.

Знайти глобальниймаксимум або мінімум (найбільше чи найменше значення функції) дещо складніше, ніж локальний екстремум, оскільки ці значення можуть досягатися у стаціонарних точках, а й у межах області визначення. Дослідити поведінку функції на межі цієї галузі не завжди легко.