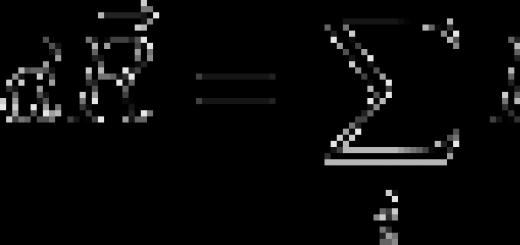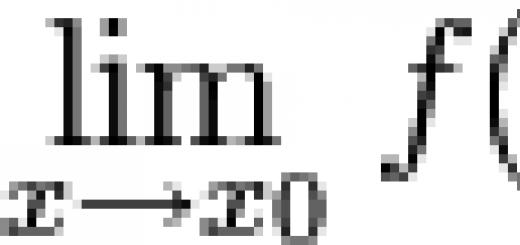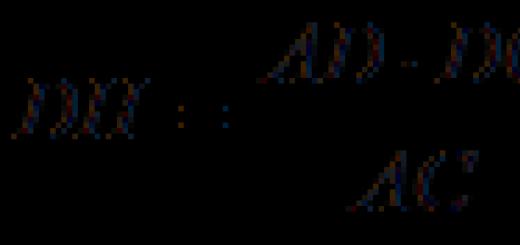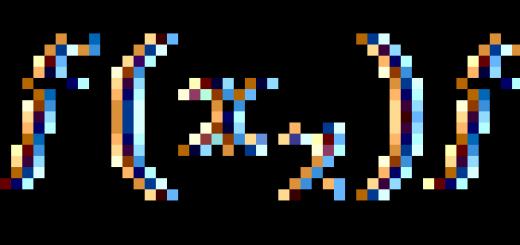\(\blacktriangleright\) Для того, щоб знайти найбільше / найменше значенняфункції на відрізку \(\) необхідно схематично зобразити графік функції на цьому відрізку.
У задачах з цієї підтеми це можна зробити за допомогою похідної: знайти проміжки зростання (\(f">0\) ) та спадання (\(f"<0\) ) функции, критические точки (где \(f"=0\) или \(f"\) не существует).

\(\blacktriangleright\) Не слід забувати, що найбільше/найменше значення функція може набувати не тільки у внутрішніх точках відрізка \(\) , а також на його кінцях.

\(\blacktriangleright\) Найбільше/найменше значення функції - це значення координати \(y=f(x)\) .

\(\blacktriangleright\) Похідна складної функції \(f(t(x))\) шукається за правилом: \[(\Large(f"(x)=f"(t)\cdot t"(x)))\]
\[\begin(array)(|r|c|c|) \hline & \text(Функція ) f(x) & \text(Похідна ) f"(x)\\ \hline \textbf(1) & c & 0\\&&\\ \textbf(2) & x^a & a\cdot x^(a-1)\\&&\\ \textbf(3) & \ln x & \dfrac1x\\&&\\ \ textbf(4) & \log_ax & \dfrac1(x\cdot \ln a)\\&&\\ \textbf(5) & e^x & e^x\\&&\\ \textbf(6) & a^x & a^x\cdot \ln a\\&&\\ \textbf(7) & \sin x & \cos x\\&&\\ \textbf(8) & \cos x & -\sin x\\ \hline \end(array) \quad \quad \quad \quad \begin(array)(|r|c|c|) \hline & \text(Функція ) f(x) & \text(Похідна ) f"(x) \\ \hline \textbf(9) & \mathrm(tg)\, x & \dfrac1(\cos^2 x)\\&&\\ \textbf(10) & \mathrm(ctg)\, x & -\ ,\dfrac1(\sin^2 x)\\&&\\ \textbf(11) & \arcsin x & \dfrac1(\sqrt(1-x^2))\\&&\\ \textbf(12) & \ arccos x & -\,\dfrac1(\sqrt(1-x^2))\\&&\\ \textbf(13) & \mathrm(arctg)\, x & \dfrac1(1+x^2)\\ &&\\ \textbf(14) & \mathrm(arcctg)\, x & -\,\dfrac1(1+x^2)\\ \hline \end(array)\]

Завдання 1 #2357

Рівень завдання: Рівний ЄДІ

Знайдіть найменше значення функції \(y = e^(x^2 - 4)\) на відрізку \([-10; -2]\) .

ОДЗ: \(x\) – довільний.

1) \

\ Отже, \(y" = 0\) при \(x = 0\) .

3) Знайдемо проміжки знаковості \(y"\) на аналізованому відрізку \([-10; -2]\) :

4) Ескіз графіка на відрізку \([-10; -2]\):

Таким чином, найменшого на \([-10; -2]\) значення функція досягає \(x = -2\) .

\ Разом: \(1\) - найменше значення функції \(y\) на \([-10; -2]\).

Відповідь: 1

Завдання 2 #2355

Рівень завдання: Рівний ЄДІ

\(y = \sqrt(2)\cdot\sqrt(x^2 + 1)\)на відрізку \([-1; 1]\).

ОДЗ: \(x\) – довільний.

1) \

Знайдемо критичні точки (тобто внутрішні точки області визначення функції, у яких її похідна дорівнює \(0\) або немає): \[\sqrt(2)\cdot\dfrac(x)(\sqrt(x^2 + 1)) = 0\qquad\Leftrightarrow\qquad x = 0\,.\]Похідна існує за будь-якого \(x\) .

2) Знайдемо проміжки знаковості \(y"\) :

3) Знайдемо проміжки знаковості \(y"\) на аналізованому відрізку \([-1; 1]\) :

4) Ескіз графіка на відрізку \([-1; 1]\):

Таким чином, найбільшого на \([-1; 1]\) значення функція досягає \(x = -1\) або \(x = 1\) . Порівняємо значення функції у цих точках.

\ Разом: \(2\) - найбільше значення функції \(y\) на \([-1; 1]\).

Відповідь: 2

Завдання 3 #2356

Рівень завдання: Рівний ЄДІ

Знайдіть найменше значення функції \(y = \cos 2x\) на відрізку \(\) .

ОДЗ: \(x\) – довільний.

1) \

Знайдемо критичні точки (тобто внутрішні точки області визначення функції, у яких її похідна дорівнює \(0\) або немає): \[-2\cdot \sin 2x = 0\qquad\Leftrightarrow\qquad 2x = \pi n, n\in\mathbb(Z)\qquad\Leftrightarrow\qquad x = \dfrac(\pi n)(2), n\in\mathbb(Z)\,.\]Похідна існує за будь-якого \(x\) .

2) Знайдемо проміжки знаковості \(y"\) :

(тут нескінченне число проміжків, у яких чергуються похідні знаки).

3) Знайдемо проміжки знаковості \(y"\) на аналізованому відрізку \(\) :

4) Ескіз графіка на відрізку \(\):

Таким чином, найменшого на \(\) значення функція досягає \(x = \dfrac(\pi)(2)\) .

\ Разом: \(-1\) - найменше значення функції \(y\) на \(\).

Відповідь: -1

Завдання 4 # 915

Рівень завдання: Рівний ЄДІ

Знайдіть найбільше значення функції

\(y = -\log_(17)(2x^2 - 2\sqrt(2)x + 2)\).

ОДЗ: \(2x^2 - 2\sqrt(2)x + 2 > 0\) . Вирішимо на ОДЗ:

1) Позначимо \(2x^2-2\sqrt(2)x+2=t(x)\) , тоді \(y(t)=-\log_(17)t\) .

Знайдемо критичні точки (тобто внутрішні точки області визначення функції, у яких її похідна дорівнює \(0\) або немає): \[-\dfrac(1)(\ln 17)\cdot\dfrac(4x-2\sqrt(2))(2x^2-2\sqrt(2)x+2) = 0qquad\Leftrightarrow\qquad 4x-2\sqrt(2) = 0\]- на ОДЗ, звідки знаходимо корінь \(x = \dfrac(\sqrt(2))(2)\). Похідна функції \(y\) не існує при \(2x^2-2\sqrt(2)x+2 = 0\) , але у даного рівняннянегативний дискримінант, отже, він не має рішень. Щоб знайти найбільше/найменше значення функції, потрібно зрозуміти, як схематично виглядає її графік.

2) Знайдемо проміжки знаковості \(y"\) :

3) Ескіз графіка:

Таким чином, найбільше значення функція досягає в \(x = \dfrac(\sqrt(2))(2)\) :

\(y\left(\dfrac(\sqrt(2))(2)\right) = -\log_(17)1 = 0\),

Разом: \ (0 \) - Найбільше значення функції \ (y \).

Відповідь: 0

Завдання 5 #2344

Рівень завдання: Рівний ЄДІ

Знайдіть найменше значення функції

\(y = \log_(3)(x^2 + 8x + 19)\).

ОДЗ: \(x^2 + 8x + 19> 0\) . Вирішимо на ОДЗ:

1) Позначимо \(x^2 + 8x + 19=t(x)\), тоді \(y(t)=\log_(3)t\).

Знайдемо критичні точки (тобто внутрішні точки області визначення функції, у яких її похідна дорівнює \(0\) або немає): \[\dfrac(1)(\ln 3)\cdot\dfrac(2x+8)(x^2 + 8x + 19) = 0qquad\Leftrightarrow\qquad 2x+8 = 0\]- На ОДЗ, звідки знаходимо корінь \ (x = -4 \). Похідна функції \(y\) не існує при \(x^2 + 8x + 19 = 0\), але у цього рівняння негативний дискримінант, отже, у нього немає рішень. Щоб знайти найбільше/найменше значення функції, потрібно зрозуміти, як схематично виглядає її графік.

2) Знайдемо проміжки знаковості \(y"\) :

3) Ескіз графіка:

Таким чином, \(x = -4\) – точка мінімуму функції \(y\) та найменше значення досягається в ній:

\(y(-4) = \log_(3)3 = 1\).

Разом: \ (1 \) - Найменше значення функції \ (y \) .

Відповідь: 1

Завдання 6 # 917

Рівень завдання: Складніше ЄДІ

Знайдіть найбільше значення функції

\(y = -e^((x^2 - 12x + 36 + 2\ln 2))\).

З практичної погляду найбільший інтерес представляє використання похідної знаходження найбільшого і найменшого значення функції. З чим це пов'язано? Максимізація прибутку, мінімізація витрат, визначення оптимального завантаження устаткування... Інакше кажучи, у багатьох сферах життя доводиться вирішувати завдання оптимізації будь-яких параметрів. А це є завдання на знаходження найбільшого і найменшого значення функції.

Слід зазначити, що найбільше і найменше значення функції зазвичай шукається на деякому інтервалі X , який є всією областю визначення функції або частиною області визначення. Сам інтервал X може бути відрізком, відкритим інтервалом , нескінченним проміжком.

У цій статті ми говоритимемо про знаходження найбільшого та найменшого значень явно заданої функціїоднієї змінної y = f (x).

Навігація на сторінці.

Найбільше та найменше значення функції – визначення, ілюстрації.

Стисло зупинимося на основних визначеннях.

Найбільшим значенням функції , що для будь-кого справедлива нерівність.

Найменшим значенням функції y=f(x) на проміжку X називають таке значення , що для будь-кого справедлива нерівність.

Ці визначення інтуїтивно зрозумілі: найбільше (найменше) значення функції – це найбільше (маленьке) значення на аналізованому інтервалі при абсцисі.

Стаціонарні точки– це значення аргументу, у яких похідна функції перетворюється на нуль.

Для чого нам стаціонарні точки при знаходженні найбільшого та найменшого значень? Відповідь це питання дає теорема Ферма. З цієї теореми випливає, що якщо функція, що диференціюється, має екстремум (локальний мінімум або локальний максимум) в деякій точці, то ця точка є стаціонарною. Таким чином, функція часто приймає своє найбільше (найменше) значення на проміжку X в одній зі стаціонарних точок цього проміжку.

Також часто найбільше та найменше значення функція може приймати у точках, у яких не існує перша похідна цієї функції, а сама функція визначена.

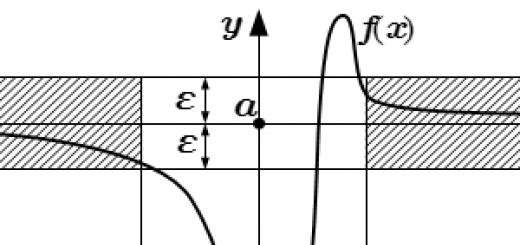
Відразу відповімо на одне з найпоширеніших питань на цю тему: "Чи завжди можна визначити найбільше (найменше) значення функції"? Ні не завжди. Іноді межі проміжку X збігаються з межами області визначення функції або інтервал X нескінченний. А деякі функції на нескінченності та на межах області визначення можуть набувати як нескінченно великі, так і нескінченно малі значення. У цих випадках нічого не можна сказати про найбільше та найменше значення функції.

Для наочності дамо графічну ілюстрацію. Подивіться малюнки – і багато проясниться.

На відрізку

На першому малюнку функція приймає найбільше (max y) і найменше (min y) значення в стаціонарних точках, що знаходяться всередині відрізка [-6; 6].

Розглянемо випадок, зображений другого малюнку. Змінимо відрізок на . У цьому прикладі найменше значення функції досягається в стаціонарній точці, а найбільше - у точці з абсцисою, що відповідає правій межі інтервалу.

На малюнку №3 граничні точки відрізка [-3;2] є абсцисами точок, що відповідають найбільшому та найменшому значенню функції.

На відкритому інтервалі

На четвертому малюнку функція приймає найбільше (max y ) і найменше (min y ) значення стаціонарних точках, що усередині відкритого інтервалу (-6;6) .

На інтервалі про найбільше значення ніяких висновків зробити не можна.

На нескінченності

У прикладі, представленому на сьомому малюнку, функція приймає найбільше значення (max y) у стаціонарній точці з абсцисою x=1, а найменше значення (min y) досягається на правій межі інтервалу. На мінус нескінченності значення функції асимптотично наближаються до y=3.

На інтервалі функція не досягає найменшого, ні найбільшого значення. При прагненні до x=2 праворуч значення функції прагнуть мінус нескінченності (пряма x=2 є вертикальною асимптотою), а при прагненні абсциси до плюс нескінченності, значення функції асимптотично наближаються до y=3 . Графічна ілюстрація цього прикладу наведено малюнку №8.

Алгоритм знаходження найбільшого та найменшого значення безперервної функції на відрізку.

Запишемо алгоритм, що дозволяє знаходити найбільше та найменше значення функції на відрізку.

1. Знаходимо область визначення функції та перевіряємо, чи міститься у ній весь відрізок .
2. Знаходимо всі точки, в яких не існує перша похідна і які містяться у відрізку (зазвичай такі точки збігаються у функцій з аргументом під знаком модуля і у статечних функційз дробно-раціональним показником). Якщо таких точок немає, переходимо до наступного пункту.
3. Визначаємо всі стаціонарні точки, що у відрізок . Для цього, прирівнюємо її до нуля, вирішуємо отримане рівняння і вибираємо відповідне коріння. Якщо стаціонарних точок немає або жодна з них не потрапляє у відрізок, переходимо до наступного пункту.
4. Обчислюємо значення функції у відібраних стаціонарних точках (якщо такі є), у точках, у яких не існує перша похідна (якщо такі є), а також при x=a та x=b .
5. З отриманих значень функції вибираємо найбільше і найменше - вони будуть шуканими найбільшим і найменшим значеннями функції відповідно.

Розберемо алгоритм при вирішенні прикладу на знаходження найбільшого та найменшого значення функції на відрізку.

приклад.

Знайти найбільше та найменше значення функції

• на відрізку;
• на відрізку [-4;-1].

Рішення.

Областью визначення функції є безліч дійсних чисел, крім нуля, тобто . Обидва відрізки потрапляють у область визначення.

Знаходимо похідну функції по:

Очевидно, похідна функції існує у всіх точках відрізків та [-4;-1].

Стаціонарні точки визначимо з рівняння. Єдиним дійсним коріннямє x=2. Ця стаціонарна точка потрапляє у перший відрізок.

Для першого випадку обчислюємо значення функції на кінцях відрізка та в стаціонарній точці, тобто при x=1, x=2 і x=4:

Отже, найбільше значення функції досягається при x=1 а найменше значення - При x = 2.

Для другого випадку обчислюємо значення функції лише на кінцях відрізка [-4;-1] (оскільки він не містить жодної стаціонарної точки):

Рішення.

Почнемо з області визначення функції. Квадратний тричлену знаменнику дробу не повинен звертатися до нуля:

Легко перевірити, що всі інтервали з умови завдання належать області визначення функції.

Продиференціюємо функцію:

Очевидно, похідна існує по всій області визначення функції.

Знайдемо стаціонарні точки. Похідна звертається в нуль при . Ця стаціонарна точка потрапляє в інтервали (-3; 1) та (-3; 2).

А тепер можна зіставити отримані у кожному пункті результати із графіком функції. Синіми пунктирними лініями позначені асимптоти.

На цьому можна закінчити із знаходженням найбільшого та найменшого значення функції. Алгоритми, розібрані у цій статті, дозволяють отримати результати при мінімумі дій. Однак буває корисно спочатку визначити проміжки зростання та зменшення функції і тільки після цього робити висновки про найбільше і найменше значення функції на якомусь інтервалі. Це дає більш ясну картину та суворе обґрунтування результатів.

Варіант 1. у

1. Графік функції у=f(x) зображений малюнку.

Вкажіть найбільше значення цієї функції 1

на відрізку [ a; b]. а 0 1 b х

1) 2,5; 2) 3; 3) 4; 4) 2.

https://pandia.ru/text/78/524/images/image003_127.gif" width="242" height="133 src="> 1) -4; 2) -2; 3) 4; 4) 2.

4. Функції у=f(x) задана на відрізку [ a; b]. у

На малюнку зображено графік її похідної

у=f ´(x). Досліджуйте на екстремуми 1 b

функцію у=f(x). У відповіді вкажіть кількість a 0 1 х

точок мінімуму.

1) 6; 2) 7; 3) 4;

5. Знайдіть найбільше значення функції у = -2х2 +8 х -7.

1) -2; 2) 7; 3) 1;

6. Знайдіть найменше значення функції на відрізку .

1) https://pandia.ru/text/78/524/images/image005_87.gif" width="17" height="48 src=">.

7. Знайдіть найменше значення функції у=|2х+3| - .

1) - https://pandia.ru/text/78/524/images/image006_79.gif" width="17" height="47"> ; 4) - .

https://pandia.ru/text/78/524/images/image009_67.gif" width="144" height="33 src="> має мінімум у точці хо=1,5?

1) 5; 2) -6; 3) 4; 4) 6.у

9. Вкажіть найбільше значення функції у=f(x) ,

1 х

0 1

1) 2,5; 2) 3; 3) -3;

у=lg(100 – x2 ).

1) 10 ; 2) 100 ; 3) 2 ; 4) 1 .

11. Знайдіть найменше значення функції у=2sin-1.

1) -1 ; 2) -3 ; 3) -2 ; 4) - .

Тест 14. Екстремуми. Найбільше (найменше) значення функції.

https://pandia.ru/text/78/524/images/image013_44.gif" width="130" height="115 src=">1. Графік функції у=f(x) зображений малюнку.

Вкажіть найменше значення цієї функції 1

на відрізку [ a; b]. а b

0 1 x

1) 0; 2) - 4 ,5; 3) -2; 4) - 3.

2. у На малюнку зображено графік функції у=f(x).

Скільки точок максимуму має функція?

1

0 1 х 1) 5; 2) 6; 3) 4; 4) 1.

3. У якій точці функція у = 2х2 +24х -25набуває найменшого значення?

https://pandia.ru/text/78/524/images/image018_37.gif" width="76" height="48"> на відрізку [-3;-1].

1) - https://pandia.ru/text/78/524/images/image020_37.gif" width="17" height="47 src=">; 2); 4) - 5.

https://pandia.ru/text/78/524/images/image022_35.gif" width="135" height="33 src="> має мінімум у точці хо=-2?

; 2) -6;; 4) 6.у

9. Вкажіть найменше значення функції у=f(x) ,

графік якої зображено малюнку. 1 х

0 1

1) -1,5; 2) -1; 3) -3;

10. Знайдіть найбільше значення функції у=log11 (121 – x2 ).

1) 11;; 3) 1;

11. Знайдіть найбільше значення функції у=2cos+3.

1) 5 ; 2) 3 ; 3) 2 ; 4) .

Відповіді :

У цій статті я розповім про алгоритм пошуку найбільшого та найменшого значенняфункції, точок мінімуму та максимуму.

З теорії нам знадобиться таблиця похіднихі правила диференціювання. Все це є у цій табличці:

Алгоритм пошуку найбільшого та найменшого значення.

Мені зручніше пояснювати на конкретному прикладі. Розглянемо:

Приклад:Знайдіть найбільше значення функції y=x^5+20x^3–65x на відрізку [–4;0].

Крок 1.Беремо похідну.

Y" = (x^5+20x^3–65x)" = 5x^4 + 20*3x^2 - 65 = 5x^4 + 60x^2 - 65

Крок 2Знаходимо точки екстремуму.

Крапкою екстремумуми називаємо такі точки, у яких функція досягає свого найбільшого чи найменшого значення.

Щоб знайти точки екстремуму, треба прирівняти похідну функцію до нуля (y" = 0)

5x^4 + 60x^2 - 65 = 0

Тепер вирішуємо це біквадратне рівняння та знайдене коріння є наші точки екстремуму.

Я розв'язую такі рівняння заміною t = x^2, тоді 5t^2 + 60t – 65 = 0.

Скоротимо рівняння на 5, отримаємо: t^2 + 12t - 13 = 0

D = 12 ^ 2 - 4 * 1 * (-13) = 196

T_(1) = (-12 + sqrt(196))/2 = (-12 + 14)/2 = 1

T_(2) = (-12 - sqrt(196))/2 = (-12 - 14)/2 = -13

Робимо зворотну заміну x^2 = t:

X_(1 та 2) = ±sqrt(1) = ±1
x_(3 і 4) = ±sqrt(-13) (виключаємо, під корінням не може бути негативних чисел, якщо звичайно не йдеться про комплексні числа)

Разом: x_(1) = 1 і x_(2) = -1 - і є наші точки екстремуму.

Крок 3Визначаємо найбільше та найменше значення.

Метод підстановки.

За умови нам було дано відрізок [b][–4;0]. Точка x=1 у цей відрізок не входить. Отже її ми не розглядаємо. Але крім точки x=-1 нам також треба розглянути ліву та праву межу нашого відрізка, тобто точки -4 та 0. Для цього підставляємо всі ці три точки у вихідну функцію. Зауважте вихідну - це ту, яка дана в умові (y=x^5+20x^3–65x), деякі починають підставляти у похідну...

Y(-1) = (-1)^5 + 20*(-1)^3 - 65*(-1) = -1 - 20 + 65 = [b]44
y(0) = (0)^5 + 20*(0)^3 - 65*(0) = 0
y(-4) = (-4)^5 + 20*(-4)^3 - 65*(-4) = -1024 - 1280 + 260 = -2044

Значить найбільше значення функції це [b]44 і досягається воно точки [b]-1, яка називається точкою максимуму функції на відрізку [-4; 0].

Ми вирішили та отримали відповідь, ми молодці, можна розслабитися. Але стоп! Вам не здається, що рахувати y(-4) якось надто складно? В умовах обмеженого часу краще скористатися іншим способом, я називаю його так:

Через проміжки знаковості.

Знаходяться ці проміжки для похідної функції, тобто нашого біквадратного рівняння.

Я роблю це так. Малюю спрямований відрізок. Розставляю точки: -4, -1, 0, 1. Не дивлячись на те, що 1 не входить у заданий відрізок, її все одно слід зазначити для того, щоб коректно визначити проміжки знакопостійності. Візьмемо яке-небудь число набагато більше 1, припустимо 100, подумки підставимо його в наше біквадратне рівняння 5 (100) ^ 4 + 60 (100) ^ 2 - 65. Навіть нічого крім стає очевидно, що в точці 100 функція має знак плюс. А значить, і на проміжки від 1 до 100 вона має знак плюс. При переході через 1 (ми йдемо праворуч наліво) функція змінить знак на мінус. При переході через точку 0 функція збереже свій знак, оскільки це лише межа відрізка, а чи не корінь рівняння. При переході через -1 функція знову змінить знак плюс.

З теорії ми знаємо, що там, де похідна функції (а ми саме для неї це креслили) змінює знак із плюсу на мінус (точка -1 у нашому випадку)функція досягає свого локального максимуму (y(-1)=44, як було пораховано раніше)на даному відрізку (це логічно дуже зрозуміло, функція перестала зростати, оскільки досягла свого максимуму і почала зменшуватися).

Відповідно, там де похідна функції міняє знак з мінусу на плюс, досягається локальний мінімум функції. Так, так, ми також знайшли точку локального мінімуму 1, а y(1) - це мінімальне значення функції на відрізку, допустимо від -1 до +∞. Зверніть велику увагу, що це лише локальний мінімум, тобто мінімум на певному відрізку. Так як дійсний (глобальний) мінімум функція досягне десь там, -∞.

На погляд перший спосіб простіше теоретично, а другий простіше з погляду арифметичних дій, але набагато складніше з погляду теорії. Адже іноді бувають випадки, коли функція не змінює знак при переході через корінь рівняння, та й взагалі можна заплутатися з цими локальними, глобальними максимумами та мінімумами, хоча Вам так і так доведеться це добре освоїти, якщо ви плануєте надходити в технічний ВНЗ(а навіщо інакше здавати профільне ЄДІ та вирішувати це завдання). Але практика і лише практика раз і назавжди навчить Вас вирішувати такі завдання. А тренуватись можете на нашому сайті. Ось.

Якщо виникли якісь питання, або щось незрозуміло – обов'язково запитайте. Я з радістю Вам відповім і внесу зміни, доповнення до статті. Пам'ятайте, ми робимо цей сайт разом!

Подивимося, як вивчити функцію за допомогою графіка. Виявляється, дивлячись на графік, можна дізнатися про все, що нас цікавить, а саме:

• область визначення функції
• область значень функції
• нулі функції
• проміжки зростання та спадання
• точки максимуму та мінімуму
• найбільше та найменше значення функції на відрізку.

Уточнимо термінологію:

Абсцисса- Це координата точки по горизонталі.
Ордината- Координата по вертикалі.
Ось абсцис- горизонтальна вісь, найчастіше звана вісь.
Вісь ординат- вертикальна вісь, або вісь.

Аргумент- незалежна змінна, від якої залежить значення функції. Найчастіше позначається.
Іншими словами, ми самі вибираємо , підставляємо у формулу функції та отримуємо .

Область визначенняфункції - безліч тих (і лише тих) значень аргументу, у яких функція існує.
Позначається: або .

На нашому малюнку область визначення функції – це відрізок. Саме на цьому відрізку намальовано графік функції. Тільки тут ця функція існує.

Область значень функції- це безліч значень, які набуває змінна . На нашому малюнку це відрізок - від найнижчого до самого верхнього значення.

Нулі функції- Точки, де значення функції дорівнює нулю, тобто . На малюнку це точки і .

Значення функції позитивнітам де . На нашому малюнку це проміжки та .
Значення функції негативнітам де . У нас це проміжок (або інтервал) від до .

Найважливіші поняття - зростання та зменшення функціїна деякій множині. Як безліч можна взяти відрізок, інтервал, об'єднання проміжків або всю числову пряму.

Функція зростає

Іншими словами, чим більше, тим більше, тобто графік йде вправо та вгору.

Функція зменшуєтьсяна множині, якщо для будь-яких і, що належать множині, з нерівності випливає нерівність.

Для спадної функції більшому значенню відповідає менше значення. Графік йде вправо та вниз.

На малюнку функція зростає проміжку і зменшується на проміжках і .

Визначимо, що таке точки максимуму та мінімуму функції.

Крапка максимуму- це внутрішня точка області визначення, така, що значення функції у ній більше, ніж у всіх досить близьких до неї точках.
Іншими словами, точка максимуму - така точка, значення функції в якій більше, ніж у сусідніх. Це локальний горбок на графіку.

На нашому малюнку – точка максимуму.

Крапка мінімуму- внутрішня точка області визначення, така, що значення функції у ній менше, ніж у всіх досить близьких до неї точках.
Тобто точка мінімуму - така, що значення функції у ній менше, ніж у сусідніх. На графіку це локальна "ямка".

На нашому малюнку – точка мінімуму.

Крапка – гранична. Вона не є внутрішньою точкою області визначення і тому не підходить для визначення точки максимуму. Адже вона не має сусідів ліворуч. Так само і на нашому графіку не може бути точкою мінімуму.

Точки максимуму та мінімуму разом називаються точками екстремуму функції. У нашому випадку це і.

А що робити, якщо потрібно знайти, наприклад, мінімум функціїна відрізку? У разі відповідь: . Тому що мінімум функції- це її значення у точці мінімуму.

Аналогічно, максимум нашої функції дорівнює. Він досягається в точці.

Можна сміливо сказати, що екстремуми функції рівні і .

Іноді у завданнях потрібно знайти найбільше та найменше значення функціїна заданому відрізку. Вони не обов'язково співпадають із екстремумами.

У нашому випадку найменше значення функціїна відрізку так само і збігається з мінімумом функції. А ось найбільше її значення на цьому відрізку дорівнює. Воно досягається у лівому кінці відрізка.

У будь-якому випадку найбільше та найменше значення безперервної функції на відрізку досягаються або в точках екстремуму, або на кінцях відрізка.