مركز الثقل الميكانيكا النظرية. طرق تحديد إحداثيات مركز الثقل. "حساب هياكل القوة"

– حساب مركز ثقل شكل مسطح محدد. يفهم العديد من القراء بشكل حدسي ما هو مركز الثقل، ولكن، مع ذلك، أوصي بتكرار المواد من أحد الدروس الهندسة التحليلية، حيث قمت بها مشكلة حول مركز ثقل المثلثوفك شفرتها في شكل يمكن الوصول إليه المعنى الجسديهذا المصطلح.

في مستقلة و مهام الاختبارللحل، كقاعدة عامة، يتم اقتراح أبسط حالة - حدود مسطحة متجانسالرقم، أي الرقم الثابت الكثافة الجسدية- الزجاج، الخشب، القصدير، ألعاب الحديد الزهر، الطفولة الصعبة، إلخ. علاوة على ذلك، افتراضيا، سنتحدث فقط عن هذه الأرقام =)

القاعدة الأولى و أبسط مثال : إذا كان الرقم المسطح لديه مركز التماثل، فهو مركز ثقل هذا الشكل. على سبيل المثال، مركز لوحة مستديرة متجانسة. إنه أمر منطقي ومفهوم في الحياة اليومية - كتلة هذا الشكل "موزعة بشكل عادل في جميع الاتجاهات" بالنسبة للمركز. لا أريد أن أقلبه.

ومع ذلك، في الواقع القاسي، من غير المرجح أن يرميك الحلو قالب شوكولاتة بيضاوي الشكل، لذلك سيتعين عليك تسليح نفسك ببعض أدوات المطبخ المهمة:

يتم حساب إحداثيات مركز ثقل الشكل المسطح المتجانس باستخدام الصيغ التالية :

, أو:

أين مساحة المنطقة (الشكل) ؛ أو باختصار شديد:

، أين

سوف نسمي التكامل تقليديًا تكامل "X"، والتكامل تكامل "Y".

ملاحظة مساعدة : لشقة محدودة غير متجانسةالأشكال التي يتم تحديد كثافتها بواسطة الوظيفة، تكون الصيغ أكثر تعقيدًا:
، أين - كتلة الشكل؛وفي حالة الكثافة الموحدة، يتم تبسيطها إلى الصيغ المذكورة أعلاه.

في الواقع، كل الحداثة تنتهي بالصيغ، والباقي هو مهارتك حل التكاملات المزدوجةبالمناسبة، الآن فرصة عظيمة للتدرب على أسلوبك وتحسينه. وكما تعلمون، ليس هناك حد للكمال =)

دعونا نلقي جزءًا من القطع المكافئ المنشط:

مثال 1

أوجد إحداثيات مركز ثقل شكل مسطح متجانس محدد بخطوط.

حل: الخطوط هنا أولية: فهي تحدد المحور السيني، والمعادلة - القطع المكافئ، والتي يمكن إنشاؤها بسهولة وسرعة باستخدام التحولات الهندسية للرسوم البيانية:

– القطع المكافئ، تم إزاحة وحدتين إلى اليسار ووحدة واحدة إلى الأسفل.

سأكمل الرسم بأكمله مرة واحدة بالنقطة النهائية لمركز ثقل الشكل:

القاعدة الثانية: إذا كان هذا الرقم لديه محاور التماثلفإن مركز ثقل هذا الشكل يقع بالضرورة على هذا المحور.

في حالتنا، الرقم متماثل بالنسبة ل مستقيمأي أننا في الواقع نعرف الإحداثي "x" للنقطة "em".

لاحظ أيضًا أن مركز الجاذبية عموديًا ينزاح بالقرب من المحور السيني، نظرًا لأن الشكل أكثر ضخامة هناك.

نعم، ربما لم يفهم الجميع تمامًا ما هو مركز الثقل: من فضلك ارفع إصبع السبابة لأعلى ثم ضع "النعل" المظلل بنقطة في ذهنك. من الناحية النظرية، لا ينبغي أن ينخفض هذا الرقم.

نجد إحداثيات مركز ثقل الشكل باستخدام الصيغ ، أين .

ترتيب اجتياز المنطقة (الشكل) واضح هنا:

انتباه!اتخاذ قرار بشأن ترتيب الاجتياز الأكثر فائدة مرة واحدة- واستخدامها للجميعالتكاملات!

1) أولا، حساب مساحة الشكل. نظرًا للبساطة النسبية للتكامل، يمكن كتابة الحل بشكل مضغوط، والشيء الرئيسي هو عدم الخلط في الحسابات:

نحن ننظر إلى الرسم ونقدر المساحة بالخلايا. اتضح أن الأمر يتعلق بالقضية.

2) تم بالفعل العثور على الإحداثي X لمركز الثقل " طريقة رسومية"، حتى تتمكن من الرجوع إلى التناظر والانتقال إلى النقطة التالية. ومع ذلك، ما زلت لا أوصي بذلك - هناك احتمال كبير أن يتم رفض الحل بعبارة "استخدم الصيغة".

يرجى ملاحظة أنه هنا لا يمكنك القيام إلا بالحسابات الذهنية - في بعض الأحيان ليس من الضروري على الإطلاق تقليل الكسور إليها القاسم المشتركأو عذاب الآلة الحاسبة.

هكذا:
، وهو ما كان مطلوبا الحصول عليه.

3) أوجد إحداثيات مركز الثقل. دعونا نحسب تكامل "اللعبة":

ولكن هنا سيكون الأمر صعبًا بدون آلة حاسبة. تحسبًا، سأعلق أنه نتيجة لضرب كثيرات الحدود، يتم الحصول على 9 حدود، وبعضها متشابه. أعطيت مصطلحات مماثلة شفويا (كما يحدث عادة في حالات مماثلة)وكتب على الفور المبلغ الإجمالي.

نتيجة ل:
، وهو مشابه جدًا للحقيقة.

على المرحلة الأخيرةبمناسبة نقطة على الرسم. وفقًا للشرط، لم يكن هناك أي شرط لرسم أي شيء، ولكن في معظم المهام، نضطر، طوعًا أو كرها، إلى رسم شكل. ولكن هناك ميزة مطلقة - التحقق المرئي والفعال للغاية من النتيجة.

إجابة:

المثالان التاليان مخصصان لك لحلهما بنفسك.

مثال 2

أوجد إحداثيات مركز ثقل شكل مسطح متجانس محدد بخطوط

بالمناسبة، إذا تخيلت كيف يقع القطع المكافئ وشاهدت النقاط التي يتقاطع عندها مع المحور، فيمكنك هنا الاستغناء عن الرسم.

وأكثر تعقيدًا:

مثال 3

أوجد مركز ثقل شكل مسطح متجانس محدد بخطوط

إذا كنت تواجه أي صعوبات في إنشاء الرسوم البيانية، فادرس (كرر) درس حول القطع المكافئةو/أو المثال رقم 11 من المادة التكاملات المزدوجة للدمى.

نماذج من الحلول في نهاية الدرس.

بالإضافة إلى ذلك، يمكن العثور على عشرات أو اثنين من الأمثلة المماثلة في الأرشيف المقابل على الصفحة حلول جاهزة للرياضيات العليا.

حسنًا، لا يسعني إلا إرضاء عشاق الرياضيات العليا، الذين يطلبون مني غالبًا تحليل المشكلات الصعبة:

مثال 4

أوجد مركز ثقل شكل مسطح متجانس محدد بخطوط. ارسم الشكل ومركز ثقله على الرسم.

حل: حالة هذه المهمة تتطلب بالفعل بشكل قاطع الانتهاء من الرسم. ولكن الشرط ليس رسميا جدا! – حتى الشخص ذو المستوى التدريبي المتوسط يمكنه أن يتخيل هذا الرقم في ذهنه:

يقطع الخط المستقيم الدائرة إلى جزأين، بالإضافة إلى جملة إضافية (سم. المتباينات الخطية) يدل على أننا نتحدث عن قطعة صغيرة مظللة.

الشكل متماثل بالنسبة لخط مستقيم (مصور بخط منقط)، لذا يجب أن يقع مركز الثقل على هذا الخط. ومن الواضح أن إحداثياتها متساوية modulo. مبدأ توجيهي ممتاز يلغي فعليًا احتمالية الحصول على إجابة خاطئة!

الآن الأخبار السيئة =) يلوح في الأفق تكامل غير سار للجذر، وهو ما درسناه بالتفصيل في المثال رقم 4 من الدرس طرق فعالة لحل التكاملات. ومن يدري ماذا سيتم رسمه هناك. ويبدو أنه بسبب وجود دائرةمربحة، ولكن ليس كل شيء بهذه البساطة. يتم تحويل معادلة الخط المستقيم إلى النموذج ولن تتحول التكاملات أيضًا إلى سكر (على الرغم من أن المعجبين التكاملات المثلثيةسوف نقدر). في هذا الصدد، هو أكثر حذرا في الحديث الإحداثيات الديكارتيةأوه.

ترتيب اجتياز الشكل:

1) احسب مساحة الشكل:

من الأكثر عقلانية أن تأخذ التكامل الأول إدراج علامة التفاضلية:

وفي التكامل الثاني نقوم بالاستبدال القياسي:

دعونا نحسب الحدود الجديدة للتكامل:

2) دعونا نجد .

هنا في التكامل الثاني تم استخدامه مرة أخرى طريقة إدراج دالة تحت العلامة التفاضلية. ممارسة واعتماد هذه الأمثل (في رأيي)تقنيات حل التكاملات القياسية

بعد الحسابات الصعبة والمستهلكة للوقت، نوجه انتباهنا مرة أخرى إلى الرسم (تذكر تلك النقاط لا نعرف بعد! ) ونحن نتلقى الرضا الأخلاقي العميق من القيمة الموجودة.

3) بناءً على التحليل الذي تم إجراؤه سابقًا، يبقى التأكد من ذلك.

عظيم:

دعونا نرسم نقطة على الرسم. ووفقا لصيغة الشرط نكتبه نهائيا إجابة:

مهمة مماثلة يمكنك حلها بنفسك:

مثال 5

أوجد مركز ثقل شكل مسطح متجانس محدد بخطوط. نفذ الرسم.

هذه المشكلة مثيرة للاهتمام لأنها تحتوي على شكل صغير الحجم إلى حد ما، وإذا ارتكبت خطأ في مكان ما، فهناك احتمال كبير "بعدم الدخول" إلى المنطقة على الإطلاق. وهو أمر جيد بالتأكيد من وجهة نظر التحكم في القرار.

نموذج للتصميم في نهاية الدرس.

في بعض الأحيان يكون الأمر منطقيًا الانتقال إلى الإحداثيات القطبية في التكاملات المزدوجة. ذلك يعتمد على هذا الرقم. لقد بحثت وبحثت عن مثال ناجح، لكن لم أجده، لذا سأوضح الحل في المشكلة التجريبية الأولى للدرس أعلاه:

اسمحوا لي أن أذكركم أنه في هذا المثال ذهبنا إلى الإحداثيات القطبية، اكتشف ترتيب اجتياز المنطقة وحساب مساحتها

دعونا نجد مركز ثقل هذا الشكل. المخطط هو نفسه: . يتم عرض القيمة مباشرة من الرسم، وينبغي إزاحة الإحداثيات "x" أقرب قليلاً إلى المحور الإحداثي، حيث يوجد الجزء الأكثر ضخامة من نصف الدائرة هناك.

في التكاملات نستخدم صيغ الانتقال القياسية:

من المعقول، على الأرجح، أنهم لم يكونوا مخطئين.

المحاضرة 4. مركز الثقل.

تتناول هذه المحاضرة القضايا التالية

1. مركز الثقل صلب.

2. إحداثيات مراكز ثقل الأجسام غير المتجانسة.

3. إحداثيات مراكز ثقل الأجسام المتجانسة.

4. طرق تحديد إحداثيات مراكز الثقل.

5. مراكز ثقل بعض الأجسام المتجانسة.

إن دراسة هذه المسائل ضرورية في المستقبل لدراسة ديناميكيات حركة الأجسام مع مراعاة الاحتكاك المنزلق والمتدحرج، ديناميكيات حركة مركز كتلة نظام ميكانيكي، العزوم الحركية، لحل المسائل في الانضباط "قوة المواد".

جلب القوى الموازية.

بعد أن فكرنا في جلب النظام المسطح والنظام المكاني التعسفي للقوى إلى المركز، نعود مرة أخرى إلى النظر في الحالة الخاصة لنظام القوى المتوازية.

جلب قوتين متوازيتين.

في سياق النظر في نظام القوى هذا، من الممكن حدوث حالات التخفيض الثلاث التالية.

1. نظام قوتين على خط واحد. دعونا نفكر في نظام يتكون من قوتين متوازيتين موجهتين في اتجاه واحد صو س، مطبق عند النقاط أو في. سنفترض أن القوى متعامدة مع هذا الجزء (الشكل 1، أ).

مع، تابعة للقطاع أ.بواستيفاء الشرط:

تكييف/شمال شرق = س/ص.(1)

الناقل الرئيسي للنظام آر سي = ص + سيساوي في المعامل مجموع هذه القوى: آر سي = ص + س.

معمع الأخذ في الاعتبار أن (1) يساوي صفراً:مج = ص ∙ تكييف- س∙ سي بي = 0.

وهكذا نتيجة الصب حصلنا على: آر سي ≠ 0, مج= 0. وهذا يعني أن المتجه الرئيسي يعادل المحصلة التي تمر عبر مركز الاختزال، أي:

محصلة القوى الخطية تساوي في معاملها مجموعها، وخط عملها يقسم القطعة التي تربط نقاط تطبيقها، بنسبة عكسية مع معاملات هذه القوى بطريقة داخلية.

لاحظ أن موقف هذه النقطة معلن تتغير إذا كانت القوات رو سبدوره زاويةألفا. نقطة مع، والتي تسمى هذه الخاصية مركز القوى الموازية.

2. نظام اثنين مضاد الخطيةوالقوى ليست متساوية في الحجم. نرجو القوة صو س، مطبق عند النقاط أو في، متوازية، موجهة في اتجاهين متعاكسين وغير متساوية في الحجم (الشكل 1، ب).

دعونا نختار نقطة لتكون مركز الاختزال مع، والذي لا يزال يرضي العلاقة (1) ويقع على نفس الخط، ولكن خارج المقطع أ.ب.

الناقل الرئيسي لهذا النظام آر سي = ص + سسيكون المعامل الآن مساوياً للفرق بين معاملات المتجهات: آر سي = س - ص.

النقطة الرئيسية فيما يتعلق بالمركز معلا يزال صفرًا:مج = ص ∙ تكييف- س∙ شمال شرق= 0 إذن

نتيجة مضاد الخطيةوالقوى غير المتساوية في المقدار تكون مساوية لفرقها، وموجهة نحو القوة الأكبر، وخط عملها يقسم القطعة التي تربط نقاط تطبيقها، بنسبة عكسية مع المقاييس الخارجية لهذه القوى.

رسم بياني 1

3. نظام اثنين مضاد الخطيةوالقوى متساوية في الحجم. لنأخذ حالة التخفيض السابقة باعتبارها الحالة الأولية. دعونا إصلاح القوة ر، والقوة سدعونا نوجه المعامل إلى القوة ر.

ثم في س → ر في الصيغة (1) العلاقة تكييف/شمال شرق → 1. هذا يعني ذلك تكييف → شمال شرق، أي المسافة تكييف →∞ .

في هذه الحالة، وحدة المتجه الرئيسي آر سي → 0، ولا يعتمد معامل اللحظة الرئيسية على موضع مركز التخفيض ويظل مساوياً للقيمة الأصلية:

مج = ص ∙ تكييف- س∙ شمال شرق = ص ∙ ( تكييف- شمال شرق) =ص ∙ أب.

لذلك، في الحد حصلنا على نظام القوى الذي آر سي = 0, مج≠ 0، ويتم إزالة مركز التخفيض إلى ما لا نهاية، والذي لا يمكن استبداله بالناتج. ليس من الصعب التعرف على قوتين في هذا النظام زوج من القوى ليس له نتيجة.

مركز نظام القوى الموازية.

النظر في النظام نقوة باي، مطبق عند النقاطأ (× ط , ذ ط , ض ط) وموازية للمحورفوق مع أورث ل(الصورة 2).

وإذا استثنينا مقدما حالة النظام المكافئ لزوج من القوى، فليس من الصعب استنادا إلى الفقرة السابقة إثبات وجود محصلتهر.

دعونا نحدد إحداثيات المركزج(س ج, ذ ج, ض ج) القوى المتوازية، أي إحداثيات نقطة تطبيق محصلة هذا النظام.

ولهذا الغرض نستخدم نظرية فارينون والتي على أساسها:

م0 (ر) = Σ م0(باي).

الصورة 2

يمكن تمثيل العزم المتجه للقوة كمنتج متجه، وبالتالي:

م 0 (ر) = ص ج× ر = Σ م0i(باي) = Σ ( ص ط× باي ).

معتبرا أن ر = عربة سكن متنقلة ∙ ل، أ باي = بفي ∙ ل واستخدام الخصائص منتج ناقلات، نحن نحصل:

ص ج × عربة سكن متنقلة ∙ ل = Σ ( ص ط × بفي ∙ ل),

ص ج ∙ رالخامس× ل = Σ ( ص ط ∙ بفي × ل) = Σ ( ص ط ∙ بفي ) × ل,

أو:

[ ص ج ر ضد - Σ ( ص ط بفي )] × ل= 0.

يكون التعبير الأخير صالحًا فقط إذا كان التعبير الموجود بين قوسين مربعين يساوي صفرًا. ولذلك حذف الفهرسالخامسومراعاة أن الناتجر = Σ باي ، ومن هنا نحصل على:

ص ج = (Σ باي ص ط )/(Σ باي ).

بإسقاط آخر مساواة متجهة على محور الإحداثيات، نحصل على المطلوب التعبير عن إحداثيات مركز القوى المتوازية:

س ج = (Σ باي × ط)/(Σ باي );

ذ ج = (Σ باي ذ ط )/(Σ باي );(2)

ض ج = (Σ باي ض ط )/(Σ باي ).

مركز ثقل الأجسام.

إحداثيات مراكز ثقل الجسم المتجانس.

فكر في وزن الجسم الصلب صوالحجم الخامسفي نظام الإحداثيات أوكيز، أين المحاور سو ذمتصلة بسطح الأرض، وبالمحور ضتهدف إلى ذروة.

إذا قمنا بتقسيم الجسم إلى أجزاء أولية ذات حجم∆ الخامس أنا فستعمل قوة الجذب على كل جزء منه∆ باي، موجهة نحو مركز الأرض. لنفترض أن أبعاد الجسم أصغر بكثير من أبعاد الأرض، فيمكن اعتبار نظام القوى المطبق على الأجزاء الأولية من الجسم غير متقارب، بل متوازي (الشكل 3)، وجميع الاستنتاجات ينطبق عليها الفصل السابق .

تين. 3

تعريف . مركز ثقل الجسم الصلب هو مركز قوى الجاذبية الموازية للأجزاء الأولية من هذا الجسم.

دعونا نتذكر ذلك جاذبية معينةجزء أساسي من الجسم يسمى نسبة وزنه∆ بايلحجم ∆ الخامس أنا : γ أنا = ∆ باي/ ∆ الخامس أنا . بالنسبة لجسم متجانس تكون هذه القيمة ثابتة:γ أنا = γ = ص/ الخامس.

استبدال ∆ في (2) باي = γ أنا ∙∆ الخامس أنا بدلاً من بايمع مراعاة الملاحظة الأخيرة وتخفيض البسط والمقام بمقدارز، نحن نحصل تعبيرات عن إحداثيات مركز ثقل جسم متجانس:

س ج = (Σ ∆ السادس∙ × ط)/(Σ ∆ السادس);

ذ ج = (Σ ∆ السادس∙ ذ ط )/(Σ ∆ السادس);(3)

ض ج = (Σ ∆ السادس∙ ض ط )/(Σ ∆ السادس).

العديد من النظريات مفيدة في تحديد مركز الثقل.

1) إذا كان لجسم متجانس مستوى تماثل، فإن مركز ثقله يقع في هذا المستوى.

إذا المحاور Xو فيتقع في هذا المستوى من التماثل، ثم لكل نقطة مع الإحداثيات. والإحداثيات حسب (3)، سيكون مساوياً للصفر، لأن في المجموعالجميع يتم تدمير الأعضاء ذوي العلامات المعاكسة في أزواج. وهذا يعني أن مركز الثقل يقعفي مستوى التماثل.

2) إذا كان جسم متجانس له محور تماثل فإن مركز ثقل الجسم يقع على هذا المحور.

في الواقع، في هذه الحالة، إذا كان المحورضارسم على طول محور التماثل لكل نقطة ذات إحداثياتيمكنك العثور على نقطة مع الإحداثياتوالإحداثيات و ، المحسوبة باستخدام الصيغ (3)، ستكون مساوية للصفر.

تم إثبات النظرية الثالثة بطريقة مماثلة.

3) إذا كان لجسم متجانس مركز تماثل فإن مركز ثقل الجسم يقع عند هذه النقطة.

وعدد قليل من التعليقات.

أولاً. فإذا أمكن تقسيم الجسم إلى أجزاء يعرف وزنها وموقع مركز ثقلها، فلا داعي للنظر في كل نقطة، وفي الصيغ (3)باي - يتم تحديده على أنه وزن الجزء المقابل و– كإحداثيات مركز ثقله.

ثانية. وإذا كان الجسم متجانسا، فإن وزن جزء واحد منه، أين - الثقل النوعي للمادة التي يتكون منها الجسم، والسادس - حجم هذا الجزء من الجسم. وستتخذ الصيغ (3) شكلاً أكثر ملاءمة. على سبيل المثال،

ومثله أين - حجم الجسم كله.

الملاحظة الثالثة. ليأخذ الجسم شكل صفيحة رفيعة ذات مساحة Fوسمك ر، ملقاة في الطائرة أوكسي. الاستبدال في (3)∆ الخامس أنا =ر ∙ ∆F أنا , نحصل على إحداثيات مركز ثقل لوحة متجانسة:

س ج = (Σ ∆ واو∙ × ط) / (Σ ∆ واو);

ذ ج = (Σ ∆ واو∙ ذ ط ) / (Σ ∆ واو).

ض ج = (Σ ∆ واو∙ ض أنا ) / (Σ ∆ واو).

أين - إحداثيات مركز ثقل الصفائح الفردية؛– مساحة الجسم الكلية .

الملاحظة الرابعة. لجسم على شكل قضيب رفيع منحني طوله لمع مساحة المقطع العرضي أالحجم الابتدائي∆ الخامس أنا = أ ∙∆ ل أنا ، لهذا إحداثيات مركز ثقل قضيب رفيع منحنيسيكون متساويا:

س ج = (Σ ∆ ل ط∙ × ط)/(Σ ∆ ل ط);

ذ ج = (Σ ∆ ل ط∙ ذ ط )/(Σ ∆ ل ط);(4)

ض ج = (Σ ∆ ل ط∙ ض ط )/(Σ ∆ ل ط).

أين - إحداثيات مركز الثقلأنا-القسم؛ .

لاحظ أن مركز الثقل، بحسب التعريف، هو نقطة هندسية؛ ويمكن أيضًا أن يقع خارج حدود جسم معين (على سبيل المثال، بالنسبة للحلقة).

ملحوظة.

في هذا القسم من الدورة لا نفرق بين الجاذبية والجاذبية ووزن الجسم. في الواقع، الجاذبية هي الفرق بين قوة الجاذبية للأرض وقوة الطرد المركزي الناتجة عن دورانها.

إحداثيات مراكز ثقل الأجسام غير المتجانسة.

إحداثيات مركز الثقل صلبة غير متجانسة(الشكل 4) في النظام المرجعي المحدد يتم تحديدها على النحو التالي:

الشكل 4

أين - الوزن لكل وحدة حجم الجسم (الثقل النوعي)

- وزن الجسم كله.

سطح غير موحد(الشكل 5)، ثم يتم تحديد إحداثيات مركز الثقل في النظام المرجعي المختار على النحو التالي:

الشكل 5

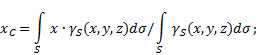
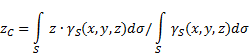
أين - الوزن لكل وحدة مساحة الجسم,

- وزن الجسم كله.

إذا كانت الصلبة خط غير موحد(الشكل 6)، ثم يتم تحديد إحداثيات مركز الثقل في النظام المرجعي المختار على النحو التالي:

الشكل 6

أين - الوزن بالنسبة لطول الجسم,

وزن الجسم كله.

طرق تحديد إحداثيات مركز الثقل.

استنادا إلى الصيغ العامة التي تم الحصول عليها أعلاه، من الممكن الإشارة إلى طرق محددة تحديد إحداثيات مراكز ثقل الأجسام.

1. تناظر.إذا كان للجسم المتجانس مستوى أو محور أو مركز تماثل (الشكل 7)، فإن مركز ثقله يقع، على التوالي، في مستوى التماثل أو محور التماثل أو في مركز التماثل.

الشكل 7

2. شق.يقتحم الجسم الرقم النهائيالأجزاء (الشكل 8)، لكل منها موقع مركز الثقل ومساحته معروفان.

الشكل 8

س = س 1 + س 2.

3.طريقة المنطقة السلبيةحالة خاصة لطريقة التقسيم (الشكل 9). ويسري على الأجسام التي لها قواطع إذا كانت مراكز ثقل الجسم دون القاطع والجزء المقطوع معروفة. يتم تمثيل الجسم على شكل صفيحة ذات انقطاع بمزيج من صفيحة صلبة (بدون انقطاع) بمساحةس 1 ومساحة الجزء المقطوع S2.

الشكل 9

س = س 1 - س 2.

4.طريقة التجميع.إنه تكملة جيدة للطريقتين الأخيرتين. بعد تقسيم الشكل إلى العناصر المكونة له، يكون من المناسب دمج بعضها مرة أخرى من أجل تبسيط الحل بعد ذلك مع مراعاة تماثل هذه المجموعة.

مراكز ثقل بعض الأجسام المتجانسة.

1) مركز ثقل القوس الدائري.النظر في القوس أ.بنصف القطرر مع الزاوية المركزية. بسبب التناظر، يقع مركز ثقل هذا القوس على المحورثور(الشكل 10).

الشكل 10

دعونا نجد الإحداثياتوفقا للصيغة . للقيام بذلك، حدد على القوس أ.بعنصر مم ’ طول، الذي يتم تحديد موضعه بالزاوية. تنسيق Xعنصر مم'سوف. استبدال هذه القيم Xود ل ومع الأخذ في الاعتبار أن التكامل يجب أن يمتد على كامل طول القوس، نحصل على:

حيث L هو طول القوس AB، ويساوي .

من هنا نجد أخيرا أن مركز ثقل القوس الدائري يقع على محور تماثله على مسافة من المركزيا متساوي

أين هي الزاوية تقاس بالراديان.

2) مركز ثقل منطقة المثلث . النظر في مثلث يقع في الطائرة أوكسي، إحداثيات رؤوسها معروفة: أ (× ط,ذ ط ), (أنا= 1،2،3). كسر المثلث إلى شرائح ضيقة موازية للجانب أ 1 أفي الشكل 2، توصلنا إلى استنتاج مفاده أن مركز ثقل المثلث يجب أن ينتمي إلى الوسيط أ 3 م 3 (الشكل 11).

الشكل 11

كسر المثلث إلى شرائح موازية للجانب أ 2 أ 3، يمكننا التحقق من أنه يجب أن يقع على الوسيط أ 1 م 1 . هكذا، يقع مركز ثقل المثلث عند نقطة تقاطع متوسطاتهوالذي كما هو معروف يفصل ثلثا من كل وسيط محسوبا من الجانب المقابل.

على وجه الخصوص، للوسيط أ 1 م 1 نحصل على، مع الأخذ في الاعتبار أن إحداثيات النقطة م 1 - هذا هو الوسط الحسابي لإحداثيات القمم أ 2 و أ 3 :

س ج = س 1 + (2/3) ∙ (سم 1 - س 1 ) = س 1 + (2/3) ∙ [(س 2 + س 3 )/2 - س 1 ] = (س 1 + س 2 + س 3 )/3.

وبالتالي فإن إحداثيات مركز ثقل المثلث هي الوسط الحسابي لإحداثيات رءوسه:

س ج =(1/3) Σ × ط ; ذ ج =(1/3) Σ ذ ط .

3) مركز ثقل مساحة القطاع الدائري.النظر في قطاع من الدائرة مع نصف القطر رمع الزاوية المركزية 2α ، تقع بشكل متناظر حول المحور ثور (الشكل 12) .

من الواضح أن ذ ج = 0، ويمكن تحديد المسافة من مركز الدائرة التي يقطع منها هذا القطاع إلى مركز ثقله بالصيغة:

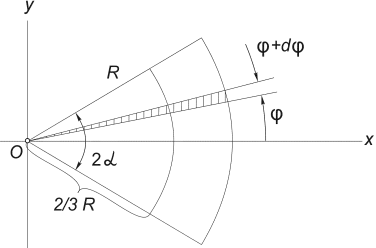
الشكل 12

أسهل طريقة لحساب هذا التكامل هي تقسيم مجال التكامل إلى قطاعات أولية بزاوية دφ . بدقة بالنسبة إلى متناهية الصغر من الدرجة الأولى، يمكن استبدال هذا القطاع بمثلث قاعدته تساوي ر × دφ والارتفاع ر. مساحة هذا المثلث مدافع =(1/2)ر 2 ∙ دφ ، ويقع مركز ثقله على مسافة 2/3 رمن الرأس، لذلك في (5) نضع س = (2/3)ر∙ كوسφ. الاستبدال في (5) F= α ر 2 نحصل على:

باستخدام الصيغة الأخيرة، نحسب، على وجه الخصوص، المسافة إلى مركز الثقل نصف دائرة.

بالتعويض α = π /2 في (2)، نحصل على: س ج = (4 ر)/(3π) ≅ 0.4 ر .

مثال 1.دعونا نحدد مركز ثقل الجسم المتجانس الموضح في الشكل. 13.

الشكل 13

حل.الجسم متجانس ويتكون من جزأين لهما شكل متماثل. إحداثيات مراكز ثقلها:

مجلداتهم:

وبالتالي فإن إحداثيات مركز ثقل الجسم

مثال 2. دعونا نوجد مركز ثقل صفيحة مثنية بزاوية قائمة. الأبعاد موجودة في الرسم (الشكل 14).

الشكل 14

حل. إحداثيات مراكز الثقل:

المناطق:

لهذا السبب:

مثال 3. على ورقة مربعة سم قطع حفرة مربعة سم (الشكل 15). دعونا نجد مركز ثقل الورقة.مثال 4. أوجد موضع مركز ثقل اللوحة الموضح في الشكل. 16. الأبعاد موضحة بالسنتيمتر.

الشكل 16

حل. دعونا نقسم اللوحة إلى أشكال (الشكل 17)، المراكزومن المعروف خطورتها.

مساحات هذه الأشكال وإحداثيات مراكز ثقلها:

1) مستطيل طول ضلعه 30 و 40 سم،س 1 =30 ∙ 40=1200 سم 2 ; × 1= 15 سم؛ في 1 = 20 سم.

2) مثلث قائمبقاعدة 50 سم وارتفاع 40 سم؛س 2 =0,5 ∙ 50 ∙ 40= 1000 سم 2 ; X 2 =30+50/3=46.7 سم؛ ص 2 =40/3 =13.3 سم؛

3) نصف دائرة نصف قطرها دائرة ص = 20 سم؛س 3 =0,5 ∙π∙ 20 2 = 628 سم 2 ; X 3 =4 ر /3 π = 8.5 سم؛ في

حل. أذكر أنه في الفيزياء كثافة الجسمρ وخطورتها النوعيةزترتبط بالعلاقة:γ = ρ ز ، أينز - التسريع السقوط الحر. للعثور على كتلة مثل هذا الجسم المتجانس، تحتاج إلى مضاعفة الكثافة بحجمها.

الشكل 19

مصطلح الكثافة "الخطية" أو "الخطية" يعني أنه لتحديد كتلة قضيب الجمالون، يجب ضرب الكثافة الخطية بطول هذا القضيب.

لحل المشكلة يمكنك استخدام طريقة التقسيم. بتمثيل الجمالون المعين كمجموع 6 قضبان فردية، نحصل على:

أينل ط طولأنا قضيب الجمالون، و× ط , ذ ط - إحداثيات مركز ثقلها.

يمكن تبسيط حل هذه المشكلة من خلال تجميع آخر 5 أشرطة من الجمالون. ومن السهل أن نرى أنهم يشكلون شكلاً يقع مركز تناظره في منتصف القضيب الرابع، حيث يقع مركز ثقل هذه المجموعة من القضبان.

وبالتالي، يمكن تمثيل الجمالون المعين بمزيج من مجموعتين فقط من القضبان.

المجموعة الأولى تتكون من العصا الأولى لذلكل 1 = 4 م،س 1 = 0 م،ذ 1 = 2 م المجموعة الثانية من القضبان تتكون من خمسة قضبان لهال 2 = 20 م،س 2 = 3 م،ذ 2 = 2 م.

تم العثور على إحداثيات مركز ثقل الجمالون باستخدام الصيغة:

س ج = (ل 1 ∙ س 1 + ل 2 ∙ س 2 )/(ل 1 + ل 2 ) = (4∙0 + 20∙3)/24 = 5/2 م؛

ذ ج = (ل 1 ∙ ذ 1 + ل 2 ∙ ذ 2 )/(ل 1 + ل 2 ) = (4∙2 + 20∙2)/24 = 2 م.

علماً بأن المركز مع تقع على خط مستقيم متصل مع 1 و مع 2 ويقسم الجزء مع 1 مع 2 بخصوص: مع 1 مع/سس 2 = (س ج - س 1 )/(س 2 - س ج ) = ل 2 / ل 1 = 2,5/0,5.

أسئلة الاختبار الذاتي

- ما يسمى مركز القوى المتوازية؟

- كيف يتم تحديد إحداثيات مركز القوى المتوازية؟

- كيفية تحديد مركز القوى المتوازية التي محصلتها صفر؟

- ما هي خصائص مراكز القوى المتوازية؟

- ما الصيغ المستخدمة لحساب إحداثيات مركز القوى المتوازية؟

- ماذا يسمى مركز ثقل الجسم؟

- لماذا يمكن اعتبار قوى الجاذبية الأرضية المؤثرة على نقطة ما على الجسم بمثابة نظام من القوى المتوازية؟

- اكتب صيغة تحديد موضع مركز ثقل الأجسام غير المتجانسة والمتجانسة، صيغة تحديد موضع مركز ثقل المقاطع المسطحة؟

- اكتب صيغة تحديد موضع مركز ثقل الجسم البسيط الأشكال الهندسية: مستطيل، مثلث، شبه منحرف ونصف دائرة؟

- ما يسمى لحظة ثابتة من المنطقة؟

- أعط مثالاً لجسم يقع مركز ثقله خارج الجسم.

- كيف تستخدم خصائص التماثل في تحديد مراكز ثقل الأجسام؟

- ما هو جوهر طريقة الأوزان السالبة؟

- أين يقع مركز ثقل القوس الدائري؟

- ما البناء الرسومي الذي يمكن استخدامه للعثور على مركز ثقل المثلث؟

- اكتب الصيغة التي تحدد مركز ثقل القطاع الدائري.

- باستخدام الصيغ التي تحدد مراكز ثقل المثلث والقطاع الدائري، اشتق صيغة مماثلة للقطاع الدائري.

- ما هي الصيغ المستخدمة لحساب إحداثيات مراكز ثقل الأجسام المتجانسة والأشكال المسطحة والخطوط؟

- ما يسمى بالعزم الثابت لمساحة الشكل المستوي بالنسبة للمحور وكيف يتم حسابه وما البعد الذي يمتلكه؟

- كيفية تحديد موضع مركز ثقل منطقة ما إذا كان موضع مراكز ثقل أجزائها الفردية معروفًا؟

- ما هي النظريات المساعدة المستخدمة لتحديد موضع مركز الثقل؟

الهدف من العمل – تحديد مركز ثقل الشكل المعقد تحليلياً وتجريبياً.

الخلفية النظرية. تتكون الأجسام المادية من الجسيمات الأولية، والتي يتم تحديد موقعها في الفضاء من خلال إحداثياتها. ويمكن اعتبار قوى جذب كل جسيم إلى الأرض نظاماً من القوى المتوازية، ويطلق على محصلة هذه القوى اسم قوة جاذبية الجسم أو وزن الجسم. مركز ثقل الجسم هو نقطة تطبيق الجاذبية.

مركز الثقل هو نقطة هندسية، والتي يمكن أن تكون موجودة خارج الجسم (على سبيل المثال، قرص به ثقب، كرة مجوفة، وما إلى ذلك). كبير أهمية عمليةلديه تعريف لمركز ثقل الصفائح المسطحة الرقيقة المتجانسة. يمكن عادة إهمال سمكها ويمكن افتراض أن مركز الجاذبية يقع في المستوى. لو خطة تنسيقيتم محاذاة xOy مع مستوى الشكل، ثم يتم تحديد موضع مركز الثقل بإحداثيتين:

أين مساحة جزء من الشكل، ()؛

– إحداثيات مركز ثقل أجزاء الشكل مم (سم).

قسم من الشكل	أ، مم 2	× ج، مم	نعم، مم
	ب	ب/2	ح/2
	ب/2	ب/3	ح/3
	ص 2 أ
عند 2α = π πR 2 /2

إجراءات العمل.

ارسم شكلاً معقدًا يتكون من 3-4 أشكال بسيطة (مستطيل، مثلث، دائرة، إلخ) بمقياس رسم 1:1 وحدد أبعاده.

ارسم محاور الإحداثيات بحيث تغطي الشكل بأكمله، وقم بتقسيم الشكل المعقد إلى أجزاء بسيطة، وحدد مساحة وإحداثيات مركز ثقل كل شكل بسيط بالنسبة لنظام الإحداثيات المحدد.

احسب إحداثيات مركز ثقل الشكل بأكمله تحليليًا. قطع هذا الشكل من الورق المقوى الرفيع أو الخشب الرقائقي. حفر فتحتين، يجب أن تكون حواف الثقوب ناعمة، ويجب أن يكون قطر الثقوب أكبر قليلاً من قطر الإبرة لتعليق الشكل.

قم أولاً بتعليق الشكل عند نقطة واحدة (الفتحة)، ثم ارسم خطًا بقلم رصاص يتزامن مع الخط الراسيا. كرر الأمر نفسه عند تعليق الشكل عند نقطة أخرى. يجب أن يتطابق مركز ثقل الشكل الذي تم العثور عليه تجريبيًا.

حدد إحداثيات مركز ثقل صفيحة رفيعة متجانسة تحليليًا. تحقق تجريبيا

خوارزمية الحل

1. الطريقة التحليلية.

أ) ارسم الرسم بمقياس رسم 1:1.

ب) قسّم الشكل المعقد إلى أشكال بسيطة

ج) حدد وارسم محاور الإحداثيات (إذا كان الشكل متماثلًا، فعندئذٍ على طول محور التماثل، وإلا على طول محيط الشكل)

د) حساب مساحة الأشكال البسيطة والشكل بأكمله

هـ) حدد موضع مركز ثقل كل شكل بسيط في الرسم

و) احسب إحداثيات مركز الثقل لكل شكل

(المحور س وص)

ز) احسب إحداثيات مركز ثقل الشكل بأكمله باستخدام الصيغة

ح) ضع علامة على موضع مركز الثقل على الرسم C (

2. التحديد التجريبي.

يمكن التحقق من صحة حل المشكلة تجريبيا. قطع هذا الشكل من الورق المقوى الرفيع أو الخشب الرقائقي. حفر ثلاثة ثقوب، يجب أن تكون حواف الثقوب ناعمة، ويجب أن يكون قطر الثقوب أكبر قليلاً من قطر الإبرة لتعليق الشكل.

قم أولاً بتعليق الشكل عند نقطة واحدة (الفتحة)، ثم ارسم خطًا بقلم رصاص يتزامن مع الخط الراسيا. كرر نفس الشيء عند تعليق الشكل في نقاط أخرى. قيمة إحداثيات مركز ثقل الشكل الموجودة عند تعليق الشكل عند نقطتين: . يجب أن يتطابق مركز ثقل الشكل الذي تم العثور عليه تجريبيًا.

3. استنتاج حول موضع مركز الثقل أثناء التحديد التحليلي والتجريبي.

يمارس

تحديد مركز ثقل مقطع مسطح تحليلياً وتجريبياً.

مثال التنفيذ

مهمة

حدد إحداثيات مركز ثقل صفيحة رفيعة متجانسة.

أنا الأسلوب التحليلي

1. يتم رسم الرسم بمقياس (عادةً ما يتم تحديد الأبعاد بالملليمتر)

2. نقوم بتقسيم الشكل المعقد إلى أشكال بسيطة.

1- المستطيل

2- المثلث (المستطيل)

3- مساحة نصف الدائرة (غير موجودة، علامة الطرح).

نجد موقف مركز الثقل لأشكال بسيطة من النقاط، و

3. ارسم محاور الإحداثيات بالشكل المناسب وحدد أصل الإحداثيات.

4. حساب مساحات الأشكال البسيطة ومساحة الشكل بأكمله. [الحجم بالسم]

(3. لا، علامة -).

مساحة الشكل بأكمله

5. ابحث عن إحداثيات النقطة المركزية. ، وفي الرسم.

6. احسب إحداثيات النقاط C 1 و C 2 و C 3

7. احسب إحداثيات النقطة C

8. حدد نقطة على الرسم

الثاني من ذوي الخبرة

إحداثيات مركز الثقل تجريبيا.

أسئلة التحكم.

1. هل من الممكن اعتبار قوة جاذبية الجسم بمثابة نظام محصلة من القوى المتوازية؟

2. هل يمكن تحديد موقع مركز ثقل الجسم كله؟

3. ما هو جوهر التحديد التجريبي لمركز ثقل الشكل المسطح؟

4. كيف يتم تحديد مركز ثقل الشكل المعقد المكون من عدة أشكال بسيطة؟

5. كيف ينبغي تقسيم الشكل المعقد بشكل عقلاني إلى أشكال بسيطة عند تحديد مركز ثقل الشكل بأكمله؟

6. ما هي الإشارة التي تحتوي عليها مساحة الثقوب في صيغة تحديد مركز الثقل؟

7. عند تقاطع أي خطوط من خطوط المثلث يقع مركز ثقله؟

8. إذا كان من الصعب تقسيم الرقم إلى عدد صغير من الأشكال البسيطة، فما هي طريقة تحديد مركز الثقل التي يمكن أن توفر الإجابة الأسرع؟

العمل التطبيقي №6

""حل المشاكل المعقدة""

الهدف من العمل: تكون قادرة على حل المشاكل المعقدة (الحركية والديناميكية)

الخلفية النظرية: السرعة هي مقياس حركي لحركة نقطة ما، وهو ما يميز سرعة التغيير في موضعها. سرعة النقطة هي ناقل يميز سرعة واتجاه حركة النقطة هذه اللحظةوقت. عند تحديد حركة نقطة بالمعادلات، فإن إسقاطات السرعة على محاور الإحداثيات الديكارتية تساوي:

يتم تحديد معامل سرعة نقطة ما بواسطة الصيغة

يتم تحديد اتجاه السرعة بواسطة جيب التمام الاتجاه:

إن خاصية سرعة تغير السرعة هي التسارع أ. تسارع نقطة ما يساوي المشتق الزمني لمتجه السرعة:

عند تحديد حركة نقطة ما، فإن معادلات إسقاط التسارع على محاور الإحداثيات تساوي:

وحدة التسريع:

وحدة التسارع الكاملة

يتم تحديد وحدة التسارع العرضي بواسطة الصيغة

يتم تحديد معامل التسارع الطبيعي بواسطة الصيغة

أين هو نصف قطر انحناء المسار عند نقطة معينة.

يتم تحديد اتجاه التسارع بواسطة جيب التمام الاتجاه

معادلة الحركة الدورانية لجسم صلب حول محور ثابت لها الشكل

السرعة الزاوية للجسم:

في بعض الأحيان يتم تحديد السرعة الزاوية بعدد الدورات في الدقيقة ويتم الإشارة إليها بالحرف. الاعتماد بين وله الشكل

التسارع الزاوي للجسم:

القوة التي تساوي حاصل ضرب كتلة نقطة معينة في تسارعها والاتجاه في الاتجاه المعاكس مباشرة لتسارع النقطة تسمى قوة القصور الذاتي.

القدرة هي الشغل الذي تبذله القوة في وحدة الزمن.

المعادلة الديناميكية الأساسية للحركة الدورانية

– عزم القصور الذاتي للجسم بالنسبة لمحور الدوران هو مجموع حاصل ضرب كتل النقاط المادية في مربع مسافاتها إلى هذا المحور

يمارس

جسم كتلته m، بمساعدة كابل ملفوف على أسطوانة قطرها d، يتحرك لأعلى أو لأسفل على طول مستوى مائل بزاوية ميل α. معادلة حركة الجسم S=f(t)، معادلة دوران الأسطوانة، حيث S بالأمتار؛ φ - بالراديان. ر – بالثواني. P وω هما، على التوالي، القوة والسرعة الزاوية على عمود الأسطوانة في لحظة نهاية التسارع أو بداية الكبح. الزمن t 1 - زمن التسارع (من السكون إلى سرعة معينة) أو زمن الكبح (من سرعة معينة إلى التوقف). معامل الاحتكاك المنزلق بين الجسم والمستوى هو -f. أهمل خسائر الاحتكاك على الأسطوانة، وكذلك كتلة الأسطوانة. عند حل المسائل، خذ g=10 m/s 2

رقم فار	ألفا، درجة	قانون الحركة	على سبيل المثال، الحركة	م، كجم	ر 1 ، ق	د، م	ف، كيلوواط	، راد/ث	F	مواطنه. كميات
		ق = 0.8 طن 2	تحت	-	-	0,20	4,0		0,20	م،ر 1
		φ=4ر2	تحت		1,0	0,30	-	-	0,16	ص، ω
		ق = 1.5 طن - ر 2	أعلى	-	-	-	4,5		0,20	م، د
		ω=15t-15t2	أعلى	-	-	0,20	3,0	-	0,14	م، ω
		ق = 0.5 طن 2	تحت		-	-	1,76		0,20	د،ر 1
		ق = 1.5 طن 2	تحت	-	0,6	0,24	9,9	-	0,10	م، ω
		ق = 0.9 طن 2	تحت		-	0,18	-		0,20	ف، ر 1
		φ=10t2	تحت		-	0,20	1,92	-	0,20	ف، ر 1
		ق=t-1.25t2	أعلى		-	-	-		0,25	ص، د
		φ=8t-20t 2	أعلى		-	0,20	-	-	0,14	ف، ω

مثال التنفيذ

المشكلة 1(الصورة 1).

الحل 1.حركة مستقيمة (الشكل 1، أ). النقطة التي تتحرك بشكل منتظم في وقت ما تلقت قانونًا جديدًا للحركة، وبعد فترة زمنية معينة توقفت. تحديد جميع الخصائص الكينماتيكية لحركة النقطة لحالتين؛ أ) الحركة على طريق مستقيم؛ ب) الحركة على طول مسار منحني نصف قطر انحناء ثابت r = 100 سم

الشكل 1 (أ).

قانون تغيير سرعة النقطة

نجد السرعة الابتدائية للنقطة من الشرط:

نجد زمن الكبح للتوقف من الحالة :

في، من هنا.

قانون حركة نقطة خلال فترة الحركة المنتظمة

المسافة التي تقطعها النقطة على طول المسار خلال فترة الكبح هي

قانون التغيير في التسارع العرضي لنقطة ما

ومن ثم يترتب على ذلك أنه خلال فترة الكبح تحركت النقطة ببطء متساوٍ، لأن التسارع العرضي يكون سالبًا وثابتًا في القيمة.

التسارع الطبيعينقاط على مسار مستقيم للحركة تساوي الصفر، أي. .

الحل 2.حركة منحنية (الشكل 1، ب).

الشكل 1 (ب)

في هذه الحالة، مقارنة بالحالة حركة مستقيمةتبقى جميع الخصائص الحركية دون تغيير، باستثناء التسارع الطبيعي.

قانون التغيير في التسارع الطبيعي لنقطة ما

التسارع الطبيعي لنقطة ما في اللحظة الأولى للفرملة

ترقيم مواضع النقاط على المسار المقبولة في الرسم: 1 – الموقف الحالىنقاط في حركة موحدة قبل بدء الكبح؛ 2 - موضع النقطة لحظة الكبح؛ 3 - الوضع الحالي للنقطة خلال فترة الكبح؛ 4- الوضع النهائي للنقطة.

المهمة 2.

يتم رفع الحمولة (الشكل 2، أ) باستخدام رافعة أسطوانية. قطر الأسطوانة d = 0.3m، وقانون دورانها هو .

استمر تسارع الأسطوانة حتى السرعة الزاوية. تحديد جميع الخصائص الحركية لحركة الأسطوانة والحمل.

حل. قانون التغير في السرعة الزاوية للأسطوانة. نجد السرعة الزاوية الأولية من الشرط: ; ولذلك، بدأ التسارع من حالة السكون. سنجد زمن التسارع من الشرط : . زاوية دوران الطبل خلال فترة التسارع.

يترتب على قانون التغيير في التسارع الزاوي للأسطوانة أنه خلال فترة التسارع تدور الأسطوانة بتسارع منتظم.

الخصائص الحركية للحمل تساوي الخصائص المقابلة لأي نقطة من حبل الجر، وبالتالي النقطة أ ملقاة على حافة الأسطوانة (الشكل 2، ب). وكما هو معروف، فإن الخصائص الخطية لنقطة من الجسم الدوار يتم تحديدها من خلال خصائصها الزاوية.

المسافة التي يقطعها الحمولة خلال فترة التسارع . سرعة الحمل في نهاية التسارع.

تسريع البضائع.

قانون حركة البضائع.

يمكن تحديد مسافة وسرعة وتسارع الحمل بشكل مختلف، من خلال قانون حركة الحمل الموجود:

المهمة 3.الحمل، الذي يتحرك بشكل منتظم لأعلى على طول مستوى دعم مائل، تلقى في وقت ما فرملة وفقًا لقانون الحركة الجديد ، حيث s بالأمتار وt بالثواني. كتلة الحمولة م = 100 كجم، معامل الاحتكاك المنزلق بين الحمولة والمستوى f = 0.25. حدد القوة F والقوة المؤثرة على حبل الجر لمدة لحظتين من الزمن: أ) حركة منتظمة قبل بدء الكبح؛

ب) لحظة الكبح الأولية. عند الحساب، خذ g=10 m/.

حل.نحدد الخصائص الحركية لحركة الحمولة.

قانون التغير في سرعة الحمل

السرعة الأولية للحمل (عند t=0)

تسارع البضائع

وبما أن التسارع سلبي، فإن الحركة تكون بطيئة.

1. حركة موحدة للحمل.

لتحديد القوة الدافعة F، نأخذ في الاعتبار توازن الحمل، والذي يتم التأثير عليه بواسطة نظام القوى المتقاربة: القوة على الكابل F، قوة جاذبية الحمل G=mg، رد فعل طبيعيدعم السطح N وقوة الاحتكاك الموجهة نحو حركة الجسم. حسب قانون الاحتكاك . نختار اتجاه المحاور الإحداثية كما هو موضح في الرسم، ونرسم معادلتي توازن للحمل:

يتم تحديد الطاقة الموجودة على الكابل قبل بدء الكبح من خلال الصيغة المعروفة

أين هو م / ث.

2. حركة بطيئة للبضائع.

وكما هو معروف، مع متفاوتة التحرك إلى الأمامالجسم فإن نظام القوى المؤثرة عليه في اتجاه الحركة غير متوازن. وفقًا لمبدأ دالمبيرت (طريقة الحركية)، يمكن اعتبار الجسم في هذه الحالة في حالة توازن مشروط إذا أضفنا إلى جميع القوى المؤثرة عليه قوة بالقصور الذاتي، يتم توجيه متجهها عكسًا لمتجه التسارع. يتم توجيه ناقل التسارع في حالتنا عكسًا لمتجه السرعة، نظرًا لأن الحمل يتحرك ببطء. نقوم بإنشاء معادلتين متوازنتين للحمل:

قم بتشغيل الكابل في بداية الكبح

أسئلة التحكم.

1. كيفية تحديد القيمة العدديةواتجاه سرعة النقطة في هذه اللحظة؟

2. ما الذي يميز المكونات العمودية والعرضية للتسارع الكلي؟

3. كيف يمكن الانتقال من التعبير عن السرعة الزاوية بالدقيقة -1 إلى التعبير عنها بالراد/الثانية؟

4. ماذا يسمى وزن الجسم؟ اسم وحدة قياس الكتلة

5. في أي حركة نقطة ماديةهل تنشأ قوة القصور الذاتي؟ ما هي قيمتها العددية وما هو اتجاهها؟

6. مبدأ دولة دالمبرت

7. هل تنشأ قوة القصور الذاتي أثناء الحركة المنحنية المنتظمة لنقطة مادية؟

8. ما هو عزم الدوران؟

9. كيف يتم التعبير عن العلاقة بين عزم الدوران والسرعة الزاوية لقوة مرسلة معينة؟

10. المعادلة الديناميكية الأساسية للحركة الدورانية.

العمل العملي رقم 7

"حساب هياكل القوة"

الهدف من العمل: تحديد القوة وأبعاد المقطع العرضي والحمل المسموح به

الخلفية النظرية.

بمعرفة عوامل القوة والخصائص الهندسية للمقطع أثناء تشوه الشد (الضغط)، يمكننا تحديد الإجهاد باستخدام الصيغ. ولفهم ما إذا كان الجزء الخاص بنا (العمود، والعتاد، وما إلى ذلك) سيتحمل الحمل الخارجي. من الضروري مقارنة هذه القيمة بالجهد المسموح به.

لذلك، معادلة القوة الثابتة

وعلى أساسه يتم حل 3 أنواع من المشاكل:

1) اختبار القوة

2) تحديد أبعاد القسم

3) تحديد الحمولة المسموح بها

لذلك، معادلة الصلابة الساكنة

وبناءً عليه، تم أيضًا حل 3 أنواع من المشكلات

معادلة قوة الشد الساكنة (الضغط).

1) النوع الأول - اختبار القوة

أي أننا نحل الطرف الأيسر ونقارنه بالإجهاد المسموح به.

2) النوع الثاني – تحديد أبعاد القسم

من الجانب الأيمن منطقة المقطع العرضي

دائرة القسم

ومن هنا القطر د

قسم المستطيل

ساحة القسم

أ = أ² (مم²)

قسم نصف دائرة

الأقسام: القناة، الشعاع I، الزاوية، الخ.

قيم المساحة - من الجدول المقبولة وفقًا لـ GOST

3) النوع الثالث هو تحديد الحمولة المسموح بها؛

اتخذت إلى الجانب الأصغر، عدد صحيح

يمارس

مهمة

أ) فحص القوة (حساب الاختبار)

بالنسبة لعارضة معينة، قم بإنشاء مخطط للقوى الطولية وتحقق من القوة في كلا القسمين. بالنسبة للمواد الخشبية (الصلب St3) تقبل

رقم الخيار
	12,5	5,3	-			-
		2,3			-	-
		4,2		-	-

ب) اختيار القسم (حساب التصميم)

بالنسبة لحزمة معينة، قم بإنشاء مخطط للقوى الطولية وحدد أبعاد المقطع العرضي في كلا القسمين. بالنسبة للمواد الخشبية (الصلب St3) تقبل

رقم الخيار
	1,9	2,5

	2,8	1,9
	3,2

ب) تحديد القوة الطولية المسموح بها

لشعاع معين، تحديد القيم المسموح بها للأحمال و،

بناء مخطط للقوى الطولية. بالنسبة للمواد الخشبية (الصلب St3) تقبل. عند حل المشكلة، افترض أن نوع التحميل هو نفسه في كلا قسمي الحزمة.

رقم الخيار
	-	-
			-	-
	-	-

مثال على إكمال المهمة

المشكلة 1(الصورة 1).

تحقق من قوة عمود مصنوع من ملفات تعريف I بحجم معين. بالنسبة لمادة العمود (الفولاذ St3)، تقبل ضغوط الشد المسموح بها وأثناء الضغط . في حالة التحميل الزائد أو التحميل الزائد بشكل كبير، حدد أحجام I-beam التي تضمن قوة العمود المثالية.

حل.

شعاع معين له قسمين 1، 2. حدود المقاطع هي الأقسام التي فيها قوى خارجية. نظرًا لأن القوى التي تحمل الحزمة تقع على طول المحور الطولي المركزي، فإن عامل قوة داخلي واحد فقط ينشأ في المقاطع العرضية - القوة الطولية، أي. هناك توتر (ضغط) للشعاع.

لتحديد القوة الطولية، نستخدم طريقة القسم. من خلال رسم قسم داخل كل قسم عقليًا، سنتخلص من الجزء السفلي الثابت من العارضة ونتركه للنظر فيه الجزء العلوي. في القسم 1، القوة الطولية ثابتة وتساوي

تشير علامة الطرح إلى أن الشعاع مضغوط في كلا القسمين.

نحن نبني مخططا للقوى الطولية. بعد رسم الخط الأساسي (الصفر) للمخطط الموازي لمحور الحزمة، نقوم برسم القيم التي تم الحصول عليها بشكل متعامد معها على مقياس تعسفي. كما ترون، تبين أن المخطط تم تحديده بخطوط مستقيمة موازية للقاعدة.

نحن نتحقق من قوة الأخشاب، أي. نحدد الإجهاد التصميمي (لكل قسم على حدة) ونقارنه بالإجهاد المسموح به. للقيام بذلك، نستخدم حالة قوة الضغط

حيث المساحة هي خاصية هندسية لقوة المقطع العرضي. من طاولة الفولاذ المدلفن نأخذ:

لشعاع I
لشعاع I

إختبار القوة:

تؤخذ قيم القوى الطولية بالقيمة المطلقة.

يتم ضمان قوة الشعاع، ومع ذلك، هناك حمل ناقص كبير (أكثر من 25٪)، وهو أمر غير مقبول بسبب الاستهلاك المفرط للمواد.

ومن شرط القوة نحدد الأبعاد الجديدة للكمرة I لكل قسم من الكمرات:
وبالتالي المنطقة المطلوبة

وفقًا لجدول GOST، نختار I-beam رقم 16، والذي؛

وبالتالي المنطقة المطلوبة

وفقًا لجدول GOST، نختار I-beam رقم 24، والذي ؛

مع أحجام I-beam المحددة، يحدث أيضًا حمل ناقص، ولكنه غير مهم (أقل من 5%)

المهمة رقم 2.

بالنسبة للعارضة ذات أبعاد المقطع العرضي المحددة، حدد قيم الحمل المسموح بها و. بالنسبة للمواد الخشبية (الفولاذ St3)، تقبل ضغوط الشد المسموح بها وأثناء الضغط .

حل.

تحتوي الحزمة المعطاة على قسمين 1، 2. هناك شد (ضغط) للحزمة.

باستخدام طريقة المقاطع نحدد القوة الطولية ونعبر عنها بالقوى المطلوبة و. نقوم بتنفيذ قسم داخل كل قسم، ونتخلص من الجزء الأيسر من العارضة ونتركه للنظر فيه الجانب الأيمن. في القسم 1، القوة الطولية ثابتة وتساوي

في القسم 2، القوة الطولية أيضًا ثابتة وتساوي

تشير علامة الزائد إلى أن العارضة ممتدة في كلا القسمين.

نحن نبني مخططا للقوى الطولية. تم تحديد المخطط بخطوط مستقيمة موازية للقاعدة.

من حالة قوة الشد نحدد قيم الأحمال المسموح بها وبعد حساب مساحات المقاطع العرضية المحددة مسبقًا:

أسئلة التحكم.

1. ما هي عوامل القوة الداخلية التي تنشأ في قسم الحزمة أثناء الشد والضغط؟

2. أكتب ظروف قوة الشد والضغط.

3. كيف يتم تحديد علامات القوة الطولية والضغط الطبيعي؟

4. كيف سيتغير الجهد إذا زادت مساحة المقطع العرضي بمقدار 4 مرات؟

5. هل تختلف ظروف القوة بالنسبة لحسابات الشد والضغط؟

6. في أي وحدات يتم قياس الجهد؟

7. أي واحد الخصائص الميكانيكيةتم اختياره كضغط نهائي للمواد المرنة والهشة؟

8. ما الفرق بين الإجهاد المحدود والإجهاد المسموح به؟

العمل العملي رقم 8

"حل المسائل لتحديد العزوم المركزية الرئيسية للقصور الذاتي للأشكال الهندسية المسطحة"

الهدف من العمل: تحديد لحظات القصور الذاتي للأجسام المسطحة ذات الشكل المعقد تحليليًا

الخلفية النظرية. يمكن التعبير عن إحداثيات مركز ثقل القسم من خلال اللحظة الثابتة:

حيث نسبة إلى محور الثور

نسبة إلى محور أوي

إن العزم الثابت لمساحة الشكل بالنسبة إلى محور يقع في نفس المستوى يساوي حاصل ضرب مساحة الشكل ومسافة مركز ثقله إلى هذا المحور. اللحظة الثابتة لها بعد. يمكن أن تكون اللحظة الثابتة موجبة أو سالبة أو تساوي الصفر (بالنسبة لأي محور مركزي).

لحظة القصور الذاتي المحورية لقسم ما هي مجموع منتجات أو تكامل المناطق الأولية المأخوذة على القسم بأكمله بمربعات مسافاتها إلى محور معين يقع في مستوى القسم قيد النظر.

لحظة محوريةيتم التعبير عن القصور الذاتي بالوحدات - . العزم المحوري للقصور الذاتي هو كمية موجبة دائمًا ولا تساوي الصفر.

تسمى المحاور التي تمر عبر مركز ثقل الشكل مركزية. تسمى لحظة القصور الذاتي حول المحور المركزي باللحظة المركزية للقصور الذاتي.

عزم القصور الذاتي حول أي محور يساوي المركز

ارسم مخططًا للنظام وحدد مركز الثقل عليه.إذا كان مركز الجاذبية الذي تم العثور عليه خارج نظام الكائنات، فقد تلقيت إجابة غير صحيحة. ربما تكون قد قمت بقياس المسافات من نقاط مرجعية مختلفة. كرر القياسات.

على سبيل المثال، إذا كان الأطفال يجلسون على الأرجوحة، فسيكون مركز الثقل في مكان ما بين الأطفال، وليس على يمين أو يسار الأرجوحة. كما أن مركز الثقل لن يتطابق أبدًا مع النقطة التي يجلس فيها الطفل.
هذه الحجج صالحة في الفضاء ثنائي الأبعاد. ارسم مربعًا يحتوي على كافة كائنات النظام. يجب أن يكون مركز الثقل داخل هذا المربع.

تحقق من حساباتك إذا حصلت على نتيجة صغيرة.إذا كانت النقطة المرجعية عند أحد طرفي النظام، فإن نتيجة صغيرة تضع مركز الثقل بالقرب من نهاية النظام. قد تكون هذه هي الإجابة الصحيحة، ولكن في الغالبية العظمى من الحالات تشير هذه النتيجة إلى وجود خطأ. عندما حسبت العزوم، هل قمت بضرب الأوزان والمسافات المقابلة لها؟ إذا أضفت الأوزان والمسافات بدلاً من الضرب، فستحصل على نتيجة أصغر بكثير.

قم بتصحيح الخطأ إذا وجدت مراكز ثقل متعددة.يحتوي كل نظام على مركز ثقل واحد فقط. إذا وجدت مراكز ثقل متعددة، فمن المرجح أنك لم تجمع كل اللحظات. مركز الجاذبية يساوي النسبةلحظة "الإجمالي" إلى الوزن "الإجمالي". ليست هناك حاجة لتقسيم "كل" لحظة على "كل" وزن: بهذه الطريقة سوف تجد موضع كل كائن.

تحقق من النقطة المرجعية إذا كانت الإجابة تختلف ببعض القيمة الصحيحة.في مثالنا، الإجابة هي 3.4 م، لنفترض أنك حصلت على الإجابة 0.4 م أو 1.4 م، أو رقم آخر ينتهي بـ ".4". هذا لأنك لم تختر الطرف الأيسر من اللوحة كنقطة بداية، بل نقطة تقع على اليمين تمامًا. في الواقع، إجابتك صحيحة بغض النظر عن النقطة المرجعية التي تختارها! فقط تذكر: النقطة المرجعية تكون دائمًا عند الموضع x = 0. إليك مثال:

في مثالنا، كانت النقطة المرجعية عند الطرف الأيسر من اللوحة، ووجدنا أن مركز الثقل كان على بعد 3.4 م من هذه النقطة المرجعية.
إذا اخترت كنقطة مرجعية نقطة تقع على بعد 1 م إلى اليمين من الطرف الأيسر للوحة، فستحصل على الإجابة 2.4 م، أي أن مركز الثقل يقع على بعد 2.4 م من النقطة المرجعية الجديدة، والتي ، بدوره، يقع على بعد متر واحد من الطرف الأيسر للوحة. وبالتالي، فإن مركز الجاذبية يقع على مسافة 2.4 + 1 = 3.4 م من الطرف الأيسر للوحة. اتضح أنها إجابة قديمة!
ملحوظة: عند قياس المسافات، تذكر أن المسافات إلى النقطة المرجعية "اليسار" سالبة، وإلى النقطة المرجعية "اليمنى" موجبة.

قياس المسافات في خطوط مستقيمة.لنفترض أن هناك طفلين على الأرجوحة، ولكن أحدهما أطول بكثير من الآخر، أو أن أحدهما معلق أسفل اللوحة بدلاً من الجلوس عليها. تجاهل هذا الاختلاف وقم بقياس المسافات على طول الخط المستقيم للوحة. قياس المسافات بالزوايا سيعطي نتائج قريبة ولكن ليست دقيقة تمامًا.

بالنسبة لمشكلة اللوح المتأرجح، تذكر أن مركز الثقل يقع بين الطرفين الأيمن والأيسر للوحة. ستتعلم لاحقًا حساب مركز ثقل الأنظمة ثنائية الأبعاد الأكثر تعقيدًا.

مؤلف: لنأخذ جسمًا ذو شكل تعسفي. هل من الممكن تعليقه على خيط بحيث يحتفظ بموضعه بعد تعليقه (أي لا يبدأ في الدوران) عندما أيالتوجه الأولي (الشكل 27.1)؟

بمعنى آخر، هل هناك نقطة يكون عندها مجموع عزوم الجاذبية المؤثرة على أجزاء مختلفة من الجسم مساويًا للصفر عندها؟ أياتجاه الجسم في الفضاء؟

قارئ: نعم أعتقد ذلك. هذه النقطة تسمى مركز ثقل الجسم.

دليل.من أجل البساطة، دعونا نفكر في جسم على شكل لوحة مسطحة ذات شكل عشوائي، موجهة بشكل عشوائي في الفضاء (الشكل 27.2). لنأخذ نظام الإحداثيات X 0فيمع البداية في مركز الكتلة - النقطة مع، ثم س ج = 0, في ج = 0.

دعونا نتخيل هذا الجسم كمجموعة عدد كبيرالجماهير النقطة م ط، يتم تحديد موضع كل منها بواسطة ناقل نصف القطر.

بحكم التعريف، مركز الكتلة هو الإحداثيات س ج = .

منذ في نظام الإحداثيات اعتمدنا س ج= 0 ثم . دعونا نضرب هذه المساواة زونحصل

كما يظهر في الشكل. 27.2، | × ط| - هذا هو كتف القوة. و إذا × ط> 0، ثم لحظة القوة م ط> 0، وإذا س ي < 0, то إم جي < 0, поэтому с учетом знака можно утверждать, что для любого × طعزم القوة سيكون متساويا م أنا = م أنا gx أنا .ثم المساواة (1) تعادل المساواة حيث م ط– لحظة الجاذبية . وهذا يعني أنه مع الاتجاه التعسفي للجسم، فإن مجموع لحظات الجاذبية المؤثرة على الجسم سيكون مساوياً للصفر بالنسبة إلى مركز كتلته.

لكي يكون الجسم الذي نفكر فيه في حالة توازن، من الضروري أن نطبق عليه عند هذه النقطة معقوة ت = ملغ، موجهة عموديا إلى أعلى. لحظة هذه القوة بالنسبة إلى النقطة معيساوي الصفر.

وبما أن تفكيرنا لم يعتمد بأي شكل من الأشكال على مدى دقة توجيه الجسم في الفضاء، فقد أثبتنا أن مركز الثقل يتزامن مع مركز الكتلة، وهو ما كنا بحاجة إلى إثباته.

المشكلة 27.1.أوجد مركز ثقل قضيب طوله عديم الوزن ل، في نهاياتها يتم تثبيت كتلتين نقطيتين ت 1 و ت 2 .

ت 1 ت 2 ل	حل. لن نبحث عن مركز الجاذبية، بل عن مركز الكتلة (لأنهما نفس الشيء). دعونا نقدم المحور X(الشكل 27.3). أرز. 27.3
س ج =?

إجابة: على مسافة من الكتلة ت 1 .

قف! قرر بنفسك: B1 – B3.

البيان 1 . إذا كان لجسم مسطح متجانس محور تماثل، فإن مركز الثقل يقع على هذا المحور.

في الواقع، لأي كتلة نقطة م ط، الواقعة على يمين محور التماثل، توجد نفس الكتلة النقطية الموجودة بشكل متناظر بالنسبة للنقطة الأولى (الشكل 27.4). في هذه الحالة، مجموع لحظات القوى.

بما أنه يمكن تمثيل الجسم بأكمله مقسمًا إلى أزواج متشابهة من النقاط، فإن إجمالي عزم الجاذبية بالنسبة لأي نقطة تقع على محور التماثل يساوي صفرًا، مما يعني أن مركز ثقل الجسم يقع على هذا المحور . وهذا يؤدي إلى نتيجة مهمة: إذا كان لجسم عدة محاور تماثل فإن مركز ثقله يقع عند تقاطع هذه المحاور(الشكل 27.5).

أرز. 27.5

البيان 2. إذا كان لجسمين كتلة ت 1 و ت 2 متصلان بواحد، ثم يقع مركز ثقل مثل هذا الجسم على قطعة خط مستقيم تربط بين مركزي ثقل الجسمين الأول والثاني (الشكل 27.6).

أرز. 27.6 أرز. 27.7

دليل.دعونا نضع الجسم المركب بحيث تكون القطعة التي تربط مراكز ثقل الأجسام رأسية. ثم مجموع عزوم جاذبية الجسم الأول بالنسبة للنقطة مع 1 يساوي صفرًا، ومجموع عزوم جاذبية الجسم الثاني بالنسبة إلى النقطة مع 2 يساوي الصفر (الشكل 27.7).

لاحظ أن كتفخطورة أي نقطة الكتلة ر طالشيء نفسه بالنسبة لأي نقطة ملقاة على القطعة مع 1 مع 2، وبالتالي عزم الجاذبية بالنسبة لأي نقطة تقع على القطعة مع 1 مع 2، نفس الشيء. وبالتالي، فإن قوة الجاذبية للجسم بأكمله تساوي صفرًا بالنسبة إلى أي نقطة على القطعة مع 1 مع 2. وبالتالي، فإن مركز ثقل الجسم المركب يقع على القطعة مع 1 مع 2 .

يتبع البيان 2 استنتاجًا عمليًا مهمًا، والذي تمت صياغته بوضوح في شكل تعليمات.

تعليمات،

كيفية العثور على مركز ثقل جسم صلب إذا كان من الممكن كسره

إلى أجزاء تكون مواقع مراكز ثقل كل منها معروفة

1. يجب استبدال كل جزء بكتلة تقع في مركز ثقل ذلك الجزء.

2. ابحث عن مركز الكتلة(وهذا هو نفس مركز الثقل) لنظام الكتل النقطية الناتج عن طريق اختيار نظام إحداثي مناسب X 0في، وفقا للصيغ:

في الواقع، دعونا نرتب الجسم المركب بحيث يكون الجزء مع 1 مع 2 ـ كان أفقياً، وعلقه على الخيوط عند نقاط مع 1 و مع 2 (الشكل 27.8، أ). من الواضح أن الجسم سيكون في حالة توازن. ولن يختل هذا التوازن إذا استبدلنا كل جسم بكتل نقطية ت 1 و ت 2 (الشكل 27.8، ب).

أرز. 27.8

قف! قرر بنفسك: C3.

المشكلة 27.2.على قمتين مثلث متساوي الاضلاعيتم وضع كرات من الكتلة تكل. تم وضع كرة كتلتها 2 عند الرأس الثالث ت(الشكل 27.9، أ). جانب المثلث أ. تحديد مركز ثقل هذا النظام.