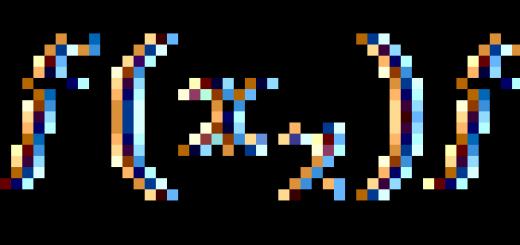Graph theory. Practical application of graph theory History of graphs

The mathematician Leonhard Euler (1707-1783) is considered to be the founder of graph theory. The history of the emergence of this theory can be traced through the correspondence of the great scientist. Here is a translation of the Latin text, which is taken from Euler's letter to the Italian mathematician and engineer Marinoni, sent from St. Petersburg on March 13, 1736 [see. pp. 41-42]:

“Once I was offered the problem of an island located in the city of Koenigsberg and surrounded by a river across which seven bridges are thrown. The question is whether anyone can continuously bypass them, passing only once through each bridge. has not yet been able to do this, but no one has proved that it is impossible. This question, although banal, seemed to me, however, noteworthy because neither geometry, nor algebra, nor combinatorial art is sufficient for its solution... through any number and any number of bridges, or not. The Konigsberg bridges are located so that they can be represented in the following figure[fig.1] , where A denotes an island, and B, C and D are parts of the continent separated from each other by river branches. The seven bridges are labeled a, b, c, d, e, f, g".

(FIGURE 1.1)

Regarding the method he discovered for solving problems of this kind, Euler wrote [see. pp. 102-104]:

"This solution, by its nature, seems to have little to do with mathematics, and it is not clear to me why this solution should be expected from a mathematician rather than from any other person, for this solution is supported by reason alone, and there is no need to involve to find this solution, any laws inherent in mathematics. So, I do not know how it turns out that questions that have very little to do with mathematics are more likely to be resolved by mathematicians than by others. "

So is it possible to get around the Königsberg bridges by passing only once through each of these bridges? To find the answer, let's continue Euler's letter to Marinoni:

0"The question is to determine whether it is possible to get around all these seven bridges, passing through each only once, or not. My rule leads to the following solution to this question. First of all, you need to look at how many sections are separated by water, - such that there is no other way from one to another, except through the bridge.In this example, there are four such sections - A, B, C, D. Next, you need to distinguish whether the number of bridges leading to these individual sections is even or odd So, in our case, five bridges lead to section A, and three bridges to the rest, i.e. The number of bridges leading to individual sections is odd, and this one is already enough to solve the problem.When this is determined, we apply the following rule: if the number of bridges leading to each individual section were even, then the bypass, about which in question, would be possible, and at the same time it would be possible to start this detour from any section. If, however, two of these numbers were odd, for only one cannot be odd, then even then the transition could take place, as prescribed, but only the beginning of the detour must necessarily be taken from one of those two sections to which no path leads. even number bridges. If, finally, there were more than two sections to which an odd number of bridges leads, then such a movement is generally impossible ... if other, more serious problems could be cited here, this method could be even more useful and should not be neglected " .

The rationale for the above rule can be found in a letter from L. Euler to his friend Eler dated April 3 of the same year. We will retell below an excerpt from this letter.

The mathematician wrote that the transition is possible if there are no more than two areas in the forking section of the river, to which an odd number of bridges leads. In order to make it easier to imagine this, we will erase the already passed bridges in the figure. It is easy to check that if we start moving in accordance with Euler's rules, cross one bridge and erase it, then the figure will show a section where again there are no more than two areas to which an odd number of bridges lead, and in the presence of areas with an odd number bridges we will be located in one of them. Continuing to move so on, we will pass through all the bridges once.

The history of the bridges of the city of Koenigsberg has a modern continuation. Let's open, for example, a school textbook on mathematics edited by N.Ya. Vilenkin for the sixth grade. In it, on page 98, under the heading of the development of mindfulness and ingenuity, we will find a problem that is directly related to the one that Euler once solved.

Problem #569. There are seven islands on the lake, which are interconnected as shown in Figure 1.2. Which island should the boat take travelers to so that they can cross each bridge and only once? Why travelers cannot be delivered to the island A?

Decision. Since this problem is similar to the Königsberg bridge problem, we will also use Euler's rule to solve it. As a result, we get the following answer: the boat must deliver travelers to the island E or F so that they can cross each bridge once. From the same Euler rule follows the impossibility of the required detour if it starts from the island A.

In conclusion, we note that the Königsberg bridge problem and similar problems, together with a set of methods for studying them, constitute a very important branch of mathematics in practical terms, called graph theory. The first work on graphs belonged to L. Euler and appeared in 1736. Later on, Koenig (1774-1833), Hamilton (1805-1865) worked on graphs, among modern mathematicians - K. Berzh, O. Ore, A. Zykov.

VLADIMIR STATE PEDAGOGICAL UNIVERSITY

ESSAY

"GRAPH THEORY"

Performed:

Zudina T.V.

Vladimir 2001

1. Introduction

2. The history of the emergence of graph theory

3. Basic definitions of graph theory

4. Basic theorems of graph theory

5. Tasks for the application of graph theory

6. Application of graph theory in school course mathematics

7. Application of graph theory in various fields science and technology

8. Recent advances in graph theory

§one. HISTORY OF GRAPH THEORY.

“Once I was offered the problem of an island located in the city of Koenigsberg and surrounded by a river across which seven bridges are thrown. The question is whether anyone can continuously bypass them, passing only once through each bridge. so far he has not been able to do this, but no one has proved that it is impossible. This question, although banal, seemed to me, however, worthy of attention because neither geometry, nor algebra, nor combinatorial art is sufficient for its solution ... After much deliberation, I found an easy rule, based on a completely convincing proof, with the help of which it is possible to immediately determine in all problems of this kind whether such a circuit can be made through any number and arbitrarily located bridges or cannot. so that they can be represented in the following figure[fig.1] , on which A stands for an island and B , C and D are parts of the continent separated from each other by river branches. The seven bridges are marked with letters a , b , c , d , e , f , g ".

(FIGURE 1.1)

Regarding the method he discovered for solving problems of this kind, Euler wrote [see. pp. 102-104]:

So is it possible to get around the Königsberg bridges by passing only once through each of these bridges? To find the answer, let's continue Euler's letter to Marinoni:

"The question is to determine whether it is possible to get around all these seven bridges, passing through each only once, or not. My rule leads to the following solution to this question. First of all, you need to look at how many sections are separated by water - such , which have no other transition from one to another, except through the bridge.In this example, there are four such sections - A , B , C , D . Next, one must distinguish whether the number of bridges leading to these individual sections is even or odd. So, in our case, five bridges lead to section A, and three bridges to the rest, i.e., the number of bridges leading to individual sections is odd, and this one is already enough to solve the problem. When this is determined, we apply the following rule: if the number of bridges leading to each individual section were even, then the bypass in question would be possible, and at the same time it would be possible to start this bypass from any section. If, however, two of these numbers were odd, for only one cannot be odd, then even then the transition could take place, as prescribed, but only the beginning of the bypass must necessarily be taken from one of those two sections to which the odd number leads. bridges. If, finally, there were more than two sections to which an odd number of bridges leads, then such a movement is generally impossible ... if other, more serious problems could be cited here, this method could be even more useful and should not be neglected " .

The rationale for the above rule can be found in a letter from L. Euler to his friend Eler dated April 3 of the same year. We will retell below an excerpt from this letter.

(FIGURE 1.2)

§2. MAIN THEOREMS OF GRAPH THEORY

Graph theory, as mentioned above, is a mathematical discipline created by the efforts of mathematicians, so its presentation includes the necessary rigorous definitions. So, let's proceed to the organized introduction of the basic concepts of this theory.

Definition 2.01. Count is called the totality finite number points called peaks graph, and pairwise connecting some of these vertices of lines, called ribs or arcs graph.

This definition can be formulated differently: count is called a non-empty set of points ( peaks) and segments ( ribs), both ends of which belong to a given set of points (see Fig. 2.1).

(FIGURE 2.1)

In what follows, the vertices of the graph will be denoted by Latin letters A , B ,C ,D. Sometimes the graph as a whole will be denoted by one capital letter.

Definition 2.02. The vertices of a graph that do not belong to any edge are called isolated .

Definition 2.03. A graph consisting only of isolated vertices is called zero - count .

Designation: O " - a graph with vertices that does not have edges (Fig. 2.2).

(FIGURE 2.2)

Definition 2.04. A graph in which each pair of vertices is connected by an edge is called complete .

Designation: U " – graph consisting of n vertices and edges connecting all possible pairs of these vertices. Such a graph can be represented as n- a square in which all diagonals are drawn (Fig. 2.3).

(FIGURE 2.3)

Definition 2.05. Degree peaks is the number of edges that the vertex belongs to.

Designation: p (A) – vertex degree A . For example, in Figure 2.1: p (A)=2, p (B)=2, p (C)=2, p (D)=1, p (E)=1.

Definition 2.06. Count, degree of all k whose vertices are the same is called homogeneous count degrees k .

Figures 2.4 and 2.5 show homogeneous graphs of the second and third degrees.

(FIGURE 2.4 and 2.5)

Definition 2.07. Supplement given count is called a graph consisting of all edges and their ends, which must be added to the original graph in order to obtain a complete graph.

Figure 2.6 shows the original graph G , consisting of four vertices and three segments, and in Figure 2.7 - the complement of this graph - the graph G " .

(FIGURE 2.6 and 2.7)

We see that in figure 2.5 the ribs AC and BD intersect at a point that is not a vertex of the graph. But there are cases when a given graph needs to be represented on a plane in such a way that its edges intersect only at the vertices (this issue will be discussed in detail later, in paragraph 5).

Definition 2.08. A graph that can be represented in a plane in such a way that its edges intersect only at the vertices is called flat .

For example, Figure 2.8 shows a planar graph that is isomorphic (equal to) the graph in Figure 2.5. However, note that not every graph is planar, although the converse is true, i.e., any planar graph can be represented in the usual way.

(FIGURE 2.8)

Definition 2.09. A polygon of a planar graph that does not contain any vertices or edges of the graph inside is called it edge .

Historically, graph theory was born more than two hundred years ago in the course of solving puzzles. For a very long time, she was away from the main directions of research of scientists, was in the realm of mathematics in the position of Cinderella, whose talents were fully revealed only when she was in the center of general attention.

The first work on graph theory, by the famous Swiss mathematician L. Euler, appeared in 1736. The impetus for the development of graph theory was at the turn of the 19th and 20th centuries, when the number of works in the field of topology and combinatorics, with which it has the closest ties, increased dramatically. kinship. Graphs began to be used in the construction of electrical circuit diagrams and molecular circuits. As a separate mathematical discipline, graph theory was first introduced in the work of the Hungarian mathematician Koenig in the 30s of the twentieth century.

AT recent times Graphs and related research methods organically permeate almost all of modern mathematics at different levels. Graph theory is considered as one of the branches of topology; it is also directly related to algebra and number theory. Graphs are effectively used in planning and management theory, scheduling theory, sociology, mathematical linguistics, economics, biology, medicine, and geography. Graphs are widely used in such areas as programming, finite automata theory, electronics, in solving probabilistic and combinatorial problems, finding the maximum flow in the network, shortest distance, maximum matching, checking the planarity of a graph, etc. As a special class, optimization problems on graphs can be distinguished. Mathematical fun and puzzles are also part of graph theory, such as the famous four-color problem, which intrigues mathematicians to this day. Graph theory is developing rapidly, finding new applications and waiting for young researchers.

Graph theory provides a simple and powerful tool for building models and solving problems of ordering objects. Currently, there are many problems where it is required to build some complex systems with the help of a certain ordering of their elements. These include scheduling industrial production, tasks of the theory of network planning and control, tactical and logical tasks, problems of building communication systems and researching information transfer processes, choosing optimal routes and flows in networks, methods for building electrical networks, identification problems in organic chemistry and methods for switching switching circuits. The same is true of a large range of economic tasks, the problems of choosing a structure social groups etc. Thus, the area of possible applications of graph theory is very wide. Combinatorial methods for finding the required ordering of objects differ significantly from classical methods for analyzing the behavior of systems using equations. In addition to the language of graph theory, the problems of ordering objects can be formulated in terms of the theory of matrices with elements zero - one.

With with good reason it can be said that graph theory is one of the simplest and most elegant branches of modern mathematics with a wide range of applications. Based on the simplest ideas and elements: points connected by lines, graph theory builds a rich variety of forms from them, endows these forms with interesting properties, and as a result becomes a useful tool in the study of a wide variety of systems. In addition, graph theory has made a great contribution to the development of methods for analyzing a wide range of combinatorial problems. If, in addition to the basic purely structural relations, some quantitative characteristics points and lines that form a graph, then instead of the concepts of a graph, you can use the concept of a network. Examples include electrical networks, work execution networks in flow network projects. At the same time, certain quantitative characteristics of energy, costs and flow are associated with the edge of the network.

MUNICIPAL AUTONOMOUS GENERAL EDUCATIONAL INSTITUTION SECONDARY EDUCATIONAL SCHOOL № 2

Prepared

Legkokonets Vladislav, 10A student

Practical use Graph Theories

Supervisor

L.I. Noskova, mathematics teacher

st.Bryukhovetskaya

2011

1.Introduction………………………………………………………………………….………….3

2. The history of the emergence of graph theory………………………………………….………..4

3.Basic definitions and theorems of graph theory……………………………….………6

4. Tasks solved with the help of graphs……………………………..……………………..8

4.1 Famous tasks………………………………….………………………...8

4.2 Some interesting tasks………………………………….……………..9

5. Application of graphs in various areas of people's lives……………………………...11

6. Problem solving……………………………………………………………………………...12

7. Conclusion………………….…………………………………………………………….13

8. List of references………….…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….

9.Appendix……………………………………………………………………….…………15

Introduction

Born in solving puzzles and entertaining games, graph theory has now become a simple, accessible and powerful tool for solving problems related to a wide range of problems. Graphs are literally ubiquitous. In the form of graphs, you can, for example, interpret road maps and electrical circuits, geographic Maps and molecules chemical compounds, connections between people and groups of people. Over the past four decades, graph theory has become one of the most rapidly developing branches of mathematics. This is driven by the demands of a rapidly expanding application area. It is used in the design of integrated circuits and control circuits, in the study of automata, logical circuits, program flowcharts, in economics and statistics, chemistry and biology, in scheduling theory. So relevance The topic is due, on the one hand, to the popularity of graphs and related research methods, and on the other hand, an undeveloped, integral system for its implementation.

The solution of many life problems requires long calculations, and sometimes these calculations do not bring success. This is what it consists research problem. The question arises: is it possible to find a simple, rational, short and elegant solution for their solution. Is it easier to solve problems if you use graphs? It determined topic of my research: "Practical Application of Graph Theory"

aim research was with the help of graphs to learn how to quickly solve practical problems.

Research hypothesis. The graph method is very important and widely used in various fields of science and human life.

Research objectives:

1. To study the literature and Internet resources on this issue.

2. Check the effectiveness of the graph method in solving practical problems.

3. Make a conclusion.

Practical significance research is that the results will undoubtedly arouse the interest of many people. Haven't any of you tried to build a family tree of your family? And how to do it correctly? The head of a transport company probably has to solve the problem of more profitable use of transport when transporting goods from a destination to several settlements. Each student faced logical transfusion tasks. It turns out they are solved with the help of graphs easily.

The following methods are used in the work: observation, search, selection, analysis.

The history of the emergence of graph theory

“Once I was given a problem about an island located in the city of Koenigsberg and surrounded by a river, across which seven bridges are thrown.

[Appendix Fig.1] The question is whether anyone can go around them continuously, passing only once through each bridge. And then I was informed that no one had yet been able to do this, but no one had proved that it was impossible. This question, although banal, seemed to me, however, worthy of attention because neither geometry, nor algebra, nor combinatorial art is sufficient for its solution. After much thought, I found an easy rule, based on a completely convincing proof, with the help of which in all problems of this kind one can immediately determine whether such a round can be made through any number and arbitrarily located bridges or cannot. The Konigsberg bridges are located so that they can be represented in the following figure [Appendix Fig.2], where A denotes an island, and B , C and D are parts of the continent separated from each other by river branches

Regarding the method he discovered for solving problems of this kind, Euler wrote:

So is it possible to get around the Königsberg bridges by passing only once through each of these bridges? To find the answer, let's continue Euler's letter to Marinoni:

"The question is to determine whether it is possible to get around all these seven bridges, passing through each only once, or not. My rule leads to the following solution to this question. First of all, you need to look at how many sections are separated by water - such , which have no other transition from one to another, except through the bridge.In this example, there are four such sections - A, B, C, D. Next, you need to distinguish whether the number of bridges leading to these individual sections is even or odd. So, in our case, five bridges lead to section A, and three bridges to the rest, i.e. The number of bridges leading to individual sections is odd, and this one is already enough to solve the problem.When this is determined, we apply the following rule : if the number of bridges leading to each individual section were even, then the detour in question would be possible, and at the same time it would be possible to start this detour from any section. would be odd, for only one be n if it cannot be even, then even then the transition could take place, as prescribed, but only the beginning of the detour must certainly be taken from one of those two sections to which an odd number of bridges leads. If, finally, there were more than two sections to which an odd number of bridges leads, then such a movement is generally impossible ... if other, more serious problems could be cited here, this method could be even more useful and should not be neglected " .

Basic definitions and theorems of graph theory

Graph theory is a mathematical discipline created by the efforts of mathematicians, so its presentation includes the necessary rigorous definitions. So, let's proceed to the organized introduction of the basic concepts of this theory.

Definition 1. A graph is a collection of a finite number of points, called the vertices of the graph, and pairwise connecting some of these vertices of lines, called the edges or arcs of the graph.

This definition can be formulated differently: a graph is a non-empty set of points (vertices) and segments (edges), both ends of which belong to a given set of points

In the future, we will denote the vertices of the graph in Latin letters A, B, C, D. Sometimes the graph as a whole will be denoted by a single capital letter.

Definition 2. The vertices of the graph that do not belong to any edge are called isolated.

Definition 3. A graph consisting only of isolated vertices is called zero - count .

Notation: O "– a graph with vertices and no edges

Definition 4. A graph in which each pair of vertices is connected by an edge is called complete.

Designation: U" – a graph consisting of n vertices and edges connecting all possible pairs of these vertices. Such a graph can be represented as an n-gon in which all diagonals are drawn

Definition 5. The degree of a vertex is the number of edges that the vertex belongs to.

Definition 6. A graph whose degrees of all k vertices are the same is called a homogeneous graph of degree k .

Definition 7. The complement of a given graph is a graph consisting of all the edges and their ends that must be added to the original graph in order to obtain a complete graph.

Definition 8. A graph that can be represented in a plane in such a way that its edges intersect only at the vertices is called planar.

Definition 9. A polygon of a planar graph that does not contain any vertices or edges of the graph inside is called its face.

The concepts of a plane graph and graph faces are used in solving problems for the "correct" coloring of various maps.

Definition 10. A path from A to X is a sequence of edges leading from A to X such that every two adjacent edges have a common vertex and no edge occurs more than once.

Definition 11. A cycle is a path where the start and end points are the same.

Definition 12. A simple cycle is a cycle that does not pass through any of the vertices of the graph more than once.

Definition 13. long way , laid on a loop , is the number of edges of this path.

Definition 14. Two vertices A and B in a graph are called connected (disconnected) if there exists (does not exist) a path leading from A to B in it.

Definition 15. A graph is called connected if every two of its vertices are connected; if the graph contains at least one pair of disconnected vertices, then the graph is called disconnected.

Definition 16. A tree is a connected graph that does not contain cycles.

A three-dimensional model of a graph-tree is, for example, a real tree with its intricately branched crown; the river and its tributaries also form a tree, but already flat - on the surface of the earth.

Definition 17. A disconnected graph consisting solely of trees is called a forest.

Definition 18. A tree, all n vertices of which are numbered from 1 to n, is called a tree with renumbered vertices.

So, we have considered the main definitions of graph theory, without which it would be impossible to prove theorems, and, consequently, to solve problems.

Problems solved using graphs

Famous Challenges

The traveling salesman problem

The traveling salesman problem is one of the famous problems in the theory of combinatorics. It was put up in 1934, and the best mathematicians broke their teeth about it.

The problem statement is the following.
The traveling salesman (traveling merchant) must leave the first city, visit cities 2,1,3..n once in an unknown order, and return to the first city. Distances between cities are known. In what order should the cities be traversed so that the closed path (tour) of the traveling salesman is the shortest?

Method for solving the traveling salesman problem

Greedy Algorithm “go to the nearest (which you have not yet entered) city.”
This algorithm is called “greedy” because in the last steps you have to pay dearly for greed.
Consider for example the network in Figure [app fig.3] representing a narrow rhombus. Let the salesman start from city 1. The “go to the nearest city” algorithm will take him to city 2, then 3, then 4; on the last step, you will have to pay for greed, returning along the long diagonal of the rhombus. The result is not the shortest, but the longest tour.

The problem of the Königsberg bridges.

The task is formulated as follows.
The city of Konigsberg is located on the banks of the Pregel River and two islands. Different parts of the city were connected by seven bridges. On Sundays, the townspeople took walks around the city. Question: is it possible to make a walk in such a way that, having left the house, come back, having passed exactly once over each bridge.
Bridges over the Pregel river are located as in the picture[Appendix Fig.1].

Consider a graph corresponding to the bridge scheme [appendix fig.2].

To answer the question of the problem, it is enough to find out whether the graph is Euler. (At least one vertex must have an even number of bridges). It is impossible, walking around the city, to go through all the bridges once and come back.

Several interesting challenges

1. "Routes".

Task 1

As you remember, the hunter dead souls Chichikov visited famous landowners once each. He visited them in the following order: Manilov, Korobochka, Nozdrev, Sobakevich, Plyushkin, Tentetnikov, General Betrishchev, Petukh, Konstanzholgo, Colonel Koshkarev. A diagram was found on which Chichikov sketched mutual arrangement estates and country roads connecting them. Determine which estate belongs to whom, if Chichikov did not pass any of the roads more than once [appendix fig.4].

Decision:

According to the road map, it can be seen that Chichikov began his journey with the E estate, and ended with the O estate. We notice that only two roads lead to the estates B and C, so Chichikov had to drive along these roads. Let's mark them with bold lines. The sections of the route passing through A are determined: AC and AB. Chichikov did not travel on the roads AE, AK and AM. Let's cross them out. Let's mark with a thick line ED ; cross out DK . Cross out MO and MN; mark with a bold line MF ; cross out FO ; we mark FH , NK and KO with a bold line. Let us find the only possible route under the given condition. And we get: the estate E - belongs to Manilov, D - Korobochka, C - Nozdrev, A - Sobakevich, V - Plyushkin, M - Tentetnikov, F - Betrishchev, N - Petukh, K - Konstanzholgo, O - Koshkarev [app fig.5].

Task 2

The figure shows a map of the area [appendix fig.6].

You can only move in the direction of the arrows. Each point can be visited no more than once. In how many ways can you get from point 1 to point 9? Which route is the shortest and which is the longest.

Decision:

Sequentially "stratify" the scheme into a tree, starting from vertex 1 [app fig.7]. Let's get a tree. Number possible ways hits from 1 to 9 is equal to the number of "hanging" vertices of the tree (there are 14 of them). Obviously the shortest path is 1-5-9; the longest is 1-2-3-6-5-7-8-9.

2 "Groups, dating"

Task 1

Participants of the music festival, having met, exchanged envelopes with addresses. Prove that:

a) an even number of envelopes were sent in total;

b) the number of participants who exchanged envelopes an odd number of times is even.

Solution: Let the festival participants be A 1 , A 2 , A 3 . . . , And n are the vertices of the graph, and the edges connect pairs of vertices representing guys who exchanged envelopes [Appendix Fig.8]

Decision:

a) the degree of each vertex A i shows the number of envelopes that participant A i gave to his friends. Total number transferred envelopes N is equal to the sum of the degrees of all vertices of the graph N = step. A 1 + step. A 2 + + . . . + step. And n -1 + step. And n , N =2p , where p is the number of graph edges, i.e. N is even. Therefore, an even number of envelopes were sent;

b) in the equality N = step. A 1 + step. A 2 + + . . . + step. And n -1 + step. And n the sum of odd terms must be even, and this can only be if the number of odd terms is even. And this means that the number of participants who exchanged envelopes an odd number of times is even.

Task 2

Once Andrei, Boris, Volodya, Dasha and Galya agreed to go to the cinema in the evening. They decided to agree on the choice of the cinema and the session by phone. It was also decided that if it was not possible to phone someone, then the trip to the cinema would be cancelled. In the evening, not everyone gathered at the cinema, and therefore the visit to the cinema fell through. The next day, they began to find out who called whom. It turned out that Andrey called Boris and Volodya, Volodya called Boris and Dasha, Boris called Andrey and Dasha, Dasha called Andrey and Volodya, and Galya called Andrey, Volodya and Boris. Who was unable to phone and therefore did not come to the meeting?

Decision:

Let's draw five points and designate them with the letters A, B, C, D, E. These are the first letters of the names. Let's connect those dots that correspond to the names of the guys who called each other.

[app fig.9]

It can be seen from the picture that each of the guys - Andrey, Boris and Volodya - phoned everyone else. That's why these guys came to the cinema. But Galya and Dasha failed to call each other (points D and D are not connected by a segment) and therefore, in accordance with the agreement, they did not come to the cinema.

The use of graphs in various areas of people's lives

In addition to the examples given, graphs are widely used in construction, electrical engineering, management, logistics, geography, mechanical engineering, sociology, programming, automation of technological processes and industries, psychology, and advertising. So, from all of the above, the practical value of graph theory irrefutably follows, the proof of which was the goal of this study.

In any field of science and technology, you meet with graphs. Graphs are wonderful mathematical objects with which you can solve mathematical, economic and logical problems, various puzzles and simplify the conditions of problems in physics, chemistry, electronics, automation. It is convenient to formulate many mathematical facts in the language of graphs. Graph theory is part of many sciences. Graph theory is one of the most beautiful and visual mathematical theories. Recently, graph theory has found more and more applications in applied issues. Even computer chemistry has emerged - a relatively young field of chemistry based on the application of graph theory.

Molecular graphs, used in stereochemistry and structural topology, chemistry of clusters, polymers, etc., are undirected graphs that display the structure of molecules [app fig.10]. The vertices and edges of these graphs correspond to the corresponding atoms and chemical bonds between them.

Molecular graphs and trees: [app fig.10] a, b - multigraphs resp. ethylene and formaldehyde; in-mol. isomers of pentane (trees 4, 5 are isomorphic to tree 2).

In the stereochemistry of organisms, the most often use molecular trees - the main trees of molecular graphs, which contain only all the vertices corresponding to C atoms. trees and the establishment of their isomorphism allow you to determine the pier. structures and find total number isomers of alkanes, alkenes and alkynes

Protein networks

Protein networks - groups of physically interacting proteins that function in a cell jointly and in a coordinated manner, controlling the interconnected processes occurring in the body [app fig. eleven].

Hierarchical system graph called a tree. Distinctive feature of a tree is that there is only one path between any two of its vertices. The tree does not contain cycles and loops.

Usually a tree representing hierarchical system, one main vertex is allocated, which is called the root of the tree. Each vertex of the tree (except the root) has only one ancestor - the object designated by it belongs to one top-level class. Any vertex of the tree can generate several descendants - vertices corresponding to lower-level classes.

For each pair of tree vertices, there is a unique path connecting them. This property is used when finding all ancestors, for example, in the male line, of any person whose family tree is presented in the form of a family tree, which is a “tree” in the sense of graph theory as well.

An example of my family tree [appendix fig.12].

One more example. The figure shows the biblical family tree [appendix fig.13].

Problem solving

1. Transport task. Let there be a base with raw materials in the city of Krasnodar, which needs to be planted in the cities of Krymsk, Temryuk, Slavyansk-on-Kuban and Timashevsk in one run, while spending as little time and fuel as possible and returning back to Krasnodar.

Decision:

First, let's create a graph of all possible routes. [app fig.14], taking into account the real roads between these settlements and the distance between them. To solve this problem, we need to create another graph, a tree [app fig.15].

For the convenience of the solution, we denote the cities with numbers: Krasnodar - 1, Krymsk - 2, Temryuk - 3, Slavyansk - 4, Timashevsk - 5.

This resulted in 24 solutions, but we only need shortest paths. Of all the solutions, only two are satisfied, these are 350 km.

Similarly, it is possible and, I think, it is necessary to calculate real transportation from one locality to others.

Logic task for transfusion. There are 8 liters of water in a bucket, and there are two pots with a capacity of 5 and 3 liters. it is required to pour 4 liters of water into a five-liter saucepan and leave 4 liters in a bucket, i.e. pour water equally into a bucket and a large saucepan.

Decision:

The situation at any moment can be described by three numbers [appendix fig.16].

As a result, we get two solutions: one in 7 moves, the other in 8 moves.

Conclusion

So, in order to learn how to solve problems, you need to understand what they are, how they are arranged, from which constituent parts they consist of what tools are used to solve problems.

Solving practical problems with the help of graph theory, it became clear that at every step, at every stage of their solution, it is necessary to apply creativity.

From the very beginning, at the first stage, it lies in the fact that you need to be able to analyze and encode the condition of the problem. The second stage is a schematic notation, which consists in the geometric representation of graphs, and at this stage the element of creativity is very important because it is far from easy to find correspondences between the elements of the condition and the corresponding elements of the graph.

When solving a transport problem or a problem of compiling a family tree, I concluded that the graph method is certainly interesting, beautiful and visual.

I was convinced that graphs are widely used in economics, management, and technology. Graph theory is also used in programming. This was not discussed in this paper, but I think that this is only a matter of time.

In this scientific work, mathematical graphs, their areas of application are considered, several problems are solved with the help of graphs. Knowledge of the basics of graph theory is necessary in various areas related to production management, business (for example, construction network diagram, mail delivery schedules). In addition, while working on a scientific work, I mastered working on a computer in text editor WORD. Thus, tasks scientific work completed.

So, from all of the above, the practical value of graph theory irrefutably follows, the proof of which was the goal of this work.

Literature

Berge K. Graph theory and its applications. -M.: IIL, 1962.

Kemeny J., Snell J., Thompson J. Introduction to finite mathematics. -M.: IIL, 1963.

Ore O. Graphs and their application. -M.: Mir, 1965.

Harary F. Graph theory. -M.: Mir, 1973.

Zykov A.A. Theory of Finite Graphs. -Novosibirsk: Nauka, 1969.

Berezina L.Yu. Graphs and their application. -M.: Education, 1979. -144 p.

"Soros Educational Journal" No. 11 1996 (Article "Flat Graphs");

Gardner M. "Mathematical leisure", M. "Mir", 1972 (chapter 35);

Olekhnik S. N., Nesterenko Yu. V., Potapov M. K. "Old entertaining problems", M. "Nauka", 1988 (part 2, section 8; appendix 4);

Appendix

Rice. 6

Rice. 7

Rice. eight

Application

Appendix

Rice. fourteen

Application

Appendix

Leonhard Euler is considered to be the father of graph theory. In 1736, in one of his letters, he formulates and proposes a solution to the problem of seven Königsberg bridges, which later became one of the classical problems of graph theory.

The first problems in graph theory were related to solving mathematical recreational problems and puzzles. Here is a retelling of an excerpt from Euler's letter dated March 13, 1736: “I was offered a problem about an island located in the city of Koenigsberg and surrounded by a river over which 7 bridges are thrown. The question is whether anyone can go around them continuously, passing only once through each bridge. And then I was informed that no one had yet been able to do this, but no one had proved that it was impossible. This question, although banal, seemed to me, however, worthy of attention because neither geometry, nor algebra, nor combinatorial art is sufficient for its solution. After much deliberation, I found an easy rule, based on a completely convincing proof, with the help of which it is possible to immediately determine in all problems of this kind whether such a round can be made through any number and arbitrarily located bridges or cannot. Königsberg bridges can be schematically depicted as follows:

Euler's rule:

1. In a graph that does not have vertices of odd degrees, there is a traversal of all edges (moreover, each edge is traversed exactly once) starting at any vertex of the graph.

2. In a graph that has two and only two odd-degree vertices, there is a bypass starting at one odd-degree vertex and ending at another.

3. In a graph with more than two odd-degree vertices, such a traversal does not exist.

There is one more type of problems related to traveling along graphs. We are talking about problems in which it is required to find a path passing through all the vertices, and no more than once through each. A cycle passing through each vertex once and only once is called a Hamiltonian line (in honor of William Rowan Hamilton, the famous Irish mathematician of the last century, who was the first to study such lines). Unfortunately, no general criterion has yet been found by which one could decide whether a given graph is Hamiltonian, and if so, find all Hamiltonian lines on it.

Formulated in the middle of the 19th century. The four color problem also looks like an entertaining problem, but attempts to solve it have led to some studies of graphs that are of theoretical and applied importance. The four-color problem is formulated as follows: “Can an area of any flat map be colored with four colors so that any two adjacent areas are painted in different colors?”. The hypothesis that the answer is yes was formulated in the middle of the 19th century. In 1890, a weaker assertion was proved, namely that any flat map can be colored with five colors. Matching any flat map its dual plane graph, obtain an equivalent formulation of the problem in terms of graphs: Is it true that the chromatic number of any plane graph is less than or equal to four? Numerous attempts to solve the problem have influenced the development of a number of areas of graph theory. In 1976, a positive solution to the problem was announced using a computer.

Another old topological problem that defied solution for a particularly long time and excited the minds of puzzle lovers is known as the “problem of electricity, gas and water supply”. In 1917, Henry E. Dudeney gave it this formulation. In each of the three houses shown in the figure, it is necessary to conduct gas, electricity and water.