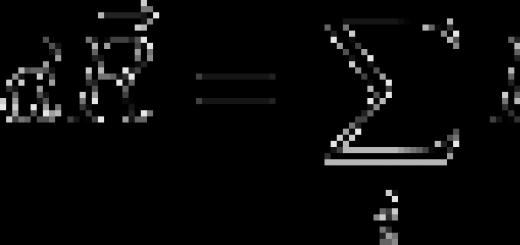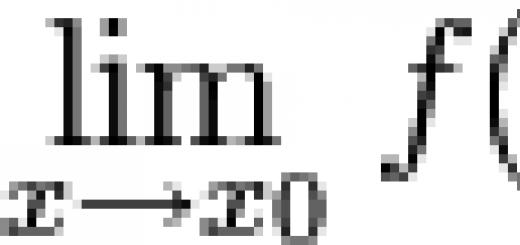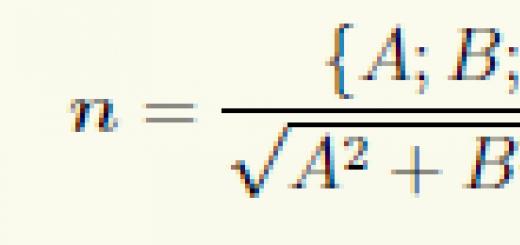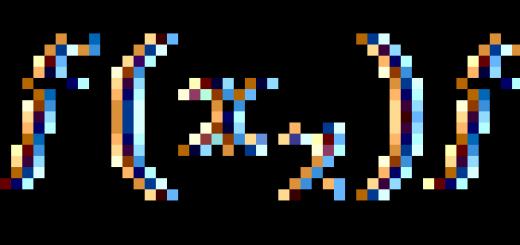In this article, we will give a definition of the distance from a point to a plane and analyze the coordinate method that allows you to find the distance from given point to a given plane in three-dimensional space. After the presentation of the theory, we will analyze in detail the solutions of several typical examples and problems.
Page navigation.
The distance from a point to a plane is a definition.
The distance from a point to a plane is determined through , one of which is a given point, and the other is the projection of a given point onto a given plane.
Let a point M 1 and a plane be given in three-dimensional space. Let's draw a straight line a through the point M 1, perpendicular to the plane. Let's denote the point of intersection of the line a and the plane as H 1 . The segment M 1 H 1 is called perpendicular, lowered from the point M 1 to the plane , and the point H 1 - the base of the perpendicular.
Definition.
is the distance from a given point to the base of a perpendicular drawn from a given point to a given plane.
The definition of the distance from a point to a plane is more common in the following form.
Definition.
Distance from point to plane is the length of the perpendicular dropped from a given point to a given plane.
It should be noted that the distance from the point M 1 to the plane , determined in this way, is the smallest of the distances from the given point M 1 to any point of the plane . Indeed, let the point H 2 lie in the plane and be different from the point H 1 . Obviously, the triangle M 2 H 1 H 2 is rectangular, in it M 1 H 1 is a leg, and M 1 H 2 is the hypotenuse, therefore, 
. By the way, the segment M 1 H 2 is called oblique drawn from point M 1 to the plane. So, the perpendicular dropped from a given point to a given plane is always less than the inclined one drawn from the same point to a given plane.
Distance from a point to a plane - theory, examples, solutions.
Some geometric problems at some stage of the solution require finding the distance from a point to a plane. The method for this is selected depending on the source data. Usually, the result is the use of either the Pythagorean theorem, or the signs of equality and similarity of triangles. If you need to find the distance from a point to a plane, which are given in three-dimensional space, then the coordinate method comes to the rescue. In this paragraph of the article, we will just analyze it.
First, we formulate the condition of the problem.
In a rectangular coordinate system Oxyz in three-dimensional space, a point is given 
, plane and it is required to find the distance from the point M 1 to the plane.
Let's look at two ways to solve this problem. The first method that allows you to calculate the distance from a point to a plane is based on finding the coordinates of the point H 1 - the base of the perpendicular dropped from the point M 1 to the plane, and then calculating the distance between the points M 1 and H 1 . The second way to find the distance from a given point to a given plane involves using the normal equation for a given plane.
The first way to calculate the distance from a point to the plane.
Let H 1 be the base of the perpendicular drawn from the point M 1 to the plane . If we determine the coordinates of the point H 1, then the required distance from the point M 1 to the plane can be calculated as the distance between the points and 
according to the formula . Thus, it remains to find the coordinates of the point H 1 .
So, algorithm for finding distance from a point up to the plane next:
The second method, suitable for finding the distance from a point to the plane.
Since we are given a plane in the rectangular coordinate system Oxyz, we can get the normal equation of the plane in the form. Then the distance from the point to the plane is calculated by the formula . The validity of this formula for finding the distance from a point to a plane is established by the following theorem.
Theorem.
Let a rectangular coordinate system Oxyz be fixed in three-dimensional space, a point and the normal equation of the plane of the form . The distance from the point M 1 to the plane is equal to the absolute value of the value of the expression on the left side of the normal equation of the plane, calculated at , that is, .
Proof.
The proof of this theorem is absolutely similar to the proof of a similar theorem given in the section Finding the distance from a point to a line.
It is easy to show that the distance from the point M 1 to the plane is equal to the modulus of the difference between the numerical projection M 1 and the distance from the origin to the plane, that is, 
, where 
- normal vector of the plane , is equal to one, - 
to the direction determined by the vector .
and by definition is , but in coordinate form . Therefore, and as required to prove.
Thus, distance from point to the plane can be calculated by substituting in the left side of the normal equation of the plane instead of x, y and z the coordinates x 1, y 1 and z 1 of the point M 1 and taking absolute value received value.
Examples of finding distance from a point to the plane.
Example.
Find distance from point 
to the plane.
Decision.
First way.
In the condition of the problem, we are given a general equation of the plane of the form , from which it can be seen that 
is the normal vector of this plane. This vector can be taken as the directing vector of the straight line a perpendicular to the given plane. Then we can write the canonical equations of a straight line in space that passes through the point and has a direction vector with coordinates , they look like .
Let's start finding the coordinates of the point of intersection of the line 
and planes. Let's denote it H 1 . To do this, we first perform the transition from the canonical equations of the straight line to the equations of two intersecting planes: 
Now let's solve the system of equations 
(if necessary, refer to the article). We use: 
Thus, .
It remains to calculate the required distance from a given point to a given plane as the distance between points and :
.
The second solution.
Let's get the normal equation of the given plane. To do this, we need to bring the general equation of the plane to normal form. Having determined the normalizing factor 
, we obtain the normal equation of the plane 
. It remains to calculate the value of the left side of the resulting equation for 
and take the module of the obtained value - this will give the desired distance from the point to plane:
So I read something on this page (http://gamedeveloperjourney.blogspot.com/2009/04/point-plane-collision-detection.html)
D = - D3DXVec3Dot(&vP1, &vNormal);
where vP1 is a point on the plane and vNormal is the normal to the plane. I'm curious how this gives you the distance from the start of the world since the result will always be 0. Also, to be clear (since I'm still a bit hazy on the D part of the 2D equation), is d in the 2D equation the distance from the line through the beginning of the world before the beginning of the plane?
math3 Answers
6
AT general case the distance between a point p and a plane can be calculated using the formula
where
and where p0 is a point in the plane.
If n has unit length, then the dot product between the vector and it is the (signed) length of the vector's projection onto the Normal
The formula you report is just a special case where the point p is the origin. In this case
Distance = This equality is technically wrong because the dot product is about vectors, not points... but still holds numerically. By writing an explicit formula, you get this (0 - p0.x)*n.x + (0 - p0.y)*n.y + (0 - p0.z)*n.z it's the same as - (p0.x*n.x + p0.y*n.y + p0.z*n.z)
The result is not always zero. The result will be zero only if the plane passes through the origin. (Here, let's assume the plane doesn't pass through the origin.) Basically, you are given a line from the origin to some point on the plane. (I.e. you have a vector from the origin to vP1). The problem with this vector is that it's most likely skewed and heading to some distant place on the plane, rather than the nearest point on the plane. So if you just took the vP1 length, you will get too much distance. What you need to do is get the projection of vP1 onto some vector that you know is perpendicular to the plane. It is, of course, vNormal. So take the dot product of vP1 and vNormal and divide it by the length of vNormal and you have your answer. (If they're kind enough to give you a vNormal that's already a magnitude one, then there's no need to split.)
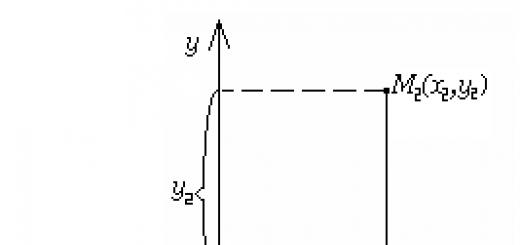
You can solve this problem with Lagrange multipliers: You know that the nearest point on the plane should look like: C=p+v Where c is the nearest point and v is a vector along the plane (which is thus orthogonal to the normal to n). You are trying to find c with the smallest norm (or squared norm). So you are trying to minimize dot(c,c) as long as v is orthogonal to n (thus dot(v,n) = 0). Thus, set the Lagrangian: L = dot(c,c) + lambda * (dot(v,n)) L = dot(p+v,p+v) + lambda * (dot(v,n)) L = dot(p,p) + 2*dot(p,v) + dot(v,v) * lambda * (dot(v,n)) And take the derivative with respect to v (and set to 0) to get: 2 * p + 2 * v + lambda * n = 0 You can solve for the lambda in the equation above by dotted, producing both sides on n to get 2 * dot(p,n) + 2 * dot(v,n) + lambda * dot(n,n) = 0 2 * dot(p,n) + lambda = 0 lambda = - 2 * dot(p,n) ) Note again that dot(n,n) = 1 and dot(v,n) = 0 (since v is in the plane and n is orthogonal to it). The Substitute lambda then returns to get: 2 * p + 2 * v - 2 * dot(p,n) * n = 0 and solve for v to get: V = dot(p,n) * n - p Then plug that back into c = p + v to get: C = dot(p,n) * n The length of this vector is |dot(p,n)| , and the sign tells you whether the point is in the direction of the normal vector from the origin, or in the opposite direction from the origin. suppose i have plane equation ax+by+cz=d, how can I find the shortest distance from the plane to the origin? I'm going backwards from this post. In this post they... Let's say the Kinect is sitting at (0,0,0) and looking in the +Z direction. Suppose there is an object at (1, 1, 1) and one of the pixels in the Kinect depth image represents that object.... I want to equalize the distance from the origin to all points where the points are given by a dataframe with two coordinates. I have all points like: x y 1 0.0 0.0 2 -4.0 -2.8 3 -7.0 -6.5 4 -9.0 -11.1... Reference Information Consider a spherical coordinate system like the one shown here: Coordinate System http://www.shokhirev.com/nikolai/projects/global/image013.gif For a particular point, we... I have a 3D scene and a camera defined with gluPerspective . I have a fixed FOV and I know the minimum distance of any geometry from the camera (it's a first person view, so it's... I have a triangle with points A, B, C and a point in space (P). How can I get the distance from a point to a plane? I need to calculate the distance from P to the plane, even though my... I want to rotate a CGPoint (red rectangle) around another CGPoint (blue rectangle) but it changes the distance from the origin (blue rectangle)...when I give 270 in the corner it creates... I need to get the center of the X, Y, Z plane, Cartesian coordinates. I have the Normal of the plane and the distance from its center point to the origin. I can place point(s) anywhere and... Given: point (x1, y1, z1) direction vector (a1, b1, c1) plane ax + by + cz + d = 0 How can I find the distance D from point to plane along this vector? Thanks I have a camera coordinate system defined by a rotation matrix R and a translation T relative to the world coordinate system. A plane is defined in camera coordinates by a normal N and a point P on it.... This article talks about determining the distance from a point to a plane. let's analyze the coordinate method, which will allow us to find the distance from a given point in three-dimensional space. To consolidate, consider examples of several tasks. The distance from a point to a plane is found by means of a known distance from a point to a point, where one of them is given, and the other is a projection onto a given plane. When a point M 1 with a plane χ is given in space, then a straight line perpendicular to the plane can be drawn through the point. H 1 is a common point of their intersection. From here we get that the segment M 1 H 1 is a perpendicular, which was drawn from the point M 1 to the plane χ, where the point H 1 is the base of the perpendicular. Definition 1 They call the distance from a given point to the base of the perpendicular, which was drawn from a given point to a given plane. The definition can be written in different formulations. Definition 2 Distance from point to plane called the length of the perpendicular, which was drawn from a given point to a given plane. The distance from the point M 1 to the plane χ is defined as follows: the distance from the point M 1 to the plane χ will be the smallest from a given point to any point in the plane. If the point H 2 is located in the χ plane and is not equal to the point H 2, then we get right triangle type M 2 H 1 H 2
, which is rectangular, where there is a leg M 2 H 1, M 2 H 2
- hypotenuse. Hence, this implies that M 1 H 1< M 1 H 2 . Тогда отрезок М 2 H 1
is considered inclined, which is drawn from the point M 1 to the plane χ. We have that the perpendicular drawn from a given point to a plane is less than the inclined one drawn from a point to a given plane. Consider this case in the figure below. There are a number geometric problems, whose solutions must contain the distance from the point to the plane. Ways to detect this may be different. To resolve, use the Pythagorean theorem or the similarity of triangles. When, according to the condition, it is necessary to calculate the distance from a point to a plane, given in a rectangular coordinate system of three-dimensional space, they solve using the coordinate method. This paragraph deals with this method. According to the condition of the problem, we have that a point in three-dimensional space with coordinates M 1 (x 1, y 1, z 1) with the plane χ is given, it is necessary to determine the distance from M 1 to the plane χ. Several solutions are used to solve. First way
This method is based on finding the distance from a point to a plane using the coordinates of the point H 1, which are the base of the perpendicular from the point M 1 to the plane χ. Next, you need to calculate the distance between M 1 and H 1. To solve the problem in the second way, the normal equation of a given plane is used. Second way
By condition, we have that H 1 is the base of the perpendicular, which was lowered from the point M 1 to the plane χ. Then we determine the coordinates (x 2, y 2, z 2) of the point H 1. The desired distance from M 1 to the χ plane is found by the formula M 1 H 1 \u003d (x 2 - x 1) 2 + (y 2 - y 1) 2 + (z 2 - z 1) 2, where M 1 (x 1, y 1 , z 1) and H 1 (x 2 , y 2 , z 2) . To solve, you need to know the coordinates of the point H 1. We have that H 1 is the point of intersection of the plane χ with the line a, which passes through the point M 1 located perpendicular to the plane χ. It follows that it is necessary to formulate the equation of a straight line passing through a given point perpendicular to a given plane. It is then that we can determine the coordinates of the point H 1 . It is necessary to calculate the coordinates of the point of intersection of the line and the plane. Algorithm for finding the distance from a point with coordinates M 1 (x 1, y 1, z 1) to the χ plane: Definition 3 Third way
In a given rectangular coordinate system O x y z there is a plane χ, then we obtain a normal equation of the plane of the form cos α · x + cos β · y + cos γ · z - p = 0 . From here we get that the distance M 1 H 1 with the point M 1 (x 1 , y 1 , z 1) drawn to the plane χ, calculated by the formula M 1 H 1 = cos α x + cos β y + cos γ z-p. This formula is valid, since it is established thanks to the theorem. Theorem If a point M 1 (x 1 , y 1 , z 1) is given in three-dimensional space, having a normal equation of the χ plane of the form cos α x + cos β y + cos γ z - p = 0, then calculating the distance from the point to plane M 1 H 1 is derived from the formula M 1 H 1 = cos α · x + cos β · y + cos γ · z - p, since x = x 1 , y = y 1 , z = z 1 . Proof The proof of the theorem is reduced to finding the distance from a point to a line. From here we get that the distance from M 1 to the χ plane is the modulus of the difference between the numerical projection of the radius vector M 1 with the distance from the origin to the χ plane. Then we get the expression M 1 H 1 = n p n → O M → - p . The normal vector of the plane χ has the form n → = cos α , cos β , cos γ , and its length is equal to one, n p n → O M → is the numerical projection of the vector O M → = (x 1 , y 1 , z 1) in the direction determined by the vector n → . Let's apply the formula for calculating scalar vectors. Then we obtain an expression for finding a vector of the form n → , O M → = n → n p n → O M → = 1 n p n → O M → = n p n → O M → , since n → = cos α , cos β , cos γ z and O M → = (x 1 , y 1 , z 1) . The coordinate form of the notation will take the form n →, O M → = cos α x 1 + cos β y 1 + cos γ z 1, then M 1 H 1 = n p n → O M → - p = cos α x 1 + cos β · y 1 + cos γ · z 1 - p . The theorem has been proven. From here we get that the distance from the point M 1 (x 1, y 1, z 1) to the plane χ is calculated by substituting into the left side of the normal equation of the plane cos α x + cos β y + cos γ z - p = 0 instead of x, y, z coordinates x 1 , y 1 and z1 relating to the point M 1 , taking the absolute value of the obtained value. Consider examples of finding the distance from a point with coordinates to a given plane. Example 1 Calculate the distance from the point with coordinates M 1 (5 , - 3 , 10) to the plane 2 x - y + 5 z - 3 = 0 . Decision
Let's solve the problem in two ways. The first method will start by calculating the direction vector of the line a . By condition, we have that the given equation 2 x - y + 5 z - 3 = 0 is the equation of the plane general view, and n → = (2, - 1, 5) is the normal vector of the given plane. It is used as a directing vector of the straight line a, which is perpendicular to the given plane. You should write the canonical equation of a straight line in space passing through M 1 (5, - 3, 10) with a direction vector with coordinates 2, - 1, 5. The equation will look like x - 5 2 = y - (- 3) - 1 = z - 10 5 ⇔ x - 5 2 = y + 3 - 1 = z - 10 5 . Intersection points should be defined. To do this, gently combine the equations into a system for the transition from the canonical to the equations of two intersecting lines. given point take for H 1. We get that x - 5 2 = y + 3 - 1 = z - 10 5 ⇔ - 1 (x - 5) = 2 (y + 3) 5 (x - 5) = 2 (z - 10) 5 ( y + 3) = - 1 (z - 10) ⇔ ⇔ x + 2 y + 1 = 0 5 x - 2 z - 5 = 0 5 y + z + 5 = 0 ⇔ x + 2 y + 1 = 0 5 x - 2 z - 5 = 0 Then you need to enable the system x + 2 y + 1 = 0 5 x - 2 z - 5 = 0 2 x - y + 5 z - 3 = 0 ⇔ x + 2 y = 1 5 x - 2 z = 5 2 x - y + 5 z = 3 Let us turn to the rule for solving the system according to Gauss: 1 2 0 - 1 5 0 - 2 5 2 - 1 5 3 ~ 1 2 0 - 1 0 - 10 - 2 10 0 - 5 5 5 ~ 1 2 0 - 1 0 - 10 - 2 10 0 0 6 0 ⇒ ⇒ z = 0 6 = 0 , y = - 1 10 10 + 2 z = - 1 , x = - 1 - 2 y = 1 We get that H 1 (1, - 1, 0) . We calculate the distance from a given point to a plane. We take points M 1 (5, - 3, 10) and H 1 (1, - 1, 0) and get M 1 H 1 \u003d (1 - 5) 2 + (- 1 - (- 3)) 2 + (0 - 10) 2 \u003d 2 30 The second solution is to first bring the given equation 2 x - y + 5 z - 3 = 0 to normal form. We determine the normalizing factor and get 1 2 2 + (- 1) 2 + 5 2 = 1 30 . From here we derive the equation of the plane 2 30 · x - 1 30 · y + 5 30 · z - 3 30 = 0 . The left side of the equation is calculated by substituting x \u003d 5, y \u003d - 3, z \u003d 10, and you need to take the distance from M 1 (5, - 3, 10) to 2 x - y + 5 z - 3 = 0 modulo. We get the expression: M 1 H 1 \u003d 2 30 5 - 1 30 - 3 + 5 30 10 - 3 30 \u003d 60 30 \u003d 2 30 Answer: 2 30 . When the χ plane is given by one of the methods of the plane definition methods section, then you first need to obtain the equation of the χ plane and calculate the desired distance using any method. Example 2 Points with coordinates M 1 (5 , - 3 , 10) , A (0 , 2 , 1) , B (2 , 6 , 1) , C (4 , 0 , - 1) are set in three-dimensional space. Calculate the distance from M 1 to the plane A B C. Decision
First you need to write down the equation of the plane passing through the given three points with coordinates M 1 (5, - 3, 10) , A (0 , 2 , 1) , B (2 , 6 , 1) , C (4 , 0 , - one) . x - 0 y - 2 z - 1 2 - 0 6 - 2 1 - 1 4 - 0 0 - 2 - 1 - 1 = 0 ⇔ x y - 2 z - 1 2 4 0 4 - 2 - 2 = 0 ⇔ ⇔ - 8x + 4y - 20z + 12 = 0 ⇔ 2x - y + 5z - 3 = 0 It follows that the problem has a solution similar to the previous one. Hence, the distance from the point M 1 to the plane A B C is 2 30 . Answer: 2 30 . Finding the distance from a given point on a plane or to a plane to which they are parallel is more convenient by applying the formula M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 - p . From here we get that the normal equations of the planes are obtained in several steps. Example 3 Find the distance from a given point with coordinates M 1 (- 3 , 2 , - 7) to coordinate plane About x y z and plane, given by the equation 2y - 5 = 0 . Decision
The coordinate plane O y z corresponds to an equation of the form x = 0. For the O y z plane, it is normal. Therefore, it is necessary to substitute the values x \u003d - 3 into the left side of the expression and take the absolute value of the distance from the point with coordinates M 1 (- 3, 2, - 7) to the plane. We get the value equal to - 3 = 3 . After the transformation, the normal equation of the plane 2 y - 5 = 0 will take the form y - 5 2 = 0 . Then you can find the required distance from the point with coordinates M 1 (- 3 , 2 , - 7) to the plane 2 y - 5 = 0 . Substituting and calculating, we get 2 - 5 2 = 5 2 - 2. Answer: The desired distance from M 1 (- 3 , 2 , - 7) to O y z has a value of 3 , and to 2 y - 5 = 0 has a value of 5 2 - 2 . If you notice a mistake in the text, please highlight it and press Ctrl+Enter
2
1
shortest distance from the plane to the origin using the equation of the plane
Does the Kinect depth image represent the distance to the origin or the distance to the XY plane?
Distance from the origin of coordinates to a point in space
spherical coordinates - distance to the plane
How to methodically choose the near clip plane distance for perspective projection?
How to get distance from point to plane in 3d?
Rotating a CG point changes the distance from the origin
Get plane center X, Y, Z, Cartesian coordinates
distance from a point to a plane in a particular direction
Converting a plane to another coordinate system 
Distance from a point to a plane - theory, examples, solutions
