Related lesson “Infinitely decreasing geometric progression”
The purpose of the lesson: introducing students to a new kind of sequence - an infinitely decreasing geometric progression.
Tasks:
formulation of the initial idea of the limit of the numerical sequence; acquaintance with another way of converting infinite periodic fractions into ordinary ones using the formula for the sum of an infinitely decreasing geometric progression;
the development of the intellectual qualities of the personality of schoolchildren, such as logical thinking, the ability for evaluative actions, generalization;
education of activity, mutual assistance, collectivism, interest in the subject.
Equipment: computer class, projector, screen.
Lesson type: lesson - learning new topic.
During the classes
I . Org. moment. Message about the topic and purpose of the lesson.
II . Updating students' knowledge.1. Checking homework.
1) Verification of basic formulas related to arithmetic and geometric progressions. Two students write down formulas at the blackboard.
2) The rest of the students do mathematical dictation on the topic "Sum Formulas".
Tasks:
№1. Find the sum of the first five terms arithmetic progression, if its first member is equal to 6 (1st option), -20 (2nd option), and the fifth member is -6 (1st option), 20 (2nd option).
№2. Find the sum of the first five members of an arithmetic progression if its first member is -20(1st option), 6(2nd option), and the difference is 10(1st option), -3(2nd option).
№3. Find the sum of the first five terms of a geometric progression if its first term is 1(1st option), -1 (2nd option), and the denominator is -2(1st option), 2(2nd option).
At the end of the dictation, selectively, two students' work is checked for evaluation, the rest perform self-examination according to ready-made solutions written on the lapels of the board.
Solutions:

Tasks
1. Arithmetic progression is given by the formula a n = 7 – 4 n. Find a 10 . (-33)
2. Arithmetic progression a 3 = 7 and a 5 = 1 . Find a 4 . (4)
3. Arithmetic progression a 3 = 7 and a 5 = 1 . Find a 17 . (-35)
4. Arithmetic progression a 3 = 7 and a 5 = 1 . Find S 17 . (-187)
5. For a geometric progression  find the fifth term.
find the fifth term. 
6. For a geometric progression  find n-th member.
find n-th member. 
7. Exponentially b 3 = 8 and b 5 = 2 . Find b 4 . (4)
8. Exponentially b
3
= 8
and b
5
= 2
. Find b
1
and
q
. 
9. Exponentially b 3 = 8 and b 5 = 2 . Find S 5 . (62)
III . Exploring a new topic(demonstration presentation).

Consider a square with a side equal to 1. Let's draw another square, the side of which is half the first square, then another one, the side of which is half the second, then the next one, and so on. Each time the side of the new square is half the previous one.
As a result, we got a sequence of sides of squares  forming a geometric progression with denominator .
forming a geometric progression with denominator .
And, what is very important, the more we build such squares, the smaller the side of the square will be. for example,

Those. as the number n increases, the terms of the progression approach zero.
With the help of this figure, one more sequence can be considered.

For example, the sequence of areas of squares:

 . And, again, if n increases indefinitely, then the area approaches zero arbitrarily close.
. And, again, if n increases indefinitely, then the area approaches zero arbitrarily close.
Let's consider one more example. An equilateral triangle with a side of 1 cm. Let's construct the next triangle with vertices in the midpoints of the sides of the 1st triangle, according to the triangle midline theorem - the side of the 2nd is equal to half the side of the first, the side of the 3rd is half the side of the 2nd, etc. Again we get a sequence of lengths of the sides of the triangles.
 at
at  .
.
If we consider a geometric progression with a negative denominator.
Then, again, with increasing numbers n the terms of the progression approach zero.
Let's pay attention to the denominators of these sequences. Everywhere the denominators were less than 1 modulo.
We can conclude: a geometric progression will be infinitely decreasing if the modulus of its denominator is less than 1.
Front work.
Definition:
A geometric progression is said to be infinitely decreasing if the modulus of its denominator is less than one.  .
.
With the help of the definition, it is possible to solve the question of whether a geometric progression is infinitely decreasing or not.
Task
Is the sequence an infinitely decreasing geometric progression if it is given by the formula:
 ;
;  .
.
Decision:
 . Let's find q
.
. Let's find q
.
 ;
;  ;
;  ;
;  .
.
this geometric progression is infinitely decreasing.
b) this sequence is not an infinitely decreasing geometric progression.

Consider a square with a side equal to 1. Divide it in half, one of the halves in half again, and so on. the areas of all the resulting rectangles form an infinitely decreasing geometric progression: ![]()
The sum of the areas of all the rectangles obtained in this way will be equal to the area of the 1st square and equal to 1. ![]()
But on the left side of this equality is the sum of an infinite number of terms.
Consider the sum of the first n terms. ![]()
According to the formula for the sum of the first n terms of a geometric progression, it is equal to  .
.
If a n increases indefinitely, then
or 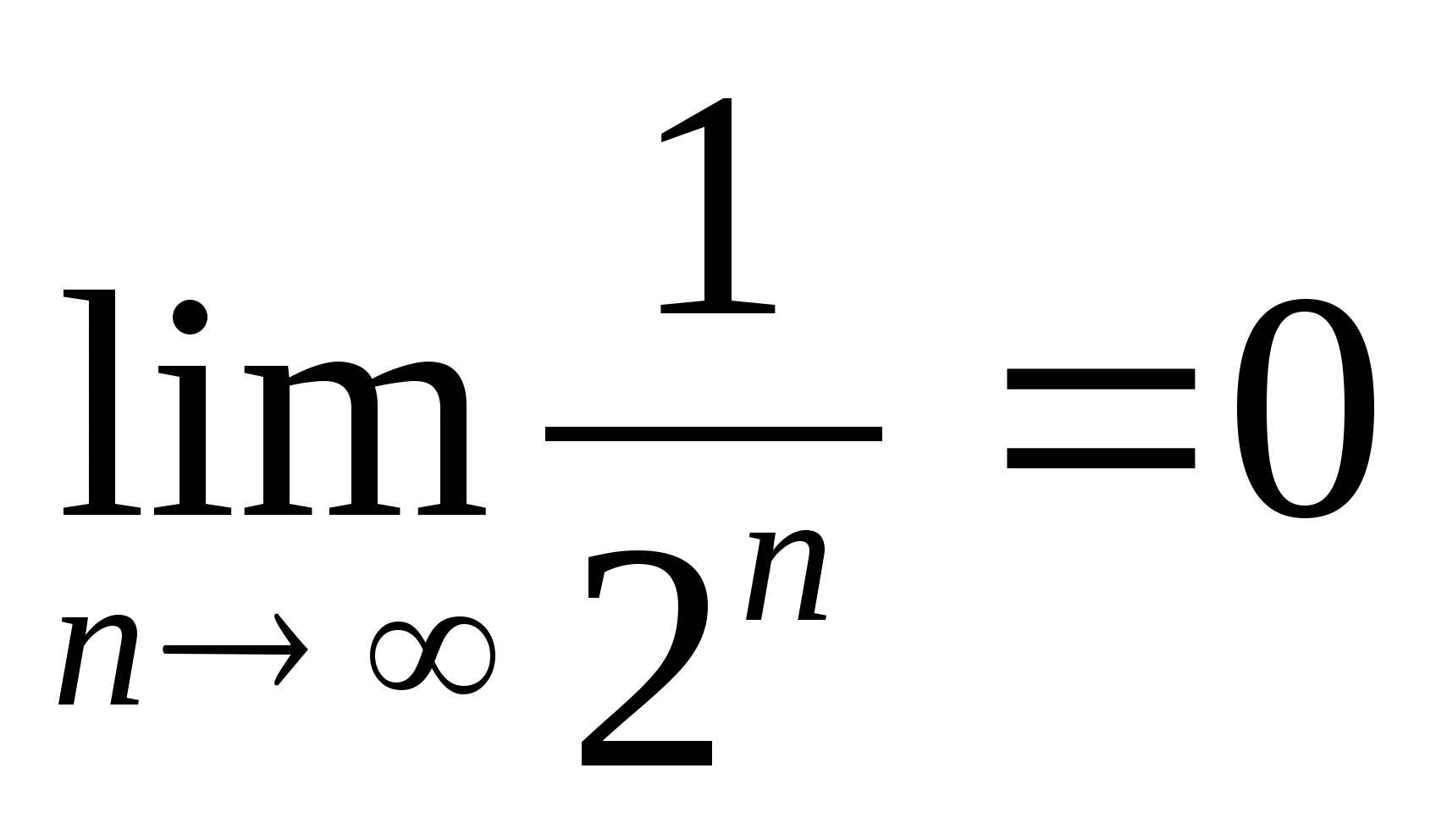 . So
. So  , i.e.
, i.e.  .
.
The sum of an infinitely decreasing geometric progression there is a sequence limit S 1 , S 2 , S 3 , …, S n , … .
For example, for a progression  ,
,
 As
As 
The sum of an infinitely decreasing geometric progression can be found using the formula  .
.
III . Reflection and Consolidation(completion of tasks).
Task number 2. Find the sum of an infinitely decreasing geometric progression with the first term 3, the second 0.3.
Decision:
Task number 3. textbook, p. 160, No. 433(1)
Find the sum of an infinitely decreasing geometric progression:
Decision:

Task number 4. Write the infinite periodic decimal fraction 0,(5) as a common fraction.
1st way. Let x = 0, (5) = 0.555 ... / 10 2nd method. 0,(5)=0.555…=

Task number 5. textbook, p. 162, No. 445(3) (independent decision)
Write the infinite periodic decimal fraction 0,(12) as a common fraction.
Answer: 0,(12)=4/33.
IV . Summarizing.
What sequence did you meet today?
Define an infinitely decreasing geometric progression.
How to prove that a geometric progression is infinitely decreasing?
Give the formula for the sum of an infinitely decreasing geometric progression.
V . Homework.
NUMERICAL SEQUENCES VI
§ l48. The sum of an infinitely decreasing geometric progression
Until now, speaking of sums, we have always assumed that the number of terms in these sums is finite (for example, 2, 15, 1000, etc.). But when solving some problems (especially higher mathematics), one has to deal with the sums of an infinite number of terms
S= a 1 + a 2 + ... + a n + ... . (1)
What are these amounts? A-priory the sum of an infinite number of terms a 1 , a 2 , ..., a n , ... is called the limit of the sum S n first P numbers when P -> ∞ :
S=S n = (a 1 + a 2 + ... + a n ). (2)
Limit (2), of course, may or may not exist. Accordingly, the sum (1) is said to exist or not to exist.
How to find out whether the sum (1) exists in each particular case? Common decision This question goes far beyond the scope of our program. However, there is one important special case which we now have to consider. We will talk about the summation of the terms of an infinitely decreasing geometric progression.
Let be a 1 , a 1 q , a 1 q 2 , ... is an infinitely decreasing geometric progression. This means that | q |< 1. Сумма первых P members of this progression is equal to
![]()
From the basic theorems on the limits of variables (see § 136) we obtain:

But 1 = 1, a q n = 0. Therefore

So, the sum of an infinitely decreasing geometric progression is equal to the first term of this progress divided by one minus the denominator of this progression.
1) The sum of the geometric progression 1, 1/3, 1/9, 1/27, ... is

and the sum of a geometric progression is 12; -6; 3; - 3 / 2 , ... equals

2) A simple periodic fraction 0.454545 ... turn into an ordinary one.
To solve this problem, we represent this fraction as an infinite sum:
The right side of this equality is the sum of an infinitely decreasing geometric progression, the first term of which is 45/100, and the denominator is 1/100. So

In the manner described, one can obtain general rule conversion of simple periodic fractions into ordinary ones (see Ch. II, § 38):
To convert a simple periodic fraction into an ordinary one, you need to do the following: put the period in the numerator decimal fraction, and in the denominator - a number consisting of nines taken as many times as there are digits in the period of the decimal fraction.
3) Mixed periodic fraction 0.58333 .... turn into an ordinary fraction.
Let's represent this fraction as an infinite sum:
On the right side of this equality, all terms, starting from 3/1000, form an infinitely decreasing geometric progression, the first term of which is 3/1000, and the denominator is 1/10. So

In the manner described, the general rule for the conversion of mixed periodic fractions into ordinary fractions can also be obtained (see Chapter II, § 38). We deliberately do not include it here. There is no need to memorize this cumbersome rule. It is much more useful to know that any mixed periodic fraction can be represented as the sum of an infinitely decreasing geometric progression and some number. And the formula
for the sum of an infinitely decreasing geometric progression, one must, of course, remember.
As an exercise, we invite you, in addition to the problems No. 995-1000 below, to once again turn to problem No. 301 § 38.
Exercises
995. What is called the sum of an infinitely decreasing geometric progression?
996. Find sums of infinitely decreasing geometric progressions:

997. For what values X progression
![]()
is infinitely decreasing? Find the sum of such a progression.
998. In equilateral triangle with a party a a new triangle is inscribed by connecting the midpoints of its sides; a new triangle is inscribed in this triangle in the same way, and so on ad infinitum.
a) the sum of the perimeters of all these triangles;
b) the sum of their areas.
999. In a square with a side a a new square is inscribed by connecting the midpoints of its sides; a square is inscribed in this square in the same way, and so on ad infinitum. Find the sum of the perimeters of all these squares and the sum of their areas.
1000. Make an infinitely decreasing geometric progression, such that its sum is equal to 25 / 4, and the sum of the squares of its terms is equal to 625 / 24.
Consider now the question of summation of an infinite geometric progression. Let us call the partial sum of a given infinite progression the sum of its first terms. Denote the partial sum by the symbol

For every infinite progression
one can compose a (also infinite) sequence of its partial sums
Let a sequence with unlimited increase have a limit
![]()
In this case, the number S, i.e., the limit of partial sums of the progression, is called the sum of an infinite progression. We will prove that an infinite decreasing geometric progression always has a sum, and derive a formula for this sum (we can also show that for an infinite progression has no sum, does not exist).
We write the expression for the partial sum as the sum of the members of the progression according to formula (91.1) and consider the limit of the partial sum at
![]()
From the theorem of item 89 it is known that for a decreasing progression ; therefore, applying the difference limit theorem, we find
(the rule is also used here: the constant factor is taken out of the sign of the limit). The existence is proved, and at the same time the formula for the sum of an infinitely decreasing geometric progression is obtained:
Equality (92.1) can also be written as
It may seem paradoxical here that the sum an infinite number terms are assigned a well-defined finite value.

A clear illustration can be given to explain this situation. Consider a square with a side equal to one(Fig. 72). Divide this square by a horizontal line into two equal parts and upper part apply to the bottom so that a rectangle is formed with sides 2 and . After that, we again divide the right half of this rectangle in half by a horizontal line and attach the upper part to the lower one (as shown in Fig. 72). Continuing this process, we are constantly transforming the original square with area equal to 1 into equal-sized figures (taking the form of a staircase with thinning steps).
With an infinite continuation of this process, the entire area of the square decomposes into an infinite number of terms - the areas of rectangles with bases equal to 1 and heights. The areas of the rectangles just form an infinite decreasing progression, its sum
i.e., as expected, is equal to the area of the square.
Example. Find the sums of the following infinite progressions:

Solution, a) We note that this progression Therefore, by the formula (92.2) we find
![]()
b) Here it means that by the same formula (92.2) we have
![]()
c) We find that this progression Therefore, this progression has no sum.
In Section 5, the application of the formula for the sum of terms of an infinitely decreasing progression to the conversion of a periodic decimal fraction into an ordinary fraction was shown.
Exercises
1. The sum of an infinitely decreasing geometric progression is 3/5, and the sum of its first four terms is 13/27. Find the first term and denominator of the progression.
2. Find four numbers that form an alternating geometric progression, in which the second term is less than the first by 35, and the third is greater than the fourth by 560.
3. Show what if sequence
forms an infinitely decreasing geometric progression, then the sequence
for any form an infinitely decreasing geometric progression. Does this assertion hold for
Derive a formula for the product of the terms of a geometric progression.
The geometric progression is the new kind number sequence, with which we have to get acquainted. For a successful acquaintance, it does not hurt to at least know and understand. Then there will be no problem with geometric progression.)
What is a geometric progression? The concept of geometric progression.
We start the tour, as usual, with the elementary. I write an unfinished sequence of numbers:
1, 10, 100, 1000, 10000, …
Can you catch a pattern and tell which numbers will go next? The pepper is clear, the numbers 100000, 1000000 and so on will go further. Even without much mental stress, everything is clear, right?)
OK. Another example. I write the following sequence:
1, 2, 4, 8, 16, …
Can you tell which numbers will go next, following the number 16 and name eighth sequence member? If you figured out that it would be the number 128, then very well. So, half the battle is in understanding meaning and key points geometric progression already done. You can grow further.)
And now we turn again from sensations to rigorous mathematics.
Key moments of a geometric progression.
Key moment #1
The geometric progression is sequence of numbers. As is progression. Nothing tricky. Just arranged this sequence differently. Hence, of course, it has another name, yes ...
Key moment #2
With the second key point, the question will be trickier. Let's go back a little and remember the key property of an arithmetic progression. Here it is: each member is different from the previous one by the same amount.
Is it possible to formulate a similar key property for a geometric progression? Think a little... Take a look at the examples given. Guessed? Yes! In a geometric progression (any!) each of its members differs from the previous one in the same number of times. Always!
In the first example, this number is ten. Whichever term of the sequence you take, it is greater than the previous one ten times.
In the second example, this is a two: each member is greater than the previous one. twice.
It is in this key point that the geometric progression differs from the arithmetic one. In an arithmetic progression, each next term is obtained adding of the same value to the previous term. And here - multiplication the previous term by the same amount. That's the difference.)
Key moment #3
This key point is completely identical to that for an arithmetic progression. Namely: each member of the geometric progression is in its place. Everything is exactly the same as in arithmetic progression and comments, I think, are unnecessary. There is the first term, there is a hundred and first, and so on. Let's rearrange at least two members - the pattern (and with it the geometric progression) will disappear. What remains is just a sequence of numbers without any logic.
That's all. That's the whole point of geometric progression.
Terms and designations.
And now, having dealt with the meaning and key points of the geometric progression, we can move on to the theory. Otherwise, what is a theory without understanding the meaning, right?
What is a geometric progression?
How is a geometric progression written? general view? No problem! Each member of the progression is also written as a letter. For arithmetic progression only, the letter is usually used "a", for geometric - letter "b". Member number, as usual, is indicated lower right index. The members of the progression themselves are simply listed separated by commas or semicolons.
Like this:
b1,b 2 , b 3 , b 4 , b 5 , b 6 , …
Briefly, such a progression is written as follows: (b n) .
Or like this, for finite progressions:
b 1 , b 2 , b 3 , b 4 , b 5 , b 6 .
b 1 , b 2 , ..., b 29 , b 30 .
Or, in short:
(b n), n=30 .
That, in fact, is all the designations. Everything is the same, only the letter is different, yes.) And now we go directly to the definition.
Definition of a geometric progression.
A geometric progression is a numerical sequence, the first term of which is non-zero, and each subsequent term is equal to the previous term multiplied by the same non-zero number.
That's the whole definition. Most of the words and phrases are clear and familiar to you. Unless, of course, you understand the meaning of a geometric progression "on the fingers" and in general. But there are also a few new phrases to which I would like to draw special attention.
First, the words: "the first term of which different from zero".
This restriction on the first term was not introduced by chance. What do you think will happen if the first term b 1 turns out to be zero? What will be the second term if each term is greater than the previous the same number of times? Let's say three times? Let's see... Multiply the first term (i.e. 0) by 3 and get... zero! And the third member? Zero too! And the fourth term is also zero! Etc…
We get just a bag of bagels a sequence of zeros:
0, 0, 0, 0, …
Of course, such a sequence has the right to life, but it is of no practical interest. Everything is so clear. Any of its members is zero. The sum of any number of members is also zero ... What interesting things can you do with it? Nothing…
The following keywords: "multiplied by the same non-zero number".
This same number also has its own special name - denominator of a geometric progression. Let's start dating.)
The denominator of a geometric progression.
Everything is simple.
The denominator of a geometric progression is a non-zero number (or value) indicating how many timeseach member of the progression more than the previous one.
Again, by analogy with the arithmetic progression, keyword which should be noted in this definition is the word "more". It means that each term of a geometric progression is obtained multiplication to this very denominator previous member.
I explain.
To calculate, let's say second member to take first member and multiply it to the denominator. For calculation tenth member to take ninth member and multiply it to the denominator.
The denominator of the geometric progression itself can be anything. Absolutely anyone! Integer, fractional, positive, negative, irrational - everyone. Except zero. This is what the word "non-zero" in the definition tells us about. Why this word is needed here - more on that later.
Denominator of a geometric progression usually denoted by a letter q.
How to find this one q? No problem! We must take any term of the progression and divide by previous term. Division is fraction. Hence the name - "the denominator of progression." The denominator, it usually sits in a fraction, yes ...) Although, logically, the value q should be called private geometric progression, similar to difference for an arithmetic progression. But agreed to call denominator. And we won't reinvent the wheel either.)
Let us define, for example, the value q for this geometric progression:
2, 6, 18, 54, …
Everything is elementary. We take any sequence number. What we want is what we take. Except the very first one. For example, 18. And divide by previous number. That is, at 6.
We get:
q = 18/6 = 3
That's all. This is the correct answer. For a given geometric progression, the denominator is three.
Let's find the denominator q for another geometric progression. For example, like this:
1, -2, 4, -8, 16, …
All the same. Whatever signs the members themselves have, we still take any sequence number (for example, 16) and divide by previous number(i.e. -8).
We get:
d = 16/(-8) = -2
And that's it.) This time the denominator of the progression turned out to be negative. Minus two. It happens.)
Let's take this progression:
1, 1/3, 1/9, 1/27, …
And again, regardless of the type of numbers in the sequence (even integers, even fractional, even negative, even irrational), we take any number (for example, 1/9) and divide by the previous number (1/3). According to the rules of operations with fractions, of course.
We get:
That's all.) Here the denominator turned out to be fractional: q = 1/3.
But such a "progression" as you?
3, 3, 3, 3, 3, …
Obviously here q = 1 . Formally, this is also a geometric progression, only with same members.) But such progressions to study and practical application not interesting. Just like progressions with solid zeros. Therefore, we will not consider them.
As you can see, the denominator of the progression can be anything - integer, fractional, positive, negative - anything! It can't just be zero. Didn't guess why?
Well, let's look at some specific example, what will happen if we take as a denominator q zero.) Let us, for example, have b 1 = 2 , a q = 0 . What will be the second term then?
We believe:
b 2 = b 1 · q= 2 0 = 0
And the third member?
b 3 = b 2 · q= 0 0 = 0
Types and behavior of geometric progressions.
With everything was more or less clear: if the difference in the progression d is positive, the progression is increasing. If the difference is negative, then the progression decreases. There are only two options. There is no third.)
But with the behavior of a geometric progression, everything will be much more interesting and diverse!)
As soon as the members behave here: they increase and decrease, and indefinitely approach zero, and even change signs, alternately rushing either to "plus" or to "minus"! And in all this diversity one must be able to understand well, yes ...
We understand?) Let's start with the simplest case.
The denominator is positive ( q >0)
With a positive denominator, firstly, the members of a geometric progression can go into plus infinity(i.e. increase indefinitely) and can go into minus infinity(i.e. decrease indefinitely). We have already got used to such behavior of progressions.
For example:
(b n): 1, 2, 4, 8, 16, …
Everything is simple here. Each member of the progression is more than the previous. And each member gets multiplication previous member on positive number +2 (i.e. q = 2 ). The behavior of such a progression is obvious: all members of the progression grow indefinitely, going into space. Plus infinity...
Now here's the progression:
(b n): -1, -2, -4, -8, -16, …
Here, too, each term of the progression is obtained multiplication previous member on positive number +2. But the behavior of such a progression is already directly opposite: each member of the progression is obtained less than previous, and all its terms decrease indefinitely, going to minus infinity.
Now let's think: what do these two progressions have in common? That's right, denominator! Here and there q = +2 . Positive number. Deuce. And here behavior These two progressions are fundamentally different! Didn't guess why? Yes! It's all about first member! It is he, as they say, who orders the music.) See for yourself.
In the first case, the first term of the progression positive(+1) and, therefore, all subsequent terms obtained by multiplying by positive denominator q = +2 , will also positive.
But in the second case, the first term negative(-one). Therefore, all subsequent members of the progression obtained by multiplying by positive q = +2 , will also be obtained negative. For "minus" to "plus" always gives "minus", yes.)
As you can see, unlike an arithmetic progression, a geometric progression can behave in completely different ways, not only depending from the denominatorq, but also depending from the first member, Yes.)
Remember: the behavior of a geometric progression is uniquely determined by its first member b 1 and denominatorq .
And now we begin the analysis of less familiar, but much more interesting cases!
Take, for example, the following sequence:
(b n): 1, 1/2, 1/4, 1/8, 1/16, …
This sequence is also a geometric progression! Each member of this progression is also obtained multiplication the previous term, by the same number. Only the number is fractional: q = +1/2 . Or +0,5 . And (important!) number, smaller one:q = 1/2<1.
What is interesting about this geometric progression? Where are its members going? Let's get a look:
1/2 = 0,5;
1/4 = 0,25;
1/8 = 0,125;
1/16 = 0,0625;
…….
What is interesting here? First, the decrease in the members of the progression is immediately striking: each of its members smaller the previous exactly 2 times. Or, according to the definition of a geometric progression, each term more previous 1/2 times, because progression denominator q = 1/2 . And from multiplying by a positive number less than one, the result usually decreases, yes ...
What more can be seen in the behavior of this progression? Do its members disappear? unlimited, going to minus infinity? Not! They disappear in a special way. At first they decrease quite quickly, and then more and more slowly. And all the while staying positive. Albeit very, very small. And what are they striving for? Didn't guess? Yes! They tend to zero!) And, pay attention, the members of our progression never reach! Only infinitely close to him. It is very important.)
A similar situation will be in such a progression:
(b n): -1, -1/2, -1/4, -1/8, -1/16, …
Here b 1 = -1 , a q = 1/2 . Everything is the same, only now the members will approach zero from the other side, from below. Staying all the time negative.)
Such a geometric progression, the members of which approaching zero indefinitely.(it doesn’t matter, on the positive or negative side), in mathematics it has a special name - infinitely decreasing geometric progression. This progression is so interesting and unusual that it will even be separate lesson .)
So, we have considered all possible positive denominators are both large ones and smaller ones. We do not consider the one itself as a denominator for the reasons stated above (remember the example with the sequence of triples ...)
To summarize:
positiveand more than one (q>1), then the members of the progression:
a) increase indefinitely (ifb 1 >0);
b) decrease indefinitely (ifb 1 <0).
If the denominator of a geometric progression positive and less than one (0< q<1), то члены прогрессии:
a) infinitely close to zero above(ifb 1 >0);
b) infinitely close to zero from below(ifb 1 <0).
It remains now to consider the case negative denominator.
The denominator is negative ( q <0)
We won't go far for an example. Why, in fact, shaggy grandmother ?!) Let, for example, the first member of the progression be b 1 = 1 , and take the denominator q = -2.
We get the following sequence:
(b n): 1, -2, 4, -8, 16, …
And so on.) Each term of the progression is obtained multiplication previous member on a negative number-2. In this case, all members in odd places (first, third, fifth, etc.) will be positive, and in even places (second, fourth, etc.) - negative. Signs are strictly interleaved. Plus-minus-plus-minus ... Such a geometric progression is called - increasing sign alternating.
Where are its members going? And nowhere.) Yes, in absolute value (i.e. modulo) the terms of our progression increase indefinitely (hence the name "increasing"). But at the same time, each member of the progression alternately throws it into the heat, then into the cold. Either plus or minus. Our progression fluctuates... Moreover, the range of fluctuations grows rapidly with each step, yes.) Therefore, the aspirations of the members of the progression to go somewhere specifically here no. Neither to plus infinity, nor to minus infinity, nor to zero - nowhere.
Consider now some fractional denominator between zero and minus one.
For example, let it be b 1 = 1 , a q = -1/2.
Then we get the progression:
(b n): 1, -1/2, 1/4, -1/8, 1/16, …
And again we have an alternation of signs! But, unlike the previous example, here there is already a clear tendency for terms to approach zero.) Only this time our terms approach zero not strictly from above or below, but again hesitating. Alternately taking either positive or negative values. But at the same time they modules are getting closer and closer to the cherished zero.)
This geometric progression is called infinitely decreasing alternating sign.
Why are these two examples interesting? And the fact that in both cases takes place alternating characters! Such a chip is typical only for progressions with a negative denominator, yes.) Therefore, if in some task you see a geometric progression with alternating members, then you will already firmly know that its denominator is 100% negative and you will not be mistaken in the sign.)
By the way, in the case of a negative denominator, the sign of the first term does not affect the behavior of the progression itself at all. Whatever the sign of the first member of the progression is, in any case, the sign of the alternation of members will be observed. The whole question is just at what places(even or odd) there will be members with specific signs.
Remember:
If the denominator of a geometric progression negative , then the signs of the terms of the progression are always alternate.
At the same time, the members themselves:
a) increase indefinitelymodulo, ifq<-1;
b) approach zero infinitely if -1< q<0 (прогрессия бесконечно убывающая).
That's all. All typical cases are analyzed.)
In the process of parsing a variety of examples of geometric progressions, I periodically used the words: "tends to zero", "tends to plus infinity", tends to minus infinity... It's okay.) These speech turns (and specific examples) are just an initial acquaintance with behavior various number sequences. An example of a geometric progression.
Why do we even need to know the progression behavior? What difference does it make where she goes? To zero, to plus infinity, to minus infinity ... What do we care about this?
The thing is that already at the university, in the course of higher mathematics, you will need the ability to work with a variety of numerical sequences (with any, not just progressions!) And the ability to imagine exactly how this or that sequence behaves - whether it increases is unlimited, whether it decreases, whether it tends to a specific number (and not necessarily to zero), or even does not tend to anything at all ... A whole section is devoted to this topic in the course of mathematical analysis - limit theory. A little more specifically, the concept limit of the number sequence. Very interesting topic! It makes sense to go to college and figure it out.)
Some examples from this section (sequences that have a limit) and in particular, infinitely decreasing geometric progression begin to learn at school. Getting used.)
Moreover, the ability to study the behavior of sequences well in the future will greatly play into the hands and will be very useful in function research. The most varied. But the ability to competently work with functions (calculate derivatives, explore them in full, build their graphs) already dramatically increases your mathematical level! Doubt? No need. Also remember my words.)
Let's look at a geometric progression in life?
In the life around us, we encounter exponential progression very, very often. Without even knowing it.)
For example, various microorganisms that surround us everywhere in huge quantities and which we do not even see without a microscope multiply precisely in geometric progression.
Let's say one bacterium reproduces by dividing in half, giving offspring in 2 bacteria. In turn, each of them, multiplying, also divides in half, giving a common offspring of 4 bacteria. The next generation will give 8 bacteria, then 16 bacteria, 32, 64 and so on. With each successive generation, the number of bacteria doubles. A typical example of a geometric progression.)
Also, some insects - aphids, flies - multiply exponentially. And rabbits sometimes, by the way, too.)
Another example of a geometric progression, closer to everyday life, is the so-called compound interest. Such an interesting phenomenon is often found in bank deposits and is called interest capitalization. What it is?
You yourself are still, of course, young. You study at school, you don't apply to banks. But your parents are adults and independent people. They go to work, earn money for their daily bread, and put some of the money in the bank, making savings.)
Let's say your dad wants to save up a certain amount of money for a family vacation in Turkey and put 50,000 rubles in the bank at 10% per annum for a period of three years with annual interest capitalization. Moreover, nothing can be done with the deposit during this entire period. You can neither replenish the deposit nor withdraw money from the account. What profit will he make in these three years?
Well, firstly, you need to figure out what 10% per annum is. It means that in a year 10% will be added to the initial deposit amount by the bank. From what? Of course, from initial deposit amount.
Calculate the amount of the account in a year. If the initial amount of the deposit was 50,000 rubles (i.e. 100%), then in a year how much interest will be on the account? That's right, 110%! From 50,000 rubles.
So we consider 110% of 50,000 rubles:
50,000 1.1 \u003d 55,000 rubles.
I hope you understand that finding 110% of the value means multiplying this value by the number 1.1? If you do not understand why this is so, remember the fifth and sixth grades. Namely - the relationship of percentages with fractions and parts.)
Thus, the increase for the first year will be 5000 rubles.
How much money will be in the account after two years? 60,000 rubles? Unfortunately (or rather, fortunately), it's not that simple. The whole trick of interest capitalization is that with each new interest accrual, these same interest will be considered already from the new amount! From the one who already is on account At the moment. And the interest accrued for the previous term is added to the initial amount of the deposit and, thus, they themselves participate in the calculation of new interest! That is, they become a full part of the total account. or general capital. Hence the name - interest capitalization.
It's in the economy. And in mathematics, such percentages are called compound interest. Or percent of percent.) Their trick is that in sequential calculation, the percentages are calculated each time from the new value. Not from the original...
Therefore, in order to calculate the sum through two years, we need to calculate 110% of the amount that will be in the account in a year. That is, already from 55,000 rubles.
We consider 110% of 55,000 rubles:
55000 1.1 \u003d 60500 rubles.
This means that the percentage increase for the second year will already be 5,500 rubles, and for two years - 10,500 rubles.
Now you can already guess that in three years the amount in the account will be 110% of 60,500 rubles. That is again 110% from the previous (last year) amounts.
Here we consider:
60500 1.1 \u003d 66550 rubles.
And now we build our monetary amounts by years in sequence:
50000;
55000 = 50000 1.1;
60500 = 55000 1.1 = (50000 1.1) 1.1;
66550 = 60500 1.1 = ((50000 1.1) 1.1) 1.1
So how? Why not a geometric progression? First member b 1 = 50000 , and the denominator q = 1,1 . Each term is strictly 1.1 times greater than the previous one. Everything is in strict accordance with the definition.)
And how many additional percentage bonuses will your dad "drop in" while his 50,000 rubles were in the bank account for three years?
We believe:
66550 - 50000 = 16550 rubles
It's bad, of course. But this is if the initial amount of the contribution is small. What if there's more? Say, not 50, but 200 thousand rubles? Then the increase for three years will already be 66,200 rubles (if you count). Which is already very good.) And if the contribution is even greater? That's what it is...
Conclusion: the higher the initial contribution, the more profitable the interest capitalization becomes. That is why deposits with interest capitalization are provided by banks for long periods. Let's say five years.
Also, all sorts of bad diseases like influenza, measles and even more terrible diseases (the same SARS in the early 2000s or plague in the Middle Ages) like to spread exponentially. Hence the scale of epidemics, yes ...) And all because of the fact that a geometric progression with whole positive denominator (q>1) - a thing that grows very fast! Remember the reproduction of bacteria: from one bacterium two are obtained, from two - four, from four - eight, and so on ... With the spread of any infection, everything is the same.)
The simplest problems in geometric progression.
Let's start, as always, with a simple problem. Purely to understand the meaning.
1. It is known that the second term of a geometric progression is 6, and the denominator is -0.5. Find the first, third and fourth terms.
So we are given endless geometric progression, well known second member this progression:
b2 = 6
In addition, we also know progression denominator:
q = -0.5
And you need to find first, third and fourth members of this progression.
Here we are acting. We write down the sequence according to the condition of the problem. Directly in general terms, where the second member is the six:
b1,6,b 3 , b 4 , …
Now let's start searching. We start, as always, with the simplest. You can calculate, for example, the third term b 3? Can! We already know (directly in the sense of a geometric progression) that the third term (b 3) more than a second (b 2 ) in "q" once!
So we write:
b 3 =b 2 · q
We substitute the six in this expression instead of b 2 and -0.5 instead q and we think. And the minus is also not ignored, of course ...
b 3 \u003d 6 (-0.5) \u003d -3
Like this. The third term turned out to be negative. No wonder: our denominator q- negative. And plus multiplied by minus, it will, of course, be minus.)
We now consider the next, fourth term of the progression:
b 4 =b 3 · q
b 4 \u003d -3 (-0.5) \u003d 1.5
The fourth term is again with a plus. The fifth term will again be with a minus, the sixth with a plus, and so on. Signs - alternate!
So, the third and fourth members were found. The result is the following sequence:
b1; 6; -3; 1.5; …
It remains now to find the first term b 1 according to the well-known second. To do this, we step in the other direction, to the left. This means that in this case, we do not need to multiply the second term of the progression by the denominator, but share.
We divide and get:
![]()
That's all.) The answer to the problem will be as follows:
-12; 6; -3; 1,5; …
As you can see, the solution principle is the same as in . We know any member and denominator geometric progression - we can find any other term. Whatever we want, we will find one.) The only difference is that addition / subtraction is replaced by multiplication / division.
Remember: if we know at least one member and denominator of a geometric progression, then we can always find any other member of this progression.
The following task, according to tradition, is from the real version of the OGE:
2.
…; 150; X; 6; 1.2; …
So how? This time there is no first term, no denominator q, just a sequence of numbers is given ... Something familiar already, right? Yes! A similar problem has already been dealt with in arithmetic progression!
Here we are not scared. All the same. Turn on your head and remember the elementary meaning of a geometric progression. We look carefully at our sequence and figure out which parameters of the geometric progression of the three main ones (the first member, denominator, member number) are hidden in it.
Member numbers? There are no member numbers, yes ... But there are four successive numbers. What this word means, I don’t see the point in explaining at this stage.) Are there two neighboring known numbers? There is! These are 6 and 1.2. So we can find progression denominator. So we take the number 1.2 and divide to the previous number. For six.
We get:
We get:
x= 150 0.2 = 30
Answer: x = 30 .
As you can see, everything is quite simple. The main difficulty lies only in the calculations. It is especially difficult in the case of negative and fractional denominators. So those who have problems, repeat the arithmetic! How to work with fractions, how to work with negative numbers, and so on... Otherwise, you will slow down mercilessly here.
Now let's change the problem a bit. Now it will get interesting! Let's remove the last number 1.2 in it. Let's solve this problem now:
3. Several consecutive terms of a geometric progression are written out:
…; 150; X; 6; …
Find the term of the progression, denoted by the letter x.
Everything is the same, only two neighboring famous we no longer have members of the progression. This is the main problem. Because the magnitude q through two neighboring terms, we can already easily determine we can't. Do we have a chance to meet the challenge? Certainly!
Let's write the unknown term " x"Directly in the sense of a geometric progression! In general terms.
Yes Yes! Directly with an unknown denominator!
On the one hand, for x we can write the following ratio:
x= 150q
On the other hand, we have every right to paint the same X through next member, through the six! Divide six by the denominator.
Like this:
x = 6/ q
Obviously, now we can equate both of these ratios. Since we are expressing the same value (x), but two different ways.
We get the equation:
Multiplying everything by q, simplifying, reducing, we get the equation:
q 2 \u003d 1/25
We solve and get:
q = ±1/5 = ±0.2
Oops! The denominator is double! +0.2 and -0.2. And which one to choose? Dead end?
Calm! Yes, the problem really has two solutions! Nothing wrong with that. It happens.) You are not surprised when, for example, you get two roots by solving the usual? It's the same story here.)
For q = +0.2 we'll get:
X \u003d 150 0.2 \u003d 30
And for q = -0,2 will:
X = 150 (-0.2) = -30
We get a double answer: x = 30; x = -30.
What does this interesting fact mean? And what exists two progressions, satisfying the condition of the problem!
Like these ones:
…; 150; 30; 6; …
…; 150; -30; 6; …
Both are suitable.) What do you think is the reason for the bifurcation of answers? Just because of the elimination of a specific member of the progression (1,2), coming after the six. And knowing only the previous (n-1)-th and subsequent (n+1)-th members of the geometric progression, we can no longer unequivocally say anything about the n-th member standing between them. There are two options - plus and minus.
But it doesn't matter. As a rule, in tasks for a geometric progression there is additional information that gives an unambiguous answer. Let's say the words: "sign-alternating progression" or "progression with a positive denominator" and so on... It is these words that should serve as a clue, which sign, plus or minus, should be chosen when making the final answer. If there is no such information, then - yes, the task will have two solutions.)
And now we decide on our own.
4. Determine if the number 20 will be a member of a geometric progression:
4 ; 6; 9; …
5. An alternating geometric progression is given:
…; 5; x ; 45; …
Find the term of the progression indicated by the letter x .
6. Find the fourth positive term of the geometric progression:
625; -250; 100; …
7. The second term of the geometric progression is -360, and its fifth term is 23.04. Find the first term of this progression.
Answers (in disarray): -15; 900; No; 2.56.
Congratulations if everything worked out!
Something doesn't fit? Is there a double answer somewhere? We read the conditions of the assignment carefully!
The last puzzle doesn't work? Nothing complicated there.) We work directly according to the meaning of a geometric progression. Well, you can draw a picture. It helps.)
As you can see, everything is elementary. If the progression is short. What if it's long? Or is the number of the desired member very large? I would like, by analogy with an arithmetic progression, to somehow get a convenient formula that makes it easy to find any member of any geometric progression by his number. Without multiplying many, many times by q. And there is such a formula!) Details - in the next lesson.
Lesson and presentation on the topic: "Number sequences. Geometric progression"
Additional materials
Dear users, do not forget to leave your comments, feedback, suggestions! All materials are checked by an antivirus program.
Teaching aids and simulators in the online store "Integral" for grade 9
Powers and Roots Functions and Graphs
Guys, today we will get acquainted with another type of progression.
The topic of today's lesson is geometric progression.
Geometric progression
Definition. A numerical sequence in which each term, starting from the second, is equal to the product of the previous one and some fixed number, is called a geometric progression.Let's define our sequence recursively: $b_(1)=b$, $b_(n)=b_(n-1)*q$,
where b and q are certain given numbers. The number q is called the denominator of the progression.
Example. 1,2,4,8,16… Geometric progression, in which the first member is equal to one, and $q=2$.
Example. 8,8,8,8… A geometric progression whose first term is eight,
and $q=1$.
Example. 3,-3,3,-3,3... A geometric progression whose first term is three,
and $q=-1$.
The geometric progression has the properties of monotonicity.
If $b_(1)>0$, $q>1$,
then the sequence is increasing.
If $b_(1)>0$, $0 The sequence is usually denoted as: $b_(1), b_(2), b_(3), ..., b_(n), ...$.
Just like in an arithmetic progression, if the number of elements in a geometric progression is finite, then the progression is called a finite geometric progression.
$b_(1), b_(2), b_(3), ..., b_(n-2), b_(n-1), b_(n)$.
Note that if the sequence is a geometric progression, then the sequence of squared terms is also a geometric progression. The second sequence has the first term $b_(1)^2$ and the denominator $q^2$.
Formula of the nth member of a geometric progression
Geometric progression can also be specified in analytical form. Let's see how to do it:$b_(1)=b_(1)$.
$b_(2)=b_(1)*q$.
$b_(3)=b_(2)*q=b_(1)*q*q=b_(1)*q^2$.
$b_(4)=b_(3)*q=b_(1)*q^3$.
$b_(5)=b_(4)*q=b_(1)*q^4$.
We can easily see the pattern: $b_(n)=b_(1)*q^(n-1)$.
Our formula is called "formula of the n-th member of a geometric progression".
Let's go back to our examples.
Example. 1,2,4,8,16… A geometric progression whose first term is equal to one,
and $q=2$.
$b_(n)=1*2^(n)=2^(n-1)$.
Example. 16,8,4,2,1,1/2… A geometric progression whose first term is sixteen and $q=\frac(1)(2)$.
$b_(n)=16*(\frac(1)(2))^(n-1)$.
Example. 8,8,8,8… A geometric progression where the first term is eight and $q=1$.
$b_(n)=8*1^(n-1)=8$.
Example. 3,-3,3,-3,3… A geometric progression whose first term is three and $q=-1$.
$b_(n)=3*(-1)^(n-1)$.
Example. Given a geometric progression $b_(1), b_(2), …, b_(n), … $.
a) It is known that $b_(1)=6, q=3$. Find $b_(5)$.
b) It is known that $b_(1)=6, q=2, b_(n)=768$. Find n.
c) It is known that $q=-2, b_(6)=96$. Find $b_(1)$.
d) It is known that $b_(1)=-2, b_(12)=4096$. Find q.
Decision.
a) $b_(5)=b_(1)*q^4=6*3^4=486$.
b) $b_n=b_1*q^(n-1)=6*2^(n-1)=768$.
$2^(n-1)=\frac(768)(6)=128$ since $2^7=128 => n-1=7; n=8$.
c) $b_(6)=b_(1)*q^5=b_(1)*(-2)^5=-32*b_(1)=96 => b_(1)=-3$.
d) $b_(12)=b_(1)*q^(11)=-2*q^(11)=4096 => q^(11)=-2048 => q=-2$.
Example. The difference between the seventh and fifth members of the geometric progression is 192, the sum of the fifth and sixth members of the progression is 192. Find the tenth member of this progression.
Decision.
We know that: $b_(7)-b_(5)=192$ and $b_(5)+b_(6)=192$.
We also know: $b_(5)=b_(1)*q^4$; $b_(6)=b_(1)*q^5$; $b_(7)=b_(1)*q^6$.
Then:
$b_(1)*q^6-b_(1)*q^4=192$.
$b_(1)*q^4+b_(1)*q^5=192$.
We got a system of equations:
$\begin(cases)b_(1)*q^4(q^2-1)=192\\b_(1)*q^4(1+q)=192\end(cases)$.
Equating, our equations get:
$b_(1)*q^4(q^2-1)=b_(1)*q^4(1+q)$.
$q^2-1=q+1$.
$q^2-q-2=0$.
We got two solutions q: $q_(1)=2, q_(2)=-1$.
Substitute successively into the second equation:
$b_(1)*2^4*3=192 => b_(1)=4$.
$b_(1)*(-1)^4*0=192 =>$ no solutions.
We got that: $b_(1)=4, q=2$.
Let's find the tenth term: $b_(10)=b_(1)*q^9=4*2^9=2048$.
The sum of a finite geometric progression
Suppose we have a finite geometric progression. Let's, as well as for an arithmetic progression, calculate the sum of its members.Let a finite geometric progression be given: $b_(1),b_(2),…,b_(n-1),b_(n)$.
Let's introduce the notation for the sum of its members: $S_(n)=b_(1)+b_(2)+⋯+b_(n-1)+b_(n)$.
In the case when $q=1$. All members of the geometric progression are equal to the first member, then it is obvious that $S_(n)=n*b_(1)$.
Consider now the case $q≠1$.
Multiply the above amount by q.
$S_(n)*q=(b_(1)+b_(2)+⋯+b_(n-1)+b_(n))*q=b_(1)*q+b_(2)*q+⋯ +b_(n-1)*q+b_(n)*q=b_(2)+b_(3)+⋯+b_(n)+b_(n)*q$.
Note:
$S_(n)=b_(1)+(b_(2)+⋯+b_(n-1)+b_(n))$.
$S_(n)*q=(b_(2)+⋯+b_(n-1)+b_(n))+b_(n)*q$.
$S_(n)*q-S_(n)=(b_(2)+⋯+b_(n-1)+b_(n))+b_(n)*q-b_(1)-(b_(2 )+⋯+b_(n-1)+b_(n))=b_(n)*q-b_(1)$.
$S_(n)(q-1)=b_(n)*q-b_(1)$.
$S_(n)=\frac(b_(n)*q-b_(1))(q-1)=\frac(b_(1)*q^(n-1)*q-b_(1)) (q-1)=\frac(b_(1)(q^(n)-1))(q-1)$.
$S_(n)=\frac(b_(1)(q^(n)-1))(q-1)$.
We have obtained the formula for the sum of a finite geometric progression.
Example.
Find the sum of the first seven terms of a geometric progression whose first term is 4 and the denominator is 3.
Decision.
$S_(7)=\frac(4*(3^(7)-1))(3-1)=2*(3^(7)-1)=4372$.
Example.
Find the fifth member of the geometric progression, which is known: $b_(1)=-3$; $b_(n)=-3072$; $S_(n)=-4095$.
Decision.
$b_(n)=(-3)*q^(n-1)=-3072$.
$q^(n-1)=1024$.
$q^(n)=1024q$.
$S_(n)=\frac(-3*(q^(n)-1))(q-1)=-4095$.
$-4095(q-1)=-3*(q^(n)-1)$.
$-4095(q-1)=-3*(1024q-1)$.
$1365q-1365=1024q-1$.
$341q=1364$.
$q=4$.
$b_5=b_1*q^4=-3*4^4=-3*256=-768$.
Characteristic property of a geometric progression
Guys, given a geometric progression. Let's consider its three consecutive members: $b_(n-1),b_(n),b_(n+1)$.We know that:
$\frac(b_(n))(q)=b_(n-1)$.
$b_(n)*q=b_(n+1)$.
Then:
$\frac(b_(n))(q)*b_(n)*q=b_(n)^(2)=b_(n-1)*b_(n+1)$.
$b_(n)^(2)=b_(n-1)*b_(n+1)$.
If the progression is finite, then this equality holds for all terms except the first and last.
If it is not known in advance what kind of sequence the sequence has, but it is known that: $b_(n)^(2)=b_(n-1)*b_(n+1)$.
Then we can safely say that this is a geometric progression.
A number sequence is a geometric progression only when the square of each of its terms is equal to the product of its two neighboring terms of the progression. Do not forget that for a finite progression this condition is not satisfied for the first and last term.
Let's look at this identity: $\sqrt(b_(n)^(2))=\sqrt(b_(n-1)*b_(n+1))$.
$|b_(n)|=\sqrt(b_(n-1)*b_(n+1))$.
$\sqrt(a*b)$ is called the average geometric numbers a and b.
The modulus of any member of a geometric progression is equal to the geometric mean of the two members adjacent to it.
Example.
Find x such that $x+2; 2x+2; 3x+3$ were three consecutive members of a geometric progression.
Decision.
Let's use the characteristic property:
$(2x+2)^2=(x+2)(3x+3)$.
$4x^2+8x+4=3x^2+3x+6x+6$.
$x^2-x-2=0$.
$x_(1)=2$ and $x_(2)=-1$.
Substitute sequentially in the original expression, our solutions:
With $x=2$, we got the sequence: 4;6;9 is a geometric progression with $q=1.5$.
With $x=-1$, we got the sequence: 1;0;0.
Answer: $x=2.$
Tasks for independent solution
1. Find the eighth first member of the geometric progression 16; -8; 4; -2 ....2. Find the tenth member of the geometric progression 11,22,44….
3. It is known that $b_(1)=5, q=3$. Find $b_(7)$.
4. It is known that $b_(1)=8, q=-2, b_(n)=512$. Find n.
5. Find the sum of the first 11 members of the geometric progression 3;12;48….
6. Find x such that $3x+4; 2x+4; x+5$ are three consecutive members of a geometric progression.