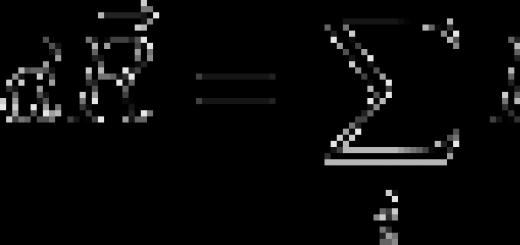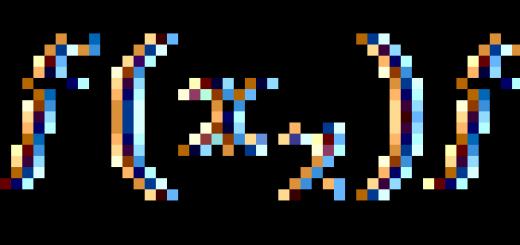How to find the coordinates of a vector from the coordinates of points. Vectors for dummies. Actions with vectors. Vector coordinates. The simplest problems with vectors. Finding the coordinates of a vector in space

Finding the coordinates of a vector is a fairly common condition for many problems in mathematics. The ability to find the coordinates of a vector will help you in other, more complex problems with related topics. In this article, we will consider the formula for finding the coordinates of a vector and several tasks.

Finding the coordinates of a vector in a plane

What is a plane? A plane is a two-dimensional space, a space with two dimensions (dimension x and dimension y). For example, paper is flat. The surface of the table is flat. Any non-volumetric figure (square, triangle, trapezium) is also a plane. Thus, if in the condition of the problem it is necessary to find the coordinates of a vector that lies on a plane, we immediately recall x and y. You can find the coordinates of such a vector as follows: AB coordinates of the vector = (xB - xA; yB - xA). It can be seen from the formula that the coordinates of the starting point must be subtracted from the coordinates of the end point.

Example:

The CD vector has start (5; 6) and end (7; 8) coordinates.
Find the coordinates of the vector itself.
Using the above formula, we get the following expression: CD = (7-5; 8-6) = (2; 2).
Thus, the coordinates of the CD vector = (2; 2).
Accordingly, the x coordinate is equal to two, the y coordinate is also two.

Finding the coordinates of a vector in space

What is space? Space is already a three-dimensional dimension, where 3 coordinates are given: x, y, z. If you need to find a vector that lies in space, the formula practically does not change. Only one coordinate is added. To find the vector, you need to subtract the start coordinates from the end coordinates. AB = (xB - xA; yB - yA; zB - zA)

Example:

Vector DF has initial (2; 3; 1) and final (1; 5; 2).
Applying the above formula, we get: Vector coordinates DF = (1-2; 5-3; 2-1) = (-1; 2; 1).
Remember, the value of the coordinates can be negative, there is no problem with that.

How to find vector coordinates online?

If for some reason you do not want to find the coordinates yourself, you can use the online calculator. First, choose the dimension of the vector. The dimension of a vector is responsible for its dimensions. Dimension 3 means that the vector is in space, dimension 2 means that it is on the plane. Next, insert the coordinates of the points into the appropriate fields and the program will determine the coordinates of the vector itself. Everything is very simple.

By clicking on the button, the page will automatically scroll down and give you the correct answer along with the solution steps.

It is recommended to study well this topic, because the concept of a vector is found not only in mathematics, but also in physics. Faculty students Information technologies also study the topic of vectors, but at a more complex level.

On the abscissa and ordinate axes are called coordinates vector. The vector coordinates are usually indicated in the form (x, y), and the vector itself as: = (x, y).

The formula for determining the coordinates of a vector for two-dimensional problems.

In the case of a two-dimensional problem, a vector with known point coordinates A(x 1; y 1) and B(x 2 ; y 2 ) can be calculated:

\u003d (x 2 - x 1; y 2 - y 1).

The formula for determining the coordinates of a vector for spatial problems.

In the case of a spatial problem, a vector with known point coordinates A (x 1; y 1;z 1 ) and B (x 2 ; y 2 ; z 2 ) can be calculated using the formula:

= (x 2 - x 1 ; y 2 - y 1 ; z 2 - z 1 ).

The coordinates give a comprehensive description of the vector, since it is possible to construct the vector itself from the coordinates. Knowing the coordinates, it is easy to calculate and vector length. (Property 3 below).

Vector coordinate properties.

1. Any equal vectors in a single coordinate system have equal coordinates.

2. Coordinates collinear vectors proportional. Provided that none of the vectors is equal to zero.

3. Square the length of any vector is equal to the sum squares it coordinates.

4.When the operation vector multiplications on the real number each of its coordinates is multiplied by this number.

5. During the operation of vector addition, we calculate the sum of the corresponding vector coordinates.

6. Scalar product of two vectors is equal to the sum of the products of their respective coordinates.

Finally, I got my hands on an extensive and long-awaited topic analytical geometry . First, a little about this section of higher mathematics…. Surely you now remembered the school geometry course with numerous theorems, their proofs, drawings, etc. What to hide, an unloved and often obscure subject for a significant proportion of students. Analytic geometry, oddly enough, may seem more interesting and accessible. What does the adjective "analytical" mean? Two stamped mathematical turns immediately come to mind: “graphic method of solution” and “analytical method of solution”. Graphic method , of course, is associated with the construction of graphs, drawings. Analytical same method involves problem solving predominantly through algebraic operations. In this regard, the algorithm for solving almost all problems of analytical geometry is simple and transparent, often it is enough to accurately apply the necessary formulas - and the answer is ready! No, of course, it will not do without drawings at all, besides, for a better understanding of the material, I will try to bring them in excess of the need.

The open course of lessons in geometry does not claim to be theoretical completeness, it is focused on solving practical problems. I will include in my lectures only what, from my point of view, is important in practical terms. If you need a more complete reference on any subsection, I recommend the following quite accessible literature:

1) A thing that, no joke, is familiar to several generations: School textbook on geometry, the authors - L.S. Atanasyan and Company. This school locker room hanger has already withstood 20 (!) reissues, which, of course, is not the limit.

2) Geometry in 2 volumes. The authors L.S. Atanasyan, Bazylev V.T.. This is literature for high school, you will need first volume. Rarely occurring tasks may fall out of my field of vision, and tutorial will provide invaluable assistance.

Both books are free to download online. In addition, you can use my archive with ready-made solutions, which can be found on the page Download higher mathematics examples.

Of the tools, I again offer my own development - software package on analytical geometry, which will greatly simplify life and save a lot of time.

It is assumed that the reader is familiar with the basic geometric concepts and figures: point, line, plane, triangle, parallelogram, parallelepiped, cube, etc. It is advisable to remember some theorems, at least the Pythagorean theorem, hello repeaters)

And now we will sequentially consider: the concept of a vector, actions with vectors, vector coordinates. Further I recommend reading the most important article Dot product of vectors, as well as Vector and mixed product of vectors. The local task will not be superfluous - Division of the segment in this regard. Based on the above information, you can equation of a straight line in a plane with the simplest examples of solutions, which will allow learn how to solve problems in geometry. The following articles are also helpful: Equation of a plane in space, Equations of a straight line in space, Basic problems on the line and plane , other sections of analytic geometry. Naturally, standard tasks will be considered along the way.

The concept of a vector. free vector

First, let's repeat the school definition of a vector. Vector called directed a segment for which its beginning and end are indicated:

In this case, the beginning of the segment is the point , the end of the segment is the point . The vector itself is denoted by . Direction is essential, if you rearrange the arrow to the other end of the segment, you get a vector, and this is already completely different vector. It is convenient to identify the concept of a vector with the movement of a physical body: you must admit that entering the doors of an institute or leaving the doors of an institute are completely different things.

It is convenient to consider individual points of a plane, space as the so-called zero vector. Such a vector has the same end and beginning.

!!! Note: Here and below, you can assume that the vectors lie in the same plane or you can assume that they are located in space - the essence of the material presented is valid for both the plane and space.

Designations: Many immediately drew attention to a stick without an arrow in the designation and said that they also put an arrow at the top! That's right, you can write with an arrow: , but admissible and record that I will use later. Why? Apparently, such a habit has developed from practical considerations, my shooters at school and university turned out to be too diverse and shaggy. AT educational literature sometimes they don’t bother with cuneiform at all, but highlight the letters in bold: , thereby implying that this is a vector.

That was the style, and now about the ways of writing vectors:

1) Vectors can be written in two capital Latin letters:
etc. While the first letter necessarily denotes the start point of the vector, and the second letter denotes the end point of the vector.

2) Vectors are also written in small Latin letters:
In particular, our vector can be redesignated for brevity by a small Latin letter .

Length or module non-zero vector is called the length of the segment. The length of the null vector is zero. Logically.

The length of a vector is denoted by the modulo sign: ,

How to find the length of a vector, we will learn (or repeat, for whom how) a little later.

That was elementary information about the vector, familiar to all schoolchildren. In analytic geometry, the so-called free vector.

If it's quite simple - vector can be drawn from any point:

We used to call such vectors equal (the definition of equal vectors will be given below), but from a purely mathematical point of view, this is the SAME VECTOR or free vector. Why free? Because in the course of solving problems you can “attach” one or another “school” vector to ANY point of the plane or space you need. This is a very cool property! Imagine a directed segment of arbitrary length and direction - it can be "cloned" an infinite number of times and at any point in space, in fact, it exists EVERYWHERE. There is such a student's proverb: Each lecturer in f ** u in the vector. After all, it’s not just a witty rhyme, everything is almost correct - a directed segment can be attached there too. But do not rush to rejoice, students themselves suffer more often =)

So, free vector- This a bunch of identical directional segments. The school definition of a vector, given at the beginning of the paragraph: “A directed segment is called a vector ...”, implies specific a directed segment taken from a given set, which is attached to a certain point in the plane or space.

It should be noted that from the point of view of physics, the concept of a free vector in general case is incorrect, and the application point matters. Indeed, a direct blow of the same force on the nose or on the forehead is enough to develop my stupid example entails different consequences. However, not free vectors are also found in the course of vyshmat (do not go there :)).

Actions with vectors. Collinearity of vectors

AT school course geometry considers a number of actions and rules with vectors: addition according to the triangle rule, addition according to the parallelogram rule, the rule of the difference of vectors, multiplication of a vector by a number, the scalar product of vectors, etc. As a seed, we repeat two rules that are especially relevant for solving problems of analytical geometry.

Rule of addition of vectors according to the rule of triangles

Consider two arbitrary non-zero vectors and :

It is required to find the sum of these vectors. Due to the fact that all vectors are considered free, we postpone the vector from end vector :

The sum of vectors is the vector . For a better understanding of the rule, it is advisable to invest in it physical meaning: let some body make a path along the vector , and then along the vector . Then the sum of the vectors is the vector of the resulting path starting at the point of departure and ending at the point of arrival. A similar rule is formulated for the sum of any number of vectors. As they say, the body can go its way strongly zigzag, or maybe on autopilot - along the resulting sum vector.

By the way, if the vector is postponed from start vector , then we get the equivalent parallelogram rule addition of vectors.

First, about the collinearity of vectors. The two vectors are called collinear if they lie on the same line or on parallel lines. Roughly speaking, we are talking about parallel vectors. But in relation to them, the adjective "collinear" is always used.

Imagine two collinear vectors. If the arrows of these vectors are directed in the same direction, then such vectors are called co-directional. If the arrows point to different sides, then the vectors will be oppositely directed.

Designations: collinearity of vectors is written with the usual parallelism icon: , while detailing is possible: (vectors are co-directed) or (vectors are directed oppositely).

work of a nonzero vector by a number is a vector whose length is equal to , and the vectors and are co-directed at and oppositely directed at .

The rule for multiplying a vector by a number is easier to understand with a picture:

We understand in more detail:

1) Direction. If the multiplier is negative, then the vector changes direction to the opposite.

2) Length. If the factor is contained within or , then the length of the vector decreases. So, the length of the vector is twice less than the length of the vector . If modulo multiplier more than one, then the length of the vector increases in time.

3) Please note that all vectors are collinear, while one vector is expressed through another, for example, . The reverse is also true: if one vector can be expressed in terms of another, then such vectors are necessarily collinear. Thus: if we multiply a vector by a number, we get collinear(relative to original) vector.

4) The vectors are codirectional. The vectors and are also codirectional. Any vector of the first group is opposite to any vector of the second group.

What vectors are equal?

Two vectors are equal if they are codirectional and have the same length. Note that co-direction implies that the vectors are collinear. The definition will be inaccurate (redundant) if you say: "Two vectors are equal if they are collinear, co-directed and have the same length."

From the point of view of the concept of a free vector, equal vectors are the same vector, which was already discussed in the previous paragraph.

Vector coordinates on the plane and in space

The first point is to consider vectors on a plane. Draw a Cartesian rectangular coordinate system and set aside from the origin single vectors and :

Vectors and orthogonal. Orthogonal = Perpendicular. I recommend slowly getting used to the terms: instead of parallelism and perpendicularity, we use the words respectively collinearity and orthogonality.

Designation: orthogonality of vectors is written with the usual perpendicular sign, for example: .

The considered vectors are called coordinate vectors or orts. These vectors form basis on surface. What is the basis, I think, is intuitively clear to many, more detailed information can be found in the article Linear (non) dependence of vectors. Vector basis.In simple words, the basis and the origin of coordinates define the entire system - this is a kind of foundation on which a full and rich geometric life boils.

Sometimes the constructed basis is called orthonormal basis of the plane: "ortho" - because the coordinate vectors are orthogonal, the adjective "normalized" means unit, i.e. the lengths of the basis vectors are equal to one.

Designation: the basis is usually written in parentheses, inside which in strict order basis vectors are listed, for example: . Coordinate vectors it is forbidden swap places.

Any plane vector the only way expressed as:
, where - numbers, which are called vector coordinates in this basis. But the expression itself called vector decompositionbasis .

Dinner served:

Let's start with the first letter of the alphabet: . The drawing clearly shows that when decomposing the vector in terms of the basis, the ones just considered are used:
1) the rule of multiplication of a vector by a number: and ;
2) addition of vectors according to the triangle rule: .

Now mentally set aside the vector from any other point on the plane. It is quite obvious that his corruption will "relentlessly follow him." Here it is, the freedom of the vector - the vector "carries everything with you." This property, of course, is true for any vector. It's funny that the basis (free) vectors themselves do not have to be set aside from the origin, one can be drawn, for example, at the bottom left, and the other at the top right, and nothing will change from this! True, you don’t need to do this, because the teacher will also show originality and draw you a “pass” in an unexpected place.

Vectors , illustrate exactly the rule for multiplying a vector by a number, the vector is co-directed with the basis vector , the vector is directed opposite to the basis vector . For these vectors, one of the coordinates is equal to zero, it can be meticulously written as follows:

And the basis vectors, by the way, are like this: (in fact, they are expressed through themselves).

And finally: , . By the way, what is vector subtraction, and why didn't I tell you about the subtraction rule? Somewhere in linear algebra, I don’t remember where, I noted that subtraction is special case addition. So, the expansions of the vectors "de" and "e" are calmly written as a sum: . Follow the drawing to see how well the good old addition of vectors according to the triangle rule works in these situations.

Considered decomposition of the form sometimes called a vector decomposition in the system ort(i.e. in the system of unit vectors). But this is not the only way to write a vector, the following option is common:

Or with an equals sign:

The basis vectors themselves are written as follows: and

That is, the coordinates of the vector are indicated in parentheses. In practical tasks, all three recording options are used.

I doubted whether to speak, but still I will say: vector coordinates cannot be rearranged. Strictly in first place write down the coordinate that corresponds to the unit vector , strictly in second place write down the coordinate that corresponds to the unit vector . Indeed, and are two different vectors.

We figured out the coordinates on the plane. Now consider vectors in three-dimensional space, everything is almost the same here! Only one more coordinate will be added. It is difficult to perform three-dimensional drawings, so I will limit myself to one vector, which for simplicity I will postpone from the origin:

Any vector three-dimensional space can the only way expand in an orthonormal basis:
, where are the coordinates of the vector (number) in the given basis.

Example from the picture: . Let's see how the vector action rules work here. First, multiplying a vector by a number: (red arrow), (green arrow) and (magenta arrow). Secondly, here is an example of adding several, in this case three, vectors: . The sum vector starts at the starting point of departure (the beginning of the vector ) and ends up at the final point of arrival (the end of the vector ).

All vectors of three-dimensional space, of course, are also free, try to mentally postpone the vector from any other point, and you will understand that its expansion "remains with it."

Similarly to the plane case, in addition to writing versions with brackets are widely used: either .

If one (or two) coordinate vectors are missing in the expansion, then zeros are put instead. Examples:
vector (meticulously ) – write down ;
vector (meticulously ) – write down ;
vector (meticulously ) – write down .

Basis vectors are written as follows:

Here, perhaps, are all the minimum theoretical knowledge necessary for solving problems of analytical geometry. Perhaps there are too many terms and definitions, so I recommend dummies to re-read and comprehend this information again. And it will be useful for any reader to refer to the basic lesson from time to time for better assimilation of the material. Collinearity, orthogonality, orthonormal basis, vector decomposition - these and other concepts will be often used in what follows. I note that the materials of the site are not enough to pass a theoretical test, a colloquium on geometry, since I carefully encrypt all theorems (besides without proofs) - to the detriment of the scientific style of presentation, but a plus for your understanding of the subject. For detailed theoretical information, I ask you to bow to Professor Atanasyan.

Now let's move on to the practical part:

The simplest problems of analytic geometry.
Actions with vectors in coordinates

The tasks that will be considered, it is highly desirable to learn how to solve them fully automatically, and the formulas memorize, don't even remember it on purpose, they will remember it themselves =) This is very important, since other problems of analytical geometry are based on the simplest elementary examples, and it will be annoying to spend extra time eating pawns. You do not need to fasten the top buttons on your shirt, many things are familiar to you from school.

The presentation of the material will follow a parallel course - both for the plane and for space. For the reason that all the formulas ... you will see for yourself.

How to find a vector given two points?

If two points of the plane and are given, then the vector has the following coordinates:

If two points in space and are given, then the vector has the following coordinates:

I.e, from the coordinates of the end of the vector you need to subtract the corresponding coordinates vector start.

The task: For the same points, write down the formulas for finding the coordinates of the vector. Formulas at the end of the lesson.

Example 1

Given two points in the plane and . Find vector coordinates

Decision: according to the corresponding formula:

Alternatively, the following notation could be used:

Aesthetes will decide like this:

Personally, I'm used to the first version of the record.

Answer:

According to the condition, it was not required to build a drawing (which is typical for problems of analytical geometry), but in order to explain some points to dummies, I will not be too lazy:

Must be understood difference between point coordinates and vector coordinates:

Point coordinates are the usual coordinates in a rectangular coordinate system. Set aside points for coordinate plane I think everyone can do it from 5-6 grade. Each point has a strict place on the plane, and they cannot be moved anywhere.

The coordinates of the same vector is its expansion with respect to the basis , in this case . Any vector is free, therefore, if desired or necessary, we can easily postpone it from some other point in the plane. Interestingly, for vectors, you can not build axes at all, a rectangular coordinate system, you only need a basis, in this case, an orthonormal basis of the plane.

The records of point coordinates and vector coordinates seem to be similar: , and sense of coordinates absolutely different, and you should be well aware of this difference. This difference, of course, is also true for space.

Ladies and gentlemen, we fill our hands:

Example 2

a) Given points and . Find vectors and .
b) Points are given and . Find vectors and .
c) Given points and . Find vectors and .
d) Points are given. Find Vectors .

Perhaps enough. These are examples for an independent decision, try not to neglect them, it will pay off ;-). Drawings are not required. Solutions and answers at the end of the lesson.

What is important in solving problems of analytical geometry? It is important to be EXTREMELY CAREFUL in order to avoid the masterful “two plus two equals zero” error. I apologize in advance if I made a mistake =)

How to find the length of a segment?

The length, as already noted, is indicated by the modulus sign.

If two points of the plane and are given, then the length of the segment can be calculated by the formula

If two points in space and are given, then the length of the segment can be calculated by the formula

Note: The formulas will remain correct if the corresponding coordinates are swapped: and , but the first option is more standard

Example 3

Decision: according to the corresponding formula:

Answer:

For clarity, I will make a drawing

Line segment - it's not a vector, and you can't move it anywhere, of course. In addition, if you complete the drawing to scale: 1 unit. \u003d 1 cm (two tetrad cells), then the answer can be checked with a regular ruler by directly measuring the length of the segment.

Yes, the solution is short, but there are a couple of important points that I would like to clarify:

First, in the answer we set the dimension: “units”. The condition does not say WHAT it is, millimeters, centimeters, meters or kilometers. Therefore, the general formulation will be a mathematically competent solution: “units” - abbreviated as “units”.

Second, let's repeat school material, which is useful not only for the considered problem:

pay attention to important technique – taking the multiplier out from under the root. As a result of the calculations, we got the result and good mathematical style involves taking the factor out from under the root (if possible). The process looks like this in more detail: . Of course, leaving the answer in the form will not be a mistake - but it is definitely a flaw and a weighty argument for nitpicking on the part of the teacher.

Here are other common cases:

Often under the root it turns out enough big number, For example . How to be in such cases? On the calculator, we check if the number is divisible by 4:. Yes, split completely, thus: . Or maybe the number can be divided by 4 again? . Thus: . The last digit of the number is odd, so dividing by 4 for the third time is clearly not possible. Trying to divide by nine: . As a result:
Ready.

Conclusion: if under the root we get a whole number that cannot be extracted, then we try to take out the factor from under the root - on the calculator we check whether the number is divisible by: 4, 9, 16, 25, 36, 49, etc.

In the course of solving various problems, roots are often found, always try to extract factors from under the root in order to avoid a lower score and unnecessary troubles with finalizing your solutions according to the teacher's remark.

Let's repeat the squaring of the roots and other powers at the same time:

Rules for actions with degrees in general view can be found in a school textbook on algebra, but I think from the examples given, everything or almost everything is already clear.

Task for an independent solution with a segment in space:

Example 4

Given points and . Find the length of the segment.

Solution and answer at the end of the lesson.