1. The rule for adding fractions with the same denominators:

Example 1:

Example 2:

Rule for adding fractions with different denominators:

Example 1:

Example 2:

Here the denominators were not multiplied, but the least common factor a2 was taken.
(The denominator is the highest power of 2.)
Additional multiplier for the first fraction 1, for the second a.

2. The rule for subtracting fractions with the same denominators:

Rule for subtracting fractions with different denominators:

3. The rule for multiplying ordinary fractions:

4. The rule for dividing fractions:

Example:

Ordinary (simple) fraction. The numerator and denominator of a fraction.
correct and not proper fraction. Mixed number.
Incomplete quotient. Integer and fractional part. Reverse fractions. A part of a unit or several of its parts is called an ordinary or simple fraction. The number of equal parts into which the unit is divided is called the denominator, and the number of parts taken is called the numerator. The fraction is written as:

Here 3 is the numerator, 7 is the denominator.

If the numerator is less than the denominator, then the fraction is less than 1 and is called proper fraction. If the numerator is equal to the denominator, then the fraction is 1. If the numerator is greater than the denominator, then the fraction is greater than 1. In both the latter cases, the fraction is called improper. If the numerator is divisible by the denominator, then this fraction is equal to the quotient: 63 / 7 = 9. If the division is performed with a remainder, then this improper fraction can be represented mixed number:

Here 9 - incomplete quotient(the integer part of the mixed number), 2 is the remainder (the numerator of the fractional part), 7 is the denominator.
Often it is necessary to solve the inverse problem - reverse a mixed number into a fraction. To do this, multiply the integer part of the mixed number by the denominator and add the numerator of the fractional part. This will be the numerator of an ordinary fraction, and the denominator remains the same.

Reciprocals are two fractions whose product is 1. For example, 3/7 and 7/3; 15/1 and 1/15 etc.

Fraction expansion. Fraction reduction. Fraction comparison.
Casting to common denominator. Addition and subtraction fractions.
Multiplication of fractions. Division of fractions
Fraction expansion.The value of a fraction does not change if its numerator and denominator are multiplied by the same non-zero number by expanding the fraction. For example,

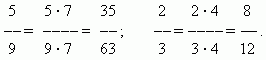
Fraction reduction. The value of a fraction does not change if its numerator and denominator are divided by the same non-zero number.. This transformation is calledfraction reduction. For example,

Fraction comparison.Of two fractions with the same numerator, the larger one is the one with the smaller denominator:

Of two fractions with the same denominators, the one with the larger numerator is greater:

To compare fractions that have different numerators and denominators, you need to expand them to bring them to a common denominator.
EXAMPLE Compare two fractions:

The transformation used here is called reducing fractions to a common denominator.
Addition and subtraction of fractions.If the denominators of fractions are the same, then in order to add the fractions, you need to add their numerators, and in order to subtract the fractions, you need to subtract their numerators (in the same order). The resulting sum or difference will be the numerator of the result; the denominator will remain the same. If the denominators of the fractions are different, you must first reduce the fractions to a common denominator. When added mixed numbers their integer and fractional parts are added separately. When subtracting mixed numbers, we recommend that you first convert them to the form of improper fractions, then subtract from one another, and then again reduce the result, if necessary, to the form of a mixed number.
EXAMPLE

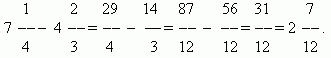
Multiplication of fractions.To multiply a number by a fraction means to multiply it by the numerator and divide the product by the denominator. Hence we have general rule multiplying fractions:to multiply fractions, you need to multiply their numerators and denominators separately and divide the first product by the second.
EXAMPLE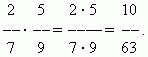
Division of fractions. In order to divide a certain number by a fraction, it is necessary to multiply this number by its reciprocal. This rule follows from the definition of division (see the Arithmetic Operations section).
EXAMPLE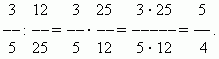

Decimal. Whole part. Decimal point.
Decimals. Properties of decimal fractions.
Periodic decimal. Period
Decimalis the result of dividing one by ten, one hundred, one thousand, etc. parts. These fractions are very convenient for calculations, since they are based on the same positional system on which counting and notation of integers are built. Due to this, the notation and rules for decimals are actually the same as for integers. When writing decimal fractions, there is no need to mark the denominator, this is determined by the place that the corresponding figure occupies. First spelled whole part numbers, then put on the rightdecimal point. The first digit after the decimal point means the number of tenths, the second - the number of hundredths, the third - the number of thousandths, etc. The numbers after the decimal point are calleddecimal places.
EXAMPLE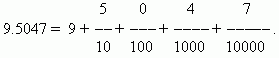
One of the advantages of decimal fractions is that they are easily reduced to the form of ordinary ones: the number after the decimal point (in our case 5047) is the numerator; the denominator is equal n -th degree 10, where n - the number of decimal places (in our case n = 4):
If the decimal fraction does not contain an integer part, then a zero is placed before the decimal point:

Properties of decimal fractions.

1. Decimal does not change if zeros are added to the right:

2. The decimal fraction does not change if you remove the zeros located
at the end of the decimal:

0.00123000 = 0.00123 .

Attention! You can not delete zeros located not at the end decimal!br />

These properties allow you to quickly multiply and divide decimals by 10, 100, 1000, and so on.

Periodic decimal contains an infinitely repeating group of digits called a period. The period is written in brackets. For example, 0.12345123451234512345… = 0.(12345).

EXAMPLE If we divide 47 by 11, we get 4.27272727… = 4.(27).

Multiplying decimals.
Division of decimals.

Addition and subtraction of decimal fractions. These operations are performed in the same way as addition and subtraction of integers. It is only necessary to write the corresponding decimal places one under the other.
EXAMPLE

Multiplying decimals. In the first step, we multiply the decimal fractions as whole numbers, without taking into account the decimal point. The following rule is then applied: the number of decimal places in the product is equal to the sum of the decimal places in all factors.
Remark : before putting the decimal point inYou can't drop zeros at the end of the product!
EXAMPLE

The sum of the numbers of decimal places in the factors is: 3 + 4 = 7. The sum of the digits in the product is 6. Therefore, you need to add one zero to the left: 0197056 and put a decimal point in front of it: 0.0197056.
Decimal division
Divide a decimal by an integer
If dividend is less than divisor, we write zero in the integer part of the quotient and put a decimal point after it. Then, without taking into account the decimal point of the dividend, we add the next digit of the fractional part to its integer part and again compare the resulting integer part of the dividend with the divisor. If the new number is again less than the divisor, put one more zero after the decimal point in the quotient and add the next digit of its fractional part to the integer part of the dividend. This process is repeated until the resulting dividend becomes greater than the divisor. After that, division is performed as for integers. If dividend is greater than or equal to the divisor, first we divide its integer part, write the result of division in private and put a decimal point. After that, the division continues, as in the case of integers.
EXAMPLE Divide 1.328 by 64.
Solution:
Division of one decimal fraction by another.
First, we transfer the decimal points in the dividend and the divisor by the number of decimal places in the divisor, that is, we make the divisor an integer. Now we perform the division, as in the previous case.
EXAMPLE Divide 0.04569 by 0.0006.
Solution: Move the decimal points 4 places to the right and divide 456.9 by 6:

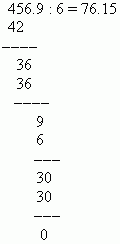
In order to convert a decimal to a common fraction, you need to take the number after the decimal point as the numerator, and take the nth power of ten as the denominator (here n is the number of decimal places). The non-zero integer part is preserved in the common fraction; the zero integer part is omitted. For example:
To convert a common fraction to a decimal, divide the numerator by the denominator according to the division rules..
EXAMPLE Convert 5 / 8 to a decimal.
Solution: Dividing 5 by 8 gives 0.625. (Check, please!).
In most cases, this process can continue indefinitely. Then it is impossible to accurately convert an ordinary fraction to a decimal. But in practice this is never required. The division is aborted if the decimal places of interest have already been received.
EXAMPLE Convert 1/3 to a decimal.
Solution: Dividing 1 by 3 will be infinite: 1:3 = 0.3333… .
Check it out please!

Multiplication and division of fractions.

Attention!
There are additional
material in Special Section 555.
For those who strongly "not very..."
And for those who "very much...")

This operation is much nicer than addition-subtraction! Because it's easier. I remind you: to multiply a fraction by a fraction, you need to multiply the numerators (this will be the numerator of the result) and the denominators (this will be the denominator). I.e:

For example:

Everything is extremely simple. And please don't look for a common denominator! Don't need it here...

To divide a fraction by a fraction, you need to flip second(this is important!) fraction and multiply them, i.e.:

For example:

If multiplication or division with integers and fractions is caught, it's okay. As with addition, we make a fraction from a whole number with a unit in the denominator - and go! For example:

In high school, you often have to deal with three-story (or even four-story!) fractions. For example:

How to bring this fraction to a decent form? Yes, very easy! Use division through two points:

But don't forget about the division order! Unlike multiplication, this is very important here! Of course, we will not confuse 4:2 or 2:4. But in a three-story fraction it is easy to make a mistake. Please note, for example:

In the first case (expression on the left):

In the second (expression on the right):

Feel the difference? 4 and 1/9!

What is the order of division? Or brackets, or (as here) the length of horizontal dashes. Develop an eye. And if there are no brackets or dashes, like:

then divide-multiply in order, left to right!

And another very simple and important trick. In actions with degrees, it will come in handy for you! Let's divide the unit by any fraction, for example, by 13/15:

The shot has turned over! And it always happens. When dividing 1 by any fraction, the result is the same fraction, only inverted.

That's all the actions with fractions. The thing is quite simple, but gives more than enough errors. Take note of practical advice, and there will be fewer of them (mistakes)!

Practical Tips:

1. The most important thing when working with fractional expressions is accuracy and attentiveness! These are not common words, not good wishes! This is a severe need! Do all the calculations on the exam as a full-fledged task, with concentration and clarity. It is better to write two extra lines in a draft than to mess up when calculating in your head.

2. In the examples with different types fractions - go to ordinary fractions.

3. We reduce all fractions to the stop.

4. We reduce multi-level fractional expressions to ordinary ones using division through two points (we follow the order of division!).

5. We divide the unit into a fraction in our mind, simply by turning the fraction over.

Here are the tasks you need to complete. Answers are given after all tasks. Use the materials of this topic and practical advice. Estimate how many examples you could solve correctly. The first time! Without a calculator! And draw the right conclusions...

Remember the correct answer obtained from the second (especially the third) time - does not count! Such is the harsh life.

So, solve in exam mode ! This is preparation for the exam, by the way. We solve an example, we check, we solve the following. We decided everything - we checked again from the first to the last. Only Then look at the answers.

Calculate:

Did you decide?

Looking for answers that match yours. I specifically wrote them down in a mess, away from the temptation, so to speak ... Here they are, the answers, written down with a semicolon.

0; 17/22; 3/4; 2/5; 1; 25.

And now we draw conclusions. If everything worked out - happy for you! Elementary calculations with fractions are not your problem! You can do more serious things. If not...

So you have one of two problems. Or both at once.) Lack of knowledge and (or) inattention. But this solvable Problems.

If you like this site...

By the way, I have a couple more interesting sites for you.)

You can practice solving examples and find out your level. Testing with instant verification. Learning - with interest!)

you can get acquainted with functions and derivatives.

496. To find X, if:

497. 1) If you add 10 1/2 to 3/10 of an unknown number, you get 13 1/2. Find an unknown number.

2) If you subtract 10 1/2 from 7/10 of an unknown number, you get 15 2/5. Find an unknown number.

498 *. If you subtract 10 from 3 / 4 of an unknown number and multiply the resulting difference by 5, you get 100. Find the number.

499 *. If an unknown number is increased by 2/3 of it, you get 60. What is this number?

500 *. If we add the same amount to an unknown number, and even 20 1/3, then we get 105 2/5. Find an unknown number.

501. 1) The yield of potatoes with a square-nest planting is on average 150 centners per 1 ha, and with a normal planting 3/5 of this amount. How many more potatoes can be harvested from an area of ​​15 hectares if potatoes are planted in a square-nest way?

2) An experienced worker made 18 parts in 1 hour, and an inexperienced worker 2/3 of this amount. How many more parts can an experienced worker produce in a 7-hour working day?

502. 1) Pioneers assembled within three days 56 kg of different seeds. On the first day, 3/14 of the total amount was collected, on the second, one and a half times more, and on the third day, the rest of the grain. How many kilograms of seeds did the pioneers collect on the third day?

2) When grinding wheat, it turned out: flour 4/5 of the total amount of wheat, semolina - 40 times less than flour, and the rest is bran. How much flour, semolina and bran separately did you get when grinding 3 tons of wheat?

503. 1) Three garages fit 460 cars. The number of cars that fit in the first garage is 3/4 of the number of cars that fit in the second, and in the third garage there are 1 1/2 times as many cars as in the first. How many cars fit in each garage?

2) The plant, which has three workshops, employs 6,000 workers. The number of workers in the second workshop is 1 1/2 times less than in the first, and the number of workers in the third workshop is 5/6 of the number of workers in the second workshop. How many workers are in each shop?

504. 1) First, 2/5 was poured from the tank with kerosene, then 1/3 of the total kerosene, and after that 8 tons of kerosene remained in the tank. How much kerosene was in the tank originally?

2) The cyclists raced for three days. On the first day they covered 4/15 of the entire journey, on the second day they covered 2/5, and on the third day the remaining 100 km. How far did the cyclists travel in three days?

505. 1) The icebreaker made its way through the ice field for three days. On the first day he covered 1/2 of the total distance, on the second day 3/5 of the remaining distance, and on the third day the remaining 24 km. Find the distance traveled by the icebreaker in three days.

2) Three detachments of schoolchildren planted trees for landscaping the village. The first detachment planted 7/20 of all the trees, the second 5/8 of the remaining trees, and the third the remaining 195 trees. How many trees did the three teams plant in total?

506. 1) A combine harvester harvested wheat from one plot in three days. On the first day he harvested from 5/18 of the total area of ​​the plot, on the second day from 7/13 of the remaining area, and on the third day from the remaining area of ​​30 1/2 hectares. On average, 20 centners of wheat were harvested from each hectare. How much wheat was harvested in the entire plot?

2) On the first day, the participants of the rally covered 3/11 of the entire path, on the second day 7/20 of the remaining path, on the third day 5/13 of the new remainder, and on the fourth day, the remaining 320 km. How long is the rally route?

507. 1) On the first day, the car covered 3/8 of the entire distance, on the second day 15/17 of what it passed on the first, and on the third day the remaining 200 km. How much gasoline was consumed if the car consumes 1 3/5 kg of gasoline for 10 km of travel?

2) The city consists of four districts. And in the first district live 4/13 of all the inhabitants of the city, in the second 5/6 of the inhabitants of the first district, in the third 4/11 of the inhabitants of the first; two districts combined, and the fourth district is home to 18,000 people. How much bread does the entire population of the city need for 3 days, if on average one person consumes 500 g per day?

508. 1) The tourist walked on the first day 10/31 of the entire path, on the second 9/10 of what he walked on the first day, and on the third the rest of the path, and on the third day he walked 12 km more than on the second day. How many kilometers did the tourist walk on each of the three days?

2) The car traveled all the way from city A to city B in three days. On the first day, the car covered 7/20 of the entire distance, on the second day, 8/13 of the remaining distance, and on the third day, the car covered 72 km less than on the first day. What is the distance between cities A and B?

509. 1) The executive committee allotted land to the workers of three factories for garden plots. The first plant was assigned 9/25 of the total number of plots, the second plant 5/9 of the number of plots allocated for the first, and the third - the rest of the plots. How many plots were allotted to the workers of three factories if the first plant was given 50 fewer plots than the third?

2) The plane delivered a shift of winterers to the polar station from Moscow in three days. On the first day he flew 2/5 of the entire path, on the second - 5/6 of the path he traveled on the first day, and on the third day he flew 500 km less than on the second day. How far did the plane fly in three days?

510. 1) The plant had three workshops. The number of workers in the first workshop is 2/5 of all factory workers; in the second workshop there are 1 1/2 times fewer workers than in the first, and in the third workshop there are 100 more workers than in the second. How many workers are in the factory?

2) The collective farm includes residents of three neighboring villages. The number of families in the first village is 3/10 of all the families of the collective farm; in the second village the number of families is 1 1/2 times greater than in the first, and in the third village the number of families is 420 fewer than in the second. How many families are on the collective farm?

511. 1) The Artel spent in the first week 1/3 of its stock of raw materials, and in the second 1/3 of the remainder. How much raw material is left in the artel if in the first week the consumption of raw materials was 3/5 tons more than in the second week?

2) Of the imported coal for heating the house in the first month, 1/6 of it was spent, and in the second month - 3/8 of the remainder. How much coal is left for heating the house if 1 3/4 more was used in the second month than in the first month?

512. 3/5 of the entire land of the collective farm is allocated for sowing grain, 13/36 of the rest is occupied by vegetable gardens and meadows, the rest of the land is forested, and the sown area of ​​the collective farm is 217 hectares more than the forest area, 1/3 of the land allotted for sowing grain is sown with rye, and the rest is wheat. How many hectares of land did the collective farm sow with wheat and how many with rye?

513. 1) The tram route is 14 3/8 km long. During this route, the tram makes 18 stops, spending on average up to 1 1/6 minutes per stop. The average tram speed along the entire route is 12 1/2 km per hour. How long does it take for a tram to make one trip?

2) Bus route 16 km. During this route, the bus makes 36 stops of 3/4 min. each on average. The average bus speed is 30 km per hour. How long does it take for a bus to make one route?

514*. 1) It is now 6 o'clock. evenings. What part is the remaining part of the day from the past and what part of the day is left?

2) A steamboat travels downstream between two cities in 3 days. and back the same distance in 4 days. How many days will the rafts float from one city to another?

515. 1) How many boards will be used to lay the floor in a room whose length is 6 2/3 m, width h 5 1/4 m, if the length of each board is 6 2/3 m, and its width is 3/80 of the length?

2) A rectangular platform has a length of 45 1/2 m, and its width is 5/13 of the length. This area is bordered by a path 4/5 m wide. Find the area of ​​the path.

516. Find the mean arithmetic numbers:

517. 1) The arithmetic mean of two numbers 6 1 / 6 . One of the numbers 3 3 / 4 . Find another number.

2) The arithmetic mean of two numbers is 14 1 / 4 . One of these numbers is 15 5 / 6 . Find another number.

518. 1) The freight train was on the road for three hours. In the first hour he walked 36 1/2 km, in the second 40 km, and in the third 39 3/4 km. Find the average speed of the train.

2) The car traveled 81 1/2 km in the first two hours, and 95 km in the next 2 1/2 hours. How many kilometers did he walk on average per hour?

519. 1) The tractor driver completed the task of plowing the land in three days. On the first day he plowed 12 1/2 ha, on the second day 15 3/4 ha, and on the third day 14 1/2 ha. How many hectares of land did a tractor driver plow on average per day?

2) A detachment of schoolchildren, making a three-day tourist trip, was on the way on the first day 6 1 / 3 hours, on the second 7 hours. and on the third day, 4 2/3 hours. How many hours on average were students on the road every day?

520. 1) Three families live in the house. The first family for lighting the apartment has 3 light bulbs, the second 4 and the third 5 bulbs. How much should each family pay for electricity if all the lamps were the same and the total electricity bill (for the whole house) was 7 1/5 rubles?

2) The polisher rubbed the floors in the apartment where three families lived. The first family had a living area of ​​36 1/2 sq. m, the second in 24 1/2 sq. m, and the third - in 43 sq. m. For all the work was paid 2 rubles. 08 kop. How much did each family pay?

521. 1) In the garden plot, potatoes were harvested from 50 bushes, 1 1/10 kg per bush, from 70 bushes, 4/5 kg per bush, from 80 bushes, 9/10 kg per bush. How many kilograms of potatoes are harvested on average from each bush?

2) A field-growing team on an area of ​​300 ha received a harvest of 20 1/2 centners of winter wheat per 1 ha, from 80 hectares 24 centners per 1 ha, and from 20 hectares - 28 1/2 centners per 1 ha. What is the average yield in a brigade from 1 hectare?

522. 1) The sum of two numbers is 7 1 / 2 . One number is greater than another by 4 4 / 5 . Find these numbers.

2) If we add the numbers expressing the width of the Tatar and Kerch Straits together, we get 11 7 / 10 km. The Tatar Strait is 3 1/10 km wider than the Kerch Strait. What is the width of each strait?

523. 1) The sum of three numbers is 35 2 / 3 . The first number is 5 1/3 greater than the second and 3 5/6 greater than the third. Find these numbers.

2) Islands New Earth, Sakhalin and Severnaya Zemlya together occupy an area of ​​196 7/10 thousand square meters. km. The area of ​​Novaya Zemlya is 44 1/10 thousand square meters. km more area Severnaya Zemlya and 5 1/5 thousand square meters. km larger than the area of ​​Sakhalin. What is the area of ​​each of the listed islands?

524. 1) The apartment consists of three rooms. The area of ​​the first room is 24 3/8 sq. m and is 13/36 of the entire area of ​​the apartment. The area of ​​the second room is 8 1/8 sq. m more than the area of ​​the third. What is the area of ​​the second room?

2) The cyclist during the three-day competition on the first day traveled 3 1/4 hours, which was 13/43 of the total travel time. On the second day he rode 1 1/2 hours more than on the third day. How many hours did the cyclist travel on the second day of the competition?

525. Three pieces of iron weigh together 17 1/4 kg. If the weight of the first piece is reduced by 1 1/2 kg, the weight of the second by 2 1/4 kg, then all three pieces will have the same weight. How much did each piece of iron weigh?

526. 1) The sum of two numbers is 15 1 / 5 . If the first number is reduced by 3 1/10 and the second is increased by 3 1/10, then these numbers will be equal. What is each number equal to?

2) There were 38 1/4 kg of cereal in two boxes. If 4 3/4 kg of cereals are poured from one box into another, then in both boxes there will be equal amounts of cereals. How many cereals are in each box?

527 . 1) The sum of two numbers is 17 17 / 30 . If you subtract 5 1/2 from the first number and add to the second, then the first will still be more than the second by 2 17/30. Find both numbers.

2) Two boxes contain 24 1/4 kg of apples. If 3 1/2 kg are transferred from the first box to the second, then in the first there will still be 3/5 kg more apples than in the second. How many kilograms of apples are in each box?

528 *. 1) The sum of two numbers is 8 11/14, and their difference is 2 3/7. Find these numbers.

2) The boat was moving along the river at a speed of 15 1/2 km per hour, and against the current 8 1/4 km per hour. What is the speed of the river?

529. 1) There are 110 cars in two garages, and in one of them there are 1 1/5 times more than in the other. How many cars are in each garage?

2) The living area of ​​an apartment consisting of two rooms is 47 1/2 sq. m. The area of ​​one room is 8/11 of the area of ​​the other. Find the area of ​​each room.

530. 1) An alloy consisting of copper and silver weighs 330 g. The weight of copper in this alloy is 5/28 of the weight of silver. How much silver and how much copper is in the alloy?

2) The sum of two numbers is 6 3 / 4 , and the quotient is 3 1 / 2 . Find these numbers.

531. The sum of three numbers is 22 1 / 2 . The second number is 3 1/2 times and the third is 2 1/4 times the first. Find these numbers.

532. 1) The difference of two numbers is 7; quotient of division more to a smaller 5 2 / 3 . Find these numbers.

2) The difference of two numbers is 29 3/8, and their multiple ratio is 8 5/6. Find these numbers.

533. In a class, the number of absent students is 3/13 of the number of those present. How many students are in the class according to the list, if there are 20 more people present than absent?

534. 1) The difference of two numbers is 3 1 / 5 . One number is 5/7 of another. Find these numbers.

2) Father older than son for 24 years. The number of the son's years is 5/13 of the father's years. How old is the father and how old is the son?

535. The denominator of a fraction is 11 more than its numerator. What is a fraction equal to if its denominator is 3 3/4 times the numerator?

No. 536 - 537 orally.

536. 1) The first number is 1/2 of the second. How many times greater is the second number than the first?

2) The first number is 3/2 of the second. What part of the first number is the second number?

537. 1) 1/2 of the first number is equal to 1/3 of the second number. What part of the first number is the second number?

2) 2/3 of the first number is equal to 3/4 of the second number. What part of the first number is the second number? What part of the second number is the first?

538. 1) The sum of two numbers is 16. Find these numbers if 1/3 of the second number is equal to 1/5 of the first.

2) The sum of two numbers is 38. Find these numbers if 2/3 of the first number is equal to 3/5 of the second.

539 *. 1) Two boys picked 100 mushrooms together. 3/8 of the number of mushrooms picked by the first boy is numerically equal to 1/4 of the number of mushrooms picked by the second boy. How many mushrooms did each boy collect?

2) The institution employs 27 people. How many men and how many women work if 2/5 of all men are equal to 3/5 of all women?

540 *. Three boys bought a volleyball. Determine the contribution of each boy, knowing that 1/2 of the contribution of the first boy is equal to 1/3 of the contribution of the second, or 1/4 of the contribution of the third, and that the contribution of the third boy is 64 kopecks more than the contribution of the first.

541 *. 1) One number is 6 greater than another. Find these numbers if 2/5 of one number is equal to 2/3 of another.

2) The difference of two numbers is 35. Find these numbers if 1/3 of the first number is equal to 3/4 of the second number.

542. 1) The first brigade can complete some work in 36 days, and the second in 45 days. How many days will it take both teams working together to complete this task?

2) A passenger train travels the distance between two cities in 10 hours, and a freight train travels this distance in 15 hours. Both trains left these cities at the same time towards each other. In how many hours will they meet?

543. 1) A fast train travels the distance between two cities in 6 1/4 hours, and a passenger train in 7 1/2 hours. In how many hours will these trains meet if they leave both cities at the same time towards each other? (Round answer to the nearest 1 hour.)

2) Two motorcyclists left two cities at the same time towards each other. One motorcyclist can travel the entire distance between these cities in 6 hours, and another in 5 hours. How many hours after the departure will the motorcyclists meet? (Round answer to the nearest 1 hour.)

544. 1) Three cars of different carrying capacity can transport some cargo, working separately: the first in 10 hours, the second in 12 hours. and the third in 15 hours In how many hours can they move the same cargo by working together?

2) Two trains leave two stations simultaneously towards each other: the first train covers the distance between these stations in 12 1/2 hours, and the second in 18 3/4 hours. How many hours after leaving will the trains meet?

545. 1) There are two taps connected to the bath. Through one of them, the bath can be filled in 12 minutes, through the other 1 1/2 times faster. How many minutes will it take to fill 5/6 of the entire bath if both taps are opened at once?

2) Two typists must retype the manuscript. The first woman can do this job in 3 1/3 days, and the second one 1 1/2 times faster. In how many days will both typists complete the work if they work at the same time?

546. 1) The pool is filled with the first pipe in 5 hours, and through the second pipe it can be emptied in 6 hours After how many hours will the entire pool be filled if both pipes are opened at the same time?

Instruction. In an hour, the pool is filled to (1 / 5 - 1 / 6 of its capacity.)

2) Two tractors plowed the field in 6 hours. The first tractor, working alone, could plow this field in 15 hours. How many hours would it take the second tractor to plow this field, working alone?

547 *. Two trains leave two stations at the same time towards each other and meet after 18 hours. after its release. How long does it take the second train to travel the distance between stations if the first train travels this distance in 1 day and 21 hours?

548 *. The pool is filled with two pipes. First, the first pipe was opened, and then after 3 3/4 hours, when half the pool was full, the second pipe was opened. After 2 1/2 hours of working together, the pool filled up. Determine the capacity of the pool if 200 buckets of water per hour were poured through the second pipe.

549. 1) A courier train left Leningrad for Moscow, which travels 1 km in 3/4 minutes. 1/2 hour after the departure of this train, a fast train left Moscow for Leningrad, the speed of which was equal to 3/4 of the speed of the courier. How far will the trains be from each other 2 1/2 hours after the departure of the courier train, if the distance between Moscow and Leningrad is 650 km?

2) From the collective farm to the city 24 km. A truck has left the collective farm and travels 1 km in 2 1/2 minutes. After 15 min. after the departure of this car from the city, a cyclist left the collective farm, at a speed half that of a truck. How long will it take for the cyclist to meet the truck after leaving?

550. 1) A pedestrian came out of one village. 4 1/2 hours after the pedestrian exited, a cyclist left in the same direction, whose speed is 2 1/2 times the speed of the pedestrian. In how many hours after the pedestrian leaves, the cyclist will overtake him?

2) A fast train travels 187 1/2 km in 3 hours, and a freight train 288 km in 6 hours. 7 1/4 hours after the departure of the freight train, an ambulance leaves in the same direction. How long will it take for the fast train to overtake the freight train?

551. 1) From two collective farms, through which the road to the district center passes, two collective farmers left at the same time to the district on horseback. The first of them traveled 8 3/4 km per hour, and the second 1 1/7 times the first. The second collective farmer overtook the first in 3 4/5 hours. Determine the distance between collective farms.

2) 26 1/3 hours after the departure of the Moscow-Vladivostok train, the average speed of which is 60 km per hour, the TU-104 aircraft took off in the same direction, at a speed 14 1/6 times the speed of the train. How many hours after the flight will the plane overtake the train?

552. 1) The distance between cities along the river is 264 km. This distance the steamer traveled downstream in 18 hours, spending 1/12 of this time on stops. The speed of the river is 1 1/2 km per hour. How long would it take a steamer to travel 87 km without stopping? standing water?

2) The motorboat traveled 207 km downstream in 13 1/2 hours, spending 1/9 of that time on stops. The speed of the river is 1 3/4 km per hour. How many miles can this boat travel in still water in 2 1/2 hours?

553. The boat on the reservoir covered a distance of 52 km without stopping in 3 hours and 15 minutes. Further, going along the river against the current, the speed of which is 1 3 / 4 km per hour, this boat traveled 28 1 / 2 km in 2 1 / 4 hours, making 3 equal stops in the process. How many minutes did the boat stop at each stop?

554. From Leningrad to Kronstadt at 12 noon. the next day a steamboat set out and covered the entire distance between these cities in 1 1/2 hours. On the way, he met another steamer that left Kronstadt for Leningrad at 12:18. and walking at a speed 1 1/4 times greater than the first. At what time did the two ships meet?

555. The train had to cover a distance of 630 km in 14 hours. Having covered 2/3 of this distance, he was delayed for 1 hour and 10 minutes. At what speed must he continue his journey in order to arrive at his destination without delay?

556. At 4 o'clock 20 min. in the morning a freight train left Kyiv for Odessa average speed 31 1/5 km per hour. After some time, a mail train left Odessa to meet it, the speed of which is 1 17/39 times the speed of the freight train, and met with a freight train 6 1/2 hours after its departure. At what time did the postal train leave Odessa if the distance between Kiev and Odessa is 663 km?

557*. The clock shows noon. How long does it take for the hour and minute hands to coincide?

558. 1) The factory has three workshops. The number of workers in the first workshop is 9/20 of all the workers of the plant, in the second workshop there are 1 1/2 times fewer workers than in the first, and in the third workshop there are 300 workers less than in the second. How many workers are in the factory?

2) There are three secondary schools in the city. The number of students in the first school is 3/10 of all students in these three schools; in the second school there are 1 1/2 times more students than in the first, and in the third school there are 420 students less than in the second. How many students are in the three schools?

559. 1) Two combine operators worked at the same site. After one combiner harvested 9/16 of the entire area, and the second 3/8 of the same area, it turned out that the first combine harvested 97 1/2 hectares more than the second. On average, 32 1/2 centners of grain were threshed from each hectare. How many quintals of grain did each combine thresh?

2) Two brothers bought a camera. One had 5/8, and the second had 4/7 of the cost of the camera, and the first had 2 rubles. 25 kop. more than the second. Each paid half the cost of the apparatus. How much money does each have?

560. 1) From city A to city B, the distance between them is 215 km, a car left at a speed of 50 km per hour. At the same time, a truck left city B for city A. How many kilometers did the car travel before meeting the truck if the speed of the truck per hour was 18/25 of the speed of the car?

2) Between cities A and B 210 km. A car left town A for town B. At the same time, a truck left city B for city A. How many kilometers did the truck travel before meeting with the car if the car was moving at a speed of 48 km per hour, and the speed of the truck per hour was 3/4 of the speed of the car?

561. The collective farm harvested wheat and rye. Wheat was sown 20 hectares more than rye. The total harvest of rye amounted to 5/6 of the total harvest of wheat with a yield of 20 centners per 1 ha for both wheat and rye. The collective farm sold 7/11 of the entire harvest of wheat and rye to the state, and left the rest of the grain to meet its needs. How many trips did the two-ton trucks need to make to take out the grain sold to the state?

562. Rye and wheat flour was brought to the bakery. The weight of wheat flour was 3/5 of the weight of rye flour, and rye flour was brought 4 tons more than wheat. How much wheat and how much rye bread will be baked by the bakery from this flour, if the baked goods are 2/5 of all flour?

563. Within three days, a team of workers completed 3/4 of the entire work to repair the highway between the two collective farms. On the first day, 2 2/5 km of this highway was repaired, on the second day 1 1/2 times more than on the first, and on the third day 5/8 of what was repaired in the first two days together. Find the length of the highway between collective farms.

564. Fill in the empty spaces in the table, where S is the area of ​​the rectangle, but- the base of the rectangle, a h-height (width) of the rectangle.

565. 1) The length of a rectangular plot of land is 120 m, and the width of the plot is 2/5 of its length. Find the perimeter and area of ​​the plot.

2) The width of the rectangular section is 250 m, and its length is 1 1/2 times the width. Find the perimeter and area of ​​the plot.

566. 1) The perimeter of a rectangle is 6 1/2 dm, its base is 1/4 dm more than the height. Find the area of ​​this rectangle.

2) The perimeter of a rectangle is 18 cm, its height is 2 1/2 cm less than the base. Find the area of ​​the rectangle.

567. Calculate the areas of the figures shown in Figure 30, dividing them into rectangles and finding the dimensions of the rectangle by measuring.

568. 1) How many sheets of dry plaster will be required to upholster the ceiling of a room whose length is 4 1/2 m and the width is 4 m, if the dimensions of the plaster sheet are 2 m x l 1/2 m?

2) How many boards 4 1/2 l long and 1/4 m wide will be required to lay a floor that is 4 1/2 m long and 3 1/2 m wide?

569. 1) A rectangular plot 560 m long and 3/4 of its length wide was sown with beans. How many seeds were required to sow the plot if 1 centner was sown per 1 hectare?

2) A wheat crop was harvested from a rectangular field at 25 centners per 1 ha. How much wheat was harvested from the whole field if the field is 800 m long and 3/8 of its length wide?

570 . 1) A rectangular plot of land, having a length of 78 3/4 m and a width of 56 4/5 m, is built up so that 4/5 of its area is occupied by buildings. Determine the area of ​​land under the buildings.

2) On a rectangular plot of land, the length of which is 9/20 km, and the width is 4/9 of its length, the collective farm proposes to plant a garden. How many trees will be planted in this garden if, on average, an area of ​​36 square meters is required for each tree?

571. 1) For normal daylight illumination of the room, it is necessary that the area of ​​\u200b\u200ball windows be at least 1/5 of the floor area. Determine if there is enough light in a room that is 5 1/2 m long and 4 m wide. Does the room have one window measuring 1 1/2 m x 2 m?

2) Using the condition of the previous problem, find out if there is enough light in your classroom.

572. 1) The barn measures 5 1/2 m x 4 1/2 m x 2 1/2 m. m of hay weighs 82 kg?

2) The woodpile has the shape of a rectangular parallelepiped, the dimensions of which are 2 1/2 m x 3 1/2 m x 1 1/2 m. What is the weight of the woodpile if 1 cu. m of firewood weighs 600 kg?

573. 1) A rectangular aquarium is filled with water up to 3/5 of the height. The length of the aquarium is 1 1/2 m, the width is 4/5 m, the height is 3/4 m. How many liters of water are poured into the aquarium?

2) The pool, having the shape of a rectangular parallelepiped, has a length of 6 1/2 m, a width of 4 m and a height of 2 m. The pool is filled with water up to 3/4 of its height. Calculate the amount of water poured into the pool.

574. A fence is to be built around a rectangular piece of land 75 m long and 45 m wide. How many cubic meters of boards should go to his device if the thickness of the board is 2 1/2 cm, and the height of the fence should be 2 1/4 m?

575. 1) What is the angle between the minute hand and the hour hand at 13:00? at 15 o'clock? at 17 o'clock? at 21 o'clock? at 23:30?

2) By how many degrees will the hour hand turn in 2 hours? 5 o'clock? 8 o'clock? 30 minutes.?

3) How many degrees does an arc equal to half a circle contain? 1/4 circle? 1/24 circle? 5 / 24 circles?

576. 1) Draw with a protractor: a) a right angle; b) an angle of 30°; c) an angle of 60°; d) an angle of 150°; e) an angle of 55°.

2) Measure the angles of the figure with a protractor and find the sum of all the angles of each figure (Fig. 31).

577. Run actions:

578. 1) A semicircle is divided into two arcs, one of which is 100° larger than the other. Find the magnitude of each arc.

2) A semicircle is divided into two arcs, one of which is 15° less than the other. Find the magnitude of each arc.

3) The semicircle is divided into two arcs, of which one is twice the other. Find the magnitude of each arc.

4) The semicircle is divided into two arcs, of which one is 5 times smaller than the other. Find the magnitude of each arc.

579. 1) The chart "Literacy of the population in the USSR" (Fig. 32) shows the number of literate per hundred people of the population. According to the diagram and its scale, determine the number of literate men and women for each of the indicated years.

Record the results in a table:

2) Using the data of the diagram "Soviet envoys to space" (Fig. 33), make up tasks.

580. 1) According to the sector diagram "Daily routine for a student of grade V" (Fig. 34), fill in the table and answer the questions: what part of the day is devoted to sleep? for homework? to school?

2) Build a pie chart about the mode of your day.

Lesson content

Adding fractions with the same denominators

Adding fractions is of two types:

1. Adding fractions with the same denominators
2. Adding fractions with different denominators

Let's start with adding fractions with the same denominators. Everything is simple here. To add fractions with the same denominators, you need to add their numerators, and leave the denominator unchanged. For example, let's add the fractions and . We add the numerators, and leave the denominator unchanged:

This example can be easily understood if we think of a pizza that is divided into four parts. If you add pizza to pizza, you get pizza:

Example 2 Add fractions and .

The answer is an improper fraction. If the end of the task comes, then it is customary to get rid of improper fractions. To get rid of an improper fraction, you need to select the whole part in it. In our case, the integer part is allocated easily - two divided by two is equal to one:

This example can be easily understood if we think of a pizza that is divided into two parts. If you add more pizzas to the pizza, you get one whole pizza:

Example 3. Add fractions and .

Again, add the numerators, and leave the denominator unchanged:

This example can be easily understood if we think of a pizza that is divided into three parts. If you add more pizzas to pizza, you get pizzas:

Example 4 Find the value of an expression

This example is solved in exactly the same way as the previous ones. The numerators must be added and the denominator left unchanged:

Let's try to depict our solution using a picture. If you add pizzas to a pizza and add more pizzas, you get 1 whole pizza and more pizzas.

As you can see, adding fractions with the same denominators is not difficult. It is enough to understand the following rules:

1. To add fractions with the same denominator, you need to add their numerators, and leave the denominator unchanged;

Adding fractions with different denominators

Now we will learn how to add fractions with different denominators. When adding fractions, the denominators of those fractions must be the same. But they are not always the same.

For example, fractions can be added because they have the same denominators.

But fractions cannot be added at once, because these fractions have different denominators. In such cases, fractions must be reduced to the same (common) denominator.

There are several ways to reduce fractions to the same denominator. Today we will consider only one of them, since the rest of the methods may seem complicated for a beginner.

The essence of this method lies in the fact that first (LCM) of the denominators of both fractions is sought. Then the LCM is divided by the denominator of the first fraction and the first additional factor is obtained. They do the same with the second fraction - the NOC is divided by the denominator of the second fraction and the second additional factor is obtained.

Then the numerators and denominators of the fractions are multiplied by their additional factors. As a result of these actions, fractions that had different denominators turn into fractions that have the same denominators. And we already know how to add such fractions.

Example 1. Add fractions and

First of all, we find the least common multiple of the denominators of both fractions. The denominator of the first fraction is the number 3, and the denominator of the second fraction is the number 2. The least common multiple of these numbers is 6

LCM (2 and 3) = 6

Now back to fractions and . First, we divide the LCM by the denominator of the first fraction and get the first additional factor. LCM is the number 6, and the denominator of the first fraction is the number 3. Divide 6 by 3, we get 2.

The resulting number 2 is the first additional factor. We write it down to the first fraction. To do this, we make a small oblique line above the fraction and write down the found additional factor above it:

We do the same with the second fraction. We divide the LCM by the denominator of the second fraction and get the second additional factor. LCM is the number 6, and the denominator of the second fraction is the number 2. Divide 6 by 2, we get 3.

The resulting number 3 is the second additional factor. We write it to the second fraction. Again, we make a small oblique line above the second fraction and write the found additional factor above it:

Now we are all set to add. It remains to multiply the numerators and denominators of fractions by their additional factors:

Look closely at what we have come to. We came to the conclusion that fractions that had different denominators turned into fractions that had the same denominators. And we already know how to add such fractions. Let's complete this example to the end:

Thus the example ends. To add it turns out.

Let's try to depict our solution using a picture. If you add pizzas to a pizza, you get one whole pizza and another sixth of a pizza:

Reduction of fractions to the same (common) denominator can also be depicted using a picture. Bringing the fractions and to a common denominator, we get the fractions and . These two fractions will be represented by the same slices of pizzas. The only difference will be that this time they will be divided into equal shares (reduced to the same denominator).

The first drawing shows a fraction (four pieces out of six) and the second picture shows a fraction (three pieces out of six). Putting these pieces together we get (seven pieces out of six). This fraction is incorrect, so we have highlighted the integer part in it. The result was (one whole pizza and another sixth pizza).

Note that we have painted this example in too much detail. IN educational institutions it is not customary to write in such a detailed manner. You need to be able to quickly find the LCM of both denominators and additional factors to them, as well as quickly multiply the additional factors found by your numerators and denominators. While at school, we would have to write this example as follows:

But there is also the other side of the coin. If detailed notes are not made at the first stages of studying mathematics, then questions of the kind “Where does that number come from?”, “Why do fractions suddenly turn into completely different fractions? «.

To make it easier to add fractions with different denominators, you can use the following step-by-step instructions:

1. Find the LCM of the denominators of fractions;
2. Divide the LCM by the denominator of each fraction and get an additional multiplier for each fraction;
3. Multiply the numerators and denominators of fractions by their additional factors;
4. Add fractions that have the same denominators;
5. If the answer turned out to be an improper fraction, then select its whole part;

Example 2 Find the value of an expression .

Let's use the instructions above.

Step 1. Find the LCM of the denominators of fractions

Find the LCM of the denominators of both fractions. The denominators of the fractions are the numbers 2, 3 and 4

Step 2. Divide the LCM by the denominator of each fraction and get an additional multiplier for each fraction

Divide the LCM by the denominator of the first fraction. LCM is the number 12, and the denominator of the first fraction is the number 2. Divide 12 by 2, we get 6. We got the first additional factor 6. We write it over the first fraction:

Now we divide the LCM by the denominator of the second fraction. LCM is the number 12, and the denominator of the second fraction is the number 3. We divide 12 by 3, we get 4. We got the second additional factor 4. We write it over the second fraction:

Now we divide the LCM by the denominator of the third fraction. LCM is the number 12, and the denominator of the third fraction is the number 4. Divide 12 by 4, we get 3. We got the third additional factor 3. We write it over the third fraction:

Step 3. Multiply the numerators and denominators of fractions by your additional factors

We multiply the numerators and denominators by our additional factors:

Step 4. Add fractions that have the same denominators

We came to the conclusion that fractions that had different denominators turned into fractions that have the same (common) denominators. It remains to add these fractions. Add up:

The addition didn't fit on one line, so we moved the remaining expression to the next line. This is allowed in mathematics. When an expression does not fit on one line, it is carried over to the next line, and it is necessary to put an equal sign (=) at the end of the first line and at the beginning of a new line. The equal sign on the second line indicates that this is a continuation of the expression that was on the first line.

Step 5. If the answer turned out to be an improper fraction, then select the whole part in it

Our answer is an improper fraction. We must single out the whole part of it. We highlight:

Got an answer

Subtraction of fractions with the same denominators

There are two types of fraction subtraction:

1. Subtraction of fractions with the same denominators
2. Subtraction of fractions with different denominators

First, let's learn how to subtract fractions with the same denominators. Everything is simple here. To subtract another from one fraction, you need to subtract the numerator of the second fraction from the numerator of the first fraction, and leave the denominator the same.

For example, let's find the value of the expression . To solve this example, it is necessary to subtract the numerator of the second fraction from the numerator of the first fraction, and leave the denominator unchanged. Let's do this:

This example can be easily understood if we think of a pizza that is divided into four parts. If you cut pizzas from a pizza, you get pizzas:

Example 2 Find the value of the expression .

Again, from the numerator of the first fraction, subtract the numerator of the second fraction, and leave the denominator unchanged:

This example can be easily understood if we think of a pizza that is divided into three parts. If you cut pizzas from a pizza, you get pizzas:

Example 3 Find the value of an expression

This example is solved in exactly the same way as the previous ones. From the numerator of the first fraction, you need to subtract the numerators of the remaining fractions:

As you can see, there is nothing complicated in subtracting fractions with the same denominators. It is enough to understand the following rules:

1. To subtract another from one fraction, you need to subtract the numerator of the second fraction from the numerator of the first fraction, and leave the denominator unchanged;
2. If the answer turned out to be an improper fraction, then you need to select the whole part in it.

Subtraction of fractions with different denominators

For example, a fraction can be subtracted from a fraction, since these fractions have the same denominators. But a fraction cannot be subtracted from a fraction, because these fractions have different denominators. In such cases, fractions must be reduced to the same (common) denominator.

The common denominator is found according to the same principle that we used when adding fractions with different denominators. First of all, find the LCM of the denominators of both fractions. Then the LCM is divided by the denominator of the first fraction and the first additional factor is obtained, which is written over the first fraction. Similarly, the LCM is divided by the denominator of the second fraction and a second additional factor is obtained, which is written over the second fraction.

The fractions are then multiplied by their additional factors. As a result of these operations, fractions that had different denominators turn into fractions that have the same denominators. And we already know how to subtract such fractions.

Example 1 Find the value of an expression:

These fractions have different denominators, so you need to bring them to the same (common) denominator.

First, we find the LCM of the denominators of both fractions. The denominator of the first fraction is the number 3, and the denominator of the second fraction is the number 4. The least common multiple of these numbers is 12

LCM (3 and 4) = 12

Now back to fractions and

Let's find an additional factor for the first fraction. To do this, we divide the LCM by the denominator of the first fraction. LCM is the number 12, and the denominator of the first fraction is the number 3. Divide 12 by 3, we get 4. We write the four over the first fraction:

We do the same with the second fraction. We divide the LCM by the denominator of the second fraction. LCM is the number 12, and the denominator of the second fraction is the number 4. Divide 12 by 4, we get 3. Write a triple over the second fraction:

Now we are all set for subtraction. It remains to multiply the fractions by their additional factors:

We came to the conclusion that fractions that had different denominators turned into fractions that had the same denominators. And we already know how to subtract such fractions. Let's complete this example to the end:

Got an answer

Let's try to depict our solution using a picture. If you cut pizzas from a pizza, you get pizzas.

This is the detailed version of the solution. Being at school, we would have to solve this example in a shorter way. Such a solution would look like this:

Reduction of fractions and to a common denominator can also be depicted using a picture. Bringing these fractions to a common denominator, we get the fractions and . These fractions will be represented by the same pizza slices, but this time they will be divided into the same fractions (reduced to the same denominator):

The first drawing shows a fraction (eight pieces out of twelve), and the second picture shows a fraction (three pieces out of twelve). By cutting off three pieces from eight pieces, we get five pieces out of twelve. The fraction describes these five pieces.

Example 2 Find the value of an expression

These fractions have different denominators, so you first need to bring them to the same (common) denominator.

Find the LCM of the denominators of these fractions.

The denominators of the fractions are the numbers 10, 3 and 5. The least common multiple of these numbers is 30

LCM(10, 3, 5) = 30

Now we find additional factors for each fraction. To do this, we divide the LCM by the denominator of each fraction.

Let's find an additional factor for the first fraction. LCM is the number 30, and the denominator of the first fraction is the number 10. Divide 30 by 10, we get the first additional factor 3. We write it over the first fraction:

Now we find an additional factor for the second fraction. Divide the LCM by the denominator of the second fraction. LCM is the number 30, and the denominator of the second fraction is the number 3. Divide 30 by 3, we get the second additional factor 10. We write it over the second fraction:

Now we find an additional factor for the third fraction. Divide the LCM by the denominator of the third fraction. LCM is the number 30, and the denominator of the third fraction is the number 5. Divide 30 by 5, we get the third additional factor 6. We write it over the third fraction:

Now everything is ready for subtraction. It remains to multiply the fractions by their additional factors:

We came to the conclusion that fractions that had different denominators turned into fractions that have the same (common) denominators. And we already know how to subtract such fractions. Let's finish this example.

The continuation of the example will not fit on one line, so we move the continuation to the next line. Don't forget about the equal sign (=) on the new line:

The answer turned out to be a correct fraction, and everything seems to suit us, but it is too cumbersome and ugly. We should make it easier. What can be done? You can reduce this fraction.

To reduce a fraction, you need to divide its numerator and denominator by (gcd) the numbers 20 and 30.

So, we find the GCD of the numbers 20 and 30:

Now we return to our example and divide the numerator and denominator of the fraction by the found GCD, that is, by 10

Got an answer

Multiplying a fraction by a number

To multiply a fraction by a number, you need to multiply the numerator of the given fraction by this number, and leave the denominator unchanged.

Example 1. Multiply the fraction by the number 1.

Multiply the numerator of the fraction by the number 1

The entry can be understood as taking half 1 time. For example, if you take pizza 1 time, you get pizza

From the laws of multiplication, we know that if the multiplicand and the multiplier are interchanged, then the product will not change. If the expression is written as , then the product will still be equal to . Again, the rule for multiplying an integer and a fraction works:

This entry can be understood as taking half of the unit. For example, if there is 1 whole pizza and we take half of it, then we will have pizza:

Example 2. Find the value of an expression

Multiply the numerator of the fraction by 4

The answer is an improper fraction. Let's take a whole part of it:

The expression can be understood as taking two quarters 4 times. For example, if you take pizzas 4 times, you get two whole pizzas.

And if we swap the multiplicand and the multiplier in places, we get the expression. It will also be equal to 2. This expression can be understood as taking two pizzas from four whole pizzas:

A number that is multiplied by a fraction and the denominator of the fraction are resolved if they have a common divisor greater than one.

For example, an expression can be evaluated in two ways.

First way. Multiply the number 4 by the numerator of the fraction, and leave the denominator of the fraction unchanged:

Second way. The quadruple being multiplied and the quadruple in the denominator of the fraction can be reduced. You can reduce these fours by 4, since the greatest common divisor for two fours is the four itself:

We got the same result 3. After reducing the fours, new numbers are formed in their place: two ones. But multiplying one with a triple, and then dividing by one does not change anything. Therefore, the solution can be written shorter:

The reduction can be performed even when we decided to use the first method, but at the stage of multiplying the number 4 and the numerator 3, we decided to use the reduction:

But for example, the expression can only be calculated in the first way - multiply 7 by the denominator of the fraction, and leave the denominator unchanged:

This is due to the fact that the number 7 and the denominator of the fraction do not have a common divisor greater than one, and, accordingly, are not reduced.

Some students mistakenly abbreviate the number being multiplied and the numerator of the fraction. You can't do this. For example, the following entry is not correct:

The reduction of the fraction implies that and numerator and denominator will be divided by the same number. In the situation with the expression, the division is performed only in the numerator, since writing this is the same as writing . We see that the division is performed only in the numerator, and no division occurs in the denominator.

Multiplication of fractions

To multiply fractions, you need to multiply their numerators and denominators. If the answer is an improper fraction, you need to select the whole part in it.

Example 1 Find the value of the expression .

Got an answer. It is desirable to reduce this fraction. The fraction can be reduced by 2. Then the final solution will take the following form:

The expression can be understood as taking a pizza from half a pizza. Let's say we have half a pizza:

How to take two-thirds from this half? First you need to divide this half into three equal parts:

And take two from these three pieces:

We'll get pizza. Remember what a pizza looks like divided into three parts:

One slice from this pizza and the two slices we took will have the same dimensions:

In other words, we are talking about the same size pizza. Therefore, the value of the expression is

Example 2. Find the value of an expression

Multiply the numerator of the first fraction by the numerator of the second fraction, and the denominator of the first fraction by the denominator of the second fraction:

The answer is an improper fraction. Let's take a whole part of it:

Example 3 Find the value of an expression

Multiply the numerator of the first fraction by the numerator of the second fraction, and the denominator of the first fraction by the denominator of the second fraction:

The answer turned out to be a correct fraction, but it will be good if it is reduced. To reduce this fraction, you need to divide the numerator and denominator of this fraction by the greatest common divisor (GCD) of the numbers 105 and 450.

So, let's find the GCD of the numbers 105 and 450:

Now we divide the numerator and denominator of our answer to the GCD that we have now found, that is, by 15

Representing an integer as a fraction

Any whole number can be represented as a fraction. For example, the number 5 can be represented as . From this, five will not change its meaning, since the expression means “the number five divided by one”, and this, as you know, is equal to five:

Reverse numbers

Now we will get acquainted with interesting topic in mathematics. It's called "reverse numbers".

Definition. Reverse to numbera is the number that, when multiplied bya gives a unit.

Let's substitute in this definition instead of a variable a number 5 and try to read the definition:

Reverse to number 5 is the number that, when multiplied by 5 gives a unit.

Is it possible to find a number that, when multiplied by 5, gives one? It turns out you can. Let's represent five as a fraction:

Then multiply this fraction by itself, just swap the numerator and denominator. In other words, let's multiply the fraction by itself, only inverted:

What will be the result of this? If we continue to solve this example, we get one:

This means that the inverse of the number 5 is the number, since when 5 is multiplied by one, one is obtained.

The reciprocal can also be found for any other integer.

You can also find the reciprocal for any other fraction. To do this, it is enough to turn it over.

Division of a fraction by a number

Let's say we have half a pizza:

Let's divide it equally between two. How many pizzas will each get?

It can be seen that after splitting half of the pizza, two equal pieces were obtained, each of which makes up a pizza. So everyone gets a pizza.

This article deals with operations on fractions. Rules for addition, subtraction, multiplication, division or exponentiation of fractions of the form A B will be formed and justified, where A and B can be numbers, numeric expressions or expressions with variables. In conclusion, examples of solutions with a detailed description will be considered.

Yandex.RTB R-A-339285-1

Rules for performing operations with numerical fractions of a general form

Numerical fractions general view have a numerator and a denominator that contain integers or numeric expressions. If we consider such fractions as 3 5 , 2 , 8 4 , 1 + 2 3 4 (5 - 2) , 3 4 + 7 8 2 , 3 - 0 , 8 , 1 2 2 , π 1 - 2 3 + π , 2 0 , 5 ln 3 , then it is clear that the numerator and denominator can have not only numbers, but also expressions of a different plan.

Definition 1

There are rules by which actions are performed with ordinary fractions. It is also suitable for fractions of a general form:

• When subtracting fractions with the same denominators, only the numerators are added, and the denominator remains the same, namely: a d ± c d \u003d a ± c d, the values ​​a, c and d ≠ 0 are some numbers or numerical expressions.
• When adding or subtracting fractions with different denominators, it is necessary to reduce to a common one, and then add or subtract the resulting fractions with the same indicators. Literally, it looks like this ab ± cd = a p ± c rs, where the values ​​a, b ≠ 0, c, d ≠ 0, p ≠ 0, r ≠ 0, s ≠ 0 are real numbers, and b p = d r = s. When p = d and r = b, then a b ± c d = a d ± c d b d.
• When multiplying fractions, an action is performed with numerators, after which with denominators, then we get a b c d \u003d a c b d, where a, b ≠ 0, c, d ≠ 0 act as real numbers.
• When dividing a fraction by a fraction, we multiply the first by the second reciprocal, that is, we swap the numerator and denominator: a b: c d \u003d a b d c.

Rationale for the rules

Definition 2

There are the following mathematical points that you should rely on when calculating:

• a fractional bar means a division sign;
• division by a number is treated as a multiplication by its reciprocal;
• application of the property of actions with real numbers;
• application of the basic property of a fraction and numerical inequalities.

With their help, you can make transformations of the form:

a d ± c d = a d - 1 ± c d - 1 = a ± c d - 1 = a ± c d ; a b ± c d = a p b p ± c r d r = a p s ± c e s = a p ± c r s ; ab cd = a db d b cb d = a d a d - 1 b c b d - 1 = = a d b c b d - 1 b d - 1 = a d b cb d b d - 1 = = (a c) (b d) - 1 = a cb d

Examples

In the previous paragraph, it was said about actions with fractions. It is after this that the fraction needs to be simplified. This topic was discussed in detail in the section on converting fractions.

First, consider the example of adding and subtracting fractions with the same denominator.

Example 1

Given fractions 8 2 , 7 and 1 2 , 7 , then according to the rule it is necessary to add the numerator and rewrite the denominator.

Solution

Then we get a fraction of the form 8 + 1 2 , 7 . After performing the addition, we get a fraction of the form 8 + 1 2 , 7 = 9 2 , 7 = 90 27 = 3 1 3 . So 8 2 , 7 + 1 2 , 7 = 8 + 1 2 , 7 = 9 2 , 7 = 90 27 = 3 1 3 .

Answer: 8 2 , 7 + 1 2 , 7 = 3 1 3

There is another way to solve. To begin with, a transition is made to the form of an ordinary fraction, after which we perform a simplification. It looks like this:

8 2 , 7 + 1 2 , 7 = 80 27 + 10 27 = 90 27 = 3 1 3

Example 2

Let us subtract from 1 - 2 3 log 2 3 log 2 5 + 1 fractions of the form 2 3 3 log 2 3 log 2 5 + 1 .

Since equal denominators are given, it means that we are calculating a fraction with the same denominator. We get that

1 - 2 3 log 2 3 log 2 5 + 1 - 2 3 3 log 2 3 log 2 5 + 1 = 1 - 2 - 2 3 3 log 2 3 log 2 5 + 1

There are examples of calculating fractions with different denominators. An important point is the reduction to a common denominator. Without this, we will not be able to perform further actions with fractions.

The process is remotely reminiscent of reduction to a common denominator. That is, a search is made for the least common divisor in the denominator, after which the missing factors are added to the fractions.

If the added fractions have no common factors, then their product can become one.

Example 3

Consider the example of adding fractions 2 3 5 + 1 and 1 2 .

Solution

In this case, the common denominator is the product of the denominators. Then we get that 2 · 3 5 + 1 . Then, when setting additional factors, we have that to the first fraction it is equal to 2, and to the second 3 5 + 1. After multiplication, the fractions are reduced to the form 4 2 3 5 + 1. The general cast 1 2 will be 3 5 + 1 2 · 3 5 + 1 . We add the resulting fractional expressions and get that

2 3 5 + 1 + 1 2 = 2 2 2 3 5 + 1 + 1 3 5 + 1 2 3 5 + 1 = = 4 2 3 5 + 1 + 3 5 + 1 2 3 5 + 1 = 4 + 3 5 + 1 2 3 5 + 1 = 5 + 3 5 2 3 5 + 1

Answer: 2 3 5 + 1 + 1 2 = 5 + 3 5 2 3 5 + 1

When we are dealing with fractions of a general form, then the least common denominator is usually not the case. It is unprofitable to take the product of numerators as a denominator. First you need to check if there is a number that is less in value than their product.

Example 4

Consider the example 1 6 2 1 5 and 1 4 2 3 5 when their product is equal to 6 2 1 5 4 2 3 5 = 24 2 4 5 . Then we take 12 · 2 3 5 as a common denominator.

Consider examples of multiplications of fractions of a general form.

Example 5

To do this, it is necessary to multiply 2 + 1 6 and 2 · 5 3 · 2 + 1.

Solution

Following the rule, it is necessary to rewrite and write the product of numerators as a denominator. We get that 2 + 1 6 2 5 3 2 + 1 2 + 1 2 5 6 3 2 + 1 . When the fraction is multiplied, reductions can be made to simplify it. Then 5 3 3 2 + 1: 10 9 3 = 5 3 3 2 + 1 9 3 10 .

Using the rule of transition from division to multiplication by a reciprocal, we get the reciprocal of the given one. To do this, the numerator and denominator are reversed. Let's look at an example:

5 3 3 2 + 1: 10 9 3 = 5 3 3 2 + 1 9 3 10

After that, they must perform multiplication and simplify the resulting fraction. If necessary, get rid of the irrationality in the denominator. We get that

5 3 3 2 + 1: 10 9 3 = 5 3 3 9 3 10 2 + 1 = 5 2 10 2 + 1 = 3 2 2 + 1 = = 3 2 - 1 2 2 + 1 2 - 1 = 3 2 - 1 2 2 2 - 1 2 = 3 2 - 1 2

Answer: 5 3 3 2 + 1: 10 9 3 = 3 2 - 1 2

This clause applies when the number or numeric expression can be represented as a fraction with a denominator equal to 1, then the action with such a fraction is considered a separate item. For example, the expression 1 6 7 4 - 1 3 shows that the root of 3 can be replaced by another 3 1 expression. Then this record will look like a multiplication of two fractions of the form 1 6 7 4 - 1 3 = 1 6 7 4 - 1 3 1 .

Performing an action with fractions containing variables

The rules discussed in the first article are applicable to operations with fractions containing variables. Consider the subtraction rule when the denominators are the same.

It is necessary to prove that A , C and D (D not equal to zero) can be any expressions, and the equality A D ± C D = A ± C D is equivalent to its range of valid values.

It is necessary to take a set of ODZ variables. Then A, C, D must take the corresponding values ​​a 0 , c 0 and d0. A substitution of the form A D ± C D results in a difference of the form a 0 d 0 ± c 0 d 0 , where, according to the addition rule, we obtain a formula of the form a 0 ± c 0 d 0 . If we substitute the expression A ± C D , then we get the same fraction of the form a 0 ± c 0 d 0 . From this we conclude that the chosen value that satisfies the ODZ, A ± C D and A D ± C D are considered equal.

For any value of the variables, these expressions will be equal, that is, they are called identically equal. This means that this expression is considered to be a provable equality of the form A D ± C D = A ± C D .

Examples of addition and subtraction of fractions with variables

When there are the same denominators, it is only necessary to add or subtract the numerators. This fraction can be simplified. Sometimes you have to work with fractions that are identically equal, but at first glance this is not noticeable, since some transformations must be performed. For example, x 2 3 x 1 3 + 1 and x 1 3 + 1 2 or 1 2 sin 2 α and sin a cos a. Most often, a simplification of the original expression is required in order to see the same denominators.

Example 6

Calculate: 1) x 2 + 1 x + x - 2 - 5 - xx + x - 2 , 2) lg 2 x + 4 x (lgx + 2) + 4 lgxx (lgx + 2) , x - 1 x - 1 + xx + 1 .

Solution

1. To make a calculation, you need to subtract fractions that have the same denominators. Then we get that x 2 + 1 x + x - 2 - 5 - x x + x - 2 = x 2 + 1 - 5 - x x + x - 2 . After that, you can open the brackets with the reduction of similar terms. We get that x 2 + 1 - 5 - x x + x - 2 = x 2 + 1 - 5 + x x + x - 2 = x 2 + x - 4 x + x - 2
2. Since the denominators are the same, it remains only to add the numerators, leaving the denominator: lg 2 x + 4 x (lgx + 2) + 4 lgxx (lgx + 2) = lg 2 x + 4 + 4 x (lgx + 2)
   The addition has been completed. It can be seen that the fraction can be reduced. Its numerator can be folded using the sum square formula, then we get (l g x + 2) 2 from the abbreviated multiplication formulas. Then we get that
   l g 2 x + 4 + 2 l g x x (l g x + 2) = (l g x + 2) 2 x (l g x + 2) = l g x + 2 x
3. Given fractions of the form x - 1 x - 1 + x x + 1 with different denominators. After the transformation, you can proceed to addition.

Let's consider a two way solution.

The first method is that the denominator of the first fraction is subjected to factorization using squares, and with its subsequent reduction. We get a fraction of the form

x - 1 x - 1 = x - 1 (x - 1) x + 1 = 1 x + 1

So x - 1 x - 1 + x x + 1 = 1 x + 1 + x x + 1 = 1 + x x + 1 .

In this case, it is necessary to get rid of irrationality in the denominator.

1 + x x + 1 = 1 + x x - 1 x + 1 x - 1 = x - 1 + x x - x x - 1

The second way is to multiply the numerator and denominator of the second fraction by x - 1 . Thus, we get rid of irrationality and proceed to adding a fraction with the same denominator. Then

x - 1 x - 1 + xx + 1 = x - 1 x - 1 + x x - 1 x + 1 x - 1 = = x - 1 x - 1 + x x - xx - 1 = x - 1 + x x - xx - 1

Answer: 1) x 2 + 1 x + x - 2 - 5 - xx + x - 2 = x 2 + x - 4 x + x - 2, 2) lg 2 x + 4 x (lgx + 2) + 4 lgxx · (lgx + 2) = lgx + 2 x , 3) ​​x - 1 x - 1 + xx + 1 = x - 1 + x x - xx - 1 .

In the last example, we found that reduction to a common denominator is inevitable. To do this, you need to simplify the fractions. To add or subtract, you always need to look for a common denominator, which looks like the product of the denominators with the addition of additional factors to the numerators.

Example 7

Calculate fraction values: 1) x 3 + 1 x 7 + 2 2, 2) x + 1 x ln 2 (x + 1) (2 x - 4) - sin xx 5 ln (x + 1) (2 x - 4) , 3) ​​1 cos 2 x - x + 1 cos 2 x + 2 cos x x + x

Solution

1. The denominator does not require any complicated calculations, so you need to choose their product of the form 3 x 7 + 2 2, then to the first fraction x 7 + 2 2 is chosen as an additional factor, and 3 to the second. When multiplying, we get a fraction of the form x 3 + 1 x 7 + 2 2 = x x 7 + 2 2 3 x 7 + 2 2 + 3 1 3 x 7 + 2 2 = = x x 7 + 2 2 + 3 3 x 7 + 2 2 = x x 7 + 2 2 x + 3 3 x 7 + 2 2
2. It can be seen that the denominators are presented as a product, which means that additional transformations are unnecessary. The common denominator will be the product of the form x 5 · ln 2 x + 1 · 2 x - 4 . From here x 4 is an additional factor to the first fraction, and ln (x + 1) to the second. Then we subtract and get:
   x + 1 x ln 2 (x + 1) 2 x - 4 - sin xx 5 ln (x + 1) 2 x - 4 = = x + 1 x 4 x 5 ln 2 (x + 1 ) 2 x - 4 - sin x ln x + 1 x 5 ln 2 (x + 1) (2 x - 4) = = x + 1 x 4 - sin x ln (x + 1) x 5 ln 2 (x + 1) (2 x - 4) = x x 4 + x 4 - sin x ln (x + 1) x 5 ln 2 (x + 1) (2 x - 4) )
3. This example makes sense when working with denominators of fractions. It is necessary to apply the formulas for the difference of squares and the square of the sum, since they will make it possible to pass to an expression of the form 1 cos x - x · cos x + x + 1 (cos x + x) 2 . It can be seen that the fractions are reduced to a common denominator. We get that cos x - x cos x + x 2 .

Then we get that

1 cos 2 x - x + 1 cos 2 x + 2 cos x x + x = = 1 cos x - x cos x + x + 1 cos x + x 2 = = cos x + x cos x - x cos x + x 2 + cos x - x cos x - x cos x + x 2 = = cos x + x + cos x - x cos x - x cos x + x 2 = 2 cos x cos x - x cos x + x2

Answer:

1) x 3 + 1 x 7 + 2 2 = x x 7 + 2 2 x + 3 3 x 7 + 2 2, 2) x + 1 x ln 2 (x + 1) 2 x - 4 - sin xx 5 ln (x + 1) 2 x - 4 = = x x 4 + x 4 - sin x ln (x + 1) x 5 ln 2 (x + 1) ( 2 x - 4) , 3) ​​1 cos 2 x - x + 1 cos 2 x + 2 cos x x + x = 2 cos x cos x - x cos x + x 2 .

Examples of multiplying fractions with variables

When multiplying fractions, the numerator is multiplied by the numerator and the denominator by the denominator. Then you can apply the reduction property.

Example 8

Multiply fractions x + 2 x x 2 ln x 2 ln x + 1 and 3 x 2 1 3 x + 1 - 2 sin 2 x - x.

Solution

You need to do the multiplication. We get that

x + 2 xx 2 ln x 2 ln x + 1 3 x 2 1 3 x + 1 - 2 sin (2 x - x) = = x - 2 x 3 x 2 1 3 x + 1 - 2 x 2 ln x 2 ln x + 1 sin (2 x - x)

The number 3 is transferred to the first place for the convenience of calculations, and you can reduce the fraction by x 2, then we get an expression of the form

3 x - 2 x x 1 3 x + 1 - 2 ln x 2 ln x + 1 sin (2 x - x)

Answer: x + 2 xx 2 ln x 2 ln x + 1 3 x 2 1 3 x + 1 - 2 sin(2 x - x) = 3 x - 2 x x 1 3 x + 1 - 2 ln x 2 ln x + 1 sin (2 x - x) .

Division

Division of fractions is similar to multiplication, since the first fraction is multiplied by the second reciprocal. If we take, for example, the fraction x + 2 x x 2 ln x 2 ln x + 1 and divide by 3 x 2 1 3 x + 1 - 2 sin 2 x - x, then this can be written as

x + 2 xx 2 ln x 2 ln x + 1: 3 x 2 1 3 x + 1 - 2 sin (2 x - x) , then replace with a product of the form x + 2 xx 2 ln x 2 ln x + 1 3 x 2 1 3 x + 1 - 2 sin (2 x - x)

Exponentiation

Let's move on to consider the action with fractions of a general form with exponentiation. If there is a degree with a natural index, then the action is considered as a multiplication of identical fractions. But it is recommended to use a general approach based on the properties of degrees. Any expressions A and C, where C is not identically equal to zero, and any real r on the ODZ for an expression of the form A C r, the equality A C r = A r C r is true. The result is a fraction raised to a power. For example, consider:

x 0 , 7 - π ln 3 x - 2 - 5 x + 1 2 , 5 = = x 0 , 7 - π ln 3 x - 2 - 5 2 , 5 x + 1 2 , 5

The order of operations with fractions

Actions on fractions are performed according to certain rules. In practice, we notice that the expression may contain several fractions or fractional expressions. Then it is necessary to perform all actions in a strict order: raise to a power, multiply, divide, then add and subtract. If there are brackets, the first action is performed in them.

Example 9

Calculate 1 - x cos x - 1 c o s x · 1 + 1 x .

Solution

Since we have same denominator, then 1 - x cos x and 1 c o s x , but it is impossible to perform subtractions according to the rule, first the actions in brackets are performed, after which the multiplication, and then the addition. Then, when calculating, we get that

1 + 1 x = 1 1 + 1 x = x x + 1 x = x + 1 x

When substituting the expression into the original one, we get that 1 - x cos x - 1 cos x · x + 1 x. When multiplying fractions, we have: 1 cos x x + 1 x = x + 1 cos x x . Having made all the substitutions, we get 1 - x cos x - x + 1 cos x · x . Now you need to work with fractions that have different denominators. We get:

x 1 - x cos x x - x + 1 cos x x = x 1 - x - 1 + x cos x x = = x - x - x - 1 cos x x = - x + 1 cos x x

Answer: 1 - x cos x - 1 c o s x 1 + 1 x = - x + 1 cos x x .

If you notice a mistake in the text, please highlight it and press Ctrl+Enter