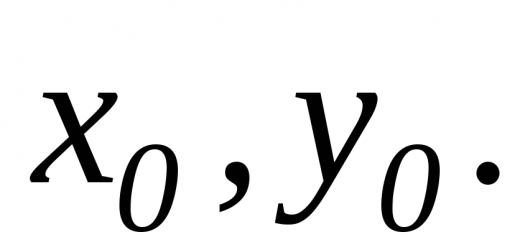1 من 22
وصف العرض التقديمي من خلال الشرائح الفردية:
الشريحة رقم 1
الدليل العلمي في الجبر الموضوع: “اللوغاريتمي و المعادلات الأسيةوأوجه عدم المساواة" أكملها: مانويلوفا ل.ن. - معلمة رياضيات، مدرسة MBOU الثانوية رقم 76، إيجيفسك، أودمورتيا
الشريحة رقم 2
المحتويات: الفصل 1. 1.1. مفهوم اللوغاريتم 1.2. خصائص اللوغاريتم 1.3. المعادلات اللوغاريتمية أ. الجزء النظريب. أمثلة 1.4. عدم المساواة اللوغاريتمية أ. الجزء النظري ب. أمثلة الفصل 2. 2.1. قوة الرقم الموجب هي 2.2. الدالة الأسية 2.3. المعادلات الأسية أ. الجزء النظري ب. أمثلة 2.4. المتباينات الأسية أ. الجزء النظري ب. أمثلة الفصل 3. 3.1. اختبار حول موضوع "المعادلات اللوغاريتمية وعدم المساواة" مستوى التعقيد الثاني مستوى التعقيد الثالث مستوى التعقيد 3.2. اختبار حول موضوع "المعادلات الأسية والمتباينات" مستوى التعقيد II مستوى التعقيد III مستوى التعقيد
الشريحة رقم 3
1.1 مفهوم اللوغاريتم y x y = b b M 1 0 n y = ax (a > 1) x y = ax (0)< a < 1) y= b M 1 0 b у Для любого положительного числа b существует, и притом только одно, число n, такое, что b = an . Это число называют логарифмом числа b по основанию a. n Логарифмом положительного числа b по основанию a (a >0, a ≠ 0) هو رقم n بحيث b = an يُشار إلى لوغاريتم الرقم الموجب b للأساس a (a > 0,a ≠ 1) على النحو التالي: n = loga b من تعريف اللوغاريتم من الواضح يتبع ذلك بالنسبة لـ a > 0 , a ≠ 1, b > 0: a loga b = b
الشريحة رقم 4
الدالة اللوغاريتمية y y x x 1 2 2 1 1 1 -1 -1 2 2 -2 -2 3 0 0 y = log2 x y = log3 x y = log⅓x y = log½x الدالة y = loga x تسمى دالة لوغاريتمية. خصائص الدالة y = loga x، لـ a > 0: مستمرة ومتزايدة على الفاصل الزمني (0;+∞)؛ إذا كان x→+∞، ثم y→+∞؛ إذا كان x→0، ثم y→ -∞. بما أن loga1=0، فمن الخاصية 1 يتبع: إذا x > 1، ثم y > 0؛ إذا 0< х < 1 ,то у < 0. Свойства функции y = loga x, при 0 < a < 1: Непрерывна и убывает на промежутке (0;+∞); Если х→ +∞, то у→ -∞; если х→0, то у→+∞. Так как loga1=0, то из свойства 1 следует: если х >1، ثم ص< 0; если 0 < х < 1 ,то у >0.
الشريحة رقم 5
اجعل a وM وN أرقامًا موجبة، مع ≠ 1 وk عدد حقيقي. إذن تكون التساويات صحيحة: 1. loga (M N) = loga M + loga N - لوغاريتم حاصل ضرب الأعداد الموجبة يساوي المبلغلوغاريتمات هذه الأرقام. 2. loga M = loga M – loga N - لوغاريتم حاصل الأعداد الموجبة N يساوي الفرق بين لوغاريتمات المقسوم والمقسوم عليه. 3. loga Mk = k · loga M - لوغاريتم قوة الرقم الموجب يساوي حاصل ضرب الأس ولوغاريتم هذا الرقم. 4. loga M = logb M → loga b = 1 - صيغة لتحويل اللوغاريتمات من logb a logb قاعدة إلى أخرى. الحالات الفردية: 1. log10 b = log b - يسمى لوغاريتم الرقم الموجب b للأساس 10 اللوغاريتم العشريأرقام ب. 2. loge b = ln b - يسمى لوغاريتم الرقم الموجب b للأساس e اللوغاريتم الطبيعيالأرقام ب 1.2 خصائص اللوغاريتمات
الشريحة رقم 6
1. ليكن a رقمًا موجبًا معينًا لا يساوي 1، ويكون b رقمًا حقيقيًا معينًا. ثم تسمى المعادلة loga x = b بأبسط معادلة لوغاريتمية. على سبيل المثال، المعادلات أ) log3 x = 3 ; (1) ب) log⅓ x = -2 ; (2) ج) log25 x + 5·log4 x·log3 x + 7·log22 x = 0 ; (3) هي أبسط المعادلات اللوغاريتمية. من خلال تعريف اللوغاريتم، إذا كان الرقم x0 يفي بسجل المساواة العددية x = b، فإن الرقم x0 هو ab، وهذا الرقم x0 = ab هو الوحيد. وبالتالي، بالنسبة لأي عدد حقيقي b، فإن المعادلة loga x = b لها جذر فريد x0 = ab. 2. المعادلات التي تتحول بعد استبدال المجهول إلى أبسط المعادلات اللوغاريتمية: أ) log5 (4x - 3) = 2؛ (4) ب) 2 + 1 = -1؛ (5) log(3x + 1) + log0.01 log(3x + 1) 1.3 المعادلات (الجزء النظري)
الشريحة رقم 7
1.3 أمثلة log3 x = 3 دعونا نعيد كتابة المعادلة على الصورة: log3 x = log3 27 فمن الواضح أن هذه المعادلة لها جذر واحد x0 = 27. الإجابة: 27. ب) log1/3 x = -2 هذه المعادلة له جذر واحد x0 = ( ⅓)-2 =9 الإجابة: 9. ج) log25 x + 5 · log4 x · log3 x + 7 · log22 x = 0 (1) بتبسيط جميع اللوغاريتمات إلى نفس الأساس، نعيد كتابة المعادلة كالتالي: 1 + 5 + 7 = 0 (2) log25 x · log5 4 · log5 3 log25 2 بما أن كل حد من المجموع الموجود بين قوسين موجب، فإن المجموع لا يساوي الصفر. لذلك، المعادلة (1)، وبالتالي المعادلة (2)، مكافئة للمعادلة log25 x = 0، التي لها جذر واحد x0 = 1. لذلك، المعادلة (1) لها جذر واحد x0 = 1. الإجابة: 1 . أ، ب – أبسط المعادلات. c هي معادلة تتحول بعد التحويلات إلى أبسط سجل. المعادلة
الشريحة رقم 8
1.3 أمثلة أ) log5 (4x – 3) = 2 (1) نقدم المعادلة الجديدة المعروفة t = 4x – 3، نعيد كتابة المعادلة على الصورة: log5 t = 2. هذه المعادلة لها جذر واحد t1 = 52 =25. للعثور على جذر المعادلة (1)، عليك حل المعادلة: 4س – 3 = 25. (2) لها جذر واحد x1 =7. ولذلك، فإن المعادلة (1) لها أيضًا جذر واحد x1=7. الجواب: 7. ب) 2 + 1 = -1 (1) سجل (3x + 1) + سجل 0.01 سجل (3x + 1) تقديم جديد غير معروف t = سجل (3x + 1) ومراعاة ذلك سجل 0.01 = -2 نعيد كتابة المعادلة (1) على الصورة: 2 + 1 = -1 (2) t - 2 t وبعد حل المعادلة النسبية (2) نجد أن لها جذرين t1 = -2 و t2 = 1. لإيجاد جميع جذور المعادلة (1) لا بد من الجمع بين جذور المعادلتين log(3x + 1) = -2 و log(3x + 1) = 1. المعادلة الأولى تعادل المعادلة 3x + 1 = 10-2، والذي له جذر واحد x1 = -0.33. المعادلة الثانية تعادل المعادلة 3x + 1 = 10، والتي لها أيضًا جذر واحد x2 = 3. الإجابة: -0.33؛ 3. أ، ب – المعادلات المخفضة إلى أبسطها عن طريق استبدال المجهول
الشريحة رقم 9
1.4 المتباينات (الجزء النظري) ليكن a رقمًا موجبًا لا يساوي 1، وb يكون رقمًا حقيقيًا. ثم المتباينات: سجل x > ب (1) سجل x< b (2) являются простейшими المتباينات اللوغاريتمية. يمكن إعادة كتابة المتباينات (1) و (2) على النحو التالي: loga x > loga x0 (3) loga x< loga x0 (4) , где x0 = ab . Если a >1، فإن الدالة y = loga x تزداد عبر مجال تعريفها بالكامل، أي. على الفاصل الزمني (0؛+∞). لذلك، لأي رقم x > x0 فهو صحيح عدم المساواة العددية loga x > loga x0 ولأي رقم x من الفاصل الزمني 0< x < x0 справедливо числовое неравенство logа x < logа x0 . Кроме того, равенство logа x = logа x0 справедливо лишь при х = х0 . Таким образом, при а >1 وأي عدد حقيقي b، فإن مجموعة جميع حلول المتباينة (3) هي الفترة (x0 ;+ ∞)، ومجموعة جميع حلول المتباينة (4) هي الفترة (0؛ x0). إذا 0< a < 1, то функция y = loga х убывает. Поэтому для любого числа x >x0 لوغا عدم المساواة العددية x صحيح< loga x0 , а для любого числа х из промежутка 0 < x < x0 справедливо числовое неравенство loga x >لوقا x0 . بالإضافة إلى ذلك، فإن loga المساواة x = loga x0 صالح فقط لـ x = x0. وهكذا، عند 0< a < 1 и любом действительном числе b множество всех решений неравенства (3) есть интервал (0; х0) , а множество всех решений неравенства (4) есть интервал (х0 ;+∞).
الشريحة رقم 10
1.4 عدم المساواة (الجزء النظري) خطة تنسيق xOy ضع في اعتبارك الرسوم البيانية للدالة y = loga x و y = b. يتقاطع الخط المستقيم y = b مع الرسم البياني للدالة y = loga x عند نقطة واحدة x0 = ab. إذا كانت a > 1، فإن النقطة المقابلة لكل x > x0 على الرسم البياني للدالة y = loga x تقع فوق الخط المستقيم y = b، أي. لكل x > x0 الإحداثي المقابل y = ax أكبر من الإحداثي ax0، ولكل x من الفاصل الزمني 0< x < x0 соответствующая точка графика функции y = loga x находится ниже прямой y = b. Если же 0 < a <1, то, наоборот, для каждого x >x0 النقطة المقابلة على الرسم البياني للدالة y = loga x تقع أسفل الخط المستقيم y = b، ولكل x من الفواصل الزمنية 0< x < x0 соответствующая точка графика функции y = loga x находится выше прямой y = b. у у х х 1 1 1 1 х0 0 0 y = b y = loga x (a >1) ص = ب ص = لوغا س (0< a < 1) х0
الشريحة رقم 11
1.4 أمثلة دعونا نحل سجل المتباينة1/3 x > -2. (1) بما أن -2 = log⅓ 9، فيمكن إعادة كتابة المتباينة (1) بالشكل log ⅓x > log ⅓ 9 (2) منذ ⅓< 1, то функция y = log⅓ x убывающая. Поэтому множество всех решений неравенства (2), а значит и неравенства (1), есть интервал 0 < x <9. Ответ: (0;9). 2. Решим неравенство log4 x >½. (3) بما أن ½ = log4 2، فيمكن إعادة كتابة المتباينة (3) بالشكل log4 x > log4 2 (4) بما أن 4 > 1، فإن الدالة y = log4 x آخذة في التزايد. ولذلك، فإن مجموعة جميع حلول المتباينة (4)، وبالتالي المتباينة (3)، هي الفترة (2;+∞). الجواب: (2;+∞). (انظر الشكل 1) x y 1 2 3 4 1 -1 0 الشكل 1 y = ½ y = log4 x
الشريحة رقم 12
1.4 أمثلة دعونا نحل المتراجحة log3 x – 3log9 x – log81 x > 1.5. (5) بما أن log9 x = (log3 x) / (log3 9) = (log3 x) / 2 = ½ (log3 x)، log81 x = (log3 x) / (log3 81) = (log3 x) / 4 = ¼ (log3 x)، فيمكن إعادة كتابة المتباينة (5) على النحو التالي: (1 – 1.5 – ¼) log3 x > 1.5 أو log3 x< log3 1/9. (6) Так как 3 >1، فإن الدالة y = log3 x آخذة في الازدياد. ولذلك، فإن مجموعة جميع حلول المتباينة (6)، وبالتالي المتباينة (5)، هي الفترة 0< x < 1/9 (рис.2) Ответ: (0 ; 1/9). y x 1 2 0 -1 y = log3 x y = -2 (рис.2) 1/9
الشريحة رقم 13
2.1 قوة العدد الموجب قوة ج مؤشر عقلانيدع a يكون رقما موجبا و p/q يكون رقم منطقي(ف ≥ 2). بحكم التعريف، الرقم a للقوة p/q هو الجذر الحسابي للقوة q لـ p للقوة p، أي. أ/ف = q√ap . نظرية. دع a يكون رقمًا موجبًا، p عددًا صحيحًا، k و q الأعداد الصحيحة, q ≥ 2, k ≥ 2. إذن فإن التساويات التالية صحيحة: أ) ap/q = (a1/p)p ؛ ب) ap/q = a pk /qk ؛ ج) ap = pq /q ; خصائص الدرجة ذات الأس العقلاني THEOREM 1. الرقم الموجب a إلى الدرجة مع أي أس عقلاني r يكون موجبًا: ar > 0 THEOREM 2. ليكن a رقمًا موجبًا، وr1 وr2 وr أرقام عقلانية. إذن الخصائص التالية صحيحة: 1. عند ضرب القوى مع الأسس النسبية لنفس العدد الموجب، تضيف الأسس: аr1 ∙ аr2 = аr1 + r2. 2. عند قسمة القوى على أسس عقلانية لنفس العدد الموجب، يتم طرح الأسس: аr1: аr2 = аr1 – r2. 3. عند رفع قوة ذات أس عقلاني لعدد موجب في درجة عقلانيةيتم ضرب الأسس: (a r1) r2 = a r1∙ r2. النظرية 3. دع a و b يكونان أرقامًا موجبة و r عددًا منطقيًا. إذن الخصائص التالية للدرجة ذات الأس العقلاني صالحة: الدرجة ذات الأس العقلاني لمنتج الأعداد الموجبة تساوي منتج نفس قوى العوامل: (ab)r = r ∙ br . القوة ذات الأس العقلاني لحاصل الأعداد الموجبة تساوي حاصل نفس قوى المقسوم والمقسوم عليه: (a / b)r = ar / br. النظرية 4. دع الرقم a > 1 و r يكون رقمًا نسبيًا. ثم ع > 1 ل ص > 0 0< ar < 1 при r < 0 ТЕОРЕМА 5. Пусть число a >1، والأرقام المنطقية r1 و r2 تلبي عدم المساواة r1< r2 . Тогда a r1 < a r2 . ТЕОРЕМА 6. Пусть число a принадлежит интервалу (0;1), а рациональные числа r1 и r2 удовлетворяют неравенству r1< r2 . Тогда a r1 < a r2 .
الشريحة رقم 14
2.2 الدالة الأسية خذ بعين الاعتبار الدالة y = a (1) ، حيث a > 0 و a ≠ 0، في مجموعة الأعداد النسبية. لكل رقم منطقي r، يتم تعريف الرقم ar. هذه هي الطريقة التي يتم بها تعريف الدالة (1) في الوقت الحالي على مجموعة الأعداد النسبية. الرسم البياني لهذه الوظيفة في نظام الإحداثيات x0y عبارة عن مجموعة من النقاط (x؛ ax)، حيث x هو أي رقم منطقي. بالنسبة لـ > 1، يظهر هذا الرسم البياني بشكل تخطيطي في الشكل (1)، وبالنسبة لـ 0< a < 1 – на рисунке (2). у у x x 1 2 1 2 3 -2 -1 -2 -1 0 1 1 2 2 Рис. 1 Рис. 2 Её называют وظيفة الأسيةمع قاعدة أ.
الشريحة رقم 15
2.3 المعادلات الأسية (الجزء النظري) 1. ليكن a عددا موجبا معطا لا يساوي 1، و b يكون رقما حقيقيا معطا. ثم تسمى المعادلة الفأس = ب (1) بأبسط معادلة أسية. على سبيل المثال، المعادلات 2x = 8، (1/3)x = 9، 25x = -25 هي أبسط المعادلات الأسية. الجذر (أو الحل) لمعادلة مجهولة x هو الرقم x0، عند استبداله في المعادلة بدلاً من x، يتم الحصول على المساواة العددية الصحيحة. حل المعادلة يعني إيجاد جميع جذورها أو إظهار عدم وجودها. بما أن ax0 > 0 لأي رقم حقيقي x0 حيث تكون المساواة العددية ax0 = b صحيحة مرضية صيغة المفرد x0 = اللوغاريتم ب. وبالتالي فإن المعادلة (1): لأن b ≥ 0 ليس لها جذور؛ بالنسبة إلى b > 0، يكون له جذر واحد x0 = loga b. 2. المعادلات التي بعد استبدال المجهول تتحول إلى أبسط المعادلات الأسية.
الشريحة رقم 16
2.3 أمثلة دعونا نحل المعادلة (1/2)x = 2 (2) بما أن 2 > 1، فإن هذه المعادلة لها جذر واحد x0 = log½ 2 = -1. الجواب: -1. دعونا نحل المعادلة 3x = 5 (3) بما أن 5 > 0، فإن هذه المعادلة لها جذر واحد x0 = log3 5. الإجابة: log3 5. حل المعادلة 25x = -25 منذ -25< 0, то это уравнение не имеет корней. Ответ: нет корней. Для отыскания корня уравнения ax = b (1) при b >0 غالبًا ما يتم كتابة هذه المعادلة كـ ax = aα، حيث α = loga b. فمن الواضح أن الجذر الوحيد لهذه المعادلة، وبالتالي المعادلة (1)، هو الرقم α. بما أن المعادلة (2) يمكن كتابتها على الصورة (1/2)x = (1/2)-1، فإن جذرها الوحيد هو x0 = -1. بما أن المعادلة (3) يمكن كتابتها بالشكل 3x = 3log 35، فإن جذرها الوحيد هو x0 = log3 5.
الشريحة رقم 17
2.3 أمثلة الآن دعونا نلقي نظرة على المعادلات التي تتحول بعد تحويلات بسيطة إلى معادلات أسية بسيطة. دعونا نحل المعادلة 5x+2 - 2 5x - 3 5x+1 = 200 (4) بما أن 5x+2 = 25 5x، 5x+1 = 5 5x، فيمكن إعادة كتابة المعادلة (4) بالشكل 5x ( 25 - 2 – 15) = 200 أو على الصورة 5x = 52 (5) من الواضح أن المعادلة (5) وبالتالي المعادلة (4) لها جذر واحد x0 = 2. الإجابة: 2. حل المعادلة 4 3x - 9 2x = 0 (6) بما أن 2x ≠ 0 لأي عدد حقيقي، فإننا بقسمة المعادلة (6) على 2x نحصل على المعادلة 4 (3/2)x - 9 = 0، (7) مكافئة للمعادلة (6). يمكن إعادة كتابة المعادلة (7) بالشكل (3/2)x = (3/2)2. (8) بما أن المعادلة (8) لها جذر واحد x0 = 2، فإن المعادلة المكافئة (6) لها جذر واحد x0 = 2. الإجابة: 2.
الشريحة رقم 18
2.3 أمثلة دعونا نحل المعادلة 9 2x2-4x + 2 - 2 · 34x2 - 8x + 3 -1 = 0. (9) بعد إعادة كتابة المعادلة (9) في الصورة 34x2 – 8x + 3 = 1، نقدم مجهولاً جديداً t = 4x2 – 8x + 3. ومن ثم يمكن إعادة كتابة المعادلة (9) في الصورة 3t = 1. (10) ) بما أن المعادلة (10) لها جذر واحد t1 = 0، إذن لإيجاد جذور المعادلة (9)، من الضروري حل المعادلة 4x2 – 8x + 3 = 0. هذه المعادلة لها جذرين x1 = 1 /2، x2 = 3/2، وبالتالي فإن المعادلة (9) لها نفس الجذور. الجواب: 1/2؛ 3/2. الآن فكر في حل المعادلات التي، بعد إدخال t مجهول جديد، تتحول إلى معادلات تربيعية أو عقلانية مجهولة t. دعونا نحل المعادلة 4x - 3 2x + 2 = 0. (11) بما أن 4x = (2x)2، فيمكن إعادة كتابة المعادلة (11) بالشكل (2x)2 - 3 2x + 2 = 0. عن طريق إدخال مجهول جديد t = 2x، نحصل على معادلة تربيعية t2 - 3t + 2 = 0، والتي لها جذرين t1 = 1، t2 = 2. ولذلك، لإيجاد جميع جذور المعادلة (11)، نحتاج إلى جمع كل جذور المعادلة (11) المعادلتان 2x = 1 و 2x = 2 وبعد حل هذه المعادلات الأسية البسيطة نجد أن جميع جذور المعادلة (11) هي x1 = 0؛ x2 = 1. الإجابة: 0؛ 1 .
الشريحة رقم 19
2.4 المتباينات الأسية (الجزء النظري) ليكن a رقمًا موجبًا لا يساوي 1، وb يكون رقمًا حقيقيًا. ثم المتباينات الفأس > ب (1) والفأس< b (2) называют простейшими показательными неравенствами. Например, неравенства: 2x < 3 , (1/3)x >4√3، 25x< -25 являются простейшими показательными неравенствами. Решением неравенства с неизвестным х называют число х0 , при подстановке которого в неравенство вместо х получается верное числовое неравенство. Решить неравенство - значит найти все его решения или показать, что их нет. Поскольку a x0 >0 لأي رقم حقيقي x0، ثم بالنسبة لـ b ≥ 0 فإن عدم المساواة a x0 > b يكون صحيحًا لأي رقم حقيقي x0، ولكن لا يوجد رقم حقيقي واحد x0 تكون فيه المتباينة العددية a x0 صحيحة< b . Таким образом, если b ≤ 0 , то множество всех решений неравенства (1) есть интервал (-∞;+∞), а неравенство (2) решений не имеет. Если же b >0، فيمكن إعادة كتابة المتباينة (1) و (2) بالشكل ax > ax0 (1) و ax< ax0 , (2) , где х0 = loga b. Рассмотрим решение неравенств (3) и (4) сначала при а >1. بما أن الدالة y = ax تتزايد بالنسبة لمثل هذه الدالة، فمن أجل أي رقم x > > ax0، ولأي رقم x > x0 يكون محور عدم المساواة العددي صحيحًا< ax0 . Кроме того, равенство ax = ax0 справедливо лишь при х = x0 .
الشريحة رقم 20
2.4 المتباينات الأسية (الجزء النظري) وبالتالي، بالنسبة لـ b > 0 وa > 1، فإن مجموعة جميع حلول المتباينة (3) هي الفترة (x0 ;+∞)، ومجموعة جميع حلول المتباينة (4) هي الفاصل الزمني (-∞; x0) حيث x0 = loga b. دعونا الآن 0< a < 1. Так как для такого а функция y = aх является убывающей, то для любого числа х >x0 محور عدم المساواة العددي صحيح< ax0 . Кроме того, равенство ax = ax0 справедливо лишь при х = x0 . Таким образом, при b >0 و 0< a < 1 множество всех решений неравенства (3) есть интервал (-∞; x0), а множество всех решений неравенства (4) есть интервал (x0 ;+∞), где x0 = loga b. Приведенное выше решение простейших показательных неравенств можно дополнить графической иллюстрацией. Рассмотрим графики функций y = aх и y = b. Ясно, что при b ≤ 0 прямая y = b не пересекает график функции y = aх, так как расположена под кривой y = aх (а, б). Поэтому для любых х выполняется неравенство ax >ب ولا يوجد x التي يكون لها محور عدم المساواة< b . При b >0 خط مستقيم y = b يتقاطع مع الرسم البياني للدالة y = ax عند نقطة واحدة x0 = loga b. 1 y y x x y = 0 y = 0 y = الفأس (أ > 1) 0 1 y = ب (ب)< 0) y = b (b < 0) 1 0 1 y = ax (0 < a < 1) a) б)
الشريحة رقم 22
2.4 أمثلة حل المتراجحة 2x< 8 . (1) Так как 8 >0، فيمكن إعادة كتابة المتباينة (1) على هيئة 2x< 23. (2) Так как 2 >1، فإن الدالة y = 2x آخذة في التزايد. لذلك، حلول المتباينة (2)، وبالتالي المتباينة (1)، كلها x< 3. Ответ: (-∞; 3). Решим неравенство (1/3)х < 5 . (3) Так как 5 >0، فيمكن إعادة كتابة عدم المساواة (3) كـ (1/3) x< (1/3) log⅓ 5 . (4) Так как 0 < 1/3 < 1, то функция y = (1/3)x убывающая. Поэтому решениями неравенства (4), а значит и неравенства (3), являются все х >سجل⅓5. الجواب: (سجل⅓ 5؛ +∞). دعونا نتأمل في متباينة تتحول إلى أبسط المتباينة بعد استبدال المجهول عدم المساواة الأسية. دعونا نحل المتراجحة 5 3x2 - 2x - 6< 1/5 . (5) Введя новое неизвестное t = 3x2 - 2x – 6, перепишем неравенство (5) в виде 5t < 5-1 . Так как 5 >1، فإن جميع الحلول لهذه المتباينة كلها ر< -1. следовательно, все решения неравенства (5) есть решения неравенства 3x2 - 2x – 6 < -1. (6) Решив عدم المساواة التربيعية(6) نجد جميع حلولها: -1< x < 5/3 . Они являются решениями неравенства (5). Ответ: (-1 ; 5/3).
المعادلات اللوغاريتمية وأنواعها وطرق حلها تركيز الانتباه: تركيز الانتباه يساوي N. ن = (عدد الإجابات الصحيحة) × 0.125 × 100%. اكتبه حالة خاصةصيغ الانتقال إلى لوغاريتم قاعدة أخرى اكتب صيغة الانتقال إلى لوغاريتم قاعدة أخرى ما هو لوغاريتم قوة الرقم والقاعدة؟ ما هو لوغاريتم القاعدة؟ ما هو لوغاريتم قوة الرقم؟ ما هو لوغاريتم الحاصل؟ ما هو لوغاريتم المنتج؟ صياغة تعريف اللوغاريتم الإجابة على السؤال
دعونا نفكر الترتيب المتبادلالرسم البياني للدالة y = log a x (a > 0, a ≠ 1) والخط المستقيم y = b. y = سجل x (a>1) y x 0 y = سجل x (0
المعادلات اللوغاريتمية وأنواعها وطرق حلها الخلاصة: الرسم البياني للدالة y = log a x (a > 0, a ≠ 1) والخط المستقيم y = b يتقاطعان عند نقطة واحدة، أي. سجل المعادلة a x = b, a > 0, a ≠ 1, x > 0 له حل فريد x 0 = a b.
تعريف: سجل المعادلة a x = b, a > 0, a ≠ 1, x > 0 يسمى أبسط معادلة لوغاريتمية. المعادلات اللوغاريتمية وأنواعها وطرق حلها مثال:
أنواع وطرق حل المعادلات اللوغاريتمية. التعريف: المعادلات اللوغاريتمية هي تلك التي تحتوي على مجهول تحت علامة اللوغاريتم أو عند قاعدة اللوغاريتم (أو كليهما). المعادلات اللوغاريتمية وأنواعها وطرق حلها
أنواع وطرق حل المعادلات اللوغاريتمية. إضافة: عند حل المعادلات اللوغاريتمية لا بد من مراعاة: المساحة القيم المقبولةاللوغاريتم: يمكن أن تظهر الكميات الموجبة فقط تحت علامة اللوغاريتم؛ عند قاعدة اللوغاريتمات توجد كميات موجبة فقط تختلف عن الوحدة؛ خصائص اللوغاريتمات. عمل التقوية. المعادلات اللوغاريتمية وأنواعها وطرق حلها
المعادلات اللوغاريتمية وأنواعها وطرق حلها أنواع وطرق حل المعادلات اللوغاريتمية. 1) أبسط المعادلات اللوغاريتمية. المثال رقم 1 الإجابة: الحل:
المعادلات اللوغاريتمية وأنواعها وطرق حلها أنواع وطرق حل المعادلات اللوغاريتمية. 2) المعادلات اللوغاريتمية، مختزلة إلى أبسط المعادلات اللوغاريتمية. المثال رقم 1 الإجابة: الحل:
المعادلات اللوغاريتمية وأنواعها وطرق حلها أنواع وطرق حل المعادلات اللوغاريتمية. 2) المعادلات اللوغاريتمية، مختزلة إلى أبسط المعادلات اللوغاريتمية. المثال رقم 2 الإجابة: الحل:
المعادلات اللوغاريتمية وأنواعها وطرق حلها أنواع وطرق حل المعادلات اللوغاريتمية. 2) المعادلات اللوغاريتمية، مختزلة إلى أبسط المعادلات اللوغاريتمية. المثال رقم 3 الإجابة: الحل:
المعادلات اللوغاريتمية وأنواعها وطرق حلها أنواع وطرق حل المعادلات اللوغاريتمية. 2) المعادلات اللوغاريتمية، مختزلة إلى أبسط المعادلات اللوغاريتمية. مثال رقم 4 الإجابة: الحل:
المعادلات اللوغاريتمية وأنواعها وطرق حلها أنواع وطرق حل المعادلات اللوغاريتمية. 3) المعادلات اللوغاريتمية، اختزال إلى المعادلات التربيعية. المثال رقم 1 الإجابة: الحل:
المعادلات اللوغاريتمية وأنواعها وطرق حلها أنواع وطرق حل المعادلات اللوغاريتمية. 3) اختزال المعادلات اللوغاريتمية إلى المعادلات التربيعية. مثال رقم 2 الإجابة: الحل: في المدى الموجود للقيم المسموح بها للمتغير x نقوم بتحويل المعادلة باستخدام خصائص اللوغاريتمات. ومع مراعاة نطاق القيم المقبولة نحصل على: 10؛ 100
المعادلات اللوغاريتمية وأنواعها وطرق حلها أنواع وطرق حل المعادلات اللوغاريتمية. 4) المعادلات اللوغاريتمية، اختزال إلى المعادلات العقلانية. مثال رقم 1 الإجابة: الحل: لنعود إلى المتغير x
المعادلات اللوغاريتمية وأنواعها وطرق حلها أنواع وطرق حل المعادلات اللوغاريتمية. 4) المعادلات اللوغاريتمية، واختزالها إلى المعادلات العقلانية. مثال رقم 2 الإجابة: الحل: في النطاق الموجود للقيم المسموح بها للمتغير x نقوم بالتحويل معادلة معينةونحصل على: لنعود إلى المتغير x:
المعادلات اللوغاريتمية وأنواعها وطرق حلها أنواع وطرق حل المعادلات اللوغاريتمية. 5) المعادلات اللوغاريتمية ذات المتغير في الأساس وتحت إشارة اللوغاريتم. مثال رقم 1 الجواب: الحل: في المدى الموجود للقيم المسموح بها للمتغير x نحول المعادلة ونحصل على: مع مراعاة مدى القيم المسموح بها للمتغير x نحصل على:
المعادلات اللوغاريتمية وأنواعها وطرق حلها أنواع وطرق حل المعادلات اللوغاريتمية. 5) المعادلات اللوغاريتمية ذات المتغير في الأساس وتحت إشارة اللوغاريتم. مثال رقم 2 الجواب: الحل: في المدى الموجود للقيم المسموح بها للمتغير x المعادلة تعادل المجموعة: مع الأخذ بعين الاعتبار مدى القيم المسموح بها للمتغير x نحصل على: 5؛ 6.
المعادلات اللوغاريتمية وأنواعها وطرق حلها
- ضمان التكرار والتعميم وتنظيم المواد المتعلقة بالموضوع؛
- تهيئة الظروف للتحكم والتحكم الذاتي في المعرفة والمهارات المكتسبة ؛
- تعزيز تكوين مهارات تطبيق التقنيات: المقارنة، التعميم، تسليط الضوء على الشيء الرئيسي، نقل المعرفة إلى وضع جديد، تطوير النظرة الرياضية؛
- تهيئة الظروف لتنمية الاهتمام المعرفي لدى الطلاب ؛
- لتنمية المسؤولية عن جودة ونتيجة العمل المنجز في الدرس والنشاط الرياضي والقدرة على العمل في مجموعات والثقافة العامة.
- مراجعة المواد النظرية. انتبه بشكل خاص إلى ODZ للدالة اللوغاريتمية.
- تنظيم طرق حل المعادلات اللوغاريتمية.
- إجراء تشخيص المعرفة.
نوع الدرس: درس التعميم وتنظيم المعرفة.
شكل الدرس: ورشة عمل
المعدات: الكتب المدرسية، المواد التعليمية، بطاقات فرديةللعمل المستقل، وأوراق تسجيل المعرفة، وجهاز عرض الوسائط.
خلال الفصول الدراسية
1. اللحظة التنظيمية
يتم تعريف الطلاب بموضوع الدرس وأهدافه، ويتم التأكيد على أهمية تكرار هذا الموضوع للتحضير لامتحان الدولة الموحدة.
2. التحقق من الواجبات المنزلية
3. تحديث المعرفة السابقة
يعمل الطلاب شفهيًا على التمارين المعروضة على الشاشة باستخدام جهاز العرض.
احسب
1 خيار 2)
الخيار 2 2)
3)
5)
4. تكوين المهارات والقدرات.
العمل في مجموعات يليه الاختبار.
1) حل المعادلات اللوغاريتمية عن طريق تعريف اللوغاريتم.
إجابة:إجابة: 256
2) المعادلات التي تم حلها عن طريق التقوية.
أولا، تحتاج إلى حل معادلة النظام، وبناء على عدم المساواة في النظام، يتم تحديد الجذور.
إجابة: 3
إجابة: 3,5المعادلات التي تم حلها عن طريق الاستبدال.
إجابة:
هذه المعادلة تعادل المعادلة
فليكن بعد ذلك
إجابة:
المعادلات التي تم حلها باللوغاريتم.
= هكذا إجابة: 0,1; 10..
.
أودز: س. لنأخذ اللوغاريتمات لكلا الجانبين للأساس 10.
أين
الجواب: 1؛ 4.
معادلات النموذج
هذه المعادلة تعادل المعادلة ل
.
يتم تحديد DZ من قبل النظام
يتم تحديد DZ من قبل النظام
إجابة: ( (0;)

حل المعادلات باستخدام خصائص مختلفة من اللوغاريتمات.
بتطبيق الصيغة نحصل على
باستبدال قيم x هذه في المعادلة الأصلية، نرى أن هذا هو جذر المعادلة، و0.1 ليس جذر المعادلة.
إجابة:
تلك المعادلات التي سببت صعوبات للطلاب يتم حلها على السبورة من قبل الطلاب الذين أكملوها.
5. دقيقة التربية البدنية
شبكوا أيديهم في «قفل»، ومدواها أمامهم، ورفعوها ومدّوها جيدًا. يقول الأطباء أنه في هذه اللحظة يتم إطلاق "إنزيم السعادة".
6. العمل المستقل
(التمرير على الشاشة والبطاقات الخاصة بكل طالب). يُطلب من الطلاب تقييم قدراتهم واختيار مستوى المهمة A أو B أو C.
بعد الانتهاء من العمل، يقدمه الطلاب للاختبار. يتم عرض الإجابات والحل القصير على الشاشة. يتم تشجيع الطلاب على فحص وتقييم عملهم من خلال تعيين علامة للعمل المستقل.
6. الواجبات المنزلية
كرر ص.6.2، 6.3. د.م. ج – 21 رقم 2 (ب، ج)، رقم 3 (د، هـ) الخياران 3 و 4.
7. ملخص الدرس
لذلك، قمنا اليوم بحل المعادلات اللوغاريتمية. الآن دعونا نلخص الطرق التي استخدمناها لحل المعادلات:
- باستخدام تعريف اللوغاريتم،
- باستخدام الهوية اللوغاريتمية الأساسية،
- باستخدام طريقة التقوية،
- إدخال متغير جديد،
- الانتقال من معادلة ذات أسس مختلفة إلى أساس واحد،
- باستخدام خصائص اللوغاريتم.
إعطاء علامات بناءً على رقم "+" في الدفتر للحل الموجود على السبورة وعلى البطاقات. تحديد أداء الطالب.
لقد وصل درسنا إلى نهايته. هل حققنا أهدافنا؟
الوقت يمر دون أن يلاحظه أحد، اليوم أنتم طلاب الصف العاشر، وغدا أنتم خريجون بالفعل. عند التحضير للامتحان، لا تعتقد أبدًا أنك لن تتمكن من التعامل مع المهمة، بل على العكس من ذلك، ارسم لنفسك صورة للنجاح ومن ثم ستنجح بالتأكيد!
الأدب:
- نيكولسكي إس إم، بوتابوف إم كيه، ريشتنيكوف إن إن، شيفكين إيه في.. الجبر وبداية التحليل الرياضي. الصف 10. البرنامج التعليمي ل المؤسسات التعليمية: المستويات الأساسية والشخصية. – م، 2009
- بوتابوف م.ك.، شيفكين أ.ف.. الجبر وبداية التحليل الرياضي. المواد التعليمية للصف العاشر. – م، 2009.
- شيبيليفا يو.في.. الجبر وبداية التحليل الرياضي. الموضوعية و الاختبارات النهائيةللصف العاشر. – م، 2009.
- ليسينكو ف.. امتحان الدولة الموحد للرياضيات 2009. الفيلق. – م، 2009.
- كلوفو أ.ج.. امتحان الدولة الموحد للرياضيات-2010 - ماجستير، 2010.
- إيرينا تي إم. الجبر. المعادلات اللوغاريتمية والمتباينات - م، 2004.
عند حل المعادلات اللوغاريتمية والمتباينات، استخدم خصائص اللوغاريتمات وكذلك خصائص الدالة اللوغاريتمية
ص = تسجيل س، أ > 0، أ 1:
1) مجال التعريف: x > 0;
2) المدى: ص ر ;
3) سجل أ × 1 = سجل أ × 2 × 1 = × 2 ؛
4) بالنسبة إلى a>1، تزداد الدالة y=log a x، بالنسبة إلى 0< a < 1 функция y=log a x убывает при всех x >0، أي.
a >1 و سجل a x 1 > سجل a x 2 x 1 >x 2 ,
0 سجل أ × 2 × 1< x 2 ;
عند الانتقال من المعادلات اللوغاريتمية (المتباينات) إلى المعادلات (المتباينات) التي لا تحتوي على علامة اللوغاريتم، ينبغي للمرء أن يأخذ في الاعتبار نطاق القيم المسموح بها (APV) للمعادلة الأصلية (المتباينة).
مسائل واختبارات في موضوع "المعادلات اللوغاريتمية"
- المعادلات اللوغاريتمية
الدروس: 4 واجبات: 25 اختبار: 1
- أنظمة المعادلات الأسية واللوغاريتمية - مظاهرة و وظيفة لوغاريتميةالصف 11
الدروس: 1 الواجبات: 15 الاختبارات: 1
- §5.1. حل المعادلات اللوغاريتمية
الدروس: 1 المهام: 38
- §7 المعادلات والمتباينات الأسية واللوغاريتمية - القسم 5. الدوال الأسية واللوغاريتمية، الصف 10
الدروس: 1 المهام: 17
- معادلة المعادلات - المعادلات والمتباينات الصف الحادي عشر
الدروس: 2 الواجبات: 9 الاختبارات: 1
عند حل المعادلات اللوغاريتمية، يكون من الضروري في كثير من الحالات استخدام خصائص لوغاريتم حاصل الضرب أو الحاصل أو الدرجة. في الحالات التي تحتوي فيها معادلة لوغاريتمية واحدة على لوغاريتمات ذات أسس مختلفة، يتم استخدامها خصائص محددةممكن فقط بعد الانتقال إلى اللوغاريتمات ذات القواعد المتساوية.
بالإضافة إلى ذلك، يجب أن يبدأ حل المعادلة اللوغاريتمية بإيجاد نطاق القيم المسموح بها (O.D.Z.) معادلة معينة، لأن أثناء عملية الحل، قد تظهر جذور غريبة. عند الانتهاء من الحل، لا تنس التحقق من الجذور التي تم العثور عليها للتأكد من انتمائها إلى O.D.Z.
يمكنك حل المعادلات اللوغاريتمية دون استخدام O.D.Z. في هذه الحالة، يعد التحقق عنصرًا إلزاميًا في الحل.
أمثلة.
حل المعادلات:
أ) سجل 3 (5س – 1) = 2.
حل:
ODZ: 5x – 1 > 0؛ س> 1/5.
سجل 3 (5س-1) = 2،
سجل 3 (5س - 1) = سجل 3 3 2،
5س - 1 =9،
س = 2.
1 خيار
- 1. أوجد حاصل ضرب جذور المعادلة: log π (x 2 + 0.1) = 0
1) - 1,21; 2) - 0,9; 3) 0,81; 4) 1,21.
- 2. أشر إلى الفترة التي تنتمي إليها جذور المعادلة: log 0.5 (x - 9) = 1 + log 0.5 5
1) (11; 13); 2) (9; 11); 3) (-12; -10); 4) [ -10; -9 ].
- 3. أشر إلى الفاصل الزمني الذي ينتمي إليه جذر المعادلة log 4 (4 - x) + log 4 x = 1
1) (-3; -1); 2) (0; 2); 3) [ 2; 3 ]; 4) [ 4; 8 ].
- 4. أوجد مجموع جذور المعادلة log √3 x 2 = log √3 (9x - 20)
1) - 13; 2) - 5; 3) 5; 4) 9.
- 5. أشر إلى الفترة التي ينتمي إليها جذر سجل المعادلة 1/3 (2س - 3) 5 = 15
1) [ -3; 2); 2) [ 2; 5); 3) [ 5; 8); 4) [ 8; 11).
- 6. . أشر إلى الفاصل الزمني الذي ينتمي إليه جذر المعادلة lg (x + 7) - log (x + 5) = 1
1) (-∞; -7); 2) (-7; -5); 3) (-5; -3); 4) (0; +∞).
- 7. حل سجل المتراجحة 3 (4 - 2x) >= 1
1) (-∞; 0,5 ]; 2) (-∞; 2 ]; 3) [ 2; + ∞); 4) [ 0,5; + ∞).
- 8. حل سجل عدم المساواة π (3x + 2)<= log π (х - 1)
1) (-2/3؛ + ∞)؛ 2) (-∞؛ - 2/3 ]؛ 3) [ -1.5؛ - 2/3]؛ 4) لا توجد حلول.
- 9. حل سجل المتراجحة 1/9 (6 - 0.3x) > -1
1) (-10; +∞); 2) (-∞; -10); 3) (-10; 20); 4) (-0,1; 20).
- 10. أوجد عدد الحلول السالبة للمتراجحة lg (x + 5)<= 2 - lg 2
15؛ 2) 4؛ 3) 10؛ 4) لا شيء
الخيار 2
- 1. أوجد حاصل ضرب جذور المعادلة: lg (x 2 + 1) = 1
1) - 99; 2) - 9; 3) 33; 4) -33.
- 2. أشر إلى الفترة التي ينتمي إليها جذر المعادلة log 4 (x - 5) = log 25 5
1) (-4; -2); 2) (6; 8); 3) (3; 6); 4) [ -8; -6 ].
- 3. أشر إلى الفاصل الزمني الذي ينتمي إليه جذر المعادلة log 0.4 (5 - 2x) - log 0.4 2 = 1
1) (-∞; -2); 2) [ -2; 1 ]; 3) [ 1; 2 ]; 4) (2; +∞).
- 4. أوجد مجموع جذور سجل المعادلة (4س - 3) = 2 سجل س
1) - 2; 2) 4; 3) -4; 4) 2.
- 5. أشر إلى الفاصل الزمني الذي ينتمي إليه جذر المعادلة سجل 2 (64x²) = 6
1) [ 5; 7]; 2) [ 9; 11 ]; 3) (3; 5); 4) [ 1; 3 ].
- 6. . حدد الفترة التي ينتمي إليها جذر المعادلة log 2 (x - 1)³ = 6 log 2 3
1) [ 0; 5); 2) [ 5; 8); 3) [ 8; 11); 4) [ 11; 14).
- 7. حل سجل عدم المساواة 0.8 (0.25 - 0.1x) > -1
1) (-∞; 2,5); 2) (-10; 2,5); 3) (2,5; + ∞); 4) (-10; + ∞).
- 8. حل سجل المتراجحة 1.25 (0.8x + 0.4)<= - l
1) (-0,5; + ∞); 2) (-∞; - 0,5 ]; 3) (-0,5; 0,5 ]; 4) (-2; 2 ] .
- 9. حل سجل المتباينة 10/3 (1 - 1.4x)< -1
1) (0,5; +∞); 2) (-∞; 0,5); 3) (1,4; 2); 4) (0,5; 5/7).
- 10. أوجد عدد الحلول الصحيحة لسجل المتراجحة 0.5 (x - 2) >= - 2
15؛ 2) 4؛ 3) كثيرة بلا حدود؛ 4) لا شيء.
مفتاح
| أ1 | أ2 | أ3 | A4 | أ5 | أ6 | أ7 | ب1 | ب2 | ج1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 خيار | 2 | 1 | 3 | 4 | 1 | 3 | 1 | 4 | 3 | 2 |
| الخيار 2 | 2 | 2 | 4 | 2 | 4 | 3 | 2 | 3 | 4 | 2 |