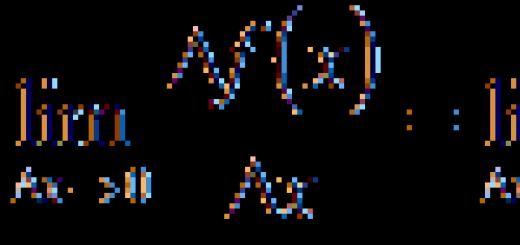Complex numbers are an extension of the set of real numbers, usually denoted by . Any complex number can be represented as a formal sum , where and are real numbers and is the imaginary unit.
Writing a complex number in the form , , is called the algebraic form of a complex number.
Properties of complex numbers. Geometric interpretation of a complex number.
Actions on complex numbers given in algebraic form:
Let's consider the rules by which arithmetic operations are performed on complex numbers.
If two complex numbers α = a + bi and β = c + di are given, then
α + β = (a + bi) + (c + di) = (a + c) + (b + d)i,
α – β = (a + bi) – (c + di) = (a – c) + (b – d)i. (eleven)
This follows from the definition of the operations of addition and subtraction of two ordered pairs of real numbers (see formulas (1) and (3)). We have received the rules for adding and subtracting complex numbers: in order to add two complex numbers, we must separately add their real parts and, accordingly, their imaginary parts; In order to subtract another from one complex number, it is necessary to subtract their real and imaginary parts, respectively.
The number – α = – a – bi is called the opposite of the number α = a + bi. The sum of these two numbers is zero: - α + α = (- a - bi) + (a + bi) = (-a + a) + (-b + b)i = 0.
To obtain the rule for multiplying complex numbers, we use formula (6), i.e., the fact that i2 = -1. Taking this relation into account, we find (a + bi)(c + di) = ac + adi + bci + bdi2 = ac + (ad + bc)i – bd, i.e.
(a + bi)(c + di) = (ac - bd) + (ad + bc)i . (12)
This formula corresponds to formula (2), which determined the multiplication of ordered pairs of real numbers.
Note that the sum and product of two complex conjugate numbers are real numbers. Indeed, if α = a + bi, = a – bi, then α = (a + bi)(a - bi) = a2 – i2b2 = a2 + b2 , α + = (a + bi) + (a - bi) = ( a + a) + (b - b)i= 2a, i.e.
α + = 2a, α = a2 + b2. (13)
When dividing two complex numbers in algebraic form, one should expect that the quotient is also expressed by a number of the same type, i.e. α/β = u + vi, where u, v R. Let us derive the rule for dividing complex numbers. Let the numbers α = a + bi, β = c + di be given, and β ≠ 0, i.e. c2 + d2 ≠ 0. The last inequality means that c and d do not simultaneously vanish (the case is excluded when c = 0, d = 0). Applying formula (12) and the second of equalities (13), we find:
Therefore, the quotient of two complex numbers is determined by the formula:
corresponding to formula (4).
Using the resulting formula for the number β = c + di, you can find its inverse number β-1 = 1/β. Assuming a = 1, b = 0 in formula (14), we obtain
This formula determines the inverse of a given complex number other than zero; this number is also complex.
For example: (3 + 7i) + (4 + 2i) = 7 + 9i;
(6 + 5i) – (3 + 8i) = 3 – 3i;
(5 – 4i)(8 – 9i) = 4 – 77i;
Operations on complex numbers in algebraic form.
55. Argument of a complex number. Trigonometric form of writing a complex number (derivation).
Arg.com.numbers. – between the positive direction of the real X axis and the vector representing the given number.
Trigon formula. Numbers: ,
DEFINITION
The algebraic form of a complex number is to write the complex number \(\z\) in the form \(\z=x+i y\), where \(\x\) and \(\y\) are real numbers, \(\i\ ) - imaginary unit satisfying the relation \(\i^(2)=-1\)
The number \(\ x \) is called the real part of the complex number \(\ z \) and is denoted by \(\ x=\operatorname(Re) z \)
The number \(\y\) is called the imaginary part of the complex number \(\z\) and is denoted by \(\y=\operatorname(Im) z\)
For example:
The complex number \(\ z=3-2 i \) and its adjoint number \(\ \overline(z)=3+2 i \) are written in algebraic form.
The imaginary quantity \(\ z=5 i \) is written in algebraic form.
In addition, depending on the problem you are solving, you can convert a complex number to a trigonometric or exponential number.
Write the number \(\z=\frac(7-i)(4)+13\) in algebraic form, find its real and imaginary parts, as well as its conjugate number.
Using the term division of fractions and the rule of adding fractions, we get:
\(\z=\frac(7-i)(4)+13=\frac(7)(4)+13-\frac(i)(4)=\frac(59)(4)-\frac( 1)(4)i\)
Therefore, the real part of the complex number \(\ z=\frac(5 g)(4)-\frac(1)(4) i \) is the number \(\ x=\operatorname(Re) z=\frac(59) (4) \) , the imaginary part is the number \(\ y=\operatorname(Im) z=-\frac(1)(4) \)
Conjugate number: \(\ \overline(z)=\frac(59)(4)+\frac(1)(4) i \)
\(\ z=\frac(59)(4)-\frac(1)(4) i \), \(\ \operatorname(Re) z=\frac(59)(4) \), \(\ \operatorname(Im) z=-\frac(1)(4) \), \(\ \overline(z)=\frac(59)(4)+\frac(1)(4) i \)
Actions of complex numbers in algebraic form comparison
Two complex numbers \(\ z_(1)=x_(1)+i y_(1) \) are said to be equal if \(\ x_(1)=x_(2) \), \(\ y_(1)= y_(2) \) i.e. Their real and imaginary parts are equal.
Determine for which x and y the two complex numbers \(\ z_(1)=13+y i \) and \(\ z_(2)=x+5 i \) are equal.
By definition, two complex numbers are equal if their real and imaginary parts are equal, i.e. \(\x=13\), \(\y=5\).
addition
Adding complex numbers \(\z_(1)=x_(1)+i y_(1)\) is done by directly summing the real and imaginary parts:
\(\ z_(1)+z_(2)=x_(1)+i y_(1)+x_(2)+i y_(2)=\left(x_(1)+x_(2)\right) +i\left(y_(1)+y_(2)\right) \)
Find the sum of complex numbers \(\ z_(1)=-7+5 i \), \(\ z_(2)=13-4 i \)
The real part of a complex number \(\ z_(1)=-7+5 i \) is the number \(\ x_(1)=\operatorname(Re) z_(1)=-7 \) , the imaginary part is the number \( \ y_(1)=\mathrm(Im) \), \(\ z_(1)=5 \) . The real and imaginary parts of the complex number \(\ z_(2)=13-4 i \) are equal to \(\ x_(2)=\operatorname(Re) z_(2)=13 \) and \(\ y_(2) respectively )=\operatorname(Im) z_(2)=-4 \) .
Therefore, the sum of complex numbers is:
\(\z_(1)+z_(2)=\left(x_(1)+x_(2)\right)+i\left(y_(1)+y_(2)\right)=(-7+ 13)+i(5-4)=6+i \)
\(\ z_(1)+z_(2)=6+i \)
Read more about adding complex numbers in a separate article: Adding complex numbers.
Subtraction
Subtraction of complex numbers \(\z_(1)=x_(1)+i y_(1)\) and \(\z_(2)=x_(2)+i y_(2)\) is performed by directly subtracting the real and imaginary parts:
\(\ z_(1)-z_(2)=x_(1)+i y_(1)-\left(x_(2)+i y_(2)\right)=x_(1)-x_(2) +\left(i y_(1)-i y_(2)\right)=\left(x_(1)-x_(2)\right)+i\left(y_(1)-y_(2)\right ) \)
find the difference of complex numbers \(\ z_(1)=17-35 i \), \(\ z_(2)=15+5 i \)
Find the real and imaginary parts of complex numbers \(\ z_(1)=17-35 i \), \(\ z_(2)=15+5 i \) :
\(\ x_(1)=\operatorname(Re) z_(1)=17, x_(2)=\operatorname(Re) z_(2)=15 \)
\(\ y_(1)=\operatorname(Im) z_(1)=-35, y_(2)=\operatorname(Im) z_(2)=5 \)
Therefore, the difference of complex numbers is:
\(\ z_(1)-z_(2)=\left(x_(1)-x_(2)\right)+i\left(y_(1)-y_(2)\right)=(17-15 )+i(-35-5)=2-40 i \)
\(\ z_(1)-z_(2)=2-40 i \) multiplication
Multiplication of complex numbers \(\ z_(1)=x_(1)+i y_(1) \) and \(\ z_(2)=x_(2)+i y_(2) \) is performed by directly creating numbers in algebraic form taking into account the property of the imaginary unit \(\i^(2)=-1\) :
\(\ z_(1) \cdot z_(2)=\left(x_(1)+i y_(1)\right) \cdot\left(x_(2)+i y_(2)\right)=x_ (1) \cdot x_(2)+i^(2) \cdot y_(1) \cdot y_(2)+\left(x_(1) \cdot i y_(2)+x_(2) \cdot i y_(1)\right)=\)
\(\ =\left(x_(1) \cdot x_(2)-y_(1) \cdot y_(2)\right)+i\left(x_(1) \cdot y_(2)+x_(2 ) \cdot y_(1)\right) \)
Find the product of complex numbers \(\ z_(1)=1-5 i \)
Complex of complex numbers:
\(\ z_(1) \cdot z_(2)=\left(x_(1) \cdot x_(2)-y_(1) \cdot y_(2)\right)+i\left(x_(1) \cdot y_(2)+x_(2) \cdot y_(1)\right)=(1 \cdot 5-(-5) \cdot 2)+i(1 \cdot 2+(-5) \cdot 5 )=15-23 i\)
\(\ z_(1) \cdot z_(2)=15-23 i \) division
The factor of complex numbers \(\z_(1)=x_(1)+i y_(1)\) and \(\z_(2)=x_(2)+i y_(2)\) is determined by multiplying the numerator and denominator to the conjugate number with the denominator:
\(\ \frac(z_(1))(z_(2))=\frac(x_(1)+i y_(1))(x_(2)+i y_(2))=\frac(\left (x_(1)+i y_(1)\right)\left(x_(2)-i y_(2)\right))(\left(x_(2)+i y_(2)\right)\left (x_(2)-i y_(2)\right))=\frac(x_(1) \cdot x_(2)+y_(1) \cdot y_(2))(x_(2)^(2) +y_(2)^(2))+i \frac(x_(2) \cdot y_(1)-x_(1) \cdot y_(2))(x_(2)^(2)+y_(2 )^(2)) \)
To divide the number 1 by the complex number \(\z=1+2i\).
Since the imaginary part of the real number 1 is zero, the factor is:
\(\ \frac(1)(1+2 i)=\frac(1 \cdot 1)(1^(2)+2^(2))-i \frac(1 \cdot 2)(1^( 2)+2^(2))=\frac(1)(5)-i \frac(2)(5)\)
\(\ \frac(1)(1+2 i)=\frac(1)(5)-i \frac(2)(5) \)
Let us recall the necessary information about complex numbers.
Complex number is an expression of the form a + bi, Where a, b are real numbers, and i- so-called imaginary unit, a symbol whose square is equal to –1, that is i 2 = –1. Number a called real part, and the number b - imaginary part complex number z = a + bi. If b= 0, then instead a + 0i they simply write a. It can be seen that the real numbers are special case complex numbers.
Arithmetic operations on complex numbers are the same as on real numbers: they can be added, subtracted, multiplied and divided by each other. Addition and subtraction occur according to the rule ( a + bi) ± ( c + di) = (a ± c) + (b ± d)i, and multiplication follows the rule ( a + bi) · ( c + di) = (ac – bd) + (ad + bc)i(here it is used that i 2 = –1). Number = a – bi called complex conjugate To z = a + bi. Equality z · = a 2 + b 2 allows you to understand how to divide one complex number by another (non-zero) complex number:
(For example, 
.)
Complex numbers have a convenient and visual geometric representation: number z = a + bi can be represented by a vector with coordinates ( a; b) on the Cartesian plane (or, which is almost the same thing, a point - the end of a vector with these coordinates). In this case, the sum of two complex numbers is depicted as the sum of the corresponding vectors (which can be found using the parallelogram rule). According to the Pythagorean theorem, the length of the vector with coordinates ( a; b) is equal to . This quantity is called module complex number z = a + bi and is denoted by | z|. The angle that this vector makes with the positive direction of the x-axis (counted counterclockwise) is called argument complex number z and is denoted by Arg z. The argument is not uniquely defined, but only up to the addition of a multiple of 2 π
radians (or 360°, if counted in degrees) - after all, it is clear that a rotation by such an angle around the origin will not change the vector. But if the vector of length r forms an angle φ
with the positive direction of the x-axis, then its coordinates are equal to ( r cos φ
; r sin φ
). From here it turns out trigonometric notation complex number: z = |z| · (cos(Arg z) + i sin(Arg z)). It is often convenient to write complex numbers in this form, because it greatly simplifies the calculations. Multiplying complex numbers in trigonometric form is very simple: z 1 · z 2 = |z 1 | · | z 2 | · (cos(Arg z 1 + Arg z 2) + i sin(Arg z 1 + Arg z 2)) (when multiplying two complex numbers, their modules are multiplied and their arguments are added). From here follow Moivre's formulas: z n = |z|n· (cos( n· (Arg z)) + i sin( n· (Arg z))). Using these formulas, it is easy to learn how to extract roots of any degree from complex numbers. Root nth degree from number z- this is a complex number w, What w n = z. It's clear that 
, And where k can take any value from the set (0, 1, ..., n- 1). This means that there is always exactly n roots n th degree of a complex number (on the plane they are located at the vertices of the regular n-gon).
Consider a quadratic equation.
Let's determine its roots.
There is no real number whose square is -1. But if we define the operator with a formula i as an imaginary unit, then the solution to this equation can be written as 
. Wherein 
And 
- complex numbers in which -1 is the real part, 2 or in the second case -2 is the imaginary part. The imaginary part is also a real number. The imaginary part multiplied by the imaginary unit means already imaginary number.
In general, a complex number has the form
z = x + iy ,
Where x, y– real numbers, – imaginary unit. In a number of applied sciences, for example, in electrical engineering, electronics, signal theory, the imaginary unit is denoted by j. Real numbers x = Re(z) And y =Im(z) are called real and imaginary parts numbers z. The expression is called algebraic form writing a complex number.
Any real number is a special case of a complex number in the form 
. An imaginary number is also a special case of a complex number 
.
Definition of the set of complex numbers C
This expression reads as follows: set WITH, consisting of elements such that x And y belong to the set of real numbers R and is an imaginary unit. Note that, etc.
Two complex numbers 
And 
are equal if and only if their real and imaginary parts are equal, i.e. And .
Complex numbers and functions are widely used in science and technology, in particular in mechanics, analysis and calculation of alternating current circuits, analog electronics, theory and signal processing, theory automatic control and other applied sciences.
- Complex number arithmetic
The addition of two complex numbers consists of adding their real and imaginary parts, i.e.
Accordingly, the difference of two complex numbers
Complex number 
called comprehensively conjugate number z =x+iy.
Complex conjugate numbers z and z * differ in the signs of the imaginary part. It's obvious that
.
Any equality between complex expressions remains valid if in this equality everywhere i replaced by -
i, i.e. go to the equality of conjugate numbers. Numbers i And –
i are algebraically indistinguishable, since 
.
The product (multiplication) of two complex numbers can be calculated as follows:
Division of two complex numbers:
Example:
- Complex plane
A complex number can be represented graphically in a rectangular coordinate system. Let us define a rectangular coordinate system in the plane (x, y).
On axis Ox we will place the real parts x, it is called real (real) axis, on the axis Oy–imaginary parts y complex numbers. It's called imaginary axis. In this case, each complex number corresponds to a certain point on the plane, and such a plane is called complex plane. Point A the complex plane will correspond to the vector OA.
Number x called abscissa complex number, number y – ordinate.
A pair of complex conjugate numbers is represented by points located symmetrically about the real axis.
 |
If on the plane we set polar coordinate system, then every complex number z determined by polar coordinates. Wherein module numbers 
is the polar radius of the point, and the angle 
- its polar angle or complex number argument z.
Modulus of a complex number 
always non-negative. The argument of a complex number is not uniquely determined. The main value of the argument must satisfy the condition 
. Each point of the complex plane also corresponds general meaning argument. Arguments that differ by a multiple of 2π are considered equal. The number zero argument is undefined.
The main value of the argument is determined by the expressions:
It's obvious that
Wherein
, 
.
Complex number representation z as
called trigonometric form complex number.
Example.
- Exponential form of complex numbers
Decomposition in Maclaurin series for real argument functions 
has the form:
For an exponential function with a complex argument z the decomposition is similar
.
The Maclaurin series expansion for the exponential function of the imaginary argument can be represented as
The resulting identity is called Euler's formula.
For a negative argument it has the form
By combining these expressions, you can define the following expressions for sine and cosine
.
Using Euler's formula, from the trigonometric form of representing complex numbers
available indicative(exponential, polar) form of a complex number, i.e. its representation in the form
,
Where 
- polar coordinates of a point with rectangular coordinates ( x,y).
The conjugate of a complex number is written in exponential form as follows.
For exponential form it is easy to determine following formulas multiplying and dividing complex numbers
That is, in exponential form, the product and division of complex numbers is simpler than in algebraic form. When multiplying, the modules of the factors are multiplied, and the arguments are added. This rule applies to any number of factors. In particular, when multiplying a complex number z on i vector z rotates counterclockwise 90
In division, the modulus of the numerator is divided by the modulus of the denominator, and the argument of the denominator is subtracted from the argument of the numerator.
Using the exponential form of complex numbers, we can obtain expressions for the well-known trigonometric identities. For example, from the identity
using Euler's formula we can write
Equating the real and imaginary parts in this expression, we obtain expressions for the cosine and sine of the sum of angles
- Powers, roots and logarithms of complex numbers
Raising a complex number to natural degree n produced according to the formula
Example. Let's calculate 
.
Let's imagine a number in trigonometric form
’
Applying the exponentiation formula, we get
By putting the value in the expression r= 1, we get the so-called Moivre's formula, with which you can determine expressions for the sines and cosines of multiple angles.
Root n-th power of a complex number z It has n different values determined by the expression
Example. Let's find it.
To do this, we express the complex number () in trigonometric form
.
Using the formula for calculating the root of a complex number, we get
Logarithm of a complex number z- this is the number w, for which . Natural logarithm complex number has infinite set values and is calculated using the formula
Consists of a real (cosine) and imaginary (sine) part. This voltage can be represented as a vector of length Um , initial phase(angle) rotating with angular velocity ω .
Moreover, if complex functions are added, then their real and imaginary parts are added. If a complex function is multiplied by a constant or real function, then its real and imaginary parts are multiplied by the same factor. Differentiation/integration of such a complex function comes down to differentiation/integration of the real and imaginary parts.
For example, differentiating the complex stress expression
is to multiply it by iω is the real part of the function f(z), and 
– imaginary part of the function. Examples: 
.
Meaning z is represented by a point in the complex z plane, and the corresponding value w- a point in the complex plane w. When displayed w = f(z) plane lines z transform into plane lines w, figures of one plane into figures of another, but the shapes of the lines or figures can change significantly.
Lesson plan.
1. Organizational moment.
2. Presentation of the material.
3. Homework.
4. Summing up the lesson.
During the classes
I. Organizational moment.
II. Presentation of the material.
Motivation.
The expansion of the set of real numbers consists of adding new numbers (imaginary) to the real numbers. The introduction of these numbers is due to the impossibility of extracting the root of a negative number in the set of real numbers.
Introduction to the concept of a complex number.
Imaginary numbers, with which we complement real numbers, are written in the form bi, Where i is an imaginary unit, and i 2 = - 1.
Based on this, we obtain the following definition of a complex number.
Definition. A complex number is an expression of the form a+bi, Where a And b- real numbers. In this case, the following conditions are met:
a) Two complex numbers a 1 + b 1 i And a 2 + b 2 i equal if and only if a 1 =a 2, b 1 =b 2.
b) The addition of complex numbers is determined by the rule:
(a 1 + b 1 i) + (a 2 + b 2 i) = (a 1 + a 2) + (b 1 + b 2) i.
c) Multiplication of complex numbers is determined by the rule:
(a 1 + b 1 i) (a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (a 1 b 2 - a 2 b 1) i.
Algebraic form of a complex number.
Writing a complex number in the form a+bi is called the algebraic form of a complex number, where A– real part, bi is the imaginary part, and b– real number.
Complex number a+bi is considered equal to zero if its real and imaginary parts are equal to zero: a = b = 0
Complex number a+bi at b = 0 considered to be the same as a real number a: a + 0i = a.
Complex number a+bi at a = 0 is called purely imaginary and is denoted bi: 0 + bi = bi.
Two complex numbers z = a + bi And = a – bi, differing only in the sign of the imaginary part, are called conjugate.
Operations on complex numbers in algebraic form.
You can perform the following operations on complex numbers in algebraic form.
1) Addition.
Definition. Sum of complex numbers z 1 = a 1 + b 1 i And z 2 = a 2 + b 2 i is called a complex number z, the real part of which is equal to the sum of the real parts z 1 And z 2, and the imaginary part is the sum of the imaginary parts of numbers z 1 And z 2, that is z = (a 1 + a 2) + (b 1 + b 2)i.
Numbers z 1 And z 2 are called terms.
Addition of complex numbers has the following properties:
1º. Commutativity: z 1 + z 2 = z 2 + z 1.
2º. Associativity: (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3).
3º. Complex number –a –bi called the opposite of a complex number z = a + bi. Complex number, opposite of complex number z, denoted -z. Sum of complex numbers z And -z equal to zero: z + (-z) = 0
Example 1: Perform addition (3 – i) + (-1 + 2i).
(3 – i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.
2) Subtraction.
Definition. Subtract from a complex number z 1 complex number z 2 z, What z + z 2 = z 1.
Theorem. The difference between complex numbers exists and is unique.
Example 2: Perform a subtraction (4 – 2i) - (-3 + 2i).
(4 – 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) i = 7 – 4i.
3) Multiplication.
Definition. Product of complex numbers z 1 =a 1 +b 1 i And z 2 =a 2 +b 2 i is called a complex number z, defined by the equality: z = (a 1 a 2 – b 1 b 2) + (a 1 b 2 + a 2 b 1)i.
Numbers z 1 And z 2 are called factors.
Multiplication of complex numbers has the following properties:
1º. Commutativity: z 1 z 2 = z 2 z 1.
2º. Associativity: (z 1 z 2)z 3 = z 1 (z 2 z 3)
3º. Distributivity of multiplication relative to addition:
(z 1 + z 2) z 3 = z 1 z 3 + z 2 z 3.
4º. z = (a + bi)(a – bi) = a 2 + b 2- real number.
In practice, multiplication of complex numbers is carried out according to the rule of multiplying a sum by a sum and separating the real and imaginary parts.
In the following example, we will consider multiplying complex numbers in two ways: by rule and by multiplying sum by sum.
Example 3: Do the multiplication (2 + 3i) (5 – 7i).
1 way. (2 + 3i) (5 – 7i) = (2× 5 – 3× (- 7)) + (2× (- 7) + 3× 5)i = = (10 + 21) + (- 14 + 15 )i = 31 + i.
Method 2. (2 + 3i) (5 – 7i) = 2× 5 + 2× (- 7i) + 3i× 5 + 3i× (- 7i) = = 10 – 14i + 15i + 21 = 31 + i.
4) Division.
Definition. Divide a complex number z 1 to a complex number z 2, means to find such a complex number z, What z · z 2 = z 1.
Theorem. The quotient of complex numbers exists and is unique if z 2 ≠ 0 + 0i.
In practice, the quotient of complex numbers is found by multiplying the numerator and denominator by the conjugate of the denominator.
Let z 1 = a 1 + b 1 i, z 2 = a 2 + b 2 i, Then
.
In the following example, we will perform division using the formula and the rule of multiplication by the number conjugate to the denominator.
Example 4. Find the quotient 
.
5) Raising to a positive whole power.
a) Powers of the imaginary unit.
Taking advantage of equality i 2 = -1, it is easy to define any positive integer power of the imaginary unit. We have:
i 3 = i 2 i = -i,
i 4 = i 2 i 2 = 1,
i 5 = i 4 i = i,
i 6 = i 4 i 2 = -1,
i 7 = i 5 i 2 = -i,
i 8 = i 6 i 2 = 1 etc.
This shows that the degree values i n, Where n– a positive integer, periodically repeated as the indicator increases by 4 .
Therefore, to raise the number i to a positive whole power, we must divide the exponent by 4 and build i to a power whose exponent is equal to the remainder of the division.
Example 5: Calculate: (i 36 + i 17) i 23.
i 36 = (i 4) 9 = 1 9 = 1,
i 17 = i 4 × 4+1 = (i 4) 4 × i = 1 · i = i.
i 23 = i 4 × 5+3 = (i 4) 5 × i 3 = 1 i 3 = - i.
(i 36 + i 17) · i 23 = (1 + i) (- i) = - i + 1= 1 – i.
b) Raising a complex number to a positive integer power is carried out according to the rule for raising a binomial to the corresponding power, since it is a special case of multiplying identical complex factors.
Example 6: Calculate: (4 + 2i) 3
(4 + 2i) 3 = 4 3 + 3× 4 2 × 2i + 3× 4× (2i) 2 + (2i) 3 = 64 + 96i – 48 – 8i = 16 + 88i.
