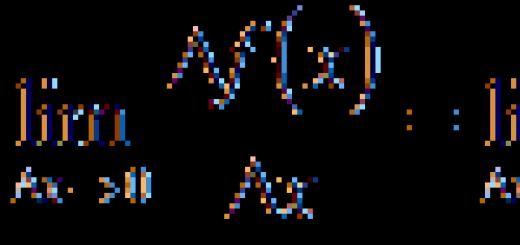The method is applicable for minimizing logical algebra functions of any number of variables.
Let's consider the case of three variables. A Boolean function in DNF can be represented in the form of all kinds of conjunctive terms that can be included in DNF:
where kО(0,1) are coefficients. The method consists in selecting coefficients in such a way that the resulting DNF is minimal.
If we now set all possible values of the variables from 000 to 111, we get 2 n (2 3 =8) equations for determining the coefficients k:
Considering the sets for which the function takes a zero value, determine the coefficients that are equal to 0 and cross them out from the equations whose right side contains 1. Of the remaining coefficients in each equation, one coefficient is equated to one, which determines the conjunction of the lowest rank. The remaining coefficients are equal to 0. So, the unit coefficients k determine the appropriate minimum form.
Example. Minimize a given function
if the values are known: 
;
;
;
;
;
;
;
.
Solution.
After crossing out the zero coefficients we get:
=1;
=1;
=1;
=1.
Let us equate the coefficient to unity 
, corresponding to the conjunction of the lowest rank and turning the last four equations to 1, and in the first equation it is advisable to equate the coefficient to 1 
. The remaining coefficients are set to 0.
Answer: type of minimized function.
It should be noted that the method of indefinite coefficients is effective when the number of variables is small and does not exceed 5-6.
Multidimensional cube
Let's consider a graphical representation of a function in the form of a multidimensional cube. Every peak n-dimensional cube can be put in correspondence with the constituent of the unit.
The subset of marked vertices is a mapping onto n-dimensional cube of a Boolean function from n variables in SDNF.
To display the function from n variables presented in any DNF, it is necessary to establish a correspondence between its miniterms and elements n-dimensional cube.
Miniterm of (n-1)th rank 
can be considered as the result of gluing two miniterms n-th rank, i.e.
=
On n-dimensional cube this corresponds to replacing two vertices that differ only in coordinate values X i, connecting these vertices with an edge (an edge is said to cover the vertices incident to it).
Thus, miniterms ( n The -1)th order corresponds to the edges of an n-dimensional cube.
Similarly, the correspondence of miniterms ( n-2)th order faces n-dimensional cube, each of which covers four vertices (and four edges).
Elements n-dimensional cube, characterized by S measurements are called S-cubes
So vertices are 0-cubes, edges are 1-cubes, faces are 2-cubes, etc.
To summarize, we can say that the miniterm ( n-S) rank in DNF for the function n variables displayed S-a cube, each S-cube covers all those cubes of lower dimension that are connected only to its vertices.
Example. In Fig. given the mapping 
Here are miniterms 
And 
correspond to 1-cubes ( S=3-2=1), and miniterm X 3
displayed to 2-cubes ( S=3-1=2).
So, any DNF is mapped to n-dimensional cube in totality S-cubes that cover all vertices corresponding to the constituent units (0-cube).
Constituents. For variables X 1
,X 2
,…X n expression 
is called the constituent of the unit, and 
- constituent of zero ( 
means either 
, or 
).
This constituent of one (zero) turns into one (zero) only with one corresponding set of variable values, which is obtained if all variables are taken equal to one (zero), and their negations equal to zero (one).
For example: constituent unit 
corresponds to the set (1011), and the constituent is zero 
- set (1001).
Since SD(K)NF is a disjunction (conjunction) of the constituents of one (zero), it can be argued that the Boolean function it represents f(x 1 , x 2 ,…, x n) turns to one (zero) only for sets of variable values x 1 , x 2 ,…, x n, corresponding to these copstitutes. On other sets this function turns to 0 (one).
The opposite statement is also true, on which it is based way of representing any Boolean function specified by the table.
To do this, it is necessary to write disjunctions (conjunctions) of the constituents of one (zero), corresponding to sets of values of variables on which the function takes a value equal to one (zero).
For example, a function given by a table
correspond
The resulting expressions can be converted to another form based on the properties of the algebra of logic.
The converse statement is also true: if some collection S-cubes covers the set of all vertices corresponding to unit values of the function, then the disjunction corresponding to these S-cubes of miniterms is the expression of this function in DNF.
They say that such a collection S-cubes (or their corresponding miniterms) forms a covering of the function. The desire for a minimal form is intuitively understood as the search for such a covering, the number S-of which there would be fewer cubes, and their dimensions S- more. The coverage corresponding to the minimum form is called the minimum coverage.
For example, for the function at=
the coating corresponds to a non-minimum shape:
rice a) at=,
a coating on rice b) at=
, rice c) at=
minimal.
Rice. Function coverage at=:
a) non-minimal; b), c) minimum.
Displaying a function on n-measured clearly and simply with n3. A four-dimensional cube can be depicted as shown in Fig., which shows the function of four variables and its minimum coverage corresponding to the expression at=
Using this method when n>4 requires such complex formations that it loses all its advantages.
MINISTRY OF SCIENCE AND EDUCATION OF THE REPUBLIC OF BASHKORTO STAN
SAOU SPO Bashkir College of Architecture and Civil Engineering
Khaliullin Askhat Adelzyanovich,
mathematics teacher at Bashkirsky
College of Architecture and Civil Engineering
UFA
2014
Introduction ___________________________________________________3
Chapter I. Theoretical aspects of using the method of uncertain coefficients_____________________________________________4
Chapter II. Searches for solutions to problems with polynomials using the method of indefinite coefficients_________________________________7
2.1.Factoring a polynomial_____________________ 7
2.2. Problems with parameters_________________________________ 10
2.3. Solving equations__________________________________________14
2.4. Functional equations______________________________19
Conclusion_________________________________________________23
List of used literature__________________________________________24
Application ________________________________________________25
Introduction.
This work is devoted to the theoretical and practical aspects of introducing the method of indefinite coefficients into the school mathematics course. The relevance of this topic is determined by the following circumstances.
No one will argue that mathematics as a science does not stand in one place, it is constantly evolving, new tasks of increased complexity appear, which often causes certain difficulties, since these tasks are usually associated with research. In recent years, such problems have been proposed at school, district and republican mathematical Olympiads, and they are also available in the Unified State Exam versions. Therefore, a special method was required that would allow at least some of them to be solved most quickly, efficiently and affordably. This work clearly presents the content of the method of indefinite coefficients, which is widely used in a wide variety of areas of mathematics, ranging from questions included in the general education course to its most advanced parts. In particular, applications of the method of indefinite coefficients in solving problems with parameters, fractional rational and functional equations are especially interesting and effective; they can easily interest anyone interested in mathematics. The main purpose of the proposed work and selection of problems is to provide ample opportunities to hone and develop the ability to find short and non-standard solutions.
This work consists of two chapters. The first discusses the theoretical aspects of using
method of uncertain coefficients, and secondly, practical and methodological aspects of such use.
The appendix to the work provides conditions for specific tasks for independent solution.
Chapter I . Theoretical aspects of use method of uncertain coefficients
“Man... was born to be a master,
ruler, king of nature, but wisdom,
with which he must rule is not given to him
from birth: it is acquired by learning"
N.I.Lobachevsky
There are various ways and methods for solving problems, but one of the most convenient, most effective, original, elegant and at the same time very simple and understandable to everyone is the method of indefinite coefficients. The method of undetermined coefficients is a method used in mathematics to find the coefficients of expressions whose form is known in advance.
Before considering the application of the method of indefinite coefficients to solving various types of problems, we present a number of theoretical information.
Let them be given
A n (x) = a 0 x n + a 1 x n-1 + a 2 x n-2 + ··· + a n-1 x + a n
B m (x ) = b 0 x m + b 1 x m -1 + b 2 x m -2 + ··· + b m-1 x + b m ,
polynomials relative X with any odds.
Theorem. Two polynomials depending on one and the same argument are identically equal if and only ifn = m and their corresponding coefficients are equala 0 = b 0 , a 1 = b 1 , a 2 = b 2 ,··· , a n -1 = b m -1 , a n = b m And T. d.
Obviously, equal polynomials take for all values X same values. Conversely, if the values of two polynomials are equal for all values X, then the polynomials are equal, that is, their coefficients at the same degreesX match up.
Therefore, the idea of applying the method of indefinite coefficients to solving problems is as follows.
Let us know that as a result of some transformations an expression of a certain type is obtained and only the coefficients in this expression are unknown. Then these coefficients are designated by letters and considered as unknowns. A system of equations is then constructed to determine these unknowns.
For example, in the case of polynomials, these equations are made from the condition that the coefficients are equal for the same powers X for two equal polynomials.
Let's demonstrate what was said above using the following specific examples, and let's start with the simplest.
So, for example, based on theoretical considerations, the fraction
can be represented as a sum
, Where
a
,
b
And
c
-
coefficients to be determined. To find them, we equate the second expression to the first:
=
and freeing ourselves from the denominator and collecting terms with the same powers on the left X, we get:
(a + b + c )X 2 + ( b - c )x - a = 2X 2 – 5 X– 1
Since the last equality must be true for all values X, then the coefficients at the same powersX right and left should be the same. Thus, three equations are obtained to determine the three unknown coefficients:
a+b+c = 2
b - c = - 5
A= 1, whence a = 1 , b = - 2 , c = 3
Hence,
=
,
the validity of this equality is easy to verify directly.
Suppose you also need to represent a fraction
as a
+
b 
+
c 
+ d
, Where a
,
b
,
c
And
d- unknown rational coefficients. We equate the second expression to the first:
a
+
b
+
c
+ d
= or, Freeing ourselves from the denominator, removing, where possible, rational factors from under the signs of the roots and bringing similar terms on the left side, we obtain:
(a-
2
b
+
3
c
) + (-
a+b
+3
d
)
+ (a+c
- 2
d
)
+
+ (b - c
+
d
)
=
1 +
-
.
But such equality is possible only in the case when the rational terms of both parts and the coefficients of the same radicals are equal. Thus, four equations are obtained for finding the unknown coefficients a , b , c And d :
a- 2b+ 3c = 1
- a+b +3 d = 1
a+c - 2 d = - 1
b
-
c
+
d= 0, whence a
= 0 ;
b
= - ;
c
= 0
;
d= , that is = -
+
.
Chapter II. Searches for solutions to problems with polynomials method of undetermined coefficients.
“Nothing contributes to the mastery of a subject better than
the way to act with him in different situations"
Academician B.V. Gnedenko
2. 1. Factoring a polynomial.
Methods for factoring polynomials:
1) placing the common factor out of brackets; 2) grouping method; 3) application of basic multiplication formulas; 4) introduction of auxiliary terms; 5) preliminary transformation of a given polynomial using certain formulas; 6) expansion by finding the roots of a given polynomial; 7) method of entering the parameter; 8)method of undetermined coefficients.
Problem 1. Factor the polynomial into real factors X 4 + X 2 + 1 .
Solution. There are no roots among the divisors of the free term of this polynomial. We cannot find the roots of the polynomial by other elementary means. Therefore, it is not possible to perform the required expansion by first finding the roots of this polynomial. It remains to look for a solution to the problem either by introducing auxiliary terms or by the method of undetermined coefficients. It's obvious that X 4 + X 2 + 1 = X 4 + X 3 + X 2 - X 3 - X 2 - X + X 2 + X + 1 =
= X 2 (X 2 + X + 1) - X (X 2 + X + 1) + X 2 + X + 1 =
= (X 2 + X + 1)(X 2 - X + 1).
The resulting quadratic trinomials have no roots and are therefore indecomposable into real linear factors.
The described method is technically simple, but difficult due to its artificiality. Indeed, it is very difficult to come up with the required auxiliary terms. Only a guess helped us find this decomposition. But
There are more reliable ways to solve such problems.
One could proceed like this: assume that the given polynomial decomposes into the product
(X 2 + A X + b )(X 2 + c X + d )
two square trinomials with integer coefficients.
Thus, we will have that
X 4 + X 2 + 1 = (X 2 + A X + b )(X 2 + c X + d )
It remains to determine the coefficientsa , b , c And d .
Multiplying the polynomials on the right side of the last equality, we get:X 4 + X 2 + 1 = X 4 +
+ (a + c ) X 3 + (b + A c + d ) X 2 + (ad + bc ) x + bd .
But since we need the right side of this equality to turn into the same polynomial that is on the left side, we will require the following conditions to be met:
a + c = 0
b + A c + d = 1
ad + bc = 0
bd = 1 .
The result is a system of four equations with four unknownsa , b , c And d . It is easy to find the coefficients from this systema = 1 , b = 1 , c = -1 And d = 1.
Now the problem is completely solved. We got:
X 4 + X 2 + 1 = (X 2 + X + 1)(X 2 - X + 1).
Problem 2. Factor the polynomial into real factors X
3
– 6
X
2
+ 14
X
– 15 .
Solution. Let us represent this polynomial in the form
X
3
– 6
X
2 + 14
X
– 15 = (X
+
A
)(X
2
+
bx
+
c) , Where a
,
b
And With
- coefficients not yet determined. Since two polynomials are identically equal if and only if the coefficients of the same powersX
are equal, then, equating the coefficients respectively forX
2
,
X
and free terms, we obtain a system of three equations with three unknowns:
a+b= - 6
ab + c = 14
ac = - 15 .
The solution to this system will be significantly simplified if we take into account that the number 3 (divisor of the free term) is the root of this equation, and, therefore,a = - 3 ,
b = - 3 And With = 5 .
Then X
3
– 6
X
2 + 14
X
– 15 = (X
– 3)(X
2
– 3
x
+
5).
The applied method of indefinite coefficients, in comparison with the above method of introducing auxiliary terms, does not contain anything artificial, but it requires the application of many theoretical principles and is accompanied by rather large calculations. For polynomials of higher degree, this method of undetermined coefficients leads to cumbersome systems of equations.
2.2.Tasks and with parameters.
In recent years, versions of the Unified State Exam have offered tasks with parameters. Their solution often causes certain difficulties. When solving problems with parameters, along with other methods, you can quite effectively use the method of indefinite coefficients. It is this method that allows you to greatly simplify their solution and quickly get an answer.
Task 3. Determine at what values of the parameter A equation 2 X 3 – 3 X 2 – 36 X + A – 3 = 0 has exactly two roots.
Solution. 1 way. Using derivative.
Let's represent this equation in the form of two functions
2x 3 – 3 X 2 – 36 X – 3 = – A .
f (x) = 2x 3 – 3 X 2 – 36 X– 3 and φ( X ) = – A .
Let's explore the functionf (x) = 2x 3 – 3 X 2 – 36 X – 3 using the derivative and schematically construct its graph (Fig. 1.).
f(
–
x
)
f
(x
) ,
f
(–
x
) –
f
(x
).
The function is neither even nor odd.
3. Let's find the critical points of the function, its intervals of increase and decrease, extrema. f / (x ) = 6 x 2 – 6 X – 36. D (f / ) = R , therefore we will find all critical points of the function by solving the equation f / (x ) = 0 .
6(X 2 – X– 6) = 0 ,
X 2 – X– 6 = 0 ,
X 1 = 3 , X 2 = – 2 by the theorem inverse to Vieta’s theorem.
f / (x ) = 6(X – 3)(X + 2).
+ max - min +
2 3 x
f
/
(x) > 0 for all X<
– 2 and X
> 3 and the function is continuous at pointsx =– 2 and X
= 3, therefore, it increases on each of the intervals (- 
; - 2] and [ 3 ; ).
f / (x ) < 0 at - 2 < X< 3, therefore, it decreases on the interval [- 2; 3 ].
X = - 2nd maximum point, because at this point the sign of the derivative changes from"+" to "-".
f (– 2) = 2· (– 8) – 3·4 – 36·(– 2) – 3 = – 16 – 12 + 72 – 3 == 72 – 31 = 41 ,
x = 3 minimum point, since at this point the sign of the derivative changes"-" to "+".
f (3) = 2·27 – 3·9 – 36·3 – 3 = 54 – 27 – 108 – 3 = – 138 + +54 = – 84.
Graph of the function φ(X ) = – A is a straight line parallel to the x-axis and passing through the point with coordinates (0; – A ). The graphs have two common points:A= 41, i.e. a =– 41 and – A= – 84, i.e. A = 84 .
at
41φ( X)
2 3 X
3 f ( x ) = 2x 3 – 3 X 2 – 36 X – 3
Method 2. Method of undetermined coefficients.
Since, according to the conditions of the problem, this equation must have only two roots, the equality is obvious:
2X 3 – 3 X 2 – 36 X + A – 3 = (x + b ) 2 (2 x + c ) ,
2X 3 – 3 X 2 – 36 X + A – 3 = 2 x 3 + (4 b + c ) x 2 + (2 b 2 + +2 bc ) x + b 2 c ,
Now equating the coefficients at the same degrees X, we obtain a system of equations
4 b + c = - 3
2b 2 + 2bc = - 36
b 2 c = a – 3 .
From the first two equations of the system we findb 2 + b – 6 = 0, whence b 1 = - 3 or b 2 = 2 . Corresponding valuesWith 1 and With 2 easy to find from the first equation of the system:With 1 = 9 or With 2 = - 11 . Finally, the desired value of the parameter can be determined from the last equation of the system:
A = b 2 c + 3 , a 1 = - 41 or a 2 = 84.
Answer: this equation has exactly two different
root at A= - 41 and A= 84 .
Task 4. Find the largest value of the parameterA , for which the equationX 3 + 5 X 2 + Oh + b = 0
with integer coefficients has three different roots, one of which is equal to – 2.
Solution. 1 way. Substituting X= - 2 to the left side of the equation, we get
8 + 20 – 2 A + b= 0, which means b = 2 a – 12 .
Since the number - 2 is a root, we can take out the common factor X + 2:
X 3 + 5 X 2 + Oh + b = X 3 + 2 X 2 + 3 X 2 + Oh + (2 a – 12) =
= x 2 (X + 2) + 3 x (X + 2) – 6 x + Oh + (2 a – 12) =
= x 2 (X + 2) + 3 x (X + 2) + (a – 6)(x +2) - 2(a – 6)+ (2 a – 12) =
= (X + 2)(X 2 + 3 x + (a – 6) ) .
By condition, there are two more roots of the equation. This means that the discriminant of the second factor is positive.
D =3 2 - 4 (a – 6) = 33 – 4 a > 0, that is A < 8,25 .
It would seem that the answer would be a = 8 . But when we substitute the number 8 into the original equation we get:
X 3 + 5 X 2 + Oh + b = X 3 + 5 X 2 + 8 X + 4 = (X + 2)(X 2 + 3 x + 2 ) =
= (X + 1) (X + 2) 2 ,
that is, the equation has only two different roots. But when a = 7 actually produces three different roots.
Method 2. Method of undetermined coefficients.
If the equation X 3 + 5 X 2 + Oh + b = 0 has a root X = - 2, then you can always pick up the numbersc And d so that in front of everyoneX equality was true
X 3 + 5 X 2 + Oh + b = (X + 2)(X 2 + With x + d ).
To find numbersc And d Let's open the brackets on the right side, add similar terms and get
X 3 + 5 X 2 + Oh + b = X 3 + (2 + With ) X 2 +(2 s + d ) X + 2 d
Equating the coefficients at the corresponding powers X we have a system
2 + With = 5
2 With + d = a
2 d = b , where c = 3 .
Hence, X 2 + 3 x + d = 0 , D = 9 – 4 d > 0 or
d
<
2.25, so d
(- ; 2 ].
The problem conditions are satisfied by the value d = 1 . The final desired value of the parameterA = 7.
ANSWER: when a = 7 this equation has three different roots.
2.3. Solving equations.
“Remember that by solving small problems you
prepare yourself to tackle big and difficult
new tasks.”
Academician S.L. Sobolev
When solving some equations, you can and should show resourcefulness and wit, and use special techniques. Mastery of a variety of transformation techniques and the ability to carry out logical reasoning is of great importance in mathematics. One of these tricks is to add and subtract some well-chosen expression or number. The stated fact itself, of course, is well known to everyone - the main difficulty is to see in a specific configuration those transformations of equations to which it is convenient and expedient to apply it.
Using a simple algebraic equation, we will illustrate one non-standard technique for solving equations.
Problem 5. Solve the equation
= 
.
Solution. Let's multiply both sides of this equation by 5 and rewrite it as follows
= 0 ; X 0; -
; 
= 0 ,
= 0 ,
= 0 or 
= 0
Let us solve the resulting equations using the method of undetermined coefficients
X 4 - X 3 –7 X – 3 = (X 2 + ah + b )(x 2 + cx + d ) = 0
X 4 - X 3 –7 X – 3 = X 4 + (a + c ) X 3 + (b + A c + d ) X 2 + (ad + bc ) x+ + bd
Equating the coefficients at X 3 , X 2 , X and free terms, we get the system
a + c = -1
b + A c + d = 0
ad + bc = -7
bd = -3, from where we find:A = -2 ; b = - 1 ;
With = 1 ; d = 3 .
So X 4 - X 3 –7X– 3 = (X 2 – 2 X – 1)(X 2 + X + 3) = 0 ,
X 2 – 2 X– 1 = 0 or X 2 + X + 3 = 0
X 1,2 = 
no roots.
Similarly we have
X 4 – 12X – 5 = (X 2 – 2 X – 1)(X 2 + 2X + 5) = 0 ,
where X 2 + 2 X + 5 = 0 , D = - 16 < 0 , нет корней.
Answer: X 1,2 =
Problem 6. Solve the equation
= 10.
Solution. To solve this equation you need to select numbersA And b so that the numerators of both fractions are the same. Therefore, we have the system:
= 0 , X 0; -1 ; -
= - 10
So the task is to find the numbersA And b , for which equality holds
(a + 6) X 2 + ah – 5 = X 2 + (5 + 2 b ) x + b
Now, according to the theorem on the equality of polynomials, it is necessary that the right side of this equality turns into the same polynomial that is on the left side.
In other words, the relations must be satisfied
a + 6 = 1
A = 5 + 2 b
– 5 = b , from where we find the valuesA = - 5 ;
b = - 5 .
At these valuesA And b equality A + b = - 10 is also fair.
= 0 , X 0; -1 ; -
= 0 ,
= 0 ,
(X 2 – 5X– 5)(X 2 + 3X + 1) = 0 ,
X 2 – 5X– 5 = 0 or X 2 + 3X + 1 = 0 ,
X 1,2 = 
, X 3,4 = 
Answer: X 1,2 = , X 3,4 =
Problem 7. Solve the equation
= 4
Solution. This equation is more complex than the previous ones and therefore we will group it this way: X 0;-1;3;-8;12
0 ,
= - 4.
From the condition of equality of two polynomials
Oh 2 + (a + 6) X + 12 = X 2 + (b + 11) x – 3 b ,
we obtain and solve a system of equations for unknown coefficientsA And b :
A = 1
a + 6 = b + 11
12 = – 3 b , where a = 1 , b = - 4 .
Polynomials - 3 – 6X + cx 2 + 8 cx And X 2 + 21 + 12 d – dx are equal to each other identically only when
With = 1
8 With - 6 = - d
3 = 21 + 12 d , With = 1 , d = - 2 .
With valuesa = 1 , b = - 4 , With = 1 , d = - 2
equality = - 4 is correct.
As a result, this equation takes the following form:
= 0 or 
= 0 or 
= 0 ,
= - 4 , 
= - 3 , 
= 1 ,
= - 
.
From the examples considered, it is clear how the skillful use of the method of indefinite coefficients,
helps to simplify the solution of a rather complex, unusual equation.
2.4. Functional equations.
“The highest purpose of mathematics... is
is to find the hidden order in
chaos that surrounds us"
N. Viner
Functional equations are a very general class of equations in which the unknown function is a certain function. A functional equation in the narrow sense of the word is understood as equations in which the desired functions are related to known functions of one or more variables using the operation of forming a complex function. A functional equation can also be considered as an expression of a property characterizing a particular class of functions
[for example, functional equation f ( x ) = f (- x ) characterizes the class of even functions, the functional equationf (x + 1) = f (x ) – class of functions having period 1, etc.].
One of the simplest functional equations is the equationf (x + y ) = f (x ) + f (y ). Continuous solutions of this functional equation have the form
f (x ) = Cx . However, in the class of discontinuous functions this functional equation has other solutions. Associated with the considered functional equation are
f (x + y ) = f (x ) · f (y ), f (x y ) = f (x ) + f (y ), f (x y ) = f (x )· f (y ),
continuous solutions, which, respectively, have the form
e cx , WITHlnx , x α (x > 0).
Thus, these functional equations can be used to define exponential, logarithmic and power functions.
The most widely used equations are those in complex functions in which the required functions are external functions. Theoretical and practical applications
It was precisely these equations that prompted outstanding mathematicians to study them.
For example, at alignment
f 2 (x) = f (x - y)· f (x + y)
N.I.Lobachevskyused when determining the angle of parallelism in my geometry.
In recent years, problems related to solving functional equations are quite often offered at mathematical Olympiads. Their solution does not require knowledge beyond the scope of the mathematics curriculum in secondary schools. However, solving functional equations often causes certain difficulties.
One of the ways to find solutions to functional equations is the method of indefinite coefficients. It can be used when the general form of the desired function can be determined by the appearance of the equation. This applies, first of all, to those cases when solutions to equations should be sought among integer or fractional rational functions.
Let us outline the essence of this technique by solving the following problems.
Task 8. Functionf
(x
) is defined for all real x and satisfies for allX
R
condition
3 f(x) - 2 f(1- x) = x 2 .
Findf (x ).
Solution. Since on the left side of this equation over the independent variable x and the values of the functionf Only linear operations are performed, and the right side of the equation is a quadratic function, then it is natural to assume that the desired function is also quadratic:
f (X) = ax 2 + bx + c , Wherea, b, c – coefficients to be determined, that is, uncertain coefficients.
Substituting the function into the equation, we arrive at the identity:
3(ax 2 + bx+c) – 2(a(1 – x) 2 + b(1 – x) + c) = x 2 .
ax 2 + (5 b + 4 a) x + (c – 2 a – 2 b) = x 2 .
Two polynomials will be identically equal if they are equal
coefficients for the same powers of the variable:
a = 1
5b + 4a = 0
c– 2 a – 2 b = 0.
From this system we find the coefficients
a = 1 , b = - , c = , Alsosatisfiesequality
3 f (x ) - 2 f (1- x ) = x 2 on the set of all real numbers. At the same time, there is suchx 0 Task 9. Functiony =f(x) for all x is defined, continuous and satisfies the conditionf (f (x)) – f(x) = 1 + 2 x . Find two such functions.
Solution. Two actions are performed on the desired function - the operation of composing a complex function and
subtraction. Considering that the right side of the equation is a linear function, it is natural to assume that the desired function is also linear:f(x) = ah +b , WhereA Andb – uncertain coefficients. Substituting this function intof (f ( (x ) = - X - 1 ;
f 2 (x ) = 2 X+ , which are solutions to the functional equationf (f (x)) – f(x) = 1 + 2 x .
Conclusion.
In conclusion, it should be noted that this work will certainly contribute to the further study of an original and effective method for solving a variety of mathematical problems, which are problems of increased difficulty and require deep knowledge of the school mathematics course and a high logical culture. Anyone who wants to independently deepen their knowledge of mathematics will also find This work contains material for reflection and interesting tasks, the solution of which will bring benefit and satisfaction.
The work, within the framework of the existing school curriculum and in a form accessible for effective perception, sets out the method of indefinite coefficients, which helps deepen the school course in mathematics.
Of course, all the possibilities of the method of indefinite coefficients cannot be demonstrated in one work. In fact, the method still requires further study and research.
List of used literature.
Glazer G.I..History of mathematics in school.-M.: Education, 1983.
Gomonov S.A. Functional equations in a school mathematics course // Mathematics at school. – 2000. –№10 .
Dorofeev G.V., Potapov M.K., Rozov N.H.. A manual on mathematics. - M.: Nauka, 1972.
Kurosh A.G.. Algebraic equations of arbitrary degrees. - M.: Nauka, 1983.
Likhtarnikov L.M.. Elementary introduction to functional equations. – St. Petersburg. : Lan, 1997.
Manturov O.V., Solntsev Yu.K., Sorokin Yu.I., Fedin N.G.. Explanatory dictionary of mathematical terms.-M.: Education, 1971
Modenov V.P.. A manual on mathematics. Part 1.-M.: Moscow State University, 1977.
Modenov V.P.. Problems with parameters. - M.: Exam, 2006.
Potapov M.K., Aleksandrov V.V., Pasichenko P.I.. Algebra and analysis of elementary functions. - M.: Nauka, 1980.
Khaliullin A.A.. You can solve it easier // Mathematics at school. – 2003 . - №8 .
Khaliullin.
4. Expand polynomial 2X 4 – 5X 3 + 9X 2 – 5X+ 3 for multipliers with integer coefficients.
5. At what value A X 3 + 6X 2 + Oh+ 12 per X+ 4 ?
6. At what value of the parameterA the equationX 3 +5 X 2 + + Oh + b = 0 with integer coefficients has two different roots, one of which is 1 ?
7. Among the roots of the polynomial X 4 + X 3 – 18X 2 + Oh + b with integer coefficients there are three equal integers. Find the value b .
8. Find the largest integer value of the parameter A, at which the equation X 3 – 8X 2 + ah +b = 0 with integer coefficients has three different roots, one of which is equal to 2.
9. At what values A And b division is performed without remainder X 4 + 3X 3 – 2X 2 + Oh + b on X 2 – 3X + 2 ?
10. Factor polynomials:
A)X 4 + 2 X 2 – X + 2 V)X 4 – 4X 3 +9X 2 –8X + 5 d)X 4 + 12X – 5
b)X 4 + 3X 2 + 2X + 3 G)X 4 – 3X –2 e)X 4 – 7X 2 + 1 .
11. Solve the equations:
A) 
= 2
= 2
f
(1 –
X
) =
X
2
.
Find f (X) .
13. Function at= f (X) in front of everyone X defined, continuous and satisfies the condition f ( f (X)) = f (X) + X. Find two such functions.
First, let's look at the theory, then we'll solve a couple of examples to reinforce the material on the expansion of a fractionally rational function into a sum of simple fractions. Let's look in detail at method of undetermined coefficients And partial value method, as well as their combinations.
The simplest fractions are often called elementary fractions.
The following are distinguished: types of simple fractions:
where A, M, N, a, p, q are numbers, and the discriminant of the denominator in fractions 3) and 4) is less than zero.
They are called fractions of the first, second, third and fourth types, respectively.
Why even break down fractions into their simplest form?
Let's give a mathematical analogy. Often you have to simplify the type of expression so that you can carry out some actions with it. So, the representation of a fractionally rational function as a sum of simple fractions is approximately the same. It is used to expand functions into power series, Laurent series and, of course, to find integrals.
For example, it requires taking integral of a fractional rational function. After decomposing the integrand into simple fractions, everything comes down to fairly simple integrals 
But about integrals in another section.
Example.
Break down the fraction into its simplest form.
Solution.
In general, the ratio of polynomials is decomposed into simple fractions if the degree of the numerator polynomial is less than the degree of the polynomial in the denominator. Otherwise, first divide the numerator polynomial by the denominator polynomial, and only then carry out the expansion of the correct fractional rational function.
Let's do the division with a column (corner): 
Therefore, the original fraction will take the form: 
Thus, we will expand into simple fractions
Algorithm for the method of undetermined coefficients.
Firstly, we factor the denominator.
In our example, everything is simple - we put x out of brackets. 
Secondly, the fraction to be expanded is represented as a sum of simple fractions with uncertain coefficients.
Here it is worth considering the types of expressions that you may have in your denominator.
Enough theory, in practice everything is clearer.
It's time to return to example. The fraction is decomposed into the sum of simple fractions of the first and third types with undetermined coefficients A, B and C. 
Third, we bring the resulting sum of simple fractions with undetermined coefficients to a common denominator and group the terms in the numerator with the same powers of x. 
That is, we came to equality: 
For x nonzero, this equality reduces to the equality of two polynomials
And two polynomials are equal if and only if the coefficients of the same powers coincide.
Fourth, we equate the coefficients for the same powers of x.
In this case, we obtain a system of linear algebraic equations with undetermined coefficients as unknowns:
Fifthly, we solve the resulting system of equations in any way (if necessary, see the article) that you like, we find the undetermined coefficients. 
At sixth, write down the answer. 
Please, do not be lazy, check your answer by bringing the resulting expansion to a common denominator.
Uncertain coefficient method is a universal method for decomposing fractions into simpler ones.
It is very convenient to use the partial value method if the denominator is a product of linear factors, that is, it has a form similar to
Let's look at an example to show the advantages of this method.
Example.
Expand a fraction 
to the simplest.
Solution.
Since the degree of the polynomial in the numerator is less than the degree of the polynomial in the denominator, we do not have to divide. Let's move on to factoring the denominator.
First, let's take x out of brackets.
We find the roots of a quadratic trinomial (for example, using Vieta’s theorem): 
Therefore, the quadratic trinomial can be written as
That is, the denominator will take the form
With a given denominator, the original fraction is decomposed into the sum of three simple fractions of the first type with undetermined coefficients:
We bring the resulting sum to a common denominator, but we do not open the brackets in the numerator and do not give similar ones for A, B and C (at this stage this is precisely the difference from the method of indefinite coefficients): 
Thus, we came to equality: 
And now, to find the undetermined coefficients, we begin to substitute “partial values” into the resulting equality, at which the denominator goes to zero, that is, x=0, x=2 and x=3 for our example.
At x=0 we have: 
At x=2 we have: 
At x=3 we have: 
Answer:
As you can see, the difference between the method of undetermined coefficients and the method of partial values is only in the method of finding unknowns. These methods can be combined to simplify calculations.
Let's look at an example.
Example.
Expand fractionally a rational expression 
to simple fractions.
Solution.
Since the degree of the numerator polynomial is less than the degree of the denominator polynomial and the denominator has already been factorized, the original expression will be presented as a sum of simple fractions of the following form:
Let's bring it to a common denominator: 
Let's equate the numerators. 
Obviously, the zeros of the denominator are the values x=1, x=-1 and x=3. We use the partial value method.
At x=1 we have: 
At x=-1 we have: 
At x=3 we have: 
It remains to find the unknowns and
To do this, we substitute the found values into the equality of numerators: 
After opening the brackets and bringing similar terms with the same powers of x, we arrive at the equality of two polynomials: 
We equate the corresponding coefficients at the same degrees, thereby compiling a system of equations for finding the remaining unknowns and . We get a system of five equations with two unknowns: 
From the first equation we immediately find, from the second equation
As a result, we get the decomposition into simple fractions: 
Note.
If we immediately decided to apply the method of undetermined coefficients, we would have to solve a system of five linear algebraic equations with five unknowns. The use of the partial value method made it possible to easily find the values of three out of five unknowns, which greatly simplified the further solution.
A rational function is a fraction of the form , the numerator and denominator of which are polynomials or products of polynomials.
Example 1. Step 2.
.
We multiply the undetermined coefficients by polynomials that are not in this individual fraction, but which are in other resulting fractions:
We open the brackets and equate the numerator of the original integrand to the resulting expression:
In both sides of the equality, we look for terms with the same powers of x and compose a system of equations from them:
.
We cancel all the x’s and get an equivalent system of equations:
.
Thus, the final expansion of the integrand into a sum of simple fractions is:
.
Example 2. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:
.
Now we begin to look for uncertain coefficients. To do this, we equate the numerator of the original fraction in the function expression to the numerator of the expression obtained after reducing the sum of fractions to a common denominator:
Now you need to create and solve a system of equations. To do this, we equate the coefficients of the variable to the corresponding degree in the numerator of the original expression of the function and similar coefficients in the expression obtained at the previous step:
We solve the resulting system:
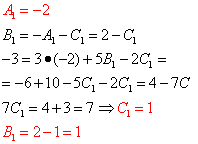
So, from here
.
Example 3. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:
We begin to look for uncertain coefficients. To do this, we equate the numerator of the original fraction in the function expression to the numerator of the expression obtained after reducing the sum of fractions to a common denominator:
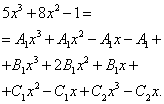
As in previous examples, we compose a system of equations:
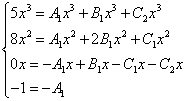
We reduce the x's and get an equivalent system of equations:
Solving the system, we obtain the following values of the uncertain coefficients:
We obtain the final decomposition of the integrand into the sum of simple fractions:
.
Example 4. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:
.
We already know from previous examples how to equate the numerator of the original fraction with the expression in the numerator obtained after decomposing the fraction into the sum of simple fractions and bringing this sum to a common denominator. Therefore, just for control purposes, we present the resulting system of equations:
Solving the system, we obtain the following values of the uncertain coefficients:
We obtain the final decomposition of the integrand into the sum of simple fractions:
Example 5. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:
.
We independently reduce this sum to a common denominator, equating the numerator of this expression to the numerator of the original fraction. The result should be the following system of equations:
Solving the system, we obtain the following values of the uncertain coefficients:
.
We obtain the final decomposition of the integrand into the sum of simple fractions:
.
Example 6. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:
We perform the same actions with this amount as in the previous examples. The result should be the following system of equations:
Solving the system, we obtain the following values of the uncertain coefficients:
.
We obtain the final decomposition of the integrand into the sum of simple fractions:
.
Example 7. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:
.
After certain actions with the resulting amount, the following system of equations should be obtained:
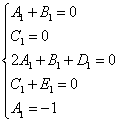
Solving the system, we obtain the following values of the uncertain coefficients:
We obtain the final decomposition of the integrand into the sum of simple fractions:
.
Example 8. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:
.
Let's make some changes to the actions that have already been brought to automaticity to obtain a system of equations. There is an artificial technique that in some cases helps to avoid unnecessary calculations. Bringing the sum of fractions to a common denominator, we obtain and equating the numerator of this expression to the numerator of the original fraction, we obtain.
