EGOROVA VICTORIA VALERIEVNA

Mathematiklehrer

höchste Qualifikationskategorie

THEMA: „IDENTALE TRANSFORMATION

LOGARITHMISCHE AUSDRÜCKE“

Kenntnisse und Fähigkeiten, die die Schüler nach dem Studium dieser Lektion beherrschen sollten:

kennen die Definition des Logarithmus einer Zahl, die grundlegende logarithmische Identität und die Eigenschaften von Logarithmen;

in der Lage sein, Transformationen von Ausdrücken durchzuführen, die Logarithmen enthalten, und Logarithmen zu berechnen.

Literatur:

1. Alimov Sh.A., Kolyagin Yu.M., Sidorov Yu.V. und andere. Algebra und die Anfänge der Analysis: ein Lehrbuch für die Klassen 10-11 Bildungsinstitutionen. – M.: Bildung, 2001.

2. Kochagin V.V., Kochagina M.V., Intensiver Vorbereitungskurs für das Einheitliche Staatsexamen. – M.: Eksmo, 2009.

3. Merzlyak A.G., Polonsky V.B., Yakir M.S., Algebraischer Simulator: Ein Handbuch für Schüler und Bewerber. – M.: Ilexa, 2005.

4. Gusev V.A., Mordkovich A.G. Mathematik: Referenzmaterialien: Ein Buch für Studenten. – M.: Bildung, 2001.

Unterrichtsplan:

Während des Unterrichts:

1) Logarithmus ist ein griechisches Wort, das aus zwei Wörtern besteht: „logos“ – Verhältnis, „arithmos“ – Zahl. Das bedeutet, dass ein Logarithmus eine Zahl ist, die ein Verhältnis misst. In einer Veröffentlichung aus dem Jahr 1614 wurde berichtet, dass Napier den Logarithmus erfunden habe. Später erstellte er logarithmische Tabellen, die uns heute als Bradis-Tabellen bekannt sind. In weniger als einem Jahrhundert haben sich Tabellen auf der ganzen Welt verbreitet und sind zu einem unverzichtbaren Computerwerkzeug geworden. Anschließend wurden sie sozusagen in ein praktisches Gerät eingebaut, das den Rechenvorgang erheblich beschleunigt – einen Rechenschieber, der bis in die siebziger Jahre des 20. Jahrhunderts verwendet wurde.

Anhang 1.

2) Logarithmus positive ZahlB bezogen auf A, Und und größer als Null und ungleich Eins ist,ist der Exponent, auf den eine Zahl erhöht werden mussA um die Nummer zu bekommenB.

Diese Gleichheit, die die Definition eines Logarithmus ausdrückt, heißtgrundlegende logarithmische Identität .

C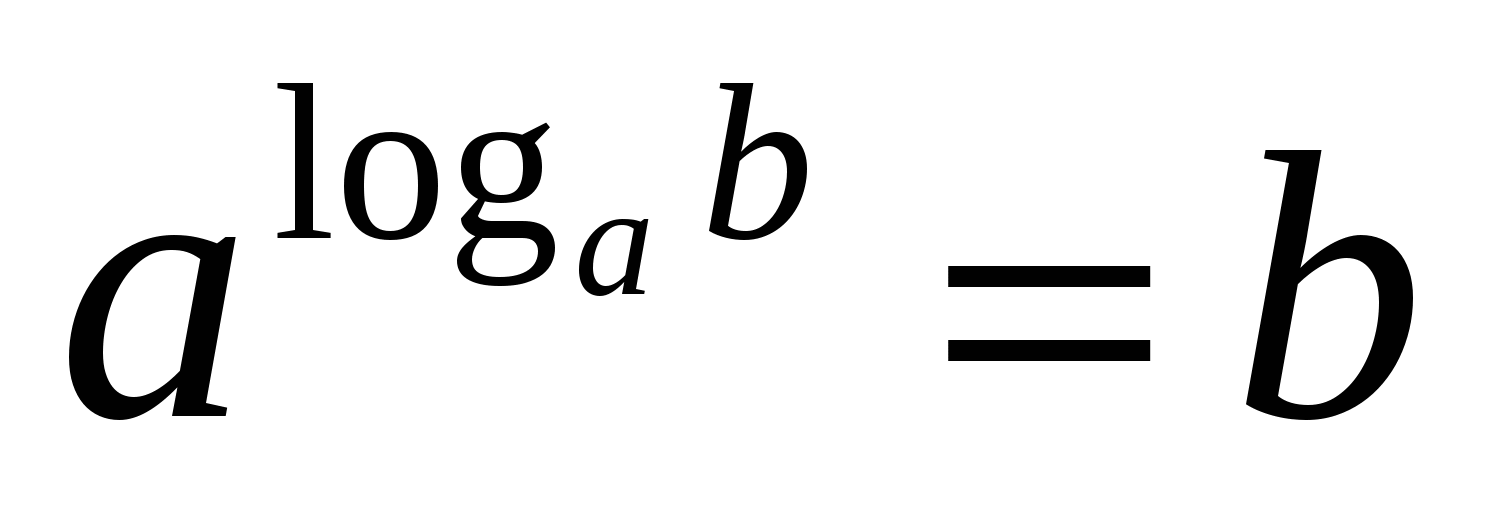

ODER 1

P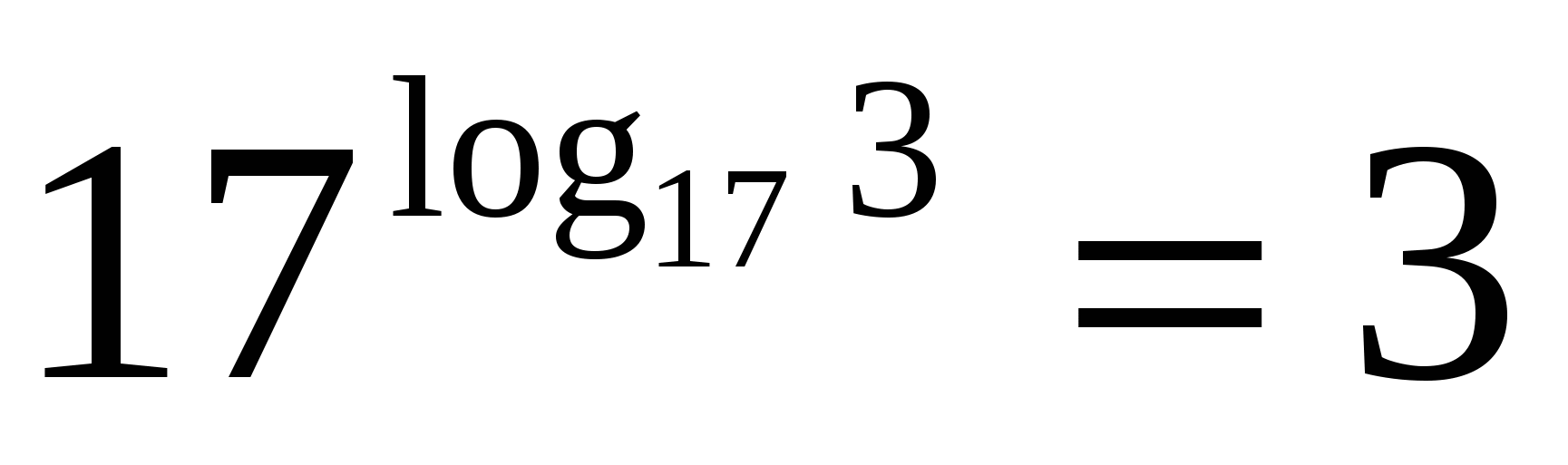

Die Basis der Potenz und die Basis des Logarithmus sind siebzehn, was bedeutet, dass der Wert des Ausdrucks gemäß der logarithmischen Grundidentität drei ist.

Lassen Sie es uns mündlich aufarbeiten:

SCH
FIR-BELLE

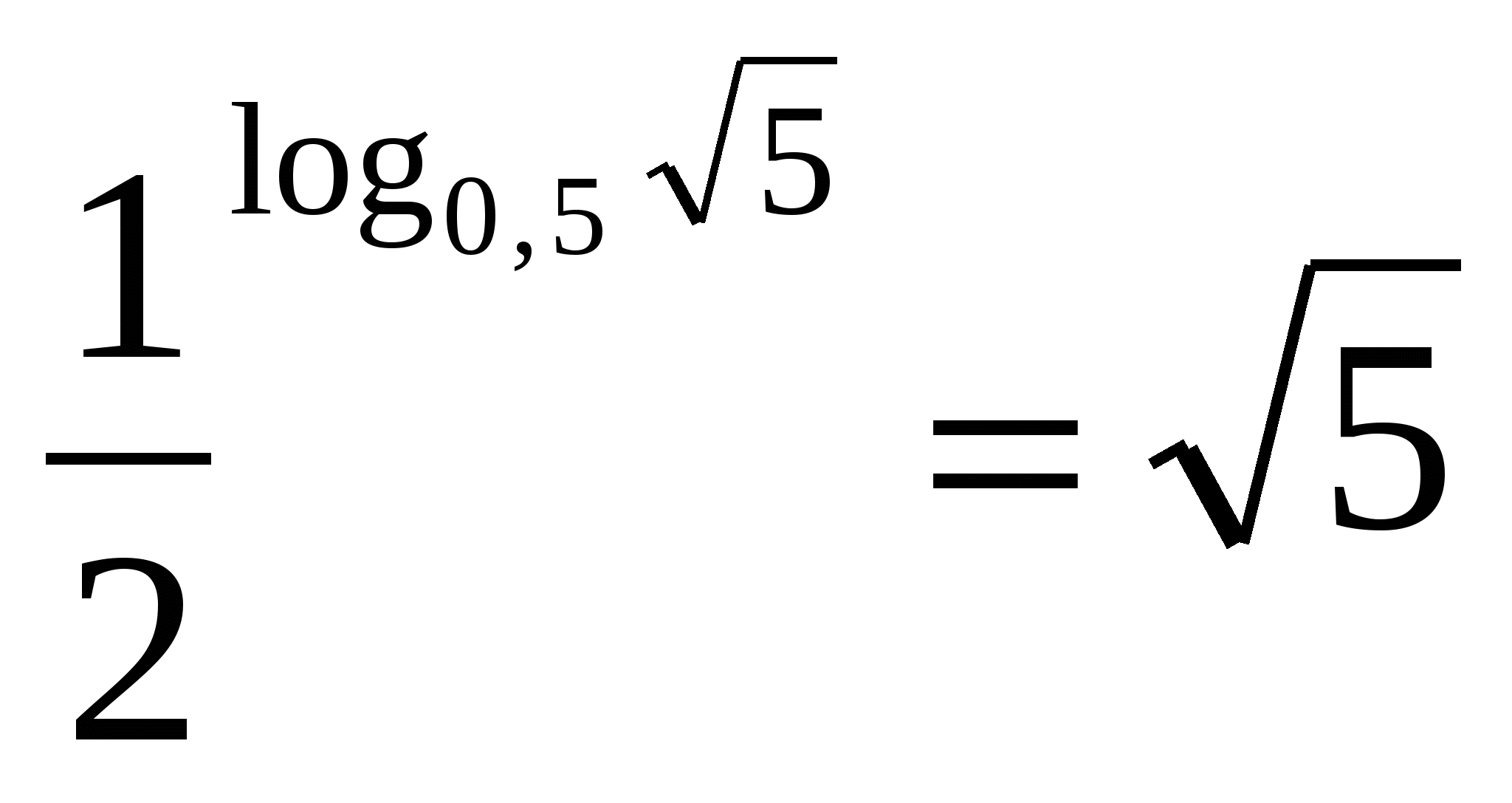
UM Der untere Teil der Sekunde ist gleich null Komma fünf, was bedeutet, dass der Ausdruck gleich der arithmetischen Quadratwurzel aus fünf ist.

P

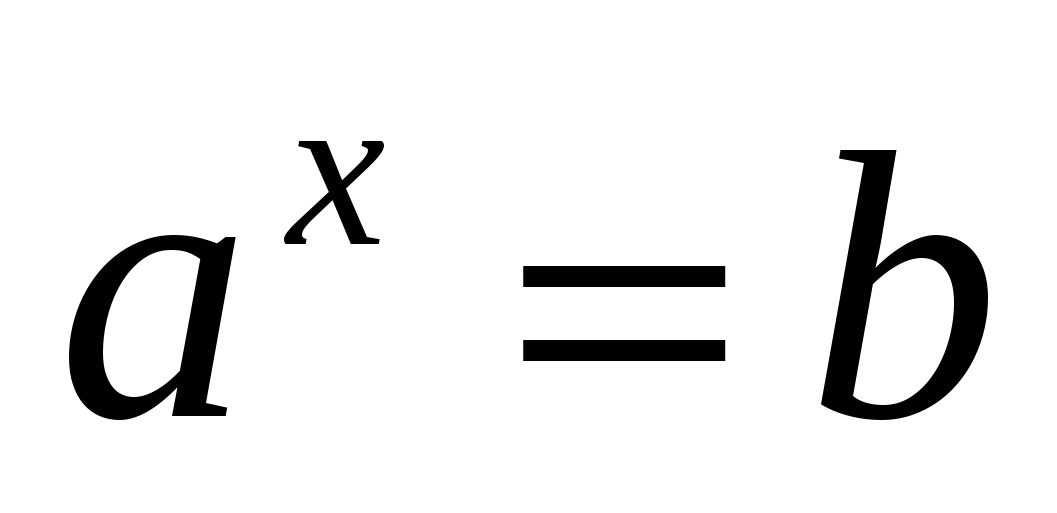Anlage 2.

Gleichwertigkeit bedeutet, dass

Aus der Definition des Logarithmus ergeben sich folgende wichtige Gleichungen:

Zum Beispiel:

P
Anhang 3.

Lass uns weitergehen zu Aufgaben zum Einheitlichen Staatsexamen:

Anhang 4.

3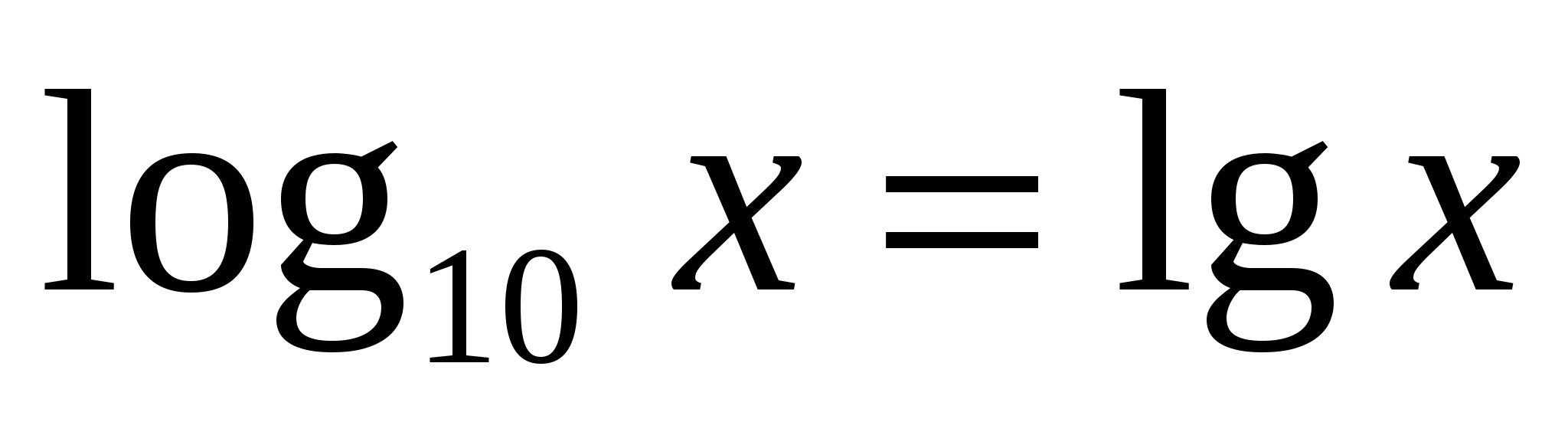
) Für den Basis-Zehn-Logarithmus gibt es eine spezielle Schreibweise und Bezeichnungdezimaler Logarithmus .

L
Basis-Kalarithmuse angerufennatürlicher Logarithmus .

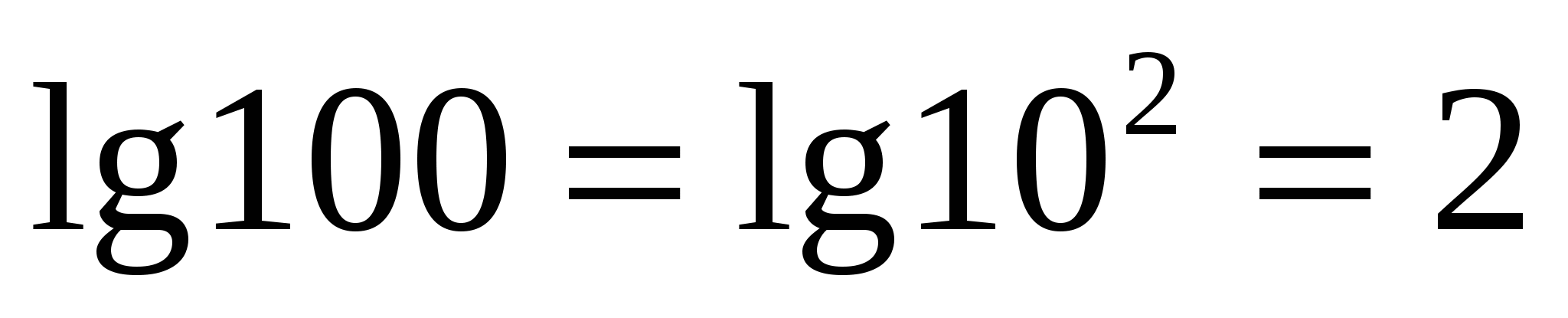
N
Zum Beispiel,

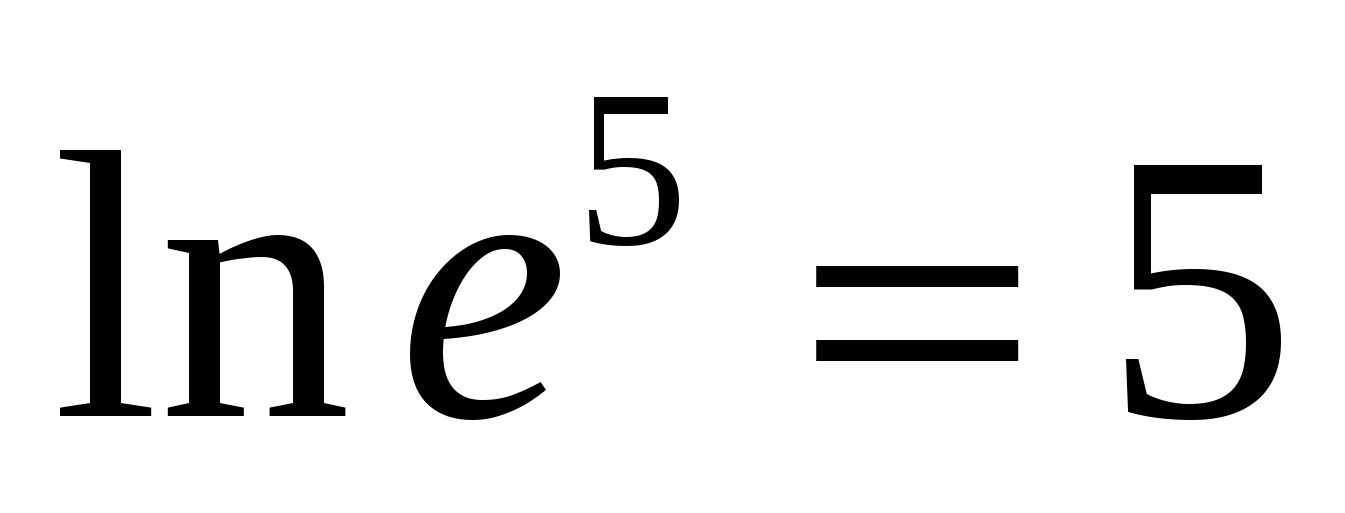
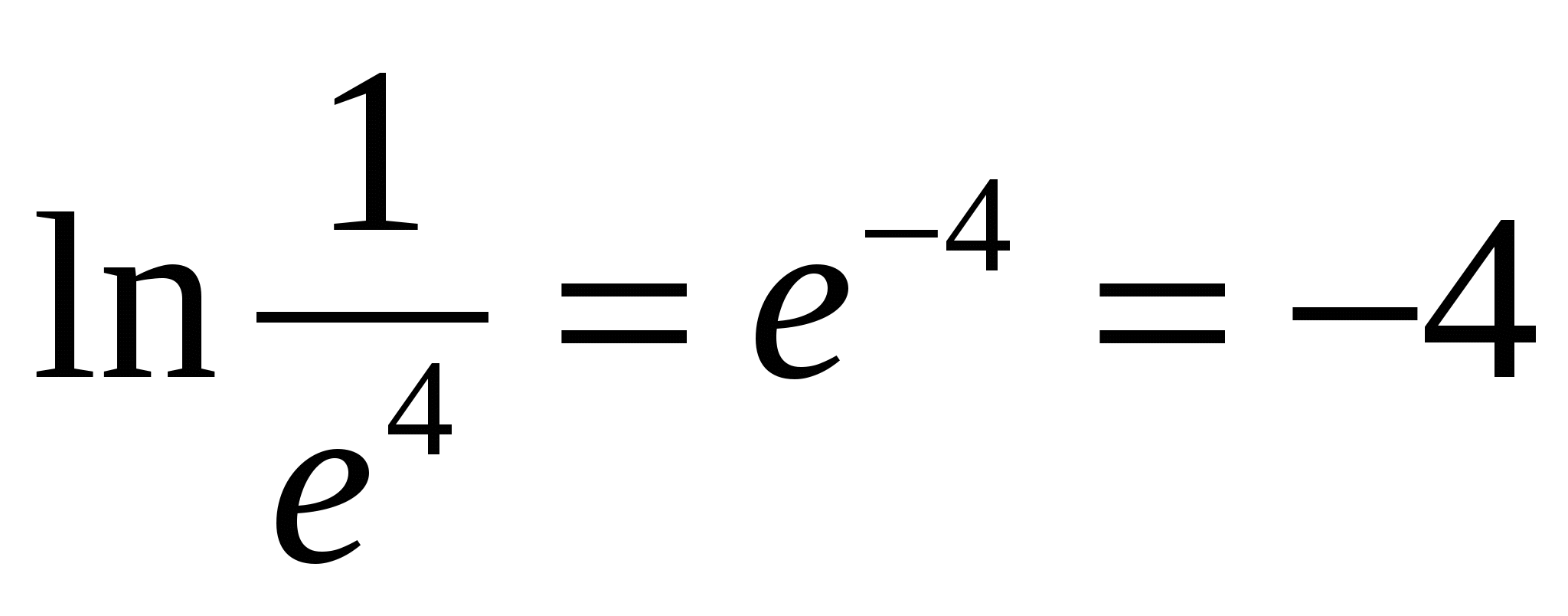
4) Die folgenden Eigenschaften ergeben sich aus der Definition eines Logarithmus. Alle Eigenschaften werden nur für positive Werte von Variablen formuliert und bewiesen, die im Logarithmuszeichen enthalten sind.

Logarithmus des Produkts zweier positiver Zahlen zur Basis A gleich der Summe Logarithmen dieser Zahlen mit derselben Basis.

TsOR 2

Zum Beispiel,

Z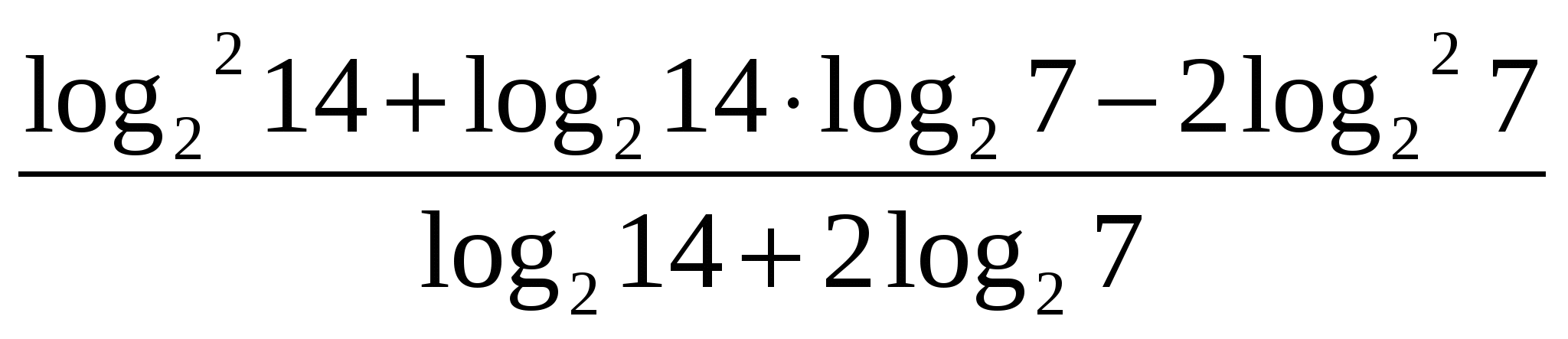
Aufgabe 1.

Aufgabe 2. Den Ausdruck vereinfachen

IN
Verwenden wir die Lösung des vorherigen Beispiels. Wir werden ersetzen

Bitte beachten Sie, dass der Logarithmus quadriert wird, daher muss die Summe quadriert werden. Mit der Formel für das Quadrat der Summe öffnen wir die Klammern. Lassen Sie uns ähnliche Begriffe vorstellen.

5) Der Logarithmus des Quotienten ist gleich der Differenz zwischen den Logarithmen des Dividenden und des Divisors.

C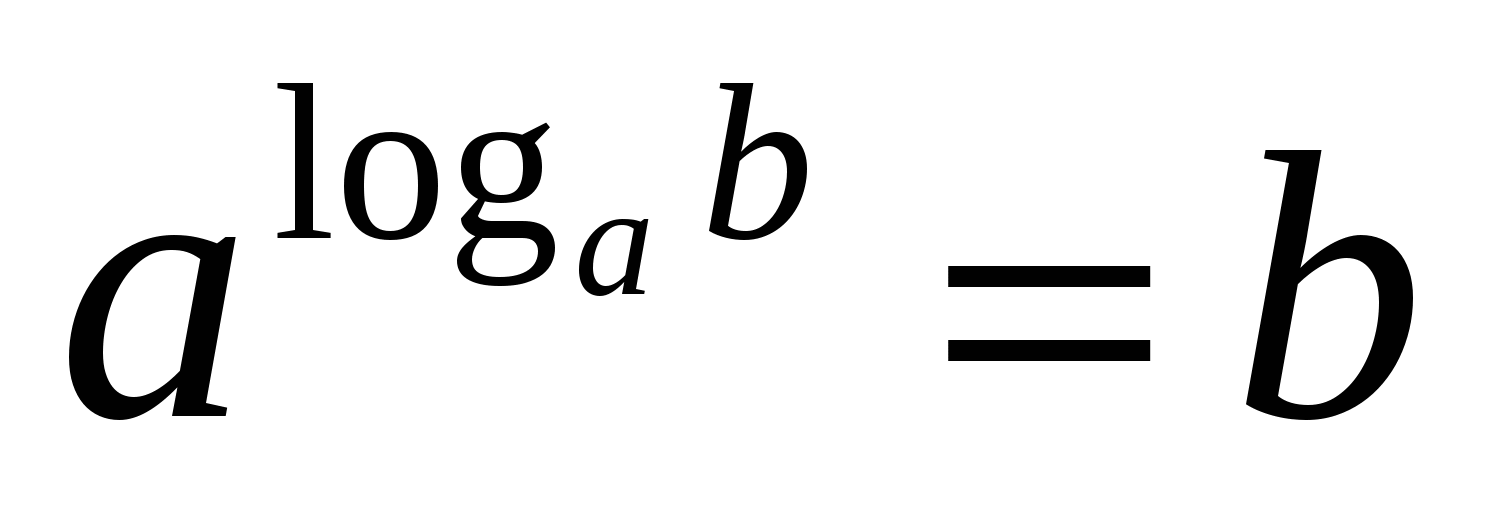

Achten Sie auf die Basis der Potenz und die Basis des Logarithmus – sie sind gleich.

ODER 3

R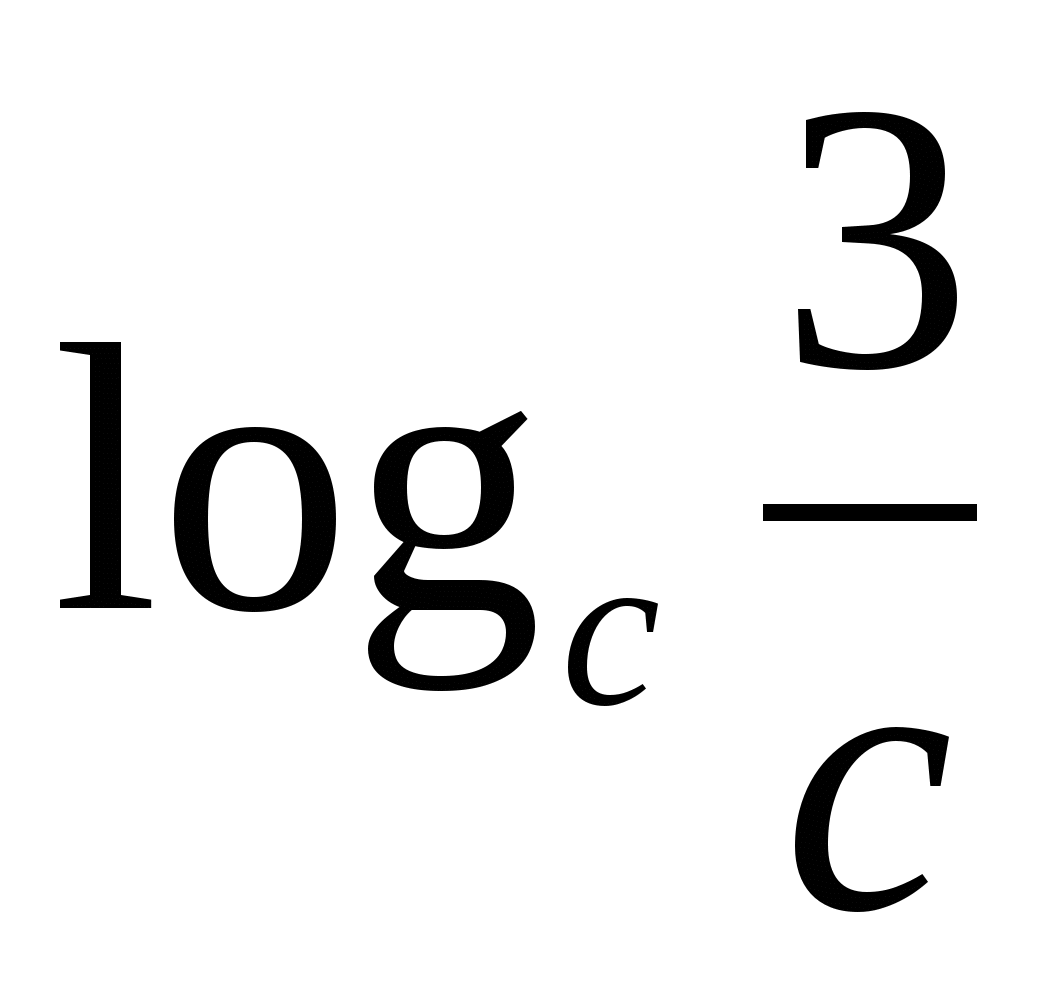

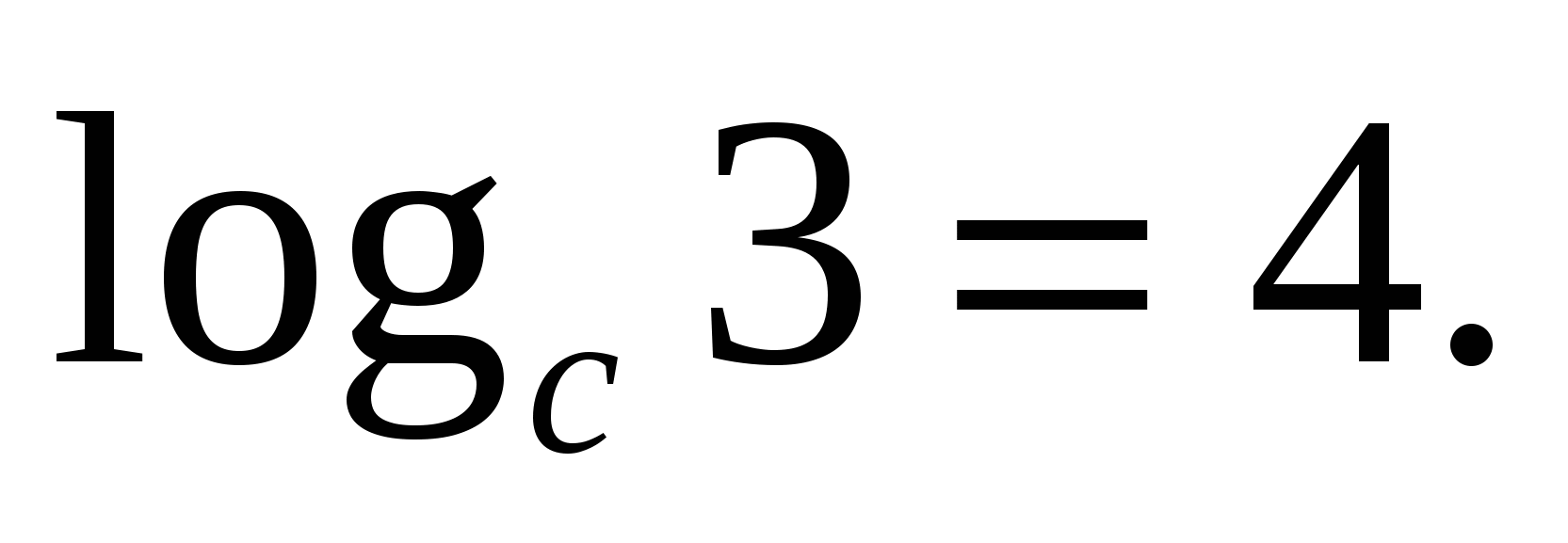Schauen wir uns die Anwendung dieser Formel anhand eines Beispiels an:

Z
Aufgabe 1. Finden Sie den Wert des Ausdrucks if

Aufgabe 2. Finden Sie den Wert B durch seinen Logarithmus

6) Logarithmus einer Potenz zur BasisA , ist gleich dem Produkt des Exponenten und des Logarithmus mit derselben Basis.

TsOR 4

Zum Beispiel,

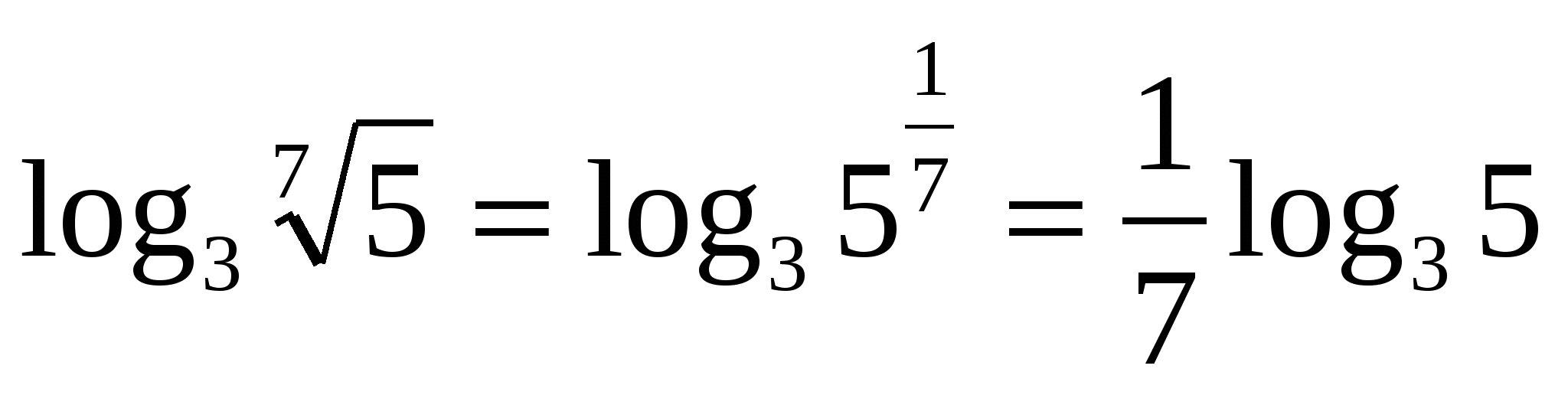
Z
Aufgabe 1. Berechnen Sie, ob

Vereinfachen wir den Ausdruck

Formel

angerufen Formel für den Übergang zu einer neuen Basis.

Z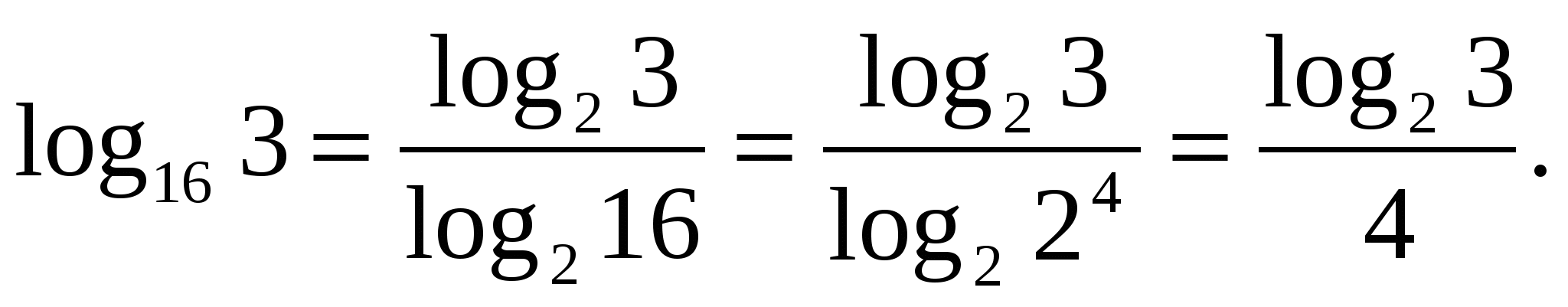

Aufgabe 1. Drücken Sie mit einem Logarithmus zur Basis 2 aus.

Aufgabe 2. Berechnung

TsOR 5

TsOR 6

Zum Beispiel,

Z

Aufgabe 1. Berechnung

Z
Aufgabe 2. Berechnung

9) Logarithmische Transformationen können nur in Fällen gestartet werden, in denen wenn Sie sich an alle Eigenschaften von Logarithmen erinnern. Nachdem wir sie wiederholt haben, werden wir Transformationsaufgaben betrachten logarithmische Ausdrücke andererseits.

Um die Summe oder Differenz logarithmischer Ausdrücke umzuwandeln, reicht es manchmal aus, die Definition eines Logarithmus und meistens die Eigenschaften des Logarithmus eines Produkts oder Quotienten zu verwenden.

Z
Aufgabe 1. Berechnung

Lassen Sie es uns auf zwei Arten lösen.

1 Weg, unter Verwendung der Definition des Logarithmus:

Methode 2, basierend auf Eigenschaft des Logarithmus eines Quotienten:

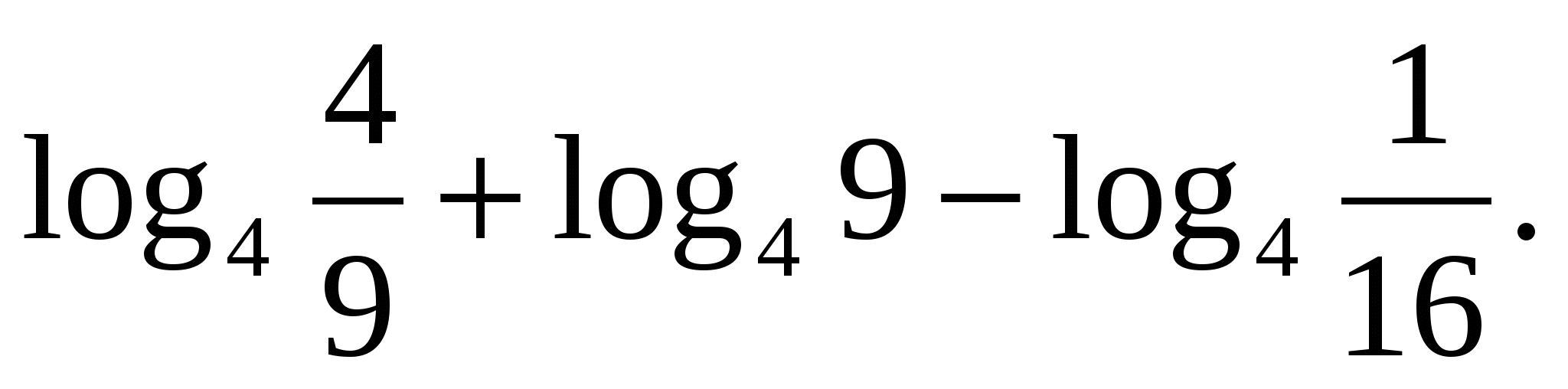
Aufgabe 2. Finden Sie die Bedeutung des Ausdrucks

Wenden wir zunächst die Formel an Logarithmus des Produkts, dann die Definition des Logarithmus.

Die grundlegende logarithmische Identität wird beim Konvertieren von Ausdrücken verwendet, die den Logarithmus als Exponenten enthalten. Die Idee solcher Operationen besteht darin, zu erhalten gleiche Gründe Potenzen und Grundlagen des Logarithmus.

Manchmal ist es notwendig, den Ausdruck umzuwandeln durch die Eigenschaften des Logarithmus und auch durch die Eigenschaften des Grades Mit der Übergangsformel können Sie problemlos von einer Basis zur anderen wechseln. In anderen Fällen sollten mehrere Eigenschaften angewendet werden.

Z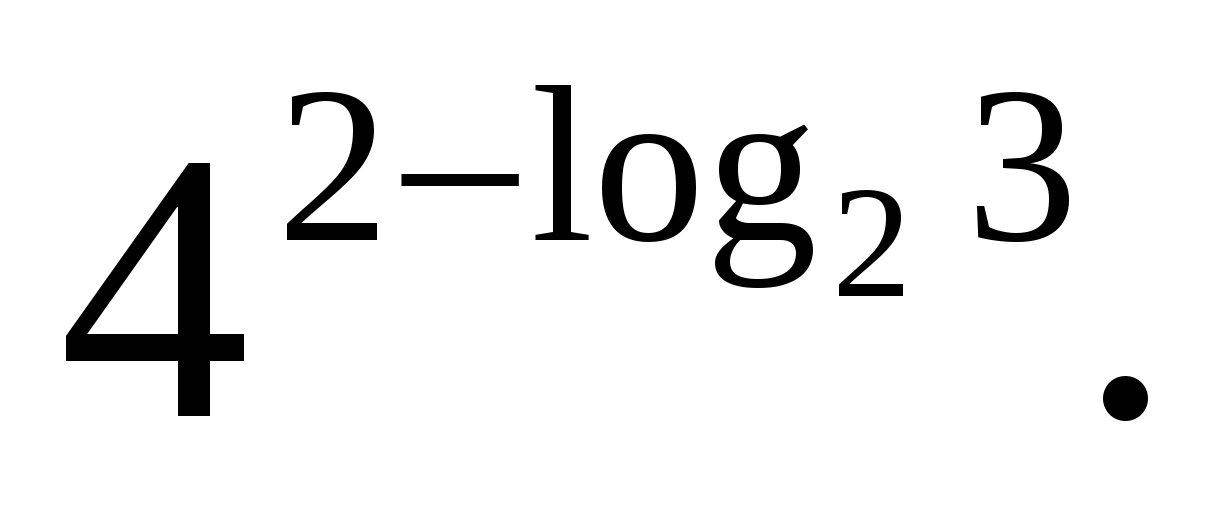
Aufgabe 3. Berechnung

Z
Aufgabe 4. Finden Sie die Bedeutung des Ausdrucks

Aufgabe 5. Finden Sie die Bedeutung des Ausdrucks

Z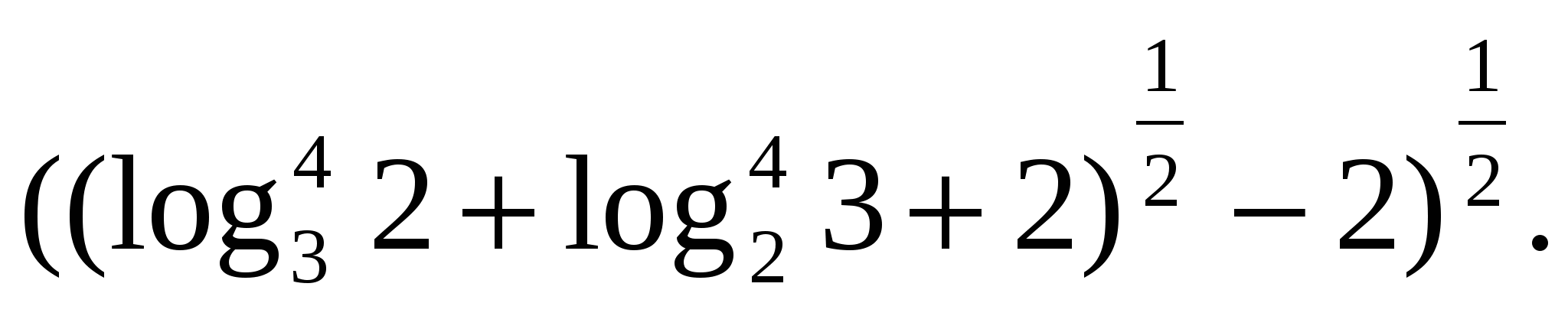
Aufgabe 6. Drücken Sie es als Differenz von Logarithmen aus

N
Die größte Schwierigkeit besteht darin, logarithmische Ausdrücke in die Wurzel umzuwandeln. Bei Transformationen müssen die Module logarithmischer Ausdrücke berücksichtigt werden, zu deren Lösung irrationale Zahlen oder eine rationale und eine irrationale Zahl verglichen werden müssen. Wir werden konsequent handeln. Schauen wir uns den Ausdruck unter dem inneren Radikal an.

Ersetzen wir es durch den ursprünglichen Ausdruck.

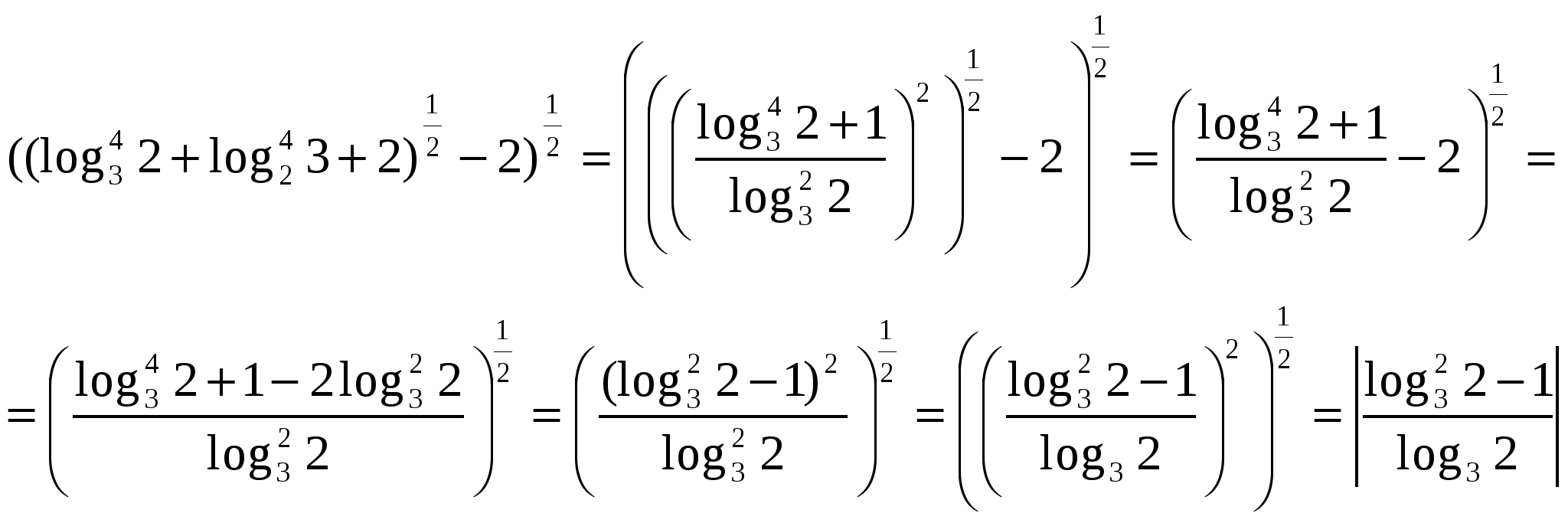Es ist zu beachten, dass die Transformation logarithmischer Ausdrücke auch beim Lösen von Gleichungen und Ungleichungen oder beim Studieren von Funktionen auftreten kann und daher in Aufgaben der Gruppen B und C in impliziter Form vorliegen kann.

10) Zusammenfassend. Fragen:

Der Logarithmus zur Basis 10 heißt

Grundlogarithmus

Hauptlogarithmus

natürlicher Logarithmus

dezimaler Logarithmus

2) Welche Werte kann es annehmen?X im Ausdruck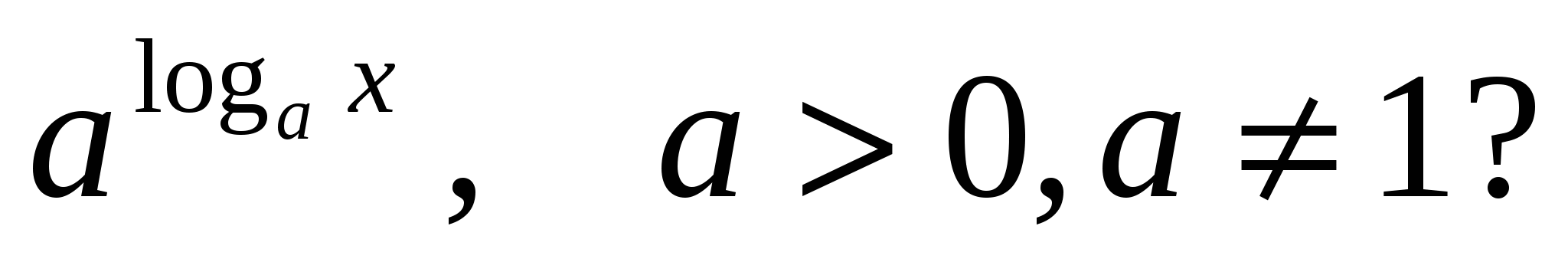

Der Wert ist nicht definiert

5) Geben Sie ein Verhältnis an, das für alle giltX ≠ 0 .

6) Geben Sie das richtige Verhältnis für die Formel für den Umzug in eine neue Basis an.

7) Geben Sie die richtige Gleichheit an

11) Kontrolltests.

Mathematik. Probandentests. Teil II. Vorbereitung auf das Einheitliche Staatsexamen 2010. 10-11 Klassen. Ed. Lysenko F.F. - Rostow o. J.: Legion, 2009. - 176 S.

Mathematik. Einheitliches Staatsexamen 2009. Thematische Tests. Teil II (B4-B8, C1-C2) Ed. Lysenko F.F. - Rostov n/D: Legion, 2008 – 160 S.

Das Handbuch besteht aus Prüfungen zu einzelnen Themen, die traditionell in Mathematikstudiengängen vorkommen und daher in der Regel in die Einheitliche Staatsprüfung einbezogen werden. Sie decken Aufgabengruppen mit erhöhtem und hohem Komplexitätsgrad des Einheitlichen Staatsexamens vollständig ab, mit Ausnahme von Textaufgaben und Geometrieaufgaben. Zu jedem Thema werden ein oder mehrere Testreihen angeboten. Jeder Satz enthält 10 Tests, jeder Test enthält 8 Aufgaben.

Der Zweck dieses Buches besteht darin, Aufgaben mit kurzen und langen Antworten zu üben. Einheitliche Staatsexamenstests. Es ist vor allem für Absolventen notwendig, die einen Abschluss erwarten gute VERWENDUNG Beurteilung sowie für Schüler der 10. Klasse, die die behandelten Themen aus der Perspektive des Einheitlichen Staatsexamens vertiefen können. Das vorgeschlagene Handbuch kann für alle Absolventen, die sich auf das Einheitliche Staatsexamen in Mathematik vorbereiten, sowie für Lehrer, die Schüler auf das Einheitliche Staatsexamen vorbereiten, nützlich sein.

Format: djvu/zip (2009 , 176 S.)

Größe: 2,5 MB

Datei herunterladen / herunterladen 14

Format: pdf (2009 , 176 S.)

Größe: 8,6 MB

Herunterladen: 14 .12.2018, Links auf Wunsch des Legion-Verlags entfernt (siehe Hinweis)

Format: djvu/zip (2008 , 160s.)

Größe: 3 MB

Datei herunterladen / herunterladen 14 .12.2018, Links auf Wunsch des Legion-Verlags entfernt (siehe Hinweis)

Format: pdf (2008 , 160s.)

Größe: 9,9 MB

Herunterladen: 14 .12.2018, Links auf Wunsch des Legion-Verlags entfernt (siehe Hinweis)

Trainings- und Methodologiekomplex„Mathematik. Einheitliches Staatsexamen-2010“ hrsg. Lysenko F.F. und Kulabukhova S.Yu. enthält Tutorials:
1. Mathematik. Vorbereitung auf das Einheitliche Staatsexamen 2010.
2. Reshebnik. Mathematik. Vorbereitung auf das Einheitliche Staatsexamen 2010.
3. Mathematik. Thematische Tests. Teil I (Grundstufe). Vorbereitung auf das Einheitliche Staatsexamen 2010. 10-11 Klassen.
4. Mathematik. Thematische Tests. Teil II. Vorbereitung auf das Einheitliche Staatsexamen 2010. 10-11 Klassen.
5. Mathematik. Thematische Tests: Geometrie, Textaufgaben. Vorbereitung auf das Einheitliche Staatsexamen 2010. 10-11 Klassen.
6. Mathematik. Sammlung der Prüfungen zum Einheitlichen Staatsexamen 2001 - 2010.
7. Mathematik. Vorbereitung auf das Einheitliche Staatsexamen 2010. Bildungs- und Ausbildungstests.
8. Taschenführer Mathematik.

Inhaltsverzeichnis
Von Autoren 11
§ 1. Identische Transformationen logarithmischer Ausdrücke 13
Option Nr. 1 13
Option Nr. 2 13
Option Nr. 3 14
Option Nr. 4 14
Option Nr. 5 15
Option Nr. 6 15
Option Nr. 7 16
Option Nr. 8 16
Option Nr. 9 17
Option Nr. 10 17
§ 2. Identische Transformationen von Ausdrücken, die Potenzen von 18 enthalten
Option Nr. 1 18
Option Nr. 2 19
Option Nr. 3 19
Option Nr. 4 20
Option Nr. 5 21
Option Nr. 6 21
Option Nr. 7 22
Option Nr. 8 23
Option Nr. 9 23
Option Nr. 10 24
§ 3. Identitätstransformationen irrationale Ausdrücke 25
Option Nr. 1 25
Option Nr. 2 25
Option Nr. 3 26
Option Nr. 4 26
Option Nr. 5 27
Option Nr. 6 28
Option Nr. 7 28
Option Nr. 8 29
Option Nr. 9 30
Option Nr. 10 30
§ 4. Gleichungssysteme 31
Option Nr. 1 31
Option Nr. 2 32
Option Nr. 3 33
Option Nr. 4 33
Option Nr. 5 34
Option Nr. 6 35
Option Nr. 7 36
Option Nr. 8 37
Option Nr. 9 38
Option Nr. 10 39
§ 5. Geometrische Bedeutung Ableitung 39
Option Nr. 1 39
Option Nr. 2 41
Option Nr. 3 43
Option Nr. 4 44
Option Nr. 5 46
Option Nr. 6 48
Option Nr. 7 50
Option Nr. 8 52
Option Nr. 9 54
Option Nr. 10 55
§ 6. Ungleichungen 56
Option Nr. 1 g 56
Option Nr. 2 57
Option Nr. 3 58
Option Nr. 4 58
Option Nr. 5 59
Option Nr. 6 60
Option Nr. 7 60
Option Nr. 8 61
Option Nr. 9 62
Option Nr. 10 63
§ 7. Irrationale Gleichungen 63
Option Nr. 1 63
Option Nr. 2 64
Option Nr. 3 65
Option Nr. 4 65
Option Nr. 5 66
Option Nr. 6 66
Option Nr. 7 67
Option Nr. 8 67
Option Nr. 9 68
Option Nr. Yu 68
§ 8. Trigonometrische Gleichungen 69
Option Nr. 1 69
Option Nr. 2 69
Option Nr. 3 70
Option Nr. 4 70
Option Nr. 5 71
Option Nr. 6 72
Option Nr. 7 72
Option Nr. 8 73
Option Nr. 9 74
Option Nr. 10 74
§ 9. Logarithmische Gleichungen 75
Option Nr. 1 75
Option Nr. 2 75
Option Nr. 3 76
Option Nr. 4 76
Option Nr. 5 77
Option Nr. 6 77
Option Nr. 7 78
Option Nr. 8 * 78
Option Nr. 9 79
Option Nr. 10 79
§ 10. Exponentialgleichungen 80
Option Nr. 1 80
Option Nr. 2 80
Option Nr. 3 81
Option Nr. 4 81
Option Nr. 5 82
Option Nr. 6 82
Option Nr. 7 83
Option Nr. 8 83
Option Nr. 9 84
Option Nr. 10 84
§elf. Periodizität, gerade und ungerade Funktionen 85
Option Nr. 1 85
Option Nr. 2 86
Option Nr. 3 87
Option Nr. 4 89
Option Nr. 5 90
Option Nr. 6 91
Option Nr. 7 92
Option Nr. 8 93
Option Nr. 9 94
Option Nr. 10 95
§ 12. Nullen komplexe Funktion. Eingeschränkte Funktion 97
Option Nr. 1 97
Option Nr. 2 97
Option Nr. 3 98
Option Nr. 4 98
Option Nr. 5 99
Option Nr. 6 99
Option Nr. 7 100
Option Nr. 8 100
Option Nr. 9 101
Option Nr. 10 101
§ 13. Definitionsbereich, Wertemenge, Monotonie der Funktionen 102
Option Nr. 1 102
Option Nr. 2 102
Option Nr. 3 103
Option Nr. 4 103
Option Nr. 5 104
Option Nr. 6 104
Option Nr. 7 105
Option Nr. 8 105
Option Nr. 9 106
Option Nr. 10 107
§ 14. Extrema einer Funktion. Der größte und kleinste Wert der Funktion 107
Option Nr. 1 107
Option Nr. 2 108
Option Nr. 3 108
Option Nr. 4 109
Option Nr. 5 109
Option Nr. 6 110
Option Nr. 7 110
Option Nr. 8 111
Option Nr. 9 111
Option Nr. 10 112
§ 15. Verschiedene Techniken zur Lösung logarithmischer Gleichungen 113
Option Nr. 1 113
Option Nr. 2 113
Option Nr. 3 114
Option Nr. 4 114
Option Nr. 5 115
Option Nr. 6 115
Option Nr. 7 116
Option Nr. 8 116
Option Nr. 9 117
Option Nr. 10 117
§ 16. Verschiedene Lösungstechniken trigonometrische Gleichungen 118
Option Nr. 1 118
Option Nr. 2 118
Option Nr. 3 118
Option Nr. 4 119
Option Nr. 5 119
Option Nr. 6 120
Option Nr. 7 120
Option Nr. 8 121
Option Nr. 9 121
Option Nr. 10 122
§ 17. Verschiedene Lösungstechniken Irrationale Gleichungen 123
Option Nr. 1 123
Option Nr. 2 123
Option Nr. 3 124
Option Nr. 4 124
Option Nr. 5 125
Option Nr. 6 125
Option Nr. 7 125
Option Nr. 8 126
Option Nr. 9 126
Option Nr. 10 127
§ 18. Gleichungen, die eine Variable unter dem Modulzeichen 127 enthalten
Option Nr. 1 127
Option Nr. 2 128
Option Nr. 3 128
Option Nr. 4 129
Option Nr. 5 129
Option Nr. 6 130
Option Nr. 7 130
Option Nr. 8 131
Option Nr. 9 131
Option Nr. 10 131
§ 19. Verschiedene Lösungstechniken Exponentialgleichungen.132
Option Nr. 1 132
Option Nr. 2 133
Option Nr. 3 133
Option Nr. 4 134
Option Nr. 5 134
Option Nr. 6 135
Option Nr. 7 135
Option Nr. 8 135
Option Nr. 9 136
Option Nr. 10 136
§ 20. Verschiedene Techniken zur Lösung kombinierter Gleichungen 137
Option Nr. 1 137
Option Nr. 2 137
Option Nr. 3 138
Option Nr. 4 138
Option Nr. 5 139
Option Nr. 6 139
Option Nr. 7 140
Option Nr. 8 140
Option Nr. 9 141
Option Nr. 10 141
§ 21. Gleichungen mit einem Parameter, der Modul 142 enthält
Option Nr. 1 142
Option Nr. 2 142
Option Nr. 3 143
Option Nr. 4 144
Option Nr. 5 144
Option Nr. 6 145
Option Nr. 7 146
Option Nr. 8 146
Option Nr. 9 147
Option Nr. 10 148
Antworten 149
§ 1. Identitätstransformationen logarithmische Ausdrücke 149
§ 2. Identische Transformationen von Ausdrücken mit Potenzen von 150
§ 3. Identische Transformationen irrationaler Ausdrücke 150
§ 4. Gleichungssysteme 151
§ 5. Geometrische Bedeutung der Ableitung 151
§ 6. Ungleichungen 152
§ 7. Irrationale Gleichungen 152
§ 8. Trigonometrische Gleichungen 153
§ 9. Logarithmische Gleichungen 153
§ 10. Exponentialgleichungen 154
§elf. Periodizität, gerade und ungerade Funktionen 154
§ 12. Nullstellen einer komplexen Funktion. Eingeschränkte Funktion 155
§ 13. Definitionsbereich, Wertemenge, Monotonie der Funktionen 156
§ 14. Extrema einer Funktion. Der größte und kleinste Wert der Funktion 158
§ 15. Verschiedene Techniken zur Lösung logarithmischer Gleichungen 159
§ 16. Verschiedene Techniken zur Lösung trigonometrischer Gleichungen 160
§ 17. Verschiedene Techniken zur Lösung irrationaler Gleichungen 164
§ 18. Gleichungen, die eine Variable unter dem Modulzeichen 165 enthalten
§ 19. Verschiedene Techniken zur Lösung von Exponentialgleichungen.166
§ 20. Verschiedene Techniken zur Lösung kombinierter Gleichungen 167
§ 21. Gleichungen mit einem Parameter, der Modul 169 enthält
Literatur 170

Aufgabe B7 gibt einen Ausdruck an, der vereinfacht werden muss. Das Ergebnis sollte eine reguläre Zahl sein, die Sie auf Ihrem Antwortbogen notieren können. Alle Ausdrücke werden herkömmlicherweise in drei Typen unterteilt:

1. Logarithmisch,
2. Indikativ,
3. Kombiniert.

Exponentielle und logarithmische Ausdrücke in reiner Form kommen praktisch nie vor. Es ist jedoch unbedingt erforderlich, zu wissen, wie sie berechnet werden.

Im Allgemeinen ist Aufgabe B7 recht einfach zu lösen und liegt durchaus im Rahmen der Fähigkeiten eines durchschnittlichen Absolventen. Der Mangel an klaren Algorithmen wird durch deren Standardisierung und Monotonie ausgeglichen. Sie können lernen, solche Probleme einfach zu lösen große Menge Ausbildung.

Logarithmische Ausdrücke

Die überwiegende Mehrheit der B7-Aufgaben beinhaltet Logarithmen in der einen oder anderen Form. Dieses Thema gilt traditionell als schwierig, da das Studium meist in der 11. Klasse stattfindet – der Ära der Massenvorbereitung auf die Abschlussprüfungen. Daher haben viele Absolventen ein sehr vages Verständnis von Logarithmen.

Aber für diese Aufgabe benötigt niemand tiefe theoretische Kenntnisse. Wir werden nur die Meisten treffen einfache Ausdrücke, die einfaches Denken erfordern und leicht selbstständig gemeistert werden können. Nachfolgend finden Sie die grundlegenden Formeln, die Sie kennen müssen, um mit Logarithmen umzugehen:

Außerdem müssen Sie in der Lage sein, Wurzeln und Brüche durch Potenzen zu ersetzen rationaler Indikator, sonst gibt es in manchen Ausdrücken einfach nichts, was man unter dem Logarithmuszeichen herausnehmen kann. Ersatzformeln:

Aufgabe. Finden Sie die Bedeutung von Ausdrücken:
log 6 270 − log 6 7,5
log 5 775 − log 5 6.2

Die ersten beiden Ausdrücke werden als Differenz der Logarithmen umgewandelt:
log 6 270 − log 6 7,5 = log 6 (270: 7,5) = log 6 36 = 2;
log 5 775 − log 5 6,2 = log 5 (775: 6,2) = log 5 125 = 3.

Um den dritten Ausdruck zu berechnen, müssen Sie Potenzen isolieren – sowohl in der Basis als auch im Argument. Lassen Sie uns zunächst den internen Logarithmus ermitteln:

Dann - extern:

Konstruktionen der Form log a log b x erscheinen vielen komplex und missverstanden. Mittlerweile ist dies nur ein Logarithmus des Logarithmus, d.h. log a (log b x ). Zuerst wird der interne Logarithmus berechnet (setze log b x = c) und dann der externe: log a c.

Demonstrative Ausdrücke

Wir nennen einen Exponentialausdruck jede Konstruktion der Form a k, wobei die Zahlen a und k beliebige Konstanten sind und a > 0. Die Methoden zum Arbeiten mit solchen Ausdrücken sind recht einfach und werden im Algebraunterricht der 8. Klasse besprochen.

Nachfolgend finden Sie die Grundformeln, die Sie unbedingt kennen müssen. Die Anwendung dieser Formeln in der Praxis bereitet in der Regel keine Probleme.

1. a n · a m = a n + m ;
2. a n / a m = a n − m ;
3. (a n ) m = a n · m ;
4. (a · b ) n = a n · b n ;
5. (a : b ) n = a n : b n .

Wenn Sie auf einen komplexen Ausdruck mit Kräften stoßen und nicht klar sind, wie Sie ihn angehen sollen, verwenden Sie eine universelle Technik – die Zerlegung in einfache Faktoren. Ergebend große Zahlen in den Graduierungsgrundlagen werden durch einfache und verständliche Elemente ersetzt. Dann müssen Sie nur noch die oben genannten Formeln anwenden – und das Problem ist gelöst.

Aufgabe. Finden Sie die Werte der Ausdrücke: 7 9 · 3 11: 21 8, 24 7: 3 6: 16 5, 30 6: 6 5: 25 2.

Lösung. Zerlegen wir alle Grundlagen der Befugnisse in einfache Faktoren:
7 9 3 11: 21 8 = 7 9 3 11: (7 3) 8 = 7 9 3 11: (7 8 3 8) = 7 9 3 11: 7 8: 3 8 = 7 3 3 = 189.
24 7: 3 6: 16 5 = (3 2 3) 7: 3 6: (2 4) 5 = 3 7 2 21: 3 6: 2 20 = 3 2 = 6.
30 6: 6 5: 25 2 = (5 3 2) 6: (3 2) 5: (5 2) 2 = 5 6 3 6 2 6: 3 5: 2 5: 5 4 = 5 2 3 2 = 150 .

Kombinierte Aufgaben

Wenn Sie die Formeln kennen, können alle exponentiellen und logarithmischen Ausdrücke buchstäblich in einer Zeile gelöst werden. Allerdings können in Aufgabe B7 Potenzen und Logarithmen zu recht starken Kombinationen kombiniert werden.

Transnistrisch Staatliche Universität

ihnen. T.G. Schewtschenko

Fakultät für Physik und Mathematik

Abteilung für Mathematische Analyse

und Methoden des Mathematikunterrichts

KURSARBEIT

„Identitätstransformationen

exponentiell und logarithmisch

Ausdrücke"

Arbeit abgeschlossen:

Schüler der Gruppe _______

Fakultät für Physik und Mathematik

_________________________

Ich habe die Arbeit überprüft:

_________________________

Tiraspol, 2003

Einleitung……………………………………………………………………………2

Kapitel 1. Identitätstransformationen und Lehrmethoden im Schulunterricht der Algebra und Beginn der Analysis……………………………………..4

§1. Bildung von Fähigkeiten zur Anwendung spezifischer Arten von Transformationen…………………………………………………………………………………….4

§2. Merkmale der Organisation eines Wissenssystems bei der Untersuchung von Identitätstransformationen.…….………………………….………..………….5

§3. Mathematikprogramm……………………………………………………….11

Kapitel 2. Identische Transformationen und Berechnungen exponentieller und logarithmischer Ausdrücke……………………………...………………13

§1. Verallgemeinerung des Abschlussbegriffs……………………………………..13

§2. Exponentialfunktion……………………………………………………..15

§3. Logarithmische Funktion…………………………………….16

Kapitel 3. Identische Transformationen exponentieller und logarithmischer Ausdrücke in der Praxis...................................... ........................................19

Fazit…………………………………………………………..24

Referenzliste……………………………………………………….25
Einführung

In diesem Kursarbeit Es werden identische Transformationen von Exponential- und Logarithmusfunktionen betrachtet, die Methodik für deren Vermittlung in einem Schulalgebrakurs und der Beginn der Analyse werden betrachtet.

Das erste Kapitel dieser Arbeit beschreibt die Methodik zur Vermittlung von Identitätstransformationen in einem Schulmathematikkurs und beinhaltet auch ein Mathematikprogramm im Kurs „Algebra und Anfänge der Analysis“ mit dem Studium exponentieller und logarithmischer Funktionen.

Das zweite Kapitel untersucht direkt die Exponential- und Logarithmusfunktionen selbst und ihre grundlegenden Eigenschaften, die bei Identitätstransformationen verwendet werden.

Im dritten Kapitel werden Beispiele und Probleme mithilfe identischer Transformationen von Exponential- und Logarithmusfunktionen gelöst.

Das Studium verschiedener Umformungen von Ausdrücken und Formeln nimmt einen erheblichen Teil der Unterrichtszeit des Kurses ein Schulmathematik. Die einfachsten Transformationen basierend auf Eigenschaften Rechenoperationen, werden bereits in produziert Grundschule und in den Klassen IV–V. Die Hauptlast bei der Entwicklung der Fähigkeiten und Fertigkeiten zur Durchführung von Transformationen trägt jedoch der Schulalgebrakurs. Dies ist sowohl auf die starke Zunahme der Zahl und Vielfalt der durchgeführten Transformationen zurückzuführen als auch auf die Komplexität der Aktivitäten zu ihrer Begründung und Klärung der Anwendbarkeitsbedingungen, auf die Identifizierung und Untersuchung der verallgemeinerten Konzepte von Identität, identischer Transformation, äquivalente Transformation, logische Konsequenz.

Die Kultur der Durchführung von Identitätstransformationen entwickelt sich auf die gleiche Weise wie die Kultur der Berechnungen, basierend auf soliden Kenntnissen der Eigenschaften von Operationen an Objekten (Zahlen, Vektoren, Polynome usw.) und Algorithmen zu ihrer Umsetzung. Sie äußert sich nicht nur in der Fähigkeit, Transformationen richtig zu begründen, sondern auch in der Fähigkeit, den kürzesten Weg zum Übergang vom ursprünglichen analytischen Ausdruck zu dem Ausdruck zu finden, der dem Zweck der Transformation am besten entspricht, in der Fähigkeit, Veränderungen zu überwachen der Bereich der Definition analytischer Ausdrücke in einer Kette identischer Transformationen, in der Geschwindigkeit und Genauigkeit der Durchführung von Transformationen.

Sicherheit Hochkultur Berechnungen und Identitätstransformationen darstellt wichtiges Problem Mathematik unterrichten. Allerdings ist dieses Problem noch lange nicht zufriedenstellend gelöst. Ein Beweis dafür sind die statistischen Daten der Behörden öffentliche Bildung, in dem Fehler und irrationale Berechnungs- und Transformationsmethoden von Schülern verschiedener Klassen bei der Durchführung gemacht werden Tests. Dies wird durch Bewertungen von Senioren bestätigt Bildungsinstitutionenüber die Qualität der mathematischen Kenntnisse und Fähigkeiten der Bewerber. Den Schlussfolgerungen der öffentlichen Bildungsbehörden und Universitäten, dass dies nicht ausreicht, kann man nur zustimmen hohes Niveau Kultur des Kalküls und Identitätstransformationen in weiterführende Schule ist eine Folge des Formalismus im Wissen der Studierenden, der Trennung von Theorie und Praxis.

Identische Transformationen und Lehrmethoden

im Schulkurs Algebra und Beginn der Analysis.

§1. Ausbildung von Anwendungskompetenzen

bestimmte Arten von Transformationen.

Das System von Techniken und Regeln zur Durchführung von Transformationen, das in der Anfangsphase der Algebra verwendet wird, hat ein sehr breites Anwendungsspektrum: Es wird im Studium des gesamten Mathematikstudiums verwendet. Gerade wegen seiner geringen Spezifität erfordert dieses System jedoch zusätzliche Transformationen, die die Strukturmerkmale der zu transformierenden Ausdrücke und die Eigenschaften neu eingeführter Operationen und Funktionen berücksichtigen. Die Beherrschung der entsprechenden Transformationsarten beginnt mit der Einführung abgekürzter Multiplikationsformeln. Anschließend werden die mit der Potenzierungsoperation verbundenen Transformationen mit verschiedenen Klassen betrachtet elementare Funktionen– exponentiell, Potenz, logarithmisch, trigonometrisch. Jede dieser Transformationsarten durchläuft eine Lernphase, in der der Schwerpunkt auf der Beherrschung ihrer charakteristischen Merkmale liegt.

Mit zunehmender Materialanhäufung wird es möglich, die Gemeinsamkeiten aller betrachteten Transformationen hervorzuheben und auf dieser Grundlage die Konzepte identischer und äquivalenter Transformationen einzuführen.

Es ist zu beachten, dass das Konzept der Identitätstransformation im Schulalgebrakurs nicht in voller Allgemeinheit, sondern nur in der Anwendung auf Ausdrücke vermittelt wird. Transformationen werden in zwei Klassen unterteilt: identische Transformationen sind Transformationen von Ausdrücken und äquivalente Transformationen sind Transformationen von Formeln. Für den Fall, dass ein Teil der Formel vereinfacht werden muss, wird in dieser Formel ein Ausdruck hervorgehoben, der als Argument für die angewandte Identitätstransformation dient. Das entsprechende Prädikat gilt als unverändert.

Was die Organisation eines integralen Systems von Transformationen (Synthese) betrifft, so besteht ihr Hauptziel darin, ein flexibles und leistungsfähiges System zu bilden; Gerät, das zur Lösung verschiedener Probleme geeignet ist pädagogische Aufgaben.

Im Laufe der Algebra und dem Beginn der Analysis verbessert sich das in seinen Grundzügen bereits gebildete ganzheitliche System von Transformationen schrittweise weiter. Es werden auch einige neue Arten von Transformationen hinzugefügt, die es jedoch nur bereichern, seine Fähigkeiten erweitern, aber seine Struktur nicht verändern. Die Methodik zum Studium dieser neuen Transformationen unterscheidet sich praktisch nicht von der im Algebra-Kurs verwendeten.

§2. Merkmale der Organisation des Aufgabensystems

beim Studium von Identitätstransformationen.

Das Grundprinzip der Organisation eines Aufgabensystems besteht darin, sie von einfach bis komplex darzustellen und dabei die Notwendigkeit zu berücksichtigen, dass die Schüler realisierbare Schwierigkeiten überwinden und etwas schaffen können Problemsituationen. Dieses Grundprinzip bedarf einer Konkretisierung in Bezug auf die Merkmale dieses Lehrmaterials. Zur Beschreibung verschiedener Aufgabensysteme in mathematischen Methoden wird das Konzept eines Übungszyklus verwendet. Der Übungszyklus zeichnet sich dadurch aus, dass in einer Übungsfolge mehrere Aspekte des Lernens und Techniken zur Anordnung des Stoffes kombiniert werden. In Bezug auf Identitätstransformationen kann die Idee eines Zyklus wie folgt gegeben werden.

Der Übungszyklus ist mit dem Studium einer Identität verbunden, um die sich andere Identitäten gruppieren, die in einem natürlichen Zusammenhang mit ihr stehen. Der Zyklus umfasst neben den exekutiven Aufgaben auch Aufgaben, die das Erkennen der Anwendbarkeit der betreffenden Identität erfordern. Die untersuchte Identität wird verwendet, um Berechnungen in verschiedenen numerischen Bereichen durchzuführen. Die Besonderheit der Identität wird berücksichtigt; insbesondere werden die damit verbundenen Redewendungen organisiert.

Die Aufgaben in jedem Zyklus sind in zwei Gruppen unterteilt. Die erste umfasst Aufgaben, die während der ersten Bekanntschaft mit der Identität durchgeführt werden. Sie dienen Unterrichtsmaterial für mehrere aufeinanderfolgende Lektionen, die durch ein Thema vereint sind. Die zweite Übungsgruppe verbindet die untersuchte Identität mit verschiedenen Anwendungen. Diese Gruppe bildet keine kompositorische Einheit – die Übungen sind hier auf verschiedene Themen verteilt.

Die beschriebene Zyklusstruktur bezieht sich auf die Phase der Entwicklung von Fähigkeiten zur Anwendung bestimmter Arten von Transformationen. An letzte Stufe– Im Stadium der Synthese werden die Zyklen verändert. Zunächst werden beide Aufgabengruppen zu einem „erweiterten“ Zyklus zusammengefasst und die hinsichtlich Formulierung oder Komplexität der Aufgabenerledigung einfachsten Aufgaben aus der ersten Gruppe ausgeschlossen. Die übrigen Aufgabentypen werden komplexer. Zweitens kommt es zu einer Verschmelzung von Zyklen im Zusammenhang mit unterschiedlichen Identitäten, wodurch die Rolle von Maßnahmen zur Anerkennung der Anwendbarkeit einer bestimmten Identität zunimmt.

Beachten wir die Merkmale von Aufgabenzyklen im Zusammenhang mit Identitäten für Elementarfunktionen. Diese Merkmale sind darauf zurückzuführen, dass erstens die entsprechenden Identitäten im Zusammenhang mit der Untersuchung von Funktionsmaterial untersucht werden und zweitens später als die Identitäten der ersten Gruppe auftreten und unter Verwendung bereits ausgebildeter Fähigkeiten zur Durchführung von Identitätstransformationen untersucht werden .

Jede neu eingeführte Elementarfunktion erweitert den Bereich der Zahlen, die individuell bezeichnet und benannt werden können, dramatisch. Daher sollte die erste Gruppe von Zyklusaufgaben Aufgaben umfassen, um eine Verbindung zwischen diesen neuen numerischen Bereichen und dem ursprünglichen Bereich herzustellen Rationale Zahlen. Lassen Sie uns Beispiele für solche Aufgaben geben.

Beispiel 1. Berechnen Sie:

Neben jedem Ausdruck wird eine Identität angegeben, in den Zyklen, für die die vorgeschlagenen Aufgaben vorhanden sein können. Der Zweck solcher Aufgaben besteht darin, die Merkmale von Datensätzen, einschließlich der Symbole neuer Operationen und Funktionen, zu beherrschen und mathematische Sprachfähigkeiten zu entwickeln.

Ein wesentlicher Teil der Verwendung von Identitätstransformationen im Zusammenhang mit Elementarfunktionen entfällt auf die Lösung irrationaler und transzendentaler Gleichungen. Die Zyklen im Zusammenhang mit der Assimilation von Identitäten umfassen nur die meisten einfache Gleichungen, aber schon hier empfiehlt es sich, an der Beherrschung der Methode zur Lösung solcher Gleichungen zu arbeiten: Reduzierung durch Ersetzen des Unbekannten durch algebraische Gleichung.

Die Abfolge der Schritte für diese Lösung ist wie folgt:

a) Finden Sie die Funktion, für die gegebene Gleichung darstellbar in der Form ;

b) Führen Sie die Substitution durch und lösen Sie die Gleichung.

c) Lösen Sie jede der Gleichungen, wobei die Menge der Wurzeln der Gleichung ist.

Bei Verwendung der beschriebenen Methode wird Schritt b) häufig implizit durchgeführt, ohne eine Notation für einzuführen. Darüber hinaus ziehen es Studierende häufig vor, von den verschiedenen Wegen, die zur Lösung führen, denjenigen auszuwählen, der schneller und einfacher zur algebraischen Gleichung führt.

Beispiel 2. Lösen Sie die Gleichung.

Erster Weg:

Zweiter Weg:

A)

B)

Hier sieht man, dass Schritt a) bei der ersten Methode schwieriger ist als bei der zweiten. Die erste Methode sei „zu Beginn schwieriger“, obwohl der weitere Lösungsverlauf deutlich einfacher sei. Andererseits bietet die zweite Methode den Vorteil, dass das Erlernen der Reduktion auf eine algebraische Gleichung einfacher und präziser ist.

Für Schulkurs Typisch sind Algebraaufgaben, bei denen der Übergang zu einer algebraischen Gleichung noch einfacher ist als in diesem Beispiel. Die Hauptaufgabe solcher Aufgaben besteht darin, Schritt c) als eigenständigen Teil des Lösungsprozesses zu identifizieren, der mit der Nutzung der Eigenschaften der untersuchten Elementarfunktion verbunden ist.

Beispiel 3. Lösen Sie die Gleichung:

A) ; B) .

Diese Gleichungen werden auf die Gleichungen: a) oder ; b) oder . Das Lösen dieser Gleichungen erfordert nur die Kenntnis der einfachsten Fakten Exponentialfunktion: seine Monotonie, Wertebereich. Wie das vorherige Beispiel können die Gleichungen a) und b) als erste Gruppe einer Reihe von Übungen zur Lösung quadratischer Exponentialgleichungen klassifiziert werden.

Somit kommen wir zu einer Einteilung der Aufgaben in Zyklen im Zusammenhang mit der Lösung transzendenter Gleichungen, die eine Exponentialfunktion beinhalten:

1) Gleichungen, die sich auf Gleichungen der Form reduzieren lassen und eine einfache, allgemeine Antwort haben: ;

2) Gleichungen, die sich auf Gleichungen reduzieren lassen, bei denen es sich um eine ganze Zahl handelt, oder bei denen;

3) Gleichungen, die sich auf Gleichungen reduzieren lassen und eine explizite Analyse der Schreibweise der Zahl erfordern.

Aufgaben für andere Elementarfunktionen können ähnlich klassifiziert werden.

Ein wesentlicher Teil der in Algebra und Algebra untersuchten Identitäten und Prinzipien der Analysekurse wird in ihnen bewiesen oder zumindest erklärt. Diese Seite des Studiums der Identitäten hat sehr wichtig für beide Kurse, da die Beweisführung in ihnen gerade in Bezug auf Identitäten mit größter Klarheit und Genauigkeit durchgeführt wird. Über dieses Material hinaus sind die Beweise in der Regel weniger vollständig und unterscheiden sich nicht immer von der verwendeten Begründung.

Die Eigenschaften arithmetischer Operationen werden als Grundlage für die Erstellung von Identitätsnachweisen verwendet.

Die pädagogische Wirkung von Berechnungen und identischen Transformationen kann auf die Entwicklung des logischen Denkens abzielen, wenn die Schüler nur systematisch aufgefordert werden, Berechnungen und identische Transformationen zu begründen, und auf die Entwicklung des funktionalen Denkens, die auf verschiedene Weise erreicht wird. Die Bedeutung von Berechnungen und identischen Transformationen für die Entwicklung von Willen, Gedächtnis, Intelligenz, Selbstbeherrschung und kreativer Initiative liegt auf der Hand.

Die Anforderungen der alltäglichen und industriellen Computerpraxis erfordern von den Studierenden die Entwicklung starker, automatisierter Fähigkeiten in rationalen Berechnungen und Identitätstransformationen. Diese Fähigkeiten werden im Laufe jeder Rechenarbeit entwickelt, es sind jedoch spezielle Trainingsübungen in schnellen Berechnungen und Transformationen erforderlich.

Wenn es in der Lektion also darum geht, logarithmische Gleichungen unter Verwendung der grundlegenden logarithmischen Identität zu lösen, ist es sinnvoll, mündliche Übungen zur Vereinfachung oder Berechnung der Werte von Ausdrücken in den Unterrichtsplan aufzunehmen: , , . Der Zweck der Übungen wird den Studierenden stets kommuniziert. Im Rahmen der Übung kann es erforderlich sein, dass Studierende einzelne Umgestaltungen, Handlungen oder die Lösung eines gesamten Problems begründen müssen, auch wenn dies nicht geplant war. Wo möglich verschiedene Wege Beim Lösen eines Problems ist es ratsam, immer Fragen zu stellen: „Wie wurde das Problem gelöst?“, „Wer hat das Problem anders gelöst?“

Die Konzepte der Identität und Identitätstransformation werden im Algebrakurs der VI. Klasse explizit eingeführt. Die Definition selbst identische Ausdrücke kann praktisch nicht verwendet werden, um die Identität zweier Ausdrücke zu beweisen und zu verstehen, dass das Wesen identischer Transformationen darin besteht, die Definitionen und Eigenschaften der im Ausdruck angegebenen Aktionen auf den Ausdruck anzuwenden oder ihm einen identischen Ausdruck hinzuzufügen gleich 0, oder um es mit dem Ausdruck zu multiplizieren, identisch gleich eins. Aber selbst wenn Studierende diese Bestimmungen beherrschen, verstehen sie oft nicht, warum diese Transformationen uns die Behauptung erlauben, dass die ursprünglichen und resultierenden Ausdrücke identisch sind, d.h. Nehmen Sie für alle Systeme (Mengen) von Variablenwerten die gleichen Werte an.

Es ist auch wichtig sicherzustellen, dass die Studierenden klar verstehen, dass solche Schlussfolgerungen identischer Transformationen Konsequenzen der Definitionen und Eigenschaften der entsprechenden Aktionen sind.

Der in den Vorjahren aufgebaute Apparat der Identitätstransformationen wird in der Jahrgangsstufe VI erweitert. Diese Erweiterung beginnt mit der Einführung einer Identität, die die Eigenschaft des Produkts von Potenzen mit denselben Basen ausdrückt: , wobei , ganze Zahlen sind.

§3. Mathematikprogramm. Im Schulkurs „Algebra und die Anfänge der Analysis“ beschäftigen sich die Studierenden systematisch mit exponentiellen und logarithmischen Funktionen und ihren Eigenschaften, identischen Transformationen logarithmischer und exponentieller Ausdrücke und deren Anwendung zur Lösung der entsprechenden Gleichungen und Ungleichungen und machen sich mit grundlegenden Konzepten und Aussagen vertraut . In der 11. Klasse umfasst der Algebraunterricht 3 Stunden pro Woche, also insgesamt 102 Stunden pro Jahr. Das Programm benötigt 36 Stunden, um Exponential-, Logarithmus- und Potenzfunktionen zu studieren. Das Programm umfasst die Betrachtung und Untersuchung der folgenden Themen: Das Konzept eines Abschlusses mit einem rationalen Exponenten. Irrationale Gleichungen lösen. Exponentialfunktion, ihre Eigenschaften und Diagramm. Identische Transformationen von Exponentialausdrücken. Exponentielle Gleichungen und Ungleichungen lösen. Logarithmus einer Zahl. Grundlegende Eigenschaften von Logarithmen. Logarithmische Funktion, ihre Eigenschaften und Diagramm. Logarithmische Gleichungen und Ungleichungen lösen. Ableitung einer Exponentialfunktion. Anzahl und natürlicher Logarithmus. Ableitung einer Potenzfunktion. Der Hauptzweck des Abschnitts über exponentielle und logarithmische Funktionen besteht darin, die Schüler mit exponentiellen, logarithmischen und Potenzfunktionen vertraut zu machen. Bringen Sie den Schülern bei, exponentielle und zu lösen logarithmische Gleichungen und Ungleichheiten. Die Konzepte der Wurzel und des Grades mit rationalem Exponenten sind eine Verallgemeinerung der Konzepte der Quadratwurzel und des Grades mit ganzzahligem Exponenten. Die Studierenden sollten darauf achten, dass die hier betrachteten Eigenschaften von Wurzeln und Potenzen mit rationalem Exponenten denen zuvor untersuchter Eigenschaften ähneln Quadratwurzeln und Grade mit ganzzahligen Exponenten. Es ist notwendig, genügend Zeit darauf zu verwenden, die Eigenschaften von Abschlüssen zu üben und die Fähigkeiten zur Identitätstransformation zu entwickeln. Konzept des Abschlusses c irrationaler Indikator wird visuell und intuitiv eingeführt. Dieses Material spielt eine Hilfsrolle und wird bei der Einführung der Exponentialfunktion verwendet. Die Untersuchung der Eigenschaften von Exponential-, Logarithmus- und Potenzfunktionen erfolgt nach dem anerkannten allgemeinen Schema zur Untersuchung von Funktionen. In diesem Fall wird eine Übersicht über die Eigenschaften in Abhängigkeit von den Parameterwerten gegeben. Illustrativ und logarithmische Ungleichungen werden basierend auf den untersuchten Eigenschaften von Funktionen gelöst. Charakteristisches Merkmal Der Kurs dient der Systematisierung und Verallgemeinerung des Wissens der Studierenden, der Festigung und Entwicklung der im Algebra-Kurs erworbenen Fähigkeiten, die sowohl beim Studium neuer Materialien als auch bei der Durchführung verallgemeinerter Wiederholungen durchgeführt wird.
Kapitel 2. Identische Transformationen und Berechnungen exponentieller und logarithmischer Ausdrücke

§1. Verallgemeinerung des Abschlussbegriffs.

Definition: Die Wurzel einer reinen Zahl ist eine Zahl, deren Potenz gleich ist.

Entsprechend diese Definition Die Wurzel einer Zahl ist die Lösung der Gleichung. Die Anzahl der Wurzeln dieser Gleichung hängt von und ab. Betrachten wir die Funktion. Wie Sie wissen, erhöht sich diese Funktion im Intervall für jeden Wert und nimmt alle Werte aus dem Intervall. Nach dem Wurzelsatz hat die Gleichung für jede eine nichtnegative Wurzel und darüber hinaus nur eine. Sie wird als arithmetische Wurzel des ten Grades einer Zahl bezeichnet und mit ; ​​bezeichnet. Die Zahl wird als Wurzelexponent bezeichnet, und die Zahl selbst wird als Wurzelausdruck bezeichnet. Das Zeichen wird auch Radikal genannt.

Definition: Man nennt die arithmetische Wurzel der Potenz einer Zahl nicht negative Zahl, dessen -ter Grad gleich ist.

Für gerade Zahlen ist die Funktion gerade. Daraus folgt, dass wenn die Gleichung zusätzlich zur Wurzel auch eine Wurzel hat. Wenn , dann gibt es eine Wurzel: ; wenn , dann hat diese Gleichung seitdem keine Wurzeln sogar Grad Jede Zahl ist nicht negativ.

Bei ungeraden Werten steigt die Funktion entlang des gesamten Zahlenstrahls; sein Bereich ist die Menge aller reellen Zahlen. Wenn wir den Wurzelsatz anwenden, finden wir, dass die Gleichung für jedes und insbesondere für eine Wurzel hat. Diese Wurzel für jeden Wert wird mit bezeichnet.

Für Wurzeln ungeraden Grades gilt die Gleichheit. Tatsächlich, d.h. Zahl ist die Wurzel von . Aber eine solche Wurzel für seltsam ist die einzige. Somit, .

Bemerkung 1: Für jeden echten

Erinnern wir uns an die bekannten Eigenschaften arithmetischer Wurzeln t-Grades.

Für jede natürliche Zahl, ganze Zahl und alle nichtnegativen ganzen Zahlen und die Gleichungen gelten:

1.

2.

3.

4.

Grad mit einem rationalen Exponenten.

Der Ausdruck ist für alle und definiert, außer im Fall von . Erinnern wir uns an die Eigenschaften solcher Kräfte.

Für alle Zahlen, alle ganzen Zahlen und die Gleichungen gilt:

Wir stellen außerdem fest, dass wenn , dann für und für .. und

Für Schüler des Einheitlichen Staatsexamens verwenden Mathematiklehrer der Sekundarschule Nr. 26 in Jakutsk einen Inhaltsfragenkatalog (Kodifizierer) für den Schulmathematikkurs, dessen Beherrschung beim Bestehen des Einheitlichen Staatsexamens 2007 geprüft wird. Wahlfachüber die Vorbereitung auf die Einheit Staatsexamen basierend auf Wiederholung, Systematisierung und Vertiefung bereits erworbener Kenntnisse. Der Unterricht findet in Form von kostenlosen... statt.