Rationale Funktion ist ein Bruch der Form , dessen Zähler und Nenner Polynome oder Produkte von Polynomen sind.

Beispiel 1. Schritt 2.

.

Wir multiplizieren die unbestimmten Koeffizienten mit Polynomen, die nicht in diesem einzelnen Bruch, sondern in anderen resultierenden Brüchen vorkommen:

Wir öffnen die Klammern und setzen den Zähler des ursprünglichen Integranden mit dem resultierenden Ausdruck gleich:

Auf beiden Seiten der Gleichheit suchen wir nach Termen mit gleichen Potenzen von x und stellen daraus ein Gleichungssystem auf:

.

Wir streichen alle x und erhalten ein äquivalentes Gleichungssystem:

.

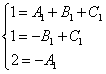Somit ist die endgültige Entwicklung des Integranden in eine Summe einfacher Brüche:

.

Beispiel 2. Schritt 2. In Schritt 1 haben wir die folgende Zerlegung des ursprünglichen Bruchs in die Summe einfacher Brüche mit unbestimmten Koeffizienten in den Zählern erhalten:

.

Jetzt beginnen wir mit der Suche nach unsicheren Koeffizienten. Dazu setzen wir den Zähler des ursprünglichen Bruchs im Funktionsausdruck mit dem Zähler des Ausdrucks gleich, den man erhält, nachdem man die Summe der Brüche auf reduziert hat gemeinsamer Nenner:

Jetzt müssen Sie ein Gleichungssystem erstellen und lösen. Dazu setzen wir die Koeffizienten der Variablen mit dem entsprechenden Grad im Zähler des ursprünglichen Ausdrucks der Funktion und ähnlichen Koeffizienten im im vorherigen Schritt erhaltenen Ausdruck gleich:

Wir lösen das resultierende System:

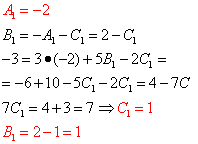
Also, von hier aus

.

Beispiel 3. Schritt 2. In Schritt 1 haben wir die folgende Zerlegung des ursprünglichen Bruchs in die Summe einfacher Brüche mit unbestimmten Koeffizienten in den Zählern erhalten:

Wir beginnen, nach unsicheren Koeffizienten zu suchen. Dazu setzen wir den Zähler des ursprünglichen Bruchs im Funktionsausdruck mit dem Zähler des Ausdrucks gleich, den man erhält, nachdem man die Summe der Brüche auf einen gemeinsamen Nenner reduziert hat:

Wie in den vorherigen Beispielen stellen wir ein Gleichungssystem auf:

Wir reduzieren die x und erhalten ein äquivalentes Gleichungssystem:

Wenn wir das System lösen, erhalten wir die folgenden Werte der unsicheren Koeffizienten:

Wir erhalten die endgültige Zerlegung des Integranden in die Summe einfacher Brüche:

.

Beispiel 4. Schritt 2. In Schritt 1 haben wir die folgende Zerlegung des ursprünglichen Bruchs in die Summe einfacher Brüche mit unbestimmten Koeffizienten in den Zählern erhalten:

.

Aus früheren Beispielen wissen wir bereits, wie man den Zähler des ursprünglichen Bruchs mit dem Ausdruck im Zähler gleichsetzt, den man erhält, nachdem man den Bruch in die Summe einfacher Brüche zerlegt und diese Summe auf einen gemeinsamen Nenner gebracht hat. Aus Gründen der Kontrolle stellen wir daher das resultierende Gleichungssystem vor:

Wenn wir das System lösen, erhalten wir die folgenden Werte der unsicheren Koeffizienten:

Wir erhalten die endgültige Zerlegung des Integranden in die Summe einfacher Brüche:

Beispiel 5. Schritt 2. In Schritt 1 haben wir die folgende Zerlegung des ursprünglichen Bruchs in die Summe einfacher Brüche mit unbestimmten Koeffizienten in den Zählern erhalten:

.

Wir reduzieren diese Summe unabhängig auf einen gemeinsamen Nenner und setzen den Zähler dieses Ausdrucks mit dem Zähler des ursprünglichen Bruchs gleich. Das Ergebnis sollte das folgende Gleichungssystem sein:

Wenn wir das System lösen, erhalten wir die folgenden Werte der unsicheren Koeffizienten:

.

Wir erhalten die endgültige Zerlegung des Integranden in die Summe einfacher Brüche:

.

Beispiel 6. Schritt 2. In Schritt 1 haben wir die folgende Zerlegung des ursprünglichen Bruchs in die Summe einfacher Brüche mit unbestimmten Koeffizienten in den Zählern erhalten:

Mit diesem Betrag führen wir die gleichen Aktionen aus wie in den vorherigen Beispielen. Das Ergebnis sollte das folgende Gleichungssystem sein:

Wenn wir das System lösen, erhalten wir die folgenden Werte der unsicheren Koeffizienten:

.

Wir erhalten die endgültige Zerlegung des Integranden in die Summe einfacher Brüche:

.

Beispiel 7. Schritt 2. In Schritt 1 haben wir die folgende Zerlegung des ursprünglichen Bruchs in die Summe einfacher Brüche mit unbestimmten Koeffizienten in den Zählern erhalten:

.

Nach bestimmten Aktionen mit der resultierenden Menge sollte sich folgendes Gleichungssystem ergeben:

Wenn wir das System lösen, erhalten wir die folgenden Werte der unsicheren Koeffizienten:

Wir erhalten die endgültige Zerlegung des Integranden in die Summe einfacher Brüche:

.

Beispiel 8. Schritt 2. In Schritt 1 haben wir die folgende Zerlegung des ursprünglichen Bruchs in die Summe einfacher Brüche mit unbestimmten Koeffizienten in den Zählern erhalten:

.

Nehmen wir einige Änderungen an den bereits automatisierten Aktionen vor, um ein Gleichungssystem zu erhalten. Es gibt eine künstliche Technik, die in manchen Fällen hilft, unnötige Berechnungen zu vermeiden. Indem wir die Summe der Brüche auf einen gemeinsamen Nenner bringen, erhalten wir und indem wir den Zähler dieses Ausdrucks mit dem Zähler des ursprünglichen Bruchs gleichsetzen, erhalten wir.

Grüße an alle, liebe Freunde!

Herzlichen Glückwunsch! Wir sind sicher beim Hauptmaterial der Integration rationaler Brüche angelangt – Methode der unsicheren Koeffizienten. Groß und mächtig.) Was ist seine Majestät und Macht? Und es liegt in seiner Vielseitigkeit. Es macht Sinn, es sich anzusehen, oder? Ich warne Sie, dass es zu diesem Thema mehrere Lektionen geben wird. Weil das Thema sehr lang ist und das Material äußerst wichtig ist.)

Ich sage gleich, dass wir uns in der heutigen Lektion (und auch in den folgenden) nicht so sehr mit Integration befassen werden, sondern... Systemlösung lineare Gleichungen! Ja Ja! Wer also Probleme mit Systemen hat, wiederholt die Matrizen, Determinanten und die Cramer-Methode. Und diejenigen Genossen, die Probleme mit Matrizen haben, bitte ich dringend, im schlimmsten Fall ihr Gedächtnis zumindest an die „schulischen“ Methoden zur Lösung von Systemen aufzufrischen – die Substitutionsmethode und die Term-für-Term-Additions-/Subtraktionsmethode.

Um unsere Bekanntschaft zu beginnen, spulen wir den Film etwas zurück. Kehren wir kurz zu den vorherigen Lektionen zurück und analysieren alle Brüche, die wir zuvor integriert haben. Direkt, ohne Methode unbestimmter Koeffizienten! Hier sind sie, diese Brüche. Ich habe sie in drei Gruppen eingeteilt.

Gruppe 1

Im Nenner - lineare Funktion entweder alleine oder bis zu einem Grad. Mit einem Wort: Der Nenner ist das Produkt identisch Klammern des Formulars (Ha).

Zum Beispiel:

(x+4) 1 = (x+4)

(x-10) 2 = (x-10)(x-10)

(2x+5) 3 = (2x+5)(2x+5)(2x+5)

Usw. Lassen Sie sich übrigens nicht durch die Klammern verwirren (4x+5) oder (2x+5) 3 mit Koeffizient k innen. Im Kern handelt es sich hierbei immer noch um Klammern des Formulars (Ha). Denn das ist das Meiste k Mit solchen Halterungen können Sie es jederzeit nach draußen bringen.

So:

Das ist alles.) Und es spielt keine Rolle, was genau im Zähler steht – einfach dx oder eine Art Polynom. Wir haben den Zähler immer in Potenzen der Klammer erweitert (x-a), wandelte den großen Bruch in die Summe der kleinen um, setzte (wo nötig) eine Klammer unter das Differential und integrierte.

Gruppe 2

Was haben diese Brüche gemeinsam?

Und das Gemeinsame ist, dass es in allen Nennern etwas gibt quadratisches TrinomAxt 2 + bx+ C. Aber nicht nur, nämlich in einer einzigen Kopie. Dabei spielt es keine Rolle, ob seine Diskriminante positiv oder negativ ist.

Solche Brüche wurden immer auf eine von zwei Arten integriert – entweder durch Erweitern des Zählers in Potenzen des Nenners oder durch Isolieren des perfekten Quadrats im Nenner und anschließendes Ersetzen der Variablen. Es hängt alles vom jeweiligen Integranden ab.

Gruppe 3

Dies waren die am schlechtesten zu integrierenden Fraktionen. Der Nenner enthält ein unzerlegbares quadratisches Trinom, und zwar bis zum Grad N. Aber wieder, in einer einzigen Kopie. Denn außer dem Trinom gibt es im Nenner keine weiteren Faktoren. Solche Brüche wurden über integriert. Entweder direkt oder darauf reduziert, nachdem das perfekte Quadrat im Nenner isoliert und anschließend die Variable ersetzt wurde.

Leider beschränkt sich die gesamte reiche Vielfalt rationaler Brüche nicht nur auf diese drei betrachteten Gruppen.

Aber was ist, wenn der Nenner ist anders Klammern? Zum Beispiel so etwas wie:

(x-1)(x+1)(x+2)

Oder gleichzeitig eine Klammer (Ha) und ein quadratisches Trinom, so etwas wie (x-10)(x 2 -2x+17)? Und in anderen ähnlichen Fällen? Gerade in solchen Fällen kommt es zur Rettung Methode der unsicheren Koeffizienten!

Ich sage gleich: Vorerst arbeiten wir nur mit richtig in Brüchen. Diejenigen, deren Zählergrad streng kleiner als der Nennergrad ist. Wie man damit umgeht, nicht richtige Brüche, detailliert in Brüchen beschrieben. Es ist notwendig, den gesamten Teil (Polynom) auszuwählen. Indem Sie den Zähler durch den Nenner mit einer Ecke dividieren oder den Zähler zerlegen – ganz wie Sie möchten. Und sogar das Beispiel wird analysiert. Und Sie werden das Polynom irgendwie integrieren. Nicht schon klein.) Aber weiter unechte Brüche Lassen Sie uns auch Beispiele lösen!

Und jetzt beginnen wir uns kennenzulernen. Im Gegensatz zu den meisten Lehrbüchern zur höheren Mathematik beginnen wir unsere Bekanntschaft nicht mit einer trockenen und schweren Theorie über den Grundsatz der Algebra, den Satz von Bezout, über die Zerlegung eines rationalen Bruchs in die Summe des einfachsten (mehr zu diesen Brüchen später) und andere langweilig, aber wir beginnen mit einem einfachen Beispiel.

Beispielsweise müssen wir das folgende unbestimmte Integral finden:

Schauen Sie sich zunächst den Integranden an. Der Nenner ist das Produkt aus drei Klammern:

(x-1)(x+3)(x+5)

Und alle Klammern anders. Daher funktioniert unsere alte Technik mit der Erweiterung des Zählers um Potenzen des Nenners dieses Mal nicht mehr: Welche Klammer soll im Zähler hervorgehoben werden? (x-1)? (x+3)? Es ist nicht klar ... Es ist auch keine gute Idee, im Nenner ein vollständiges Quadrat zu wählen: Da gibt es ein Polynom dritte Grad (wenn Sie alle Klammern multiplizieren). Was zu tun ist?

Beim Betrachten unserer Fraktion entsteht ein ganz natürliches Verlangen... Geradezu unwiderstehlich! Aus unserer großen Fraktion, die unbequem integrieren, irgendwie drei kleine machen. Zumindest so:

Warum sollten Sie nach dieser besonderen Art suchen? Und das alles, weil unser Anfangsanteil bereits in dieser Form vorliegt komfortabel für Integration! Fassen wir den Nenner jedes kleinen Bruchs zusammen und - vorwärts.)

Ist eine solche Zerlegung überhaupt möglich? Gute Nachrichten! Der entsprechende Satz in der Mathematik besagt: Ja, du kannst! Eine solche Zerlegung existiert und ist einzigartig.

Aber es gibt ein Problem: die Koeffizienten A, IN Und MIT Wir Tschüss wir wissen es nicht. Und jetzt wird unsere Hauptaufgabe genau sein Identifizieren Sie sie. Finden Sie heraus, was unsere Buchstaben bedeuten A, IN Und MIT. Daher der Name - Methode unsicher Koeffizienten Beginnen wir unsere fabelhafte Reise!

Wir haben also eine Gleichheit, die uns zum Tanzen bringt:

Bringen wir alle drei Brüche rechts auf einen gemeinsamen Nenner und addieren:

Jetzt können wir die Nenner getrost verwerfen (da sie gleich sind) und die Zähler einfach gleichsetzen. Alles ist wie immer

Nächster Schritt Öffnen Sie alle Klammern(Koeffizienten A, IN Und MIT Tschüss lieber draußen lassen):

Und jetzt (wichtig!) richten wir unsere gesamte Struktur auf der rechten Seite aus nach Dienstalter der Abschlüsse: Zuerst sammeln wir alle Terme mit x 2 auf einem Stapel, dann nur mit x und schließlich sammeln wir die freien Terme. Tatsächlich präsentieren wir einfach ähnliche und gruppieren die Terme nach Potenzen von x.

So:

Lassen Sie uns nun das Ergebnis verstehen. Links ist unser ursprüngliches Polynom. Zweiter Grad. Der Zähler unseres Integranden. Auch rechts ein Polynom zweiten Grades. Nase unbekannte Koeffizienten. Diese Gleichheit muss gültig sein, wenn alle akzeptable Werte X. Die Brüche links und rechts waren gleich (entsprechend unserer Bedingung)! Das bedeutet, dass sie Zähler und (d. h. unsere Polynome) sind ebenfalls gleich. Daher die Koeffizienten bei den gleichen Potenzen von x Diese Polynome müssen haben sei gleich!

Wir beginnen mit dem höchsten Abschluss. Vom Platz. Mal sehen, welche Art von Koeffizienten wir haben X 2 links und rechts. Rechts sehen wir die Summe der Koeffizienten A+B+C, und auf der linken Seite ist eine Zwei. So entsteht unsere erste Gleichung.

Wir schreiben auf:

A+B+C = 2

Essen. Die erste Gleichung ist fertig.)

Als nächstes folgen wir einer abnehmenden Trajektorie – wir betrachten Terme mit X in der ersten Potenz. Rechts bei X haben wir 8A+4B+2C. Bußgeld. Und was haben wir mit dem X auf der linken Seite? Hm... Links gibt es überhaupt keinen Begriff mit einem X! Es gibt nur 2x 2 - 3. Was tun? Sehr einfach! Dies bedeutet, dass der Koeffizient von x auf der linken Seite ist gleich Null! Wir können unsere linke Seite so schreiben:

Und was? Wir haben jedes Recht.) Daher sieht die zweite Gleichung so aus:

8 A+4 B+2 C = 0

Nun, das ist praktisch alles. Es bleibt die Gleichsetzung der freien Begriffe:

15A-5B-3C = -3

Kurz gesagt, die Gleichsetzung der Koeffizienten für die gleichen Potenzen von x erfolgt nach dem folgenden Schema:

Alle drei unserer Gleichheiten müssen erfüllt sein gleichzeitig. Deshalb stellen wir aus unseren geschriebenen Gleichungen ein System zusammen:

Für einen fleißigen Schüler ist das System nicht das schwierigste – drei Gleichungen und drei Unbekannte. Entscheiden Sie, wie Sie möchten. Sie können die Cramer-Methode durch Matrizen mit Determinanten verwenden, Sie können die Gauß-Methode verwenden, Sie können sogar die übliche Schulsubstitution verwenden.

Zunächst werde ich dieses System so lösen, wie Kulturstudenten solche Systeme normalerweise lösen. Nämlich die Cramer-Methode.

Wir beginnen die Lösung mit der Erstellung einer Systemmatrix. Ich möchte Sie daran erinnern, dass diese Matrix nur eine Platte ist, die aus besteht Koeffizienten für Unbekannte.

Da ist sie:

Lassen Sie uns zunächst einmal rechnen Determinante der Systemmatrix. Oder kurz gesagt: Systemdeterminante. Es wird normalerweise bezeichnet griechischer Brief∆ („Delta“):

Großartig, die Systemdeterminante ist nicht Null (-48).≠0) . Aus der Theorie linearer Gleichungssysteme bedeutet diese Tatsache, dass unser System konsistent ist und hat eine einzigartige Lösung.

Der nächste Schritt ist die Berechnung Determinanten von Unbekannten ∆A, ∆B, ∆C. Ich möchte Sie daran erinnern, dass jede dieser drei Determinanten aus der Hauptdeterminante des Systems erhalten wird, indem die Spalten mit Koeffizienten für die entsprechenden Unbekannten durch eine Spalte mit freien Termen ersetzt werden.

Also bilden wir die Determinanten und berechnen:

Ich werde die Technik zur Berechnung von Determinanten dritter Ordnung hier nicht im Detail erläutern. Und frag nicht. Dies wird eine völlige Abweichung vom Thema sein.) Diejenigen, die sich mit dem Thema befassen, verstehen, wovon wir sprechen. Und vielleicht haben Sie bereits genau erraten, wie ich diese drei Determinanten berechnet habe.)

Das war’s, alles ist fertig.)

Auf diese Weise lösen gebildete Schüler normalerweise Systeme. Aber... Nicht alle Studenten sind mit ihnen befreundet und qualifiziert. Leider. Für einige diese einfache Konzepte Die höhere Mathematik wird für immer ein chinesischer Buchstabe und ein mysteriöses Monster im Nebel bleiben ...

Nun, insbesondere für solch unkultivierte Studenten schlage ich eine vertrautere Lösung vor – Methode zur sequentiellen Eliminierung von Unbekannten. Tatsächlich handelt es sich hierbei um eine fortgeschrittene „schulische“ Substitutionsmethode. Es wird nur noch mehr Schritte geben.) Aber das Wesentliche ist dasselbe. Als Erstes werde ich die Variable entfernen MIT. Um dies zu tun, werde ich es zum Ausdruck bringen MIT aus der ersten Gleichung und setze sie in die zweite und dritte ein:

Wir vereinfachen, bringen ähnliche mit und erhalten ein neues System, bereits mit zwei Unbekannt:

In diesem neuen System ist es nun auch möglich, eine der Variablen durch eine andere auszudrücken. Aber die aufmerksamsten Schüler werden wahrscheinlich bemerken, dass die Koeffizienten vor der Variablen stehen B – Gegenteil. Zwei und minus zwei. Daher ist es sehr praktisch, beide Gleichungen zu addieren, um die Variable zu eliminieren IN und lass nur den Brief A.

Wir fügen den linken und rechten Teil hinzu und verkürzen ihn gedanklich 2B Und -2B und löse die Gleichung nur relativ A:

Essen. Der erste Koeffizient wurde gefunden: A = -1/24.

Bestimmen Sie den zweiten Koeffizienten IN. Zum Beispiel aus der oberen Gleichung:

Von hier aus erhalten wir:

Großartig. Der zweite Koeffizient wurde ebenfalls gefunden: B = -15/8 . Es ist noch ein Brief übrig MIT. Um es zu bestimmen, verwenden wir die oberste Gleichung, in der wir es ausdrücken A Und IN:

Also:

OK, jetzt ist alles vorbei. Unbekannte Quoten gefunden! Egal ob durch Cramer oder durch Einwechslung. Hauptsächlich, Rechts gefunden.)

Daher wird unsere Zerlegung eines großen Bruchs in die Summe kleiner Brüche so aussehen:

Und lassen Sie sich nicht von den resultierenden Bruchkoeffizienten verwirren: Bei diesem Verfahren (der Methode der unbestimmten Koeffizienten) ist dies das häufigste Phänomen. :) :)

Jetzt ist es sehr ratsam zu überprüfen, ob wir unsere Koeffizienten richtig ermittelt haben A, B Und MIT. Deshalb nehmen wir jetzt den Entwurf und erinnern uns an die achte Klasse – wir fügen alle drei unserer kleinen Brüche wieder hinzu.

Wenn wir den ursprünglichen großen Bruch erhalten, ist alles in Ordnung. Nein – das heißt, schlag mich und suche nach einem Fehler.

Der gemeinsame Nenner wird offensichtlich 24(x-1)(x+3)(x+5) sein.

Gehen:

Ja!!! Wir haben den ursprünglichen Bruch erhalten. Das musste überprüft werden. Alles ist gut. Also schlagen Sie mich bitte nicht.)

Kehren wir nun zu unserem ursprünglichen Integral zurück. Er ist in dieser Zeit nicht einfacher geworden, ja. Aber jetzt, wo unser Bruchteil in eine Summe kleiner Bruchteile zerlegt wurde, ist es ein wahres Vergnügen geworden, ihn zu integrieren!

Überzeugen Sie sich selbst! Wir fügen unsere Entwicklung in das ursprüngliche Integral ein.

Wir bekommen:

Wir nutzen die Eigenschaften der Linearität und teilen unser großes Integral in eine Summe kleiner Integrale auf, wobei wir alle Konstanten außerhalb der Integralzeichen platzieren.

Wir bekommen:

Und die resultierenden drei kleinen Integrale sind bereits leicht zu berechnen .

Wir setzen die Integration fort:

Das ist alles.) Und fragen Sie mich in dieser Lektion nicht, woher die Logarithmen in der Antwort kommen! Wer sich erinnert, weiß Bescheid und wird alles verstehen. Und für diejenigen, die sich nicht erinnern, folgen wir den Links. Ich stelle sie nicht einfach dort hin.

Endgültige Antwort:

Hier ist so eine schöne Dreifaltigkeit: drei Logarithmen – ein Feigling, ein Erfahrener und ein Dummkopf. :) Und versuchen Sie, eine so knifflige Antwort sofort zu erraten! Ja, nur die Methode der unbestimmten Koeffizienten hilft.) Tatsächlich untersuchen wir dies zu diesem Zweck. Was, wie und wo.

Als Trainingsübung schlage ich vor, dass Sie die Methode üben und den folgenden Bruch integrieren:

Üben Sie, finden Sie das Integral, finden Sie es nicht schwierig! Die Antwort sollte etwa so lauten:

Die Methode der unbestimmten Koeffizienten ist eine mächtige Sache. Es spart sogar in der aussichtslosesten Situation, wenn man trotzdem einen Bruch umwandelt. Und hier könnten einige aufmerksame und interessierte Leser eine Reihe von Fragen haben:

- Was tun, wenn das Polynom im Nenner überhaupt nicht faktorisiert ist?

- WIE sollte man nach der Zerlegung eines großen rationalen Bruchs in die Summe kleiner Brüche suchen? In irgendeiner Form? Warum genau dies und nicht das?

- Was ist zu tun, wenn bei der Erweiterung des Nenners mehrere Faktoren berücksichtigt werden? Oder Klammern in Potenzen wie (x-1) 2? In welcher Form sollten wir nach Zersetzung suchen?

- Was tun, wenn der Nenner neben einfachen Klammern der Form (x-a) gleichzeitig ein unzerlegbares quadratisches Trinom enthält? Sagen wir x 2 +4x+5? In welcher Form sollten wir nach Zersetzung suchen?

Nun ist es an der Zeit, gründlich zu verstehen, woher die Beine wachsen. In den nächsten Lektionen.)

MINISTERIUM FÜR WISSENSCHAFT UND BILDUNG DER REPUBLIK BASCHKORTO STAN

SAOU SPO Baschkirische Hochschule für Architektur und Bauingenieurwesen

Khaliullin Askhat Adelzyanovich,

Mathematiklehrer in Baschkirisch

Hochschule für Architektur und Bauingenieurwesen

UFA

2014

Einleitung ___________________________________________________3

Kapitel ICH. Theoretische Aspekte der Verwendung der Methode der unsicheren Koeffizienten_____________________________________________4

Kapitel II. Sucht nach Lösungen für Probleme mit Polynomen mit der Methode der unbestimmten Koeffizienten_________________________________7

2.1.Faktorisierung eines Polynoms_____________________ 7

2.2. Probleme mit Parametern_________________________________ 10

2.3. Gleichungen lösen________________________________________14

2.4. Funktionsgleichungen______________________________19

Fazit_________________________________________________23

Liste der verwendeten Literatur________________________________________24

Anwendung ________________________________________________25

Einführung.

diese Arbeit widmet sich den theoretischen und praktischen Aspekten der Einführung der Methode der unbestimmten Koeffizienten in den schulischen Mathematikunterricht. Die Relevanz dieses Themas wird durch die folgenden Umstände bestimmt.

Niemand wird behaupten, dass die Mathematik als Wissenschaft nicht an einem Ort steht, sie sich ständig weiterentwickelt, neue Aufgaben mit zunehmender Komplexität entstehen, was oft gewisse Schwierigkeiten mit sich bringt, da diese Aufgaben meist mit Forschung verbunden sind. Solche Aufgaben in letzten Jahren wurden in der Schule, im Bezirk und bei den Republikanern angeboten mathematische Olympiaden, es gibt sie auch in Optionen für das einheitliche Staatsexamen. Deshalb war es notwendig spezielle Methode, wodurch zumindest einige davon am schnellsten, effizientesten und kostengünstigsten gelöst werden könnten. Diese Arbeit stellt den Inhalt der Methode der unbestimmten Koeffizienten klar dar, die in einer Vielzahl von Bereichen der Mathematik weit verbreitet ist und von Fragen des allgemeinbildenden Kurses bis hin zu seinen fortgeschrittensten Teilen reicht. Insbesondere Anwendungen der Methode der unbestimmten Koeffizienten bei der Lösung von Problemen mit Parametern, gebrochenen rationalen und funktionalen Gleichungen sind besonders interessant und effektiv; Sie können jeden, der sich für Mathematik interessiert, leicht interessieren. Der Hauptzweck der vorgeschlagenen Arbeit und Auswahl der Probleme besteht darin, umfassende Möglichkeiten zur Verbesserung und Entwicklung der Fähigkeit zu bieten, kurze und nicht standardmäßige Lösungen zu finden.

Diese Arbeit besteht aus zwei Kapiteln. Im ersten Teil werden die theoretischen Aspekte der Verwendung erörtert

Methode der unsicheren Koeffizienten und zweitens praktische und methodische Aspekte einer solchen Verwendung.

Der Anhang zur Arbeit liefert Bedingungen für konkrete Aufgaben zur eigenständigen Lösung.

Kapitel ICH . Theoretische Aspekte der Nutzung Methode der unsicheren Koeffizienten

„Der Mensch... wurde geboren, um ein Meister zu sein,

Herrscher, König der Natur, aber Weisheit,

mit der er herrschen muss, ist ihm nicht gegeben

von Geburt an: es wird durch Lernen erworben“

N. I. Lobatschewski

Existieren verschiedene Wege und Methoden zur Lösung von Problemen, aber eine der bequemsten, effektivsten, originellsten, elegantesten und gleichzeitig sehr einfachen und für jedermann verständlichen Methode ist die Methode der unbestimmten Koeffizienten. Die Methode der unbestimmten Koeffizienten ist eine in der Mathematik verwendete Methode, um die Koeffizienten von Ausdrücken zu ermitteln, deren Form im Voraus bekannt ist.

Bevor wir die Anwendung der Methode der unbestimmten Koeffizienten zur Lösung verschiedener Arten von Problemen betrachten, präsentieren wir eine Reihe theoretischer Informationen.

Lass sie gegeben werden

A N (X) = A 0 X N + A 1 X n-1 + A 2 X n-2 + ··· + A n-1 X + A N

B M (X ) = B 0 X M + B 1 X M -1 + B 2 X M -2 + ··· + B m-1 X + B M ,

Polynome relativ X mit irgendwelchen Chancen.

Satz. Zwei Polynome abhängig von eins und Das gleiche Argument ist genau dann identisch gleich, wennN = M und ihre entsprechenden Koeffizienten sind gleichA 0 = B 0 , A 1 = B 1 , A 2 = B 2 ,··· , A N -1 = B M -1 , A N = B M Und T. D.

Offensichtlich gelten für alle Werte gleiche Polynome X gleiche Werte. Umgekehrt, wenn die Werte zweier Polynome für alle Werte gleich sind X, dann die Polynome sind gleich, das heißt, ihre Koeffizienten haben den gleichen GradX zusammenpassen.

Daher ist die Idee, die Methode der unbestimmten Koeffizienten zur Lösung von Problemen anzuwenden, wie folgt.

Lassen Sie uns wissen, dass als Ergebnis einiger Transformationen ein Ausdruck eines bestimmten Typs erhalten wird und nur die Koeffizienten in diesem Ausdruck unbekannt sind. Dann werden diese Koeffizienten mit Buchstaben bezeichnet und als Unbekannte betrachtet. Anschließend wird ein Gleichungssystem erstellt, um diese Unbekannten zu bestimmen.

Im Fall von Polynomen werden diese Gleichungen beispielsweise unter der Bedingung erstellt, dass die Koeffizienten für die gleichen Potenzen gleich sind X für zwei gleiche Polynome.

Was oben gesagt wurde, zeigen wir im Folgenden konkrete Beispiele, und fangen wir mit dem Einfachsten an.

So ergibt sich beispielsweise aufgrund theoretischer Überlegungen der Bruch

kann als Summe dargestellt werden

, Wo A , B Und C - zu bestimmende Koeffizienten. Um sie zu finden, setzen wir den zweiten Ausdruck mit dem ersten gleich:

=

und uns vom Nenner zu befreien und Begriffe mit den gleichen Befugnissen auf der linken Seite zu sammeln X, wir bekommen:

(A + B + C )X 2 + ( B - C )x - a = 2X 2 – 5 X– 1

Da die letzte Gleichheit für alle Werte gelten muss X, dann sind die Koeffizienten gleich großX rechts und links sollten gleich sein. Somit werden drei Gleichungen zur Bestimmung der drei unbekannten Koeffizienten erhalten:

a+b+c = 2

B - C = - 5

A= 1, daher A = 1 , B = - 2 , C = 3

Somit,

=
,

Die Gültigkeit dieser Gleichheit lässt sich leicht direkt überprüfen.

Angenommen, Sie müssen auch einen Bruch darstellen

als A + B
+ C
+ D
, Wo A , B , C Und D- unbekannte rationale Koeffizienten. Wir setzen den zweiten Ausdruck mit dem ersten gleich:

A + B
+ C
+ D
=
oder, Wenn wir uns vom Nenner befreien, wenn möglich rationale Faktoren unter den Zeichen der Wurzeln entfernen und ähnliche Begriffe auf die linke Seite bringen, erhalten wir:

(A- 2 B + 3 C ) + (- a+b +3 D )
+ (a+c - 2 D )
+

+ (b - c + D )
= 1 +
-
.

Eine solche Gleichheit ist jedoch nur dann möglich, wenn die rationalen Terme beider Teile und die Koeffizienten derselben Radikale gleich sind. Somit werden vier Gleichungen zum Finden der unbekannten Koeffizienten erhalten A , B , C Und D :

A- 2b+ 3C = 1

- a+b +3 D = 1

a+c - 2 D = - 1

B - C + D= 0, daher A = 0 ; B = - ; C = 0 ; D= , das heißt
= -
+
.

Kapitel II. Sucht nach Lösungen für Probleme mit Polynomen Methode der unbestimmten Koeffizienten.

„Nichts trägt besser zur Beherrschung eines Fachs bei als

die Art und Weise, in verschiedenen Situationen mit ihm umzugehen“

Akademiker B.V. Gnedenko

2. 1. Faktorisieren eines Polynoms.

Methoden zur Faktorisierung von Polynomen:

1) Setzen des gemeinsamen Faktors aus Klammern; 2) Gruppierungsmethode; 3) Anwendung grundlegender Multiplikationsformeln; 4) Einführung von Hilfstermen; 5) vorläufige Transformation eines gegebenen Polynoms unter Verwendung bestimmter Formeln; 6) Erweiterung durch Finden der Wurzeln eines gegebenen Polynoms; 7) Methode zur Eingabe des Parameters; 8)Methode der unbestimmten Koeffizienten.

Aufgabe 1. Zerlegen Sie das Polynom in reelle Faktoren X 4 + X 2 + 1 .

Lösung. Es gibt keine Wurzeln zwischen den Teilern des freien Termes dieses Polynoms. Wir können die Wurzeln des Polynoms nicht mit anderen elementaren Mitteln finden. Daher ist es nicht möglich, die erforderliche Entwicklung durchzuführen, indem zunächst die Wurzeln dieses Polynoms ermittelt werden. Es bleibt nach einer Lösung des Problems zu suchen, entweder durch Einführung von Hilfstermen oder durch die Methode der unbestimmten Koeffizienten. Es ist klar, dass X 4 + X 2 + 1 = X 4 + X 3 + X 2 - X 3 - X 2 - X + X 2 + X + 1 =

= X 2 (X 2 + X + 1) - X (X 2 + X + 1) + X 2 + X + 1 =

= (X 2 + X + 1)(X 2 - X + 1).

Die resultierenden quadratischen Trinome haben keine Wurzeln und sind daher nicht in reelle lineare Faktoren zerlegbar.

Die beschriebene Methode ist technisch einfach, aber aufgrund ihrer Künstlichkeit schwierig. Tatsächlich ist es sehr schwierig, die erforderlichen Hilfsbegriffe zu finden. Nur eine Vermutung half uns, diese Zerlegung zu finden. Aber

Es gibt zuverlässigere Möglichkeiten, solche Probleme zu lösen.

Man könnte so vorgehen: Angenommen, das gegebene Polynom zerfällt in das Produkt

(X 2 + A X + B )(X 2 + C X + D )

zwei quadratische Trinome mit ganzzahligen Koeffizienten.

Das werden wir also haben

X 4 + X 2 + 1 = (X 2 + A X + B )(X 2 + C X + D )

Es bleibt die Bestimmung der KoeffizientenA , B , C Und D .

Wenn wir die Polynome auf der rechten Seite der letzten Gleichung multiplizieren, erhalten wir:X 4 + X 2 + 1 = X 4 +

+ (a + c ) X 3 + (B + A C + D ) X 2 + (Anzeige + v. Chr ) x + bd .

Aber da müssen wir rechter Teil Da sich diese Gleichheit in dasselbe Polynom verwandelt hat, das auf der linken Seite steht, benötigen wir die Erfüllung folgenden Bedingungen:

a + c = 0

B + A C + D = 1

Anzeige + v. Chr = 0

bd = 1 .

Das Ergebnis ist ein System aus vier Gleichungen mit vier UnbekanntenA , B , C Und D . Es ist einfach, die Koeffizienten aus diesem System zu ermittelnA = 1 , B = 1 , C = -1 Und D = 1.

Jetzt ist das Problem vollständig gelöst. Wir bekamen:

X 4 + X 2 + 1 = (X 2 + X + 1)(X 2 - X + 1).

Aufgabe 2. Faktorisieren Sie das Polynom in reelle Faktoren X 3 – 6 X 2 + 14 X – 15 .

Lösung. Stellen wir dieses Polynom in der Form dar

X 3 – 6 X 2 + 14 X – 15 = (X + A )(X 2 + bx + C) , Wo A , B Und Mit - Koeffizienten noch nicht bestimmt. Denn zwei Polynome sind genau dann identisch gleich, wenn die Koeffizienten die gleichen Potenzen habenX sind dann gleich, wobei die Koeffizienten jeweils gleichgesetzt werdenX 2 , X und freien Termen erhalten wir ein System aus drei Gleichungen mit drei Unbekannten:

a+b= - 6

ab + c = 14

ac = - 15 .

Die Lösung dieses Systems wird erheblich vereinfacht, wenn wir berücksichtigen, dass die Zahl 3 (Teiler des freien Termes) die Wurzel ist gegebene Gleichung, und deshalbA = - 3 ,

B = - 3 Und Mit = 5 .

Dann X 3 – 6 X 2 + 14 X – 15 = (X – 3)(X 2 – 3 X + 5).

Die angewandte Methode der unbestimmten Koeffizienten enthält im Vergleich zur obigen Methode der Einführung von Hilfstermen nichts Künstliches, erfordert jedoch die Anwendung vieler theoretischer Prinzipien und geht mit ziemlich umfangreichen Berechnungen einher. Für Polynome mehr hochgradig Diese Methode der unbestimmten Koeffizienten führt zu umständlichen Gleichungssystemen.

2.2.Aufgaben und mit Parametern.

In den letzten Jahren wurden in Versionen des Einheitlichen Staatsexamens Aufgaben mit Parametern angeboten. Ihre Lösung bereitet oft gewisse Schwierigkeiten. Bei der Lösung von Problemen mit Parametern können Sie neben anderen Methoden auch die Methode der unbestimmten Koeffizienten sehr effektiv verwenden. Mit dieser Methode können Sie die Lösung erheblich vereinfachen und schnell eine Antwort erhalten.

Aufgabe 3. Bestimmen Sie, bei welchen Werten der Parameter vorliegt A Gleichung 2 X 3 – 3 X 2 – 36 X + A – 3 = 0 hat genau zwei Wurzeln.

Lösung. 1 Weg. Ableitung verwenden.

Stellen wir diese Gleichung in Form von zwei Funktionen dar

2x 3 – 3 X 2 – 36 X – 3 = – A .

F (X) = 2x 3 – 3 X 2 – 36 X– 3 und φ( X ) = – A .

Lassen Sie uns die Funktion untersuchenF (X) = 2x 3 – 3 X 2 – 36 X – 3 Verwenden Sie die Ableitung und konstruieren Sie schematisch ihren Graphen (Abb. 1.).

F( – X )F (X ) , F (– X ) – F (X ). Die Funktion ist weder gerade noch ungerade.

3. Finden wir die kritischen Punkte der Funktion, ihre Anstiegs- und Abfallintervalle, Extrema. F / (X ) = 6 X 2 – 6 X – 36. D (F / ) = R , daher werden wir alle kritischen Punkte der Funktion finden, indem wir die Gleichung lösen F / (X ) = 0 .

6(X 2 – X– 6) = 0 ,

X 2 – X– 6 = 0 ,

X 1 = 3 , X 2 = – 2 nach Satz, Umkehrung des Satzes Vieta.

F / (X ) = 6(X – 3)(X + 2).

+ max - Mindest +

2 3 X

F / (X) > 0 für alle X< - 2 und X > 3 und die Funktion ist punktweise stetigx =- 2 und X = 3, daher nimmt es in jedem der Intervalle zu (- ; - 2] und [ 3 ; ).

F / (X ) < 0 bei - 2 < X< 3, daher nimmt es im Intervall [- 2; 3 ].

X = - 2. maximaler Punkt, weil An diesem Punkt ändert sich das Vorzeichen der Ableitung„+“ bis „-“.

F (– 2) = 2· (– 8) – 3·4 – 36·(– 2) – 3 = – 16 – 12 + 72 – 3 == 72 – 31 = 41 ,

x = 3 Mindestpunkt, da sich an dieser Stelle das Vorzeichen der Ableitung ändert„-“ bis „+“.

F (3) = 2·27 – 3·9 – 36·3 – 3 = 54 – 27 – 108 – 3 = – 138 + +54 = – 84.

Graph der Funktion φ(X ) = – A ist eine gerade Linie parallel zur x-Achse und durch den Punkt mit den Koordinaten (0; – A ). Die Diagramme haben zwei gemeinsame Punkte:A= 41, d.h. a =– 41 und – A= – 84, d.h. A = 84 .

bei

41φ( X)

2 3 X

3 F ( X ) = 2x 3 – 3 X 2 – 36 X – 3

Methode 2. Methode unbestimmter Koeffizienten.

Da diese Gleichung nach den Bedingungen des Problems nur zwei Wurzeln haben darf, liegt die Gleichheit auf der Hand:

2X 3 – 3 X 2 – 36 X + A – 3 = (x + B ) 2 (2 X + C ) ,

2X 3 – 3 X 2 – 36 X + A – 3 = 2 X 3 + (4 B + C ) X 2 + (2 B 2 + +2 v. Chr ) X + B 2 C ,

Nun werden die Koeffizienten mit den gleichen Graden gleichgesetzt X, erhalten wir ein Gleichungssystem

4 b + c = - 3

2B 2 + 2bc = - 36

B 2 C = A – 3 .

Aus den ersten beiden Gleichungen des Systems finden wirB 2 + B – 6 = 0, daher B 1 = - 3 oder B 2 = 2 . Entsprechende WerteMit 1 und Mit 2 leicht aus der ersten Gleichung des Systems zu finden:Mit 1 = 9 oder Mit 2 = - 11 . Abschließend lässt sich der gewünschte Wert des Parameters aus der letzten Gleichung des Systems ermitteln:

A = B 2 C + 3 , A 1 = - 41 oder A 2 = 84.

Antwort: Diese Gleichung hat genau zwei verschiedene

root bei A= - 41 und A= 84 .

Problem 4. Finden Höchster Wert ParameterA , für die die GleichungX 3 + 5 X 2 + Oh + B = 0

mit ganzzahligen Koeffizienten hat drei verschiedene Wurzeln, von denen eine gleich – 2 ist.

Lösung. 1 Weg. Ersetzen X= - 2 auf der linken Seite der Gleichung erhalten wir

8 + 20 – 2 A + B= 0, was bedeutet B = 2 A – 12 .

Da die Zahl - 2 eine Wurzel ist, können wir den gemeinsamen Faktor herausnehmen X + 2:

X 3 + 5 X 2 + Oh + B = X 3 + 2 X 2 + 3 X 2 + Oh + (2 A – 12) =

= X 2 (X + 2) + 3 X (X + 2) – 6 X + Oh + (2 A – 12) =

= X 2 (X + 2) + 3 X (X + 2) + (A – 6)(X +2) - 2(A – 6)+ (2 A - 12) =

= (X + 2)(X 2 + 3 X + (A – 6) ) .

Bedingt durch die Bedingung gibt es zwei weitere Wurzeln der Gleichung. Dies bedeutet, dass die Diskriminante des zweiten Faktors positiv ist.

D =3 2 - 4 (A – 6) = 33 – 4 A > 0, das heißt A < 8,25 .

Es scheint, dass die Antwort lauten würde a = 8 . Aber wenn wir die Zahl 8 in die ursprüngliche Gleichung einsetzen, erhalten wir:

X 3 + 5 X 2 + Oh + B = X 3 + 5 X 2 + 8 X + 4 = (X + 2)(X 2 + 3 X + 2 ) =

= (X + 1) (X + 2) 2 ,

das heißt, die Gleichung hat nur zwei verschiedene Wurzeln. Aber wenn a = 7 erzeugt tatsächlich drei verschiedene Wurzeln.

Methode 2. Methode unbestimmter Koeffizienten.

Wenn die Gleichung X 3 + 5 X 2 + Oh + B = 0 hat eine Wurzel X = - 2, dann können Sie die Zahlen jederzeit abrufenC Und D damit vor allenX Gleichheit war wahr

X 3 + 5 X 2 + Oh + B = (X + 2)(X 2 + Mit X + D ).

Zahlen findenC Und D Öffnen wir die Klammern auf der rechten Seite, fügen ähnliche Begriffe hinzu und erhalten

X 3 + 5 X 2 + Oh + B = X 3 + (2 + Mit ) X 2 +(2 s + D ) X + 2 D

Gleichsetzen der Koeffizienten bei den entsprechenden Potenzen X Wir haben ein System

2 + Mit = 5

2 Mit + D = A

2 D = B , Wo c = 3 .

Somit, X 2 + 3 X + D = 0 , D = 9 – 4 D > 0 oder

D < 2,25, also D (- ; 2 ].

Die Problembedingungen werden durch den Wert erfüllt D = 1 . Der endgültige gewünschte Wert des ParametersA = 7.

ANTWORT: Wann a = 7 Diese Gleichung hat drei verschiedene Wurzeln.

2.3. Gleichungen lösen.

„Denken Sie daran, indem Sie kleine Probleme lösen

Bereiten Sie sich darauf vor, Großes und Schwieriges in Angriff zu nehmen

neue Aufgaben.“

Akademiker S.L. Sobolev

Beim Lösen einiger Gleichungen können und sollten Sie Einfallsreichtum und Witz zeigen und spezielle Techniken anwenden. Die Beherrschung verschiedener Transformationstechniken und die Fähigkeit zum logischen Denken sind in der Mathematik unerlässlich sehr wichtig. Einer dieser Tricks besteht darin, einen ausgewählten Ausdruck oder eine bestimmte Zahl zu addieren und zu subtrahieren. Die dargelegte Tatsache selbst ist natürlich jedem bekannt – die Hauptschwierigkeit besteht darin, in einer bestimmten Konfiguration diejenigen Transformationen von Gleichungen zu sehen, auf die es bequem und zweckmäßig ist, sie anzuwenden.

Anhand einer einfachen algebraischen Gleichung veranschaulichen wir eine nicht standardmäßige Technik zum Lösen von Gleichungen.

Aufgabe 5. Lösen Sie die Gleichung

=
.

Lösung. Lassen Sie uns beide Seiten dieser Gleichung mit 5 multiplizieren und sie wie folgt umschreiben

= 0 ; X 0; -
;

= 0 ,

= 0 ,

= 0 oder
= 0

Lösen wir die resultierenden Gleichungen mit der Methode der unbestimmten Koeffizienten

X 4 - X 3 –7 X – 3 = (X 2 + ah + B )(X 2 + cx + D ) = 0

X 4 - X 3 –7 X – 3 = X 4 + (a + c ) X 3 + (B + A C + D ) X 2 + (Anzeige + v. Chr ) x+ + bd

Gleichsetzung der Koeffizienten bei X 3 , X 2 , X und kostenlose Konditionen, wir bekommen das System

a + c = -1

B + A C + D = 0

Anzeige + v. Chr = -7

bd = -3, woher wir finden:A = -2 ; B = - 1 ;

Mit = 1 ; D = 3 .

Also X 4 - X 3 –7X– 3 = (X 2 – 2 X – 1)(X 2 + X + 3) = 0 ,

X 2 – 2 X– 1 = 0 oder X 2 + X + 3 = 0

X 1,2 =
Keine Wurzeln.

Ebenso haben wir

X 4 – 12X – 5 = (X 2 – 2 X – 1)(X 2 + 2X + 5) = 0 ,

Wo X 2 + 2 X + 5 = 0 , D = - 16 < 0 , нет корней.

Antwort: X 1,2 =

Aufgabe 6. Lösen Sie die Gleichung

= 10.

Lösung. Um diese Gleichung zu lösen, müssen Sie Zahlen auswählenA Und B sodass die Zähler beider Brüche gleich sind. Deshalb haben wir das System:

= 0 , X 0; -1 ; -

= - 10

Die Aufgabe besteht also darin, die Zahlen zu findenA Und B , für die Gleichheit gilt

(ein + 6) X 2 + ach – 5 = X 2 + (5 + 2 B ) X + B

Nach dem Satz über die Gleichheit der Polynome ist es nun notwendig, dass die rechte Seite dieser Gleichheit in dasselbe Polynom übergeht wie auf der linken Seite.

Mit anderen Worten: Die Beziehungen müssen erfüllt sein

ein + 6 = 1

A = 5 + 2 B

– 5 = B , von wo aus wir die Werte findenA = - 5 ;

B = - 5 .

Bei diesen WertenA Und B Gleichwertigkeit A + B = - 10 ist auch fair.

= 0 , X 0; -1 ; -

= 0 ,

= 0 ,

(X 2 – 5X– 5)(X 2 + 3X + 1) = 0 ,

X 2 – 5X– 5 = 0 oder X 2 + 3X + 1 = 0 ,

X 1,2 =
, X 3,4 =

Antwort: X 1,2 =
, X 3,4 =

Aufgabe 7. Lösen Sie die Gleichung

= 4

Lösung. Diese Gleichung ist komplexer als die vorherigen und daher werden wir sie wie folgt gruppieren: X 0;-1;3;-8;12

0 ,

= - 4.

Aus der Bedingung der Gleichheit zweier Polynome

Oh 2 + (ein + 6) X + 12 = X 2 + (B + 11) X – 3 B ,

Wir erhalten und lösen ein Gleichungssystem für unbekannte KoeffizientenA Und B :

A = 1

ein + 6 = B + 11

12 = – 3 B , Wo a = 1 , B = - 4 .

Polynome - 3 – 6X + cx 2 + 8 cx Und X 2 + 21 + 12 D – dx sind einander nur dann identisch, wenn

Mit = 1

8 Mit - 6 = - D

3 = 21 + 12 D , Mit = 1 , D = - 2 .

Mit Wertena = 1 , B = - 4 , Mit = 1 , D = - 2

Gleichwertigkeit
= - 4 ist richtig.

Infolgedessen nimmt diese Gleichung die folgende Form an:

= 0 oder
= 0 oder
= 0 ,

= - 4 , = - 3 , = 1 , = -
.

Aus den betrachteten Beispielen wird deutlich, wie der geschickte Einsatz der Methode der unbestimmten Koeffizienten,

hilft, die Lösung einer ziemlich komplexen, ungewöhnlichen Gleichung zu vereinfachen.

2.4. Funktionsgleichungen.

„Der höchste Zweck der Mathematik... ist

ist es, die verborgene Ordnung darin zu finden

Chaos, das uns umgibt“

N. Viner

Funktionsgleichungen sind sehr allgemeine Klasse Gleichungen, in denen die erforderliche Funktion eine bestimmte Funktion ist. Unter einer Funktionsgleichung im engeren Sinne werden Gleichungen verstanden, bei denen die gewünschten Funktionen durch die Bildung einer komplexen Funktion mit bekannten Funktionen einer oder mehrerer Variablen in Beziehung gesetzt werden. Eine Funktionsgleichung kann auch als Ausdruck einer Eigenschaft betrachtet werden, die eine bestimmte Klasse von Funktionen charakterisiert

[zum Beispiel Funktionsgleichung F ( X ) = F (- X ) charakterisiert die Klasse der geraden Funktionen, die FunktionsgleichungF (X + 1) = F (X ) – Klasse von Funktionen mit Periode 1 usw.].

Eine der einfachsten Funktionsgleichungen ist die GleichungF (X + j ) = F (X ) + F (j ). Kontinuierliche Lösungen dieser Funktionsgleichung haben die Form

F (X ) = CX . In der Klasse der unstetigen Funktionen hat diese Funktionsgleichung jedoch andere Lösungen. Mit der betrachteten Funktionsgleichung verbunden sind

F (X + j ) = F (X ) · F (j ), F (X j ) = F (X ) + F (j ), F (X j ) = F (X )· F (j ),

kontinuierliche Lösungen, die jeweils die Form haben

e cx , MITlnX , X α (X > 0).

Also diese Funktionsgleichungen können zur Bestimmung von Exponential-, Logarithmus- und Potenzfunktionen verwendet werden.

Am häufigsten werden Gleichungen für komplexe Funktionen verwendet, bei denen die erforderlichen Funktionen externe Funktionen sind. Theoretisch und praktische Anwendungen

Es waren genau diese Gleichungen, die herausragende Mathematiker dazu veranlassten, sie zu studieren.

Zum Beispiel, bei Ausrichtung

F 2 (X) = F (X - j)· F (X + j)

N. I. LobatschewskiWird zur Bestimmung des Parallelitätswinkels in meiner Geometrie verwendet.

In den letzten Jahren werden bei Mathematikolympiaden häufig Aufgaben zur Lösung von Funktionsgleichungen angeboten. Ihre Lösung erfordert keine Kenntnisse, die über den Rahmen des Mathematikprogramms hinausgehen Weiterführende Schulen. Allerdings bereitet die Lösung von Funktionsgleichungen oft gewisse Schwierigkeiten.

Eine Möglichkeit, Lösungen für Funktionsgleichungen zu finden, ist die Methode der unbestimmten Koeffizienten. Es kann verwendet werden, wenn Aussehen Gleichungen ermittelt werden können generelle Form die gewünschte Funktion. Dies gilt vor allem für die Fälle, in denen Lösungen für Gleichungen unter ganzzahligen oder gebrochenen rationalen Funktionen gesucht werden sollen.

Lassen Sie uns die Essenz dieser Technik skizzieren, indem wir die folgenden Probleme lösen.

Aufgabe 8. FunktionF (X ) ist für alle reellen x definiert und erfüllt für alleX R Zustand

3 F(X) - 2 F(1- X) = X 2 .

FindenF (X ).

Lösung. Da auf der linken Seite dieser Gleichung die unabhängige Variable x und die Werte der Funktion stehenF Es werden nur lineare Operationen ausgeführt, und die rechte Seite der Gleichung ist quadratische Funktion, dann ist es natürlich anzunehmen, dass die erforderliche Funktion auch quadratisch ist:

F (X) = Axt 2 + bx + C , WoA, B, C – zu bestimmende Koeffizienten, also unsichere Koeffizienten.

Wenn wir die Funktion in die Gleichung einsetzen, erhalten wir die Identität:

3(Axt 2 + bx+ c) – 2(A(1 – X) 2 + B(1 – X) + C) = X 2 .

Axt 2 + (5 B + 4 A) X + (C – 2 A – 2 B) = X 2 .

Zwei Polynome sind identisch gleich, wenn sie gleich sind

Koeffizienten für die gleichen Potenzen der Variablen:

A = 1

5B + 4A = 0

C– 2 A – 2 B = 0.

Aus diesem System ermitteln wir die Koeffizienten

A = 1 , B = - , C = , AuchbefriedigtGleichwertigkeit

3 F (X ) - 2 F (1- X ) = X 2 auf der Menge aller reellen Zahlen. Gleichzeitig gibt es solcheX 0 Aufgabe 9. Funktiony =F(X) für alle x ist definiert, stetig und erfüllt die BedingungF (F (X)) – F(X) = 1 + 2 X . Finden Sie zwei solcher Funktionen.

Lösung. An der gewünschten Funktion werden zwei Aktionen ausgeführt – der Vorgang des Zusammenstellens einer komplexen Funktion und

Subtraktion. Wenn man bedenkt, dass die rechte Seite der Gleichung eine lineare Funktion ist, ist es naheliegend anzunehmen, dass die gewünschte Funktion ebenfalls linear ist:F(X) = ah +B , WoA UndB – unsichere Koeffizienten. Ersetzen dieser Funktion inF (F ( (X ) = - X - 1 ;

F 2 (X ) = 2 X+ , die Lösungen der Funktionsgleichung sindF (F (X)) – F(X) = 1 + 2 X .

Abschluss.

Abschließend ist festzuhalten, dass diese Arbeit sicherlich zur weiteren Erforschung des Originals und beitragen wird effektive Methode Lösung einer Vielzahl mathematischer Probleme, bei denen es sich um Probleme mit erhöhtem Schwierigkeitsgrad handelt, die tiefe Kenntnisse des schulischen Mathematikunterrichts und eine hohe logische Kultur erfordern. Wer seine Mathematikkenntnisse selbstständig vertiefen möchte, findet in dieser Arbeit auch Stoff zur Reflexion und interessante Probleme , deren Lösung Nutzen und Zufriedenheit bringen wird.

In der Arbeit im Bestehenden Lehrplan und in einer für eine effektive Wahrnehmung zugänglichen Form wird die Methode der unbestimmten Koeffizienten vorgestellt, die zur Vertiefung des Schulunterrichts in Mathematik beiträgt.

Natürlich können nicht alle Möglichkeiten der Methode der unbestimmten Koeffizienten in einer Arbeit aufgezeigt werden. Tatsächlich bedarf die Methode noch weiterer Studien und Forschung.

Liste der verwendeten Literatur.

Glazer G.I..Geschichte der Mathematik in der Schule.-M.: Bildung, 1983.

Gomonov S.A. Funktionsgleichungen in Schulkurs Mathematik // Mathematik in der Schule. – 2000. –№10 .

Dorofeev G.V., Potapov M.K., Rozov N.H.. Ein Handbuch zur Mathematik. - M.: Nauka, 1972.

Kurosh A.G.. Algebraische Gleichungen willkürliche Abschlüsse.-M.: Nauka, 1983.

Likhtarnikov L.M.. Grundlegende Einführung in Funktionsgleichungen. - St. Petersburg. : Lan, 1997.

Manturov O.V., Solntsev Yu.K., Sorokin Yu.I., Fedin N.G.. Erklärendes Wörterbuch mathematischer Begriffe.-M.: Bildung, 1971

Modenov V.P.. Ein Handbuch zur Mathematik. Teil 1.-M.: Moskauer Staatliche Universität, 1977.

Modenov V.P.. Probleme mit Parametern. - M.: Prüfung, 2006.

Potapov M.K., Aleksandrov V.V., Pasichenko P.I.. Algebra und Analyse elementarer Funktionen. - M.: Nauka, 1980.

Khaliullin A.A.. Du kannst es einfacher lösen // Mathematik in der Schule. – 2003 . - №8 .

Khaliullin.

4. Erweitern Sie Polynom 2X 4 – 5X 3 + 9X 2 – 5X+ 3 für Multiplikatoren mit ganzzahligen Koeffizienten.

5. Zu welchem ​​​​Wert A X 3 + 6X 2 + Oh+ 12 pro X+ 4 ?

6. Bei welchem ​​Wert des ParametersA Die gleichungX 3 +5 X 2 + + Oh + B = 0 mit ganzzahligen Koeffizienten hat zwei verschiedene Wurzeln, von denen eine 1 ist ?

7. Unter den Wurzeln des Polynoms X 4 + X 3 – 18X 2 + Oh + B Bei ganzzahligen Koeffizienten gibt es drei gleiche ganze Zahlen. Finden Sie den Wert B .

8. Finden Sie den größten ganzzahligen Wert des Parameters A, bei dem die Gleichung X 3 – 8X 2 + ah +B = 0 mit ganzzahligen Koeffizienten hat drei verschiedene Wurzeln, von denen eine gleich 2 ist.

9. Bei welchen Werten A Und B Die Division erfolgt ohne Rest X 4 + 3X 3 – 2X 2 + Oh + B An X 2 – 3X + 2 ?

10. Faktorpolynome:

A)X 4 + 2 X 2 – X + 2 V)X 4 – 4X 3 +9X 2 –8X + 5 D)X 4 + 12X – 5

B)X 4 + 3X 2 + 2X + 3 G)X 4 – 3X –2 e)X 4 – 7X 2 + 1 .

11. Lösen Sie die Gleichungen:

A)
= 2 = 2 F (1 – X ) = X 2 .

Finden F (X) .

13. Funktion bei= F (X) Vor allen X definiert, kontinuierlich ist und die Bedingung erfüllt F ( F (X)) = F (X) + X. Finden Sie zwei solcher Funktionen.

Integration einer gebrochenrationalen Funktion.
Methode mit unsicheren Koeffizienten

Wir arbeiten weiterhin an der Integration von Brüchen. Wir haben uns in der Lektion bereits mit Integralen einiger Arten von Brüchen befasst, und diese Lektion kann gewissermaßen als Fortsetzung betrachtet werden. Um den Stoff erfolgreich zu verstehen, sind grundlegende Integrationsfähigkeiten erforderlich. Wenn Sie also gerade erst mit dem Studium von Integralen begonnen haben, also ein Anfänger sind, müssen Sie mit dem Artikel beginnen Unbestimmtes Integral. Beispiele für Lösungen.

Seltsamerweise werden wir uns jetzt nicht so sehr mit der Suche nach Integralen beschäftigen, sondern... mit der Lösung linearer Gleichungssysteme. Diesbezüglich dringend Ich empfehle, an der Lektion teilzunehmen. Sie müssen nämlich mit Substitutionsmethoden („Schulmethode“ und der Methode der Term-für-Term-Addition (Subtraktion) von Systemgleichungen) vertraut sein.

Was ist eine gebrochene rationale Funktion? In einfachen Worten Eine gebrochenrationale Funktion ist ein Bruch, dessen Zähler und Nenner Polynome oder Produkte von Polynomen enthalten. Darüber hinaus sind die Brüche komplexer als die im Artikel behandelten Einige Brüche integrieren.

Integration einer echten gebrochenrationalen Funktion

Gleich ein Beispiel und ein typischer Algorithmus zur Lösung des Integrals einer gebrochenrationalen Funktion.

Beispiel 1

Schritt 1. Das erste, was wir IMMER tun, wenn wir ein Integral einer gebrochenen rationalen Funktion lösen, ist die Klärung der folgenden Frage: ist der Bruch richtig? Dieser Schritt wird mündlich ausgeführt, und jetzt werde ich erklären, wie:

Zuerst schauen wir uns den Zähler an und finden es heraus Senior-Abschluss Polynom:

Die führende Potenz des Zählers ist zwei.

Jetzt schauen wir uns den Nenner an und finden es heraus Senior-Abschluss Nenner. Der naheliegendste Weg besteht darin, die Klammern zu öffnen und ähnliche Begriffe einzufügen, aber Sie können es auch einfacher machen: jede Finden Sie in Klammern den höchsten Abschluss

und gedanklich multiplizieren: - somit ist der höchste Grad des Nenners gleich drei. Es liegt auf der Hand, dass wir, wenn wir die Klammern tatsächlich öffnen, keinen Grad größer als drei erhalten.

Abschluss: Hauptgrad des Zählers STRENG ist kleiner als die höchste Potenz des Nenners, was bedeutet, dass der Bruch echt ist.

Wenn in diesem Beispiel der Zähler das Polynom 3, 4, 5 usw. enthielt. Grad, dann wäre der Bruch falsch.

Jetzt betrachten wir nur die richtigen gebrochenen rationalen Funktionen. Der Fall, dass der Grad des Zählers größer oder gleich dem Grad des Nenners ist, wird am Ende der Lektion besprochen.

Schritt 2. Lassen Sie uns den Nenner faktorisieren. Schauen wir uns unseren Nenner an:

Im Allgemeinen ist dies bereits ein Produkt von Faktoren, aber dennoch fragen wir uns: Ist es möglich, etwas anderes zu erweitern? Das Ziel der Folter wird zweifellos das quadratische Trinom sein. Lass uns entscheiden quadratische Gleichung:

Die Diskriminante ist größer als Null, was bedeutet, dass das Trinom tatsächlich faktorisiert werden kann:

Allgemeine Regel: ALLES, was im Nenner berücksichtigt werden kann – wir berücksichtigen es

Beginnen wir mit der Formulierung einer Lösung:

Schritt 3. Mit der Methode der unbestimmten Koeffizienten entwickeln wir den Integranden in eine Summe einfacher (Elementar-)Brüche. Jetzt wird es klarer.

Schauen wir uns unsere Integrandenfunktion an:

Und, wissen Sie, irgendwie taucht intuitiv der Gedanke auf, dass es schön wäre, unseren großen Bruchteil in mehrere kleine umzuwandeln. Zum Beispiel so:

Es stellt sich die Frage: Ist das überhaupt möglich? Lasst uns aufatmen, der entsprechende Satz der mathematischen Analysis besagt: ES IST MÖGLICH. Eine solche Zerlegung existiert und ist einzigartig.

Es gibt nur einen Haken: Die Chancen stehen gut Tschüss Wir wissen es nicht, daher der Name – die Methode der unbestimmten Koeffizienten.

Wie Sie vermutet haben, sind nachfolgende Körperbewegungen so, kein Lachen! wird darauf abzielen, sie einfach zu ERKENNEN – herauszufinden, wem sie gewachsen sind.

Seien Sie vorsichtig, ich werde es nur einmal ausführlich erklären!

Beginnen wir also mit dem Tanzen von:

Auf der linken Seite bringen wir den Ausdruck auf einen gemeinsamen Nenner:

Jetzt können wir die Nenner getrost loswerden (da sie gleich sind):

Auf der linken Seite öffnen wir die Klammern, berühren die unbekannten Koeffizienten aber vorerst nicht:

Gleichzeitig wiederholen wir Schulordnung Polynome multiplizieren. Als ich Lehrer war, lernte ich, diese Regel mit ernstem Gesicht auszusprechen: Um ein Polynom mit einem Polynom zu multiplizieren, müssen Sie jeden Term eines Polynoms mit jedem Term des anderen Polynoms multiplizieren.

Aus Sicht einer klaren Erklärung ist es besser, die Koeffizienten in Klammern zu setzen (obwohl ich das persönlich aus Zeitgründen nie mache):

Wir stellen ein System linearer Gleichungen auf.
Zuerst suchen wir nach höheren Abschlüssen:

Und wir schreiben die entsprechenden Koeffizienten in die erste Gleichung des Systems:

Denken Sie gut an den folgenden Punkt. Was würde passieren, wenn es auf der rechten Seite überhaupt kein s gäbe? Sagen wir mal, würde es auch ohne Quadrat zur Geltung kommen? In diesem Fall müsste in der Gleichung des Systems rechts eine Null gesetzt werden: . Warum Null? Aber weil man auf der rechten Seite immer dasselbe Quadrat mit Nullen belegen kann: Wenn auf der rechten Seite keine Variablen und/oder ein freier Term stehen, dann setzen wir Nullen auf die rechten Seiten der entsprechenden Gleichungen des Systems.

Die entsprechenden Koeffizienten schreiben wir in die zweite Gleichung des Systems:

Und schließlich Mineralwasser, wir wählen kostenlose Mitglieder aus.

Äh... das war ein Scherz. Spaß beiseite – Mathematik ist eine ernstzunehmende Wissenschaft. In unserer Institutsgruppe lachte niemand, als die Assistenzprofessorin sagte, sie würde die Terme entlang des Zahlenstrahls verteilen und die größten auswählen. Lasst uns ernst werden. Obwohl... wer das Ende dieser Lektion noch erlebt, wird immer noch leise lächeln.

Das System ist fertig:

Wir lösen das System:

(1) Aus der ersten Gleichung drücken wir sie aus und setzen sie in die zweite und dritte Gleichung des Systems ein. Tatsächlich war es möglich, (oder einen anderen Buchstaben) aus einer anderen Gleichung auszudrücken, aber in diesem Fall ist es vorteilhaft, es aus der ersten Gleichung auszudrücken, da dort die kleinsten Chancen.

(2) Wir präsentieren ähnliche Begriffe in der 2. und 3. Gleichung.

(3) Wir addieren die 2. und 3. Gleichung Term für Term und erhalten so die Gleichheit, woraus folgt

(4) Wir setzen es in die zweite (oder dritte) Gleichung ein, wo wir das finden

(5) Setzen Sie und in die erste Gleichung ein und erhalten Sie .

Wenn Sie Schwierigkeiten mit den Lösungsmethoden des Systems haben, üben Sie diese im Unterricht. Wie löst man ein lineares Gleichungssystem?

Nach dem Lösen des Systems ist es immer sinnvoll, die gefundenen Werte zu überprüfen und zu ersetzen jeden Gleichung des Systems, als Ergebnis sollte alles „konvergieren“.

Fast dort. Die Koeffizienten wurden gefunden und:

Der fertige Auftrag sollte etwa so aussehen:

Wie Sie sehen, bestand die Hauptschwierigkeit der Aufgabe darin, ein System linearer Gleichungen (richtig!) zusammenzustellen und (richtig!) zu lösen. Und im Endstadium ist alles gar nicht so schwer: Wir nutzen die Linearitätseigenschaften des unbestimmten Integrals und integrieren. Bitte beachten Sie, dass wir unter jedem der drei Integrale „frei“ haben komplexe Funktion Ich habe über die Besonderheiten seiner Integration in den Unterricht gesprochen Methode zur Variablenänderung im unbestimmten Integral.

Prüfen: Differenzieren Sie die Antwort:

Die ursprüngliche Integrandenfunktion wurde erhalten, was bedeutet, dass das Integral korrekt gefunden wurde.
Bei der Überprüfung mussten wir den Ausdruck auf einen gemeinsamen Nenner bringen, und das ist kein Zufall. Die Methode der unbestimmten Koeffizienten und die Reduzierung eines Ausdrucks auf einen gemeinsamen Nenner sind wechselseitig inverse Aktionen.

Beispiel 2

Finden Sie das unbestimmte Integral.

Kehren wir zum Bruch aus dem ersten Beispiel zurück: . Es ist leicht zu erkennen, dass im Nenner alle Faktoren UNTERSCHIEDLICH sind. Es stellt sich die Frage, was zu tun ist, wenn beispielsweise folgender Bruch gegeben ist: ? Hier haben wir Grade im Nenner, oder mathematisch gesehen: Vielfache. Darüber hinaus gibt es ein quadratisches Trinom, das nicht faktorisiert werden kann (es ist leicht zu überprüfen, ob die Diskriminante der Gleichung vorliegt). ist negativ, daher kann das Trinom nicht faktorisiert werden). Was zu tun ist? Summenentwicklung elementare Brüche wird aussehen wie mit unbekannten Koeffizienten oben oder etwas anderes?

Beispiel 3

Führen Sie eine Funktion ein

Schritt 1.Überprüfen, ob wir einen richtigen Bruch haben
Hauptzähler: 2
Höchster Nennergrad: 8
, was bedeutet, dass der Bruch korrekt ist.

Schritt 2. Ist es möglich, etwas im Nenner zu berücksichtigen? Offensichtlich nicht, es ist bereits alles geplant. Das quadratische Trinom kann aus den oben genannten Gründen nicht zu einem Produkt entwickelt werden. Haube. Weniger Arbeit.

Schritt 3. Stellen wir uns eine gebrochenrationale Funktion als Summe elementarer Brüche vor.
In diesem Fall hat die Erweiterung die folgende Form:

Schauen wir uns unseren Nenner an:
Bei der Zerlegung einer gebrochenrationalen Funktion in eine Summe elementarer Brüche lassen sich drei grundlegende Punkte unterscheiden:

1) Wenn der Nenner einen „einsamen“ Faktor in der ersten Potenz enthält (in unserem Fall), dann setzen wir oben einen unbestimmten Koeffizienten (in unserem Fall). Die Beispiele Nr. 1, 2 bestanden nur aus solchen „einsamen“ Faktoren.

2) Wenn der Nenner hat mehrere Multiplikator, dann müssen Sie es wie folgt zerlegen:
- das heißt, alle Grade von „X“ vom ersten bis zum n-ten Grad nacheinander durchlaufen. In unserem Beispiel gibt es zwei Mehrfachfaktoren: und , schauen Sie sich die von mir angegebene Erweiterung noch einmal an und stellen Sie sicher, dass sie genau nach dieser Regel erweitert werden.

3) Wenn der Nenner ein unzerlegbares Polynom zweiten Grades enthält (in unserem Fall), müssen Sie beim Zerlegen im Zähler schreiben lineare Funktion mit unsicheren Koeffizienten (in unserem Fall mit unsicheren Koeffizienten und ).

Tatsächlich gibt es noch einen vierten Fall, über den ich aber schweigen werde, da er in der Praxis äußerst selten vorkommt.

Beispiel 4

Führen Sie eine Funktion ein als Summe elementarer Brüche mit unbekannten Koeffizienten.

Dies ist ein Beispiel, das Sie selbst lösen können. Komplette Lösung und die Antwort am Ende der Lektion.
Befolgen Sie den Algorithmus strikt!

Wenn Sie die Prinzipien verstehen, nach denen Sie eine gebrochenrationale Funktion in eine Summe entwickeln müssen, können Sie fast jedes Integral des betrachteten Typs durchforsten.

Beispiel 5

Finden Sie das unbestimmte Integral.

Schritt 1. Offensichtlich ist der Bruch richtig:

Schritt 2. Ist es möglich, etwas im Nenner zu berücksichtigen? Dürfen. Hier ist die Summe der Würfel . Faktorisieren Sie den Nenner mithilfe der abgekürzten Multiplikationsformel

Schritt 3. Mit der Methode der unbestimmten Koeffizienten entwickeln wir den Integranden in eine Summe elementarer Brüche:

Bitte beachten Sie, dass das Polynom nicht faktorisiert werden kann (überprüfen Sie, ob die Diskriminante negativ ist), daher setzen wir oben eine lineare Funktion mit unbekannten Koeffizienten und nicht nur einen Buchstaben.

Wir bringen den Bruch auf einen gemeinsamen Nenner:

Lassen Sie uns das System zusammenstellen und lösen:

(1) Wir drücken aus der ersten Gleichung aus und setzen sie in die zweite Gleichung des Systems ein (dies ist die rationalste Methode).

(2) Ähnliche Terme präsentieren wir in der zweiten Gleichung.

(3) Wir addieren die zweite und dritte Gleichung des Systems Term für Term.

Alle weiteren Berechnungen erfolgen grundsätzlich mündlich, da das System einfach ist.

(1) Wir schreiben die Summe der Brüche entsprechend den gefundenen Koeffizienten auf.

(2) Wir nutzen die Linearitätseigenschaften des unbestimmten Integrals. Was geschah im zweiten Integral? Mit dieser Methode können Sie sich im letzten Absatz der Lektion vertraut machen. Einige Brüche integrieren.

(3) Wir nutzen wieder die Eigenschaften der Linearität. Im dritten Integral beginnen wir, das vollständige Quadrat zu isolieren (vorletzter Absatz der Lektion). Einige Brüche integrieren).

(4) Wir nehmen das zweite Integral, im dritten wählen wir das vollständige Quadrat.

(5) Nehmen Sie das dritte Integral. Bereit.

Die Methode ist zur Minimierung logischer Algebrafunktionen einer beliebigen Anzahl von Variablen anwendbar.

Betrachten wir den Fall von drei Variablen. Eine boolesche Funktion in DNF kann in Form aller Arten von Konjunktiven dargestellt werden, die in DNF enthalten sein können:

wobei kО(0,1) Koeffizienten sind. Die Methode besteht darin, Koeffizienten so auszuwählen, dass der resultierende DNF minimal ist.

Wenn wir nun alle möglichen Werte der Variablen von 000 bis 111 setzen, erhalten wir 2 n (2 3 =8) Gleichungen zur Bestimmung der Koeffizienten k:

Bestimmen Sie unter Berücksichtigung der Mengen, für die die Funktion einen Nullwert annimmt, die Koeffizienten, die gleich 0 sind, und streichen Sie sie aus den Gleichungen, deren rechte Seite 1 enthält. Von den verbleibenden Koeffizienten in jeder Gleichung wird ein Koeffizient mit eins gleichgesetzt, was bestimmt die Konjunktion des niedrigsten Ranges. Die übrigen Koeffizienten sind gleich 0. Also die Einheitskoeffizienten k Bestimmen Sie die geeignete Mindestform.

Beispiel. Minimieren gegebene Funktion

wenn die Werte bekannt sind: ; ; ; ; ; ; ; .

Lösung.

Nach dem Durchstreichen der Nullkoeffizienten erhalten wir:

=1;

=1;

=1.

Setzen wir den Koeffizienten, der der Konjunktion des niedrigsten Rangs entspricht, mit eins gleich und drehen die letzten vier Gleichungen auf 1, und in der ersten Gleichung ist es ratsam, den Koeffizienten mit 1 gleichzusetzen. Die restlichen Koeffizienten werden auf 0 gesetzt.

Antwort: Art der minimierten Funktion.

Es ist zu beachten, dass die Methode der unbestimmten Koeffizienten effektiv ist, wenn die Anzahl der Variablen klein ist und 5-6 nicht überschreitet.

Mehrdimensionaler Würfel

Betrachten wir eine grafische Darstellung einer Funktion in Form eines mehrdimensionalen Würfels. Jeder Gipfel N-dimensionaler Würfel kann mit dem Konstituenten der Einheit korrespondiert werden.

Die Teilmenge der markierten Eckpunkte ist eine Abbildung auf N-dimensionaler Würfel einer booleschen Funktion aus N Variablen in SDNF.

Zur Anzeige der Funktion ab N Für die in jedem DNF dargestellten Variablen ist es notwendig, eine Entsprechung zwischen seinen Minitermen und Elementen herzustellen N-dimensionaler Würfel.

Ein Miniterm vom Rang (n-1) kann als Ergebnis des Zusammenklebens zweier Miniterms betrachtet werden N-ter Rang, d.h.

An N Bei einem -dimensionalen Würfel entspricht dies dem Ersetzen zweier Eckpunkte, die sich nur in den Koordinatenwerten unterscheiden x i, diese Eckpunkte mit einer Kante verbinden (eine Kante soll die mit ihr inzidenten Eckpunkte abdecken).

Somit sind Miniterme ( N Die -1)te Ordnung entspricht den Kanten eines n-dimensionalen Würfels.

Ebenso ist die Entsprechung von Miniterms ( N Gesichter der -2. Ordnung N-dimensionaler Würfel, der jeweils vier Eckpunkte (und vier Kanten) umfasst.

Elemente N-dimensionaler Würfel, gekennzeichnet durch S Messungen werden aufgerufen S-Würfel

Scheitelpunkte sind also 0-Würfel, Kanten sind 1-Würfel, Flächen sind 2-Würfel usw.

Zusammenfassend können wir sagen, dass der Miniterm ( n-S) Rang im DNF für die Funktion N Variablen angezeigt S- jeweils ein Würfel S-cube umfasst alle Würfel niedrigerer Dimension, die nur mit seinen Eckpunkten verbunden sind.

Beispiel. In Abb. angesichts der Zuordnung

Hier entsprechen die Miniterme und 1-Würfeln ( S=3-2=1) und Miniterm x 3 wird in 2 Würfeln angezeigt ( S=3-1=2).

Es wird also jedem DNF zugeordnet N-dimensionaler Würfel in seiner Gesamtheit S-Würfel, die alle Eckpunkte abdecken, die den konstituierenden Einheiten entsprechen (0-Würfel).

Bestandteile. Für Variablen x 1,x 2,…x n Ausdruck heißt Konstituent der Einheit und - ein Bestandteil von Null (bedeutet entweder oder).

Diese Konstituente von Eins (Null) wird nur mit einem entsprechenden Satz von Variablenwerten zu Eins (Null), die man erhält, wenn alle Variablen gleich Eins (Null) und ihre Negationen gleich Null (Eins) angenommen werden.

Zum Beispiel: Der Konstituent Eins entspricht der Menge (1011) und der Konstituent Null - setzen (1001).

Da SD(K)NF eine Disjunktion (Konjunktion) der Konstituenten von Eins (Null) ist, kann argumentiert werden, dass es sich um die boolesche Funktion handelt, die es darstellt F(x 1 ,x 2 ,…,x n) wird nur für Sätze von Variablenwerten zu Eins (Null). x 1 ,x 2 ,…,x n, entsprechend diesen Kostituierten. Bei anderen Sätzen wird diese Funktion auf 0 (eins) gesetzt.

Es trifft auch die umgekehrte Aussage zu, auf der sie beruht Möglichkeit, eine beliebige Formel in Form einer Formel darzustellen Durch die Tabelle angegebene boolesche Funktion.

Dazu ist es notwendig, die Disjunktionen (Konjunktionen) der Konstituenten von Eins (Null) aufzuschreiben, die den Wertemengen der Variablen entsprechen, auf denen die Funktion einen Wert annimmt, gleich eins(null).

Zum Beispiel eine durch eine Tabelle gegebene Funktion

entsprechen

Die resultierenden Ausdrücke können basierend auf den Eigenschaften der Algebra der Logik in eine andere Form umgewandelt werden.

Die umgekehrte Aussage gilt auch: wenn eine Sammlung S-cubes deckt die Menge aller entsprechenden Eckpunkte ab Einzelwerte Funktionen, dann die diesen entsprechende Disjunktion S-cubes of miniterms ist der Ausdruck dieser Funktion in DNF.

Sie sagen, dass eine solche Sammlung S-cubes (oder ihre entsprechenden Miniterme) bilden eine Abdeckung der Funktion. Der Wunsch nach einer Minimalform wird intuitiv als Suche nach einer solchen Hülle, der Zahl, verstanden S-von denen es weniger Würfel gäbe, und deren Abmessungen S- mehr. Die der Mindestform entsprechende Deckung wird als Mindestdeckung bezeichnet.

Zum Beispiel für die Funktion bei= Die Beschichtung passt sich einer nicht-minimalen Form an.