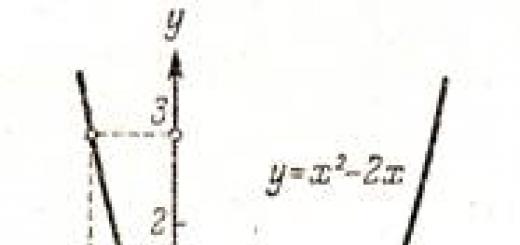صيغة لحساب خطأ القياس النسبي. كيفية حساب خطأ القياسات المباشرة؟ قيم الكميات لتوزيع الطالب t(n) بثقة

الحلول والأجوبة:

الخطأ المطلق

خطأ نسبي

قواعد حساب الأخطاء

ماذا تعلمنا؟

تم العثور على الخطأ المطلق للحسابات بواسطة الصيغة:

توضح علامة المعامل أننا لا نهتم بالقيمة الأكبر والقيمة الأقل. مهم، الى اي مدىانحرفت النتيجة التقريبية عن القيمة الدقيقة في اتجاه أو آخر.

تم العثور على الخطأ النسبي للحسابات بواسطة الصيغة:
، أو نفس الشيء:

يظهر الخطأ النسبي بأي نسبةانحرفت النتيجة التقريبية عن القيمة الدقيقة. هناك نسخة من الصيغة بدون الضرب بنسبة 100%، ولكن من الناحية العملية أرى دائمًا الإصدار أعلاه مع النسب المئوية.

بعد إشارة قصيرة، دعونا نعود إلى مشكلتنا، والتي قمنا فيها بحساب القيمة التقريبية للدالة باستخدام التفاضلية.

دعونا نحسب القيمة الدقيقةالوظائف باستخدام الآلة الحاسبة الدقيقة:
بالمعنى الدقيق للكلمة، لا تزال القيمة تقريبية، لكننا سنعتبرها دقيقة. تحدث مثل هذه المشاكل.

دعونا نحسب الخطأ المطلق:

دعونا نحسب الخطأ النسبي:
، تم الحصول على أجزاء من الألف من النسبة المئوية، وبالتالي فإن الفرق قدم مجرد تقدير تقريبي ممتاز.

إجابة: ، خطأ حسابي مطلق، خطأ حسابي نسبي

المثال التالي لحل مستقل:

مثال 4

عند نقطة . حساب قيمة أكثر دقة للدالة عند نقطة معينة، وتقدير الخطأ المطلق والنسبي في الحسابات.

نموذج تقريبي للتصميم النهائي والإجابة في نهاية الدرس.

لقد لاحظ العديد من الأشخاص أن الجذور تظهر في جميع الأمثلة التي تم النظر فيها. هذا ليس من قبيل الصدفة، في معظم الحالات، يتم اقتراح وظائف ذات جذور في المشكلة قيد النظر.

لكن بالنسبة للقراء الذين يعانون، فقد قمت بحفر مثال صغير باستخدام أركسين:

مثال 5

احسب قيمة الدالة تقريبًا باستخدام التفاضل عند هذه النقطة

هذا المثال القصير والمفيد أيضًا يمكنك حله بنفسك. واسترحت قليلاً حتى أتمكن بقوة متجددة من التفكير في المهمة الخاصة:

مثال 6

قم بإجراء الحساب التقريبي باستخدام التفاضل، مع تقريب النتيجة إلى منزلتين عشريتين.

حل:ما الجديد في المهمة؟ يتطلب الشرط تقريب النتيجة إلى منزلتين عشريتين. لكن هذا ليس هو الهدف؛ أعتقد أن مشكلة التقريب المدرسي ليست صعبة بالنسبة لك. والحقيقة هي أننا حصلنا على ظل مع حجة، والتي يتم التعبير عنها بالدرجات. ماذا يجب أن تفعل عندما يُطلب منك حل دالة مثلثية بالدرجات؟ على سبيل المثال , إلخ.

خوارزمية الحل هي نفسها بشكل أساسي، أي أنه من الضروري، كما في الأمثلة السابقة، تطبيق الصيغة

دعونا نكتب وظيفة واضحة

يجب تقديم القيمة في النموذج . سوف تقدم مساعدة جدية جدول قيم الدوال المثلثية . بالمناسبة، بالنسبة لأولئك الذين لم يطبعوا، أوصي بذلك، حيث سيتعين عليك البحث هناك طوال دورة دراسة الرياضيات العليا.

وبتحليل الجدول نلاحظ وجود قيمة ظل "جيدة" تقترب من 47 درجة:

هكذا:

بعد التحليل الأولي يجب تحويل الدرجات إلى راديان. نعم، وبهذه الطريقة فقط!

في هذا المثال، مباشرة من الجدول المثلثييمكنك معرفة ما. استخدام صيغة تحويل الدرجات إلى راديان: (يمكن العثور على الصيغ في نفس الجدول).

ما يلي هو صيغة:

هكذا: (نستخدم القيمة للحسابات). يتم تقريب النتيجة، كما هو مطلوب حسب الشرط، إلى منزلتين عشريتين.

إجابة:

مثال 7

قم بالحساب التقريبي باستخدام التفاضل، وقم بتقريب النتيجة إلى ثلاث منازل عشرية.

هذا مثال عليك حله بنفسك. الحل الكاملوالإجابة في نهاية الدرس.

كما ترون، لا يوجد شيء معقد، فنحن نحول الدرجات إلى راديان ونلتزم بخوارزمية الحل المعتادة.

الحسابات التقريبية باستخدام التفاضل الكلي لدالة من متغيرين

سيكون كل شيء مشابهًا جدًا جدًا، لذلك إذا أتيت إلى هذه الصفحة خصيصًا لهذه المهمة، فإنني أوصي أولاً بالنظر إلى مثالين على الأقل من الفقرة السابقة.

لدراسة فقرة يجب أن تكون قادرا على العثور عليها المشتقات الجزئية من الدرجة الثانية ، أين كنا سنكون لولاهم؟ في الدرس أعلاه، قمت بالإشارة إلى دالة لمتغيرين باستخدام الحرف . فيما يتعلق بالمهمة قيد النظر، فمن الملائم أكثر استخدام الترميز المكافئ.

كما هو الحال في حالة دالة ذات متغير واحد، يمكن صياغة حالة المشكلة بطرق مختلفة، وسأحاول النظر في جميع الصياغات التي تمت مواجهتها.

مثال 8

حل:بغض النظر عن كيفية كتابة الشرط، في الحل نفسه للإشارة إلى الوظيفة، أكرر، من الأفضل عدم استخدام الحرف "zet"، ولكن .

وهنا صيغة العمل:

ما أمامنا هو في الواقع الأخت الكبرى لصيغة الفقرة السابقة. لقد زاد المتغير فقط. ماذا يمكنني أن أقول، نفسي ستكون خوارزمية الحل هي نفسها بشكل أساسي!

وفقًا للشرط، يلزم إيجاد القيمة التقريبية للدالة عند هذه النقطة.

دعونا نمثل الرقم 3.04 كـ . الكعكة نفسها تطلب أن تؤكل:
,

دعونا نمثل الرقم 3.95 كـ . لقد حان الدور إلى النصف الثاني من كولوبوك:
,

ولا تنظر إلى كل حيل الثعلب، فهناك كولوبوك - عليك أن تأكله.

لنحسب قيمة الدالة عند النقطة:

نجد تفاضل الدالة عند نقطة ما باستخدام الصيغة:

ويترتب على الصيغة أننا بحاجة إلى إيجاد المشتقات الجزئية الترتيب الأول وحساب قيمها عند النقطة .

لنحسب المشتقات الجزئية من الدرجة الأولى عند النقطة:

مجموع التفاضل عند النقطة:

وهكذا، وفقا للصيغة، القيمة التقريبية للدالة عند النقطة:

لنحسب القيمة الدقيقة للدالة عند النقطة:

هذه القيمة دقيقة تماما.

يتم حساب الأخطاء باستخدام الصيغ القياسية، والتي تمت مناقشتها بالفعل في هذه المقالة.

الخطأ المطلق:

خطأ نسبي:

الجواب: الخطأ المطلق: الخطأ النسبي:

مثال 9

احسب القيمة التقريبية للدالة عند نقطة ما باستخدام التفاضل الإجمالي، قم بتقدير الخطأ المطلق والنسبي.

هذا مثال عليك حله بنفسك. أي شخص يلقي نظرة فاحصة على هذا المثال سوف يلاحظ أن الأخطاء الحسابية كانت ملحوظة للغاية. حدث هذا للسبب التالي: في المشكلة المقترحة، تكون زيادات الوسائط كبيرة جدًا: .

النمط العام هو هذاأ - كلما زادت هذه الزيادات قيمه مطلقه، كلما انخفضت دقة الحسابات. لذلك، على سبيل المثال، بالنسبة لنقطة مماثلة ستكون الزيادات صغيرة: وستكون دقة الحسابات التقريبية عالية جدًا.

تنطبق هذه الميزة أيضًا على حالة دالة ذات متغير واحد (الجزء الأول من الدرس).

مثال 10

حل:لنحسب هذا التعبير تقريبًا باستخدام التفاضل الإجمالي لدالة ذات متغيرين:

الفرق عن الأمثلة 8-9 هو أننا نحتاج أولاً إلى إنشاء دالة مكونة من متغيرين: . أعتقد أن الجميع يفهم بشكل حدسي كيفية تكوين الوظيفة.

القيمة 4.9973 قريبة من "خمسة"، وبالتالي: , .
القيمة 0.9919 قريبة من "واحد" لذلك نفترض: , .

لنحسب قيمة الدالة عند النقطة:

نجد التفاضل عند نقطة ما باستخدام الصيغة:

للقيام بذلك، نحسب المشتقات الجزئية من الدرجة الأولى عند النقطة.

المشتقات هنا ليست الأبسط، ويجب الحذر:

;

مجموع التفاضل عند النقطة:

وبالتالي فإن القيمة التقريبية لهذا التعبير هي:

لنحسب قيمة أكثر دقة باستخدام الآلة الحاسبة الدقيقة: 2.998899527

لنجد الخطأ الحسابي النسبي:

إجابة: ،

مجرد توضيح لما سبق، في المشكلة التي تم النظر فيها، زيادات الوسائط صغيرة جدًا، وتبين أن الخطأ صغير جدًا.

مثال 11

باستخدام التفاضل الكامل لدالة مكونة من متغيرين، احسب قيمة هذا التعبير تقريبًا. حساب نفس التعبير باستخدام حاسبة صغيرة. تقدير خطأ الحساب النسبي كنسبة مئوية.

هذا مثال لك لحله بنفسك. نموذج تقريبي للتصميم النهائي في نهاية الدرس.

كما لوحظ بالفعل، فإن الضيف الأكثر شيوعا في هذا النوع من المهام هو نوع من الجذور. ولكن من وقت لآخر هناك وظائف أخرى. ومثال بسيط أخير للاسترخاء:

مثال 12

باستخدام التفاضل الإجمالي لدالة مكونة من متغيرين، احسب قيمة الدالة if تقريبًا

الحل أقرب إلى أسفل الصفحة. مرة أخرى، انتبه إلى صياغة مهام الدرس، في أمثلة مختلفةفي الممارسة العملية، قد تكون الصياغة مختلفة، لكن هذا لا يغير جوهر الحل وخوارزميته بشكل أساسي.

بصراحة، كنت متعبًا بعض الشيء لأن المادة كانت مملة بعض الشيء. لم يكن قول هذا في بداية المقال أمرًا تربويًا، لكنه أصبح الآن ممكنًا بالفعل =) في الواقع، لا تكون المشكلات في الرياضيات الحسابية عادةً معقدة للغاية، وليست مثيرة للاهتمام للغاية، وربما يكون الشيء الأكثر أهمية هو عدم ارتكاب أي خطأ في الحسابات العادية.

نرجو ألا تمحى مفاتيح الآلة الحاسبة الخاصة بك!

مثال 2:

حل:نحن نستخدم الصيغة:
في هذه الحالة: ، ،

هكذا:

إجابة:

مثال 4:

حل:نحن نستخدم الصيغة:
في هذه الحالة: , ,

هكذا:

لنحسب قيمة أكثر دقة للدالة باستخدام الآلة الحاسبة الدقيقة:

الخطأ المطلق:

خطأ نسبي:

إجابة: ، خطأ حسابي مطلق، خطأ حسابي نسبي

مثال 5:

حل:نحن نستخدم الصيغة:

في هذه الحالة: , ,

هكذا:

إجابة:

مثال 7:

حل:نحن نستخدم الصيغة:
في هذه الحالة: ، ،

المعنى الحقيقي الكمية الماديةيكاد يكون من المستحيل تحديد ذلك بدقة مطلقة، لأنه ترتبط أي عملية قياس بعدد من الأخطاء أو بمعنى آخر عدم الدقة. يمكن أن تكون أسباب الأخطاء مختلفة جدًا. وقد يرتبط حدوثها بعدم الدقة في تصنيع وضبط جهاز القياس، وذلك بسبب الخصائص الفيزيائية للكائن قيد الدراسة (على سبيل المثال، عند قياس قطر سلك ذو سمك غير منتظم، فإن النتيجة تعتمد بشكل عشوائي على اختيار موقع القياس)، وأسباب عشوائية، وما إلى ذلك.

تتمثل مهمة المجرب في تقليل تأثيرها على النتيجة، وكذلك الإشارة إلى مدى قرب النتيجة التي تم الحصول عليها من النتيجة الحقيقية.

هناك مفاهيم المطلقة و خطأ نسبي.

تحت الخطأ المطلقستفهم القياسات الفرق بين نتيجة القياس والقيمة الحقيقية للكمية المقاسة:

∆x ط =x ط -x و (2)

حيث ∆x i هو الخطأ المطلق للقياس i، x i _ هو نتيجة القياس i، x هي القيمة الحقيقية للقيمة المقاسة.

عادة ما تكون نتيجة أي قياس فيزيائي مكتوبة بالصيغة التالية:

حيث تكون القيمة المتوسطة الحسابية للقيمة المقاسة، الأقرب إلى القيمة الحقيقية (سيتم عرض صحة x و≈ أدناه)، وهي خطأ القياس المطلق.

ينبغي فهم المساواة (3) بطريقة تجعل القيمة الحقيقية للكمية المقاسة تقع في الفترة [ - , + ].

الخطأ المطلق هو كمية بعدية لها نفس البعد مثل الكمية المقاسة.

الخطأ المطلق لا يصف بشكل كامل دقة القياسات المأخوذة. في الواقع، إذا قمنا بقياس قطع بطول 1 متر و5 مم بنفس الخطأ المطلق ± 1 مم، فإن دقة القياسات ستكون لا تضاهى. ولذلك، جنبا إلى جنب مع خطأ القياس المطلق، يتم حساب الخطأ النسبي.

خطأ نسبيالقياسات هي نسبة الخطأ المطلق إلى القيمة المقاسة نفسها:

الخطأ النسبي هو كمية بلا أبعاد. ويتم التعبير عنها كنسبة مئوية:

في المثال أعلاه، الأخطاء النسبية هي 0.1% و20%. وهي تختلف بشكل ملحوظ عن بعضها البعض، على الرغم من أن القيم المطلقة هي نفسها. الخطأ النسبي يعطي معلومات حول الدقة

أخطاء القياس

وفقا لطبيعة المظاهر وأسباب حدوث الأخطاء، يمكن تقسيمها إلى الفئات التالية: مفيدة، منهجية، عشوائية، وأخطاء (أخطاء جسيمة).

تحدث الأخطاء إما بسبب خلل في الجهاز، أو انتهاك المنهجية أو الشروط التجريبية، أو تكون ذات طبيعة ذاتية. ومن الناحية العملية، يتم تعريفها على أنها نتائج تختلف بشكل حاد عن غيرها. للقضاء على حدوثها، من الضروري توخي الحذر والدقة عند العمل مع الأجهزة. يجب استبعاد النتائج التي تحتوي على أخطاء من النظر (تجاهلها).

أخطاء الصك. إذا كان جهاز القياس يعمل بشكل جيد ومضبوط، فيمكن إجراء القياسات عليه بدقة محدودة يحددها نوع الجهاز. من المعتاد اعتبار خطأ أداة أداة المؤشر مساويًا لنصف أصغر تقسيم لمقياسها. في الأجهزة ذات القراءة الرقمية، يُعادل خطأ الأداة قيمة أصغر رقم واحد من مقياس الأداة.

الأخطاء النظامية هي الأخطاء التي يكون حجمها وإشارتها ثابتين بالنسبة لسلسلة القياسات بأكملها التي يتم إجراؤها بنفس الطريقة وباستخدام نفس أدوات القياس.

عند إجراء القياسات، من المهم ليس فقط أن تأخذ في الاعتبار الأخطاء المنهجية، ولكن من الضروري أيضا ضمان القضاء عليها.

يتم تقسيم الأخطاء المنهجية بشكل تقليدي إلى أربع مجموعات:

1) الأخطاء التي تكون طبيعتها معروفة ويمكن تحديد حجمها بدقة تامة. مثل هذا الخطأ هو، على سبيل المثال، تغيير في الكتلة المقاسة في الهواء، والتي تعتمد على درجة الحرارة والرطوبة وضغط الهواء، وما إلى ذلك؛

2) الأخطاء التي تكون طبيعتها معروفة ولكن حجم الخطأ نفسه غير معروف. وتشمل هذه الأخطاء الأخطاء التي يسببها جهاز القياس: عطل في الجهاز نفسه، أو مقياس لا يتوافق مع القيمة الصفرية، أو فئة دقة الجهاز؛

3) الأخطاء التي قد لا يكون هناك شك في وجودها، ولكن حجمها يمكن أن يكون كبيرا في كثير من الأحيان. تحدث مثل هذه الأخطاء غالبًا في القياسات المعقدة. مثال بسيطومثل هذا الخطأ هو قياس كثافة بعض العينات التي تحتوي على تجويف بداخلها؛

4) الأخطاء الناجمة عن خصائص كائن القياس نفسه. على سبيل المثال، عند قياس التوصيل الكهربائي للمعدن، يتم أخذ قطعة من الأسلاك من الأخير. يمكن أن تحدث الأخطاء في حالة وجود أي عيب في المادة - صدع أو سماكة السلك أو عدم التجانس الذي يغير مقاومته.

الأخطاء العشوائية هي أخطاء تتغير بشكل عشوائي في الإشارة والحجم في ظل ظروف مماثلة لقياسات متكررة لنفس الكمية.

معلومات ذات صله.

تُستخدم الأخطاء المطلقة والنسبية لتقييم عدم الدقة في الحسابات المعقدة للغاية. كما أنها تستخدم في أبعاد مختلفةولتقريب نتائج الحساب. دعونا نلقي نظرة على كيفية تحديد الخطأ المطلق والنسبي.

الخطأ المطلق في الرقماستدعاء الفرق بين هذا الرقم وقيمته الدقيقة.
لنلقي نظرة على مثال : هناك 374 طالبا في المدرسة. إذا قمنا بتقريب هذا الرقم إلى 400، فإن خطأ القياس المطلق هو 400-374=26.

لحساب الخطأ المطلق، تحتاج إلى طرح الرقم الأصغر من الرقم الأكبر.

هناك صيغة للخطأ المطلق. دعونا نشير إلى الرقم الدقيق بالحرف A، والحرف a هو التقريب للرقم الدقيق. الرقم التقريبي هو رقم يختلف قليلاً عن الرقم المحدد وعادةً ما يحل محله في العمليات الحسابية. ثم ستبدو الصيغة كما يلي:

Δأ=أ-أ. ناقشنا أعلاه كيفية العثور على الخطأ المطلق باستخدام الصيغة.

ومن الناحية العملية، الخطأ المطلق لا يكفي لتقييم القياس بدقة. نادراً ما يكون من الممكن معرفة القيمة الدقيقة للكمية المقاسة من أجل حساب الخطأ المطلق. عند قياس كتاب طوله 20 سم مع وجود خطأ قدره 1 سم، يمكن اعتبار القياس به خطأ كبير. ولكن إذا حدث خطأ بمقدار 1 سم عند قياس جدار بطول 20 مترًا، فيمكن اعتبار هذا القياس دقيقًا قدر الإمكان. لذلك، في الممارسة العملية أكثر مهملديه تعريف لخطأ القياس النسبي.

سجل الخطأ المطلق للرقم باستخدام العلامة ±. على سبيل المثال يبلغ طول لفة ورق الحائط 30 م ± 3 سم ويسمى حد الخطأ المطلق بالحد الأقصى للخطأ المطلق.

خطأ نسبييسمون نسبة الخطأ المطلق للرقم إلى الرقم نفسه. لحساب الخطأ النسبي في المثال مع الطلاب نقسم 26 على 374. نحصل على الرقم 0.0695 ونحوله إلى نسبة ونحصل على 6%. ويشار إلى الخطأ النسبي كنسبة مئوية لأنه كمية بلا أبعاد. الخطأ النسبي هو تقدير دقيق لخطأ القياس. إذا أخذنا خطأ مطلقًا قدره 1 سم عند قياس طول المقاطع 10 سم و10 م، فإن الأخطاء النسبية ستكون 10٪ و0.1٪ على التوالي. بالنسبة لقطعة بطول 10 سم، يكون الخطأ 1 سم كبيرًا جدًا، وهذا خطأ بنسبة 10٪. ولكن بالنسبة لقطعة من عشرة أمتار، لا يهم 1 سم، فقط 0.1٪.

هناك أخطاء منهجية وعشوائية. المنهجي هو الخطأ الذي يظل دون تغيير أثناء القياسات المتكررة. الخطأ العشوائي ينشأ نتيجة تأثير العوامل الخارجية على عملية القياس ومن الممكن أن تغير قيمته.

هناك عدة قواعد لتقدير الأخطاء الاسمية:

عند جمع وطرح الأرقام، من الضروري إضافة أخطائها المطلقة؛
عند قسمة وضرب الأرقام، من الضروري إضافة أخطاء نسبية؛
عند رفعه إلى قوة، يتم ضرب الخطأ النسبي بالأس.

تتم كتابة الأرقام التقريبية والدقيقة باستخدام الكسور العشرية. يتم أخذ القيمة المتوسطة فقط، حيث أن القيمة الدقيقة يمكن أن تكون طويلة بلا حدود. لفهم كيفية كتابة هذه الأرقام، عليك أن تتعرف على الأرقام الحقيقية والمشكوك فيها.

الأرقام الحقيقية هي تلك الأرقام التي تتجاوز رتبتها الخطأ المطلق للرقم. إذا كان رقم الشكل أقل من الخطأ المطلق، فإنه يسمى مشكوك فيه. على سبيل المثال ، بالنسبة للكسر 3.6714 مع خطأ 0.002، فإن الأرقام الصحيحة ستكون 3،6،7، والمشكوك فيها ستكون 1 و 4. ولم يتبق سوى الأرقام الصحيحة في تسجيل الرقم التقريبي. سيبدو الكسر في هذه الحالة هكذا - 3.67.

رقم القياس

5.4. حساب الخطأ الكلي

الخطأ المطلق

; .

5. الخطأ النسبي، أو دقة القياس

; ه = 0.5%.

6. سجل النتيجة النهائية

يتم كتابة النتيجة النهائية للقيمة قيد الدراسة في النموذج

ملحوظة. في التسجيل النهائي، يجب أن يكون عدد أرقام النتيجة والخطأ المطلق هو نفسه.

6. التمثيل البياني لنتائج القياس

غالبًا ما يتم عرض نتائج القياسات الفيزيائية في شكل رسوم بيانية. تتمتع الرسوم البيانية بعدد من المزايا المهمة والخصائص القيمة:

أ) جعل من الممكن تحديد نوع الاعتماد الوظيفي والحدود التي يكون صالحًا ضمنها؛

ب) السماح بإجراء مقارنة واضحة للبيانات التجريبية مع المنحنى النظري؛

ج) عند إنشاء رسم بياني، يقومون بتنعيم القفزات أثناء الوظيفة التي تنشأ بسبب أخطاء عشوائية؛

د) جعل من الممكن تحديد كميات معينة أو إجراء التمايز الرسومي والتكامل وحل المعادلات وما إلى ذلك.

الرسوم البيانية، كقاعدة عامة، مصنوعة على ورق خاص (ملليمتر، لوغاريتمي، شبه لوغاريتمي). ومن المعتاد أن يرسم المتغير المستقل على طول المحور الأفقي، أي القيمة التي يحدد قيمتها المجرب نفسه، وعلى المحور الرأسي - القيمة التي يحددها. يجب أن يؤخذ في الاعتبار أن تقاطع محاور الإحداثيات لا يجب أن يتزامن مع القيم الصفرية لـ x و y. عند اختيار أصل الإحداثيات، يجب أن تسترشد بحقيقة أن منطقة الرسم بأكملها مستخدمة بالكامل (الشكل 2.).

على محاور إحداثيات الرسم البياني، لا يتم الإشارة إلى أسماء أو رموز الكميات فحسب، بل يتم أيضًا الإشارة إلى وحدات قياسها. يجب اختيار المقياس على طول محاور الإحداثيات بحيث تقع النقاط المقاسة على كامل مساحة الورقة. في هذه الحالة، يجب أن يكون المقياس بسيطًا بحيث لا تضطر عند رسم النقاط على الرسم البياني إلى إجراء حسابات حسابية في رأسك.

يجب تصوير النقاط التجريبية على الرسم البياني بدقة ووضوح. ومن المفيد رسم النقاط التي تم الحصول عليها في ظل ظروف تجريبية مختلفة (على سبيل المثال، التدفئة والتبريد) بألوان مختلفة أو برموز مختلفة. إذا كان خطأ التجربة معروفًا، فبدلاً من النقطة، من الأفضل تصوير صليب أو مستطيل، تتوافق أبعاده على طول المحاور مع هذا الخطأ. لا ينصح بربط النقاط التجريبية مع بعضها البعض بخط متقطع. يجب رسم المنحنى على الرسم البياني بسلاسة، مع التأكد من أن النقاط التجريبية تقع أعلى المنحنى وأسفله، كما هو موضح في الشكل 3.

عند إنشاء الرسوم البيانية، بالإضافة إلى نظام الإحداثيات بمقياس موحد، يتم استخدام ما يسمى بالمقاييس الوظيفية. من خلال تحديد الوظائف المناسبة x وy، يمكنك الحصول على خط أبسط على الرسم البياني مقارنة بالبناء التقليدي. غالبًا ما يكون هذا ضروريًا عند تحديد صيغة لرسم بياني معين لتحديد معلماته. تُستخدم المقاييس الوظيفية أيضًا في الحالات التي يكون فيها من الضروري تمديد أو تقصير أي قسم من المنحنى على الرسم البياني. المقياس الوظيفي الأكثر استخدامًا هو المقياس اللوغاريتمي (الشكل 4).

يتم استخدام الأخطاء المطلقة والنسبية لتقييم دقة القياسات. الخطأ المطلق هو الفرق بين العدد الدقيق والتقريبي. الخطأ النسبي هو نسبة الخطأ المطلق لعدد ما إلى الرقم نفسه. ومن الناحية العملية، يتم استخدام الخطأ النسبي لأنه أكثر دقة.

للقياسات المباشرة

1. دع جهدين يقاسان مرة واحدة على الفولتميتر ش 1 = 10 فولت، ش 2 = 200 فولت. يتميز الفولتميتر بالخصائص التالية: فئة الدقة d فئة t = 0.2، شالحد الأقصى = 300 فولت.

دعونا نحدد الأخطاء المطلقة والنسبية لهذه القياسات.

وبما أن كلا القياسين تم إجراؤهما على نفس الجهاز، فإن D ش 1 = د ش 2 ويتم حسابها باستخدام الصيغة (ب.4)

وفقا للتعريف، والأخطاء النسبية ش 1 و ش 2 متساوون على التوالي

ε 1 = 0.6 ∙ فولت / 10 فولت = 0.06 = 6%،

ε 2 = 0.6 ∙ فولت / 200 فولت = 0.003 = 0.3%.

من النتائج المعطاة للحسابات ε 1 و ε 2 يتضح أن ε 1 أكبر بكثير من ε 2.

يؤدي هذا إلى القاعدة: يجب عليك اختيار جهاز به حد قياس بحيث تكون القراءات في الثلث الأخير من المقياس.

2. دع بعض الكمية تقاس عدة مرات، أي يتم إنتاجها نالقياسات الفردية لهذه الكمية فأس 1 ، فأس 2 ,...,فأس 3 .

ثم لحساب الخطأ المطلق يتم تنفيذ العمليات التالية:

1) باستخدام الصيغة (ب.5) تحديد قيمة الوسط الحسابي أ 0 القيمة المقاسة؛

2) احسب مجموع الانحرافات التربيعية للقياسات الفردية عن الوسط الحسابي الموجود، وباستخدام الصيغة (ب.6)، حدد جذر متوسط مربع الخطأ، الذي يميز الخطأ المطلق لقياس واحد لقياسات مباشرة متعددة لقيمة معينة ;

3) يتم حساب الخطأ النسبي ε باستخدام الصيغة (B.2).

حساب الخطأ المطلق والنسبي

بالقياس غير المباشر

يعد حساب الأخطاء في القياسات غير المباشرة مهمة أكثر تعقيدًا، حيث أن القيمة المطلوبة في هذه الحالة هي دالة للكميات المساعدة الأخرى، والتي يكون قياسها مصحوبًا بظهور أخطاء. عادة، في القياسات، باستثناء الأخطاء، تكون الأخطاء العشوائية صغيرة جدًا مقارنة بالقيمة المقاسة. فهي صغيرة جدًا بحيث تكون الثانية أو أكثر درجات عاليةالأخطاء تقع خارج نطاق دقة القياس ويمكن إهمالها. نظرا لصغر الأخطاء في الحصول على صيغة الخطأ
تُستخدم طرق حساب التفاضل والتكامل لقياس كمية تم قياسها بشكل غير مباشر. عند قياس كمية ما بشكل غير مباشر، عندما يتم قياس الكميات المرتبطة ببعض العلاقات الرياضية المرغوبة بشكل مباشر، فمن الملائم أكثر تحديد الخطأ النسبي أولاً ثم
باستخدام الخطأ النسبي الموجود، احسب خطأ القياس المطلق.

يوفر حساب التفاضل والتكامل أبسط طريقة لتحديد الخطأ النسبي في القياس غير المباشر.

اتركي الكمية المطلوبة أيرتبط بالاعتماد الوظيفي مع عدة كميات مستقلة قابلة للقياس مباشرة س 1 ,
س 2 , ..., س ك، أي.

أ= F(س 1 , س 2 , ..., س ك).

لتحديد الخطأ النسبي للقيمة أخذ اللوغاريتم الطبيعي لطرفي المساواة

ln أ= سجل F(س 1 , س 2 , ..., س ك).

ثم يتم حساب الفرق اللوغاريتم الطبيعيالمهام
أ= F(س 1 ,س 2 , ..., س ك),

dln أ=dln F(س 1 , س 2 , ..., س ك)

يتم تنفيذ جميع التحويلات والتبسيطات الجبرية الممكنة في التعبير الناتج. بعد ذلك، يتم استبدال جميع رموز التفاضل d برموز الخطأ D، ويتم استبدال الإشارات السالبة أمام تفاضلات المتغيرات المستقلة بأخرى موجبة، أي يتم أخذ الحالة الأكثر سلبية، عندما يتم جمع جميع الأخطاء. في هذه الحالة، يتم حساب الحد الأقصى للخطأ في النتيجة.

مع ذلك قال

ولكن ε = د أ / أ

هذا التعبيرهي صيغة الخطأ النسبي للكمية أوفي القياسات غير المباشرة، فإنه يحدد الخطأ النسبي للقيمة المطلوبة، من خلال الأخطاء النسبية للقيم المقاسة. وبعد حساب الخطأ النسبي باستخدام الصيغة (ب.11)،
تحديد الخطأ المطلق للقيمة أكمنتج للخطأ النسبي والقيمة المحسوبة أأي.

د أ = ε أ، (في 12)

حيث يتم التعبير عن ε كرقم بلا أبعاد.

لذلك، ينبغي حساب الأخطاء النسبية والمطلقة للكمية المقاسة بشكل غير مباشر بالتسلسل التالي:

1) خذ الصيغة التي يتم من خلالها حساب القيمة المطلوبة (صيغة الحساب)؛

2) خذ اللوغاريتم الطبيعي لطرفي الصيغة الحسابية؛

3) محسوبة التفاضلية الكاملةاللوغاريتم الطبيعي للكمية المطلوبة؛

4) يتم تنفيذ جميع التحويلات والتبسيطات الجبرية الممكنة في التعبير الناتج؛

5) يتم استبدال رمز التفاضل d برمز الخطأ D، بينما يتم استبدال جميع العلامات السالبة أمام تفاضل المتغيرات المستقلة بأخرى موجبة (قيمة الخطأ النسبي ستكون الحد الأقصى) وتكون صيغة الخطأ النسبي مُقتَنىً؛

6) يتم حساب الخطأ النسبي للقيمة المقاسة؛

7) على أساس الخطأ النسبي المحسوب، يتم حساب الخطأ المطلق القياس غير المباشرحسب الصيغة (ب.12).

دعونا نلقي نظرة على عدة أمثلة لحساب الأخطاء النسبية والمطلقة في القياسات غير المباشرة.

1. الكمية المطلوبة أالمتعلقة بكميات قابلة للقياس مباشرة X, في, ضنسبة

أين أو ب- القيم الثابتة.

2. خذ اللوغاريتم الطبيعي للتعبير (ب.13)

3. احسب التفاضل الإجمالي للوغاريتم الطبيعي للكمية المطلوبة أأي أننا نفرق (ب.13)

4. نقوم بإجراء التحولات. باعتبار أن د أ= 0 منذ ذلك الحين أ= ثابت، كوس في/الخطيئة ذ=ctg ذ، نحن نحصل:

5. استبدال الرموز التفاضلية برموز الخطأ وعلامة الطرح أمام التفاضل بعلامة الزائد.

6. نحسب الخطأ النسبي للقيمة المقاسة.

7. بناءً على الخطأ النسبي المحسوب، يتم حساب الخطأ المطلق للقياس غير المباشر وفق الصيغة (ب.12)، أي.

يتم تحديد الطول الموجي اللون الأصفراستخدام الخط الطيفي للزئبق صريف الحيود(باستخدام التسلسل المقبول لحساب الأخطاء النسبية والمطلقة لطول الموجة الصفراء).

1. يتم تحديد الطول الموجي للون الأصفر في هذه الحالة بالصيغة:

أين مع- ثابت محزوز الحيود (القيمة المقاسة بشكل غير مباشر)؛ φ ث – زاوية حيود الخط الأصفر للداخل في هذا التسلسلالطيف (الكمية المقاسة مباشرة)؛ كز – ترتيب الطيف الذي تم فيه الرصد.

يتم حساب ثابت صريف الحيود بواسطة الصيغة

أين كح – ترتيب طيف الخط الأخضر؛ з з – الطول الموجي المعروف للون الأخضر ( з з – ثابت)؛ φз – زاوية الحيود للخط الأخضر بترتيب طيفي معين (القيمة المقاسة مباشرة).

ثم مع مراعاة التعبير (ب.15)

(ب.16)

أين كح، كز - الأشياء القابلة للملاحظة، والتي تعتبر ثابتة؛ φ ح، φ ث – هم
كميات قابلة للقياس مباشرة.

التعبير (B.16) هو صيغة حسابية للطول الموجي الأصفر المحدد باستخدام محزوز الحيود.

4. د كض = 0؛ د كث = 0؛ د з = 0، منذ ذلك الحين كح، كز و  ح – قيم ثابتة؛

ثم

5. (ب.17)

حيث Dφ w، Dφ h – الأخطاء المطلقة في قياس زاوية حيود اللون الأصفر
وخطوط الطيف الخضراء.

6. احسب الخطأ النسبي للطول الموجي الأصفر.

7. احسب الخطأ المطلق للطول الموجي الأصفر:

د  و = ε  و.

تقدير أخطاء نتائج القياس

أخطاء القياس وأنواعها

يتم إجراء أي قياسات دائمًا مع بعض الأخطاء المرتبطة بمحدودية دقة أدوات القياس، والاختيار الخاطئ والخطأ في طريقة القياس، وفسيولوجية المجرب، وخصائص الأشياء التي يتم قياسها، والتغيرات في ظروف القياس، وما إلى ذلك. تتضمن مهمة القياس العثور ليس فقط على القيمة نفسها، ولكن أيضًا خطأ القياس، أي الفاصل الزمني الذي من المرجح أن تقع فيه القيمة الحقيقية للكمية المقاسة. على سبيل المثال، عند قياس فترة زمنية t باستخدام ساعة توقيت بقيمة قسمة قدرها 0.2 ثانية، يمكننا القول أن قيمتها الحقيقية موجودة في الفاصل الزمني من https://pandia.ru/text/77/496/images/image002_131 .gif" width="85 " height="23 src=">с..gif" width="16" height="17 src="> وX هي القيم الحقيقية والمقاسة للكمية قيد الدراسة، على التوالى. الكمية تسمى الخطأ المطلق(خطأ) القياس، والإعراب الذي يميز دقة القياس يسمى خطأ نسبي.

من الطبيعي تمامًا أن يرغب المُجرِّب في إجراء كل قياس بأكبر قدر ممكن من الدقة، ولكن مثل هذا النهج لا يُنصح به دائمًا. كلما أردنا قياس هذه الكمية أو تلك بدقة أكبر، كلما زادت تعقيد الأدوات التي يجب أن نستخدمها، وكلما زادت المدة التي تتطلبها هذه القياسات. ولذلك، فإن دقة النتيجة النهائية يجب أن تتوافق مع الغرض من التجربة. تقدم نظرية الأخطاء توصيات حول كيفية إجراء القياسات وكيفية معالجة النتائج بحيث يكون الخطأ في حده الأدنى.

عادةً ما يتم تقسيم جميع الأخطاء التي تنشأ أثناء القياسات إلى ثلاثة أنواع - أخطاء منهجية أو عشوائية أو أخطاء أو أخطاء جسيمة.

أخطاء منهجيةتنتج عن الدقة المحدودة في تصنيع الأجهزة (أخطاء الأجهزة)، وأوجه القصور في طريقة القياس المختارة، وعدم دقة معادلة الحساب، والتركيب غير الصحيح للجهاز، وما إلى ذلك. وبالتالي، تحدث الأخطاء المنهجية بسبب عوامل تعمل بنفس الطريقة عندما يتم تكرار نفس القياسات عدة مرات. وحجم هذا الخطأ يتكرر بشكل منهجي أو يتغير وفقا لقانون معين. يمكن التخلص من بعض الأخطاء المنهجية (من السهل دائمًا تحقيق ذلك عمليًا) عن طريق تغيير طريقة القياس، وإدخال تصحيحات على قراءات الأجهزة، ومراعاة التأثير المستمر للعوامل الخارجية.

على الرغم من أن الخطأ المنهجي (الآلي) في القياسات المتكررة يعطي انحرافًا عن القيمة المقاسة المعنى الحقيقيطريق واحد، لا نعرف أبدًا أي طريق. لذلك، يتم كتابة خطأ الصك بعلامة مزدوجة

أخطاء عشوائيةتنتج عن عدد كبير من الأسباب العشوائية (التغيرات في درجة الحرارة، الضغط، اهتزاز المباني، وما إلى ذلك)، والتي تختلف تأثيراتها على كل قياس ولا يمكن أخذها في الاعتبار مسبقًا. كما تحدث أخطاء عشوائية نتيجة لنقص حواس المجرب. تتضمن الأخطاء العشوائية أيضًا الأخطاء الناتجة عن خصائص الجسم المقاس.

من المستحيل استبعاد الأخطاء العشوائية في القياسات الفردية، ولكن من الممكن تقليل تأثير هذه الأخطاء على النتيجة النهائية عن طريق إجراء قياسات متعددة. إذا تبين أن الخطأ العشوائي أقل بكثير من الخطأ الآلي (المنهجي)، فلا فائدة من تقليل القيمة بشكل أكبر خطأ عشوائيعن طريق زيادة عدد القياسات. إذا كان الخطأ العشوائي أكبر من خطأ الجهاز فيجب زيادة عدد القياسات لتقليل قيمة الخطأ العشوائي وجعله أقل من أو بنفس حجم خطأ الجهاز.

الأخطاء أو الأخطاء- هذه قراءات غير صحيحة على الجهاز، وتسجيل غير صحيح للقراءة، وما إلى ذلك. كقاعدة عامة، تكون الأخطاء الناجمة عن الأسباب المحددة ملحوظة بوضوح، لأن القراءات المقابلة تختلف بشكل حاد عن القراءات الأخرى. يجب القضاء على الأخطاء عن طريق قياسات التحكم. وبالتالي، فإن عرض الفاصل الزمني الذي تقع فيه القيم الحقيقية للكميات المقاسة لن يتم تحديده إلا من خلال أخطاء عشوائية ومنهجية.

2. تقدير الخطأ المنهجي (الأداة).

للقياسات المباشرةيتم حساب قيمة الكمية المقاسة مباشرة على مقياس جهاز القياس. يمكن أن يصل الخطأ في القراءة إلى عدة أعشار من تقسيم المقياس. عادة، في مثل هذه القياسات، يعتبر الخطأ المنهجي مساويا لنصف تقسيم مقياس أداة القياس. على سبيل المثال، عند القياس باستخدام الفرجار بقيمة تقسيم تبلغ 0.05 مم، فإن قيمة خطأ قياس الأداة تساوي 0.025 مم.

رقمي أدوات القياسإعطاء قيمة الكميات التي يقيسونها مع وجود خطأ، يساوي القيمةوحدة واحدة من الرقم الأخير على مقياس الأداة. لذا، إذا أظهر الفولتميتر الرقمي قيمة 20.45 مللي فولت، فإن خطأ القياس المطلق يساوي مللي فولت.

تنشأ أيضًا أخطاء منهجية عند استخدام القيم الثابتة المحددة من الجداول. في مثل هذه الحالات، يفترض أن يكون الخطأ مساويًا لنصف آخر رقم مهم. على سبيل المثال، إذا كانت قيمة كثافة الفولاذ في الجدول 7.9∙103 كجم/م3، فإن الخطأ المطلق في هذه الحالة يساوي https://pandia.ru/text/77/496/images/image009_52. gif" width= "123" height="24 src=">يتم استخدام الصيغة

, (1)

حيث https://pandia.ru/text/77/496/images/image012_40.gif" width="16" height="24">، هي مشتقات جزئية للدالة بالنسبة للمتغير https://pandia. ru/text/77 /496/images/image014_34.gif" width="65 height=44" height="44">.

المشتقات الجزئية فيما يتعلق بالمتغيرات دو حسوف تكون متساوية

https://pandia.ru/text/77/496/images/image017_27.gif" width = "71" height = "44 src = ">.

وبالتالي، فإن صيغة تحديد الخطأ المنهجي المطلق عند قياس حجم الأسطوانة وفقًا لها لها الشكل التالي

أين توجد أخطاء في الأجهزة عند قياس قطر وارتفاع الأسطوانة

3. تقدير الخطأ العشوائي.

فترة الثقة واحتمال الثقة

https://pandia.ru/text/77/496/images/image016_30.gif" width = "12 ارتفاع = 23" ارتفاع = "23">.gif" width = "45" ارتفاع = "21 src = "> - دالة توزيع الأخطاء العشوائية (الأخطاء)، التي تحدد احتمالية الخطأ، σ – متوسط مربع الخطأ.

الكمية σ ليست متغيرة عشوائية وتميز عملية القياس. إذا لم تتغير شروط القياس، تبقى σ قيمة ثابتة. يسمى مربع هذه الكمية تشتت القياس.كلما كان التشتت أصغر، كلما كان انتشار القيم الفردية أصغر وكلما زادت دقة القياسات.

القيمة الدقيقة لمتوسط مربع الخطأ σ، وكذلك القيمة الحقيقية للقيمة المقاسة، غير معروفة. وهناك ما يسمى بالتقدير الإحصائي لهذه المعلمة، والذي بموجبه يكون متوسط مربع الخطأ مساوياً لمتوسط مربع الخطأ للوسط الحسابي. يتم تحديد قيمتها بواسطة الصيغة

, (3)

حيث https://pandia.ru/text/77/496/images/image027_14.gif" width="15" height="17"> هو الوسط الحسابي للقيم التي تم الحصول عليها؛ ن- عدد القياسات.

كيف عدد أكبرالقياسات، كلما قل https://pandia.ru/text/77/496/images/image027_14.gif" width="15" height="17 src=">، والخطأ العشوائي المطلق، ثم ستكون نتيجة القياس مكتوبًا بالشكل https://pandia.ru/text/77/496/images/image029_11.gif" width="45" height="19"> إلى ، والذي يحتوي على القيمة الحقيقية للكمية المقاسة μ، يسمى فاصل الثقة.نظرًا لأن https://pandia.ru/text/77/496/images/image025_16.gif" width="19 height=24" height="24"> قريب من σ. للعثور على فاصل الثقة واحتمال الثقة باستخدام يتم استخدام عدد قليل من القياسات التي نتعامل معها أثناء العمل المخبري توزيع احتمالات الطلاب.هذا هو التوزيع الاحتمالي متغير عشوائي، مُسَمًّى معامل الطالب، يعطي قيمة فاصل الثقة في كسور جذر متوسط مربع الخطأ للوسط الحسابي.

لا يعتمد التوزيع الاحتمالي لهذه الكمية على σ2، ولكنه يعتمد بشكل كبير على عدد التجارب ن.مع تزايد عدد التجارب نيميل توزيع الطلاب إلى التوزيع الغوسي.

يتم جدولة وظيفة التوزيع (الجدول 1). قيمة معامل الطالب تكون عند تقاطع الخط المقابل لعدد القياسات ن، والعمود المقابل لاحتمال الثقة α

الجدول 1.

باستخدام بيانات الجدول، يمكنك:

1) تحديد فاصل الثقة، مع وجود احتمال معين؛

2) حدد فاصل الثقة وحدد احتمالية الثقة.

بالنسبة للقياسات غير المباشرة، متوسط مربع الخطأ لقيمة المتوسط الحسابي للدالة تحسب بواسطة الصيغة

. (5)

يتم تحديد فاصل الثقة واحتمال الثقة بنفس الطريقة كما في حالة القياسات المباشرة.

تقدير خطأ القياس الكلي. سجل النتيجة النهائية.

سيتم تحديد الخطأ الإجمالي لنتيجة القياس للقيمة X على أنه القيمة الجذرية لمتوسط مربع الأخطاء المنهجية والعشوائية

, (6)

أين δ –خطأ في الأداة، Δ X- خطأ عشوائي.

يمكن أن تكون X كمية يتم قياسها بشكل مباشر أو غير مباشر.

، α=…، ه=… (7)

يجب أن يؤخذ في الاعتبار أن صيغ نظرية الخطأ نفسها صالحة عدد كبيرقياسات. ولذلك، يتم تحديد قيمة العشوائية، وبالتالي الخطأ الإجمالي، عند صغير نمع خطأ كبير. عند حساب Δ Xعند قياس عدد القياسات، يوصى بتحديد رقم واحد مهم إذا كان أكثر من 3 واثنين إذا كان الرقم الأول شخصية هامةأقل من 3. على سبيل المثال، إذا كان Δ X= 0.042، ثم نتخلص من 2 ونكتب Δ X= 0.04، وإذا Δ X=0.123، ثم نكتب Δ X=0,12.

يجب أن يكون عدد أرقام النتيجة والخطأ الإجمالي هو نفسه. ولذلك، يجب أن يكون الوسط الحسابي للخطأ هو نفسه. ولذلك، يتم حساب الوسط الحسابي أولاً برقم واحد أكثر من القياس، وعند تسجيل النتيجة يتم تحسين قيمته إلى عدد أرقام الخطأ الإجمالي.

4. منهجية حساب أخطاء القياس.

أخطاء القياسات المباشرة

عند معالجة نتائج القياسات المباشرة، يوصى باعتماد الترتيب التالي للعمليات.

قياسات المحدد المعلمة المادية ن مرات وبنفس الظروفويتم تسجيل النتائج في جدول. إذا كانت نتائج بعض القياسات تختلف بشكل حاد في القيمة عن قياسات أخرى، فسيتم تجاهلها باعتبارها أخطاء إذا لم يتم تأكيدها بعد التحقق منها. يتم حساب الوسط الحسابي للقياسات المتطابقة n. يتم اعتبارها القيمة الأكثر احتمالية للكمية المقاسة

تم العثور على الأخطاء المطلقة للقياسات الفردية ويتم حساب مربعات الأخطاء المطلقة للقياسات الفردية (Δ Xط)2 يتم تحديد جذر متوسط مربع الخطأ للوسط الحسابي

تم تعيين قيمة احتمال الثقة α. من المعتاد في مختبرات الورش ضبط α=0.95. تم العثور على معامل الطالب لاحتمال ثقة معين α وعدد القياسات المأخوذة (انظر الجدول).

يتم تحديد الخطأ الإجمالي

يتم تقدير الخطأ النسبي لنتيجة القياس

النتيجة النهائية مكتوبة في النموذج

ج α=… ه=…%.

5. خطأ القياسات غير المباشرة

عند تقييم القيمة الحقيقية لقيمة تم قياسها بشكل غير مباشر https://pandia.ru/text/77/496/images/image045_6.gif" width="75" height="24">، يمكن استخدام طريقتين.

الطريقة الأولىتستخدم إذا كانت القيمة ذمحدد في ظروف مختلفةخبرة. في هذه الحالة، يتم حساب كل من القيم ومن ثم يتم تحديد الوسط الحسابي لجميع القيم يي

تم العثور على الخطأ المنهجي (الآلي) بناءً على الأخطاء الآلية المعروفة لجميع القياسات باستخدام الصيغة. ويعرف الخطأ العشوائي في هذه الحالة بأنه خطأ القياس المباشر.

الطريقة الثانيةينطبق إذا كانت هذه الوظيفة ذتم تحديدها عدة مرات بنفس القياسات..gif" width="75" height="24">. في ممارساتنا المخبرية، يتم استخدام الطريقة الثانية لتحديد الكمية المقاسة بشكل غير مباشر في كثير من الأحيان ذ.يتم العثور على الخطأ المنهجي (الآلي) كما في الطريقة الأولى على أساس الأخطاء الآلية المعروفة لجميع القياسات باستخدام الصيغة

. (10)

للعثور على الخطأ العشوائي لقياس غير مباشر، يتم أولاً حساب جذر متوسط الأخطاء المربعة للوسط الحسابي للقياسات الفردية. ومن ثم يتم العثور على متوسط مربع الخطأ للقيمة ذ.تحديد احتمالية الثقة α، وإيجاد معامل الطالب https://pandia.ru/text/77/496/images/image048_2.gif" width="83" height="23">، مع α=… E=…% .

6. مثال على تصميم العمل المخبري

العمل المختبري رقم 1

تحديد حجم الاسطوانة

مُكَمِّلات:الفرجار بقيمة قسمة 0.05 مم، ميكرومتر بقيمة قسمة 0.01 مم، جسم أسطواني.

الهدف من العمل:التعرف على أبسط القياسات الفيزيائية، وتحديد حجم الأسطوانة، وحساب الأخطاء في القياسات المباشرة وغير المباشرة.

قم بقياس قطر الاسطوانة 5 مرات على الأقل باستخدام الفرجار وارتفاعها بالميكرومتر.

صيغة حسابية لحساب حجم الاسطوانة

حيث d هو قطر الاسطوانة؛ ح – الارتفاع.

نتائج القياس

الجدول 2.