ЕГОРОВА ВИКТОРИЯ ВАЛЕРЬЕВНА

Учитель математики

высшей квалификационной категории

ТЕМА: «ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ

ЛОГАРИФМИЧЕСКИХ ВЫРАЖЕНИЙ»

Знания и навыки, которыми должны овладеть учащиеся после изучения данного урока:

знать определение логарифма числа, основное логарифмическое тождество, свойства логарифмов;

уметь выполнять преобразования выражений, содержащих логарифмы, вычислять логарифмы.

Литература:

1. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. и др. Алгебра и начала анализа: учебник для 10-11 классов общеобразовательных учреждений. – М.: Просвещение, 2001.

2. Кочагин В.В., Кочагина М.В., Интенсивный курс подготовки к ЕГЭ. – М.:Эксмо, 2009.

3. Мерзляк А.Г., Полонский В.Б., Якир М.С., Алгебраический тренажер: Пособие для школьников и абитуриентов. – М.:Илекса, 2005.

4. Гусев В.А., Мордкович А.Г. Математика: Справочные материалы: Книга для учащихся. – М.: Просвещение, 2001.

План урока:

Ход урока:

1) Логарифм – это греческое слово, которое состоит из 2-х слов: “логос”- отношение, “аритмос”- число. Значит, логарифм есть число, измеряющее отношение. В публикации тысяча шестьсот четырнадцатого года сообщалось, что Непер изобрёл логарифмы. Позже им были составлены логарифмические таблицы, которые теперь известны нам как таблицы Брадиса. Менее чем за одно столетие таблицы распространились по всему миру и сделались незаменимым вычислительным средством. В дальнейшем они были, как бы встроены в удобное устройство, чрезвычайно ускоряющее процесс вычисления – логарифмическую линейку, которой пользовались до семидесятых годов двадцатого века.

Приложение 1.

2) Логарифмом положительного числа b по основанию a , причём а больше нуля и не равно единицы, называется показатель степени, в которую нужно возвести число a , чтобы получить число b.

Это равенство, выражающее определение логарифма, называется основным логарифмическим тождеством .

Ц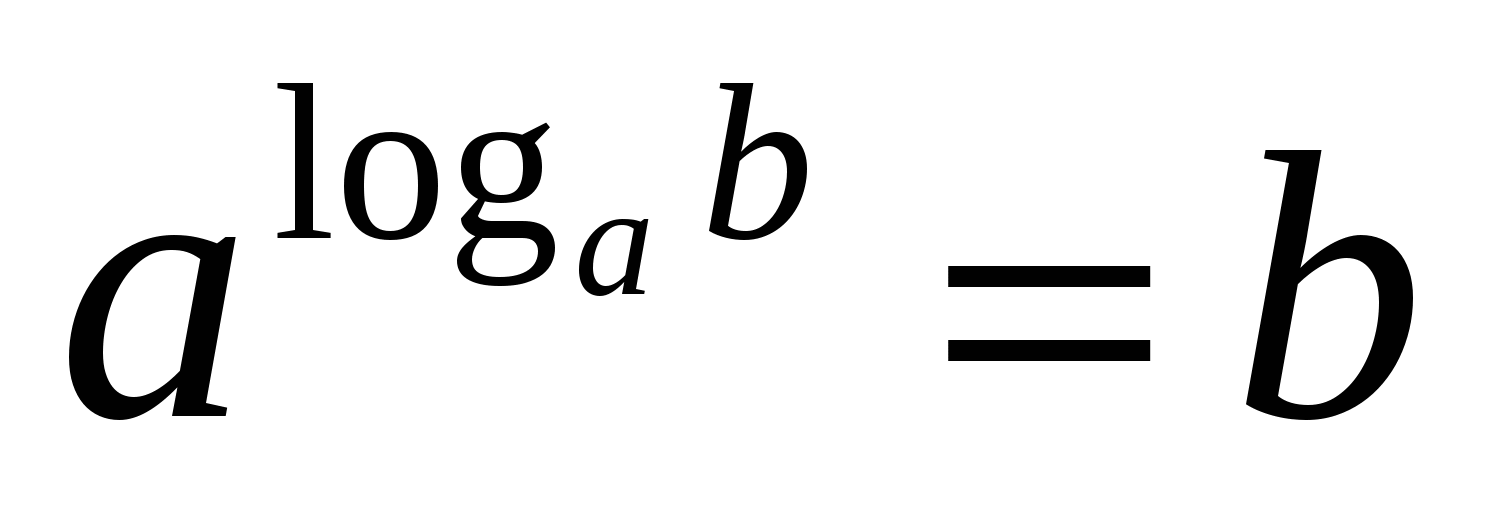

ОР 1

П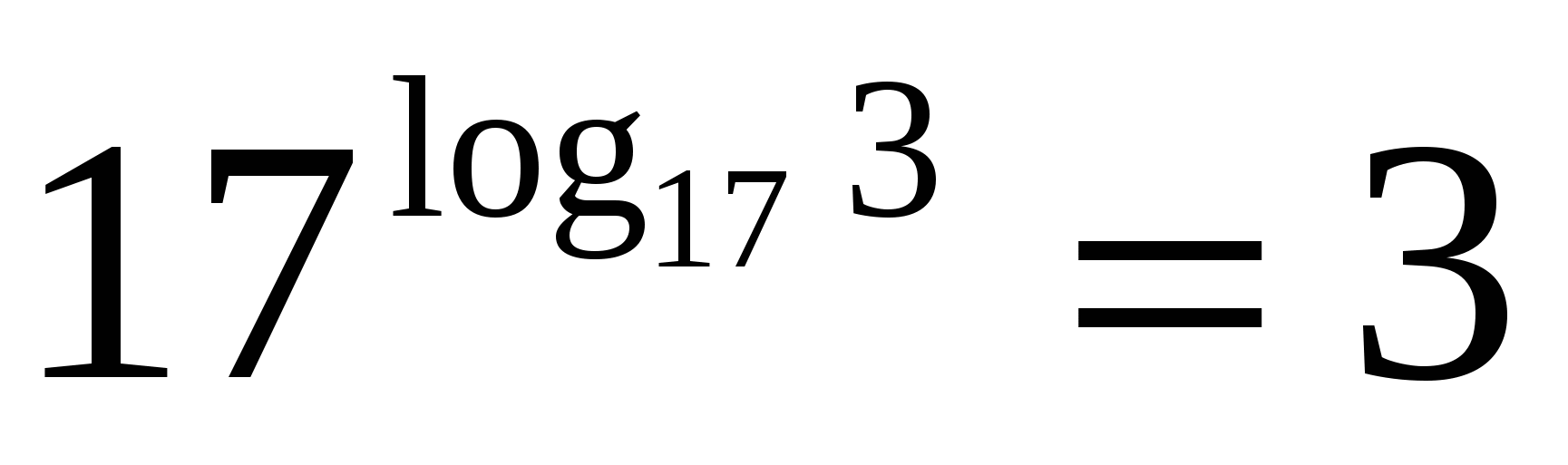

Основание степени и основание логарифма семнадцать, значит по основному логарифмическому тождеству значение выражения равно трём.

Оработаем устно:

Щ
ЕЛЧОК

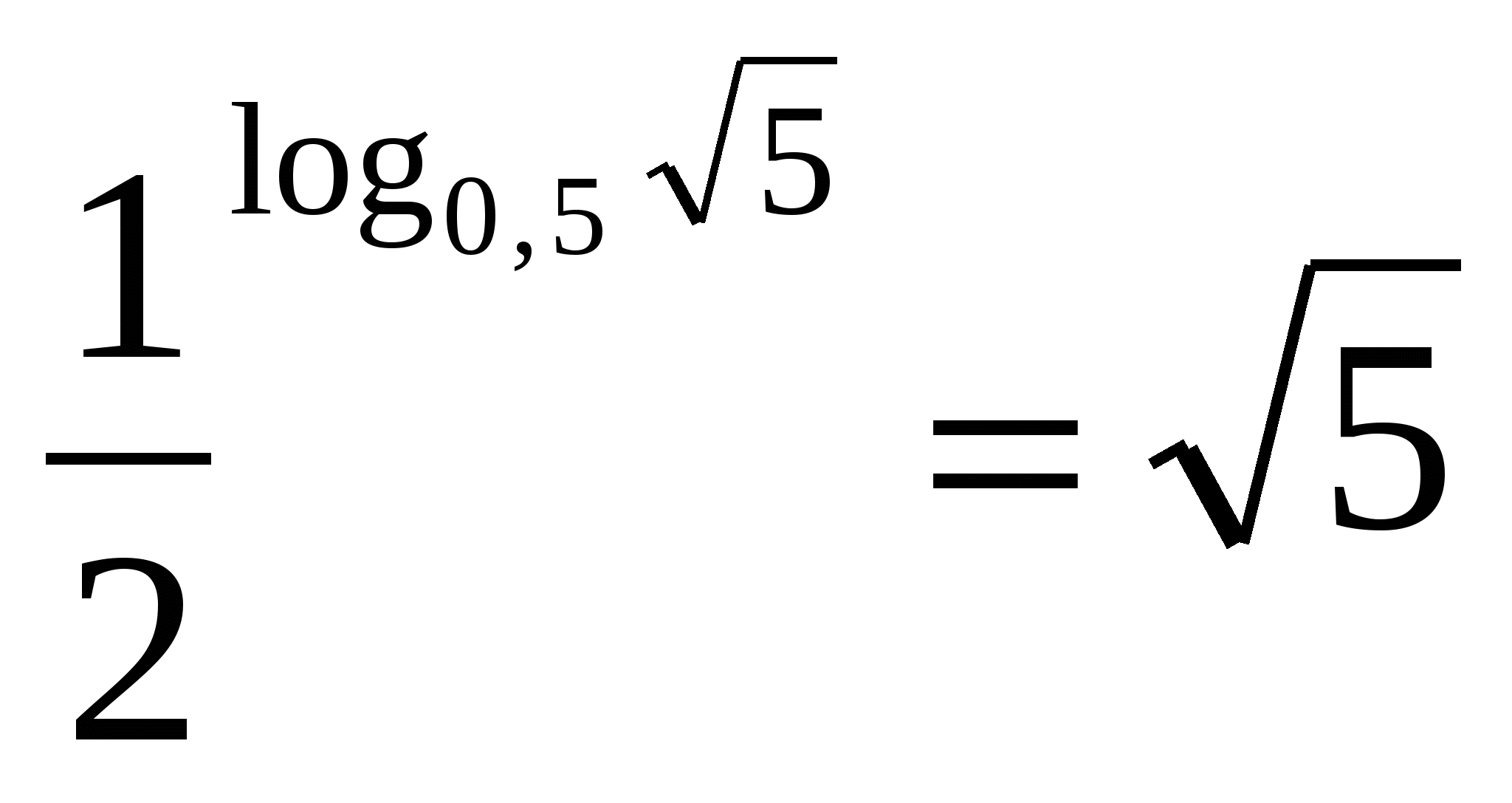
Одна вторая равна нуль целых пяти десятым, значит выражение равно арифметическому квадратному корню из пяти.

П

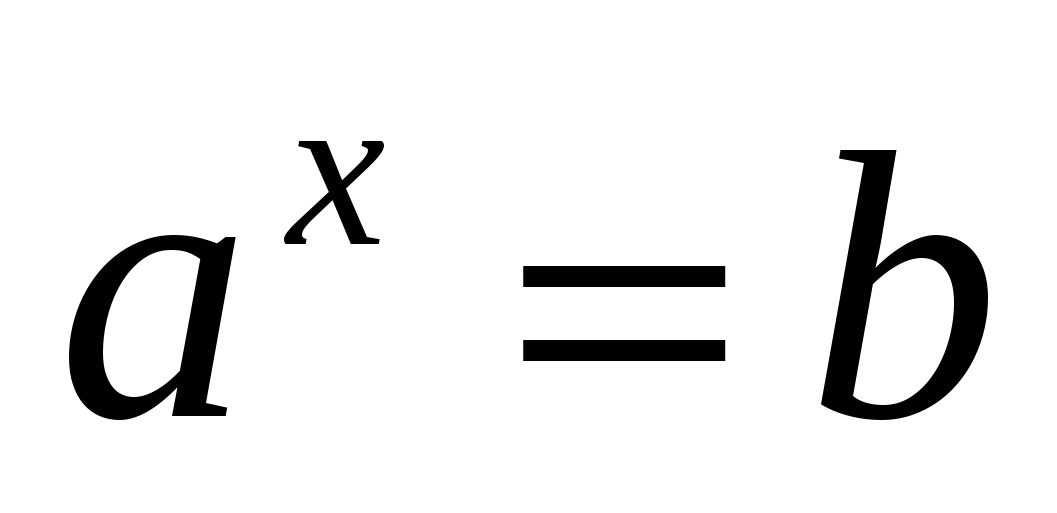риложение 2.

Равенство означает, что

Из определения логарифма получаются следующие важные равенства:

Например:

П
риложение 3.

Перейдем к заданиям ЕГЭ:

Приложение 4.

3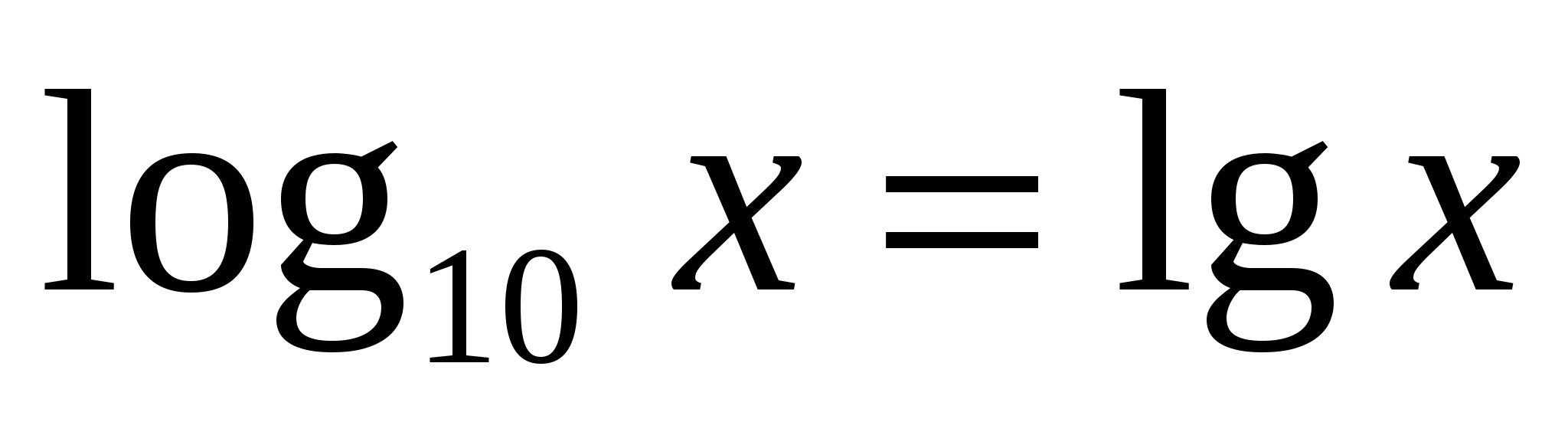
) Для логарифма по основанию десять существует специальное обозначение и название десятичный логарифм .

Л
огарифм по основанию е называется натуральным логарифмом .

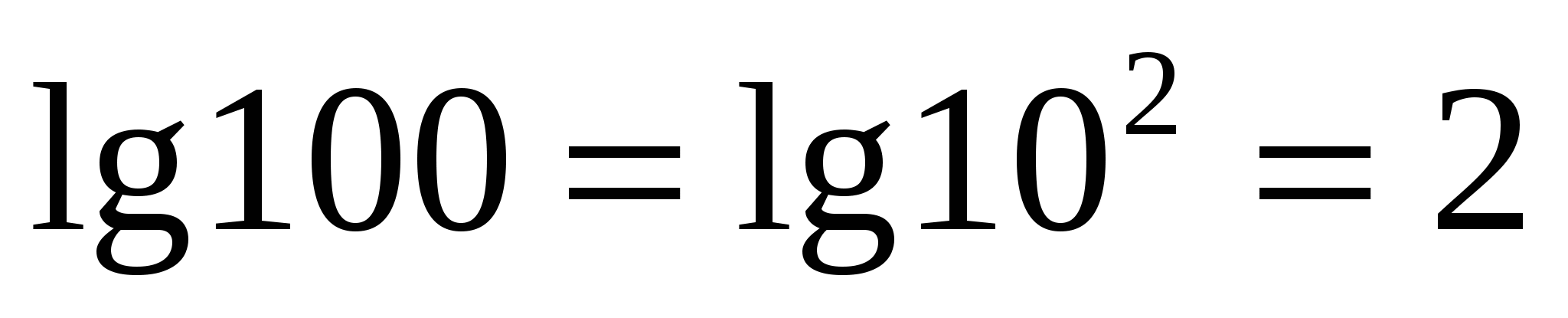
Н
апример,

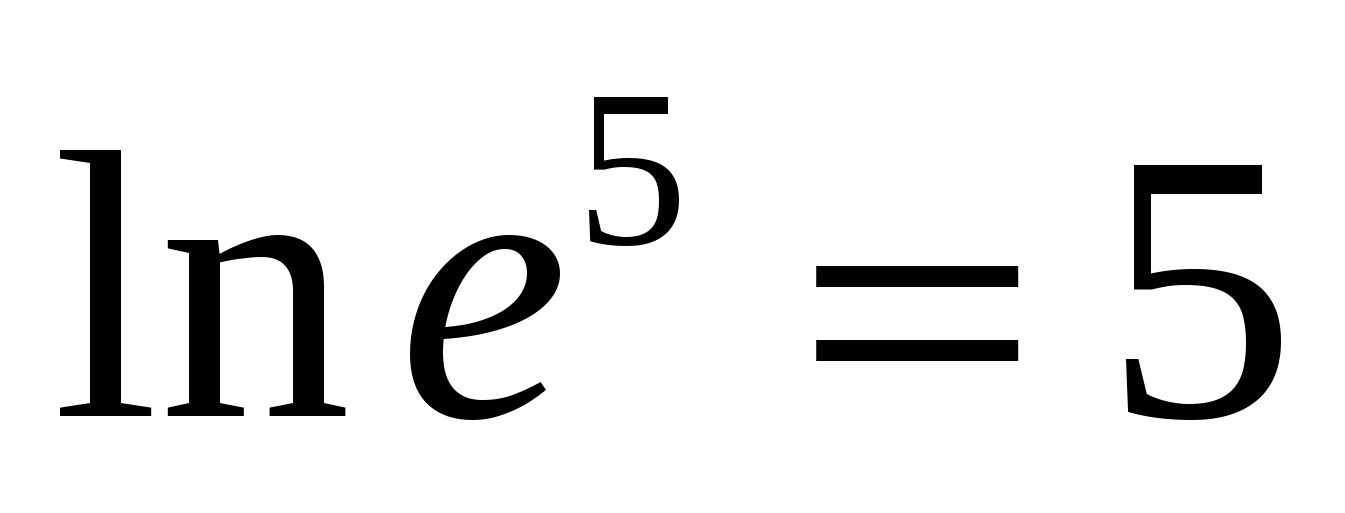
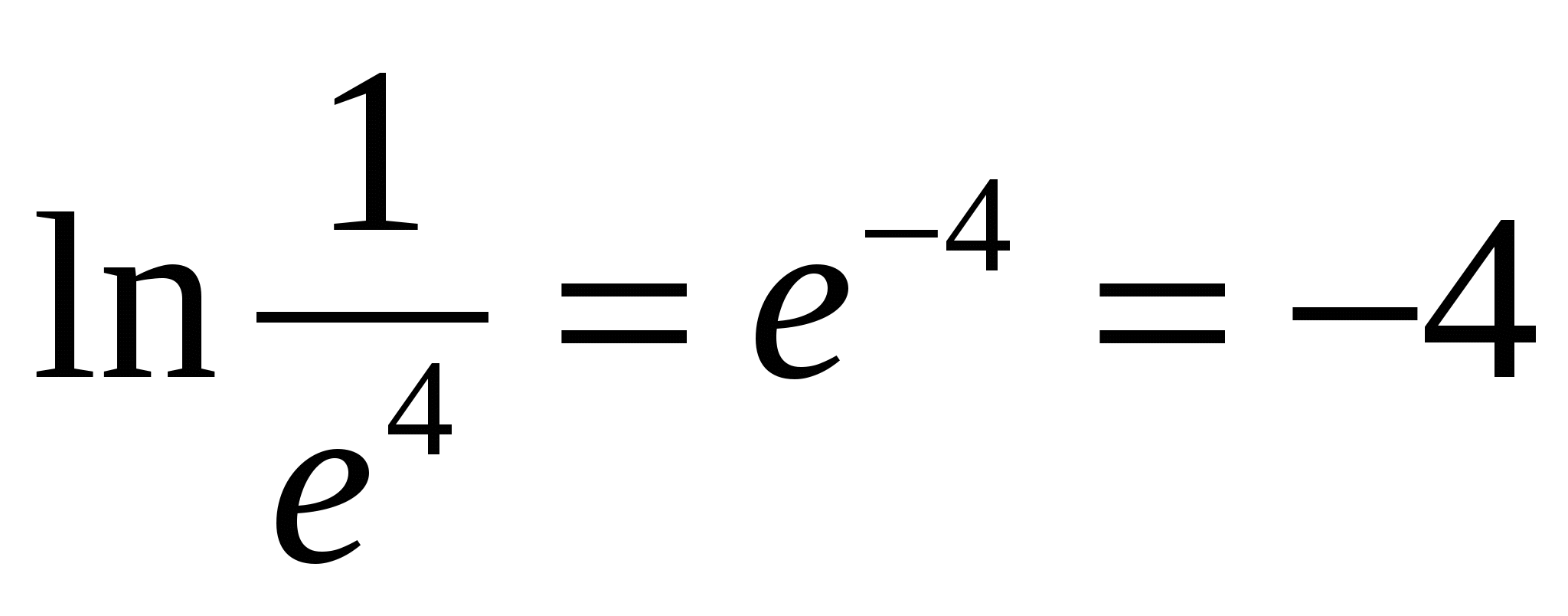
4) Из определения логарифма вытекают следующие его свойства. Все свойства формулируются и доказываются только для положительных значений переменных, содержащихся под знаками логарифмов.

Логарифм произведения двух положительных чисел по основанию а равен сумме логарифмов этих чисел с тем же основанием.

ЦОР 2

Например,

З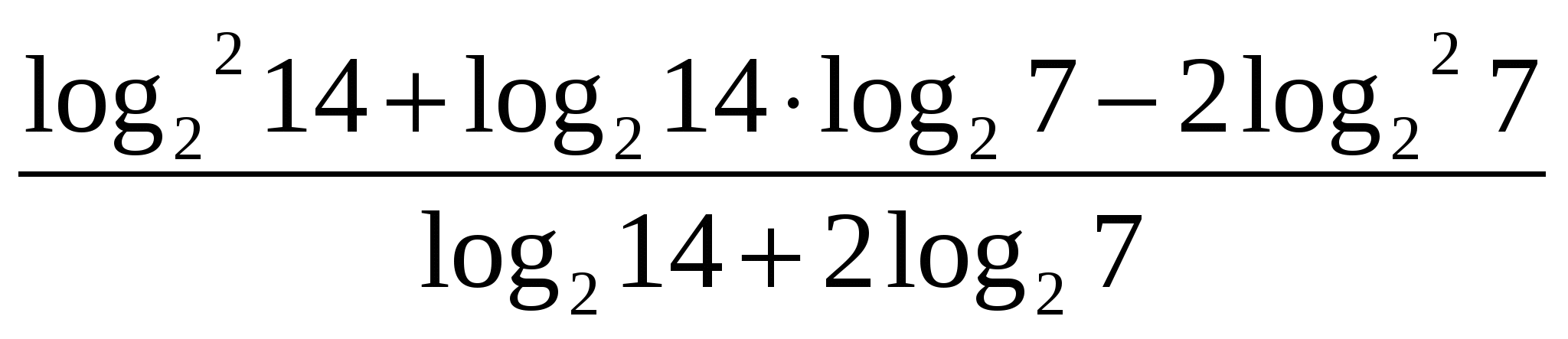
адание 1.

Задание 2. Упростите выражение

В
оспользуемся решением предыдущего примера. Заменим

Обратите внимание на то, что логарифм в квадрате, поэтому и сумму необходимо возвести в квадрат. Применяя формулу квадрата суммы, раскроем скобки. Приведём подобные слагаемые.

5) Логарифм частного равен разности логарифмов делимого и делителя.

Ц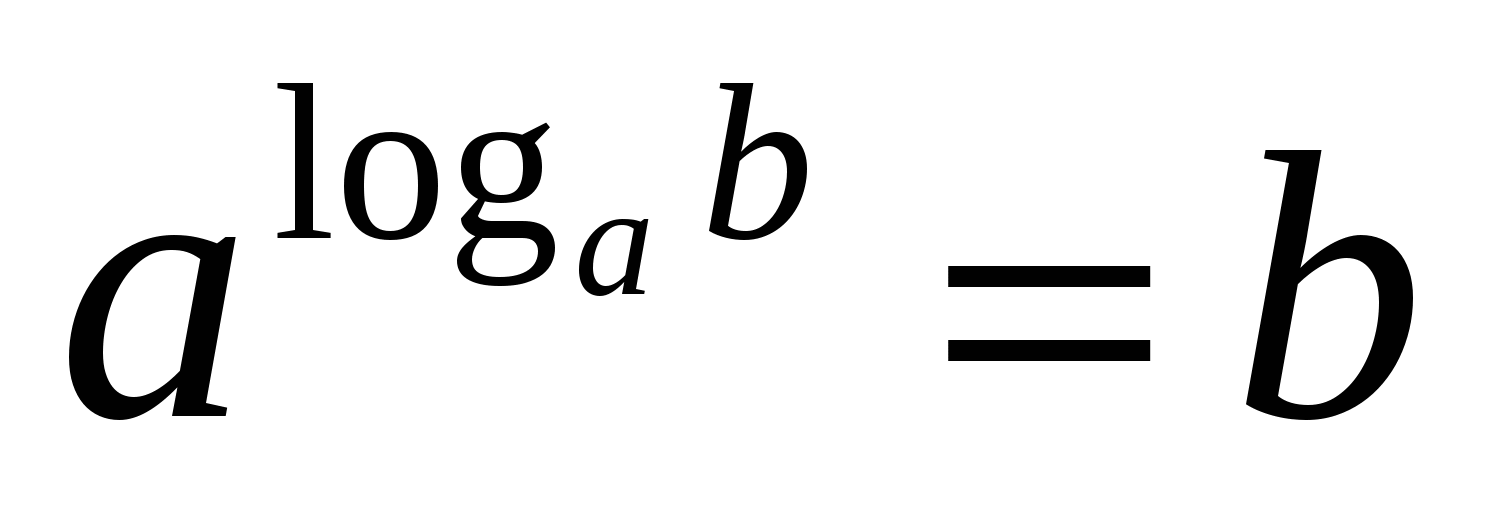

Обратите внимание на основание степени и основание логарифма – они одинаковы.

ОР 3

Р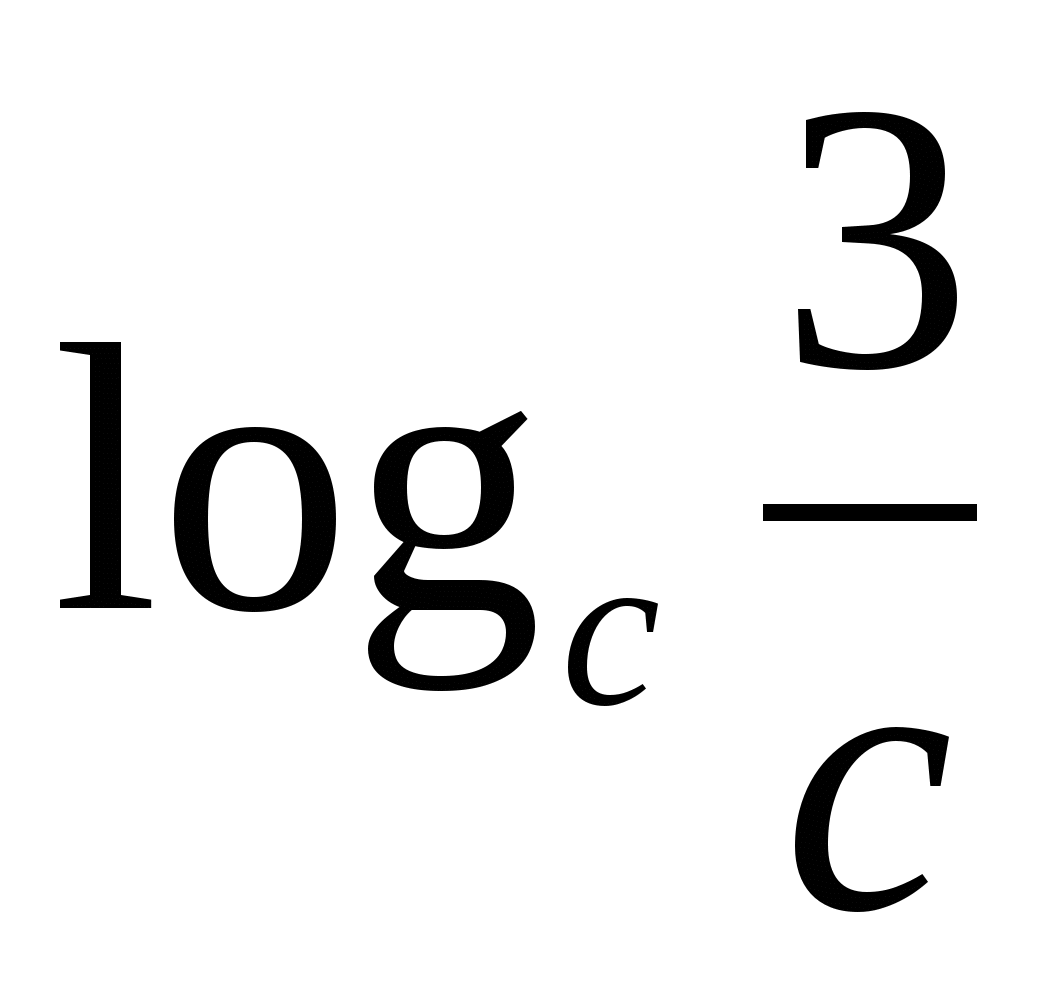

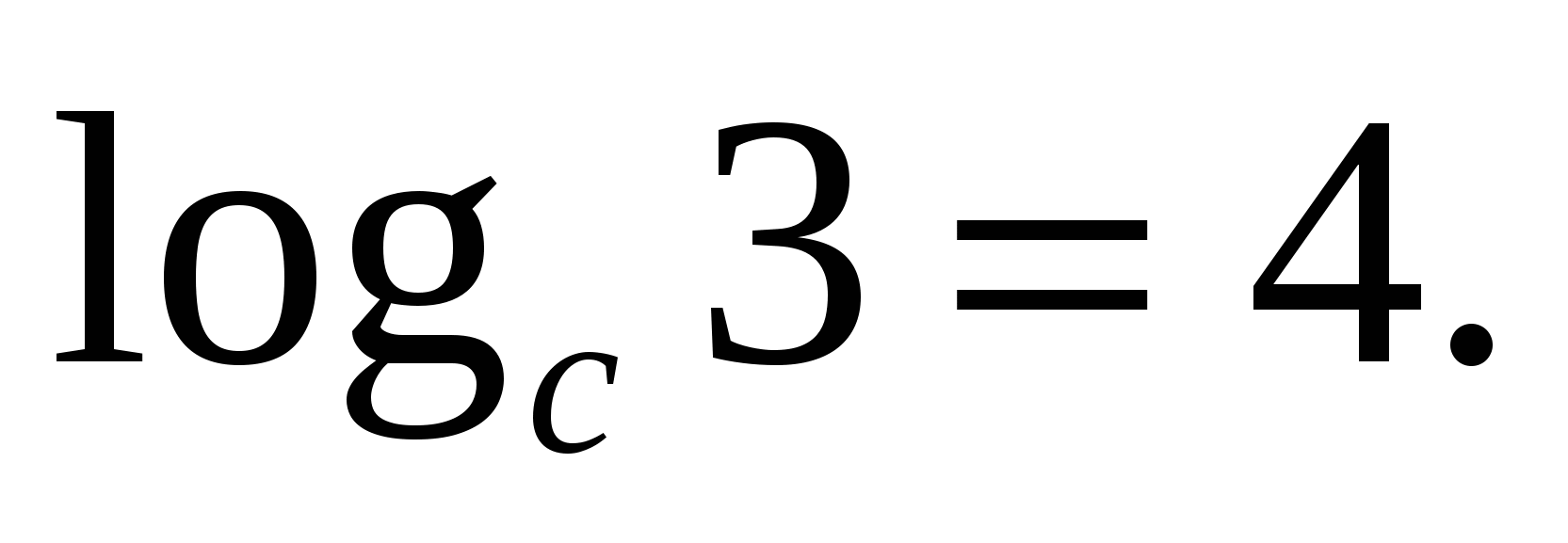ассмотрим применение этой формулы на примере:

З
адание 1. Найдите значение выражения, если

Задание 2. Найдите значение b по его логарифму

6) Логарифм степени по основанию а , равен произведению показателя степени на логарифм по тому же основанию.

ЦОР 4

Например,

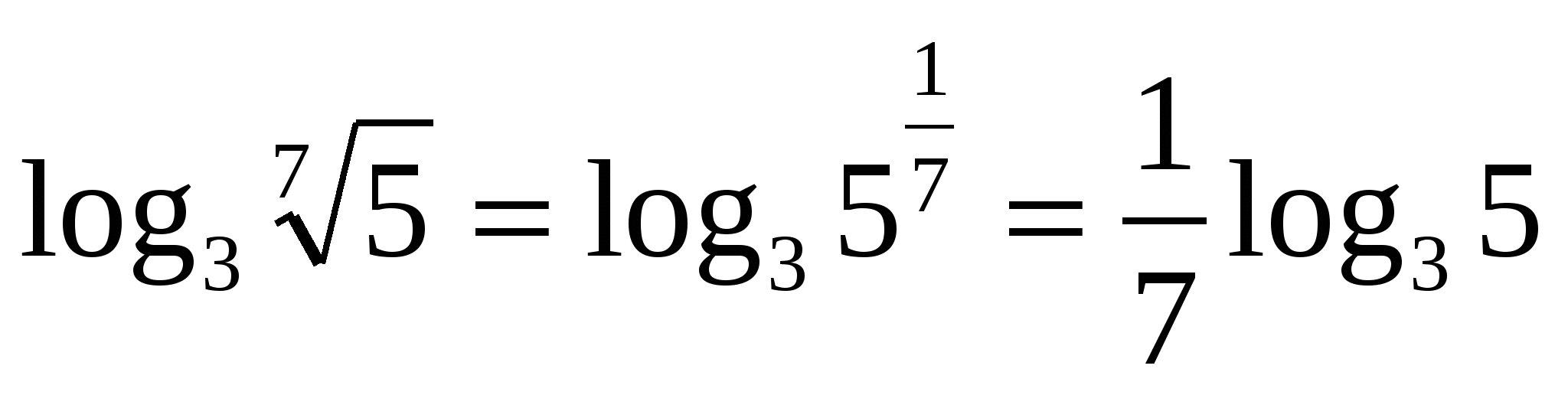
З
адание 1. Вычислите, если

Упростим выражение

Формула

называется формулой перехода к новому основанию.

З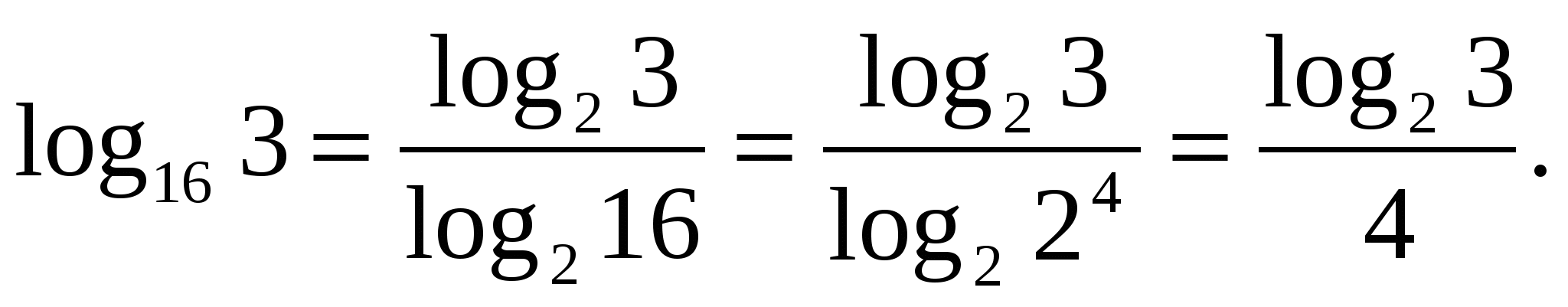

адание 1. Выразить через логарифм с основанием 2.

Задание 2. Вычислите

ЦОР 5

ЦОР 6

Например,

З

адание 1. Вычислите

З
адание 2. Вычислите

9) К логарифмическим преобразованиям можно приступать, только в том случаи, если вы запомнили все свойства логарифмов. Повторив их, рассмотрим задания на преобразования логарифмических выражений с другой стороны.

Для преобразования суммы или разности логарифмических выражений иногда достаточно использовать определение логарифма, а чаще всего свойства логарифма произведения или частного.

З
адание 1. Вычислите

Решим двумя способами.

1 способ, используя определение логарифма:

2 способ, опираясь на свойство логарифма частного:

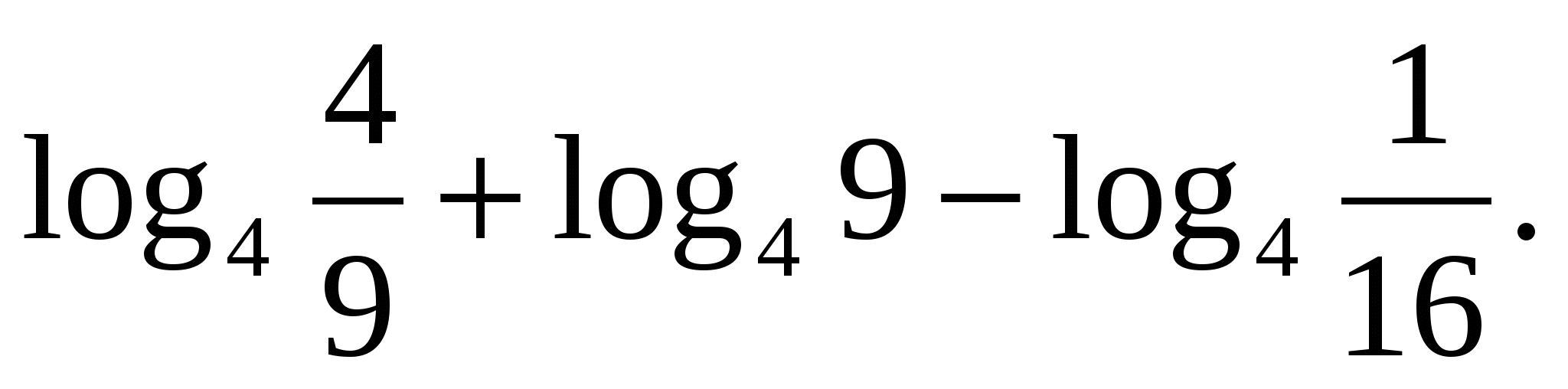
Задание 2. Найдите значение выражения

Применим сначала формулу логарифма произведения, затем определение логарифма.

Основное логарифмическое тождество используется при преобразовании выражений, содержащих логарифм в показателе степени. Идея таких операций заключается в получении равных основания степени и основания логарифма.

Иногда необходимо преобразовывать выражение по свойствам логарифма и по свойствам степени, так же можно легко перейти от одного основания к другому, используя формулу перехода. В других случаях следует применять несколько свойств.

З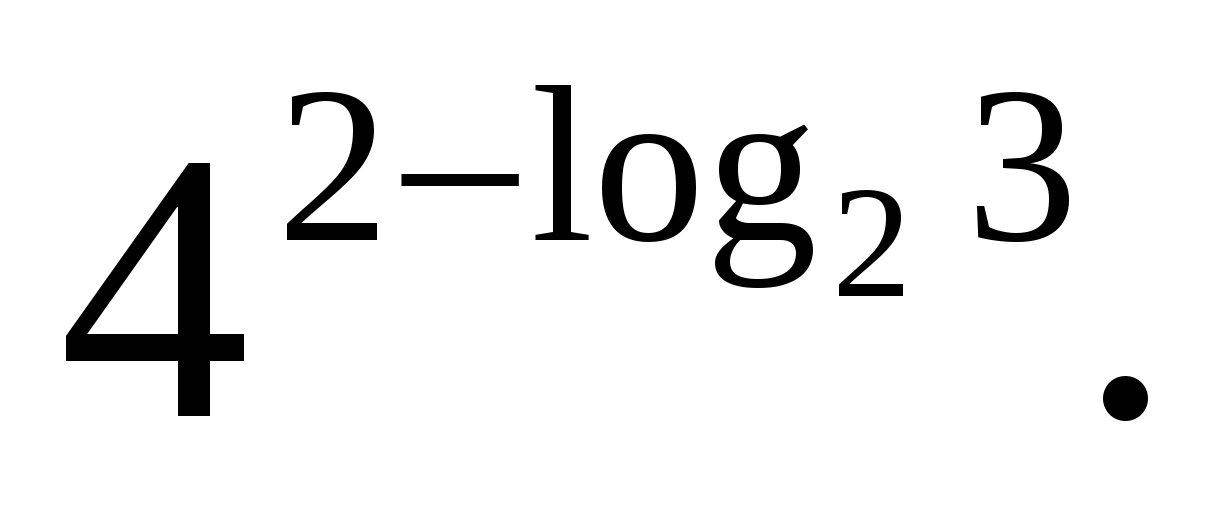
адание 3. Вычислите

З
адание 4. Найдите значение выражения

Задание 5. Найдите значение выражения

З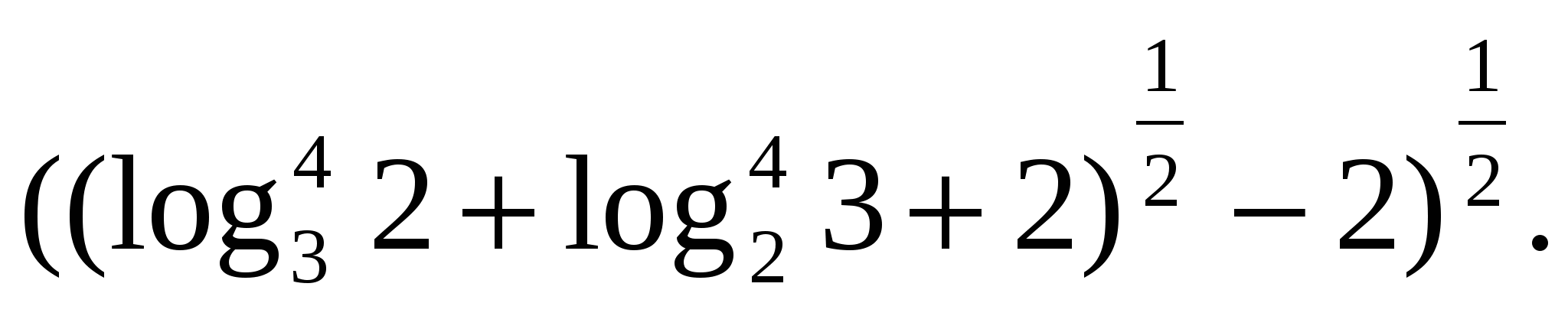
адание 6. Представьте в виде разности логарифмов

Н
аибольшую трудность представляют преобразования логарифмических выражений, находящихся под радикалом. В процессе преобразований приходится рассматривать модули логарифмических выражений, для раскрытия которых требуется сравнить иррациональные числа или рациональное и иррациональное число. Будем действовать последовательно. Рассмотрим выражение, стоящее под внутренним радикалом.

Подставим в исходное выражение.

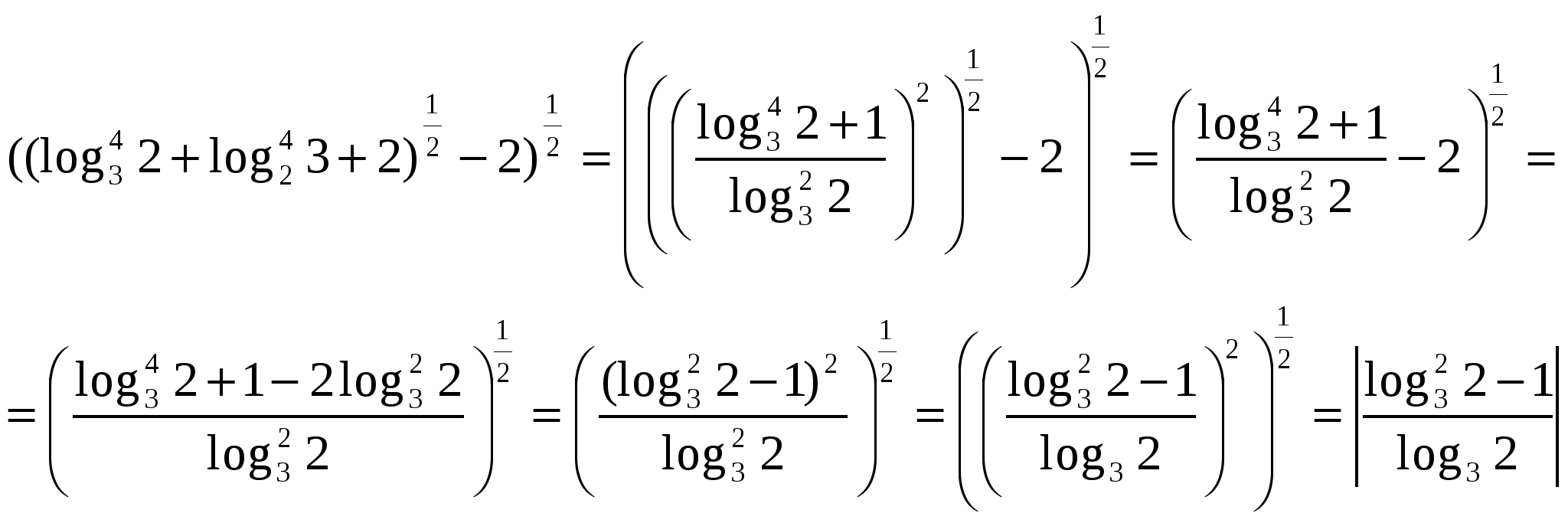Следует отметить, что с преобразованием логарифмических выражений можно встретиться и при решении уравнений и неравенств или исследовании функций, поэтому в неявном виде они могут присутствовать и в заданиях групп В и С.

10) Подведение итогов.Вопросы:

Логарифм по основанию 10 называется

основным логарифмом

главным логарифмом

натуральным логарифмом

десятичным логарифмом

2) Какие значения может принимать x в выражении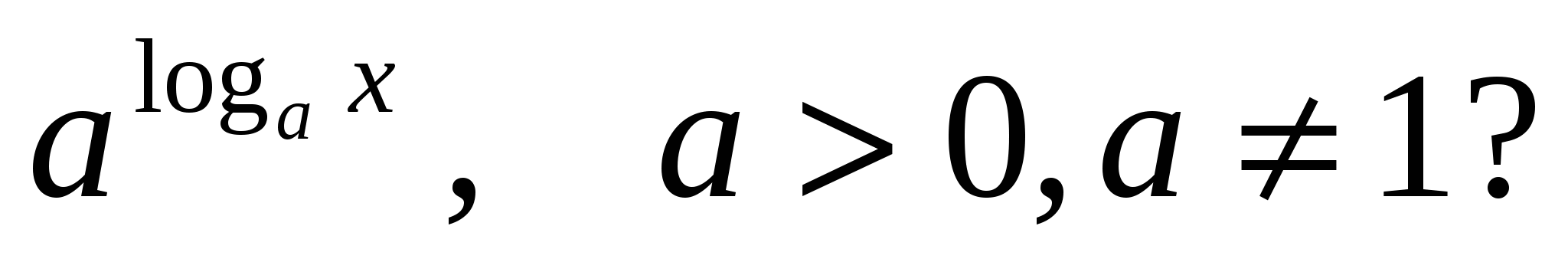

Значение не определено

5) Укажите соотношение, которое верно для всех x ≠ 0 .

6) Укажите верное соотношение для формулы перехода к новому основанию.

7) Укажите верное равенство при

11) Контрольное тестирование.

Математика. Тематические тесты. Часть II. Подготовка к ЕГЭ-2010. 10-11 классы. Под ред. Лысенко Ф.Ф. - Ростов н/Д.: Легион, 2009. - 176с.

Математика. ЕГЭ-2009. Тематические тесты. Ч.II (В4-В8, С1-С2) Под ред. Лысенко Ф.Ф. - Ростов н/ Д: Легион, 2008 - 160 с.

Пособие состоит из тестов по отдельным темам, которые являются традиционными в курсе математики и потому, как правило, входят в ЕГЭ. Они полностью охватывают группы заданий повышенного и высокого уровня сложности ЕГЭ, кроме текстовых задач и задач по геометрии. По каждой теме предлагается один или более комплектов тестов. В каждом комплекте по 10 тестов, в каждом тесте содержится 8 заданий.

Цель настоящей книги - отработать задания с кратким и развернутым ответом тестов ЕГЭ. Она необходима в первую очередь выпускникам, рассчитывающим получить на ЕГЭ хорошую оценку, а также учащимся 10-х классов, которые могут закрепить пройденные темы под углом зрения ЕГЭ. Предлагаемое пособие может быть полезно всем выпускникам, готовящимся к ЕГЭ по математике, а также педагогам, осуществляющим подготовку учащихся к ЕГЭ.

Формат: djvu / zip (2009 , 176с.)

Размер: 2,5 Мб

Скачать / Download файл 14

Формат: pdf (2009 , 176с.)

Размер: 8 ,6 Мб

Скачать: 14 .12.2018г, ссылки удалены по требованию изд-ва "Легион" (см. примечание)

Формат: djvu / zip (2008 , 160с.)

Размер: 3 Мб

Скачать / Download файл 14 .12.2018г, ссылки удалены по требованию изд-ва "Легион" (см. примечание)

Формат: pdf (2008 , 160с.)

Размер: 9 ,9 Мб

Скачать: 14 .12.2018г, ссылки удалены по требованию изд-ва "Легион" (см. примечание)

Учебно-методический комплекс "Математика. ЕГЭ-2010" под ред. Лысенко Ф.Ф. и Кулабухова С.Ю. включает учебные пособия:
1. Математика. Подготовка к ЕГЭ-2010.
2. Решебник. Математика. Подготовка к ЕГЭ-2010.
3. Математика. Тематические тесты. Часть I (базовый уровень). Подготовка к ЕГЭ-2010. 10-11 классы.
4. Математика. Тематические тесты. Часть II. Подготовка к ЕГЭ-2010. 10-11 классы.
5. Математика. Тематические тесты: геометрия, текстовые задачи. Подготовка к ЕГЭ-2010. 10-11 классы.
6. Математика. Сборник тестов ЕГЭ 2001 - 2010.
7. Математика. Подготовка к ЕГЭ-2010. Учебно-тренировочные тесты.
8. Карманный справочник по математике.

Оглавление
От авторов 11
§ 1. Тождественные преобразования логарифмических выражений 13
Вариант №1 13
Вариант №2 13
Вариант №3 14
Вариант №4 14
Вариант №5 15
Вариант №6 15
Вариант №7 16
Вариант №8 16
Вариант №9 17
Вариант №10 17
§ 2. Тождественные преобразования выражений, содержащих степень 18
Вариант №1 18
Вариант №2 19
Вариант №3 19
Вариант №4 20
Вариант №5 21
Вариант №6 21
Вариант №7 22
Вариант №8 23
Вариант №9 23
Вариант №10 24
§ 3. Тождественные преобразования иррациональных выражений 25
Вариант №1 25
Вариант №2 25
Вариант №3 26
Вариант №4 26
Вариант №5 27
Вариант №6 28
Вариант №7 28
Вариант №8 29
Вариант №9 30
Вариант №10 30
§ 4. Системы уравнений 31
Вариант №1 31
Вариант №2 32
Вариант №3 33
Вариант №4 33
Вариант №5 34
Вариант №6 35
Вариант №7 36
Вариант №8 37
Вариант №9 38
Вариант №10 39
§ 5. Геометрический смысл производной 39
Вариант №1 39
Вариант №2 41
Вариант №3 43
Вариант №4 44
Вариант №5 46
Вариант №6 48
Вариант №7 50
Вариант №8 52
Вариант №9 54
Вариант №10 55
§ 6. Неравенства 56
Вариант №1 г 56
Вариант №2 57
Вариант №3 58
Вариант №4 58
Вариант №5 59
Вариант №6 60
Вариант №7 60
Вариант №8 61
Вариант №9 62
Вариант №10 63
§ 7. Иррациональные уравнения 63
Вариант №1 63
Вариант №2 64
Вариант №3 65
Вариант №4 65
Вариант №5 66
Вариант №6 66
Вариант №7 67
Вариант №8 67
Вариант №9 68
Вариант №Ю 68
§ 8. Тригонометрические уравнения 69
Вариант №1 69
Вариант №2 69
Вариант №3 70
Вариант №4 70
Вариант №5 71
Вариант №6 72
Вариант №7 72
Вариант №8 73
Вариант №9 74
Вариант №10 74
§ 9. Логарифмические уравнения 75
Вариант №1 75
Вариант №2 75
Вариант №3 76
Вариант №4 76
Вариант №5 77
Вариант №6 77
Вариант №7 78
Вариант №8 * 78
Вариант №9 79
Вариант №10 79
§ 10. Показательные уравнения 80
Вариант №1 80
Вариант №2 80
Вариант №3 81
Вариант №4 81
Вариант №5 82
Вариант №6 82
Вариант №7 83
Вариант №8 83
Вариант №9 84
Вариант №10 84
§11. Периодичность, чётность и нечётность функций 85
Вариант №1 85
Вариант №2 86
Вариант №3 87
Вариант №4 89
Вариант №5 90
Вариант №6 91
Вариант №7 92
Вариант №8 93
Вариант №9 94
Вариант №10 95
§ 12. Нули сложной функции. Ограниченность функции 97
Вариант №1 97
Вариант №2 97
Вариант №3 98
Вариант №4 98
Вариант №5 99
Вариант №6 99
Вариант №7 100
Вариант №8 100
Вариант №9 101
Вариант №10 101
§ 13. Область определения, множество значений, монотонность функций 102
Вариант №1 102
Вариант №2 102
Вариант №3 103
Вариант №4 103
Вариант №5 104
Вариант №6 104
Вариант №7 105
Вариант №8 105
Вариант №9 106
Вариант №10 107
§ 14. Экстремумы функции. Наибольшее и наименьшее значения функции 107
Вариант №1 107
Вариант №2 108
Вариант №3 108
Вариант №4 109
Вариант №5 109
Вариант №6 110
Вариант №7 110
Вариант №8 111
Вариант №9 111
Вариант №10 112
§ 15. Различные приёмы при решении логарифмических уравнений 113
Вариант №1 113
Вариант №2 113
Вариант №3 114
Вариант №4 114
Вариант №5 115
Вариант №6 115
Вариант №7 116
Вариант №8 116
Вариант №9 117
Вариант №10 117
§ 16. Различные приёмы при решении тригонометрических уравнений 118
Вариант №1 118
Вариант №2 118
Вариант №3 118
Вариант №4 119
Вариант №5 119
Вариант №6 120
Вариант №7 120
Вариант №8 121
Вариант №9 121
Вариант №10 122
§ 17. Различные приёмы при решении иррациональных уравнений 123
Вариант №1 123
Вариант №2 123
Вариант №3 124
Вариант №4 124
Вариант №5 125
Вариант №6 125
Вариант №7 125
Вариант №8 126
Вариант №9 126
Вариант № 10 127
§ 18. Уравнения, содержащие переменную под знаком модуля 127
Вариант №1 127
Вариант №2 128
Вариант №3 128
Вариант №4 129
Вариант №5 129
Вариант №6 130
Вариант №7 130
Вариант №8 131
Вариант №9 131
Вариант №10 131
§ 19. Различные приёмы при решении показательных уравнений.132
Вариант №1 132
Вариант №2 133
Вариант №3 133
Вариант №4 134
Вариант №5 134
Вариант №6 135
Вариант №7 135
Вариант №8 135
Вариант №9 136
Вариант №10 136
§ 20. Различные приёмы при решении комбинированных уравнений 137
Вариант №1 137
Вариант №2 137
Вариант №3 138
Вариант №4 138
Вариант №5 139
Вариант №6 139
Вариант №7 140
Вариант №8 140
Вариант №9 141
Вариант №10 141
§ 21. Уравнения с параметром, содержащие модуль 142
Вариант №1 142
Вариант №2 142
Вариант №3 143
Вариант №4 144
Вариант №5 144
Вариант №6 145
Вариант №7 146
Вариант №8 146
Вариант №9 147
Вариант №10 148
Ответы 149
§ 1. Тождественные преобразования логарифмических выражений 149
§ 2. Тождественные преобразования выражений, содержащих степень 150
§ 3. Тождественные преобразования иррациональных выражений 150
§ 4. Системы уравнений 151
§ 5. Геометрический смысл производной 151
§ 6. Неравенства 152
§ 7. Иррациональные уравнения 152
§ 8. Тригонометрические уравнения 153
§ 9. Логарифмические уравнения 153
§ 10. Показательные уравнения 154
§11. Периодичность, четность и нечетность функций 154
§ 12. Нули сложной функции. Ограниченность функции 155
§ 13. Область определения, множество значений, монотонность функций 156
§ 14. Экстремумы функции. Наибольшее и наименьшее значения функции 158
§ 15. Различные приемы при решении логарифмических уравнений 159
§ 16. Различные приемы при решении тригонометрических уравнений 160
§ 17. Различные приемы при решении иррациональных уравнений 164
§ 18. Уравнения, содержащие переменную под знаком модуля 165
§ 19. Различные приемы при решении показательных уравнений.166
§ 20. Различные приемы при решении комбинированных уравнений 167
§ 21. Уравнения с параметром, содержащие модуль 169
Литература 170

В задаче B7 дается некоторое выражение, которое нужно упростить. В результате должно получиться обычное число, которое можно записать в бланке ответов. Все выражения условно делятся на три типа:

1. Логарифмические,
2. Показательные,
3. Комбинированные.

Показательные и логарифмические выражения в чистом виде практически не встречаются. Однако знать, как они вычисляются, совершенно необходимо.

В целом, задача B7 решается достаточно просто и вполне под силу среднему выпускнику. Отсутствие четких алгоритмов компенсируется в ней стандартностью и однообразностью. Научиться решать такие задачи можно просто за счет большого количества тренировок.

Логарифмические выражения

Подавляющее большинство задач B7 содержат логарифмы в том или ином виде. Эта тема традиционно считается сложной, поскольку ее изучение приходится, как правило, на 11 класс — эпоху массовой подготовки к выпускным экзаменам. В результате многие выпускники имеют весьма смутное представление о логарифмах.

Но в этой задаче никто и не требует глубоких теоретических познаний. Нам будут встречаться лишь самые простые выражения, которые требуют незамысловатых рассуждений и вполне могут быть освоены самостоятельно. Ниже приведены основные формулы, которые надо знать, чтобы справиться с логарифмами:

Кроме того, надо уметь заменять корни и дроби на степени с рациональным показателем, иначе в некоторых выражениях выносить из под знака логарифма будет просто нечего. Формулы замены:

Задача. Найти значения выражений:
log 6 270 − log 6 7,5
log 5 775 − log 5 6,2

Первые два выражения преобразуются как разность логарифмов:
log 6 270 − log 6 7,5 = log 6 (270: 7,5) = log 6 36 = 2;
log 5 775 − log 5 6,2 = log 5 (775: 6,2) = log 5 125 = 3.

Для вычисления третьего выражения придется выделять степени — как в основании, так и в аргументе. Для начала найдем внутренний логарифм:

Затем — внешний:

Конструкции вида log a log b x многим кажутся сложными и непонятыми. А между тем, это всего лишь логарифм от логарифма, т.е. log a (log b x ). Сначала вычисляется внутренний логарифм (положим log b x = c ), а затем внешний: log a c .

Показательные выражения

Будем называть показательным выражением любую конструкцию вида a k , где числа a и k — произвольные постоянные, причем a > 0. Методы работы с такими выражениями достаточно просты и рассматриваются на уроках алгебры 8-го класса.

Ниже приведены основные формулы, которые обязательно надо знать. Применение этих формул на практике, как правило, не вызывает проблем.

1. a n · a m = a n + m ;
2. a n / a m = a n − m ;
3. (a n ) m = a n · m ;
4. (a · b ) n = a n · b n ;
5. (a : b ) n = a n : b n .

Если встретилось сложное выражение со степенями, и не понятно, как к нему подступиться, используют универсальный прием — разложение на простые множители. В результате большие числа в основаниях степеней заменяются простыми и понятными элементами. Затем останется лишь применить указанные выше формулы — и задача будет решена.

Задача. Найти значения выражений: 7 9 · 3 11: 21 8 , 24 7: 3 6: 16 5 , 30 6: 6 5: 25 2 .

Решение. Разложим все основания степеней на простые множители:
7 9 · 3 11: 21 8 = 7 9 · 3 11: (7 · 3) 8 = 7 9 · 3 11: (7 8 · 3 8) = 7 9 · 3 11: 7 8: 3 8 = 7 · 3 3 = 189.
24 7: 3 6: 16 5 = (3 · 2 3) 7: 3 6: (2 4) 5 = 3 7 · 2 21: 3 6: 2 20 = 3 · 2 = 6.
30 6: 6 5: 25 2 = (5 · 3 · 2) 6: (3 · 2) 5: (5 2) 2 = 5 6 · 3 6 · 2 6: 3 5: 2 5: 5 4 = 5 2 · 3 · 2 = 150.

Комбинированные задачи

Если знать формулы, то все показательные и логарифмические выражения решаются буквально в одну строчку. Однако в задаче B7 степени и логарифмы могут объединяться, образуя довольно неслабые комбинации.

Приднестровский государственный университет

им. Т.Г. Шевченко

Физико-математический факультет

Кафедра математического анализа

и методики преподавания математики

КУРСОВАЯ РАБОТА

«Тождественные преобразования

показательных и логарифмических

выражений»

Работу выполнила:

студентка _______ группы

физико-математического ф-та

_________________________

Работу проверила:

_________________________

Тирасполь, 2003г.

Введение……………………………………………………………………2

Глава 1. Тождественные преобразования и методика преподавания в школьном курсе алгебры и начала анализа……………………………………..4

§1. Формирование навыков применения конкретных видов преобразований…………………………………………………………………………….4

§2. Особенности организации системы знаний при изучении тождественных преобразований.…….………………………….………..………….5

§3. Программа по математике ……………………………………….11

Глава 2. Тождественные преобразования и вычисления показательных и логарифмических выражений……………………………...…………………13

§1. Обобщение понятия степени……………………………………..13

§2. Показательная функция…………………………………………..15

§3. Логарифмическая функция……………………………………….16

Глава 3. Тождественные преобразования показательных и логарифмических выражений на практике..........................................................................19

Заключение………………………………………………………………..24

Список использованной литературы…………………………………….25
Введение

В данной курсовой работе будет рассмотрено тождественные преобразования показательной и логарифмической функции, рассмотрена методика преподавания их в школьном курсе алгебры и начала анализа.

Первая глава данной работы описывает методику преподавания тождественных преобразований в школьном курсе математики, так же включает программу по математике в курсе «Алгебры и начала анализа» с изучением показательной и логарифмической функции.

Вторая глава рассматривает непосредственно саму показательную и логарифмическую функции, их основные свойства, используемые при тождественных преобразованиях.

Третья глава – решение примеров и задач с использованием тождественных преобразований показательной и логарифмической функции.

Изучение различных преобразований выражений и формул занимает значительную часть учебного времени в курсе школьной математики. Простейшие преобразования, опирающиеся на свойства арифметических операций, производятся уже в начальной школе и в IV–V классах. Но основную нагрузку по формированию умений и навыков выполнения преобразований несет на себе курс школьной алгебры. Это связано как с резким увеличением числа и разнообразия совершаемых преобразований, так и с усложнением деятельности по их обоснованию и выяснению условий применимости, с выделением и изучением обобщенных понятий тождества, тождественного преобразования, равносильного преобразования, логического следования.

Культура выполнения тождественных преобразований развивается так же, как и культура вычислений, на основе прочных знаний свойств операций над объектами (числами, векторами, многочленами и т. д.) и алгоритмов их выполнения. Она проявляется не только в умении правильно обосновать преобразования, но и в умении найти кратчайший путь перехода от исходного аналитического выражения к выражению, наиболее соответствующему цели преобразования, в умении проследить за изменением области определения аналитических выражений в цепочке тождественных преобразований, в быстроте и безошибочности выполнения преобразований.

Обеспечение высокой культуры вычислений и тождественных преобразований представляет важную проблему обучения математике. Однако эта проблема решается еще далеко не удовлетворительно. Доказательство этому – статистические данные органов народного образования, в которых ежегодно констатируются ошибки и нерациональные приемы вычислений и преобразований, допускаемые учащимися различных классов при выполнении контрольных работ. Это подтверждается и отзывами высших учебных заведений о качестве математических знаний и навыков абитуриентов. Нельзя не согласиться с выводами органов народного образования и вузов о том, что недостаточно высокий уровень культуры вычислений и тождественных преобразований в средней школе является следствием формализма в знаниях учащихся, отрыва теории от практики.

Тождественные преобразования и методика преподавания

в школьном курсе алгебры и начала анализа.

§1. Формирование навыков применения

конкретных видов преобразований.

Система приемов и правил проведения преобразований, используемая на этапе начал алгебры, имеет очень широкую область приложений: она используется в изучении всего курса математики. Однако именно в силу своей малой специфичности эта система нуждается в дополнительных преобразованиях, учитывающих особенности структуры преобразуемых выражений и свойства вновь вводимых операций и функций. Освоение соответствующих видов преобразований начинается с введения формул сокращенного умножения. Затем рассматриваются преобразования, связанные с операцией возведения в степень, с различными классами элементарных функций – показательных, степенных, логарифмических, тригонометрических. Каждый из этих типов преобразований проходит этап изучения, на котором внимание сосредоточивается на усвоении их характерных особенностей.

По мере накопления материала появляется возможность выделить и общие черты всех рассматриваемых преобразований и на этой основе ввести понятия тождественного и равносильного преобразований.

Следует обратить внимание на то, что понятие тождественного преобразования дается в школьном курсе алгебры не в полной общности, а только в применении к выражениям. Преобразования разделяются на два класса: тождественные преобразования – это преобразования выражений, и равносильные – преобразования формул. В случае, когда возникает потребность в упрощении одной части формулы, в этой формуле выделяется выражение, которое и служит аргументом применяемого тождественного преобразования. Соответствующий предикат при этом считается неизменным.

Что касается организации целостной системы преобразований (синтез), то основная её цель состоит в формировании гибкого и мощного; аппарата, пригодного для использования в решении разнообразных учебных заданий.

В курсе алгебры и начал анализа целостная система преобразований, в основных чертах уже сформированная, продолжает постепенно совершенствоваться. К ней также добавляются некоторые новые виды преобразований, однако они только обогащают ее, расширяют ее возможности, но не меняют ее структуру. Методика изучения этих новых преобразований практически не отличается от применяемой в курсе алгебры.

§2. Особенности организации системы заданий

при изучении тождественных преобразований.

Основной принцип организации любой системы заданий – предъявление их от простого к сложному с учетом необходимости преодоления учениками посильных трудностей и создания проблемных ситуаций. Указанный основной принцип требует конкретизации применительно к особенностям данного учебного материала. Для описания различных систем заданий в методике математики используется понятие цикла упражнений. Цикл упражнений характеризуется соединением в последовательности упражнений нескольких аспектов изучения и приемов расположения материала. По отношению к тождественным преобразованиям представление о цикле может быть дано следующим образом.

Цикл упражнений связан с изучением одного тождества, вокруг которого группируются другие тождества, находящиеся с ним в естественной связи. В состав цикла наряду с исполнительными входят задания, требующие распознавания применимости рассматриваемого тождества. Изучаемое тождество применяется для проведения вычислений на различных числовых областях. Учитывается специфика тождества; в частности, организуются связанные с ним обороты речи.

Задания в каждом цикле разбиты на две группы. К первой относятся задания, выполняемые при первоначальном знакомстве с тождеством. Они служат учебным материалом для нескольких идущих подряд уроков, объединенных одной темой. Вторая группа упражнений связывает изучаемое тождество с различными приложениями. Эта группа не образует композиционного единства – упражнения здесь разбросаны по различным темам.

Описанная структура цикла относится к этапу формирования навыков применения конкретных видов преобразований. На заключительном этапе – этапе синтеза циклы видоизменяются. Во-первых, объединяются обе группы заданий, образующие «развернутый» цикл, причем из первой группы исключаются наиболее простые по формулировкам или по сложности выполнения задания. Оставшиеся типы заданий усложняются. Во-вторых, происходит слияние циклов, относящихся к различным тождествам, в силу чего повышается роль действий по распознаванию применимости того или иного тождества.

Отметим особенности циклов заданий, связанных с тождествами для элементарных функций. Эти особенности обусловлены тем, что, во-первых, соответствующие тождества изучаются в связи с изучением функционального материала и, во-вторых, они появляются позже тождеств первой группы и изучаются с использованием уже сформированных навыков проведения тождественных преобразований.

Каждая вновь вводимая элементарная функция резко расширяет область чисел, которые могут быть обозначены и названы индивидуально. Поэтому в первую группу заданий циклов должны войти задания на установление связи этих новых числовых областей с исходной областью рациональных чисел. Приведем примеры таких заданий.

Пример 1. Вычислить:

Рядом с каждым выражением указано тождество, в циклах по которым могут присутствовать предлагаемые задания. Цель таких заданий – в освоении особенностей записей, включающих символы новых операций и функций, и в развитии навыков математической речи.

Значительная часть использования тождественных преобразований, связанных с элементарными функциями, приходится на решение иррациональных и трансцендентных уравнений. В циклы, относящиеся к усвоению тождеств, входят только наиболее простые уравнения, но уже здесь целесообразно проводить работу по усвоению приема решения таких уравнений: сведение его путем замены неизвестного к алгебраическому уравнению.

Последовательность шагов при этом способе решения такова:

а) найти функцию , для которой данное уравнение представимо в виде ;

б) произвести подстановку и решить уравнение ;

в) решить каждое из уравнений , где – множество корней уравнения .

При использовании описанного способа зачастую шаг б) выполняется в неявном виде, без введения обозначения для . Кроме того, ученики зачастую предпочитают из различных путей, ведущих к нахождению ответа, выбирать тот, который быстрее и проще приводит к алгебраическому уравнению.

Пример 2. Решить уравнение .

Первый способ:

Второй способ:

а)

б)

Здесь видно, что при первом способе шаг а) сложнее, чем при втором. Первым способом «труднее начать», хотя дальнейший ход решения значительно проще. С другой стороны, у второго способа имеются достоинства, состоящие в большей легкости, большей отработанности в обучении сведения к алгебраическому уравнению.

Для школьного курса алгебры типичны задания, в которых переход к алгебраическому уравнению осуществляется даже еще проще, чем в данном примере. Основная нагрузка таких заданий относится к выделению шага в) как самостоятельной части процесса решения, связанного с использованием свойств изучаемой элементарной функции.

Пример 3. Решить уравнение:

а) ; б) .

Эти уравнения сводятся к уравнениям: а) или ; б) или . Для решения этих уравнений требуется знание лишь простейших фактов о показательной функции: ее монотонность, область значений. Как и задание предыдущего примера, уравнения а) и б) можно отнести к первой группе цикла упражнений на решение квадратно-показательных уравнений.

Таким образом, приходим к классификации заданий в циклах, относящихся к решению трансцендентных уравнений, включающих показательную функцию:

1) уравнения, сводящиеся к уравнениям вида и имеющие простой, общий по форме ответ: ;

2) уравнения, сводящиеся к уравнениям , где – целое число, или , где ;

3) уравнения, сводящиеся к уравнениям и требующие явного анализа формы, в которой записано число .

Аналогично можно классифицировать задания и для других элементарных функций.

Значительная часть тождеств, изучаемых в курсах алгебры и алгебры и начал анализа, доказывается в них или, по крайней мере, поясняется. Эта сторона изучения тождеств имеет большое значение для обоих курсов, поскольку доказательные рассуждения в них с наибольшей четкостью и строгостью проводятся именно по отношению к тождествам. За пределами этого материала доказательства обычно менее полны, они не всегда выделяются из состава применяемых средств обоснования.

В качестве опоры, на которой строятся доказательства тождеств, используются свойства арифметических операций.

Воспитательное воздействие вычислений и тождественных преобразований может быть, направлено на развитие логического мышления, если только от учащихся будут систематически требоваться обоснования вычислений и тождественных преобразований, на развитие функционального мышления, что достигается различными путями. Совершенно очевидно значение вычислений и тождественных преобразований в развитии воли, памяти, сообразительности, самоконтроля, творческой инициативы.

Запросы бытовой, производственной вычислительной практики требуют формирования у учащихся прочных, автоматизированных навыков рациональных вычислений и тождественных преобразований. Эти навыки вырабатываются в процессе любой вычислительной работы, тем не менее, необходимы специальные тренировочные упражнения в быстрых вычислениях и преобразованиях.

Так, если на уроке предполагается решение логарифмических уравнений с использованием основного логарифмического тождества , то полезно в план урока включить устные упражнения на упрощение или вычисление значений выражений: , , . Цель упражнений всегда сообщается учащимся. В ходе выполнения упражнения может возникнуть необходимость потребовать от учащихся обоснований отдельных преобразований, действий или решения всей задачи, даже если это не планировалось. Там, где возможны различные способы решения задачи, желательно всегда ставить вопросы: «Каким способом решалась задача?», «Кто решил задачу другим способом?»

Понятия тождества и тождественного преобразования, они явно вводятся в курсе алгебры VI класса. Само определение тождественных выражений не может быть практически использовано для доказательства тождественности двух выражений, и понять, что сущность тождественных преобразований состоит в применении к выражению определений и свойств тех действий, которые указаны в выражении, или в прибавлении к нему выражения, тождественно равного 0, или в умножении его на выражение, тождественно равное единице. Но, даже усвоив эти положения, учащиеся часто не понимают, почему указанные преобразования позволяют утверждать, что исходное и полученное выражение тождественны, т.е. принимают одинаковые значения при любых системах (наборах) значений переменных.

Важно так же добиться, что бы учащиеся хорошо понимали, что такие выводы тождественных преобразований, являются следствиями определений и свойств соответствующих действий.

Аппарат тождественных преобразований, накопленный в предшествующие годы, в VI классе расширяется. Это расширение начинается введением тождества, выражающего свойство произведения степеней с одинаковыми основаниями: , где , – целые числа.

§3. Программа по математике. В школьном курсе «Алгебра и начала анализа» учащиеся систематически изучают показательную и логарифмическую функции и их свойства, тождественные преобразования логарифмических и показательных выражений и их применение к решению соответствующих уравнений и неравенств, знакомятся с основными понятиями, утверждениями. В XI классе на уроки алгебры уходит по 3 часа в неделю, всего получается 102 часа в год. На изучение показательной, логарифмической и степенной функции по программе уходит 36 часов. В программу входит рассмотрение и изучение следующих вопросов: Понятие о степени с рациональным показателем. Решение иррациональных уравнений. Показательная функция, её свойства и график. тождественные преобразования показательных выражений. Решение показательных уравнений и неравенств. Логарифм числа. Основные свойства логарифмов. Логарифмическая функция, её свойства и график. Решение логарифмических уравнений и неравенств. Производная показательной функции. Число и натуральный логарифм. Производная степенной функции. Основной целью раздела изучения показательной и логарифмической функции является ознакомление учащихся с показательной, логарифмической и степенной функцией; научить учащихся решать показательные и логарифмические уравнения и неравенства. Понятия корня -ой степени и степени с рациональным показателем являются обобщением понятий квадратного корня и степени с целым показателем. Следует обратить внимание учащихся, что рассматриваемые здесь свойства корней и степеней с рациональным показателем аналогичны тем свойствам, которыми обладают изученные ранее квадратные корни и степени с целыми показателями. Необходимо уделить достаточно времени отработке свойств степеней и формированию навыков тождественных преобразований. Понятие степени с иррациональным показателем вводится на наглядно-интуитивной основе. Этот материал играет вспомогательную роль и используется при введении показательной функции. Изучение свойств показательной, логарифмической и степенной функции построено в соответствии с принятой общей схемой исследования функций. При этом обзор свойств дается в зависимости от значений параметров. Показательные и логарифмические неравенства решаются с опорой на изученные свойства функций. Характерной особенностью курса являются систематизация и обобщение знаний учащихся, закрепление и развитие умений и навыков, полученных в курсе алгебры, что осуществляется как при изучении нового материала, так и при проведении обобщающего повторения.
Глава 2. Тождественные преобразования и вычисления показательных и логарифмических выражений

§1. Обобщение понятия степени.

Определение: Корнем -ой степени из чиста называется такое число, -я степень которого равна .

Согласно данному определению корень -ой степени из числа – это решение уравнения . Число корней этого уравнения зависит от и . Рассмотрим функцию . Как известно, на промежутке эта функция при любом возрастает и принимает все значения из промежутка . По теореме о корне уравнение для любого имеет неотрицательный корень и при том только один. Его называют арифметическим корнем -ой степени из числа и обозначают ; число называют показателем корня, а само число – подкоренным выражением. Знак называют так же радикалом.

Определение: Арифметическим корнем -ой степени из числа называют неотрицательное число, -я степень которого равна .

При четных функция четна. Отсюда следует, что если , то уравнение , кроме корня , имеет также корень . Если , то корень один: ; если , то это уравнение корней не имеет, поскольку четная степень любого числа неотрицательна.

При нечетных значениях функция возрастает на всей числовой прямой; её область значений – множество всех действительных чисел. Применяя теорему о корне, находим, что уравнение имеет один корень при любом и, в частности, при . Этот корень для любого значения обозначают .

Для корней нечетной степени справедливо равенство . В самом деле, , т.е. число – есть корень -й степени из . Но такой корень при нечетном единственный. Следовательно, .

Замечание 1: Для любого действительного

Напомним известные свойства арифметических корней -ой степени.

Для любого натурального , целого и любых неотрицательных целых чисел и справедливы равенства:

1.

2.

3.

4.

Степень с рациональным показателем.

Выражение определено для всех и , кроме случая при . Напомним свойства таких степеней.

Для любых чисел , и любых целых чисел и справедливы равенства:

Отметим так же, что если , то при и при .. и

Учащихся к ЕГЭ, учителя математики СОШ №26 г.Якутска используют перечень вопросов содержания (кодификатор) школьного курса математики, усвоение которых проверяется при сдачи единого государственного экзамена 2007г. Элективный курс по подготовке к Единому Государственному Экзамену основан на повторении, систематизации и углублении знаний полученных ранее. Занятия проходят в форме свободного...