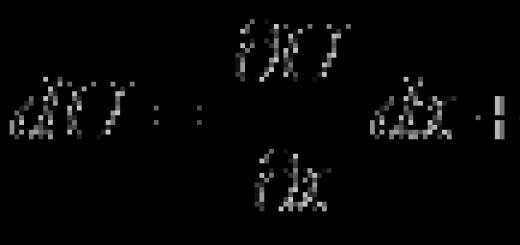The 19th century is the beginning of a new, fourth period in the history of mathematics - the period of modern mathematics.

We already know that one of the main directions in the development of mathematics in the fourth period is the strengthening of the rigor of proofs in all mathematics, especially the restructuring of mathematical analysis on a logical basis. In the second half of the 18th century. numerous attempts were made to rebuild mathematical analysis: the introduction of the definition of a limit (D'Alembert et al.), the definition of the derivative as the limit of a ratio (Euler et al.), the results of Lagrange and Carnot, etc., but these works lacked a system, and sometimes they were unsuccessful. However, they prepared the ground on which perestroika in the 19th century. could be implemented. In the 19th century This direction of development of mathematical analysis became the leading one. It was taken up by O. Cauchy, B. Bolzano, K. Weierstrass and others.

1. Augustin Louis Cauchy (1789−1857) graduated from the Ecole Polytechnique and the Institute of Communications in Paris. Since 1816, member of the Paris Academy and professor at the Ecole Polytechnique. In 1830−1838 During the years of the republic, he was in exile because of his monarchist beliefs. Since 1848, Cauchy became a professor at the Sorbonne - University of Paris. He published more than 800 papers on mathematical analysis, differential equations, theory of functions of a complex variable, algebra, number theory, geometry, mechanics, optics, etc. The main areas of his scientific interests were mathematical analysis and theory of functions of a complex variable.

Cauchy published his lectures on analysis, delivered at the Polytechnic School, in three works: “A Course in Analysis” (1821), “Summary of Lectures on Infinitesimal Calculus” (1823), “Lecture on Applications of Analysis to Geometry”, 2 volumes (1826, 1828). In these books, for the first time, mathematical analysis is built on the basis of the theory of limits. they marked the beginning of a radical restructuring of mathematical analysis.

Cauchy gives the following definition of the limit of a variable: “If the values ​​successively assigned to the same variable approach a fixed value indefinitely, so that in the end they differ from it as little as possible, then the latter is called the limit of all others.” The essence of the matter is expressed well here, but the words “as little as desired” themselves need definition, and in addition, the definition of the limit of a variable, and not the limit of a function, is formulated here. Next, the author proves various properties of limits.

Then Cauchy gives the following definition of the continuity of a function: a function is called continuous (at a point) if an infinitesimal increment in the argument generates an infinitesimal increment in the function, i.e., in modern language

Then he has various properties of continuous functions.

The first book also examines the theory of series: it gives the definition of the sum of a number series as the limit of its partial sum, introduces a number of sufficient criteria for the convergence of number series, as well as power series and the region of their convergence - all this in both the real and complex domains.

He presents differential and integral calculus in his second book.

Cauchy defines the derivative of a function as the limit of the ratio of the increment of the function to the increment of the argument, when the increment of the argument tends to zero, and the differential as the limit of the ratio It follows from this that. The usual derivative formulas are discussed next; in this case, the author often uses Lagrange's mean value theorem.

In integral calculus, Cauchy first puts forward the definite integral as a basic concept. He also introduces it for the first time as the limit of integral sums. Here we prove an important theorem on the integrability of a continuous function. His indefinite integral is defined as a function of the argument that. In addition, expansions of functions in Taylor and Maclaurin series are considered here.

In the second half of the 19th century. a number of scientists: B. Riemann, G. Darboux and others found new conditions for the integrability of a function and even changed the very definition of a definite integral so that it could be applied to the integration of some discontinuous functions.

In the theory of differential equations, Cauchy was mainly concerned with proofs of fundamentally important existence theorems: the existence of a solution to an ordinary differential equation, first of the first and then of the th order; existence of a solution for a linear system of partial differential equations.

In the theory of functions of a complex variable, Cauchy is the founder; Many of his articles are devoted to it. In the 18th century Euler and d'Alembert laid only the beginning of this theory. In the university course on the theory of functions of a complex variable, we constantly come across the name of Cauchy: the Cauchy - Riemann conditions for the existence of a derivative, the Cauchy integral, the Cauchy integral formula, etc.; many theorems on residues of a function are also due to Cauchy. B. Riemann, K. Weierstrass, P. Laurent and others also obtained very important results in this area.

Let's return to the basic concepts of mathematical analysis. In the second half of the century, it became clear that the Czech scientist Bernard Bolzano (1781 - 1848) had done a lot in the field of substantiating analysis before Cauchy and Weierschtrass. Before Cauchy, he gave definitions of the limit, continuity of a function and the convergence of a number series, proved a criterion for the convergence of a number sequence, and also, long before it appeared in Weierstrass, the theorem: if a number set is bounded above (below), then it has an exact upper ( exact bottom edge. He considered a number of properties of continuous functions; Let us remember that in the university course of mathematical analysis there are the Bolzano–Cauchy and Bolzano–Weierstrass theorems on functions continuous on an interval. Bolzano also investigated some issues of mathematical analysis, for example, he constructed the first example of a function that is continuous on a segment, but does not have a derivative at any point on the segment. During his lifetime, Bolzano was able to publish only five small works, so his results became known too late.

2. In mathematical analysis, the lack of a clear definition of a function was felt more and more clearly. A significant contribution to resolving the dispute about what is meant by function was made by the French scientist Jean Fourier. He studied the mathematical theory of thermal conductivity in solids and, in connection with this, used trigonometric series (Fourier series)

these series later became widely used in mathematical physics, a science that deals with mathematical methods for studying partial differential equations encountered in physics. Fourier proved that any continuous curve, regardless of what dissimilar parts it is composed of, can be defined by a single analytical expression - a trigonometric series, and that this can also be done for some curves with discontinuities. Fourier's study of such series once again raised the question of what is meant by a function. Can such a curve be considered to define a function? (This is a renewal of the old 18th century debate about the relationship between function and formula at a new level.)

In 1837, the German mathematician P. Direchle first gave a modern definition of a function: “is a function of a variable (on an interval if each value (on this interval) corresponds to a completely specific value, and it does not matter how this correspondence is established - by an analytical formula, a graph, a table, or even just words." Noteworthy is the addition: "it does not matter how this correspondence is established." Direchle's definition received general recognition quite quickly. However, it is now customary to call the correspondence itself a function.

3. The modern standard of rigor in mathematical analysis first appeared in the works of Weierstrass (1815−1897). He worked for a long time as a mathematics teacher in gymnasiums, and in 1856 became a professor at the University of Berlin. The listeners of his lectures gradually published them in the form of separate books, thanks to which the content of Weierstrass's lectures became well known in Europe. It was Weierstrass who began to systematically use language in mathematical analysis. He gave a definition of the limit of a sequence, a definition of the limit of a function in language (which is often incorrectly called the Cauchy definition), rigorously proved theorems on limits and the so-called Weierstrass theorem on the limit of a monotone sequence: an increasing (decreasing) sequence, bounded from above (from below), has a finite limit. He began to use the concepts of the exact upper and exact lower bounds of a numerical set, the concept of a limit point of a set, proved the theorem (which has another author - Bolzano): a bounded numerical set has a limit point, and examined some properties of continuous functions. Weierstrass devoted many works to the theory of functions of a complex variable, substantiating it with the help of power series. He also studied the calculus of variations, differential geometry and linear algebra.

4. Let us dwell on the theory of infinite sets. Its creator was the German mathematician Cantor. Georg Kantor (1845-1918) worked for many years as a professor at the University of Halle. He published works on set theory starting in 1870. He proved the uncountability of the set of real numbers, thus establishing the existence of nonequivalent infinite sets, introduced the general concept of the power of a set, and elucidated the principles for comparing powers. Cantor built a theory of transfinite, “improper” numbers, attributing the lowest, smallest transfinite number to the power of a countable set (in particular, the set of natural numbers), to the power of the set of real numbers - a higher, larger transfinite number, etc.; this gave him the opportunity to construct an arithmetic of transfinite numbers, similar to the ordinary arithmetic of natural numbers. Cantor systematically applied actual infinity, for example, the possibility of completely “exhausting” the natural series of numbers, while before him in mathematics of the 19th century. only potential infinity was used.

Cantor's set theory aroused objections from many mathematicians when it appeared, but recognition gradually came when its enormous importance for the justification of topology and the theory of functions of a real variable became clear. But logical gaps remained in the theory itself; in particular, paradoxes of set theory were discovered. Here is one of the most famous paradoxes. Let us denote by the set all such sets that are not elements of themselves. Does the inclusion also hold and is not an element since, by condition, only such sets are included as elements that are not elements of themselves; if the condition holds, inclusion is a contradiction in both cases.

These paradoxes were associated with the internal inconsistency of some sets. It became clear that not just any sets can be used in mathematics. The existence of paradoxes was overcome by the creation already at the beginning of the 20th century. axiomatic set theory (E. Zermelo, A. Frenkel, D. Neumann, etc.), which, in particular, answered the question: what sets can be used in mathematics? It turns out that you can use the empty set, the union of given sets, the set of all subsets of a given set, etc.

Philosophy is considered the focus of all sciences, since it included the first sprouts of literature, astronomy, literature, natural science, mathematics and other areas. Over time, each field developed independently, mathematics was no exception. The first “hint” of analysis is considered to be the theory of decomposition into infinitesimal quantities, which many minds tried to approach, but it was vague and had no basis. This is due to an attachment to the old school of science, which was strict in its formulations. Isaac Newton came very close to forming the foundations, but was too late. As a result, mathematical analysis owes its emergence as a separate system to the philosopher Gottfried Leibniz. It was he who introduced to the scientific world such concepts as minimum and maximum, inflection points and convexity of the graph of a function, and formulated the foundations of differential calculus. From this moment on, mathematics is officially divided into elementary and higher.

Mathematical analysis. Our days

Any specialty, be it technical or humanitarian, includes analysis in the course of study. The depth of study varies, but the essence remains the same. Despite all the “abstractness,” it is one of the pillars on which natural science in its modern understanding rests. With his help, physics and economics developed, he is able to describe and predict the activities of the stock exchange, and help in building an optimal portfolio of shares. Introduction to mathematical analysis is based on elementary concepts:

• multitudes;
• basic operations on sets;
• properties of operations on sets;
• functions (otherwise known as mappings);
• types of functions;
• sequences;
• number lines;
• sequence limit;
• properties of limits;
• continuity of function.

It is worth highlighting separately such concepts as set, point, straight line, plane. All of them have no definitions, since they are the basic concepts on which all mathematics is built. All that can be done in the process is to explain what exactly they mean in individual cases.

Limit as a continuation

The fundamentals of mathematical analysis include limit. In practice, it represents the value to which a sequence or function strives, comes as close as desired, but does not reach it. It is denoted as lim; consider a special case of the limit of the function: lim (x-1)= 0 for x→1. From this simplest example it is clear that as x→1 the entire function tends to 0, since if we substitute the limit into the function itself, we get (1-1)=0. More detailed information, from elementary to complex special cases, is presented in a kind of “Bible” of analysis - the works of Fichtenholtz. It examines mathematical analysis, limits, their derivation and further application. For example, derivation of the number e (Euler's constant) would be impossible without the theory of limits. Despite the dynamic abstractness of the theory, limits are actively used in practice in economics and sociology. For example, you cannot do without them when calculating interest on a bank deposit.

English: Wikipedia is making the site more secure. You are using an old web browser that will not be able to connect to Wikipedia in the future. Please update your device or contact your IT administrator.

中文: 维基百科正在使网站更加安全。您正在使用旧的浏览器，请更新IT ）。

Spanish: Wikipedia está haciendo el sitio más seguro. Usted está utilizando un navegador web viejo que no será capaz de conectarse a Wikipedia en el futuro. Actualice su dispositivo o contacte a su administrador informático. Más abajo hay una actualización más larga y más técnica en inglés.

ﺎﻠﻋﺮﺒﻳﺓ: ويكيبيديا تسعى لتأمين الموقع أكثر من ذي قبل. أنت تستخدم متصفح وب قديم لن يتمكن من الاتصال بموقع ويكيبيديا في المستقبل. يرجى تحديث جهازك أو الاتصال بغداري تقنية المعلومات الخاص بك. يوجد تحديث فني أطول ومغرق في التقنية باللغة الإنجليزية تاليا.

Français: Wikipédia va bientôt augmenter la securité de son site. Vous utilisez actuellement un navigateur web ancien, qui ne pourra plus se connecter à Wikipédia lorsque ce sera fait. Merci de mettre à jour votre appareil ou de contacter votre administrateur informatique à cette fin. Des informations supplémentaires plus techniques et en anglais sont disponibles ci-dessous.

日本語: ? ??? IT 情報は以下に英語で提供しています。

German: Wikipedia erhöht die Sicherheit der Webseite. Du benutzt einen alten Webbrowser, der in Zukunft nicht mehr auf Wikipedia zugreifen können wird. Bitte aktualisiere dein Gerät oder sprich deinen IT-Administrator an. Ausführlichere (und technisch detailliertere) Hinweise findest Du unten in englischer Sprache.

Italiano: Wikipedia sta rendendo il sito più sicuro. Stay usando un browser web che non sarà in grado di connettersi a Wikipedia in futuro. Per favore, aggiorna il tuo dispositivo o contatta il tuo amministratore informatico. Più in basso è disponibile un aggiornamento più dettagliato e tecnico in inglese.

Magyar: Biztonságosabb lesz a Wikipédia. A böngésző, amit használsz, nem lesz képes kapcsolódni a jövőben. Használj modernebb szoftvert vagy jelezd a problémát a rendszergazdádnak. Alább olvashatod a részletesebb magyarázatot (angolul).

Svenska: Wikipedia gör sidan mer säker. Du använder en äldre webbläsare som inte kommer att kunna läsa Wikipedia i framtiden. Uppdatera din enhet eller kontakta din IT-administratör. Det finns en längre och mer teknisk förklaring på engelska längre ned.

हिन्दी: विकिपीडिया साइट को और अधिक सुरक्षित बना रहा है। आप एक पुराने वेब ब्राउज़र का उपयोग कर रहे हैं जो भविष्य में विकिपीडिया से कनेक्ट नहीं हो पाएगा। कृपया अपना डिवाइस अपडेट करें या अपने आईटी व्यवस्थापक से संपर्क करें। नीचे अंग्रेजी में एक लंबा और अधिक तकनीकी अद्यतन है।

We are removing support for insecure TLS protocol versions, specifically TLSv1.0 and TLSv1.1, which your browser software relies on to connect to our sites. This is usually caused by outdated browsers, or older Android smartphones. Or it could be interference from corporate or personal "Web Security" software, which actually downgrades connection security.

You must upgrade your web browser or otherwise fix this issue to access our sites. This message will remain until Jan 1, 2020. After that date, your browser will not be able to establish a connection to our servers.

In the history of mathematics, we can roughly distinguish two main periods: elementary and modern mathematics. The milestone from which it is customary to count the era of new (sometimes called higher) mathematics was the 17th century - the century of the appearance of mathematical analysis. By the end of the 17th century. I. Newton, G. Leibniz and their predecessors created the apparatus of a new differential calculus and integral calculus, which forms the basis of mathematical analysis and even, perhaps, the mathematical basis of all modern natural science.

Mathematical analysis is a vast area of ​​mathematics with a characteristic object of study (variable quantity), a unique research method (analysis by means of infinitesimals or by means of passages to limits), a certain system of basic concepts (function, limit, derivative, differential, integral, series) and constantly improving and a developing apparatus, the basis of which is differential and integral calculus.

Let's try to give an idea of ​​what kind of mathematical revolution occurred in the 17th century, what characterizes the transition associated with the birth of mathematical analysis from elementary mathematics to what is now the subject of research in mathematical analysis, and what explains its fundamental role in the entire modern system of theoretical and applied knowledge .

Imagine that in front of you is a beautifully executed color photograph of a stormy ocean wave rushing onto the shore: a powerful stooped back, a steep but slightly sunken chest, a head already tilted forward and ready to fall with a gray mane tormented by the wind. You stopped the moment, you managed to catch the wave, and you can now carefully study it in every detail without haste. A wave can be measured, and using the tools of elementary mathematics, you can draw many important conclusions about this wave, and therefore all its ocean sisters. But by stopping the wave, you deprived it of movement and life. Its origin, development, running, the force with which it hits the shore - all this turned out to be outside your field of vision, because you do not yet have either a language or a mathematical apparatus suitable for describing and studying not static, but developing, dynamic processes, variables and their relationships.

“Mathematical analysis is no less comprehensive than nature itself: it determines all tangible relationships, measures times, spaces, forces, temperatures.” J. Fourier

Movement, variables and their relationships surround us everywhere. Various types of motion and their patterns constitute the main object of study of specific sciences: physics, geology, biology, sociology, etc. Therefore, precise language and corresponding mathematical methods for describing and studying variable quantities turned out to be necessary in all areas of knowledge to approximately the same extent as numbers and arithmetic are necessary when describing quantitative relationships. So, mathematical analysis forms the basis of the language and mathematical methods for describing variables and their relationships. Nowadays, without mathematical analysis, it is impossible not only to calculate space trajectories, the operation of nuclear reactors, the movement of ocean waves and patterns of cyclone development, but also to economically manage production, resource distribution, organization of technological processes, predict the course of chemical reactions or changes in the number of various species interconnected in nature animals and plants, because all of these are dynamic processes.

Elementary mathematics was mainly the mathematics of constant quantities, it studied mainly the relationships between the elements of geometric figures, the arithmetic properties of numbers and algebraic equations. Its attitude to reality can to some extent be compared with an attentive, even thorough and complete study of each fixed frame of a film that captures the changing, developing living world in its movement, which, however, is not visible in a separate frame and which can only be observed by looking the tape as a whole. But just as cinema is unthinkable without photography, so modern mathematics is impossible without that part of it that we conventionally call elementary, without the ideas and achievements of many outstanding scientists, sometimes separated by tens of centuries.

Mathematics is united, and the “higher” part of it is connected with the “elementary” part in much the same way as the next floor of a house under construction is connected with the previous one, and the width of the horizons that mathematics opens to us in the world around us depends on which floor of this building we managed to reach rise. Born in the 17th century. mathematical analysis has opened up the possibilities for scientific description, quantitative and qualitative study of variables and motion in the broad sense of the word.

What are the prerequisites for the emergence of mathematical analysis?

By the end of the 17th century. The following situation has arisen. Firstly, within the framework of mathematics itself over many years, some important classes of problems of the same type have accumulated (for example, problems of measuring areas and volumes of non-standard figures, problems of drawing tangents to curves) and methods for solving them in various special cases have appeared. Secondly, it turned out that these problems are closely related to the problems of describing arbitrary (not necessarily uniform) mechanical motion, and in particular with the calculation of its instantaneous characteristics (speed, acceleration at any time), as well as with finding the distance traveled for movement occurring at a given variable speed. The solution to these problems was necessary for the development of physics, astronomy, and technology.

Finally, thirdly, by the middle of the 17th century. the works of R. Descartes and P. Fermat laid the foundations of the analytical method of coordinates (the so-called analytical geometry), which made it possible to formulate geometric and physical problems of heterogeneous origin in the general (analytical) language of numbers and numerical dependencies, or, as we now say, numerical functions.

The confluence of these circumstances led to the fact that at the end of the 17th century. two scientists - I. Newton and G. Leibniz - independently of each other managed to create a mathematical apparatus for solving these problems, summing up and generalizing individual results of their predecessors, including the ancient scientist Archimedes and contemporaries of Newton and Leibniz - B. Cavalieri, B. Pascal , D. Gregory, I. Barrow. This apparatus formed the basis of mathematical analysis - a new branch of mathematics that studies various developing processes, i.e. relationships between variables, which in mathematics are called functional dependencies or, in other words, functions. By the way, the term “function” itself was required and naturally arose precisely in the 17th century, and by now it has acquired not only general mathematical, but also general scientific significance.

Initial information about the basic concepts and mathematical apparatus of analysis is given in the articles “Differential calculus” and “Integral calculus”.

In conclusion, I would like to dwell on only one principle of mathematical abstraction, common to all mathematics and characteristic of analysis, and in this regard explain in what form mathematical analysis studies variables and what is the secret of such universality of its methods for studying all kinds of specific developing processes and their interrelations .

Let's look at a few illustrative examples and analogies.

Sometimes we no longer realize that, for example, a mathematical relation written not for apples, chairs or elephants, but in an abstract form abstracted from specific objects, is an outstanding scientific achievement. This is a mathematical law that, as experience shows, is applicable to various specific objects. This means that by studying in mathematics the general properties of abstract, abstract numbers, we thereby study the quantitative relationships of the real world.

For example, from a school mathematics course it is known that, therefore, in a specific situation you could say: “If they don’t give me two six-ton ​​dump trucks to transport 12 tons of soil, then I can ask for three four-ton dump trucks and the work will be done, and if they give me only one four-ton dump truck, then she will have to make three flights.” Thus, the abstract numbers and numerical patterns that are now familiar to us are associated with their specific manifestations and applications.

The laws of change in specific variables and developing processes of nature are related in approximately the same way to the abstract, abstract form-function in which they appear and are studied in mathematical analysis.

For example, an abstract ratio may reflect the dependence of a cinema's box office on the number of tickets sold, if 20 is 20 kopecks - the price of one ticket. But if we are riding a bicycle on a highway, traveling 20 km per hour, then this same ratio can be interpreted as the relationship between the time (hours) of our cycling trip and the distance covered during this time (kilometers). You can always say that, for example, a change of several times leads to a proportional (i.e., the same number of times) change in the value of , and if , then the opposite conclusion is also true. This means, in particular, to double the box office of a movie theater, you will have to attract twice as many spectators, and in order to travel twice as far on a bicycle at the same speed, you will have to ride twice as long.

Mathematics studies both the simplest dependence and other, much more complex dependences in a general, abstract form, abstracted from a particular interpretation. The properties of a function or methods for studying these properties identified in such a study will be of the nature of general mathematical techniques, conclusions, laws and conclusions applicable to each specific phenomenon in which the function studied in abstract form occurs, regardless of what area of ​​knowledge this phenomenon belongs to .

So, mathematical analysis as a branch of mathematics took shape at the end of the 17th century. The subject of study in mathematical analysis (as it appears from modern positions) are functions, or, in other words, dependencies between variable quantities.

With the advent of mathematical analysis, mathematics became accessible to the study and reflection of developing processes in the real world; mathematics included variables and motion.

Antiquity

During the ancient period, some ideas appeared that later led to integral calculus, but in that era these ideas were not developed in a rigorous, systematic manner. Calculations of volumes and areas, one of the purposes of integral calculus, can be found in the Moscow mathematical papyrus from Egypt (c. 1820 BC), but the formulas are more like instructions, without any indication of the method, and some are simply erroneous. In the era of Greek mathematics, Eudoxus (c. 408-355 BC) used the exhaustion method to calculate areas and volumes, which anticipates the concept of limit, and later this idea was further developed by Archimedes (c. 287-212 BC) , inventing heuristics that resemble methods of integral calculus. The exhaustion method was later invented in China by Liu Hui in the 3rd century AD, which he used to calculate the area of ​​a circle. In the 5th AD, Zu Chongzhi developed a method for calculating the volume of a sphere, which would later be called Cavalieri's principle.

Middle Ages

In the 14th century, Indian mathematician Madhava Sangamagrama and the Kerala School of Astronomy and Mathematics introduced many components of calculus, such as Taylor series, approximation of infinite series, integral test of convergence, early forms of differentiation, term-by-term integration, iterative methods for solving nonlinear equations, and determining what area under the curve is its integral. Some consider Yuktibhāṣā to be the first work on mathematical analysis.

Modern era

In Europe, the seminal work was the treatise of Bonaventura Cavalieri, in which he argued that volumes and areas can be calculated as the sum of the volumes and areas of an infinitely thin section. The ideas were similar to what Archimedes outlined in his Method, but this treatise of Archimedes was lost until the first half of the 20th century. Cavalieri's work was not recognized because his methods could lead to erroneous results, and he gave infinitesimals a dubious reputation.

Formal research into infinitesimal calculus, which Cavalieri combined with finite difference calculus, was taking place in Europe around this time. Pierre Fermat, claiming that he borrowed it from Diophantus, introduced the concept of "quasi-equality" (English: adequality), which was equality up to an infinitesimal error. John Wallis, Isaac Barrow and James Gregory also made major contributions. The last two, around 1675, proved the second fundamental theorem of calculus.

Reasons

In mathematics, foundations refer to a strict definition of a subject, starting from precise axioms and definitions. At the initial stage of the development of calculus, the use of infinitesimal quantities was considered to be lax, and was severely criticized by a number of authors, most notably Michel Rolle and Bishop Berkeley. Berkeley excellently described the infinitesimals as "ghosts of dead quantities" in his book The Analyst in 1734. Developing a rigorous foundation for calculus occupied mathematicians for more than a century after Newton and Leibniz, and is still to some extent an active area of ​​research today.

Several mathematicians, including Maclaurin, tried to prove the validity of the use of infinitesimals, but this was only done 150 years later with the work of Cauchy and Weierstrass, who finally found a way to evade the simple “little things” of infinitesimals, and the beginnings were made differential and integral calculus. In Cauchy's writings we find a universal range of fundamental approaches, including the definition of continuity in terms of infinitesimals and the (somewhat imprecise) prototype of the (ε, δ)-definition of limit in the definition of differentiation. In his work, Weierstrass formalizes the concept of limit and eliminates infinitesimal quantities. After this work of Weierstrass, the general basis of calculus became limits, and not infinitesimal quantities. Bernhard Riemann used these ideas to give a precise definition of the integral. Additionally, during this period, the ideas of calculus were generalized to Euclidean space and to the complex plane.

In modern mathematics, the basics of calculus are included in the branch of real analysis, which contains complete definitions and proofs of the theorems of calculus. The scope of calculus research has become much broader. Henri Lebesgue developed the theory of set measures and used it to determine integrals of all but the most exotic functions. Laurent Schwartz introduced generalized functions, which can be used to calculate the derivatives of any function in general.

The introduction of limits determined not the only strict approach to the basis of calculus. An alternative would be, for example, Abraham Robinson's non-standard analysis. Robinson's approach, developed in the 1960s, uses technical tools from mathematical logic to extend the system of real numbers to infinitesimal and infinitely large numbers, as in the original Newton-Leibniz concept. These numbers, called hyperreals, can be used in the ordinary rules of calculus, much as Leibniz did.

Importance

Although some ideas of calculus had previously been developed in Egypt, Greece, China, India, Iraq, Persia, and Japan, the modern use of calculus began in Europe in the 17th century, when Isaac Newton and Gottfried Wilhelm Leibniz built on the work of earlier mathematicians to build on its basic principles. The development of calculus was based on the earlier concepts of instantaneous motion and area under a curve.

Differential calculus is used in calculations related to speed and acceleration, curve slope, and optimization. Applications of integral calculus include calculations involving areas, volumes, arc lengths, centers of mass, work and pressure. More complex applications include calculations of power series and Fourier series.

Calculus [ ] is also used to gain a more accurate understanding of the nature of space, time and motion. For centuries, mathematicians and philosophers have wrestled with the paradoxes associated with dividing by zero or finding the sum of an infinite series of numbers. These questions arise when studying motion and calculating areas. The ancient Greek philosopher Zeno of Elea gave several famous examples of such paradoxes. Calculus provides tools for resolving these paradoxes, in particular limits and infinite series.

Limits and infinitesimals

Notes

1. Morris Kline, Mathematical thought from ancient to modern times, Vol. I
2. Archimedes, Method, in The Works of Archimedes ISBN 978-0-521-66160-7
3. Dun, Liu; Fan, Dainian; Cohen, Son Robertne. A comparison of Archimdes" and Liu Hui"s studies of circles (English): journal. - Springer, 1966. - Vol. 130. - P. 279. - ISBN 0-792-33463-9., Chapter, p. 279
4. Zill, Dennis G.; Wright, Scott; Wright, Warren S. Calculus: Early Transcendentals (undefined). - 3. - Jones & Bartlett Learning (English)Russian, 2009. - P. xxvii. - ISBN 0-763-75995-3.,Extract of page 27
5. Indian mathematics
6. von Neumann, J., "The Mathematician", in Heywood, R. B., ed., The Works of the Mind, University of Chicago Press, 1947, pp. 180-196. Reprinted in Bródy, F., Vámos, T., eds., The Neumann Compedium, World Scientific Publishing Co. Pte. Ltd., 1995, ISBN 9810222017, pp. 618-626.
7. André Weil: Number theory. An approach through history. From Hammurapi to Legendre. Birkhauser Boston, Inc., Boston, MA, 1984, ISBN 0-8176-4565-9, p. 28.
8. Leibniz, Gottfried Wilhelm. The Early Mathematical Manuscripts of Leibniz. Cosimo, Inc., 2008. Page 228. Copy
9. Unlu, Elif Maria Gaetana Agnesi (undefined) . Agnes Scott College (April 1995). Archived from the original on September 5, 2012.

Links

• Ron Larson, Bruce H. Edwards (2010). "Calculus", 9th ed., Brooks Cole Cengage Learning. ISBN 978-0-547-16702-2
• McQuarrie, Donald A. (2003). Mathematical Methods for Scientists and Engineers, University Science Books. ISBN 978-1-891389-24-5
• James Stewart (2008). Calculus: Early Transcendentals, 6th ed., Brooks Cole Cengage Learning.