Schwerpunkttheoretische Mechanik. Methoden zur Bestimmung der Koordinaten des Schwerpunkts. „Berechnung von Tragwerken auf Festigkeit“

– Berechnen des Schwerpunkts einer flach begrenzten Figur. Viele Leser verstehen intuitiv, wo der Schwerpunkt liegt, dennoch empfehle ich, den Stoff aus einer der Lektionen zu wiederholen analytische Geometrie, wo ich rumgemacht habe Problem über den Schwerpunkt eines Dreiecks und entschlüsselte es in einer zugänglichen Form physikalische Bedeutung diese Bezeichnung.

In unabhängiger und Testaufgaben Für die Lösung wird in der Regel der einfachste Fall vorgeschlagen - ein flach begrenzter Fall homogen Zahl, also eine konstante Zahl physikalische Dichte– Spielzeug aus Glas, Holz, Blech, Gusseisen, schwierige Kindheit usw. Außerdem werden wir standardmäßig nur über solche Zahlen sprechen =)

Die erste Regel und einfachstes Beispiel : wenn eine flache Figur hat Zentrum der Symmetrie, dann ist es der Schwerpunkt dieser Figur. Zum Beispiel die Mitte einer runden homogenen Platte. Es ist logisch und im Alltag verständlich – die Masse einer solchen Figur ist relativ zum Zentrum „gerecht in alle Richtungen verteilt“. Ich möchte es nicht umdrehen.

In der harten Realität ist es jedoch unwahrscheinlich, dass sie Ihnen eine Süßigkeit zuwerfen Elliptische Schokoladentafel, also müssen Sie sich mit einigen ernsthaften Küchenutensilien ausrüsten:

Die Koordinaten des Schwerpunkts einer flachen homogenen begrenzten Figur werden mit berechnet die folgenden Formeln :

, oder:

, wo ist die Fläche der Region (Abbildung); oder ganz kurz:

, Wo

Konventionell nennen wir das Integral „X“-Integral und das Integral „Y“-Integral.

Hilfehinweis : für Wohnung begrenzt heterogen Figuren, deren Dichte durch die Funktion angegeben wird, sind die Formeln komplexer:
, Wo – Masse der Figur;im Falle einer gleichmäßigen Dichte werden sie zu den obigen Formeln vereinfacht.

Tatsächlich endet die ganze Neuheit bei den Formeln, der Rest ist Ihr Können Lösen Sie DoppelintegraleÜbrigens ist jetzt eine großartige Gelegenheit, Ihre Technik zu üben und zu verbessern. Und der Perfektion sind bekanntlich keine Grenzen gesetzt =)

Dazu noch eine belebende Portion Parabeln:

Beispiel 1

Finden Sie die Koordinaten des Schwerpunkts einer homogenen flachen Figur, die durch Linien begrenzt ist.

Lösung: Die Linien hier sind elementar: Sie definieren die x-Achse und die Gleichung – eine Parabel, die mit einfach und schnell konstruiert werden kann geometrische Transformationen von Graphen:

– Parabel, um 2 Einheiten nach links und 1 Einheit nach unten verschoben.

Ich werde die gesamte Zeichnung auf einmal mit dem fertigen Schwerpunktpunkt der Figur vervollständigen:

Regel zwei: wenn die Figur hat Symmetrieachse, dann liegt der Schwerpunkt dieser Figur notwendigerweise auf dieser Achse.

In unserem Fall ist die Figur symmetrisch in Bezug auf gerade, das heißt, wir kennen tatsächlich bereits die „x“-Koordinate des Punktes „em“.

Beachten Sie auch, dass vertikal der Schwerpunkt näher zur x-Achse verschoben wird, da die Figur dort massiver ist.

Ja, vielleicht hat noch nicht jeder ganz verstanden, was der Schwerpunkt ist: Heben Sie bitte Ihren Zeigefinger nach oben und platzieren Sie gedanklich die schattierte „Sohle“ mit einem Punkt darauf. Theoretisch dürfte die Zahl nicht sinken.

Die Koordinaten des Schwerpunkts der Figur ermitteln wir anhand der Formeln , Wo .

Die Reihenfolge des Durchquerens des Bereichs (Abbildung) ist hier ersichtlich:

Aufmerksamkeit! Entscheidung über die vorteilhafteste Durchlaufreihenfolge einmal- und nutzen Sie es für alle Integrale!

1) Berechnen Sie zunächst die Fläche der Figur. Aufgrund der relativen Einfachheit des Integrals kann die Lösung kompakt geschrieben werden; Hauptsache, man darf sich bei den Berechnungen nicht verwirren:

Wir schauen uns die Zeichnung an und schätzen die Fläche anhand der Zellen. Es stellte sich heraus, dass es um den Fall ging.

2) Die X-Koordinate des Schwerpunkts wurde bereits gefunden“ grafische Methode", damit Sie sich auf die Symmetrie beziehen und mit dem nächsten Punkt fortfahren können. Allerdings empfehle ich dies trotzdem nicht – es besteht eine hohe Wahrscheinlichkeit, dass die Lösung mit der Formulierung „Verwenden Sie die Formel“ abgelehnt wird.


Bitte beachten Sie, dass Sie hier nur mit Kopfrechnen auskommen – manchmal ist es gar nicht nötig, Brüche auf zu reduzieren gemeinsamer Nenner oder den Rechner quälen.

Auf diese Weise:
, was benötigt wurde, um erhalten zu werden.

3) Finden Sie die Ordinate des Schwerpunkts. Berechnen wir das „Spiel“-Integral:

Aber hier wäre es ohne Taschenrechner schwierig. Zur Sicherheit möchte ich anmerken, dass man durch die Multiplikation von Polynomen 9 Terme erhält, von denen einige ähnlich sind. Ähnliche Begriffe habe ich mündlich dargelegt (wie es normalerweise in ähnlichen Fällen geschieht) und notierte sofort den Gesamtbetrag.

Ergebend:
, was der Wahrheit sehr, sehr ähnlich ist.

An letzte Stufe Markieren Sie einen Punkt auf der Zeichnung. Gemäß der Bedingung gab es keine Verpflichtung, etwas zu zeichnen, aber bei den meisten Aufgaben sind wir wohl oder übel gezwungen, eine Figur zu zeichnen. Aber es gibt ein absolutes Plus – eine visuelle und durchaus effektive Überprüfung des Ergebnisses.

Antwort:

Die folgenden beiden Beispiele können Sie selbst lösen.

Beispiel 2

Finden Sie die Koordinaten des Schwerpunkts einer homogenen flachen Figur, die durch Linien begrenzt ist

Wenn Sie sich übrigens vorstellen, wie die Parabel angeordnet ist, und sehen, an welchen Punkten sie die Achse schneidet, dann können Sie hier tatsächlich auf eine Zeichnung verzichten.

Und noch komplizierter:

Beispiel 3

Finden Sie den Schwerpunkt einer homogenen flachen Figur, die durch Linien begrenzt ist

Wenn Sie Schwierigkeiten beim Erstellen von Diagrammen haben, lernen Sie (wiederholen) Lektion über Parabeln und/oder Beispiel Nr. 11 des Artikels Doppelte Integrale für Dummies.

Beispiellösungen am Ende der Lektion.

Darüber hinaus finden sich im entsprechenden Archiv auf der Seite ein Dutzend oder zwei ähnliche Beispiele Vorgefertigte Lösungen für die höhere Mathematik.

Nun, ich kann nicht anders, als Fans der höheren Mathematik zu erfreuen, die mich oft bitten, schwierige Probleme zu analysieren:

Beispiel 4

Finden Sie den Schwerpunkt einer homogenen flachen Figur, die durch Linien begrenzt ist. Zeichnen Sie die Figur und ihren Schwerpunkt in die Zeichnung ein.

Lösung: Der Zustand dieser Aufgabe erfordert bereits unbedingt die Fertigstellung der Zeichnung. Aber die Anforderung ist nicht so formell! – Selbst ein durchschnittlich trainierter Mensch kann sich diese Zahl vorstellen:

Eine gerade Linie schneidet einen Kreis in zwei Teile und einen Zusatzsatz (cm. Lineare Ungleichungen) zeigt an, dass es sich um ein kleines schattiertes Stück handelt.

Die Figur ist symmetrisch zu einer geraden Linie (dargestellt durch eine gestrichelte Linie), daher sollte der Schwerpunkt auf dieser Linie liegen. Und natürlich sind seine Koordinaten gleich Modulo. Eine ausgezeichnete Richtlinie, die die Möglichkeit einer falschen Antwort praktisch ausschließt!

Jetzt die schlechte Nachricht =) Am Horizont zeichnet sich ein unangenehmes Integral der Wurzel ab, das wir im Beispiel Nr. 4 der Lektion ausführlich untersucht haben Effiziente Methoden zur Lösung von Integralen. Und wer weiß, was dort sonst noch gezeichnet wird. Es scheint, dass es an der Anwesenheit liegt Kreis profitabel, aber nicht alles ist so einfach. Die Geradengleichung wird in die Form umgewandelt und die Integrale werden sich auch nicht als Zucker herausstellen (obwohl Fans trigonometrische Integrale Wird schätzen). In dieser Hinsicht ist es sorgfältiger, näher darauf einzugehen Kartesischen Koordinaten Oh.

Die Reihenfolge beim Durchlaufen der Figur:

1) Berechnen Sie die Fläche der Figur:

Es ist rationaler, das erste Integral zu nehmen Subsumieren des Differentialzeichens:

Und im zweiten Integral führen wir den Standardersatz durch:


Berechnen wir die neuen Integrationsgrenzen:

2) Finden wir .

Hier im 2. Integral wurde es erneut verwendet Methode, eine Funktion unter dem Differentialzeichen zu subsumieren. Üben und übernehmen Sie diese optimal (meiner Meinung nach) Techniken zur Lösung von Standardintegralen.

Nach schwierigen und zeitaufwändigen Berechnungen wenden wir uns wieder der Zeichnung zu (Denken Sie daran, dass Punkte wir wissen es noch nicht! ) und wir empfinden tiefe moralische Befriedigung aus dem gefundenen Wert.

3) Basierend auf der zuvor durchgeführten Analyse muss noch sichergestellt werden, dass .

Großartig:

Lassen Sie uns einen Punkt ziehen auf der Zeichnung. Entsprechend dem Wortlaut der Bedingung schreiben wir diese als endgültig nieder Antwort:

Eine ähnliche Aufgabe, die Sie selbst lösen können:

Beispiel 5

Finden Sie den Schwerpunkt einer homogenen flachen Figur, die durch Linien begrenzt ist. Führen Sie die Zeichnung aus.

Dieses Problem ist interessant, weil es sich um eine relativ kleine Figur handelt und wenn man irgendwo einen Fehler macht, besteht eine hohe Wahrscheinlichkeit, dass man den Bereich überhaupt nicht „betritt“. Was aus Sicht der Entscheidungskontrolle sicherlich gut ist.

Ein Musterentwurf am Ende der Lektion.

Manchmal macht es Sinn Übergang zu Polarkoordinaten in Doppelintegralen. Es kommt auf die Figur an. Ich suchte und suchte nach einem erfolgreichen Beispiel, konnte es aber nicht finden, daher werde ich die Lösung im ersten Demoproblem der obigen Lektion demonstrieren:


Ich möchte Sie daran erinnern, dass wir in diesem Beispiel darauf eingegangen sind Polar Koordinaten, fand die Reihenfolge der Durchquerung des Gebiets heraus und berechnete seine Fläche

Finden wir den Schwerpunkt dieser Figur. Das Schema ist das gleiche: . Der Wert ist direkt aus der Zeichnung ersichtlich und die „x“-Koordinate sollte etwas näher an die Ordinatenachse verschoben werden, da sich dort der massivere Teil des Halbkreises befindet.

Bei Integralen verwenden wir Standardübergangsformeln:


Plausibel und höchstwahrscheinlich haben sie sich nicht geirrt.

Vorlesung 4. Schwerpunkt.

In dieser Vorlesung werden folgende Themen behandelt

1. Schwerpunkt solide.

2. Koordinaten der Schwerpunkte inhomogener Körper.

3. Koordinaten der Schwerpunkte homogener Körper.

4. Methoden zur Bestimmung der Koordinaten von Schwerpunkten.

5. Schwerpunkte einiger homogener Körper.

Die Untersuchung dieser Fragen ist in Zukunft notwendig, um die Dynamik der Bewegung von Körpern unter Berücksichtigung von Gleit- und Rollreibung, die Dynamik der Bewegung des Massenschwerpunkts eines mechanischen Systems und kinetische Momente zu untersuchen und Probleme in der zu lösen Disziplin „Festigkeit der Werkstoffe“.

Parallele Kräfte bringen.

Nachdem wir darüber nachgedacht haben, ein flaches System und ein beliebiges räumliches Kräftesystem ins Zentrum zu bringen, kehren wir wieder zur Betrachtung des Sonderfalls eines Systems paralleler Kräfte zurück.

Bringt zwei parallele Kräfte.

Im Zuge der Betrachtung eines solchen Kräftesystems sind die folgenden drei Reduktionsfälle möglich.

1. System zweier kollinearer Kräfte. Betrachten wir ein System aus zwei parallelen Kräften, die in eine Richtung gerichtet sind P Und Q, punktuell angewendet A Und IN. Wir gehen davon aus, dass die Kräfte senkrecht zu diesem Segment wirken (Abb. 1, A).

MIT, zum Segment gehörend AB und die Bedingung erfüllen:

Wechselstrom/NE = Q/P.(1)

Hauptvektor des Systems R C = P + Q ist im Modul gleich der Summe dieser Kräfte: R C = P + Q.

MIT unter Berücksichtigung von (1) ist gleich Null:MC = P ∙ Wechselstrom- Q∙ CB = 0.

Als Ergebnis des Castings haben wir also Folgendes erhalten: R C ≠ 0, MC= 0. Dies bedeutet, dass der Hauptvektor der durch das Reduktionszentrum verlaufenden Resultierenden entspricht, d. h.:

Die Resultierende kollinearer Kräfte hat den gleichen Modul wie ihre Summe, und ihre Wirkungslinie teilt das Segment, das die Punkte ihrer Anwendung verbindet, im umgekehrten Verhältnis zu den Modulen dieser Kräfte auf interne Weise.

Beachten Sie die Position des Punktes MIT wird sich nicht ändern, wenn die Kräfte R Und Q einen Winkel drehenα. Punkt MIT, das diese Eigenschaft hat, heißt Zentrum paralleler Kräfte.

2. Zweiersystem antikollinear und Kräfte, die nicht gleich groß sind. Möge die Stärke P Und Q, punktuell angewendet A Und IN, parallel, in entgegengesetzte Richtungen gerichtet und ungleich groß (Abb. 1, B).

Wählen wir einen Punkt als Reduktionszentrum MIT, die immer noch die Beziehung (1) erfüllt und auf derselben Linie, aber außerhalb des Segments liegt AB.

Der Hauptvektor dieses Systems R C = P + Q Der Modul ist nun gleich der Differenz zwischen den Modulen der Vektoren: R C = Q - P.

Der wichtigste Punkt bezüglich der Mitte MIT ist immer noch Null:MC = P ∙ Wechselstrom- Q∙ NE= 0, also

Resultierend antikollinear und Kräfte, deren Größe nicht gleich ist, sind gleich ihrer Differenz, auf die größere Kraft gerichtet, und ihre Wirkungslinie teilt das Segment, das die Punkte ihrer Anwendung verbindet, im umgekehrten Verhältnis zu den äußeren Modulen dieser Kräfte.

Abb.1

3. Zweiersystem antikollinear und Kräfte gleicher Größe. Nehmen wir den vorherigen Reduktionsfall als Ausgangsfall. Lasst uns die Kraft reparieren R, und Stärke Q Richten wir den Modul auf die Kraft aus R.

Dann um Q → R in Formel (1) die Beziehung Wechselstrom/NE → 1. Das bedeutet das Wechselstrom → NE, also die Entfernung Wechselstrom →∞ .

In diesem Fall das Modul des Hauptvektors R C → 0, und der Modul des Hauptmoments hängt nicht von der Position des Reduktionszentrums ab und bleibt gleich dem ursprünglichen Wert:

MC = P ∙ Wechselstrom- Q∙ NE = P ∙ ( Wechselstrom- NE) =P ∙ AB.

Im Grenzfall haben wir also ein Kräftesystem erhalten, für das R C = 0, MC≠ 0, und das Reduktionszentrum wird ins Unendliche verschoben, das nicht durch die Resultierende ersetzt werden kann. Es ist also nicht schwer, ein paar Kräfte in diesem System zu erkennen Ein Kräftepaar hat keine Resultierende.

Zentrum des Systems paralleler Kräfte.

Betrachten Sie das System N Stärke P ich, punktuell angewendetA i (x i , y i , z i) und parallel zur AchseOv mit orth l(Abb. 2).

Wenn wir den Fall eines Systems, das einem Kräftepaar entspricht, von vornherein ausschließen, ist es auf der Grundlage des vorherigen Absatzes nicht schwierig, die Existenz seiner Resultierenden zu beweisenR.

Bestimmen wir die Koordinaten des ZentrumsC(X C, j C, z C) parallele Kräfte, also die Koordinaten des Angriffspunkts der Resultierenden dieses Systems.

Zu diesem Zweck verwenden wir den Satz von Varignon, der darauf basiert:

M0 (R) = Σ M0(P ich).

Abb.2

Das Vektormoment einer Kraft kann als Vektorprodukt dargestellt werden, daher:

M 0 (R) = r c× R = Σ M0i(P ich) = Σ ( r i× P ich ).

Bedenkt, dass R = Rv ∙ l, A P ich = Pvi ∙ l und Nutzung der Eigenschaften Vektorprodukt, wir bekommen:

r c × Rv ∙ l = Σ ( r i × Pvi ∙ l),

r c ∙ R v× l = Σ ( r i ∙ Pvi × l) = Σ ( r i ∙ Pvi ) × l,

oder:

[ r c R v - Σ ( r i Pvi )] × l= 0.

Der letzte Ausdruck ist nur gültig, wenn der Ausdruck in eckigen Klammern gleich Null ist. Daher wird der Index weggelassenvund unter Berücksichtigung der resultierendenR = Σ P ich , von hier aus erhalten wir:

r c = (Σ P ich r i )/(Σ P ich ).

Indem wir die letzte Vektorgleichheit auf die Koordinatenachse projizieren, erhalten wir das erforderliche Ergebnis Ausdruck für die Koordinaten des Mittelpunkts paralleler Kräfte:

x c = (Σ P ich x i)/(Σ P ich );

y c = (Σ P ich y i )/(Σ P ich );(2)

z c = (Σ P ich z i )/(Σ P ich ).

Schwerpunkt der Körper.

Koordinaten der Schwerpunkte eines homogenen Körpers.

Stellen Sie sich eine starre Körperwägung vor P und Lautstärke V im Koordinatensystem Oxyz, wo sind die Achsen X Und j mit der Erdoberfläche und der Achse verbunden z auf den Zenit gerichtet.

Wenn wir den Körper in elementare Teile mit Volumen zerlegen∆ V ich , dann wirkt die Anziehungskraft auf jeden Teil davon∆ P ich, auf den Mittelpunkt der Erde gerichtet. Nehmen wir an, dass die Abmessungen des Körpers deutlich kleiner sind als die Abmessungen der Erde, dann kann das auf die Elementarteile des Körpers ausgeübte Kräftesystem als nicht konvergierend, sondern parallel betrachtet werden (Abb. 3) und alle Schlussfolgerungen des vorherigen Kapitels gelten hierfür.

Abb. 3

Definition . Der Schwerpunkt eines festen Körpers ist der Mittelpunkt paralleler Schwerkraftkräfte der Elementarteile dieses Körpers.

Erinnern wir uns daran spezifisches Gewicht eines elementaren Körperteils nennt man das Verhältnis seines Gewichts∆ P ich zum Volumen ∆ V ich : γ ich = ∆ P ich/ ∆ V ich . Für einen homogenen Körper ist dieser Wert konstant:γ ich = γ = P/ V.

Einsetzen von ∆ in (2) P ich = γ ich ∙∆ V ich anstatt P ich, unter Berücksichtigung der letzten Bemerkung und Reduzierung von Zähler und Nenner umG, wir bekommen Ausdrücke für die Koordinaten des Schwerpunkts eines homogenen Körpers:

x c = (Σ ∆ V i∙ x i)/(Σ ∆ V i);

y c = (Σ ∆ V i∙ y i )/(Σ ∆ V i);(3)

z c = (Σ ∆ V i∙ z i )/(Σ ∆ V i).

Zur Bestimmung des Schwerpunkts sind mehrere Theoreme hilfreich.

1) Wenn ein homogener Körper eine Symmetrieebene hat, liegt sein Schwerpunkt in dieser Ebene.

Wenn die Achsen X Und bei in dieser Symmetrieebene gelegen, dann für jeden Punkt mit Koordinaten. Und die Koordinate nach (3) wird gleich Null sein, weil in der Summe Alle Mitglieder mit entgegengesetzten Vorzeichen werden paarweise zerstört. Das bedeutet, dass der Schwerpunkt lokalisiert ist in der Symmetrieebene.

2) Wenn ein homogener Körper eine Symmetrieachse hat, dann liegt der Schwerpunkt des Körpers auf dieser Achse.

In diesem Fall nämlich, wenn die AchsezZeichnen Sie für jeden Punkt mit Koordinaten entlang der SymmetrieachseSie können einen Punkt mit Koordinaten finden und Koordinaten und , berechnet nach Formeln (3), ist gleich Null.

Der dritte Satz wird auf ähnliche Weise bewiesen.

3) Wenn ein homogener Körper ein Symmetriezentrum hat, dann liegt in diesem Punkt der Schwerpunkt des Körpers.

Und noch ein paar Kommentare.

Erste. Wenn der Körper in Teile zerlegt werden kann, für die Gewicht und Lage des Schwerpunkts bekannt sind, muss nicht jeder Punkt berücksichtigt werden, und in den Formeln (3) P ich – bestimmt als Gewicht des entsprechenden Teils und– als Koordinaten seines Schwerpunkts.

Zweite. Wenn der Körper homogen ist, dann das Gewicht eines einzelnen Teils davon, Wo - spezifisches Gewicht des Materials, aus dem der Körper besteht, und V i - das Volumen dieses Körperteils. Und Formeln (3) werden eine bequemere Form annehmen. Zum Beispiel,

Und ebenso, wo - Volumen des gesamten Körpers.

Dritte Anmerkung. Lassen Sie den Körper die Form einer dünnen Platte mit einer Fläche haben F und Dicke T, im Flugzeug liegend Oxy. Einsetzen in (3)∆ V ich =T ∙ ∆F ich , wir erhalten die Koordinaten des Schwerpunkts einer homogenen Platte:

x c = (Σ ∆ F i∙ x i) / (Σ ∆ F i);

y c = (Σ ∆ F i∙ y i ) / (Σ ∆ F i).

z c = (Σ ∆ F i∙ z ich ) / (Σ ∆ F i).

Wo – Koordinaten des Schwerpunkts einzelner Platten;– gesamter Körperbereich.

Vierte Anmerkung. Für einen Körper in Form eines dünnen, gebogenen Stabes der Länge L mit Querschnittsfläche A elementarer Band∆ V ich = A ∙∆ L ich , Deshalb Koordinaten des Schwerpunkts eines dünnen gebogenen Stabes wird gleich sein:

x c = (Σ ∆ L ich∙ x i)/(Σ ∆ L ich);

y c = (Σ ∆ L ich∙ y i )/(Σ ∆ L ich);(4)

z c = (Σ ∆ L ich∙ z i )/(Σ ∆ L ich).

Wo – Koordinaten des Schwerpunktsich-ter Abschnitt; .

Beachten Sie, dass der Schwerpunkt laut Definition ein geometrischer Punkt ist; es kann auch außerhalb der Grenzen eines bestimmten Körpers liegen (z. B. bei einem Ring).

Notiz.

In diesem Kursabschnitt wird nicht zwischen Schwerkraft, Schwerkraft und Körpergewicht unterschieden. In Wirklichkeit ist die Schwerkraft die Differenz zwischen der Gravitationskraft der Erde und der durch ihre Rotation verursachten Zentrifugalkraft.

Koordinaten der Schwerpunkte inhomogener Körper.

Schwerpunktkoordinaten inhomogener Feststoff(Abb.4) im gewählten Bezugssystem werden wie folgt ermittelt:

Abb.4

Wo - Gewicht pro Volumeneinheit eines Körpers (spezifisches Gewicht)

- ganzes Körpergewicht.

ungleichmäßige Oberfläche(Abb. 5), dann werden die Koordinaten des Schwerpunkts im gewählten Bezugssystem wie folgt bestimmt:

Abb.5

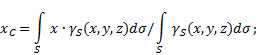
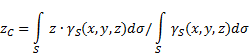
Wo - Gewicht pro Körperflächeneinheit,

- ganzes Körpergewicht.

Wenn der Feststoff ist ungleichmäßige Linie(Abb. 6), dann werden die Koordinaten des Schwerpunkts im gewählten Bezugssystem wie folgt bestimmt:

Abb.6

Wo - Gewicht pro Körperlänge,

Gesamtkörpergewicht.

Methoden zur Bestimmung der Koordinaten des Schwerpunkts.

Basierend auf den oben erhaltenen allgemeinen Formeln ist es möglich, spezifische Methoden anzugeben Bestimmung der Koordinaten der Schwerpunkte von Körpern.

1. Symmetrie. Besitzt ein homogener Körper eine Ebene, Achse oder ein Symmetriezentrum (Abb. 7), so liegt sein Schwerpunkt jeweils in der Symmetrieebene, Symmetrieachse bzw. im Symmetriezentrum.

Abb.7

2. Aufteilen. Der Körper bricht ein letzte Zahl Teile (Abb. 8), für die jeweils die Lage des Schwerpunkts und die Fläche bekannt sind.

Abb.8

S =S 1 +S 2.

3.Negativflächenmethode. Ein Sonderfall der Partitionierungsmethode (Abb. 9). Sie gilt für Körper mit Aussparungen, wenn die Schwerpunkte des Körpers ohne Aussparung und des ausgeschnittenen Teils bekannt sind. Ein Körper in Form einer Platte mit Ausschnitt wird durch eine Kombination einer massiven Platte (ohne Ausschnitt) mit einer Fläche dargestellt S 1 und die Fläche des geschnittenen Teils S2.

Abb.9

S = S 1 - S 2.

4.Gruppierungsmethode. Es ist eine gute Ergänzung zu den letzten beiden Methoden. Nachdem man eine Figur in ihre Bestandteile zerlegt hat, ist es sinnvoll, einige davon wieder zu kombinieren, um dann die Lösung unter Berücksichtigung der Symmetrie dieser Gruppe zu vereinfachen.

Schwerpunkte einiger homogener Körper.

1) Schwerpunkt eines Kreisbogens. Betrachten Sie den Bogen AB RadiusR mit Zentralwinkel. Aus Symmetriegründen liegt der Schwerpunkt dieses Bogens auf der AchseOchse(Abb. 10).

Abb.10

Finden wir die Koordinate nach der Formel . Wählen Sie dazu den Bogen aus AB Element MM ’ Länge, dessen Position durch den Winkel bestimmt wird. Koordinate X Element MM' Wille. Ersetzen dieser Werte X Und D l und unter Berücksichtigung der Tatsache, dass das Integral über die gesamte Länge des Bogens ausgedehnt werden muss, erhalten wir:

wobei L die Länge des Bogens AB ist, gleich .

Von hier aus stellen wir schließlich fest, dass der Schwerpunkt eines Kreisbogens auf seiner Symmetrieachse im Abstand vom Mittelpunkt liegt O gleich

Wo ist der Winkel? gemessen im Bogenmaß.

2) Schwerpunkt der Dreiecksfläche. Betrachten Sie ein Dreieck, das in der Ebene liegt Oxy, deren Koordinaten der Eckpunkte bekannt sind: A i (x i,y i ), (ich= 1,2,3). Brechen Sie das Dreieck in schmale Streifen parallel zur Seite A 1 A 2 kommen wir zu dem Schluss, dass der Schwerpunkt des Dreiecks zum Median liegen muss A 3 M 3 (Abb. 11).

Abb.11

Ein Dreieck in seitlich parallele Streifen brechen A 2 A 3 können wir überprüfen, dass es auf dem Median liegen muss A 1 M 1 . Auf diese Weise, Der Schwerpunkt eines Dreiecks liegt im Schnittpunkt seiner Mediane, der bekanntlich von jedem Median einen dritten Teil abtrennt, gerechnet von der entsprechenden Seite.

Insbesondere für den Median A 1 M 1 erhalten wir unter Berücksichtigung der Koordinaten des Punktes M 1 - Dies ist das arithmetische Mittel der Koordinaten der Eckpunkte A 2 und A 3 :

x c = X 1 + (2/3) ∙ (XM 1 - X 1 ) = X 1 + (2/3) ∙ [(X 2 + X 3 )/2 - X 1 ] = (X 1 + X 2 + X 3 )/3.

Somit sind die Koordinaten des Schwerpunkts des Dreiecks das arithmetische Mittel der Koordinaten seiner Eckpunkte:

X C =(1/3) Σ x i ; j C =(1/3) Σ y i .

3) Schwerpunkt der Fläche eines Kreissektors. Betrachten Sie einen Kreissektor mit Radius R mit Zentrierwinkel 2α , symmetrisch um die Achse angeordnet Ochse (Abb. 12) .

Es ist klar, dass j C = 0, und der Abstand vom Mittelpunkt des Kreises, aus dem dieser Sektor geschnitten wird, zu seinem Schwerpunkt kann durch die Formel bestimmt werden:

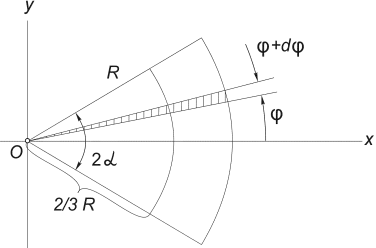
Abb.12

Der einfachste Weg, dieses Integral zu berechnen, besteht darin, das Integrationsgebiet in Elementarsektoren mit einem Winkel zu unterteilen Dφ . Auf Infinitesimalzahlen erster Ordnung genau kann ein solcher Sektor durch ein Dreieck mit einer Basis gleich ersetzt werden R × Dφ und Höhe R. Die Fläche eines solchen Dreiecks dF =(1/2)R 2 ∙ Dφ , und sein Schwerpunkt liegt in einem Abstand von 2/3 R vom Scheitelpunkt, deshalb setzen wir in (5). X = (2/3)R∙ cosφ. Einsetzen in (5) F= α R 2, wir erhalten:

Mit der letzten Formel berechnen wir insbesondere den Abstand zum Schwerpunkt Halbkreis.

Wenn wir α = π /2 in (2) einsetzen, erhalten wir: X C = (4 R)/(3π) ≅ 0,4 R .

Beispiel 1.Bestimmen wir den Schwerpunkt des in Abb. gezeigten homogenen Körpers. 13.

Abb.13

Lösung.Der Körper ist homogen und besteht aus zwei Teilen mit symmetrischer Form. Koordinaten ihrer Schwerpunkte:

Ihre Bände:

Daher die Koordinaten des Schwerpunkts des Körpers

Beispiel 2. Finden wir den Schwerpunkt einer im rechten Winkel gebogenen Platte. Die Abmessungen finden Sie in der Zeichnung (Abb. 14).

Abb.14

Lösung. Koordinaten der Schwerpunkte:

0.

Bereiche:

Deshalb:
Beispiel 3. Auf einem quadratischen Blatt cm quadratisches Loch schneiden cm (Abb. 15). Lassen Sie uns den Schwerpunkt des Blattes ermitteln. Beispiel 4. Finden Sie die Position des Schwerpunkts der in Abb. gezeigten Platte. 16. Die Abmessungen werden in Zentimetern angegeben.

Abb.16

Lösung. Teilen wir die Platte in Figuren auf (Abb. 17), Zentren deren Schweregrad bekannt ist.

Die Flächen dieser Figuren und die Koordinaten ihrer Schwerpunkte:

1) ein Rechteck mit Seitenlängen von 30 und 40 cm,S 1 =30 ∙ 40=1200 cm 2 ; x 1=15 cm; bei 1 =20 cm.

2) rechtwinkliges Dreieck mit einer Grundfläche von 50 cm und einer Höhe von 40 cm;S 2 =0,5 ∙ 50 ∙ 40= 1000 cm 2 ; X 2 =30+50/3=46,7cm; y 2 =40/3 =13,3 cm;

3) Halbkreisradiuskreis R = 20 cm;S 3 =0,5 ∙π∙ 20 2 =628 cm 2 ; X 3 =4 R /3 π =8,5 cm; bei

Lösung. Denken Sie daran, dass in der Physik die Dichte eines Körpers giltρ und sein spezifisches GewichtGhängen durch die Beziehung zusammen:γ = ρ G , WoG - Beschleunigung freier Fall. Um die Masse eines solchen homogenen Körpers zu ermitteln, müssen Sie die Dichte mit seinem Volumen multiplizieren.

Abb.19

Der Begriff „linear“ oder „lineare“ Dichte bedeutet, dass zur Bestimmung der Masse eines Halsstabes die lineare Dichte mit der Länge dieses Stabes multipliziert werden muss.

Um das Problem zu lösen, können Sie die Partitionierungsmethode verwenden. Wenn wir ein gegebenes Fachwerk als Summe von 6 einzelnen Stäben darstellen, erhalten wir:

WoL ich Längeich der Halsstab undx i , y i - Koordinaten seines Schwerpunkts.

Die Lösung dieses Problems kann durch die Gruppierung der letzten 5 Stäbe des Fachwerks vereinfacht werden. Es ist leicht zu erkennen, dass sie eine Figur bilden, deren Symmetriezentrum in der Mitte des vierten Stabes liegt, wo sich der Schwerpunkt dieser Stabgruppe befindet.

Somit kann ein gegebenes Fachwerk durch eine Kombination von nur zwei Stabgruppen dargestellt werden.

Die erste Gruppe besteht aus der ersten RuteL 1 = 4m,X 1 = 0 m,j 1 = 2 m. Die zweite Stabgruppe besteht aus fünf StäbenL 2 = 20 m,X 2 = 3m,j 2 = 2 m.

Die Koordinaten des Schwerpunkts des Fachwerks werden mit der Formel ermittelt:

X C = (L 1 ∙ X 1 + L 2 ∙ X 2 )/(L 1 + L 2 ) = (4∙0 + 20∙3)/24 = 5/2 m;

j C = (L 1 ∙ j 1 + L 2 ∙ j 2 )/(L 1 + L 2 ) = (4∙2 + 20∙2)/24 = 2 m.

Beachten Sie, dass die Mitte MIT liegt auf der Verbindungsgeraden MIT 1 und MIT 2 und teilt das Segment MIT 1 MIT 2 zu: MIT 1 MIT/SS 2 = (X C - X 1 )/(X 2 - X C ) = L 2 / L 1 = 2,5/0,5.

Fragen zum Selbsttest

- Wie nennt man das Zentrum paralleler Kräfte?

- Wie werden die Koordinaten des Mittelpunkts paralleler Kräfte bestimmt?

- Wie bestimmt man den Mittelpunkt paralleler Kräfte, deren Resultierende Null ist?

- Welche Eigenschaften hat der Mittelpunkt paralleler Kräfte?

- Mit welchen Formeln werden die Koordinaten des Mittelpunkts paralleler Kräfte berechnet?

- Wie nennt man den Schwerpunkt eines Körpers?

- Warum kann man die auf einen Punkt eines Körpers wirkenden Gravitationskräfte der Erde als ein System paralleler Kräfte auffassen?

- Geben Sie die Formel zur Bestimmung der Schwerpunktlage inhomogener und homogener Körper und die Formel zur Bestimmung der Schwerpunktlage flacher Abschnitte an?

- Schreiben Sie die Formel zur Bestimmung der Lage des Schwerpunkts eines einfachen Menschen auf geometrische Formen: Rechteck, Dreieck, Trapez und Halbkreis?

- Was nennt man das statische Flächenmoment?

- Geben Sie ein Beispiel für einen Körper, dessen Schwerpunkt außerhalb des Körpers liegt.

- Wie werden die Eigenschaften der Symmetrie zur Bestimmung der Schwerpunkte von Körpern genutzt?

- Was ist das Wesentliche an der Methode der negativen Gewichte?

- Wo liegt der Schwerpunkt eines Kreisbogens?

- Mit welcher grafischen Konstruktion lässt sich der Schwerpunkt eines Dreiecks ermitteln?

- Schreiben Sie die Formel auf, die den Schwerpunkt eines Kreissektors bestimmt.

- Leiten Sie mithilfe von Formeln, die die Schwerpunkte eines Dreiecks und eines Kreissektors bestimmen, eine ähnliche Formel für ein Kreissegment ab.

- Mit welchen Formeln werden die Koordinaten der Schwerpunkte homogener Körper, flacher Figuren und Linien berechnet?

- Wie nennt man das statische Moment der Fläche einer ebenen Figur relativ zur Achse, wie berechnet man es und welche Dimension hat es?

- Wie lässt sich die Lage des Schwerpunkts einer Fläche bestimmen, wenn die Lage der Schwerpunkte ihrer einzelnen Teile bekannt ist?

- Welche Hilfssätze werden verwendet, um die Lage des Schwerpunkts zu bestimmen?

Ziel der Arbeit – den Schwerpunkt einer komplexen Figur analytisch und experimentell bestimmen.

Theoretischer Hintergrund. Materielle Körper bestehen aus Elementarteilchen, deren Position im Raum durch ihre Koordinaten bestimmt wird. Die Anziehungskräfte jedes Teilchens auf die Erde können als System paralleler Kräfte betrachtet werden. Die Resultierende dieser Kräfte wird als Schwerkraft des Körpers oder als Gewicht des Körpers bezeichnet. Der Schwerpunkt eines Körpers ist der Angriffspunkt der Schwerkraft.

Der Schwerpunkt liegt geometrischer Punkt, die sich außerhalb des Körpers befinden kann (z. B. eine Scheibe mit einem Loch, eine Hohlkugel usw.). Groß praktische Bedeutung hat eine Definition des Schwerpunkts dünner, flacher, homogener Platten. Ihre Dicke kann in der Regel vernachlässigt werden und es kann davon ausgegangen werden, dass der Schwerpunkt in einer Ebene liegt. Wenn Koordinatenebene Wenn xOy mit der Ebene der Figur ausgerichtet ist, wird die Position des Schwerpunkts durch zwei Koordinaten bestimmt:

wo ist die Fläche eines Teils der Figur, ();

– Koordinaten des Schwerpunkts der Teile der Figur, mm (cm).

Ausschnitt einer Figur A, mm 2 X c ,mm Yc, mm

bh b/2 h/2

BH/2 b/3 h/3
R 2a
Bei 2α = π πR 2 /2

Arbeitsablauf.

Zeichnen Sie eine Figur mit komplexer Form, bestehend aus 3-4 einfachen Figuren (Rechteck, Dreieck, Kreis usw.) im Maßstab 1:1 und geben Sie ihre Abmessungen an.

Zeichnen Sie die Koordinatenachsen so, dass sie die gesamte Figur abdecken, zerlegen Sie die komplexe Figur in einfache Teile und bestimmen Sie die Fläche und die Koordinaten des Schwerpunkts jeder einfachen Figur relativ zum ausgewählten Koordinatensystem.

Berechnen Sie analytisch die Koordinaten des Schwerpunkts der gesamten Figur. Schneiden Sie diese Figur aus dünnem Karton oder Sperrholz aus. Bohren Sie zwei Löcher, die Kanten der Löcher sollten glatt sein und der Durchmesser der Löcher sollte etwas größer sein als der Durchmesser der Nadel zum Aufhängen der Figur.

Hängen Sie die Figur zunächst an einem Punkt (Loch) auf und zeichnen Sie mit einem Bleistift eine Linie, die mit dem Lot übereinstimmt. Wiederholen Sie das Gleiche, wenn Sie die Figur an einer anderen Stelle aufhängen. Der experimentell ermittelte Schwerpunkt der Figur muss übereinstimmen.

Bestimmen Sie die Koordinaten des Schwerpunkts einer dünnen homogenen Platte analytisch. Prüfen Sie experimentell

Lösungsalgorithmus

1. Analytische Methode.

a) Zeichnen Sie die Zeichnung im Maßstab 1:1.

b) Zerlegen Sie eine komplexe Figur in einfache

c) Koordinatenachsen auswählen und zeichnen (wenn die Figur symmetrisch ist, dann entlang der Symmetrieachse, andernfalls entlang der Kontur der Figur)



d) Berechnen Sie die Fläche einfacher Figuren und der gesamten Figur

e) Markieren Sie die Position des Schwerpunkts jeder einfachen Figur in der Zeichnung

f) Berechnen Sie die Koordinaten des Schwerpunkts jeder Figur

(x- und y-Achse)

g) Berechnen Sie mit der Formel die Koordinaten des Schwerpunkts der gesamten Figur

h) Markieren Sie die Lage des Schwerpunkts auf Zeichnung C (

2. Experimentelle Bestimmung.

Die Richtigkeit der Lösung des Problems kann experimentell überprüft werden. Schneiden Sie diese Figur aus dünnem Karton oder Sperrholz aus. Bohren Sie drei Löcher, die Kanten der Löcher sollten glatt sein und der Durchmesser der Löcher sollte etwas größer sein als der Durchmesser der Nadel zum Aufhängen der Figur.

Hängen Sie die Figur zunächst an einem Punkt (Loch) auf und zeichnen Sie mit einem Bleistift eine Linie, die mit dem Lot übereinstimmt. Wiederholen Sie dasselbe, wenn Sie die Figur an anderen Stellen aufhängen. Der Wert der Koordinaten des Schwerpunkts der Figur, der ermittelt wird, wenn die Figur an zwei Punkten aufgehängt wird: . Der experimentell ermittelte Schwerpunkt der Figur muss übereinstimmen.

3. Aussage über die Lage des Schwerpunktes bei der analytischen und experimentellen Bestimmung.

Übung

Bestimmen Sie den Schwerpunkt eines flachen Abschnitts analytisch und experimentell.

Ausführungsbeispiel

Aufgabe

Bestimmen Sie die Koordinaten des Schwerpunkts einer dünnen homogenen Platte.

I Analytische Methode

1. Die Zeichnung ist maßstabsgetreu (Maße werden üblicherweise in mm angegeben)

2. Wir zerlegen eine komplexe Figur in einfache.

1- Rechteck

2- Dreieck (Rechteck)

3- Fläche des Halbkreises (existiert nicht, Minuszeichen).

Wir ermitteln die Lage des Schwerpunkts einfacher Punktfiguren und

3. Zeichnen Sie die Koordinatenachsen nach Bedarf ein und markieren Sie den Koordinatenursprung.

4. Berechnen Sie die Flächen einfacher Figuren und die Fläche der gesamten Figur. [Größe in cm]

(3. Nein, Zeichen -).

Fläche der gesamten Figur

5. Finden Sie die Koordinate des Mittelpunkts. , und in der Zeichnung.

6. Berechnen Sie die Koordinaten der Punkte C 1, C 2 und C 3



7. Berechnen Sie die Koordinaten von Punkt C

8. Markieren Sie einen Punkt auf der Zeichnung

II Erfahren

Koordinaten des Schwerpunkts experimentell.

Kontrollfragen.

1. Ist es möglich, die Schwerkraft eines Körpers als resultierendes System paralleler Kräfte zu betrachten?

2. Kann der Schwerpunkt des gesamten Körpers lokalisiert werden?

3. Was ist das Wesentliche an der experimentellen Bestimmung des Schwerpunkts einer flachen Figur?

4. Wie wird der Schwerpunkt einer komplexen Figur bestimmt, die aus mehreren einfachen Figuren besteht?

5. Wie sollte eine Figur mit komplexer Form bei der Bestimmung des Schwerpunkts der gesamten Figur rational in einfache Figuren unterteilt werden?

6. Welches Vorzeichen hat die Fläche der Löcher in der Formel zur Bestimmung des Schwerpunkts?

7. Im Schnittpunkt welcher Linien des Dreiecks liegt sein Schwerpunkt?

8. Wenn es schwierig ist, eine Figur in eine kleine Anzahl einfacher Figuren zu zerlegen, welche Methode zur Bestimmung des Schwerpunkts kann die schnellste Antwort liefern?

Praktische Arbeit №6

„Komplexe Probleme lösen“

Ziel der Arbeit: komplexe Probleme (Kinematik, Dynamik) lösen können

Theoretischer Hintergrund: Geschwindigkeit ist ein kinematisches Maß für die Bewegung eines Punktes und charakterisiert die Geschwindigkeit der Änderung seiner Position. Die Geschwindigkeit eines Punktes ist ein Vektor, der die Geschwindigkeit und Bewegungsrichtung eines Punktes charakterisiert dieser Moment Zeit. Bei der Angabe der Bewegung eines Punktes durch Gleichungen sind die Geschwindigkeitsprojektionen auf den kartesischen Koordinatenachsen gleich:

Der Geschwindigkeitsmodul eines Punktes wird durch die Formel bestimmt

Die Richtung der Geschwindigkeit wird durch den Richtungskosinus bestimmt:

Das Merkmal der Geschwindigkeitsänderungsgeschwindigkeit ist die Beschleunigung a. Die Beschleunigung eines Punktes ist gleich der zeitlichen Ableitung des Geschwindigkeitsvektors:

Bei der Angabe der Bewegung eines Punktes lauten die Gleichungen für die Projektion der Beschleunigung auf die Koordinatenachsen wie folgt:


Beschleunigungsmodul:

Volles Beschleunigungsmodul

Der Tangentialbeschleunigungsmodul wird durch die Formel bestimmt

Der normale Beschleunigungsmodul wird durch die Formel bestimmt

wo ist der Krümmungsradius der Flugbahn an einem bestimmten Punkt.

Die Richtung der Beschleunigung wird durch den Richtungskosinus bestimmt

Die Gleichung der Rotationsbewegung eines starren Körpers um eine feste Achse hat die Form

Winkelgeschwindigkeit des Körpers:

Manchmal wird die Winkelgeschwindigkeit durch die Anzahl der Umdrehungen pro Minute charakterisiert und mit dem Buchstaben bezeichnet. Die Abhängigkeit zwischen und hat die Form

Winkelbeschleunigung des Körpers:

Eine Kraft, die dem Produkt der Masse eines gegebenen Punktes mit seiner Beschleunigung und der Richtung in der Richtung, die der Beschleunigung des Punktes direkt entgegengesetzt ist, entspricht, wird Trägheitskraft genannt.

Leistung ist die Arbeit, die eine Kraft pro Zeiteinheit verrichtet.

Grundlegende Dynamikgleichung für Rotationsbewegungen

– Das Trägheitsmoment des Körpers relativ zur Rotationsachse ist die Summe der Produkte der Massen materieller Punkte mit dem Quadrat ihrer Abstände zu dieser Achse

Übung

Ein Körper der Masse m bewegt sich mit Hilfe eines auf einer Trommel mit dem Durchmesser d aufgewickelten Seils entlang einer schiefen Ebene mit einem Neigungswinkel α auf oder ab. Gleichung der Körperbewegung S=f(t), Gleichung der Trommelrotation, wobei S in Metern angegeben ist; φ - im Bogenmaß; t – in Sekunden. P und ω sind jeweils die Leistung und die Winkelgeschwindigkeit an der Trommelwelle zum Zeitpunkt des Endes der Beschleunigung bzw. des Beginns des Bremsens. Zeit t 1 – Beschleunigungszeit (vom Ruhezustand auf eine bestimmte Geschwindigkeit) oder Bremszeit (von einer bestimmten Geschwindigkeit bis zum Stillstand). Der Gleitreibungskoeffizient zwischen Körper und Ebene beträgt –f. Reibungsverluste an der Trommel sowie die Masse der Trommel sind zu vernachlässigen. Nehmen Sie beim Lösen von Problemen g=10 m/s 2 an

Nr. var α, Grad Bewegungsgesetz Zum Beispiel Bewegung m, kg t 1 , s d, m P, kW , rad/s F Def. Mengen
S=0,8t 2 Runter - - 0,20 4,0 0,20 m,t 1
φ=4t 2 Runter 1,0 0,30 - - 0,16 P,ω
S=1,5t-t 2 hoch - - - 4,5 0,20 m, d
ω=15t-15t 2 hoch - - 0,20 3,0 - 0,14 m,ω
S=0,5t 2 Runter - - 1,76 0,20 d,t 1
S=1,5t 2 Runter - 0,6 0,24 9,9 - 0,10 m,ω
S=0,9t 2 Runter - 0,18 - 0,20 P, t 1
φ=10t 2 Runter - 0,20 1,92 - 0,20 P, t 1
S=t-1,25t 2 hoch - - - 0,25 P,d
φ=8t-20t 2 hoch - 0,20 - - 0,14 P, ω

Ausführungsbeispiel

Problem 1(Bild 1).

Lösung 1. Geradlinige Bewegung (Abbildung 1, a). Ein Punkt, der sich zu einem bestimmten Zeitpunkt gleichmäßig bewegte, erhielt ein neues Bewegungsgesetz und blieb nach einer bestimmten Zeit stehen. Bestimmen Sie alle kinematischen Eigenschaften der Punktbewegung für zwei Fälle; a) Bewegung auf einem geraden Weg; b) Bewegung entlang einer gekrümmten Bahn mit konstantem Krümmungsradius r=100cm

Abbildung 1(a).

Gesetz der Änderung der Punktgeschwindigkeit

Die Anfangsgeschwindigkeit des Punktes ermitteln wir aus der Bedingung:

Wir finden die Bremszeit, um aus der Bedingung anzuhalten:

at , von hier .

Bewegungsgesetz eines Punktes während einer Periode gleichförmiger Bewegung

Die vom Punkt entlang der Flugbahn während der Bremsperiode zurückgelegte Strecke beträgt

Gesetz der Änderung der Tangentialbeschleunigung eines Punktes

Daraus folgt, dass sich der Punkt während der Bremsperiode gleichermaßen langsam bewegte, da die Tangentialbeschleunigung negativ und von konstantem Wert ist.

Normale Beschleunigung Punkte auf einer geradlinigen Bewegungsbahn ist gleich Null, d.h. .

Lösung 2. Krummlinige Bewegung (Abbildung 1, b).

Abbildung 1(b)

In diesem Fall im Vergleich zum Fall geradlinige Bewegung Mit Ausnahme der normalen Beschleunigung bleiben alle kinematischen Eigenschaften unverändert.

Gesetz der Änderung der Normalbeschleunigung eines Punktes

Normale Beschleunigung eines Punktes im ersten Moment der Bremsung

Die in der Zeichnung akzeptierte Nummerierung der Punktpositionen auf der Flugbahn: 1 – aktuelle Position Punkte in gleichmäßiger Bewegung, bevor das Bremsen beginnt; 2 – Position des Punktes zum Zeitpunkt des Bremsens; 3 – aktuelle Position des Punktes während der Bremszeit; 4 – Endposition des Punktes.


Aufgabe 2.

Die Last (Abb. 2, a) wird mit einer Trommelwinde angehoben. Der Durchmesser der Trommel beträgt d=0,3 m und das Rotationsgesetz lautet .

Die Beschleunigung der Trommel dauerte bis zur Winkelgeschwindigkeit. Bestimmen Sie alle kinematischen Eigenschaften der Trommel- und Lastbewegung.

Lösung. Gesetz der Änderung der Trommelwinkelgeschwindigkeit. Die Anfangswinkelgeschwindigkeit ermitteln wir aus der Bedingung: ; daher begann die Beschleunigung aus dem Ruhezustand. Die Beschleunigungszeit ermitteln wir aus der Bedingung: . Trommeldrehwinkel während der Beschleunigungsperiode.

Aus dem Änderungsgesetz der Winkelbeschleunigung der Trommel folgt, dass sich die Trommel während der Beschleunigungsperiode mit gleichmäßiger Beschleunigung dreht.

Die kinematischen Eigenschaften der Last entsprechen den entsprechenden Eigenschaften eines beliebigen Punktes des Zugseils und damit des Punktes A, der auf dem Trommelrand liegt (Abb. 2, b). Bekanntlich werden die linearen Eigenschaften eines Punktes eines rotierenden Körpers durch seine Winkeleigenschaften bestimmt.

Die von der Last während der Beschleunigungsperiode zurückgelegte Strecke. Geschwindigkeit der Last am Ende der Beschleunigung.

Beschleunigung der Ladung.

Gesetz des Güterverkehrs.

Der Abstand, die Geschwindigkeit und die Beschleunigung der Last könnten durch das gefundene Bewegungsgesetz der Last unterschiedlich bestimmt werden:


Aufgabe 3. Die Last, die sich entlang einer geneigten Auflageebene gleichmäßig nach oben bewegte, wurde irgendwann gemäß dem neuen Bewegungsgesetz abgebremst , wobei s in Metern und t in Sekunden angegeben ist. Masse der Last m = 100 kg, Gleitreibungskoeffizient zwischen Last und Ebene f = 0,25. Bestimmen Sie die Kraft F und die Leistung am Zugseil für zwei Zeitpunkte: a) gleichmäßige Bewegung vor Beginn des Bremsens;

b) Anfangsmoment der Bremsung. Gehen Sie bei der Berechnung von g=10 m/ aus.

Lösung. Wir ermitteln die kinematischen Eigenschaften der Lastbewegung.

Gesetz der Änderung der Lastgeschwindigkeit

Anfangsgeschwindigkeit der Last (bei t=0)

Frachtbeschleunigung

Da die Beschleunigung negativ ist, ist die Bewegung langsam.

1. Gleichmäßige Bewegung der Last.

Um die Antriebskraft F zu bestimmen, betrachten wir das Gleichgewicht der Last, auf das ein System konvergierender Kräfte einwirkt: die Kraft auf das Seil F, die Schwerkraft der Last G=mg, normale Reaktion Auflagefläche N und Reibungskraft, die auf die Bewegung des Körpers gerichtet ist. Nach dem Reibungsgesetz gilt . Wir wählen die Richtung der Koordinatenachsen, wie in der Zeichnung dargestellt, und stellen zwei Gleichgewichtsgleichungen für die Belastung auf:

Die Leistung am Kabel vor Beginn des Bremsvorgangs wird nach der bekannten Formel ermittelt

Wo ist m/s.

2. Langsame Bewegung der Ladung.

Bekanntlich mit Unebenheiten Vorwärtsbewegung Körper ist das in Bewegungsrichtung auf ihn einwirkende Kräftesystem nicht ausgeglichen. Nach dem d'Alembert-Prinzip (kinetostatische Methode) kann in diesem Fall davon ausgegangen werden, dass sich der Körper im bedingten Gleichgewicht befindet, wenn wir zu allen auf ihn einwirkenden Kräften eine Trägheitskraft hinzufügen, deren Vektor dem Beschleunigungsvektor entgegengesetzt gerichtet ist. Der Beschleunigungsvektor ist in unserem Fall dem Geschwindigkeitsvektor entgegengesetzt gerichtet, da sich die Last langsam bewegt. Wir erstellen zwei Gleichgewichtsgleichungen für die Last:

Schalten Sie das Kabel zu Beginn des Bremsens ein

Kontrollfragen.

1. So ermitteln Sie numerischer Wert und die Richtung der Geschwindigkeit des Punktes im Moment?

2. Was charakterisiert die Normal- und Tangentialkomponente der Gesamtbeschleunigung?

3. Wie kommt man von der Angabe der Winkelgeschwindigkeit in min -1 zur Angabe in rad/s?

4. Wie nennt man das Körpergewicht? Nennen Sie die Maßeinheit für die Masse

5. Bei welcher Bewegung materieller Punkt entsteht Trägheitskraft? Welchen Zahlenwert hat sie und welche Richtung hat sie?

6. State-d'Alembert-Prinzip

7. Entsteht die Trägheitskraft bei der gleichmäßigen krummlinigen Bewegung eines materiellen Punktes?

8. Was ist Drehmoment?

9. Wie drückt sich der Zusammenhang zwischen Drehmoment und Winkelgeschwindigkeit bei gegebener übertragener Leistung aus?

10. Grundlegende Dynamikgleichung für Rotationsbewegungen.

Praktische Arbeit Nr. 7

„Berechnung von Tragwerken auf Festigkeit“

Ziel der Arbeit: Bestimmen Sie Festigkeit, Querschnittsabmessungen und zulässige Belastung

Theoretischer Hintergrund.

Wenn wir die Kraftfaktoren und geometrischen Eigenschaften des Abschnitts während der Zugverformung (Druckverformung) kennen, können wir die Spannung anhand der Formeln bestimmen. Und um zu verstehen, ob unser Teil (Welle, Zahnrad usw.) äußeren Belastungen standhält. Dieser Wert muss mit der zulässigen Spannung verglichen werden.

Also die statische Festigkeitsgleichung

Darauf aufbauend werden 3 Arten von Problemen gelöst:

1) Festigkeitstest

2) Bestimmung der Abschnittsabmessungen

3) Bestimmung der zulässigen Belastung

Also die Gleichung der statischen Steifigkeit

Darauf aufbauend werden auch 3 Arten von Problemen gelöst

Gleichung der statischen Zugfestigkeit (Druckfestigkeit).

1) Erster Typ – Festigkeitstest

,

d.h. wir lösen die linke Seite und vergleichen sie mit der zulässigen Spannung.

2) Zweiter Typ – Bestimmung der Abschnittsabmessungen

von der rechten Seite die Querschnittsfläche

Abschnittskreis

daher der Durchmesser d

Rechteckiger Abschnitt

Schnittquadrat

A = a² (mm²)

Halbkreisabschnitt

Abschnitte: Kanal, I-Träger, Winkel usw.

Flächenwerte - aus der Tabelle, akzeptiert nach GOST

3) Der dritte Typ ist die Bestimmung der zulässigen Belastung;

auf die kleinere Seite genommen, ganze Zahl

ÜBUNG

Aufgabe

A) Festigkeitsnachweis (Prüfberechnung)

Erstellen Sie für einen bestimmten Balken ein Diagramm der Längskräfte und überprüfen Sie die Festigkeit in beiden Abschnitten. Für Holzwerkstoff (Stahl St3) akzeptieren

Option Nr.
12,5 5,3 - -
2,3 - -
4,2 - -

B) Auswahl des Abschnitts (Entwurfsberechnung)

Erstellen Sie für einen bestimmten Balken ein Diagramm der Längskräfte und bestimmen Sie die Querschnittsabmessungen in beiden Abschnitten. Für Holzwerkstoff (Stahl St3) akzeptieren

Option Nr.
1,9 2,5
2,8 1,9
3,2

B) Bestimmung der zulässigen Längskraft

Bestimmen Sie für einen bestimmten Balken die zulässigen Werte der Lasten und ,

Erstellen Sie ein Diagramm der Längskräfte. Für Holzmaterial (Stahl St3) akzeptieren Sie . Gehen Sie bei der Lösung des Problems davon aus, dass die Belastungsart auf beiden Trägerabschnitten gleich ist.

Option Nr.
- -
- -
- -

Beispiel für die Erledigung einer Aufgabe

Problem 1(Bild 1).

Überprüfen Sie die Festigkeit einer Säule aus I-Profilen einer bestimmten Größe. Für das Säulenmaterial (Stahl St3) sind die zulässigen Zugspannungen zu berücksichtigen und während der Komprimierung . Wählen Sie im Falle einer Überlastung oder erheblichen Unterlast I-Trägergrößen aus, die eine optimale Stützenfestigkeit gewährleisten.

Lösung.

Ein gegebener Balken hat zwei Abschnitte 1, 2. Die Grenzen der Abschnitte sind die Abschnitte, in denen die äußere Kräfte. Da die den Balken belastenden Kräfte entlang seiner Mittellängsachse liegen, entsteht in den Querschnitten nur ein innerer Kraftfaktor – die Längskraft, d.h. Es liegt eine Spannung (Druck) des Balkens vor.

Zur Bestimmung der Längskraft verwenden wir die Schnittmethode. Indem wir in jedem Abschnitt gedanklich einen Abschnitt zeichnen, verwerfen wir den unteren festen Teil des Balkens und überlassen ihn der Betrachtung Oberer Teil. Im Abschnitt 1 ist die Längskraft konstant und gleich

Das Minuszeichen zeigt an, dass der Balken in beiden Abschnitten gestaucht ist.

Wir erstellen ein Diagramm der Längskräfte. Nachdem wir die Basislinie (Nulllinie) des Diagramms parallel zur Strahlachse gezeichnet haben, tragen wir die erhaltenen Werte senkrecht dazu in einem willkürlichen Maßstab ein. Wie Sie sehen können, wurde das Diagramm durch gerade Linien parallel zur Basis umrissen.

Wir prüfen die Festigkeit des Holzes, d.h. Wir ermitteln die Bemessungsspannung (für jeden Abschnitt separat) und vergleichen sie mit der zulässigen. Dazu verwenden wir die Druckfestigkeitsbedingung

wobei die Fläche ein geometrisches Merkmal der Stärke des Querschnitts ist. Aus der Walzstahltabelle nehmen wir:

für I-Träger
für I-Träger

Krafttest:

Die Werte der Längskräfte werden in Absolutwerten angenommen.

Die Festigkeit des Trägers ist gewährleistet, allerdings kommt es zu einer erheblichen Unterlast (mehr als 25 %), die aufgrund des übermäßigen Materialverbrauchs nicht akzeptabel ist.

Aus der Festigkeitsbedingung ermitteln wir die neuen Abmessungen des I-Trägers für jeden Abschnitt des Trägers:
Daher die benötigte Fläche

Gemäß der GOST-Tabelle wählen wir I-Träger Nr. 16, für den;

Daher die benötigte Fläche

Gemäß der GOST-Tabelle wählen wir I-Träger Nr. 24, für den ;

Bei den gewählten I-Trägergrößen tritt auch eine Unterlast auf, die jedoch unbedeutend ist (weniger als 5 %).

Aufgabe Nr. 2.

Bestimmen Sie für einen Balken mit gegebenen Querschnittsabmessungen die zulässigen Belastungswerte und . Bei Holzwerkstoff (Stahl St3) zulässige Zugspannungen berücksichtigen und während der Komprimierung .

Lösung.

Der gegebene Balken besteht aus zwei Abschnitten 1, 2. Der Balken unterliegt einer Spannung (Druck).

Mit der Schnittmethode ermitteln wir die Längskraft, indem wir sie durch die erforderlichen Kräfte ausdrücken und. Indem wir innerhalb jedes Abschnitts einen Abschnitt ausführen, verwerfen wir den linken Teil des Balkens und überlassen ihn der Betrachtung rechte Seite. Im Abschnitt 1 ist die Längskraft konstant und gleich

Im Abschnitt 2 ist die Längskraft ebenfalls konstant und gleich

Das Pluszeichen zeigt an, dass der Balken in beiden Abschnitten gestreckt ist.

Wir erstellen ein Diagramm der Längskräfte. Das Diagramm wird durch gerade Linien parallel zur Basis dargestellt.

Aus dem Zustand der Zugfestigkeit ermitteln wir die zulässigen Belastungswerte und berechnen zuvor die Flächen der gegebenen Querschnitte:

Kontrollfragen.

1. Welche Schnittgrößen entstehen im Balkenquerschnitt bei Zug und Druck?

2. Notieren Sie die Zug- und Druckfestigkeitsbedingungen.

3. Wie werden die Zeichen von Längskraft und Normalspannung zugeordnet?

4. Wie ändert sich die Spannung, wenn sich die Querschnittsfläche um das Vierfache vergrößert?

5. Unterscheiden sich die Festigkeitsbedingungen bei Zug- und Druckberechnungen?

6. In welchen Einheiten wird die Spannung gemessen?

7. Welches mechanische Eigenschaften als höchste Belastung für duktile und spröde Materialien gewählt?

8. Was ist der Unterschied zwischen Grenz- und zulässiger Belastung?

Praktische Arbeit Nr. 8

„Lösen von Problemen zur Bestimmung der wichtigsten zentralen Trägheitsmomente flacher geometrischer Figuren“

Ziel der Arbeit: Bestimmen Sie analytisch die Trägheitsmomente flacher Körper komplexer Form

Theoretischer Hintergrund. Die Koordinaten des Schwerpunkts des Abschnitts können durch das statische Moment ausgedrückt werden:

wo relativ zur Ox-Achse

relativ zur Oy-Achse

Das statische Moment der Fläche einer Figur relativ zu einer in derselben Ebene liegenden Achse ist gleich dem Produkt aus der Fläche der Figur und dem Abstand ihres Schwerpunkts zu dieser Achse. Das statische Moment hat eine Dimension. Das statische Moment kann positiv, negativ oder gleich Null sein (relativ zu einer beliebigen Mittelachse).

Das axiale Trägheitsmoment eines Abschnitts ist die Summe der Produkte oder Integrale von Elementarflächen über den gesamten Abschnitt mit den Quadraten ihrer Abstände zu einer bestimmten Achse, die in der Ebene des betrachteten Abschnitts liegt.

Axiales Moment Trägheit wird in Einheiten ausgedrückt - . Das axiale Trägheitsmoment ist eine Größe, die immer positiv und ungleich Null ist.

Die durch den Schwerpunkt der Figur verlaufenden Achsen werden als Zentralachsen bezeichnet. Das Trägheitsmoment um die Mittelachse wird Zentralträgheitsmoment genannt.

Das Trägheitsmoment um jede Achse ist gleich dem Mittelpunkt

Zeichnen Sie ein Diagramm des Systems und markieren Sie darauf den Schwerpunkt. Liegt der gefundene Schwerpunkt außerhalb des Objektsystems, haben Sie eine falsche Antwort erhalten. Möglicherweise haben Sie Entfernungen von verschiedenen Referenzpunkten gemessen. Wiederholen Sie die Messungen.

  • Wenn Kinder beispielsweise auf einer Schaukel sitzen, liegt der Schwerpunkt irgendwo zwischen den Kindern und nicht rechts oder links von der Schaukel. Außerdem wird der Schwerpunkt nie mit dem Punkt übereinstimmen, an dem das Kind sitzt.
  • Diese Argumente gelten im zweidimensionalen Raum. Zeichnen Sie ein Quadrat, das alle Objekte des Systems enthält. Der Schwerpunkt sollte innerhalb dieses Quadrats liegen.

Überprüfen Sie Ihre Mathematik, wenn Sie ein kleines Ergebnis erhalten. Wenn der Referenzpunkt an einem Ende des Systems liegt, liegt der Schwerpunkt bei einem kleinen Ergebnis nahe am Ende des Systems. Dies mag die richtige Antwort sein, aber in den allermeisten Fällen weist dieses Ergebnis auf einen Fehler hin. Haben Sie bei der Berechnung der Momente die entsprechenden Gewichte und Abstände multipliziert? Wenn Sie statt der Multiplikation die Gewichte und Abstände addieren würden, würden Sie ein viel kleineres Ergebnis erhalten.

Korrigieren Sie den Fehler, wenn Sie mehrere Schwerpunkte gefunden haben. Jedes System hat nur einen Schwerpunkt. Wenn Sie mehrere Schwerpunkte gefunden haben, haben Sie höchstwahrscheinlich nicht alle Momente addiert. Schwerpunkt gleich dem Verhältnis„Gesamtmoment“ zu „Gesamtgewicht“. Es ist nicht nötig, „jeden“ Moment durch „jedes“ Gewicht zu dividieren: Auf diese Weise finden Sie die Position jedes Objekts.

  • Überprüfen Sie den Referenzpunkt, wenn die Antwort um einen ganzzahligen Wert abweicht. In unserem Beispiel ist die Antwort 3,4 m. Nehmen wir an, Sie haben die Antwort 0,4 m oder 1,4 m oder eine andere Zahl erhalten, die auf „.4“ endet. Dies liegt daran, dass Sie nicht das linke Ende des Bretts als Ausgangspunkt gewählt haben, sondern einen Punkt, der ein ganzes Stück rechts liegt. Tatsächlich ist Ihre Antwort richtig, egal welchen Bezugspunkt Sie wählen! Denken Sie daran: Der Referenzpunkt befindet sich immer an der Position x = 0. Hier ein Beispiel:

    • In unserem Beispiel befand sich der Referenzpunkt am linken Ende des Bretts und wir stellten fest, dass der Schwerpunkt 3,4 m von diesem Referenzpunkt entfernt lag.
    • Wenn Sie als Bezugspunkt einen Punkt wählen, der 1 m rechts vom linken Ende der Tafel liegt, erhalten Sie als Antwort 2,4 m. Das heißt, der Schwerpunkt liegt 2,4 m vom neuen Bezugspunkt entfernt , wiederum befindet sich 1 m vom linken Ende der Tafel entfernt. Somit liegt der Schwerpunkt in einem Abstand von 2,4 + 1 = 3,4 m vom linken Ende des Bretts. Es stellte sich heraus, dass es sich um eine alte Antwort handelte!
    • Hinweis: Beachten Sie beim Messen von Entfernungen, dass die Entfernungen zum „linken“ Referenzpunkt negativ und zum „rechten“ Referenzpunkt positiv sind.

  • Messen Sie Entfernungen in geraden Linien. Angenommen, es sitzen zwei Kinder auf einer Schaukel, aber ein Kind ist viel größer als das andere, oder ein Kind hängt unter dem Brett, anstatt darauf zu sitzen. Ignorieren Sie diesen Unterschied und messen Sie die Abstände entlang der geraden Linie der Platine. Das Messen von Entfernungen in Winkeln führt zu ähnlichen, aber nicht ganz genauen Ergebnissen.

    • Denken Sie beim Problem mit dem Wippbrett daran, dass der Schwerpunkt zwischen dem rechten und dem linken Ende des Bretts liegt. Später lernen Sie, den Schwerpunkt komplexerer zweidimensionaler Systeme zu berechnen.

    • Autor: Nehmen wir einen Körper beliebiger Form. Ist es möglich, es an einem Faden aufzuhängen, damit es nach dem Aufhängen seine Position beibehält (d. h. nicht anfängt, sich zu drehen), wenn beliebig Erstorientierung (Abb. 27.1)?

    Mit anderen Worten: Gibt es einen Punkt, relativ zu dem die Summe der auf verschiedene Körperteile wirkenden Schwerkraftmomente gleich Null wäre? beliebig Körperorientierung im Raum?

    Leser: Ja, ich denke schon. Dieser Punkt heißt Schwerpunkt des Körpers.

    Nachweisen. Betrachten wir der Einfachheit halber einen Körper in Form einer flachen Platte beliebiger Form, beliebig im Raum ausgerichtet (Abb. 27.2). Nehmen wir das Koordinatensystem X 0bei mit dem Anfang im Massenschwerpunkt - Punkt MIT, Dann x C = 0, bei C = 0.

    Stellen wir uns diesen Körper als eine Sammlung vor große Zahl Punktmassen m i, deren Position jeweils durch den Radiusvektor angegeben wird.

    Per Definition ist der Schwerpunkt und die Koordinate x C = .

    Da wir das Koordinatensystem übernommen haben x C= 0, dann . Multiplizieren wir diese Gleichheit mit G und wir bekommen

    Wie aus Abb. ersichtlich ist. 27,2, | x i| - Das ist die Schulter der Macht. Und wenn x i> 0, dann das Kraftmoment M i> 0, und wenn x j < 0, то Mj < 0, поэтому с учетом знака можно утверждать, что для любого x i das Kraftmoment wird gleich sein M i = m i gx i . Dann ist Gleichheit (1) äquivalent zu Gleichheit, wobei M i– Moment der Schwerkraft. Dies bedeutet, dass bei beliebiger Ausrichtung des Körpers die Summe der auf den Körper einwirkenden Schwerkraftmomente relativ zu seinem Massenschwerpunkt gleich Null ist.

    Damit der Körper, den wir betrachten, im Gleichgewicht ist, ist es notwendig, den Punkt auf ihn anzuwenden MIT Gewalt T = mg, senkrecht nach oben gerichtet. Das Moment dieser Kraft relativ zum Punkt MIT gleich Null.

    Da unsere Überlegungen in keiner Weise davon abhingen, wie genau der Körper im Raum ausgerichtet ist, haben wir bewiesen, dass der Schwerpunkt mit dem Massenschwerpunkt zusammenfällt, was wir beweisen mussten.

    Aufgabe 27.1. Finden Sie den Schwerpunkt eines schwerelosen Stabs der Länge l, an deren Enden zwei Punktmassen befestigt sind T 1 und T 2 .

    T 1 T 2 l Lösung. Wir werden nicht nach dem Schwerpunkt suchen, sondern nach dem Massenschwerpunkt (da dies dasselbe ist). Lassen Sie uns die Achse vorstellen X(Abb. 27.3). Reis. 27.3
    x C =?

    Antwort: im Abstand von der Masse T 1 .

    STOPPEN! Entscheiden Sie selbst: B1–B3.

    Aussage 1 . Wenn ein homogener flacher Körper eine Symmetrieachse hat, liegt der Schwerpunkt auf dieser Achse.

    Tatsächlich für jede Punktmasse m i, rechts von der Symmetrieachse gelegen, befindet sich die gleiche Punktmasse symmetrisch zur ersten (Abb. 27.4). In diesem Fall ist die Summe der Kraftmomente .

    Da der gesamte Körper in gleichartige Punktpaare unterteilt dargestellt werden kann, ist das Gesamtschwerkraftmoment relativ zu jedem Punkt, der auf der Symmetrieachse liegt, gleich Null, was bedeutet, dass der Schwerpunkt des Körpers auf dieser Achse liegt . Dies führt zu einer wichtigen Schlussfolgerung: Besitzt ein Körper mehrere Symmetrieachsen, so liegt der Schwerpunkt im Schnittpunkt dieser Achsen(Abb. 27.5).

    Reis. 27.5

    Aussage 2. Wenn zwei Körper Massen haben T 1 und T Wenn zwei Körper zu einem verbunden sind, liegt der Schwerpunkt eines solchen Körpers auf einem geraden Liniensegment, das die Schwerpunkte des ersten und zweiten Körpers verbindet (Abb. 27.6).

    Reis. 27.6 Reis. 27.7

    Nachweisen. Positionieren wir den zusammengesetzten Körper so, dass das Segment, das die Schwerpunkte der Körper verbindet, vertikal ist. Dann die Summe der Schwerkraftmomente des ersten Körpers relativ zum Punkt MIT 1 ist gleich Null und die Summe der Schwerkraftmomente des zweiten Körpers relativ zum Punkt MIT 2 ist gleich Null (Abb. 27.7).

    beachte das Schulter Schwerkraft einer beliebigen Punktmasse t i das Gleiche gilt für jeden Punkt, der auf dem Segment liegt MIT 1 MIT 2 und damit das Schwerkraftmoment relativ zu jedem auf dem Segment liegenden Punkt MIT 1 MIT 2, das Gleiche. Folglich ist die Schwerkraft des gesamten Körpers relativ zu jedem Punkt auf dem Segment Null MIT 1 MIT 2. Somit liegt der Schwerpunkt des Verbundkörpers auf dem Segment MIT 1 MIT 2 .

    Eine wichtige praktische Schlussfolgerung ergibt sich aus Aussage 2, die klar in Form einer Anleitung formuliert ist.

    Anweisungen,

    Wie findet man den Schwerpunkt eines festen Körpers, wenn dieser zerbrochen werden kann?

    in Teile zerlegen, wobei die Lage der Schwerpunkte jedes einzelnen bekannt ist

    1. Jedes Teil sollte durch eine Masse ersetzt werden, die sich im Schwerpunkt dieses Teils befindet.

    2. Finden Massezentrum(und das ist dasselbe wie der Schwerpunkt) des resultierenden Systems von Punktmassen, wobei ein geeignetes Koordinatensystem gewählt wird X 0bei, nach den Formeln:

    In der Tat ordnen wir den zusammengesetzten Körper so an, dass er segmentiert ist MIT 1 MIT 2 war horizontal und hängte es punktuell an Fäden auf MIT 1 und MIT 2 (Abb. 27.8, A). Es ist klar, dass der Körper im Gleichgewicht sein wird. Und dieses Gleichgewicht wird nicht gestört, wenn wir jeden Körper durch Punktmassen ersetzen T 1 und T 2 (Abb. 27.8, B).

    Reis. 27.8

    STOPPEN! Entscheiden Sie selbst: C3.

    Aufgabe 27.2. Auf zwei Gipfeln gleichseitiges Dreieck Massenkugeln werden platziert T jeden. Am dritten Scheitelpunkt wird eine Kugel mit der Masse 2 platziert T(Abb. 27.9, A). Dreiecksseite A. Bestimmen Sie den Schwerpunkt dieses Systems.

    T 2T A Reis. 27.9
    x C = ? bei C = ?

    Lösung. Lassen Sie uns das Koordinatensystem vorstellen X 0bei(Abb. 27.9, B). Dann

    ,

    .

    Antwort: x C = A/2; ; Der Schwerpunkt liegt auf halber Höhe ANZEIGE.



    Lesen Sie auch:

    Kategorien:

    Beliebt: