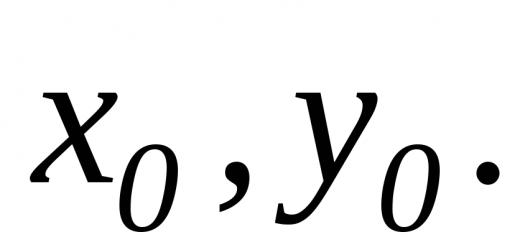Newton's law of universal gravitation allows us to measure one of the most important physical characteristics of a celestial body - its mass.

Mass can be determined:

a) from measurements of gravity on the surface of a given body (gravimetric method),

b) according to Kepler’s third refined law,

c) from the analysis of observed disturbances produced by a celestial body in the movements of other celestial bodies.

1. The first method is used on Earth.

Based on the law of gravity, the acceleration g on the Earth's surface is:

where m is the mass of the Earth, and R is its radius.

g and R are measured at the Earth's surface. G = const.

With the currently accepted values ​​of g, R, G, the mass of the Earth is obtained:

m = 5.976.1027g = 6.1024kg.

Knowing the mass and volume, you can find the average density. It is equal to 5.5 g/cm3.

2. According to Kepler’s third law, it is possible to determine the relationship between the mass of the planet and the mass of the Sun if the planet has at least one satellite and its distance from the planet and the period of revolution around it are known.

where M, m, mc are the masses of the Sun, the planet and its satellite, T and tc are the periods of revolution of the planet around the Sun and the satellite around the planet, A And ac- the distances of the planet from the Sun and the satellite from the planet, respectively.

From the equation it follows

The M/m ratio for all planets is very high; the ratio m/mc is very small (except for the Earth and the Moon, Pluto and Charon) and can be neglected.

The M/m ratio can be easily found from the equation.

For the case of the Earth and the Moon, you must first determine the mass of the Moon. This is very difficult to do. The problem is solved by analyzing the disturbances in the movement of the Earth that the Moon causes.

3. By precise determinations of the apparent positions of the Sun in its longitude, changes with a monthly period, called “lunar inequality,” were discovered. The presence of this fact in the apparent motion of the Sun indicates that the center of the Earth describes a small ellipse during the month around the common center of mass "Earth - Moon", located inside the Earth, at a distance of 4650 km. from the center of the Earth.

The position of the Earth-Moon center of mass was also found from observations of the small planet Eros in 1930 - 1931.

Based on disturbances in the movements of artificial Earth satellites, the ratio of the masses of the Moon and the Earth turned out to be 1/81.30.

In 1964, the International Astronomical Union adopted it as const.

From the Kepler equation we obtain for the Sun a mass = 2.1033g, which is 333,000 times greater than that of the Earth.

The masses of planets that do not have satellites are determined by the disturbances they cause in the movement of the Earth, Mars, asteroids, comets, and by the disturbances they produce on each other.

One of the striking examples of the triumph of the law of universal gravitation is the discovery of the planet Neptune. In 1781, the English astronomer William Herschel discovered the planet Uranus. Its orbit was calculated and a table of the positions of this planet was compiled for many years to come. However, a check of this table, carried out in 1840, showed that its data diverges from reality.

Scientists have suggested that the deviation in the movement of Uranus is caused by the attraction of an unknown planet located even further from the Sun than Uranus. Knowing the deviations from the calculated trajectory (disturbances in the movement of Uranus), the Englishman Adams and the Frenchman Leverrier, using the law of universal gravitation, calculated the position of this planet in the sky. Adams finished his calculations early, but the observers to whom he reported his results were in no hurry to check. Meanwhile, Leverrier, having completed his calculations, indicated to the German astronomer Halle the place where to look for the unknown planet. On the very first evening, September 28, 1846, Halle, pointing the telescope at the indicated location, discovered a new planet. She was named Neptune.

In the same way, the planet Pluto was discovered on March 14, 1930. The discovery of Neptune, made, as Engels put it, “at the tip of a pen,” is the most convincing proof of the validity of Newton’s law of universal gravitation.

Using the law of universal gravitation, you can calculate the mass of planets and their satellites; explain phenomena such as the ebb and flow of water in the oceans, and much more.

The forces of universal gravity are the most universal of all the forces of nature. They act between any bodies that have mass, and all bodies have mass. There are no barriers to the forces of gravity. They act through any body.

Determination of the mass of celestial bodies

Newton's law of universal gravitation allows us to measure one of the most important physical characteristics of a celestial body - its mass.

The mass of a celestial body can be determined:

a) from measurements of gravity on the surface of a given body (gravimetric method);

b) according to Kepler’s third (refined) law;

c) from the analysis of observed disturbances produced by a celestial body in the movements of other celestial bodies.

The first method is applicable only to Earth for now, and is as follows.

Based on the law of gravitation, the acceleration of gravity on the Earth's surface is easily found from formula (1.3.2).

The acceleration of gravity g (more precisely, the acceleration of the component of gravity due only to the force of gravity), as well as the radius of the Earth R, is determined from direct measurements on the Earth's surface. The gravitational constant G was determined quite accurately from the experiments of Cavendish and Jolly, well known in physics.

With the currently accepted values ​​of g, R and G, formula (1.3.2) yields the mass of the Earth. Knowing the mass of the Earth and its volume, it is easy to find the average density of the Earth. It is equal to 5.52 g/cm3

The third, refined Kepler's law allows us to determine the relationship between the mass of the Sun and the mass of the planet if the latter has at least one satellite and its distance from the planet and the period of revolution around it are known.

Indeed, the motion of a satellite around a planet is subject to the same laws as the motion of a planet around the Sun and, therefore, Kepler’s third equation can be written in this case as follows:

where M is the mass of the Sun, kg;

t - mass of the planet, kg;

m c - satellite mass, kg;

T is the period of revolution of the planet around the Sun, s;

t c is the period of revolution of the satellite around the planet, s;

a - distance of the planet from the Sun, m;

a c is the distance of the satellite from the planet, m;

Dividing the numerator and denominator of the left-hand side of the fraction of this equation pa t and solving it for masses, we get

The ratio for all planets is very high; the ratio, on the contrary, is small (except for the Earth and its satellite the Moon) and can be neglected. Then in equation (2.2.2) there will only be one unknown relation left, which can be easily determined from it. For example, for Jupiter the inverse ratio determined in this way is 1: 1050.

Since the mass of the Moon, the only satellite of the Earth, is quite large compared to the mass of the Earth, the ratio in equation (2.2.2) cannot be neglected. Therefore, to compare the mass of the Sun with the mass of the Earth, it is necessary to first determine the mass of the Moon. Accurately determining the mass of the Moon is a rather difficult task, and it is solved by analyzing those disturbances in the Earth's motion that are caused by the Moon.

Under the influence of lunar gravity, the Earth must describe an ellipse around the common center of mass of the Earth-Moon system within a month.

By accurately determining the apparent positions of the Sun in its longitude, changes with a monthly period, called “lunar inequality,” were discovered. The presence of a “lunar inequality” in the apparent motion of the Sun indicates that the center of the Earth actually describes a small ellipse during the month around the common center of mass “Earth-Moon”, located inside the Earth, at a distance of 4650 km from the center of the Earth. This made it possible to determine the ratio of the mass of the Moon to the mass of the Earth, which turned out to be equal. The position of the center of mass of the Earth-Moon system was also found from observations of the small planet Eros in 1930-1931. These observations gave a value for the ratio of the masses of the Moon and the Earth. Finally, based on disturbances in the movements of artificial Earth satellites, the ratio of the masses of the Moon and the Earth turned out to be equal. The latter value is the most accurate, and in 1964 the International Astronomical Union accepted it as the final value among other astronomical constants. This value was confirmed in 1966 by calculating the mass of the Moon from the rotation parameters of its artificial satellites.

With the known ratio of the masses of the Moon and the Earth from equation (2.26), it turns out that the mass of the Sun is M ? 333,000 times the mass of the Earth, i.e.

Mz = 2 10 33 g.

Knowing the mass of the Sun and the ratio of this mass to the mass of any other planet that has a satellite, it is easy to determine the mass of this planet.

The masses of planets that do not have satellites (Mercury, Venus, Pluto) are determined from an analysis of the disturbances that they produce in the movement of other planets or comets. So, for example, the masses of Venus and Mercury are determined by the disturbances that they cause in the movement of the Earth, Mars, some small planets (asteroids) and the comet Encke-Backlund, as well as by the disturbances they produce on each other.

earth planet universe gravity

Mass is one of the most important characteristics of celestial bodies. But how can you determine the mass of a celestial body? Newton proved that a more accurate formula for Kepler's third law is:

where M 1 and M 2 are the masses of any celestial bodies, and m 1 and m 2 are, respectively, the masses of their satellites. In particular, the planets are satellites of the Sun. We see that the refined formula of this law differs from the approximate one by the presence of a factor containing masses. If by M 1 = M 2 = M we mean the mass of the Sun, and by m 1 and m 2 the masses of two different planets, then the ratio

will differ little from unity, since m 1 and m 2 are very small compared to the mass of the Sun. In this case, the exact formula will not differ noticeably from the approximate one.

Kepler's refined third law allows us to determine the masses of planets with satellites and the mass of the Sun. To determine the mass of the Sun, we rewrite the formula of this law in the following form, comparing the movement of the Moon around the Earth with the movement of the Earth around the Sun:

where T z i a z is the period of revolution of the Earth (year) and the semi-major axis of its orbit, T l and a l is the period of revolution of the Moon around the Earth and the semi-major axis of its orbit, M c is the mass of the Sun, M z is the mass of the Earth, m l - mass of the Moon. The mass of the Earth is insignificant compared to the mass of the Sun, and the mass of the Moon is small (1:81) compared to the mass of the Earth. Therefore, the second terms in the sums can be discarded without making a big mistake. Having solved the equation for M c / M z we have:

This formula allows you to determine the mass of the Sun, expressed in masses of the Earth. It is about 333,000 Earth masses.

To compare the masses of the Earth and another planet, for example Jupiter, in the original formula index 1 must be attributed to the movement of the Moon around the Earth with mass M 1 and 2 - to the movement of any satellite around Jupiter with mass M 2.

The masses of planets that do not have satellites are determined by the disturbances that their attraction produces in the movement of neighboring planets or in the movement of comets and asteroids.

1. Determine the mass of Jupiter by comparing the Jupiter system with a satellite with the Earth - Moon system, if the first satellite of Jupiter is 422,000 km away from it and has an orbital period of 1.77 days. The data for the Moon should be known to you.
2. Calculate at what distance from the Earth on the Earth - Moon line there are those points at which the attractions of the Earth and the Moon are equal, knowing that the distance between the Moon and the Earth is equal to 60 radii of the Earth, and the masses of the Earth and the Moon are in the ratio 81: 1.

The mass of the Sun can be found from the condition that the Earth’s gravity towards the Sun manifests itself as a centripetal force that holds the Earth in its orbit (for simplicity, we will consider the Earth’s orbit to be a circle)

Here is the mass of the Earth, the average distance of the Earth from the Sun. Denoting the length of the year in seconds through we have. Thus

from where, substituting numerical values, we find the mass of the Sun:

The same formula can be applied to calculate the mass of any planet that has a satellite. In this case, the average distance of the satellite from the planet, the time of its revolution around the planet, the mass of the planet. In particular, by the distance of the Moon from the Earth and the number of seconds in a month, the mass of the Earth can be determined using the indicated method.

The mass of the Earth can also be determined by equating the weight of a body to the gravitation of this body towards the Earth, minus that component of gravity that manifests itself dynamically, imparting to a given body participating in the daily rotation of the Earth a corresponding centripetal acceleration (§ 30). The need for this correction disappears if, for such a calculation of the mass of the Earth, we use the acceleration of gravity that is observed at the poles of the Earth. Then, denoting by the average radius of the Earth and by the mass of the Earth, we have:

where does the earth's mass come from?

If the average density of the globe is denoted by then, obviously, Hence the average density of the globe is equal to

The average density of mineral rocks in the upper layers of the Earth is approximately Therefore, the core of the globe must have a density significantly exceeding

The study of the density of the Earth at various depths was undertaken by Legendre and continued by many scientists. According to the conclusions of Gutenberg and Haalck (1924), approximately the following values ​​of the Earth's density occur at various depths:

The pressure inside the globe, at great depths, is apparently enormous. Many geophysicists believe that already at depth the pressure should reach atmospheres per square centimeter. In the Earth's core, at a depth of about 3000 kilometers or more, the pressure may reach 1-2 million atmospheres.

As for the temperature in the depths of the globe, it is certain that it is higher (the temperature of lava). In mines and boreholes, the temperature rises on average by one degree for every one. It is assumed that at a depth of about 1500-2000 ° and then remains constant.

Rice. 50. Relative sizes of the Sun and planets.

The complete theory of planetary motion, set forth in celestial mechanics, makes it possible to calculate the mass of a planet from observations of the influence that a given planet has on the motion of some other planet. At the beginning of the last century, the planets Mercury, Venus, Earth, Mars, Jupiter, Saturn, and Uranus were known. It was observed that the motion of Uranus exhibited some "irregularities" which indicated that there was an unobserved planet behind Uranus influencing the motion of Uranus. In 1845, the French scientist Le Verrier and, independently of him, the Englishman Adams, having studied the movement of Uranus, calculated the mass and location of the planet, which no one had yet observed. Only after this the planet was found in the sky exactly in the place indicated by the calculations; this planet was named Neptune.

In 1914, astronomer Lovell similarly predicted the existence of another planet even further from the Sun than Neptune. Only in 1930 this planet was found and named Pluto.

Basic information about the major planets

(see scan)

The table below contains basic information about the nine major planets of the solar system. Rice. 50 illustrates the relative sizes of the Sun and planets.

In addition to the listed large planets, about 1,300 very small planets, so-called asteroids (or planetoids), are known. Their orbits are mainly located between the orbits of Mars and Jupiter.

Delitant 75 · 03-10-2014

Masses of celestial bodies (methods of determination)
The basis for determining the masses of celestial bodies is the law of universal gravitation, expressed by:
$F=Gcdot((mathfrak M)_1(mathfrak M)_2over (r^2))$ (1)
where F is the force of mutual attraction of the masses $(mathfrak M)_1$ and $(mathfrak M)_2$, proportional to their product and inversely proportional to the square of the distance r between their centers. In astronomy, it is often (but not always) possible to neglect the size of the celestial bodies themselves in comparison with the distances separating them, the difference in their shape from an exact sphere, and to liken celestial bodies to material points in which all their mass is concentrated.
Proportionality coefficient G =$6.67cdot 10^(-8) mbox(cm)^3cdot mbox(g)^(-1)cdot mbox(s)^(-2)$ called. gravitational constant or constant of gravity. It is found from a physical experiment with torsion balances, which make it possible to determine the force of gravity. interactions of bodies of known mass.
In the case of free falling bodies, the force F acting on the body is equal to the product of the mass of the body $(mathfrak M)$ and the acceleration of free fall g. Acceleration g can be determined, for example, by the period T of oscillations of a vertical pendulum: $T=2pisqrt(l/g)$, where l is the length of the pendulum. At latitude 45o and at sea level g= 9.806 m/s2.
Substituting the expression for the forces of gravity $F=(mathfrak M)cdot g$ into formula (1) leads to the dependence $g=G(mathfrak M)_oplus/R_oplus^2$, where $(mathfrak M)_oplus$ - the mass of the Earth, and $R_oplus$ is the radius of the globe. In this way, the mass of the Earth was determined $(mathfrak M)_oplusapprox 6.0cdot 10^(27)$ g. Determination of the mass of the Earth yavl. the first link in the chain of determining the masses of other celestial bodies (Sun, Moon, planets, and then stars). The masses of these bodies are found based either on Kepler's 3rd law (see Kepler's laws), or on the rule: distances of k.-l. masses from the general center of mass are inversely proportional to the masses themselves. This rule allows you to determine the mass of the Moon. From measurements of the exact coordinates of the planets and the Sun, it was found that the Earth and the Moon with a period of one month move around the barycenter - the center of mass of the Earth - Moon system. The distance of the center of the Earth from the barycenter is 0.730 $R_oplus$ (it is located inside the globe). Wed. The distance of the center of the Moon from the center of the Earth is 60.08 $R_oplus$. Hence the ratio of the distances of the centers of the Moon and the Earth from the barycenter is 1/81.3. Since this ratio is the inverse of the ratio of the masses of the Earth and the Moon, the mass of the Moon
$(mathfrak M)_Л=(mathfrak M)_oplus/81.3approx 7.35cdot 10^(25)$ g.
The mass of the Sun can be determined by applying Kepler's 3rd law to the motion of the Earth (along with the Moon) around the Sun and the motion of the Moon around the Earth:
$(a_oplus^3over (T_oplus^2((mathfrak M)_odot+(mathfrak M)_oplus)))=(a_(L)^3over (T_(L)^2((mathfrak M)_oplus+(mathfrak M)_( L))))$ , (2)
where a are the semimajor axes of the orbits, T are the periods (stellar or sidereal) of revolution. Neglecting $(mathfrak M)_oplus$ in comparison with $(mathfrak M)_odot$, we obtain the ratio $(mathfrak M)_odot/((mathfrak M)_oplus+(mathfrak M)_(L))$ equal to 329390. Hence $ (mathfrak M)_odotapprox 3.3cdot 10^(33)$ g, or approx. $3.3cdot 10^5 (mathfrak M)_oplus$.
The masses of planets with satellites are determined in a similar way. The masses of planets that do not have satellites are determined by the disturbances they exert on the motion of their neighboring planets. The theory of perturbed planetary motion made it possible to suspect the existence of the then unknown planets Neptune and Pluto, to find their masses, and to predict their position in the sky.
The mass of a star (besides the Sun) can be determined with relatively high reliability only if it is physical component of a visual double star (see Double Stars), the distance to the cut is known. Kepler's third law in this case gives the sum of the masses of the components (in units $(mathfrak M)_odot$):
$(mathfrak M)_1+(mathfrak M)_2=((a"")^3over ((pi"")^3))cdot (1over(P^2))$ ,
where a"" is the semimajor axis (in arc seconds) of the true orbit of the satellite around the main (usually brighter) star, which in this case is considered stationary, P is the orbital period in years, $pi""$ is the parallax of the system (in seconds of arc). The value $a""/pi""$ gives the semi-major axis of the orbit in a. e. If it is possible to measure the angular distances of $ ho$ components from the common center of mass, then their ratio will give a value inverse to the mass ratio: $ ho_1/ ho_2=(mathfrak M)_2/(mathfrak M)_1$. The found sum of masses and their ratio make it possible to obtain the mass of each star separately. If the components of a binary have approximately the same brightness and similar spectra, then the half-sum of masses $((mathfrak M)_1+(mathfrak M)_2)/2$ gives a correct estimate of the mass of each component without addition. determining their relationship.
For other types of double stars (eclipsing binaries and spectroscopic binaries), there are a number of possibilities to approximately determine the masses of stars or estimate their lower limit (i.e., the values ​​​​below which their masses cannot be).
The totality of data on the masses of the components of approximately one hundred binary stars of different types made it possible to discover important statistical data. the relationship between their masses and luminosities (see Mass-luminosity relationship). It makes it possible to estimate the masses of single stars by their luminosities (in other words, by their absolute magnitudes). Abs. stellar magnitudes M are determined by the formula: M = m + 5 + 5 log $pi$ - A(r) , (3) where m is the apparent stellar magnitude in the selected optical. range (in a certain photometric system, for example U, B or V; see Astrophotometry), $pi$ - parallax and A(r) - the amount of interstellar absorption of light in the same optical range. range in a given direction up to a distance of $r=1/pi$.
If the parallax of the star is not measured, then the approximate value of abs. stellar magnitude can be determined by its spectrum. To do this, it is necessary that the spectrogram allows not only to find out the spectral class of the star, but also to estimate the relative intensities of certain spectrum pairs. lines sensitive to the "absolute magnitude effect". In other words, it is first necessary to determine the luminosity class of a star - whether it belongs to one of the sequences on the spectrum-luminosity diagram (see Hertzsprung-Russell diagram), and by luminosity class - its absolute value. size. According to the abs. obtained in this way. magnitude, you can find the mass of the star using the mass-luminosity relationship (only white dwarfs and pulsars do not obey this relationship).
Another method for estimating the mass of a star involves measuring gravity. redshift spectrum. lines in its gravitational field. In a spherically symmetric gravitational field, it is equivalent to the Doppler redshift $Delta v_r=0.635 (mathfrak M)/R$, where $(mathfrak M)$ is the mass of the star in units. mass of the Sun, R is the radius of the star in units. radius of the Sun, and $Delta v_r$ is expressed in km/s. This relationship was verified using those white dwarfs that are part of binary systems. For them, the radii, masses and true radial velocities vr, which are projections of the orbital velocity, were known.
Invisible (dark) satellites, discovered near certain stars from observed fluctuations in the position of the star associated with its motion around the common center of mass (see Invisible satellites of stars), have masses less than 0.02 $(mathfrak M)_odot$. They probably didn't show up. self-luminous bodies and are more like planets.
From determinations of the masses of stars, it turned out that they range from approximately 0.03 $(mathfrak M)_odot$ to 60 $(mathfrak M)_odot$. The largest number of stars have masses from 0.3 $(mathfrak M)_odot$ to 3 $(mathfrak M)_odot$. Wed. the mass of stars in the immediate vicinity of the Sun is $approx 0.5 (mathfrak M)_odot$, i.e. $approx$1033 The difference in the masses of stars turns out to be much smaller than their difference in luminosity (the latter can reach tens of millions). The radii of stars are also very different. This leads to a striking difference between them. densities: from $5cdot 10^(-5)$ to $3cdot 10^5$ g/cm3 (cf. solar density 1.4 g/cm3).
The mass of an open star cluster can be determined by adding up the masses of all its members, the luminosities of which are determined by their apparent brightness and distance to the cluster, and the masses by the mass-luminosity relationship.
The mass of a globular star cluster cannot always be estimated by counting stars, because in the central region of most of these clusters, images of individual stars in photographs taken with optimal exposure merge into one luminous spot. There are methods for estimating the total mass of the entire cluster based on statistical data. principles. So, for example, the application of the virial theorem (see Virial theorem) allows us to estimate the cluster mass $(mathfrak M)_(ck)$ (in $(mathfrak M)_odot$) from the cluster radius r (pc) and cf. quadratic deviation $ar((Delta v)^2)$ of the radial velocity of individual stars (in km/s) from the average. its values ​​(i.e., from the radial velocity of the cluster as a whole):
$(mathfrak M)_(ck)approx 800 ar((Delta v)^2)cdot r$ .
If counting the stars that are members of a globular cluster is possible, then the total mass of the cluster can be determined as the sum of the products $(mathfrak M)_i cdot varphi(M_i)$, where $varphi(M_i)$ is the luminosity function of this cluster, i.e. number of stars falling on different abs intervals. stellar magnitudes Mi (usually they are calculated in intervals equal to 1m), and $(mathfrak M)_i$ is the mass corresponding to a given abs. magnitude Mi from the mass-luminosity relationship. Thus, the total mass of the cluster is $(mathfrak M)_(ck)=sumlimits_i (mathfrak M)_icdot varphi(M_i)$, where the sum is taken from the brightest to the faintest members of the cluster.
The method for determining the mass of the Galaxy $(mathfrak M)_Г$ is based on the fact of rotation of the Galaxy. The stability of the rotation suggests a centripetal. the acceleration for each star, in particular for the Sun, is determined by the attraction of the Galaxy’s matter within the solar orbit. The sun is attracted to the galaxy. center with a force $F_0=G(mathfrak M)_0(mathfrak M)_odot/R_0^2$, where R0 is the distance of the Sun from the Galactic core, equal to $3cdot 10^(22)$ cm. The force F0 imparts to the Sun an acceleration of $g_0 =G(mathfrak M)_0/R_0^2$, which is equal to the centrifugal acceleration of the Sun $v_0^2/R_0$ (without taking into account the influence of the outer part of the Galaxy and provided that surfaces of equal density are ellipsoidal in its inner part). Own galactic the speed of the Sun (the so-called circular speed at a distance R0 from the center) $v_0approx$220 km/s, hence $g_0=v_0^2/R_0approx 1.6cdot 10^(-8)$ cm/s2. The mass of the Galaxy, excluding its parts external to the galactic trajectory of the Sun, $(mathfrak M)_Gapprox g_0R_0/Gapprox 2.2cdot 10^(44)$ g. The mass of the Galaxy in spherical. volume with a radius of $approx$15 kpc, according to similar calculations, is equal to $approx 1.5cdot 10^(11) (mathfrak M)_odot$. This also takes into account the mass of all diffuse (scattered) matter in the Galaxy.
The mass of a spiral galaxy can be determined by studying its rotation, e.g. from an analysis of the radial velocity curve measured at various points on the major axis of the visible ellipse of the galaxy. At every point in the galaxy there is a centripetal. the force is proportional to the mass of the regions closer to the center of the galaxy and depends on the law of changes in the density of the galaxy with distance from its center. Spectroscopic observations in optical range made it possible to construct rotation curves of spiral galaxies up to distances of 20-25 kpc from the center (and for a number of high-luminosity galaxies up to 40 kpc or more). Up to these distances, the circular speed does not decrease with increasing R, i.e. The mass of the galaxy continues to grow with distance. Thus, galaxies have hidden mass. The mass of the invisible (non-luminous) matter of galaxies can be 10 or more times greater than the mass of the luminous matter; Presumably, hidden mass can exist in the form of very faint low-mass stars or black holes or in the form of elementary particles (for example, neutrinos, if they have rest mass).
For slowly rotating galaxies, such as, for example, elliptical. galaxies, it is difficult to obtain radial velocity curves, but it is possible to expand the spectrum. lines estimate avg. the speed of the stars in the system and, comparing it with the true size of the galaxy, determine its mass. The more avg. the speed of stars, the greater the mass of the galaxy should be (with the same dimensions). The relationship between the mass, size of the galaxy and cf. the speed of stars follows from the condition of stationarity of the system.
Another method for estimating the mass of component galaxies of binary systems is similar to the method for estimating the masses of components of spectroscopic binary stars (the error does not exceed 20%). Established statistics are also used. relationship between mass and integral. luminosity of galaxies of various types (a kind of mass-luminosity relationship for galaxies). Luminosity is determined by visible integral. stellar magnitude and distance, which is estimated by the red shift of lines in the spectrum. Wed. The mass of galaxies included in a galaxy cluster is estimated from the number of galaxies in the cluster and its total mass, which is statistically determined from the dispersion of the radial velocities of the galaxies, just as the total mass of a star cluster is estimated based on the virial theorem.
The currently known masses of galaxies range from ~105$(mathfrak M)_odot$ (so-called dwarf galaxies) to 1012$(mathfrak M)_odot$ (supergiant elliptical galaxies, for example galaxy M 87), i.e. . The ratio of galaxy masses reaches 107.
Accuracy of determination of astronomical masses. objects depends on the accuracy of determining all quantities included in the corresponding files. The mass of the Earth is determined with an error of $pm$0.05%, the mass of the Moon is $pm$0.1%. The error in determining the mass of the Sun is also $pm$0.1%, it depends on the accuracy of determining the astronomical unit (cf. distance to the Sun). Actually, that means. degree, the accuracy of determining the mass depends on the accuracy of measuring the distance to the space object, in the case of double stars - on the distance between them, on the linear dimensions of the bodies, etc. The masses of the planets are known with an error of $pm$0.05 to $pm$0.7%. The masses of stars are determined with an error of 20 to 60%. The uncertainty in determining the masses of galaxies can be characterized by the coefficient. 2-5 (the mass can be several times greater or less), if the distance to them is reliably determined.
Lit.:
Struve O., Linde B., Pillans E., Elementary Astronomy, trans. from English, 2nd ed., M., 1967; Sagitov M.U., Constant of gravity and mass of the Earth, M., 1969; Klimishin I.A., Relativistic Astronomy, M., 1983.
(P.G. Kulikovsky)