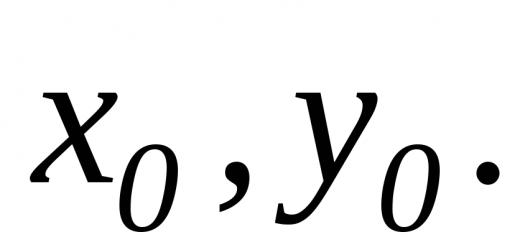Def. The set w is called a linear space, and its element. -vectors if:

*law is specified (+) according to cat. any two elements x, y from w are associated with an element called. their sum [x + y]

*a law is given (* for the number a), according to the cat element x from w and a, an element from w is compared, called the product of x and a [ax];

* completed

the following requirements (or axioms):

Trace c1. zero vector (ctv 0 1 and 0 2. by a3: 0 2 + 0 1 = 0 2 and 0 1 + 0 2 = 0 1. by a1 0 1 + 0 2 = 0 2 + 0 1 => 0 1 = 0 2.)

c2. .(ctv, a4)

c3. 0 vect.(a7)

c4. a(number)*0=0.(a6,c3)

c5. x (*) -1 =0 vector, opposite to x, i.e. (-1)x = -x. (a5,a6)

c6. In w, the subtraction action is defined: the vector x is called the difference of vectors b and a, if x + a = b, and is denoted x = b - a.

Number n called dimension lin. pr-a L , if in L there is a system of n lin. nezav. vectors, and any system of n+1 vector - lin. dependent dim L= n. Space L called n-dimensional.

An ordered collection of n lines. nezav. vectors n dimensional independent. space – basis

Theorem. Each vector X can be represented in a unique way as a line. Combinations of basis vectors

Let (1) be the basis of an n-dimensional linear. pr-va V, i.e. a collection of linearly independent vectors. The set of vectors will be linear. dependent, because their n+ 1.

Those. there are numbers that are not all equal to zero at the same time, what does that have to do with it (otherwise (1) are linearly dependent).

Then where is the vector decomposition x by basis(1) .

This expression is unique, because if another expression exists (**)

subtracting equality (**) from (*),

we get

Because are linearly independent, then . Chtd

Theorem. If - lin. independent vectors of the space V and each vector x from V can be represented through , then these vectors form a basis of V

Doc: (1)-lin.independent =>the document remains that is linear-independent. According to the convention Each vector a is expressed through (1): , consider , rang≤n => among the columns no more than n are linearly independent, but m > n=> m columns are linearly dependent => s=1, n

That is, the vectors are linear dependent

Thus, the space V is n-dimensional and (1) its basis

№4Def. Subset L lin. production V is called lin. cond. of this space if, with respect to the operations (+) and (*a) specified in V, the subspace L is a linear space

Theorem The set l of vectors of space V is linear. A subspace of this space performs

(advance) let (1) and (2) be satisfied, in order for L to be a subsimple.V it remains to prove that all the axioms of lin are satisfied. pr-va.

(-x): -x+x=0 d. a(x + y) = ax + ay;

(a-b) and (e-h) follows from the validity of V; let us prove (c)

(necessity) Let L be lin. subspace of this space, then (1) and (2) are satisfied by virtue of the definition of lines. pr-va

Def. A collection of all kinds of lines. combinations of some elements (x j) lin. the product is called a linear shell

Theorem an arbitrary set of all lines. combinations of vectors V with real. coefficient is lin. subpr V (linear shell given system of vectors lin. pr. is the linear subpr of this pr. )

ODA.Non-empty subset of L line vectors. production V is called lin. subspace if:

a) the sum of any vectors from L belongs to L

b) the product of each vector from L by any number belongs to L

Sum of two subspacesLis again a subspaceL

1) Let y 1 +y 2 (L 1 +L 2)<=>y 1 =x 1 +x 2, y 2 =x’ 1 +x’ 2, where (x 1,x’ 1) L 1, (x 2,x’ 2) L 2. y 1 +y 2 =(x 1 +x 2)+(x' 1 +x' 2)=(x 1 +x' 1)+(x 2 +x' 2), where (x 1 +x' 1 ) L 1 , (x 2 +x' 2) L 2 => the first condition of a linear subspace is satisfied.

ay 1 =ax 1 +ax 2, where (ax 1) L 1, (ax 2) L 2 => because (y 1 +y 2) (L 1 +L 2) , (ly 1) (L 1 +L 2) => conditions are met => L 1 +L 2 is a linear subspace.

The intersection of two subdivisions.L 1 AndL 2 lin. pr-vaL is also a subsp. this space.

Consider two arbitrary vectors x,y, belonging to the intersection of subspaces, and two arbitrary numbers a,b:.

According to def. intersections of sets:

=> by definition of a subspace of a linear space:,.

T.K. vector ax + by belongs to many L 1, and many L 2, then it belongs, by definition, to the intersection of these sets. Thus:

ODA.They say that V is the direct sum of its subdivisions. if and b) this decomposition is unique

b") Let us show that b) is equivalent to b’)

When b) is true b’)

All sorts of (M, N) from intersect only along the zero vector

Let ∃ z ∈

Fair returnL=

contradiction

Theorem To (*) is necessary and sufficient for the union of bases ( formed the basis of space

(Required) let (*) and vectors be bases of subsets. and there is an expansion in ; x is expanded over the basis L, in order to assert that ( constitute a basis, it is necessary to prove their linear independence; they all contain 0 0=0+...+0. Due to the uniqueness of the expansion of 0 over : => due to the linear independence of the basis => ( – basis

(Ext.) Let ( form the basis of L a unique decomposition (**) at least one decomposition exists. By uniqueness (*) => uniqueness (**)

Comment. The dimension of the direct sum is equal to the sum of the dimensions of the subspace

Any non-singular quadratic matrix can serve as a transition matrix from one basis to another

Let in n dimensional linear space V there are two bases and

(1) =A, where the elements * and ** are not numbers, but we will extend certain operations on a numeric matrix to such rows.

Because otherwise the vectors ** would be linear dependent

Back. If then the columns of A are linearly independent =>form a basis

Coordinates And related by the relation , Where transition matrix elements

Let the decomposition of the elements of the “new” basis into the “old” one be known

Then the equalities are true

But if a linear combination of linearly independent elements is 0 then =>

Basic Linear Dependence Theorem

If (*) is linearly expressed through (**) Thatn<= m

Let us prove by induction on m

m=1: system (*) contains 0 and lin. manager - impossible

let it be true for m=k-1

let's prove for m=k

It may turn out that 1) , i.e. v-ry (1) are lin.comb. lin. in-ditch (2)System (1) linear undependable, because is part of lin.nezav. systems (*). Because in system (2) there are only k-1 vectors, then by the induction hypothesis we obtain k+1

Lemma 1 : If in a matrix of size n n at least one row (column) is zero, then the rows (columns) of the matrix are linearly dependent.

Proof: Let the first line be zero, then

Where a 1 0. That's what was required.

Definition: A matrix whose elements located below the main diagonal are equal to zero is called triangular:

and ij = 0, i>j.

Lemma 2: The determinant of a triangular matrix is ​​equal to the product of the elements of the main diagonal.

The proof is easy to carry out by induction on the dimension of the matrix.

Theorem O linear independence vectors.

A)Necessity: linearly dependent D=0 .

Proof: Let them be linearly dependent, j=,

that is, there are a j , not all equal to zero, j= , What a 1 A 1 + a 2 A 2 + ... a n A n = , A j – matrix columns A. Let, for example, a n¹0.

We have a j * = a j / a n , j£ n-1a 1 * A 1 + a 2 * A 2 + ... a n -1 * A n -1 + A n = .

Let's replace the last column of the matrix A on

A n * = a 1 * A 1 + a 2 * A 2 + ... a n -1 A n -1 + A n = .

According to the above-proven property of the determinant (it will not change if another column multiplied by a number is added to any column in the matrix), the determinant of the new matrix is ​​equal to the determinant of the original one. But in the new matrix one column is zero, which means that, expanding the determinant over this column, we get D=0, Q.E.D.

b)Adequacy: Size matrix n nwith linearly independent rows It can always be reduced to a triangular form using transformations that do not change the absolute value of the determinant. Moreover, from the independence of the rows of the original matrix, it follows that its determinant is equal to zero.

1. If in the size matrix n n with linearly independent rows element a 11 is equal to zero, then the column whose element a 1 j ¹ 0. According to Lemma 1, such an element exists. The determinant of the transformed matrix may differ from the determinant of the original matrix only in sign.

2. From lines with numbers i>1 subtract the first line multiplied by the fraction a i 1 /a 11. Moreover, in the first column of rows with numbers i>1 will result in zero elements.

3. Let's start calculating the determinant of the resulting matrix by decomposing over the first column. Since all elements in it except the first are equal to zero,

D new = a 11 new (-1) 1+1 D 11 new,

Where d 11 new is the determinant of a matrix of smaller size.

Next, to calculate the determinant D 11 repeat steps 1, 2, 3 until the last determinant turns out to be the determinant of the size matrix 1 1. Since step 1 only changes the sign of the determinant of the matrix being transformed, and step 2 does not change the value of the determinant at all, then, up to the sign, we will ultimately obtain the determinant of the original matrix. In this case, since due to the linear independence of the rows of the original matrix, step 1 is always satisfied, all elements of the main diagonal will turn out to be unequal to zero. Thus, the final determinant, according to the described algorithm, is equal to the product of non-zero elements on the main diagonal. Therefore, the determinant of the original matrix is ​​not equal to zero. Q.E.D.

Appendix 2

The functions are called linearly independent, If

(only a trivial linear combination of functions that is identically equal to zero is allowed). In contrast to the linear independence of vectors, here the linear combination is identical to zero, and not equality. This is understandable, since the equality of a linear combination to zero must be satisfied for any value of the argument.

The functions are called linearly dependent, if there is a non-zero set of constants (not all constants are equal to zero) such that (there is a non-trivial linear combination of functions identically equal to zero).

Theorem.In order for functions to be linearly dependent, it is necessary and sufficient that any of them is linearly expressed through the others (represented as their linear combination).

Prove this theorem yourself; it is proven in the same way as a similar theorem about the linear dependence of vectors.

Vronsky's determinant.

The Wronski determinant for functions is introduced as a determinant whose columns are the derivatives of these functions from zero (the functions themselves) to the n-1st order.

.

Theorem. If the functions are linearly dependent, then

Proof. Since the functions are linearly dependent, then any of them is linearly expressed through the others, for example,

The identity can be differentiated, so

Then the first column of the Wronski determinant is linearly expressed through the remaining columns, so the Wronski determinant is identically equal to zero.

Theorem.In order for solutions to a linear homogeneous differential equation nth order were linearly dependent, it is necessary and sufficient that.

Proof. Necessity follows from the previous theorem.

Adequacy. Let's fix some point. Since , the columns of the determinant calculated at this point are linearly dependent vectors.

, that the relations are satisfied

Since a linear combination of solutions to a linear homogeneous equation is its solution, we can introduce a solution of the form

A linear combination of solutions with the same coefficients.

Note that this solution satisfies zero initial conditions; this follows from the system of equations written above. But the trivial solution of a linear homogeneous equation also satisfies the same zero initial conditions. Therefore, from Cauchy’s theorem it follows that the introduced solution is identically equal to the trivial one, therefore,

therefore the solutions are linearly dependent.

Consequence.If the Wronski determinant, built on solutions of a linear homogeneous equation, vanishes at least at one point, then it is identically equal to zero.

Proof. If , then the solutions are linearly dependent, therefore, .

Theorem.1. For linear dependence of solutions it is necessary and sufficient(or ).

2. For linear independence of solutions it is necessary and sufficient.

Proof. The first statement follows from the theorem and corollary proved above. The second statement can be easily proven by contradiction.

Let the solutions be linearly independent. If , then the solutions are linearly dependent. Contradiction. Hence, .

Let . If the solutions are linearly dependent, then , hence, a contradiction. Therefore, the solutions are linearly independent.

Consequence.The vanishing of the Wronski determinant at least at one point is a criterion for the linear dependence of solutions to a linear homogeneous equation.

The difference between the Wronski determinant and zero is a criterion for the linear independence of solutions to a linear homogeneous equation.

Theorem.The dimension of the space of solutions to a linear homogeneous equation of the nth order is equal to n.

Proof.

a) Let us show that there exist n linearly independent solutions to a linear homogeneous differential equation of the nth order. Let's consider solutions , satisfying the following initial conditions:

...........................................................

Such solutions exist. Indeed, according to Cauchy’s theorem, through the point passes through a single integral curve—the solution. Through the point the solution passes through the point

- solution, through a point - solution .

These solutions are linearly independent, since .

b) Let us show that any solution to a linear homogeneous equation is linearly expressed through these solutions (is their linear combination).

Let's consider two solutions. One - an arbitrary solution with initial conditions . Fair ratio

Theorem 1. (On the linear independence of orthogonal vectors). Let Then the system of vectors is linearly independent.

Let's make a linear combination ∑λ i x i =0 and consider the scalar product (x j , ∑λ i x i)=λ j ||x j || 2 =0, but ||x j || 2 ≠0⇒λ j =0.

Definition 1. Vector systemor (e i ,e j)=δ ij - Kronecker symbol, called orthonormal (ONS).

Definition 2. For an arbitrary element x of an arbitrary infinite-dimensional Euclidean space and an arbitrary orthonormal system of elements, the Fourier series of an element x over the system is called a formally composed infinite sum (series) of the form , in which the real numbers λ i are called the Fourier coefficients of the element x in the system, where λ i =(x,e i).

A comment. (Naturally, the question arises about the convergence of this series. To study this issue, let us fix an arbitrary number n and find out what distinguishes nth partial the sum of the Fourier series of any other linear combination of the first n elements of an orthonormal system.)

Theorem 2. For any fixed number n, among all sums of the form, the nth partial sum of the Fourier series of the element has the smallest deviation from the element x according to the norm of a given Euclidean space

Taking into account the orthonormality of the system and the definition of the Fourier coefficient, we can write

The minimum of this expression is achieved at c i =λ i, since in this case the non-negative first sum on the right side always vanishes, and the remaining terms do not depend on c i.

Example. Consider the trigonometric system

in the space of all Riemann integrable functions f(x) on the segment [-π,π]. It is easy to check that this is an ONS, and then the Fourier Series of the function f(x) has the form where .

A comment. (The trigonometric Fourier series is usually written in the form Then )

An arbitrary ONS in an infinite-dimensional Euclidean space without additional assumptions, generally speaking, is not a basis of this space. On an intuitive level, without giving strict definitions, we will describe the essence of the matter. In an arbitrary infinite-dimensional Euclidean space E, consider the ONS, where (e i ,e j)=δ ij is the Kronecker symbol. Let M be a subspace of Euclidean space, and k=M ⊥ be a subspace orthogonal to M such that Euclidean space E=M+M ⊥ . The projection of the vector x∈E onto the subspace M is the vector ∈M, where

We will look for those values ​​of the expansion coefficients α k for which the residual (squared residual) h 2 =||x-|| 2 will be the minimum:

h 2 =||x-|| 2 =(x-,x-)=(x-∑α k e k ,x-∑α k e k)=(x,x)-2∑α k (x,e k)+(∑α k e k ,∑α k e k)= ||x|| 2 -2∑α k (x,e k)+∑α k 2 +∑(x,e k) 2 -∑(x,e k) 2 =||x|| 2 +∑(α k -(x,e k)) 2 -∑(x,e k) 2 .

It is clear that this expression will take a minimum value at α k =0, which is trivial, and at α k =(x,e k). Then ρ min =||x|| 2 -∑α k 2 ≥0. From here we obtain Bessel’s inequality ∑α k 2 ||x|| 2. At ρ=0 an orthonormal system of vectors (ONS) is called a complete orthonormal system in the Steklov sense (PONS). From here we can obtain the Steklov-Parseval equality ∑α k 2 =||x|| 2 - the “Pythagorean theorem” for infinite-dimensional Euclidean spaces that are complete in the sense of Steklov. Now it would be necessary to prove that in order for any vector in space to be uniquely represented in the form of a Fourier series converging to it, it is necessary and sufficient for the Steklov-Parseval equality to hold. The system of vectors pic=""> ONB forms? system of vectors Consider for the partial sum of the series Then like the tail of a convergent series. Thus, the system of vectors is a PONS and forms an ONB.

Example. Trigonometric system

in the space of all Riemann-integrable functions f(x) on the segment [-π,π] is a PONS and forms an ONB.