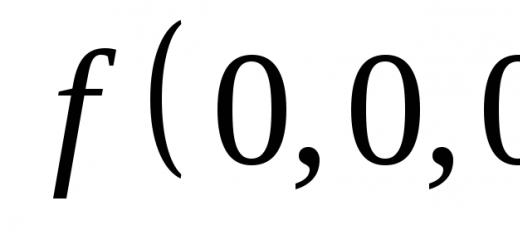If the condition is true, then action 1 is performed, otherwise action 2 is performed.
Example. Let cell E2 store information about the points scored by the applicant. If the number of points is less than 10, then he is accepted into the university, otherwise - not. The formula will look like this:
IF (E2>10; “accepted”; “not accepted”).
A conditional function can be nested. Let the same university have a rule: if an applicant scores 9 points, then he is conditionally admitted.
IF(E2>=10;"accepted";IF(E2=9;"conditionally accepted";"not accepted"))
Logic is the science of laws and forms of thinking
Logic is a science that studies methods of substantiating judgments, proof, thinking and logical conclusion. IN
Mathematical logic uses methods of algebra or the theory of algorithms for this purpose.
Algebra of logic (Boolean algebra) is a branch of mathematics that studies methods of operating with logical (Boolean)
variables that take only two values - true and false.
Algebra of logic is a branch of mathematical logic in which logical operations on statements are studied.
Statements can be true, false, or contain truth and falsehood in different proportions.
Mathematical logic (theoretical logic, symbolic logic) is a branch of mathematics that studies
proofs and questions of the foundations of mathematics.
A logical statement is a statement that can always be associated with one of two logical
values false (0, false, false) or true (1, true, true). A logical statement is usually denoted
in capital Latin letters. An expressive form is a logical statement in which one
from objects is replaced by a variable. When substituting a value in place of a variable, the expressive form
turns into a statement.
Example: A(x) = “It is raining in city x” A is an expressive form, x is an object.
The negation of a logical statement is a logical statement that takes the value “true” if the original
the statement is false, and vice versa.
The conjunction of two logical statements is a logical statement that is true only if they
simultaneously true.
A disjunction of two logical statements is a logical statement that is true only when at least one of
them true.
The implication of two logical statements A and B is a logical statement that is false only if B is false and
A is true.
Equivalence (equivalence) of two logical statements is a logical statement that is true only if
when they are both true and false.
Quantifier logical statement with universal quantifier () - logical statement, true
only if for each object x from a given population the statement A(x) is true.
Quantifier logical statement with existence quantifier () - logical statement, true
only if in a given population there is an object x such that the statement A(x) is true.
A statement (judgment) is a sentence that can be true (true) or false
An assertion is a proposition that needs to be proven or disproved.
Reasoning is a chain of statements or statements related to each other in a certain way
http://profbeckman.narod.ru/EVM Inference is a logical operation, as a result of which one or more given judgments is obtained
(deduces) a new judgment
A logical expression is a record or oral statement, which, along with constants, necessarily includes
variable quantities (objects). Depending on the values of these variables, a Boolean expression may
take one of two possible values: TRUE (logical 1) or FALSE (logical 0)
Complex logical expression is a logical expression composed of one or more simple (or
complex) logical expressions connected using logical operations.
The word logic means a set of rules that govern the thinking process. The term itself
“logic” comes from the ancient Greek logos, meaning “word, thought, concept, reasoning, law.”
Formal logic is the science of the forms and laws of thinking. The laws of logic are reflected in the human mind
properties, connections and relationships of objects in the surrounding world. Logic as a science allows you to build formal
models of the surrounding world, distracting from the content side. Basic forms of thinking
are concepts, judgments and inferences.
A concept is a form of thinking that identifies the essential features of an object or class of objects,
distinguishing him from others. For example, a computer, a person, students.
Judgments are a form of thinking in which the connection between an object and its
a sign, a relationship between objects or the fact of the existence of an object and which can be either
true or false. The linguistic form of expressing a judgment is a declarative sentence.
Interrogative and incentive sentences are not judgments. Judgments are not considered with
from the point of view of their meaning and content, but only from the point of view of their truth or falsity. True
there will be a judgment in which the connection of concepts correctly reflects the properties and relationships of real objects.
“Twice two equals four” is a true proposition, but “The processor is designed for printing” is false.
Judgments can be simple or complex. “Spring has come and the rooks have arrived” is a complex proposition,
consisting of two simple ones. Simple judgments (statements) express the connection between two concepts. Complex -
consist of several simple propositions.
Inference is a thinking technique that allows, on the basis of one or more premise judgments,
obtain a new judgment (knowledge or conclusion). Examples of inferences are proofs of theorems in
geometry. According to the rules of formal logic, the premises of an inference can only be true
judgments. Then the conclusion will be true. Otherwise, you may come to a false conclusion.
Research in the algebra of logic is closely related to the study of statements (although statements are
subject of study of formal logic). With the help of statements we establish properties, relationships
between objects. A statement is true if it adequately reflects this connection, otherwise it
Mathematical logic studies the application of mathematical methods to solve
logical tasks and construction of logical circuits that underlie the operation of any computer.
Judgments in mathematical logic are called statements or logical expressions. Like
just as the branch of mathematics of algebras was developed to describe operations on variables, so also for
processing of logical expressions in mathematical logic, propositional algebra, or algebra, was created
Thus, the algebra of logic is a section of mathematical logic in which logical
operations on statements. Statements can be true or false.
Propositional logic served as the main mathematical tool in the creation
computers. It can easily be converted into bit logic: the truth of a statement is indicated by one
bit (0 - FALSE, 1 - TRUE); then the operation takes on the meaning of subtraction from unity; ∨ -
non-modular addition; & (or ∧) - multiplication; ↔ - equality; ⊕ - in the literal sense of addition by
modulo 2 (exclusive OR - XOR); - the sum does not exceed 1 (that is, AB = (A + B)<= 1).
Subsequently, Boolean algebra was generalized from propositional logic by introducing characteristic
for the logic of statements of axioms. This made it possible to consider, for example, qubit logic, triple
logic (when there are three options for the truth of a statement: “true”, “false” and “undefined”), etc.
Truth tables
It is convenient to describe logical operations by the so-called truth tables, which reflect the results of calculations of complex statements for different values of the original simple statements. Simple statements are denoted by variables (for example, A and B).
Question 2: During the learning process, the student must remember a certain amount of important information. If he does not do this, then the process of cognition or problem solving will slow down, therefore, to facilitate the memorization process, it is important to teach schoolchildren to use mnemonic rules.
Mnemonics - the art of memorization - helps us learn cumbersome formulas or rules, translating them into the language of funny associations, consonant phrases or poems. There are many mnemonic rules.
Colors of the spectrum in order (red, orange, yellow, green, blue, indigo, violet):
1) Every Hunter Wants to Know Where the Pheasant Sits;
2) How Once Jacques the City Bell-Ringer Broke the Lantern;
3) Why do Deer Live in Winter Without Their Imaginations?
4) Enchanting Autumn - Living New Year B "e White Porcelain
Remembering the order of the planets (from the Sun and to the Sun): Pluto, Neptune, Uranus, Saturn, Jupiter, Mars, Earth, Venus, Mercury
1) The Planets are Not Difficult for the Youngest Kid to Remember, Knowing Venus, Mercury;
2) Between the Wolves, the Little Bunny Tossed, Whispered, Stumbled, Fell - Didn’t Get Up;
3) You can fly beyond Mars with a Jewelly Turn Off Our Planet;
4) Little Bear Bite the Ham with Raspberries, Nimble Gopher Stole the Penknife;
5) Great Zdіbnosti looming Little Yurko Spivav Ukrainian Folk Songs
To remember the spectral types of stars:
1) "ABOUT h, B e a F ine G irl K iss M e";
2) One Shaved Englishman Chewed Dates Like Carrots.
Moon phases:
To distinguish the first quarter from the last, an observer located in the northern hemisphere can use the following mnemonic rule. If the month looks like the letter “C”, then it is Aging - this is the last quarter. If it is turned in the opposite direction and then, mentally placing a stick on it, you can get the letter “R”, then the month is “Growing”, that is, this is the first quarter.
Physical formulas
1) Mass formula: We find the mass of a body by multiplying the density by the volume;
2) The average speed of thermal motion of a particle is remembered as follows: Three Cots per Meat;
3) Formula of Archimedean power: Rozha - Wow!
4) Law of electrolysis: M ace WHALE A
Prefixes:
Lived THREE ram: Milli, Micro, Nano.
The key word here is three. The exponents of these prefixes differ from each other by just three (10 -3,10 -6,10 -9).
To remember cathodic and anodic processes in electrochemistry there is the following mnemonic rule:
- At the anode, the anions are oxidized.
- At the cathode, cations are reduced.
In the first line, all words begin with a vowel, in the second - with a consonant.
Roman numerals:
To fix in memory the letter designations of numbers in descending order, there is a mnemonic rule:
M s D arim WITH face-to-face L imons, X vatit V seven I X.
Respectively M(1000), D(500), C(100), L(50), X(10), V(5), I (1)
Introduction to Using Data Types and Field Properties
show all
This article provides an overview of data types and field properties and includes a reference topic that details data types. This article also provides a brief description of lookup fields. Lookup fields that allow multiple values at once are not discussed in this article. For links to more information about lookup fields that allow multiple values at once, see see also.
In this article
· General information
· Data Type Reference
General information
Each table field has properties. These properties determine the characteristics of the fields and the features of working with them. The most important property of a field is its data type. The data type of a field determines what kind of data can be stored in it. For example, a field with a Text data type can store data that contains text and numeric characters, but a field with a Numeric data type can store only numeric data.
The data type of a field determines many other important characteristics of the field. For example:
· Using a field in expressions.
· Maximum size of the field value.
· Possibility of field indexing.
· Acceptable field data formats.
When you create a new field in design mode, you specify the field's data type and (optionally) its other properties.

Contacts table in design mode
Data type
Field properties
When you create a field in Datasheet view, the field type is set automatically. If a field is created in Datasheet view by using a field template or by using an existing field from another table, the data type is already defined in the template or in the other table. If you create a field using data entry in Datasheet view, the data type is assigned to the field by Microsoft Office Access based on the values you enter. If you enter values whose data type is different from the field's data type, the user may be prompted to select a data type.
In Datasheet view, you can change the data type of a field and its properties Field Format, Indexed field And Obligatory field.

Contacts table in table view
Create a field by entering data into a blank column.
Adjusting a field's data type and other properties using the tab Table mode on the tape.
Data types
You can think of a field's data type as a set of characteristics that apply to all the values contained in the field and that determine what kind of values those values can be. For example, values stored in a field with the Text data type can consist only of letters, numbers, and a limited set of punctuation characters. In addition, such a field can contain no more than 255 characters.
Access provides 10 different data types:
· The attachment. Files such as digital photographs. You can put multiple types of data into one record. This data type was not available in earlier versions of Access.
· Counter. Numbers automatically generated for each entry.
· Monetary. Values of monetary amounts.
· Date Time. Date and time values.
· MEMO field. Large text fragments, as well as formatted text. For example, the MEMO field is typically used to describe a product in detail.
· Numerical. Numeric values, such as distances. Note that there is a separate data type for monetary values.
· OLE object field. OLE objects, such as Word documents.
· Text. Short alphanumeric values, such as last names or postal addresses.
· Logical. Boolean values.
ADVICE. Sometimes the data in a field appears to have one data type, when in fact the field has a different data type. For example, a field may appear to contain numeric values, but it actually contains text values, such as room numbers. Expressions are often used to compare or convert between values of different data types.
Lookup fields
You can set the field data type to Substitution Wizard. This launches the Lookup Wizard, which creates a lookup field. A lookup field displays either a list of values obtained from a table or query, or a constant set of values specified by the user when the field is created.
In the Lookup Wizard, you can either enter a constant list of values or specify the source from which you want to get the values, such as a field in a table. The lookup field data type can be Text or Numeric, depending on the user's selection in the Lookup Wizard.
NOTE. Lookup fields have an additional set of field properties located on the tab Substitution in area Field properties.
For more information about lookup fields, see see also.
Field properties
After you have created a field and specified its data type, you can set additional properties for the field. The field's data type determines what other properties of the field can be set. For example, you can control the size of a text field by setting its property Field size.
For numeric and currency fields, the property Field size is important because it determines the range of field values. For example, single-byte numeric fields can only contain integers in the range 0 to 255.
Property Field size also determines the amount of disk space required for each numeric field value. Depending on the field size, a number can occupy exactly 1, 2, 4, 8, 12, or 16 bytes.
NOTE. For text fields and MEMO fields, the size of the field values may vary. For these data types, the property Field size specifies the maximum disk space that can be used for a single value.
For more information about field properties and the roles they play for different data types, see the Data Type Reference section of this article.
Related information.
Let's introduce the concept random events. Since in the future we will consider only random events, then, starting from this moment, we will, as a rule, simply call them events.
Any set elementary outcomes, or, in other words, an arbitrary subset spaces of elementary outcomes, called event .
Elementary outcomes that are elements of the subset (event) under consideration are called elementary outcomes, favorable this event , or forming This event .
We will denote events in capital Latin letters, providing them with indices if necessary, for example: A, IN 1 ,WITH 3, etc.
They say that the event A happened (or occurred) if any of the elementary outcomes appeared as a result of the experience.
Note 1. For the convenience of presenting the material, the term “event” as a subset of the space of elementary events Ω is identified with the term “an event occurred as a result of an experience,” or “an event consists in the appearance of some elementary outcomes.”
So in example 2, where  , event A is a subset
, event A is a subset  . But we will also say that the event A– is the appearance of any of the elementary outcomes
. But we will also say that the event A– is the appearance of any of the elementary outcomes 
Example 1.5. In example 2 it was shown that when throwing a die once
 ,
,
Where  - an elementary outcome consisting in loss i points. Consider the following events: A– getting an even number of points; IN- getting an odd number of points; WITH– rolling out a number of points that is a multiple of three. It's obvious that
- an elementary outcome consisting in loss i points. Consider the following events: A– getting an even number of points; IN- getting an odd number of points; WITH– rolling out a number of points that is a multiple of three. It's obvious that
 ,
,
 ,
,
An event consisting of all elementary outcomes, i.e. An event that necessarily occurs in a given experience is called a veridical event.
A reliable event is indicated by the letter Ω .
Event  , opposite to the reliable event Ω, is called impossible. Obviously an impossible event
, opposite to the reliable event Ω, is called impossible. Obviously an impossible event  cannot appear as a result of experience. For example, getting more than six points when throwing a die. We will denote an impossible event by
cannot appear as a result of experience. For example, getting more than six points when throwing a die. We will denote an impossible event by  Ø.
Ø.
An impossible event does not contain a single elementary event. It corresponds to the so-called “empty set”, which does not contain a single point.
Geometrically, random events are represented by sets of points in the region Ω, i.e. regions lying inside Ω (Fig. 1.1). A reliable event corresponds to the entire region Ω.
In probability theory, various operations are performed on events, the totality of which forms the so-called algebra of events, closely related to the algebra of logic, widely used in modern computers.


Rice. 1.1 Fig. 1.2
To consider problems of event algebra, we introduce basic definitions.
The two events are called equivalent (equivalent) , if they consist of the same elementary events. The equivalence of events is indicated by the equal sign:
A=IN.
Event B is called a consequence of the event A:
A IN,
IN,
If from appearance A follows the appearance IN. Obviously, if A IN And IN
IN And IN A, That A=IN, If A
A, That A=IN, If A IN And IN
IN And IN WITH, That A
WITH, That A WITH(Fig. 1.2).
WITH(Fig. 1.2).
Amount or unification two events A And IN this event is called WITH, which consists either in the implementation of an event A, or events IN, or events A And IN together. Conventionally it is written like this:
WITH=A+IN or WITH=A IN.
IN.
The sum of any number events A 1 ,A 2 , … , A n is called an event WITH, which consists in the implementation of at least one of these events and is written in the form
 or
or 
The work or combination (intersection) two events A And IN called event WITH, which also consists in the implementation of the event A, and events IN. Conventionally it is written like this:
WITH=AB or WITH=A IN.
IN.
The product of any number of events is determined similarly. Event WITH, equivalent to the product n events A 1 ,A 2 , … , A n is written as
 or
or  .
.
The sum and product of events have the following properties.
A+IN=IN+A.
(A+IN)+WITH=A+(IN+WITH)=A+IN+WITH.
AB=VA.
(AB)WITH=A(Sun)=ABC.
A(IN+WITH)=AB+AC.
Most of them are easy to check yourself. We recommend using a geometric model.
Let us give a proof of the 5th property.
Event A(IN+WITH) consists of elementary events that belong to and A And IN+WITH, i.e. event A and at least one of the events IN,WITH. In other words, A(IN+WITH) is a set of elementary events belonging to either the event AB, or event AC, i.e. event AB+AC. Geometrically event A(IN+WITH) represents the common part of the areas A And IN+WITH(Fig. 1.3.a), and the event AB+AC– merging areas AB And AC(Fig. 1.3.b), i.e. the same area A(IN+WITH).

Rice. 1.3.a Fig. 1.3.b
Event WITH, consisting in the fact that the event A happens and the event IN doesn't happen, it's called difference events A And IN. Conventionally it is written like this:
WITH=A-IN.
Events A And IN are called joint , if they can appear in the same trial. This means that there are such elementary events that are part of and A And IN simultaneously (Fig. 1.4).
Events A And IN are called incompatible
, if the appearance of one of them excludes the appearance of the other, i.e. If AB= Ø. In other words, there is not a single elementary event that would be part of and A And IN simultaneously (Fig. 1.5). In particular, the opposite events  And
And  always incompatible.
always incompatible.

Rice. 1.4 Fig. 1.5
Events  are called pairwise incompatible
, if any two of them are inconsistent.
are called pairwise incompatible
, if any two of them are inconsistent.
Events  form full group
, if they are pairwise inconsistent and add up to a reliable event, i.e. if for any i,
k
form full group
, if they are pairwise inconsistent and add up to a reliable event, i.e. if for any i,
k
 Ø;
Ø;
 .
.
Obviously, each elementary event must be part of one and only one event of the complete group  . Geometrically, this means that the entire region Ω region
. Geometrically, this means that the entire region Ω region  divided by n parts that do not have common points with each other (Fig. 1.6).
divided by n parts that do not have common points with each other (Fig. 1.6).

Opposite events  And
And  represent the simplest case of a complete group.
represent the simplest case of a complete group.
General statement of the problem: the probabilities of some events are known, and you need to calculate the probabilities of other events that are associated with these events. In these problems, there is a need for operations with probabilities such as addition and multiplication of probabilities.
For example, while hunting, two shots are fired. Event A- hitting a duck with the first shot, event B- hit from the second shot. Then the sum of events A And B- hit with the first or second shot or with two shots.
Problems of a different type. Several events are given, for example, a coin is tossed three times. You need to find the probability that either the coat of arms will appear all three times, or that the coat of arms will appear at least once. This is a probability multiplication problem.
Addition of probabilities of incompatible events
Addition of probabilities is used when you need to calculate the probability of a combination or logical sum of random events.
Sum of events A And B denote A + B or A ∪ B. The sum of two events is an event that occurs if and only if at least one of the events occurs. It means that A + B– an event that occurs if and only if the event occurred during observation A or event B, or simultaneously A And B.
If events A And B are mutually inconsistent and their probabilities are given, then the probability that one of these events will occur as a result of one trial is calculated using the addition of probabilities.
Probability addition theorem. The probability that one of two mutually incompatible events will occur is equal to the sum of the probabilities of these events:
For example, while hunting, two shots are fired. Event A– hitting a duck with the first shot, event IN– hit from the second shot, event ( A+ IN) – a hit from the first or second shot or from two shots. So, if two events A And IN– incompatible events, then A+ IN– the occurrence of at least one of these events or two events.
Example 1. There are 30 balls of the same size in a box: 10 red, 5 blue and 15 white. Calculate the probability that a colored (not white) ball will be picked up without looking.
Solution. Let us assume that the event A- “the red ball is taken”, and the event IN- “The blue ball was taken.” Then the event is “a colored (not white) ball is taken.” Let's find the probability of the event A:
and events IN:
![]()
Events A And IN– mutually incompatible, since if one ball is taken, then it is impossible to take balls of different colors. Therefore, we use the addition of probabilities:
![]()
The theorem for adding probabilities for several incompatible events. If events constitute a complete set of events, then the sum of their probabilities is equal to 1:
The sum of the probabilities of opposite events is also equal to 1:
![]()
Opposite events form a complete set of events, and the probability of a complete set of events is 1.
Probabilities of opposite events are usually indicated in small letters p And q. In particular,
from which the following formulas for the probability of opposite events follow:
Example 2. The target in the shooting range is divided into 3 zones. The probability that a certain shooter will shoot at the target in the first zone is 0.15, in the second zone – 0.23, in the third zone – 0.17. Find the probability that the shooter will hit the target and the probability that the shooter will miss the target.
Solution: Find the probability that the shooter will hit the target:
Let's find the probability that the shooter will miss the target:
![]()
More complex problems, in which you need to use both addition and multiplication of probabilities, can be found on the page "Various problems involving addition and multiplication of probabilities".
Addition of probabilities of mutually simultaneous events
Two random events are called joint if the occurrence of one event does not exclude the occurrence of a second event in the same observation. For example, when throwing a die the event A The number 4 is considered to be rolled out, and the event IN– rolling an even number. Since 4 is an even number, the two events are compatible. In practice, there are problems of calculating the probabilities of the occurrence of one of the mutually simultaneous events.
Probability addition theorem for joint events. The probability that one of the joint events will occur is equal to the sum of the probabilities of these events, from which the probability of the common occurrence of both events is subtracted, that is, the product of the probabilities. The formula for the probabilities of joint events has the following form:
Since events A And IN compatible, event A+ IN occurs if one of three possible events occurs: or AB. According to the theorem of addition of incompatible events, we calculate as follows:
Event A will occur if one of two incompatible events occurs: or AB. However, the probability of the occurrence of one event from several incompatible events is equal to the sum of the probabilities of all these events:
Likewise:
Substituting expressions (6) and (7) into expression (5), we obtain the probability formula for joint events:
When using formula (8), it should be taken into account that events A And IN can be:
- mutually independent;
- mutually dependent.
Probability formula for mutually independent events:
Probability formula for mutually dependent events:
If events A And IN are inconsistent, then their coincidence is an impossible case and, thus, P(AB) = 0. The fourth probability formula for incompatible events is:
Example 3. In auto racing, when you drive the first car, you have a better chance of winning, and when you drive the second car. Find:
- the probability that both cars will win;
- the probability that at least one car will win;
1) The probability that the first car will win does not depend on the result of the second car, so the events A(the first car wins) and IN(the second car will win) – independent events. Let's find the probability that both cars win:
2) Find the probability that one of the two cars will win:
![]()
More complex problems, in which you need to use both addition and multiplication of probabilities, can be found on the page "Various problems involving addition and multiplication of probabilities".
Solve the addition of probabilities problem yourself, and then look at the solution
Example 4. Two coins are tossed. Event A- loss of the coat of arms on the first coin. Event B- loss of the coat of arms on the second coin. Find the probability of an event C = A + B .
Multiplying Probabilities
Probability multiplication is used when the probability of a logical product of events must be calculated.
In this case, random events must be independent. Two events are said to be mutually independent if the occurrence of one event does not affect the probability of the occurrence of the second event.
Probability multiplication theorem for independent events. Probability of simultaneous occurrence of two independent events A And IN is equal to the product of the probabilities of these events and is calculated by the formula:
Example 5. The coin is tossed three times in a row. Find the probability that the coat of arms will appear all three times.
Solution. The probability that the coat of arms will appear on the first toss of a coin, the second time, and the third time. Let's find the probability that the coat of arms will appear all three times:
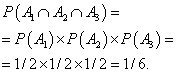
Solve probability multiplication problems on your own and then look at the solution
Example 6. There is a box of nine new tennis balls. To play, three balls are taken, and after the game they are put back. When choosing balls, played balls are not distinguished from unplayed balls. What is the probability that after three games there will be no unplayed balls left in the box?
Example 7. 32 letters of the Russian alphabet are written on cut-out alphabet cards. Five cards are drawn at random one after another and placed on the table in order of appearance. Find the probability that the letters will form the word "end".
Example 8. From a full deck of cards (52 sheets), four cards are taken out at once. Find the probability that all four of these cards will be of different suits.
Example 9. The same task as in example 8, but each card after being removed is returned to the deck.
More complex problems, in which you need to use both addition and multiplication of probabilities, as well as calculate the product of several events, can be found on the page "Various problems involving addition and multiplication of probabilities".
The probability that at least one of the mutually independent events will occur can be calculated by subtracting from 1 the product of the probabilities of opposite events, that is, using the formula.
You can perform various actions on events, thereby receiving other events. Let us define these actions.
Definition 2.13.
If during any trial in which an event occurs A, an event occurs IN, then the event A called special case events V.
They also say that A entails B, and they write: ( A invested in IN) or (Fig. 2.1).
For example, let the event A is the appearance of two points when throwing a die, and the event IN consists in the appearance of an even number of points when throwing a die B = (2; 4; 6). Then the event A there is a special case of the event IN, since two is an even number. We can write it down.

Rice. 2.1 . Event A- a special case of an event IN
Definition 2.14.
If A entails IN, A IN entails A, then these events equivalent , since they advance together or do not advance together.
From what (follows) A = B.
For example, A- an event consisting in the fact that an even number less than three is rolled on a die. This event is equivalent to the event IN, consisting in the fact that the number 2 fell on the dice.
Definition 2.15.
An event consisting of the joint occurrence of both events and A, And IN, called intersection these events A∩B, or work these events AB(Fig. 2.2).

Rice. 2.2. Crossing Events
For example, let the event A consists of getting an even number of points when throwing a die, then its occurrence is favored by elementary events consisting of getting 2, 4 and 6 points. A -(2; 4; 6). Event IN consists of getting more than three points when throwing a dice, then its occurrence is favored by elementary events consisting of getting 4, 5 and 6 points. IN= (4; 5; 6). Then by the intersection or product of events A And IN there will be an event consisting in the loss of an even number of points greater than three (the event is also carried out A, and event IN):
A∩B =AB={4; 6}.
The intersection of events, one of which A- a queen falling out of a deck of cards, and another IN- if a club falls out, there will be a queen of clubs.
Note. If two events A And IN are incompatible, then their joint offensive is impossible AB = 0.
Definition 2.16.
Event consisting of the occurrence or event A, or events IN(at least one of the events, at least one of these events) is called their union A And IN, or the sum of events A And IN and is denoted by A+B (Fig. 2.3).

Rice. 2.3. Merging Events
For example, event A consists of getting an even number of points when throwing a die, then its occurrence is favored by elementary events consisting of getting 2, 4 and 6 points, or A -(2; 4; 6). Event IN consists of getting more than three points when throwing a dice, then its occurrence is favored by elementary events consisting of getting 4, 5 and 6 points, or B = (4; 5; 6). Then by the union, or the sum of events A And IN there will be an event consisting in the loss of at least one of them - either an even number of points, or a number of points greater than three (either the event is fulfilled A, or event IN):
A ∩ B =A +B={2; 4; 5; 6}.
Definition 2.17.
An event that is an event A does not occur, is called the opposite of the event A and is denoted by Ā (Fig. 2.4).

Rice. 2.4. Opposite events
For example, let the event A consists of getting an even number of points when throwing a die, then its occurrence is favored by elementary events consisting of getting 2, -4 and 6 points, or A =(2; 4; 6). Then the event Ā consists of rolling out an odd number of points, and its occurrence is facilitated by elementary events consisting of rolling out 1st, 3rd and 5th points. Ā ={1;3;5}.
Definition 2.18.
Event (A and B), consisting in the fact that A happens and does not happen is called the difference of events A And IN and is denoted by A-B. However, we can do without this designation, since it follows from the definition that A - B -(Fig. 2.5).

Rice. 2.5. Event difference A And IN
For example, let the event A consists of getting an even number of points when throwing a die, then A =(2; 4; 6). Event IN consists of rolling a number of points greater than three. IN= {4; 5; 6}.
Then - an event consisting in the loss of a number of points of no more than three, and its occurrence is favored by elementary events consisting in the loss of 1, 2 and 3 points. = {1; 2; 3}.
By difference of events A And IN there will be an event consisting of an event being executed A and the event is not executed IN. Its onset is favored by an elementary event consisting of rolling 2 points:
A-B= A∩= {2}.
Definitions sums and products events extend to a larger number of events:
A + B + ... + N =(A or IN, or or N) (2.1)
there is an event consisting of the occurrence at least one from events A, B, ... N;
AB... N =(A And IN and... and N), (2.2)
there is an event consisting of joint offensive all events A, B, ... N.
The sum and product of an infinite number of events are defined similarly A 1, A 2, ... A p, ...
Note that, nevertheless, some rules of algebra are preserved for actions on events. For example, there is a commutative law (communicability):
A + B = B + A, AB = BA,(2.3)
the distributive law (distributivity) is satisfied:
(A + B) C = AC + BC,(2.4)
since the left and right sides represent the event that event C and at least one of the events occur A And IN. The combinational law (associativity) is also valid:
A+(B + C) = (A+B)+ C = A+B + C;
A(BC) = (AB)C = ABC.(2.5)
In addition, there are also equalities that would seem absurd in ordinary algebra. For example, for any A, B, C:
AA=A(2.6)
A+A= A(2.7)
A+AB= A(2.8)
AB + C = (A+C)(B+C)(2.9)
Opposite events are related:
· the law of double negation:
= A;(2.10)
law of excluded middle
A + = Ω. (their sum is a reliable event); (2.11)
law of contradiction:
A =Ø (product of their impossible event). (2.12)
Equalities (2.6)-(2.12) are proven for statements in the course of discrete mathematics. We invite the reader to check this for themselves using the definitions of the sum and product of events.
If B = A 1 + A 2 +... + A p and events A pairwise incompatible, i.e. each is incompatible with the others: A j A k= Ø at i≠k they say that the event B is divided into special cases A 1, A 2, ..., A p. For example, event IN, consisting of rolling an odd number of points, is divided into special cases E 1, E 3, E 5, consisting of rolling 1, 3 and 5 points respectively.
Based on the definition of actions on events, we can give a clearer definition to the complete group of events.
Definition 2.19.
If A 1 + A 2 +... + A p = Ω , i.e. if at least one of the events A 1 + A 2 +... + A p must certainly come true and if at the same time A j pairwise incompatible (i.e. a reliable event Ω divided into special cases A 1 + A 2 +... + A p), then they say that events A 1 + A 2 +... + A p form a complete group of events. Thus, if A 1 + A 2 +... + A p- a complete group of events, then during each trial one and only one of the events necessarily occurs A 1 + A 2 +... + A p.
For example, when throwing a die, the complete group of events also consists of the events E 1, E 2, E 3, E 4, E 5 And E 6, consisting of rolling 1, 2, 3,4, 5 and 6 points respectively.
Transcript
1 Answers = A 5 12 = A3 7 = 7 3 = a) 126; b) P(4, 5, 6) = a) P 4 = 24; b) P(2, 2) = C22 4 C2 8 = , 30, 60, Insufficient, 9, Actions on events An event is called random or possible if the outcome of the test leads to the occurrence or non-occurrence of this event. For example, a coat of arms falling out when throwing a coin; the appearance of a side with a number of points equal to 3 when throwing a die. An event is called reliable if it is sure to occur under test conditions. For example, drawing a white ball from an urn containing only white balls; getting no more than 6 points when throwing a die. An event is called impossible if it certainly will not occur under test conditions. For example, getting seven points when throwing one die; drawing more than four aces from a regular deck of cards. Random events are designated by Latin letters of the alphabet A, B, C and so on. Events can be joint or non-joint. Events are called incompatible if, under test conditions, the occurrence of one of them excludes the occurrence of the others. For example, the loss of a coat of arms and tails in one toss of a coin; hit and miss with one shot. Events are called joint if, under test conditions, the occurrence of one of them does not exclude the occurrence of the others. For example, hitting a target and missing while shooting from two rifles at the same time; two coats of arms appearing when throwing two coins. Events are called equally possible if, under the conditions of a given test, the possibility of each of these events occurring is the same. Examples of equally possible events: a coat of arms falling out and a tail falling out in one toss of a coin; 13
2 The number of points from 1 to 6 is rolled when one dice is thrown. Event C, consisting of the occurrence of at least one of the events A or B, is called the sum (union) of events and is denoted C = A + B (C = A B). Event C, consisting of the joint occurrence of events A and B, is called the product (intersection) of these events and is denoted C = A B (C = A B). The event C, which consists in the fact that the event a does not occur, is called the opposite and is denoted by A. The sum of the opposite events is the certain event Ω, that is, A + A = Ω. The product of opposite events is an impossible event (V), that is, A A = V. The set of possible events forms a complete group if at least one of these events appears as a result of the tests: n A i = Ω. i=1 For example, when throwing a die, rolls from one to six make up the complete group of events Event A of the four light bulbs being tested are all defective; Event B All light bulbs are good. What do the events mean: 1) A + B; 2) A B; 3) A; 4) B? Solution. 1) Event A is that all light bulbs are defective, and event B is that all light bulbs are good. The sum of events A+B means that all light bulbs must be either defective or good. 2) Event A B light bulbs must be both defective and good, so event A B is impossible. 3) A all the light bulbs are defective, therefore A at least one light bulb is good quality. 4) B all the light bulbs are good quality, therefore B at least one light bulb is defective. 14
3 2.2. One number is taken at random from the table of random numbers. Event A the selected number is divided by 2, event B the selected number is divided by 3. What do the events mean: 1) A+B; 2) A B; 3) A B? Solution. 1) The sum of eventsa + B is an event consisting of the occurrence of at least one of the events A or B, that is, a randomly selected number must be divisible by either 2, or 3, or 6. 2) The product of events A B means that events A and B occur simultaneously. Therefore, the selected number must be divisible by 6. 3) A B the selected number is not divisible by Two shooters fire one shot at the same target. Event A: the first shooter hits the target; event B the second shooter hits the target. What do the events mean: a) A + B; b) A B; c) A + B; d) A B? Solution. a) Event A+B means: at least one of the shooters hits the target; b) event A B means: both shooters hit the target; c) event A+B means: at least one misses; d) events A B means: both make mistakes. Two chess players play the same game. Event A will be won by the first player, event B by the second player. Which event should be added to the specified population to form a complete group of events? Solution. Event C draw Given two duplicate blocks a 1 and a 2. Write down the event that the system is closed. Solution. Let us introduce the following notation: A 1 event, consisting in the fact that block a 1 is operational; a1 a A 2 2 event, consisting in the fact that block a 2 is operational; S is an event that the system is closed. The blocks are redundant, so the system will be closed in the case when at least one of the blocks is operational, that is, S = A 1 + A A system of three blocks a 1, a 2, b is given. Record events - 15
4 The point is that the system is closed. Solution. Let us introduce the notation: A 1 a a 1 2 b the following event, consisting in the fact that block a 1 is operational; A 2 event, consisting in the fact that block a 2 is operational; B event, consisting in the fact that block b is operational; S is an event that the system is closed. Let's split the system into two parts. The closure of a system consisting of duplicate blocks, as we see, can be written as the event A 1 + A 2. For the closure of the entire system, the serviceability of block B is always required, therefore S = (A 1 + A 2) B. Problems for independent solution 2.7 . One number is taken at random from the table of random numbers. Event A the selected number is divisible by 5, event B this number ends in zero. What do the events mean: 1) A+B; 2) A B; 3) A B; 4) A B? 2.8. Three shooters are shooting at a target. Events: A 1 hit on the target by the first shooter; A 2 hit by the second shooter; A 3 hit by the third shooter. Make a complete group of events. The box contains several balls of the same size, but different colors: white, red, blue. Event K i a red ball taken at random; event B i is white; event C i is blue. Two balls are taken out in a row (i = 1, 2 is the serial number of the balls taken out). Write down the following events: a) event A, the second ball taken at random turns out to be blue; b) event A; c) event B are both balls red? Make a complete group of events Three shots are fired at the target. Given events A i (i = 1, 2, 3) hitting the target with the i-th shot. Express the following events in terms of A i and A i: 1) not a single hit in 16
5 goal; 2) one hit on the target; 3) two hits on the target; 4) three hits on target; 5) at least one hit on the target; 6) at least one miss. Are the following events incompatible: a) experience of tossing a coin; events: A the appearance of the coat of arms, B the appearance of the number; b) two shots at a target; events: A at least one hit, B at least one miss. Are the following events equally possible: a) experience of tossing a coin; events: A the appearance of the coat of arms, B the appearance of the number; b) experience of tossing a bent coin; events: A the appearance of the coat of arms, B the appearance of the number; c) experience: shooting at a target; events: A hit, B miss Do the following events form a complete group of events: a) experience of tossing a coin; events: A coat of arms, B figure; b) experience of tossing two coins; events: A two coats of arms, B two numbers Throwing a die. Let's denote the events: A - 6 points are rolled out, B - 3 points are rolled out, C - an even number of points are rolled out; D rolling a number of points that is a multiple of three. What are the relationships between these events? Let A, B, C be arbitrary events. What do the following events mean: ABC; ABC; A+BC; ABC +ABC+ +ABC; ABC + ABC + ABC + ABC? Using arbitrary events A, B, C, find expressions for the following events: a) only event A occurred; b) A and B happened, C did not happen; c) all three events occurred; d) at least one of these events occurred; e) at least two events occurred; f) one and only one event occurred; g) two and only two events occurred; 17
ELEMENTS OF PROBABILITY THEORY. Probability theory is a branch of mathematics that studies the patterns that arise in random trials. The outcome of the test is random in relation to the test, if during this
1 Basic concepts of combinatorics 1 Appendix Definition The product of all natural numbers from 1 to n inclusive is called n-factorial and written Example Calculate 4! 3! n! 1 3 n 4!-3!= 1 3 4 1 3 4 18
Reliable event. An event is called reliable if it is sure to occur when a certain set of conditions are met. Symbol: Ω (true). Impossible event. An event that
TOPIC 1. BASIC CONCEPTS OF PROBABILITY THEORY. CLASSICAL AND GEOMETRIC PROBABILITIES The subject of probability theory. The concept of a random event. Space of elementary events. Classic and geometric
1.1. Classical definition of probability The basic concept of probability theory is the concept of a random event. A random event is an event that, if certain conditions are met, can
Basic provisions of the theory of probability A random event relative to certain conditions is an event that, when these conditions are met, can either occur or not occur. Probability theory has
( σ-algebra - field of random events - first group of Kolmogorov’s axioms - second group of Kolmogorov’s axioms - basic formulas of probability theory - probability addition theorem - conditional probability
Subject of probability theory In various branches of science and technology, situations often arise when the result of each of the many experiments carried out cannot be predicted in advance, but it can be studied
CONTENTS TOPIC III. INTRODUCTION TO PROBABILITY THEORY... 2 1. REFERENCES... 2 1.1. BASIC CONCEPTS AND DEFINITIONS... 2 1.2. ACTIONS ON RANDOM EVENTS... 4 1.3. CLASSICAL DEFINITION
LESSON 3 INTRODUCTION TO PROBABILITY THEORY METHODOLOGICAL RECOMMENDATIONS MISS 2013 I APPROVED: D.E. Kaputkin Chairman of the Educational and Methodological Commission for the implementation of the Agreement with the Department of Education of the cities.
1.6. Independent tests. Bernoulli's formula When solving probabilistic problems, one often encounters situations in which the same test is repeated many times and the outcome of each test is
Probability. What is this? Probability theory, as the name suggests, deals with probabilities. We are surrounded by many things and phenomena about which, no matter how developed science is, it is impossible to make accurate predictions.
Practical lesson 1. Determination of probability Properties of random events 1. [Ventzel E.S., 1.1.] Do the following groups of events form a complete group: a) Experience throwing a coin; events: b) Throwing experience
SUBJECT. THEOREMS OF ADDITION AND MULTIPLICATION OF PROBABILITIES Operations on random events. Algebra of events. The concept of compatibility of events. Complete group of events. Dependence and independence of random events. Conditional
Lecture 2. Theorems of addition and multiplication of probabilities Sum and product of an event The sum or union of several events is an event consisting of the occurrence of at least one of these
Mathematics (BkPl-100) M.P. Kharlamov 2011/2012 academic year, 1st semester Lecture 5. Topic: Combinatorics, introduction to probability theory 1 Topic: Combinatorics Combinatorics is a branch of mathematics that studies
Lesson topic: “The simplest probabilistic problems.” 11th grade Mathematics teacher N.S. Pereverzyeva Municipal Educational Institution Lyceum 6 It is remarkable that science, which began with the consideration of gambling, promises to become the most important
Elements of probability theory. Plan. 1. Events, types of events. 2. Probability of an event a) Classic probability of an event. b) Statistical probability of an event. 3. Algebra of events a) Sum of events. Probability
Topic 33 “Probabilities of events” We all quite often say “it’s incredible”, “it’s more likely that”, “it’s unlikely”, etc. when we try to predict the occurrence of this or that event. Wherein
Federal Agency for Education Tomsk State University of Control Systems and Radioelectronics N. E. Lugina PRACTICUM ON PROBABILITY THEORY Textbook Tomsk 2006 Reviewers: Ph.D.
TTÜ VIRUMAA KOLLEDŽ RAR0530 Tõenäosusteooria ja matemaatiline statistika Lecture 1 Random events Actions on events Õppejõud: I. Gusseva PROBABILITY THEORY Introduction Probability theory deals with
PROBABILITY OF A RANDOM EVENT Kolmogorov's axioms In 1933, A. N. Kolmogorov in his book “Basic Concepts of Probability Theory” gave an axiomatic justification for the theory of probability. "This means that after
Homework 1 “Probability Theory” Task 1. 1.1. There are five tickets worth one ruble, three tickets worth three rubles and two tickets worth five rubles. Three tickets are taken at random. Determine probability
Test in applied mathematics for 2nd year students of the correspondence course of higher education school, direction of preparation 03/08/01 construction Option 1 1) A natural number not exceeding
Practical work 3 Algebra of events. Addition and multiplication of probabilities Purpose of the work: to master the calculation of the probabilities of joint events, determining the probability using the sum and product formulas. Equipment
MINISTRY OF EDUCATION OF THE RUSSIAN FEDERATION VOLGOGRAD STATE TECHNICAL UNIVERSITY VOLGA POLYTECHNIC INSTITUTE DEPARTMENT OF MATHEMATICS Probability theory (introduction) Part 1 Methodological
Department of Mathematics and Computer Science Mathematics Educational and methodological complex for secondary vocational education students studying using distance technologies Module 6 Elements of probability theory and mathematical statistics
BASIC CONCEPTS OF PROBABILITY THEORY. 3.1. Random events. Each science, when studying the phenomena of the material world, operates with certain concepts, among which there are necessarily fundamental ones;
Practical work 2 Topic 2 Total probability formula and Bayes formula Repetition of experiments (Bernoulli scheme). We will say that the events H 1, H 2, H n form a complete group if, as a result of the experiment:
13 Addition and multiplication of probabilities Event A is called a special case of event B if when A occurs, B also occurs. It is written: Events A and B are called equal if each of them is special
COMBINATORY PROBABILITY Topic 5 Translation carried out with the support of IT Akadeemia Lecture content 1 Introduction 2 3 4 Next paragraph 1 Introduction 2 3 4 Problem... Problem... Problem... ... and solution: Girl
Lecture Topic: ALGEBRA OF EVENTS BASIC THEOREMS ABOUT PROBABILITY Algebra of events The sum of events is the event S = +, which consists in the occurrence of at least one of them The product of events is called
Lecture 9. Classical definition of probability Probability theory is a mathematical science that allows, from the probabilities of some random events, to find the probabilities of other random events related in some way
CHECK TASKS Test 1 Option 1 1. Among the 0 ceramic products received at the store, there are 4 defective ones. To check the quality, the merchandiser selects two products at random. Find probability
( definitions - random event - operations on events probability on a discrete space of elementary outcomes classical definition of probability example hypergeometric distribution example
PRACTICAL Basic formulas of combinatorics Types of events Actions on events Classical probability Geometric probability Basic formulas of combinatorics Combinatorics studies the numbers of combinations,
LECTURE 1 PROBABILITY THEORY Probability theory is a science that studies patterns in random phenomena. A random phenomenon is a phenomenon that, when the same thing is repeated repeatedly,
1 Probability Experimental data are processed using various methods. Typically, a researcher, having received experimental data on one or several groups of subjects and determined from them
Basics of probability theory Lecture 2 Contents 1. Conditional probability 2. Probability of a product of events 3. Probability of a sum of events 4. Formula of total probability Dependent and independent events Definition
Topic: Probability Theory Discipline: Mathematics Authors: Nefedova G.A. Date: 9.0.0. The probability of a random event may be equal. 0.5. 3. 0. 0.7 5..5 6. - 7. 0.3. The probability of a reliable event is equal.
Probability theory Lecture plan P About probability theory as a science P Basic definitions of probability theory P Frequency of a random event Determination of probability P 4 Application of combinatorics to counting
In terms of S, the event that the system is not closed can be written: S = A 1 A 2 +B = (A 1 + A 2)+B. 2.18. Similar to solving problems 2.5, 2.6, we obtain S = A(B 1 +B 2) C D; S = A + B 1 B 2 + C
Topic 8 Discrete random variables. Often the result of a random experiment is a number. For example, you can throw a die and get one of the numbers:,3,4,5,6. You can drive to a gas station
Conditional probability. Probability multiplication theorem Number:..B Problem: The probability of the joint occurrence of independent events A and B is determined by the formula Answers:). P(A) PA(B)). P(A) + P(B)).
Lecture 10 TOPIC Basics of probability theory (part 2). Author: Maxim Igorevich Pisarevsky, Teacher at the Pre-University Training Center of National Research Nuclear University MEPhI. Moscow, 2017 Definitions and properties Basic definitions of the theory
Assignment Solving problems in probability theory Topic: “Probability of a random event.” Task. The coin is tossed three times in a row. By the outcome of the experiment we mean the sequence X X X. where each
Test 01 1. Random events and their classification. 2. Mathematical expectation of a random variable. 3. There are 15 red, 9 blue and 6 green balls in a box. 6 balls are drawn at random. What is the probability
LESSON 1 RANDOM EVENTS The main concept of natural science is the concept of experiment, regardless of whether this experiment is carried out by nature or by a researcher. Conventionally, we will assume that the experiment
Solving problems from the collection Chudesenko Theory of Probability Problems -0. Option 6 Problem. Two dice are thrown. Determine the probability that: a) the sum of the number of points does not exceed N; b) work
TOMSK STATE UNIVERSITY Faculty of Economics PRACTICUM ON PROBABILITY THEORY AND MATHEMATICAL STATISTICS FOR ECONOMISTS PART Tomsk 06 APPROVED by the Department of Mathematical Methods and Information
1 PART I. PROBABILITY THEORY CHAPTER 1. 1. Elements of combinatorics Definition 1. Examples: Definition. -factorial is a number denoted by!, and! = 1** * for all natural numbers 1, ; Besides,
Paragraph: General concepts Probability theory Random events Definition: Probability theory is a mathematical science that studies quantitative patterns in random phenomena. Probability theory is not
Assessment tools for ongoing monitoring of academic performance, intermediate certification based on the results of mastering the discipline and educational and methodological support for students’ independent work 1 Test options
Vorobiev V.V. "Lyceum" of Kalachinsk, Omsk Region Workshop on solving problems in probability theory and mathematical statistics. An important role in studying topics in probability theory and statistics is played by
A.V. Clubless Theory of Probability Textbook Nizhny Novgorod 06 Ministry of Education and Science of the Russian Federation Federal State Budgetary Educational Institution of Higher Professional Education
Chudesenko's problem book, probability theory, option Two dice are thrown. Determine the probability that: a the sum of the number of points does not exceed N; b the product of the number of points does not exceed N; V
Compiled by: Associate Professor of the Department of Medical and Biological Physics Romanova N.Yu. Probability theory 1 lecture Introduction. Probability theory is a mathematical science that studies the patterns of random phenomena.
MVDubatovskaya Probability theory and mathematical statistics Lecture 3 Methods for determining probabilities 0 Classical determination of probabilities We will call any of the possible results of an experiment elementary
1. The train consists of 12 cars. Each of the 7 passengers chooses any carriage at random. Find the probabilities of the following events: A = (all passengers boarded the first three cars); B = (all passengers boarded in different
Elements of probability theory Random events Deterministic processes In science and technology, processes are considered whose outcome can be predicted with confidence: If a difference is applied to the ends of the conductor
Federal Agency for Education State educational institution of higher professional education "NATIONAL RESEARCH TOMSK POLYTECHNIC UNIVERSITY" LECTURE ON THEORY
1 Classic definition of probability 1 A deck of 3 cards is carefully shuffled Find the probability that all four aces are in the deck one after the other, without interspersing other cards Solution Number
Lecture 3 CONDITIONAL PROBABILITY AND INDEPENDENCE OF EVENTS COMPLETE PROBABILITY FORMULA AND BAYES' THEOREM PURPOSE OF THE LECTURE: to define the concepts of conditional probability and independence of events; construct a multiplication rule
CONTROL TASKS Assignment. You need to solve the problem corresponding to the number of your option. The box contains reels of four colors: white 5 red green blue 0. What is the probability that at random
1. There are 14 apples in the basket, including 4 red ones. They took out 4 apples at random (without returning). Find the probability that you got exactly 3 red ones. 2. A list of 20 business calls is drawn up randomly.
1. The numbers 1,..., n are arranged in random order. Find the probability that the numbers 1, 2 and 3 are located next to each other in the given order. 2. Out of ten teams, four make it to the finals. Assuming that each
FEDERAL STATE BUDGETARY EDUCATIONAL INSTITUTION OF HIGHER PROFESSIONAL EDUCATION "Chelyabinsk State Academy of Culture and Art" Department of Informatics PROBABILITY THEORY
TOPIC 1 Combinatorics Calculation of probabilities Problem 1B 17 teams take part in the national football cup. How many ways are there to distribute gold, silver and bronze medals? Because the