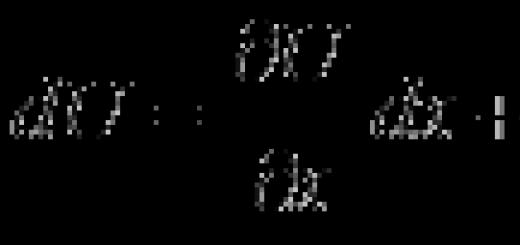Описание решения. Уравнения в полных дифференциалах Найти функцию по ее полному дифференциалу примеры

Постановка задачи в двумерном случае

Восстановление функции нескольких переменных по ее полному дифференциалу

9.1. Постановка задачи в двумерном случае. 72

9.2. Описание решения. 72

Это одно из приложений криволинейного интеграла II рода.

Дано выражение полного дифференциала функции двух переменных:

Найти функцию .

1. Так как не всякое выражение вида является полным дифференциалом некоторой функции U (x ,y ), то необходимо проверить корректность постановки задачи, то есть проверить необходимое и достаточное условие полного дифференциала, которое для функции 2-х переменных имеет вид . Это условие следует из эквивалентности утверждений (2) и (3) в теореме предыдущего параграфа. Если обозначенное условие выполнено, то задача имеет решение, то есть функцию U (x ,y ) восстановить можно; если условие не выполнено, то задача не имеет решения, то есть функцию восстановить нельзя.

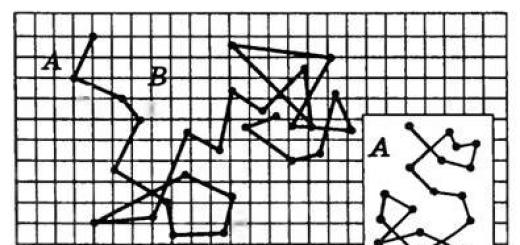
2. Найти функцию по ее полному дифференциалу можно, например, с помощью криволинейного интеграла II рода, вычислив его от по линии, соединяющей фиксированную точку (x 0 ,y 0) и переменную точку (x;y ) (Рис. 18 ):

Таким образом получено, что криволинейный интеграл II рода от полного дифференциала dU (x ,y ) равен разности значений функции U (x ,y ) в конечной и начальной точках линии интегрирования.

Зная теперь этот результат, нужно подставить вместо dU в криволинейный интеграл выражение и провести вычисление интеграла по ломаной (ACB ), учитывая его независимость от формы линии интегрирования:

на (AC ): на (СВ ) :

(1)

Таким образом, получена формула, с помощью которой восстанавливается функция 2-х переменных по ее полному дифференциалу .

3. Восстановить функцию по ее полному дифференциалу можно только с точностью до постоянного слагаемого, так как d (U + const) = dU . Поэтому в результате решения задачи получаем множество функций, отличающихся друг от друга на постоянное слагаемое.

Примеры (восстановление функции двух переменных по ее полному дифференциалу)

1. Найти U (x ,y ), если dU = (x 2 – y 2)dx – 2xydy .

Проверяем условие полного дифференциала функции двух переменных:

Условие полного дифференциала выполнено, значит, функцию U (x ,y ) восстановить можно.

Проверка: – верно.

Ответ: U (x ,y ) = x 3 /3 – xy 2 + C .

2. Найти функцию , такую что

Проверяем необходимые и достаточные условия полного дифференциала функции трех переменных: , , , если дано выражение .

В решаемой задаче

все условия полного дифференциала выполнены, следовательно, функцию восстановить можно (задача поставлена корректно).

Будем восстанавливать функцию с помощью криволинейного интеграла II рода, вычислив его по некоторой линии, соединяющей фиксированную точку и переменную точку , так как

(это равенство выводится так же, как и в двумерном случае).

С другой стороны, криволинейный интеграл II рода от полного дифференциала не зависит от формы линии интегрирования, поэтому его проще всего считать по ломаной, состоящей из отрезков, параллельных осям координат. При этом в качестве фиксированной точки можно взять для просто ты взять точку с конкретными числовыми координатами, отслеживая лишь только, чтобы в этой точке и на всей линии интегрирования выполнилось условие существования криволинейного интеграла (то есть чтобы функции , и были непрерывными). С учетом этого замечания в данной задаче можно взять фиксированной точкой, например, точку М 0 . Тогда на каждой из звеньев ломаной будем иметь

10.2. Вычисление поверхностного интеграла I рода. 79

10.3. Некоторые приложения поверхностного интеграла I рода. 81

некоторых функций. Если восстановить функцию по ее полному дифференциалу, то найдем общий интеграл дифференциального уравнения. Ниже поговорим о методе восстановления функции по ее полному дифференциалу .

Левая часть дифференциального уравнения - это полный дифференциал некоторой функции U(x, y) = 0 , если выполняется условие .

Т.к. полный дифференциал функции U(x, y) = 0 это , значит, при выполнении условия утверждают, что .

Тогда, .

Из первого уравнения системы получаем . Функцию находим, воспользовавшись вторым уравнением системы:

Таким образом мы найдем искомую функцию U(x, y) = 0 .

Пример.

Найдем общее решение ДУ .

Решение.

В нашем примере . Условие выполняется, потому что:

Тогда, левая часть начального ДУ является полным дифференциалом некоторой функции U(x, y) = 0 . Нам необходимо найти эту функцию.

Т.к. является полным дифференциалом функции U(x, y) = 0 , значит:

Интегрируем по x 1-е уравнение системы и дифференцируем по y результат:

Из 2-го уравнения системы получаем . Значит:

Где С - произвольная постоянная.

Т.о., и общим интегралом заданного уравнения будет .

Есть второй метод вычисления функции по ее полному дифференциалу . Он состоит во взятии криволинейного интеграла от фиксированной точки (x 0 , y 0) до точки с переменными координатами (x, y) : . В таком случае значение интеграла не зависимо от пути интегрирования. Удобно брать в качестве пути интегрирования ломаную, звенья которой параллельны осям координат.

Пример.

Найдем общее решение ДУ .

Решение.

Проверяем выполнение условия :

Т.о., левая часть ДУ является полным дифференциалом некоторой функции U(x, y) = 0 . Найдем эту функцию, вычислив криволинейный интеграл от точки (1; 1) до (x, y) . Как путь интегрирования берем ломаную: первый участок ломаной пройдем по прямой y = 1 от точки (1, 1) до(x, 1) , вторым участком пути берем отрезок прямой от точки (x, 1) до (x, y) :

Значит, общее решение ДУ выглядит так: .

Пример.

Определим общее решение ДУ .

Решение.

Т.к. , значит, условие не выполняется, тогда, левая часть ДУ не будет полным дифференциалом функции и нужно использовать второй способ решения (это уравнение является дифференциальным уравнением с разделяющимися переменными).

Может случиться, что левая часть дифференциального уравнения

является полным дифференциалом некоторой функции :

и следовательно, уравнение (7) принимает вид .

Если функция является решением уравнения (7), то , и, следовательно,

где - постоянная, и наоборот, если некоторая функция обращает в тождество конечное уравнение (8), то, дифференцируя полученное тождество, получим , и следовательно, , где - произвольная постоянная, является общим интегралом исходного уравнения.

Если даны начальные значения , то постоянная определяется из (8) и

является искомым частным интегралом. Если в точке , то уравнение (9) определяет как неявную функцию от .

Для того, чтобы левая часть уравнения (7) являлась полным дифференциалом некоторой функции , необходимо и достаточно, чтобы

Если это условие, указанное Эйлером, выполнено, то уравнение (7) легко интегрируется. Действительно, . С другой стороны, . Следовательно,

При вычислении интеграла величина рассматривается как постоянная, поэтому является произвольной функцией от . Для определения функции дифференцируем найденную функцию по и, так как , получим

Из этого уравнения определяем и, интегрируя, находим .

Как известно из курса математического анализа, еще проще можно определить функцию по ее полному дифференциалу , взяв криволинейный интеграл от между некоторой фиксированной точкой и точкой с переменными координатами по любому пути:

Чаще всего в качестве пути интегрирования удобно брать ломаную, составленную из двух звеньев, параллельных осям координат; в этом случае

Пример. .

Левая часть уравнения является полным дифференциалом некоторой функции , так как

Следовательно, общий интеграл имеет вид

Можно применить и другой метод определения функции :

За начальную точку выбираем, например, начало координат, в качестве пути интегрирования -ломаную. Тогда

и общий интеграл имеет вид

Что совпадает с предыдущим результатом, приводя к общему знаменателю.

В некоторых случаях, когда левая часть уравнения (7) не является полным дифференциалом, легко удается подобрать функцию , после умножения на которую левая часть уравнения (7) превращается в полный дифференциал . Такая функция называется интегрирующим множителем . Заметим, что умножение на интегрирующий множитель может привести к появлению лишних частных решений, обращающих этот множитель в нуль.

Пример . .

Очевидно, что после умножения на множитель левая часть превращается в полный дифференциал. Действительно, после умножения на получим

или, интегрируя, . Умножая на 2 и потенцируя, будем иметь .

Конечно, далеко не всегда интегрирующий множитель подбирается столь легко. В общем случае для нахождения интегрирующего множителя надо подобрать хотя бы одно не равное тождественно нулю частное решение уравнения в частных производных , или в развернутом виде

которое после деления на и переноса некоторых слагаемых в другую часть равенства приводится к виду

В общем случае интегрирование этого уравнения в частных производных является задачей отнюдь не более простой, чем интегрирование исходного уравнения, однако в некоторых случаях подбор частного решения уравнения (11) не представляет затруднений.

Кроме того, считая, что интегрирующий множитель является функцией только одного аргумента (например, является функцией только или только , или функцией только , или только и т.д.), можно уже без труда проинтегрировать уравнение (11) и указать условия, при которых интегрирующий множитель рассматриваемого вида существует. Тем самым выделяются классы уравнений, для которых интегрирующий множитель легко может быть найден.

Например, найдем условия, при которых уравнение имеет интегрирующий множитель, зависящий только от , т.е. . При этом уравнение (11) упрощается и приобретает вид , откуда, считая непрерывной функцией от , получим

Если является функцией только от , то интегрирующий множитель, зависящий лишь от , существует и равен (12), в противном случае интегрирующего множителя вида не существует.

Условие существования интегрирующего множителя, зависящего только от , выполнено, например, для линейного уравнения или . Действительно, и, следовательно, . Совершенно аналогично могут быть найдены условия существования интегрирующих множителей вида и т.д.

Пример. Имеет ли уравнение интегрирующий множитель вида ?

Обозначим . Уравнение (11) при принимает вид , откуда или

Для существования интегрирующего множителя заданного вида необходимо и в предположении непрерывности достаточно, чтобы была функцией только . В данном случае , следовательно, интегрирующий множитель существует и равен (13). При получим . Умножая исходное уравнение на , приведем его к виду

Интегрируя, получим , а после потенцирования будем иметь , или в полярных координатах - семейство логарифмических спиралей.

Пример . Найти форму зеркала, отражающего параллельно данному направлению все лучи, выходящие из заданной точки.

Поместим начало координат в заданную точку и направим ось абсцисс параллельно заданному в условиях задачи направлению. Пусть луч падает на зеркало в точке . Рассмотрим сечение зеркала плоскостью , проходящее через ось абсцисс и точку . Проведем касательную к рассматриваемому сечению поверхности зеркала в точке . Так как угол падения луча равен углу отражения, то треугольник - равнобедренный. Следовательно,

Полученное однородное уравнение легко интегрируется заменой переменных , но еще проще, освободившись от иррациональности в знаменателе, переписать его в виде . Это уравнение имеет очевидный интегрирующий множитель , , , (семейство парабол).

Эта задача еще проще решается в координатах и , где , при этом уравнение сечения искомых поверхностей приобретает вид .

Можно доказать существование интегрирующего множителя, или, что то же самое, существование ненулевого решения уравнения в частных производных (11) в некоторой области, если функции и имеют непрерывные производные и по крайней мере одна из этих функций не обращается в нуль. Следовательно, метод интегрирующего множителя можно рассматривать как общий метод интегрирования уравнений вида , однако ввиду трудности нахождения интегрирующего множителя этот метод чаще всего применяется в тех случаях, когда интегрирующий множитель очевиден.

В этой теме мы рассмотрим метод восстановления функции по ее полному дифференциалу, дадим примеры задач с полным разбором решения.

Бывает так, что дифференциальные уравнения (ДУ) вида P (x , y) d x + Q (x , y) d y = 0 могут содержать в левых частях полные дифференциалы некоторых функций. Тогда мы можем найти общий интеграл ДУ, если предварительно восстановим функцию по ее полному дифференциалу.

Пример 1

Рассмотрим уравнение P (x , y) d x + Q (x , y) d y = 0 . В записи левой его части содержится дифференциал некоторой функции U (x , y) = 0 . Для этого должно выполняться условие ∂ P ∂ y ≡ ∂ Q ∂ x .

Полный дифференциал функции U (x , y) = 0 имеет вид d U = ∂ U ∂ x d x + ∂ U ∂ y d y . С учетом условия ∂ P ∂ y ≡ ∂ Q ∂ x получаем:

P (x , y) d x + Q (x , y) d y = ∂ U ∂ x d x + ∂ U ∂ y d y

∂ U ∂ x = P (x , y) ∂ U ∂ y = Q (x , y)

Преобразовав первое уравнение из полученной системы уравнений, мы можем получить:

U (x , y) = ∫ P (x , y) d x + φ (y)

Функцию φ (y) мы можем найти из второго уравнения полученной ранее системы:
∂ U (x , y) ∂ y = ∂ ∫ P (x , y) d x ∂ y + φ y " (y) = Q (x , y) ⇒ φ (y) = ∫ Q (x , y) - ∂ ∫ P (x , y) d x ∂ y d y

Так мы нашли искомую функцию U (x , y) = 0 .

Пример 2

Найдите для ДУ (x 2 - y 2) d x - 2 x y d y = 0 общее решение.

Решение

P (x , y) = x 2 - y 2 , Q (x , y) = - 2 x y

Проверим, выполняется ли условие ∂ P ∂ y ≡ ∂ Q ∂ x:

∂ P ∂ y = ∂ (x 2 - y 2) ∂ y = - 2 y ∂ Q ∂ x = ∂ (- 2 x y) ∂ x = - 2 y

Наше условие выполняется.

На основе вычислений мы можем сделать вывод, что левая часть исходного ДУ является полным дифференциалом некоторой функции U (x , y) = 0 . Нам нужно найти эту функцию.

Так как (x 2 - y 2) d x - 2 x y d y является полным дифференциалом функции U (x , y) = 0 , то

∂ U ∂ x = x 2 - y 2 ∂ U ∂ y = - 2 x y

Интегрируем по x первое уравнение системы:

U (x , y) = ∫ (x 2 - y 2) d x + φ (y) = x 3 3 - x y 2 + φ (y)

Теперь дифференцируем по y полученный результат:

∂ U ∂ y = ∂ x 3 3 - x y 2 + φ (y) ∂ y = - 2 x y + φ y " (y)

Преобразовав второе уравнение системы, получаем: ∂ U ∂ y = - 2 x y . Это значит, что
- 2 x y + φ y " (y) = - 2 x y φ y " (y) = 0 ⇒ φ (y) = ∫ 0 d x = C

где С – произвольная постоянная.

Получаем: U (x , y) = x 3 3 - x y 2 + φ (y) = x 3 3 - x y 2 + C . Общим интегралом исходного уравнения является x 3 3 - x y 2 + C = 0 .

Разберем еще один метод нахождения функции по известному полному дифференциалу. Он предполагает применение криволинейного интеграла от фиксированной точки (x 0 , y 0) до точки с переменными координатами (x , y) :

U (x , y) = ∫ (x 0 , y 0) (x , y) P (x , y) d x + Q (x , y) d y + C

В таких случаях значение интеграла никак не зависит от пути интегрирования. Мы можем взять в качестве пути интегрировании ломаную, звенья которой располагаются параллельно осям координат.

Пример 3

Найдите общее решение дифференциального уравнения (y - y 2) d x + (x - 2 x y) d y = 0 .

Решение

Проведем проверку, выполняется ли условие ∂ P ∂ y ≡ ∂ Q ∂ x:

∂ P ∂ y = ∂ (y - y 2) ∂ y = 1 - 2 y ∂ Q ∂ x = ∂ (x - 2 x y) ∂ x = 1 - 2 y

Получается, что левая часть дифференциального уравнения представлена полным дифференциалом некоторой функции U (x , y) = 0 . Для того, чтобы найти эту функцию, необходимо вычислить криволинейный интеграл от точки (1 ; 1) до (x , y) . Возьмем в качестве пути интегрирования ломаную, участки которой пройдут по прямой y = 1 от точки (1 , 1) до (x , 1) , а затем от точки (x , 1) до (x , y) :

∫ (1 , 1) (x , y) y - y 2 d x + (x - 2 x y) d y = = ∫ (1 , 1) (x , 1) (y - y 2) d x + (x - 2 x y) d y + + ∫ (x , 1) (x , y) (y - y 2) d x + (x - 2 x y) d y = = ∫ 1 x (1 - 1 2) d x + ∫ 1 y (x - 2 x y) d y = (x y - x y 2) y 1 = = x y - x y 2 - (x · 1 - x · 1 2) = x y - x y 2

Мы получили общее решение дифференциального уравнения вида x y - x y 2 + C = 0 .

Пример 4

Определите общее решение дифференциального уравнения y · cos x d x + sin 2 x d y = 0 .

Решение

Проверим, выполняется ли условие ∂ P ∂ y ≡ ∂ Q ∂ x .

Так как ∂ (y · cos x) ∂ y = cos x , ∂ (sin 2 x) ∂ x = 2 sin x · cos x , то условие выполняться не будет. Это значит, что левая часть дифференциального уравнения не является полным дифференциалом функции. Это дифференциальное уравнение с разделяющимися переменными и для его решения подходят другие способы решения.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Дифференциальным называется уравнение вида

P (x,y )dx + Q (x,y )dy = 0 ,

где левая часть является полным дифференциалом какой-либо функции двух переменных.

Обозначим неизвестную функцию двух переменных (её-то и требуется найти при решении уравнений в полных дифференциалах) через F и скоро вернёмся к ней.

Первое, на что следует обратить внимание: в правой части уравнения обязательно должен быть нуль, а знак, соединяющий два члена в левой части, должен быть плюсом.

Второе - должно соблюдаться некоторое равенство, которое является подтверждением того, что данное дифференциальное уравнение является уравнением в полных дифференциалах. Эта проверка является обязательной частью алгоритма решения уравнений в полных дифференциалах (он во втором параграфе этого урока), так процесс поиска функции F достаточно трудоёмкий и важно на начальном этапе убедиться в том, что мы не потратим время зря.

Итак, неизвестную функцию, которую требуется найти, обозначили через F . Сумма частных дифференциалов по всем независимым переменным даёт полный дифференциал. Следовательно, если уравнение является уравнением в полных дифференциалах, левая часть уравнения представляет собой сумму частных дифференциалов. Тогда по определению

dF = P (x,y )dx + Q (x,y )dy .

Вспоминаем формулу вычисления полного дифференциала функции двух переменных:

Решая два последних равенства, можем записать

Первое равенство дифференцируем по переменной "игрек", второе - по переменной "икс":

что является условием того, что данное дифференциальное уравнение действительно представляет собой уравнение в полных дифференциалах.

Алгоритм решения дифференциальных уравнений в полных дифференциалах

Шаг 1. Убедиться, что уравнение является уравнением в полных дифференциалах. Для того, чтобы выражение было полным дифференциалом некоторой функции F (x, y ) , необходимо и достаточно, чтобы . Иными словами, нужно взять частную производную по x и частную производную по y другого слагаемого и, если эти производные равны, то уравнение является уравнением в полных дифференциалах.

Шаг 2. Записать систему уравнений из частных производных, составляющих функцию F :

Шаг 3. Проинтегрировать первое уравнение системы - по x (y F :

,
y .

Альтернативный вариант (если так интеграл найти проще) - проинтегрировать второе уравнение системы - по y (x остаётся константой и выносится за знак интеграла). Таким образом так же восстанавливается функция F :

,
где - пока неизвестная функция от х .

Шаг 4. Результат шага 3 (найденный общий интеграл) продифференцировать по y (в альтернативном варианте - по x ) и приравнять ко второму уравнению системы:

а в альтернативном варианте - к первому уравнению системы:

Из полученного уравнения определяем (в альтернативном варианте )

Шаг 5. Результат шага 4 интегрировать и найти (в альтернативном варианте найти ).

Шаг 6. Результат шага 5 подставить в результат шага 3 - в восстановленную частным интегрированием функцию F . Произвольную постоянную C чаще записывают после знака равенства - в правой части уравнения. Таким образом получаем общее решение дифференциального уравнения в полных дифференциалах. Оно, как уже говорилось, имеет вид F (x, y ) = C .

Примеры решений дифференциальных уравнений в полных дифференциалах

Пример 1.

Шаг 1. уравнением в полных дифференциалах x одного слагаемого в левой части выражения

и частную производную по y другого слагаемого
уравнением в полных дифференциалах .

Шаг 2. F :

Шаг 3. по x (y остаётся константой и выносится за знак интеграла). Таким образом восстанавливаем функцию F :

где - пока неизвестная функция от y .

Шаг 4. y

Шаг 5.

Шаг 6. F . Произвольную постоянную C :
.

Какая ошибка возможна здесь с наибольшей вероятностью? Самые распространённые ошибки - принять частный интеграл по одной из переменных за обычный интеграл произведения функций и пытаться интегрировать по частям или заменной переменной а также принять частную производную двух сомножителей за производную произведения функций и искать производную по соответствующей формуле.

Это надо запомнить: при вычислении частного интеграла по одной из переменной другая является константой и выносится за знак интеграла, а при вычислении частной производной по одной из переменной другая также является константой и производная выражения находится как производная "действующей" переменной, умноженной на константу.

Среди уравнений в полных дифференциалах не редкость - примеры с экспонентой. Таков следующий пример. Он же примечателен и тем, что в его решении используется альтернативный вариант.

Пример 2. Решить дифференциальное уравнение

Шаг 1. Убедимся, что уравнение является уравнением в полных дифференциалах . Для этого находим частную производную по x одного слагаемого в левой части выражения

и частную производную по y другого слагаемого
. Эти производные равны, значит, уравнение является уравнением в полных дифференциалах .

Шаг 2. Запишем систему уравнений из частных производных, составляющих функцию F :

Шаг 3. Проинтегрируем второе уравнение системы - по y (x остаётся константой и выносится за знак интеграла). Таким образом восстанавливаем функцию F :

где - пока неизвестная функция от х .

Шаг 4. Результат шага 3 (найденный общий интеграл) продифференцируем по х

и приравняем к первому уравнению системы:

Из полученного уравнения определяем :
.

Шаг 5. Результат шага 4 интегрируем и находим :
.

Шаг 6. Результат шага 5 подставляем в результат шага 3 - в восстановленную частным интегрированием функцию F . Произвольную постоянную C записываем после знака равенства. Таким образом получаем общее решение дифференциального уравнения в полных дифференциалах :
.

В следующем примере возвращаемся от альтернативного варианта к основному.

Пример 3. Решить дифференциальное уравнение

Шаг 1. Убедимся, что уравнение является уравнением в полных дифференциалах . Для этого находим частную производную по y одного слагаемого в левой части выражения

и частную производную по x другого слагаемого
. Эти производные равны, значит, уравнение является уравнением в полных дифференциалах .

Шаг 2. Запишем систему уравнений из частных производных, составляющих функцию F :

Шаг 3. Проинтегрируем первое уравнение системы - по x (y остаётся константой и выносится за знак интеграла). Таким образом восстанавливаем функцию F :

где - пока неизвестная функция от y .

Шаг 4. Результат шага 3 (найденный общий интеграл) продифференцируем по y

и приравняем ко второму уравнению системы:

Из полученного уравнения определяем :
.

Шаг 5. Результат шага 4 интегрируем и находим :

Пример 4. Решить дифференциальное уравнение

Шаг 1. Убедимся, что уравнение является уравнением в полных дифференциалах . Для этого находим частную производную по y одного слагаемого в левой части выражения

и частную производную по x другого слагаемого
. Эти производные равны, значит, уравнение является уравнением в полных дифференциалах.

Шаг 2. Запишем систему уравнений из частных производных, составляющих функцию F :