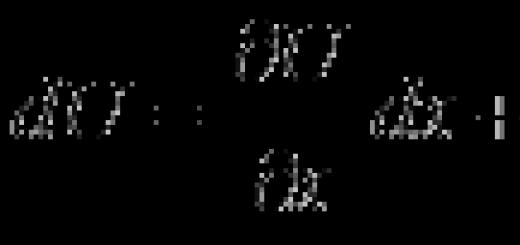XIX век является началом нового, четвертого периода в истории математики – периода современной математики.

Мы уже знаем , что одним из главных направлений развития математики в четвертом периоде является усиление строгости доказательств во всей математике, особенно перестройка математического анализа на логической основе. Во второй половинеXVIII в. делались многократные попытки перестройки математического анализа: введение определения предела (Даламбер и др.), определение производной как предела отношения (Эйлер и др.), результаты Лагранжа и Карно и т. д., но этим работам не хватало системы, а иногда они были неудачны. Однако они готовили почву, на которой перестройка в XIX в. смогла быть осуществлена. В XIX в. это направление развития математического анализа стало ведущим. Им занялись О.Коши, Б. Больцано, К. Вейерштрасс и др.

1.Огюстен Луи Коши (1789−1857) окончил в Париже Политехническую школу и Институт путей сообщения. С 1816 г. член Парижской академии и профессор Политехнической школы. В 1830−1838 гг. в годы республики он был в эмиграции из-за своих монархистских убеждений. С 1848 г. Коши стал профессором Сорбонны – Парижского университета. Он опубликовал более 800 работ по математическому анализу, дифференциальным уравнениям, теории функций комплексной переменной, алгебре, теории чисел, геометрии, механике, оптике и др. Главными областями его научных интересов были математический анализ и теория функций комплексной переменной.

Свои лекции по анализу, прочитанные в Политехнической школе, Коши издал в трех сочинениях: «Курс анализа» (1821), «Резюме лекций по исчислению бесконечно малых» (1823), «Лекция по приложениям анализа к геометрии», 2 тома (1826, 1828). в этих книгах впервые математический анализ строится на основе теории пределов. они означали начало коренной перестройки математического анализа.

Коши дает следующее определение предела переменной: « Если значения, последовательно приписываемые одной и той же переменной, неограниченно приближаются к фиксированному значению, так что в конце концов отличаются от него сколь угодно мало, то последнее называют пределом всех остальных». Суть дела здесь выражена хорошо, но слова « сколь угодно мало» сами нуждаются в определении, а кроме того, здесь формулируется определение предела переменной, а не предела функции. Далее автор доказывает различные свойства пределов.

Затем Коши приводит такое определение непрерывности функции: функция называется непрерывной (в точке), если бесконечно малое приращение аргумента порождает бесконечно малое приращение функции, т.е., на современном языке

Потом у него следуют различные свойства непрерывных функций.

В первой книге рассматривает также теорию рядов: дает определение суммы числового ряда как предела его частичной суммы, вводит ряд достаточных признаков сходимости числовых рядов, а также степенные ряды и область их сходимости – все это как в действительной, так и в комплексной области.

Дифференциальное и интегральное исчисление он излагает во второй книге.

Коши дает определение производной функции как предела отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, и дифференциал, как предела отношения приОтсюда следует, что. Далее рассматриваются обычные формулы производных; при этом автор часто использует теорему Лагранжа о средних значениях.

В интегральном исчислении Коши впервые выдвигает в качестве основного понятия определенный интеграл. Он вводит его также впервые, как предел интегральных сумм. Здесь же доказывается важная теорема об интегрируемости непрерывной функции. Неопределенный интеграл у него определяется как такая функцияаргументачтоКроме того, здесь рассматриваются разложения функций в ряды Тейлора и Маклорена.

Во второй половине XIX в. ряд ученых: Б. Риман, Г. Дарбу и др. нашли новые условия интегрируемости функции и даже изменили само определение определенного интеграла таким образом, чтобы его можно было применить к интегрированию некоторых разрывных функций.

В теории дифференциальных уравнений Коши занимался, главным образом, доказательствами принципиально важных теорем существования: существования решения обыкновенного дифференциального уравнения сначала первого, а потом -го порядка; существования решения для линейной системы уравнений с частными производными.

В теории функций комплексной переменной Коши является основоположником; ей посвящены многие его статьи. В XVIII в. Эйлер и Даламбер положили лишь начало этой теории. В вузовском курсе теории функций комплексной переменной мы постоянно встречаем имя Коши: условия Коши − Римана существования производной, интеграл Коши, интегральная формула Коши и т.д.; многие теоремы о вычетах функции также принадлежат Коши. В этой области получили весьма важные результаты также Б.Риман, К. Вейерштрасс, П. Лоран и др.

Вернемся к основным понятиям математического анализа. Во второй половине века выяснилось, что в области обоснования анализа многое сделал до Коши и Вейерщтрасса чешский ученый Бернард Больцано (1781 – 1848). Он до Коши дал определения предела, непрерывности функции и сходимости числового ряда, доказал критерий сходимости числовой последовательности, а также, задолго до того, как она появилась у Вейерштрасса, теорему: если числовое множество ограниченно сверху (снизу), то оно имеет точную верхнюю (точную нижнюю) грань. Он рассмотрел ряд свойств непрерывных функций; вспомним, что в вузовском курсе математического анализа имеются теоремы Больцано – Коши и Больцано – Вейерштрасса о функциях, непрерывных на отрезке. Больцано исследовал и некоторые вопросы математического анализа, например, построил первый пример функции, непрерывной на отрезке, но не имеющей производной ни в одной точке отрезка. При жизни Больцано смог опубликовать только пять небольших работ, поэтому его результаты стали известны слишком поздно.

2.В математическом анализе все явственнее чувствовалось отсутствие четкого определения функции. Значительный вклад в решение спора о том, что понимать под функцией, внес французский ученый Жан Фурье. Он занимался математической теорией теплопроводности в твердом теле и в связи с этим использовал тригонометрические ряды (ряды Фурье)

эти ряды позднее стали широко применяться в математической физике – науке, которая занимается математическими методами исследования встречающихся в физике дифференциальных уравнений в частных производных. Фурье доказал, что любую непрерывную кривую, независимо от того, из каких разнородных частей она составлена, можно задать единым аналитическим выражением – тригонометрическим рядом, и что это можно сделать и для некоторых кривых с разрывами. Исследование таких рядов, проведенное Фурье, вновь поставило вопрос, что же понимать под функцией. Можно ли считать, что подобная кривая задает функцию? (Это возобновление старого спора XVIII в о соотношении между функцией и формулой на новом уровне.)

В 1837 г. немецкий математик П. Дирехле впервые дал современное определение функции: « есть функция переменной(на отрезкеесли каждому значению(на этом отрезке) соответствует совершенно определенное значение, причем безразлично, каким образом установлено это соответствие – аналитической формулой, графиком, таблицей либо даже просто словами». Обращает на себя внимание добавление: «безразлично, каким образом установлено это соответствие». Определение Дирехле получило общее признание довольно быстро. Правда, сейчас принято функцией называть само соответствие.

3.Современный стандарт строгости в математическом анализе впервые появился в работах Вейерштрасса (1815−1897) долгое время работал учителем математики в гимназиях, а в 1856 г. стал профессором Берлинского университета. Слушатели его лекций постепенно издавали их в виде отдельных книг, благодаря чему содержание лекций Вейерштрасса стало хорошо известным в Европе. Именно Вейерштрасс стал систематически употреблять в математическом анализе язык Он дал определение предела последовательности, определение предела функции на языке(которое часто неправильно называют определением Коши), строго доказал теоремы о пределах и так называемую теорему Вейерштрасса о пределе монотонной последовательности: возрастающая (убывающая) последовательность, ограниченная сверху (снизу), имеет конечный предел. Он стал использовать понятия точной верхней и точной нижней грани числового множества, понятие предельной точки множества, доказал теорему (у которой есть и другой автор – Больцано): ограниченное числовое множество имеет предельную точку, рассмотрел некоторые свойства непрерывных функций. Много работ Вейерштрасс посвятил теории функций комплексной переменной, обосновав ее с помощью степенных рядов. Он занимался также вариационным исчислением, дифференциальной геометрией и линейной алгеброй.

4.Остановимся еще на теории бесконечных множеств. Ее создателем был немецкий математик Кантор. Георг Кантор (18451918) много лет работал профессором университета в Галле. Работы по теории множеств опубликовал, начиная с 1870г. Он доказал несчетность множества действительных чисел, установив, таким образом, существование неэквивалентных бесконечных множеств, ввел общее понятие мощности множества, выяснил принципы сравнения мощностей. Кантор построил теорию трансфинитных, «несобственных» чисел, приписав низшее, наименьшее трансфинитное число мощности счетного множества (в частности, множества натуральных чисел), мощности множества действительных чисел – более высокое, большее трансфинитное число, и т.д.; это дало ему возможность построить арифметику трансфинитных чисел, похожую на обычную арифметику натуральных чисел. Кантор систематически применял актуальную бесконечность, например, возможность полностью «исчерпать» натуральный ряд чисел, в то время как до него в математикеXIX в. использовалась лишь потенциальная бесконечность.

Теория множеств Кантора при своем появлении вызвала возражения многих математиков, но постепенно пришло признание тогда, когда стало ясным ее огромное значение для обоснования топологии и теории функций действительной переменной. Но оставались логические пробелы в самой теории, в частности, были обнаружены парадоксы теории множеств. Вот один из наиболее известных парадоксов. Обозначим через множество всех таких множеств, которые не являются элементами самих себя. Выполняется ли включениетакже и не является элементомтак как по условию ввходят в качестве элементов только такие множества, которые не являются элементами самих себя; если жето по условию выполняется включениепротиворечие в обоих случаях.

Эти парадоксы были связаны с внутренней противоречивостью некоторых множеств. Становилось ясным, что в математике можно пользоваться не любыми множествами. Существование парадоксов было преодолено созданием уже в начале XX в. аксиоматической теории множеств (Э. Цермело, а. Френкелем, Д. Нейманом и др.), которая, в частности, отвечала на вопрос: какими множествами можно пользоваться в математике? Оказывается, можно пользоваться пустым множеством, объединением данных множеств, множеством всех подмножеств данного множества и др.

Средоточием всех наук считается философия, так как именно она включала в себя первые ростки литературы, астрономии, литературы, естествознания, математики и прочих направлений. С течением времени каждая область развивалась самостоятельно, математика не стала исключением. Первым «намеком» на анализ считается теория разложения на бесконечно малые величины, к которой пытались подступиться многие умы, однако она носила туманный характер и не имела под собой базы. Это связано с привязанностью к старой школе науки, которая была строга в своих формулировках. Исаак Ньютон был очень близок к тому, чтобы сформировать основы, но опоздал. В итоге своему появлению как обособленной системе математический анализ обязан философу Готфриду Лейбницу. Именно он в работах представил научному миру такие понятия, как минимум и максимум, точки перегиба и выпуклости графика функции, сформулировал основы дифференциального исчисления. С этого момента математику официально разделяют на элементарную и высшую.

Математический анализ. Наши дни

Любая специальность, будь она технической или гуманитарной, включает в курс обучения анализ. Глубина изучения разнится, но суть остается неизменной. Несмотря на всю «абстрактность», он является одним из столпов, на котором держится естествознание в современном его понимании. С его помощью получили развитие физика и экономика, он способен описать и спрогнозировать деятельность фондовой биржи, помочь в построении оптимального портфеля акций. Введение в математический анализ базируется на элементарных понятиях:

• множества;
• основные операции над множествами;
• свойства операций над множествами;
• функции (иначе - отображения);
• типы функций;
• последовательности;
• числовые прямые;
• предел последовательности;
• свойства пределов;
• непрерывность функции.

Стоит выделить отдельно такие понятия, как множество, точка, прямая, плоскость. Все они не имеют определений, так как являются базовыми понятиями, на которых строится вся математика. Все, что можно сделать в процессе работы - это пояснить, что именно они означают в отдельно взятых случаях.

Предел как продолжение

К основам математического анализа относится предел. На практике он представляет собой величину, к которой стремится последовательность или функция, подходит сколь угодно близко, но не достигает ее. Обозначается он как lim, рассмотрим частный случай предела функции: lim (x-1)= 0 при х→1. Из этого простейшего примера видно, что при х→1 вся функция стремится к 0, так как если подставить предел в саму функцию, то получим (1-1)=0. Подробнее, от элементарных до усложненных частных случаев, информация изложена в своеобразной «Библии» анализа - работах Фихтенгольца. Там рассматривается в разрезе математический анализ, пределы, их вывод и дальнейшее применение. Например, вывод числа e (константа Эйлера) был бы невозможен без теории пределов. Несмотря на динамическую абстрактность теории, пределы активно используются на практике все в той же экономике и социологии. Например, без них не обойтись при начислении процентов по банковскому вкладу.

English: Wikipedia is making the site more secure. You are using an old web browser that will not be able to connect to Wikipedia in the future. Please update your device or contact your IT administrator.

中文: 维基百科正在使网站更加安全。您正在使用旧的浏览器，这在将来无法连接维基百科。请更新您的设备或联络您的IT管理员。以下提供更长，更具技术性的更新（仅英语）。

Español: Wikipedia está haciendo el sitio más seguro. Usted está utilizando un navegador web viejo que no será capaz de conectarse a Wikipedia en el futuro. Actualice su dispositivo o contacte a su administrador informático. Más abajo hay una actualización más larga y más técnica en inglés.

ﺎﻠﻋﺮﺒﻳﺓ: ويكيبيديا تسعى لتأمين الموقع أكثر من ذي قبل. أنت تستخدم متصفح وب قديم لن يتمكن من الاتصال بموقع ويكيبيديا في المستقبل. يرجى تحديث جهازك أو الاتصال بغداري تقنية المعلومات الخاص بك. يوجد تحديث فني أطول ومغرق في التقنية باللغة الإنجليزية تاليا.

Français: Wikipédia va bientôt augmenter la sécurité de son site. Vous utilisez actuellement un navigateur web ancien, qui ne pourra plus se connecter à Wikipédia lorsque ce sera fait. Merci de mettre à jour votre appareil ou de contacter votre administrateur informatique à cette fin. Des informations supplémentaires plus techniques et en anglais sont disponibles ci-dessous.

日本語: ウィキペディアではサイトのセキュリティを高めています。ご利用のブラウザはバージョンが古く、今後、ウィキペディアに接続できなくなる可能性があります。デバイスを更新するか、IT管理者にご相談ください。技術面の詳しい更新情報は以下に英語で提供しています。

Deutsch: Wikipedia erhöht die Sicherheit der Webseite. Du benutzt einen alten Webbrowser, der in Zukunft nicht mehr auf Wikipedia zugreifen können wird. Bitte aktualisiere dein Gerät oder sprich deinen IT-Administrator an. Ausführlichere (und technisch detailliertere) Hinweise findest Du unten in englischer Sprache.

Italiano: Wikipedia sta rendendo il sito più sicuro. Stai usando un browser web che non sarà in grado di connettersi a Wikipedia in futuro. Per favore, aggiorna il tuo dispositivo o contatta il tuo amministratore informatico. Più in basso è disponibile un aggiornamento più dettagliato e tecnico in inglese.

Magyar: Biztonságosabb lesz a Wikipédia. A böngésző, amit használsz, nem lesz képes kapcsolódni a jövőben. Használj modernebb szoftvert vagy jelezd a problémát a rendszergazdádnak. Alább olvashatod a részletesebb magyarázatot (angolul).

Svenska: Wikipedia gör sidan mer säker. Du använder en äldre webbläsare som inte kommer att kunna läsa Wikipedia i framtiden. Uppdatera din enhet eller kontakta din IT-administratör. Det finns en längre och mer teknisk förklaring på engelska längre ned.

हिन्दी: विकिपीडिया साइट को और अधिक सुरक्षित बना रहा है। आप एक पुराने वेब ब्राउज़र का उपयोग कर रहे हैं जो भविष्य में विकिपीडिया से कनेक्ट नहीं हो पाएगा। कृपया अपना डिवाइस अपडेट करें या अपने आईटी व्यवस्थापक से संपर्क करें। नीचे अंग्रेजी में एक लंबा और अधिक तकनीकी अद्यतन है।

We are removing support for insecure TLS protocol versions, specifically TLSv1.0 and TLSv1.1, which your browser software relies on to connect to our sites. This is usually caused by outdated browsers, or older Android smartphones. Or it could be interference from corporate or personal "Web Security" software, which actually downgrades connection security.

You must upgrade your web browser or otherwise fix this issue to access our sites. This message will remain until Jan 1, 2020. After that date, your browser will not be able to establish a connection to our servers.

В истории математики условно можно выделить два основных периода: элементарной и современной математики. Рубежом, от которого принято вести отсчет эпохи новой (иногда говорят - высшей) математики, стал XVII век – век появления математического анализа. К концу XVII в. И. Ньютоном, Г. Лейбницем и их предшественниками был создан аппарат нового дифференциального исчисления и интегрального исчисления, составляющий основу математического анализа и даже, пожалуй, математическую основу всего современного естествознания.

Математический анализ – это обширная область математики с характерным объектом изучения (переменной величиной), своеобразным методом исследования (анализом посредством бесконечно малых или посредством предельных переходов), определенной системой основных понятий (функция, предел, производная, дифференциал, интеграл, ряд) и постоянно совершенствующимся и развивающимся аппаратом, основу которого составляют дифференциальное и интегральное исчисления.

Попробуем дать представление о том, какая математическая революция произошла в XVII в., чем характеризуется связанный с рождением математического анализа переход от элементарной математики к той, что ныне составляет предмет исследований математического анализа и чем объясняется его фундаментальная роль во всей современной системе теоретических и прикладных знаний.

Представьте себе, что перед вами прекрасно выполненная цветная фотография набегающей на берег штормовой океанской волны: могучая сутуловатая спина, крутая, но чуть впалая грудь, уже наклоненная вперед и готовая упасть голова с терзаемой ветром седой гривой. Вы остановили мгновение, вам удалось поймать волну, и вы можете теперь без спешки внимательно изучать ее во всех подробностях. Волну можно измерить, и, пользуясь средствами элементарной математики, вы сделаете много важных выводов об этой волне, а значит, и всех ее океанских сестрах. Но, остановив волну, вы лишили ее движения и жизни. Ее зарождение, развитие, бег, сила, с которой она обрушивается на берег, - все это оказалось вне вашего поля зрения, потому что вы не располагаете пока ни языком, ни математическим аппаратом, пригодными для описания и изучения не статических, а развивающихся, динамических процессов, переменных величин и их взаимосвязей.

«Математический анализ не менее всеобъемлющ, чем сама природа: он определяет все ощутимые взаимосвязи, измеряет времена, пространства, силы, температуры». Ж. Фурье

Движение, переменные величины и их взаимосвязи окружают нас повсюду. Различные виды движения и их закономерности составляют основной объект изучения конкретных наук: физики, геологии, биологии, социологии и др. Поэтому точный язык и соответствующие математические методы описания и изучения переменных величин оказались необходимыми во всех областях знания примерно в той же степени, в какой числа и арифметика необходимы при описании количественных соотношений. Так вот, математический анализ и составляет основу языка и математических методов описания переменных величин и их взаимосвязей. В наши дни без математического анализа невозможно не только рассчитать космические траектории, работу ядерных реакторов, бег океанской волны и закономерности развития циклона, но и экономично управлять производством, распределением ресурсов, организацией технологических процессов, прогнозировать течение химических реакций или изменение численности различных взаимосвязанных в природе видов животных и растений, потому что все это - динамические процессы.

Элементарная математика была в основном математикой постоянных величин, она изучала главным образом соотношения между элементами геометрических фигур, арифметические свойства чисел и алгебраические уравнения. Ее отношение к действительности в какой-то мере можно сравнить с внимательным, даже тщательным и полным изучением каждого фиксированного кадра киноленты, запечатлевшей изменчивый, развивающийся живой мир в его движении, которого, однако, не видно на отдельном кадре и которое можно наблюдать, только посмотрев ленту в целом. Но как кино немыслимо без фотографии, так и современная математика невозможна без той ее части, которую мы условно называем элементарной, без идей и достижений многих выдающихся ученых, разделенных порой десятками столетий.

Математика едина, и «высшая» ее часть связана с «элементарной» примерно так же, как следующий этаж строящегося дома связан с предшествующим, и ширина горизонтов, которые математика открывает нам в окружающий мир, зависит от того, на какой этаж этого здания нам удалось подняться. Родившийся в XVII в. математический анализ открыл нам возможности для научного описания, количественного и качественного изучения переменных величин и движения в широком смысле этого слова.

Каковы же предпосылки появления математического анализа?

К концу XVII в. сложилась следующая ситуация. Во-первых, в рамках самой математики за долгие годы накопились некоторые важные классы однотипных задач (например, задачи измерения площадей и объемов нестандартных фигур, задачи проведения касательных к кривым) и появились методы их решения в различных частных случаях. Во-вторых, оказалось, что эти задачи теснейшим образом связаны с задачами описания произвольного (не обязательно равномерного) механического движения, и в частности с вычислением его мгновенных характеристик (скорости, ускорения в любой момент времени), а также с нахождением величины пройденного пути для движения, происходящего с заданной переменной скоростью. Решение этих проблем было необходимо для развития физики, астрономии, техники.

Наконец, в-третьих, к середине XVII в. трудами Р. Декарта и П. Ферма были заложены основы аналитического метода координат (так называемой аналитической геометрии), позволившие сформулировать разнородные по своему происхождению геометрические и физические задачи на общем (аналитическом) языке чисел и числовых зависимостей, или, как мы теперь говорим, числовых функций.

Стечение этих обстоятельств и привело к тому, что в конце XVII в. двум ученым – И. Ньютону и Г. Лейбницу – независимо друг от друга удалось создать для решения названных задач математический аппарат, подытоживший и обобщивший отдельные результаты предшественников, среди которых и ученый древности Архимед и современники Ньютона и Лейбница – Б. Кавальери, Б. Паскаль, Д. Грегори, И. Барроу. Этот аппарат и составил основу математического анализа – нового раздела математики, изучающего различные развивающиеся процессы, т.е. взаимосвязи переменных величин, которые в математике называют функциональными зависимостями или, иначе, функциями. Кстати, сам термин «функция» потребовался и естественно возник именно в XVII в., а к настоящему времени он приобрел не только общематематическое, но и общенаучное значение.

Начальные сведения об основных понятиях и математическом аппарате анализа даны в статьях «Дифференциальное исчисление» и «Интегральное исчисление».

В заключение хотелось бы остановиться только на одном общем для всей математики и характерном для анализа принципе математического абстрагирования и в этой связи объяснить, в каком виде математический анализ изучает переменные величины и в чем секрет такой универсальности его методов для изучения всевозможных конкретных развивающихся процессов и их взаимосвязей.

Рассмотрим несколько поясняющих примеров и аналогий.

Мы порой уже не отдаем себе отчета в том, что, например, математическое соотношение , написанное не для яблок, стульев или слонов, а в отвлеченном от конкретных объектов абстрактном виде, - выдающееся научное завоевание. Это математический закон, который, как показывает опыт, применим к различным конкретным объектам. Значит, изучая в математике общие свойства отвлеченных, абстрактных чисел, мы тем самым изучаем количественные соотношения реального мира.

Например, из школьного курса математики известно, что , поэтому в конкретной ситуации вы могли бы сказать: «Если мне для перевозки 12 т грунта не выделят два шеститонных самосвала, то можно запросить три четырехтонки и работа будет выполнена, а если дадут только одну четырехтонку, то ей придется сделать три рейса». Так привычные теперь для нас отвлеченные числа и числовые закономерности связаны с их конкретными проявлениями и приложениями.

Примерно так же связаны законы изменения конкретных переменных величин и развивающихся процессов природы с той абстрактной, отвлеченной формой-функцией, в которой они появляются и изучаются в математическом анализе.

Например, абстрактное соотношение может быть отражением зависимости кассового сбора у кинотеатра от количества проданных билетов, если 20 – это 20 копеек – цена одного билета. Но если мы едем по шоссе на велосипеде, проезжая 20 км в час, то это же соотношение можно истолковать как взаимосвязь времени (часов) нашей велосипедной прогулки и покрытого за это время расстояния (километров)., вы всегда можете утверждать, что, например, изменение в несколько раз приводит к пропорциональному (т.е. во столько же раз) изменению величины , а если , то верно и обратное заключение. Значит, в частности, для увеличения кассового сбора кинотеатра в два раза вам придется привлечь вдвое больше зрителей, а для того, чтобы на велосипеде с той же скоростью проехать вдвое большее расстояние, вам придется ехать вдвое дольше.

Математика изучает и простейшую зависимость , и другие, значительно более сложные зависимости в отвлеченном от частной интерпретации, общем, абстрактном виде. Выявленные в таком исследовании свойства функции или методы изучения этих свойств будут носить характер общих математических приемов, заключений, законов и выводов, применимых к каждому конкретному явлению, в котором встречается изученная в абстрактном виде функция, независимо от того, к какой области знания это явление относится.

Итак, математический анализ как раздел математики оформился в конце XVII в. Предметом изучения в математическом анализе (как он представляется с современных позиций) являются функции, или, иначе, зависимости между переменными величинами.

С возникновением математического анализа математике стало доступно изучение и отражение развивающихся процессов реального мира; в математику вошли переменные величины и движение.

Античность

В античный период появились некоторые идеи, которые в дальнейшем привели к интегральному исчислению, но в ту эпоху эти идеи не были развиты строгим, систематическим образом. Расчёты объёмов и площадей, являющиеся одной из целей интегрального исчисления, можно найти в московском математическом папирусе из Египта (ок. 1820 до н. э.), но формулы являются скорее инструкциями, без каких-либо указаний на метод, а некоторые просто ошибочны. В эпоху греческой математики Евдокс (ок. 408-355 до н. э.) для вычисления площадей и объёмов использовал метод исчерпывания , который предвосхищает понятие предела, а позже эту идею дальше развил Архимед (ок. 287-212 до н. э.), изобретя эвристики , которые напоминают методы интегрального исчисления. Метод исчерпывания позже изобрёл в Китае Лю Хуэй в III веке нашей эры, который он использовал для вычисления площади круга. В V нашей эры Цзу Чунчжи разработал метод вычисления объёма шара, который позже назовут принципом Кавальери .

Средневековье

В XIV веке индийский математик Мадхава Сангамаграма и астрономо-математическая школа Керала ввели многие компоненты исчисления, такие как ряды Тейлора , аппроксимацию бесконечных рядов , интегральный признак сходимости , ранние формы дифференцирования, почленное интегрирование, итерационные методы для решения нелинейных уравнений и определение того, что площадь под кривой является её интегралом. Некоторые считают, что «Юктибхаза» (Yuktibhāṣā) является первым трудом по математическому анализу.

Современная эпоха

В Европе основополагающим трудом стал трактат Бонавентура Кавальери , в котором он утверждал, что объёмы и площади могут быть рассчитаны как суммы объёмов и площадей бесконечно тонкого сечения. Идеи были похожи на то, что изложил Архимед в работе «Метод», но этот трактат Архимеда был утерян до первой половины XX века. Работа Кавальери не была признана, так как его методы могли привести к ошибочным результатам, и бесконечно малым величинам он создал сомнительную репутацию.

Формальное исследование исчисления бесконечно малых, которое Кавальери соединил с исчислением конечных разностей , проводилось в Европе примерно в это же время. Пьер Ферма , утверждая, что он заимствовал это из Диофанта , ввёл понятие «квази-равенства» (англ. adequality ), которое представляло собой равенство с точностью до бесконечно малой ошибки. Большой вклад внесли также Джон Валлис , Исаак Барроу и Джеймс Грегори . Последние два около 1675 года доказали вторую фундаментальную теорему исчисления .

Основания

В математике основания относятся к строгому определению предмета, отталкиваясь от точных аксиом и определений. На начальном этапе развития исчисления использование бесконечно малых величин считалось нестрогим, оно подвергалось жёсткой критике рядом авторов, в первую очередь Мишелем Роллем и епископом Беркли . Беркли превосходно описал бесконечно малые как «призраки умерших количеств» в своей книге «The Analyst» в 1734 году. Разработка строгих основ для исчисления заняло математиков на протяжении более столетия после Ньютона и Лейбница, и до сих пор сегодня в некоторой степени является активной областью исследований.

Несколько математиков, в том числе Маклорен , пытались доказать обоснованность использования бесконечно малых, но это удалось сделать только 150 лет спустя трудами Коши и Вейерштрасса , которые наконец-то нашли средства, как уклониться от простых «мелочёвок» бесконечно малых величин, и были положены начала дифференциального и интегрального исчисления. В трудах Коши мы находим универсальный спектр основополагающих подходов, в том числе определение непрерывности в терминах бесконечно малых и (несколько неточный) прототип (ε, δ)-определения предела в определении дифференцирования. В своём труде Вейерштрасс формализует понятие предела и устраняет бесконечно малые величины. После этого труда Вейерштрасса общей основой исчисления стали пределы, а не бесконечно малые величины. Бернхард Риман использовал эти идеи, чтобы дать точное определение интеграла. Кроме того, в этот период идеи исчисления были обобщены на евклидово пространство и на комплексную плоскость .

В современной математике основы исчисления включаются в раздел вещественного анализа , который содержит полные определения и доказательства теорем исчисления. Сфера исследований исчисления стала значительно шире. Анри Лебег разработал теорию мер множества и использовал её для определения интегралов от всех функций, кроме самых экзотических. Лоран Шварц ввёл в рассмотрение обобщённые функции , которые можно использовать для вычисления производных любой функции вообще.

Введение пределов определило не единственный строгий подход к основанию исчисления. Альтернативой может быть, например, нестандартный анализ Абрахама Робинсона . Подход Робинсона, разработанный в 1960-е годы, использует технические средства из математической логики для расширения системы вещественных чисел бесконечно малыми и бесконечно большими числами, как это было в исходной концепции Ньютона-Лейбница. Эти числа, называемые гипердействительными , можно использовать в обычных правилах исчисления, подобно тому, как это делал Лейбниц.

Важность

Хотя некоторые идеи исчисления ранее были разработаны в Египте , Греции , Китае , Индии , Ираке, Персии и Японии , современное использование исчисления началось в Европе в XVII веке, когда Исаак Ньютон и Готфрид Вильгельм Лейбниц построили на базе работ предшествующих математиков его основные принципы. Развитие исчисления было основано на более ранних концепциях мгновенного движения и площади под кривой.

Дифференциальное исчисление применяется в расчётах, связанных со скоростью и ускорением , углом наклона кривой и оптимизацией . Применение интегрального исчисления включает расчёты с участием площадей , объёмов , длин дуг , центров масс , работы и давления . Более сложные приложения включают расчёты степенных рядов и рядов Фурье .

Исчисление [ ] также используется для получения более точного представления о природе пространства, времени и движения. Веками математики и философы боролись с парадоксами, связанными с делением на ноль или нахождением суммы бесконечного ряда чисел. Эти вопросы возникают при изучении движения и вычислении площадей. Древнегреческий философ Зенон Элейский дал несколько известных примеров таких парадоксов . Исчисление предоставляет инструменты для разрешения этих парадоксов, в частности, пределы и бесконечные ряды.

Пределы и бесконечно малые величины

Примечания

1. Morris Kline, Mathematical thought from ancient to modern times , Vol. I
2. Archimedes, Method , in The Works of Archimedes ISBN 978-0-521-66160-7
3. Dun, Liu; Fan, Dainian; Cohen, Robert Sonné. A comparison of Archimdes" and Liu Hui"s studies of circles (англ.) : journal. - Springer, 1966. - Vol. 130 . - P. 279 . - ISBN 0-792-33463-9 . , Chapter, p. 279
4. Zill, Dennis G.; Wright, Scott; Wright, Warren S. Calculus: Early Transcendentals (неопр.) . - 3. - Jones & Bartlett Learning (англ.) русск. , 2009. - С. xxvii. - ISBN 0-763-75995-3 . , Extract of page 27
5. Indian mathematics
6. von Neumann, J., «The Mathematician», in Heywood, R. B., ed., The Works of the Mind , University of Chicago Press, 1947, pp. 180-196. Reprinted in Bródy, F., Vámos, T., eds., The Neumann Compedium , World Scientific Publishing Co. Pte. Ltd., 1995, ISBN 9810222017 , pp. 618-626.
7. André Weil: Number theory. An approach through history. From Hammurapi to Legendre. Birkhauser Boston, Inc., Boston, MA, 1984, ISBN 0-8176-4565-9 , p. 28.
8. Leibniz, Gottfried Wilhelm. The Early Mathematical Manuscripts of Leibniz. Cosimo, Inc., 2008. Page 228. Copy
9. Unlu, Elif Maria Gaetana Agnesi (неопр.) . Agnes Scott College (April 1995). Архивировано 5 сентября 2012 года.

Ссылки

• Ron Larson, Bruce H. Edwards (2010). «Calculus», 9th ed., Brooks Cole Cengage Learning. ISBN 978-0-547-16702-2
• McQuarrie, Donald A. (2003). Mathematical Methods for Scientists and Engineers , University Science Books. ISBN 978-1-891389-24-5
• James Stewart (2008). Calculus: Early Transcendentals , 6th ed., Brooks Cole Cengage Learning.