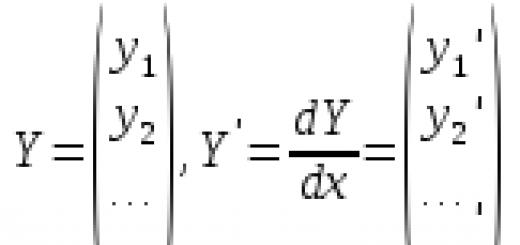Решение систем линейных уравнений методом Гаусса.
Пусть нам требуется найти решение системы из n
линейных уравнений с n
неизвестными переменными
определитель основной матрицы которой отличен от нуля.
Суть метода Гаусса состоит в последовательном исключении неизвестных переменных: сначала исключается x 1 из всех уравнений системы, начиная со второго, далее исключается x 2 из всех уравнений, начиная с третьего, и так далее, пока в последнем уравнении останется только неизвестная переменная x n . Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называется прямым ходом метода Гаусса . После завершения прямого хода метода Гаусса из последнего уравнения находитсяx n , с помощью этого значения из предпоследнего уравнения вычисляется x n-1 , и так далее, из первого уравнения находится x 1 . Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называется обратным ходом метода Гаусса .
Кратко опишем алгоритм исключения неизвестных переменных.
Будем считать, что , так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменную x 1
из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на , к третьему уравнению прибавим первое, умноженное на , и так далее, к n-ому
уравнению прибавим первое, умноженное на . Система уравнений после таких преобразований примет вид
где , а  .
.
К такому же результату мы бы пришли, если бы выразили x 1 через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x 1 исключена из всех уравнений, начиная со второго.
Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке
Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на , и так далее, к n-ому
уравнению прибавим второе, умноженное на . Система уравнений после таких преобразований примет вид
где , а  . Таким образом, переменная x 2
исключена из всех уравнений, начиная с третьего.
. Таким образом, переменная x 2
исключена из всех уравнений, начиная с третьего.
Далее приступаем к исключению неизвестной x 3
, при этом действуем аналогично с отмеченной на рисунке частью системы
Так продолжаем прямой ход метода Гаусса пока система не примет вид
С этого момента начинаем обратный ход метода Гаусса: вычисляем x n из последнего уравнения как , с помощью полученного значения x n находим x n-1 из предпоследнего уравнения, и так далее, находим x 1 из первого уравнения.
Пример.
Решите систему линейных уравнений  методом Гаусса.
методом Гаусса.
В данной статье метод рассматривается как способ решения Метод является аналитическим, то есть позволяет написать алгоритм решения в общем виде, а потом уже подставлять туда значения из конкретных примеров. В отличие от матричного метода или формул Крамера, при решении системы линейных уравнений методом Гаусса можно работать и с теми, что имеют решений бесконечно много. Или не имеют его вовсе.
Что значит решить методом Гаусса?
Для начала необходимо нашу систему уравнений записать в Выглядит это следующим образом. Берется система:
Коэффициенты записываются в виде таблицы, а справа отдельным столбиком - свободные члены. Столбец со свободными членами отделяется для удобства Матрица, включающая в себя этот столбец, называется расширенной.

Далее основную матрицу с коэффициентами нужно привести к верхней треугольной форме. Это основной момент решения системы методом Гаусса. Проще говоря, после определенных манипуляций матрица должна выглядеть так, чтобы в ее левой нижней части стояли одни нули:

Тогда, если записать новую матрицу опять как систему уравнений, можно заметить, что в последней строке уже содержится значение одного из корней, которое затем подставляется в уравнение выше, находится еще один корень, и так далее.
Это описание решения методом Гаусса в самых общих чертах. А что получится, если вдруг у системы нет решения? Или их бесконечно много? Чтобы ответить на эти и еще множество вопросов, необходимо рассмотреть отдельно все элементы, использующиеся при решении методом Гаусса.
Матрицы, их свойства
Никакого скрытого смысла в матрице нет. Это просто удобный способ записи данных для последующих операций с ними. Бояться их не надо даже школьникам.
Матрица всегда прямоугольная, потому что так удобнее. Даже в методе Гаусса, где все сводится к построению матрицы треугольного вида, в записи фигурирует прямоугольник, только с нулями на том месте, где нет чисел. Нули можно не записывать, но они подразумеваются.
Матрица имеет размер. Ее "ширина" - число строк (m), "длина" - число столбцов (n). Тогда размер матрицы A (для их обозначения обычно используются заглавные латинские буквы) будет обозначаться как A m×n . Если m=n, то эта матрица квадратная, и m=n - ее порядок. Соответственно, любой элемент матрицы A можно обозначить через номер его строки и столбца: a xy ; x - номер строки, изменяется , y - номер столбца, изменяется .
В - это не основной момент решения. В принципе, все операции можно выполнять непосредственно с самими уравнениями, однако запись получится куда более громоздкая, и в ней будет гораздо легче запутаться.
Определитель
Еще у матрицы есть определитель. Это очень важная характеристика. Выяснять его смысл сейчас не стоит, можно просто показать, как он вычисляется, а потом рассказать, какие свойства матрицы он определяет. Наиболее простой способ нахождения определителя - через диагонали. В матрице проводятся воображаемые диагонали; элементы, находящиеся на каждой из них, перемножаются, а затем полученные произведения складываются: диагонали с наклоном вправо - со знаком "плюс", с наклоном влево - со знаком "минус".

Крайне важно отметить, что вычислять определитель можно только у квадратной матрицы. Для прямоугольной матрицы можно сделать следующее: из количества строк и количества столбцов выбрать наименьшее (пусть это будет k), а затем в матрице произвольным образом отметить k столбцов и k строк. Элементы, находящиеся на пересечении выбранных столбцов и строк, составят новую квадратную матрицу. Если определитель такой матрицы будет числом, отличным от нуля, то назовется базисным минором первоначальной прямоугольной матрицы.
Перед тем как приступить к решению системы уравнений методом Гаусса, не мешает посчитать определитель. Если он окажется нулевым, то сразу можно говорить, что у матрицы количество решений либо бесконечно, либо их вообще нет. В таком печальном случае надо идти дальше и узнавать про ранг матрицы.
Классификация систем
Существует такое понятие, как ранг матрицы. Это максимальный порядок ее определителя, отличного от нуля (если вспомнить про базисный минор, можно сказать, что ранг матрицы - порядок базисного минора).
По тому, как обстоят дела с рангом, СЛАУ можно разделить на:
- Совместные. У совместных систем ранг основной матрицы (состоящей только из коэффициентов) совпадает с рангом расширенной (со столбцом свободных членов). Такие системы имеют решение, но необязательно одно, поэтому дополнительно совместные системы делят на:
- - определенные - имеющие единственное решение. В определенных системах равны ранг матрицы и количество неизвестных (или число столбцов, что есть одно и то же);
- - неопределенные - с бесконечным количеством решений. Ранг матриц у таких систем меньше количества неизвестных.
- Несовместные. У таких систем ранги основной и расширенной матриц не совпадают. Несовместные системы решения не имеют.
Метод Гаусса хорош тем, что позволяет в ходе решения получить либо однозначное доказательство несовместности системы (без вычисления определителей больших матриц), либо решение в общем виде для системы с бесконечным числом решений.
Элементарные преобразования
До того как приступить непосредственно к решению системы, можно сделать ее менее громоздкой и более удобной для вычислений. Это достигается за счет элементарных преобразований - таких, что их выполнение никак не меняет конечный ответ. Следует отметить, что некоторые из приведенных элементарных преобразований действительны только для матриц, исходниками которых послужили именно СЛАУ. Вот список этих преобразований:
- Перестановка строк. Очевидно, что если в записи системы поменять порядок уравнений, то на решение это никак не повлияет. Следовательно, в матрице этой системы также можно менять местами строки, не забывая, конечно, про столбец свободных членов.
- Умножение всех элементов строки на некоторый коэффициент. Очень полезно! С помощью него можно сократить большие числа в матрице или убрать нули. Множество решений, как обычно, не изменится, а выполнять дальнейшие операции станет удобнее. Главное, чтобы коэффициент не был равен нулю.
- Удаление строк с пропорциональными коэффициентами. Это отчасти следует из предыдущего пункта. Если две или более строки в матрице имеют пропорциональные коэффициенты, то при умножении/делении одной из строк на коэффициент пропорциональности получаются две (или, опять же, более) абсолютно одинаковые строки, и можно убрать лишние, оставив только одну.
- Удаление нулевой строки. Если в ходе преобразований где-то получилась строка, в которой все элементы, включая свободный член, - ноль, то такую строку можно назвать нулевой и выкинуть из матрицы.
- Прибавление к элементам одной строки элементов другой (по соответствующим столбцам), умноженных на некоторый коэффициент. Самое неочевидное и самое важное преобразование из всех. На нем стоит остановиться поподробнее.
Прибавление строки, умноженной на коэффициент
Для простоты понимания стоит разобрать этот процесс по шагам. Берутся две строки из матрицы:
a 11 a 12 ... a 1n | b1
a 21 a 22 ... a 2n | b 2
Допустим, необходимо ко второй прибавить первую, умноженную на коэффициент "-2".
a" 21 = a 21 + -2×a 11
a" 22 = a 22 + -2×a 12
a" 2n = a 2n + -2×a 1n
Затем в матрице вторая строка заменяется на новую, а первая остается без изменений.
a 11 a 12 ... a 1n | b1
a" 21 a" 22 ... a" 2n | b 2
Необходимо заметить, что коэффициент умножения можно подобрать таким образом, чтобы в результате сложения двух строк один из элементов новой строки был равен нулю. Следовательно, можно получить уравнение в системе, где на одну неизвестную будет меньше. А если получить два таких уравнения, то операцию можно проделать еще раз и получить уравнение, которое будет содержать уже на две неизвестных меньше. А если каждый раз превращать в ноль один коэффициент у всех строк, что стоят ниже исходной, то можно, как по ступенькам, спуститься до самого низа матрицы и получить уравнение с одной неизвестной. Это и называется решить систему методом Гаусса.
В общем виде
Пусть существует система. Она имеет m уравнений и n корней-неизвестных. Записать ее можно следующим образом:

Из коэффициентов системы составляется основная матрица. В расширенную матрицу добавляется столбец свободных членов и для удобства отделяется чертой.
- первая строка матрицы умножается на коэффициент k = (-a 21 /a 11);
- первая измененная строка и вторая строка матрицы складываются;
- вместо второй строки в матрицу вставляется результат сложения из предыдущего пункта;
- теперь первый коэффициент в новой второй строке равен a 11 × (-a 21 /a 11) + a 21 = -a 21 + a 21 = 0.
Теперь выполняется та же серия преобразований, только участвуют первая и третья строки. Соответственно, в каждом шаге алгоритма элемент a 21 заменяется на a 31 . Потом все повторяется для a 41 , ... a m1 . В итоге получается матрица, где в строках первый элемент равен нулю. Теперь нужно забыть о строке номер один и выполнить тот же алгоритм, начиная со второй строки:
- коэффициент k = (-a 32 /a 22);
- с "текущей" строкой складывается вторая измененная строка;
- результат сложения подставляется в третью, четвертую и так далее строки, а первая и вторая остаются неизменными;
- в строках матрицы уже два первых элемента равны нулю.
Алгоритм надо повторять, пока не появится коэффициент k = (-a m,m-1 /a mm). Это значит, что в последний раз алгоритм выполнялся только для нижнего уравнения. Теперь матрица похожа на треугольник, или имеет ступенчатую форму. В нижней строчке имеется равенство a mn × x n = b m . Коэффициент и свободный член известны, и корень выражается через них: x n = b m /a mn . Полученный корень подставляется в верхнюю строку, чтобы найти x n-1 = (b m-1 - a m-1,n ×(b m /a mn))÷a m-1,n-1 . И так далее по аналогии: в каждой следующей строке находится новый корень, и, добравшись до "верха" системы, можно отыскать множество решений . Оно будет единственным.
Когда нет решений
Если в одной из матричных строк все элементы, кроме свободного члена, равны нулю, то уравнение, соответствующее этой строке, выглядит как 0 = b. Оно не имеет решения. И поскольку такое уравнение заключено в систему, то и множество решений всей системы - пустое, то есть она является вырожденной.
Когда решений бесконечное количество
Может получиться так, что в приведенной треугольной матрице нет строк с одним элементом-коэффициентом уравнения, и одним - свободным членом. Есть только такие строки, которые при переписывании имели бы вид уравнения с двумя или более переменными. Значит, у системы имеется бесконечное число решений. В таком случае ответ можно дать в виде общего решения. Как это сделать?
Все переменные в матрице делятся на базисные и свободные. Базисные - это те, которые стоят "с краю" строк в ступенчатой матрице. Остальные - свободные. В общем решении базисные переменные записываются через свободные.
Для удобства матрица сначала переписывается обратно в систему уравнений. Потом в последнем из них, там, где точно осталась только одна базисная переменная, она остается с одной стороны, а все остальное переносится в другую. Так делается для каждого уравнения с одной базисной переменной. Потом в остальные уравнения, там, где это возможно, вместо базисной переменной подставляется полученное для нее выражение. Если в результате опять появилось выражение, содержащее только одну базисную переменную, она оттуда опять выражается, и так далее, пока каждая базисная переменная не будет записана в виде выражения со свободными переменными. Это и есть общее решение СЛАУ.
Можно также найти базисное решение системы - дать свободным переменным любые значения, а потом для этого конкретного случая посчитать значения базисных переменных. Частных решений можно привести бесконечно много.
Решение на конкретных примерах
Вот система уравнений.

Для удобства лучше сразу составить ее матрицу

Известно, что при решении методом Гаусса уравнение, соответствующее первой строке, в конце преобразований останется неизменным. Поэтому выгодней будет, если левый верхний элемент матрицы будет наименьшим - тогда первые элементы остальных строк после операций обратятся в ноль. Значит, в составленной матрице выгодно будет на место первой строки поставить вторую.
вторая строка: k = (-a 21 /a 11) = (-3/1) = -3
a" 21 = a 21 + k×a 11 = 3 + (-3)×1 = 0
a" 22 = a 22 + k×a 12 = -1 + (-3)×2 = -7
a" 23 = a 23 + k×a 13 = 1 + (-3)×4 = -11
b" 2 = b 2 + k×b 1 = 12 + (-3)×12 = -24
третья строка: k = (-a 3 1 /a 11) = (-5/1) = -5
a" 3 1 = a 3 1 + k×a 11 = 5 + (-5)×1 = 0
a" 3 2 = a 3 2 + k×a 12 = 1 + (-5)×2 = -9
a" 3 3 = a 33 + k×a 13 = 2 + (-5)×4 = -18
b" 3 = b 3 + k×b 1 = 3 + (-5)×12 = -57
Теперь, чтобы не запутаться, необходимо записать матрицу с промежуточными результатами преобразований.

Очевидно, что такую матрицу можно сделать более удобной для восприятия с помощью некоторых операций. Например, из второй строки можно убрать все "минусы", умножая каждый элемент на "-1".
Стоит также заметить, что в третьей строке все элементы кратны трем. Тогда можно сократить строку на это число, умножая каждый элемент на "-1/3" (минус - заодно, чтобы убрать отрицательные значения).

Выглядит гораздо приятнее. Теперь надо оставить в покое первую строку и поработать со второй и третьей. Задача - прибавить к третьей строке вторую, умноженную на такой коэффициент, чтобы элемент a 32 стал равен нулю.
k = (-a 32 /a 22) = (-3/7) = -3/7 (если в ходе некоторых преобразований в ответе получилось не целое число, рекомендуется для соблюдения точности вычислений оставить его "как есть", в виде обыкновенной дроби, а уже потом, когда получены ответы, решать, стоит ли округлять и переводить в другую форму записи)
a" 32 = a 32 + k×a 22 = 3 + (-3/7)×7 = 3 + (-3) = 0
a" 33 = a 33 + k×a 23 = 6 + (-3/7)×11 = -9/7
b" 3 = b 3 + k×b 2 = 19 + (-3/7)×24 = -61/7
Снова записывается матрица с новыми значениями.
| 1 | 2 | 4 | 12 |
| 0 | 7 | 11 | 24 |
| 0 | 0 | -9/7 | -61/7 |
Как видно, полученная матрица уже имеет ступенчатый вид. Поэтому дальнейшие преобразования системы по методу Гаусса не требуются. Что здесь можно сделать, так это убрать из третьей строки общий коэффициент "-1/7".

Теперь все красиво. Дело за малым - записать матрицу опять в виде системы уравнений и вычислить корни
x + 2y + 4z = 12 (1)
7y + 11z = 24 (2)
Тот алгоритм, по которому сейчас будут находиться корни, называется обратным ходом в методе Гаусса. В уравнении (3) содержится значение z:
y = (24 - 11×(61/9))/7 = -65/9
И первое уравнение позволяет найти x:
x = (12 - 4z - 2y)/1 = 12 - 4×(61/9) - 2×(-65/9) = -6/9 = -2/3
Такую систему мы имеем право назвать совместной, да еще и определенной, то есть имеющей единственное решение. Ответ записывается в следующей форме:
x 1 = -2/3, y = -65/9, z = 61/9.
Пример неопределенной системы
Вариант решения определенной системы методом Гаусса разобран, теперь необходимо рассмотреть случай, если система неопределенная, то есть для нее можно найти бесконечно много решений.
х 1 + х 2 + х 3 + х 4 + х 5 = 7 (1)
3х 1 + 2х 2 + х 3 + х 4 - 3х 5 = -2 (2)
х 2 + 2х 3 + 2х 4 + 6х 5 = 23 (3)
5х 1 + 4х 2 + 3х 3 + 3х 4 - х 5 = 12 (4)
Сам вид системы уже настораживает, потому что количество неизвестных n = 5, а ранг матрицы системы уже точно меньше этого числа, потому что количество строк m = 4, то есть наибольший порядок определителя-квадрата - 4. Значит, решений существует бесконечное множество, и надо искать его общий вид. Метод Гаусса для линейных уравнений позволяет это сделать.
Сначала, как обычно, составляется расширенная матрица.

Вторая строка: коэффициент k = (-a 21 /a 11) = -3. В третьей строке первый элемент - еще до преобразований, поэтому не надо ничего трогать, надо оставить как есть. Четвертая строка: k = (-а 4 1 /а 11) = -5
Умножив элементы первой строки на каждый их коэффициентов по очереди и сложив их с нужными строками, получаем матрицу следующего вида:

Как можно видеть, вторая, третья и четвертая строки состоят из элементов, пропорциональных друг другу. Вторая и четвертая вообще одинаковые, поэтому одну из них можно убрать сразу, а оставшуюся умножить на коэффициент "-1" и получить строку номер 3. И опять из двух одинаковых строк оставить одну.
Получилась такая матрица. Пока еще не записана система, нужно здесь определить базисные переменные - стоящие при коэффициентах a 11 = 1 и a 22 = 1, и свободные - все остальные.

Во втором уравнении есть только одна базисная переменная - x 2 . Значит, ее можно выразить оттуда, записав через переменные x 3 , x 4 , x 5 , являющиеся свободными.
Подставляем полученное выражение в первое уравнение.
Получилось уравнение, в котором единственная базисная переменная - x 1 . Проделаем с ней то же, что и с x 2 .
Все базисные переменные, которых две, выражены через три свободные, теперь можно записывать ответ в общем виде.

Также можно указать одно из частных решений системы. Для таких случаев в качестве значений для свободных переменных выбирают, как правило, нули. Тогда ответом будет:
16, 23, 0, 0, 0.
Пример несовместной системы
Решение несовместных систем уравнений методом Гаусса - самое быстрое. Оно заканчивается сразу же, как только на одном из этапов получается уравнение, не имеющее решения. То есть этап с вычислением корней, достаточно долгий и муторный, отпадает. Рассматривается следующая система:
x + y - z = 0 (1)
2x - y - z = -2 (2)
4x + y - 3z = 5 (3)
Как обычно, составляется матрица:
| 1 | 1 | -1 | 0 |
| 2 | -1 | -1 | -2 |
| 4 | 1 | -3 | 5 |
И приводится к ступенчатому виду:
k 1 = -2k 2 = -4
| 1 | 1 | -1 | 0 |
| 0 | -3 | 1 | -2 |
| 0 | 0 | 0 | 7 |
После первого же преобразования в третьей строке содержится уравнение вида
не имеющее решения. Следовательно, система несовместна, и ответом будет пустое множество.
Преимущества и недостатки метода
Если выбирать, каким методом решать СЛАУ на бумаге ручкой, то метод, который был рассмотрен в этой статье, выглядит наиболее привлекательно. В элементарных преобразованиях гораздо труднее запутаться, чем в том случается, если приходится искать вручную определитель или какую-нибудь хитрую обратную матрицу. Однако, если использовать программы для работы с данными такого типа, например, электронные таблицы, то оказывается, что в таких программах уже заложены алгоритмы вычисления основных параметров матриц - определитель, миноры, обратная и и так далее. А если быть уверенным в том, что машина посчитает эти значения сама и не ошибется, целесообразней использовать уже матричный метод или формул Крамера, потому что их применение начинается и заканчивается вычислением определителей и обратными матрицами.
Применение
Поскольку решение методом Гаусса представляет из себя алгоритм, а матрица - это, фактически, двумерный массив, его можно использовать при программировании. Но поскольку статья позиционирует себя, как руководство "для чайников", следует сказать, что самое простое, куда метод можно запихнуть - это электронные таблицы, например, Excel. Опять же, всякие СЛАУ, занесенные в таблицу в виде матрицы, Excel будет рассматривать как двумерный массив. А для операций с ними существует множество приятных команд: сложение (складывать можно только матрицы одинаковых размеров!), умножение на число, перемножение матриц (также с определенными ограничениями), нахождение обратной и транспонированной матриц и, самое главное, вычисление определителя. Если это трудоемкое занятие заменить одной командой, можно гораздо быстрее определять ранг матрицы и, следовательно, устанавливать ее совместность или несовместность.
Метод Гаусса был предложен известнейшим немецким математиком Карлом Фридрихом Гауссом (1777 - 1855) и является одним из наиболее универсальных методов решения СЛАУ. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении задачи, расширенная матрица системы с помощью элементарных преобразований над ее строками приводится к ступенчатому виду. Далее последовательно находятся все неизвестные, начиная снизу вверх.
Принцип метода Гаусса
Метод Гаусса включает в себя прямой (приведение расширенной матрицы к ступенчатому виду, то есть получение нулей под главной диагональю) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы. Прямой ход и называется методом Гаусса, обратный - методом Гаусса-Жордана, который отличается от первого только последовательностью исключения переменных.
Метод Гаусса идеально подходит для решения систем содержащих больше трех линейных уравнений, для решения систем уравнений, которые не являются квадратными (чего не скажешь про метод Крамера и матричный метод). То есть метод Гаусса - наиболее универсальный метод для нахождения решения любой системы линейных уравнений, он работает в случае, когда система имеет бесконечно много решений или несовместна.
Примеры решения систем уравнений
Пример
Задание. Решить СЛАУ методом Гаусса.
Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент равнялся 1 (это мы делаем для упрощения вычислений):

Все элементы третьей строки делим на два (или, что тоже самое, умножаем на ):


От третьей строки отнимаем вторую, умноженную на 3:

Умножив третью строку на , получаем:

Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Надо обнулить элемент , для этого от второй строки отнимем третью.
Карл Фридрих Гаусс, величайший математик долгое время колебался, выбирая между философией и математикой. Возможно, именно такой склад ума позволил ему столь заметно "наследить" в мировой науке. В частности, создав "Метод Гаусса" ...
Почти 4 года статьи этого сайта касались школьного образования, в основном, со стороны философии, принципов (не)понимания, внедряемых в сознание детей. Приходит время бОльшей конкретики, примеров и методов... Я верю, что именно такой подход к привычным, запутанным и важным областям жизни дает лучшие результаты.
Мы, люди так устроены, что сколько ни говори об абстрактном мышлении , но понимание всегда происходит через примеры . Если примеры отсутствуют, то принципы уловить невозможно... Как невозможно оказаться на вершине горы иначе, как пройдя весь ее склон от подножия.
Тоже и со школой: пока живых историй недостаточно мы инстинктивно продолжаем считать ее местом, где детей учат понимать.
Например, обучая методу Гаусса...
Метод Гаусса в 5 классе школы
Оговорюсь сразу: метод Гаусса имеет гораздо более широкое применение, например, при решении систем линейных уравнений . То, о чем мы будем говорить, проходят в 5 классе. Это начала , уяснив которые, гораздо легче разобраться в более "продвинутых вариантах". В этой статье мы говорим о методе (способе) Гаусса при нахождении суммы ряда
Вот пример, который принес из школы мой младший сын, посещающий 5 класс московской гимназии.
Школьная демонстрация метода Гаусса
Учитель математики с использованием интерактивной доски (современные методы обучения ) показал детям презентацию истории "создания метода" маленьким Гауссом.
Школьный учитель выпорол маленького Карла (устаревший метод, нынче в школах не применяется) за то, что тот,
вместо того, чтобы последовательно складывая числа от 1 до 100 найти их сумму заметил , что пары чисел, равно отстоящие от краев арифметической прогрессии, в сумме дают одно и то же число. например, 100 и 1, 99 и 2. Посчитав количество таких пар, маленький Гаусс почти моментально решил предложенную учителем задачу. За что и был подвергнут экзекуции на глазах изумленной публики. Чтобы остальным думать было неповадно.
Что сделал маленький Гаусс, развивший чувство числа ? Заметил некоторую особенность числового ряда с постоянным шагом (арифметической прогрессии). И именно это сделало его впоследствии великим ученым, умеющим замечать , обладающим чувством, инстинктом понимания .
Этим и ценна математика, развивающая способность видеть общее в частном - абстрактное мышление . Поэтому большинство родителей и работодателей инстинктивно считают математику важной дисциплиной ...
"Математику уже затем учить надо, что она ум в порядок приводит.
М.В.Ломоносов".
Однако, последователи тех, кто порол розгами будущих гениев, превратили Метод в нечто противоположное. Как 35 лет назад говорил мой научный руководитель: "Занаучили вопрос". Или как сказал вчера о методе Гаусса мой младший сын: "Может не стоит из этого большую науку делать-то, а?"
Последствия творчества "ученых" видны по уровню нынешней школьной математики, уровню ее преподавания и понимания "Царицы наук" большинством.
Однако, продолжим...
Методы объяснения метода Гаусса в 5 классе школы
Учитель математики московской гимназии, объясняя метод Гаусса по-Виленкину, усложнил задание.
Что, если разность (шаг) арифметической прогрессии будет не единица, а другое число? Например, 20.
Задача, которую он дал пятиклассникам:
20+40+60+80+ ... +460+480+500
Прежде, чем познакомиться с гимназическим методом, заглянем в Сеть: как это делают школьные учителя - репетиторы по математике?..
Метод Гаусса: объяснение №1
Известный репетитор на своем канале YOUTUBE приводит следующие рассуждения:
"запишем числа от 1 до 100 следующим образом:
сначала ряд чисел от 1 до 50, а строго под ним другой ряд чисел от 50 до 100, но в обратной последовательности"
1, 2, 3, ... 48, 49, 50
100, 99, 98 ... 53, 52, 51
"Обратите внимание: сумма каждой пары чисел из верхнего и нижнего рядов одинакова и равняется 101 ! Посчитаем количество пар, оно составляет 50 и умножим сумму одной пары на количество пар! Вуаля: Ответ готов!".
"Если вы не смогли понять - не расстраивайтесь!", - три раза в процессе объяснения повторил учитель. "Этот метод вы будете проходить в 9 классе!"
Метод Гаусса: объяснение №2
Другой репетитор, менее известный (судя по числу просмотров) использует более научный подход, предлагая алгоритм решения из 5 пунктов, которые необходимо выполнить последовательно.
Для непосвященных: 5 это одно из чисел Фибоначчи, традиционно считающееся магическим. Метод из 5 шагов всегда более научен, чем метод, например, из 6 шагов. ... И это вряд ли случайность, скорее всего, Автор - скрытый приверженец теории Фибоначчи
Дана арифметическая прогрессия: 4, 10, 16 ... 244, 250, 256 .
Алгоритм нахождения суммы чисел ряда методом Гаусса:
4, 10, 16 ... 244, 250, 256
256, 250, 244 ... 16, 10, 4
При этом нужно помнить о правиле "Плюс один" : к полученному частному необходимо прибавить единицу: иначе мы получим результат, меньший на единицу, чем истинное число пар: 42 + 1 = 43.
Это и есть искомая сумма арифметической прогрессии от 4 до 256 с разницей 6 !
Метод Гаусса: объяснение в 5 классе московской гимназии
А вот как требовалось решить задачу нахождения суммы ряда:
20+40+60+ ... +460+480+500
в 5 классе московской гимназии, учебник Виленкина (со слов моего сына).
Показав презентацию, учительница математики показала пару примеров по методу Гаусса и дала классу задачу по нахождению суммы чисел ряда с шагом 20.
При этом требовалось следующее:
Как видим, это более компактная и эффективная методика: число 3 - также член последовательности Фибоначчи

Мои комментарии к школьной версии метода Гаусса
Великий математик определенно выбрал бы философию, если бы предвидел, во что превратят его "метод" последователи немецкого учителя , выпоровшего Карла розгами. Он узрел бы и символизм, и диалектическую спираль и неумирающую глупость "учителей", пытающихся измерить алгеброй непонимания гармонию живой математической мысли ....
Между прочим: знаете ли вы. что наша система образования уходит корнями в немецкую школу 18 - 19 веков?
Но Гаусс выбрал математику.
В чем суть его метода?
В упрощении . В наблюдении и схватывании простых закономерностей чисел. В превращении сухой школьной арифметики в интересное и увлекательное занятие , активизирующее в мозге желание продолжать, а не блокирующее высокозатратную умственную деятельность.
Разве возможно одной из приведенных "модификаций метода" Гаусса посчитать сумму чисел арифметической прогрессии почти моментально ? По "алгоритмам" маленький Карл гарантированно избежал бы порки, воспитал отвращение к математике и подавил на корню свои творческие импульсы.
Почему репетитор так настойчиво советовал пятиклассникам "не бояться непонимания" метода, убеждая, что "такие" задачи они будут решать аж в 9 классе? Психологически безграмотное действие . Удачным приемом было отметить : "Видите? Вы уже в 5 классе можете решать задачи, которые будете проходить только через 4 года! Какие вы молодцы!".
Для использования метода Гаусса достаточно уровня 3 класса , когда нормальные дети уже умеют складывать, умножать и делить 2 -3 значные числа. Проблемы возникают из-за неспособности взрослых учителей, "не въезжающих", как объяснить простейшие вещи нормальным человеческим языком, не то что математическим... Не способных заинтересовать математикой и напрочь отбивающих охоту даже у "способных".
Или, как прокомментировал мой сын: "делающих из этого большую науку".
Метод Гаусса, мои объяснения
Нашему ребенку мы с супругой объясняли этот "метод", кажется, еще до школы...
Простота вместо усложнения или игра в вопросы - ответы
""Посмотри, вот числа от 1 до 100. Что ты видишь?"
Дело не в том, что именно увидит ребенок. Фокус в том, чтобы он стал смотреть.
"Как можно их сложить?" Сын уловил, что такие вопросы не задаются "просто так" и нужно взглянуть на вопрос "как-то по-другому, иначе, чем он делает обычно"
Не важно, увидит ли ребенок решение сразу, это маловероятно. Важно, чтобы он перестал бояться смотреть, или как я говорю: "шевелил задачу" . Это начало пути к пониманию
"Что легче: сложить, например, 5 и 6 или 5 и 95?" Наводящий вопрос... Но ведь любое обучение и сводится к "наведению" человека на "ответ" - любым приемлемым для него способом.
На этом этапе уже могут возникнуть догадки о том, как "сэкономить" на вычислениях.
Все, что мы сделали - намекнули: "лобовой, линейный" метод счета - не единственно возможный. Если ребенок это усек, то впоследствии он выдумает еще много таких методов, ведь это интересно!!! И он точно избежит "непонимания" математики, не будет испытывать к ней отвращение. Он получил победу!
Если ребенок обнаружил , что сложение пар чисел, дающих в сумме сотню, плевое занятие, то "арифметическая прогрессия с разницей 1" - довольно муторная и неинтересная для ребенка вещь - вдруг для него обрела жизнь . Из хаоса возник порядок, а это всегда вызывает энтузиазм: так мы устроены !
Вопрос на засыпку: зачем после полученного ребенком озарения вновь загонять его в рамки сухих алгоритмов, к тому же функционально бесполезных в этом случае?!
Зачем заставлять тупо переписывать числа последовательности в тетрадь: чтобы даже у способных не возникло и единого шанса на понимание? Статистически, конечно, а ведь массовое образование заточено на "статистику" ...
Куда делся ноль?
И все-таки складывать числа, дающие в сумме 100 для ума гораздо более приемлемо, чем дающие 101 ...
"Школьный метод Гаусса" требует именно этого: бездумно складывать равноотстоящие от центра прогрессии пары чисел, несмотря ни на что .
А если посмотреть?
Все-таки ноль - величайшее изобретение человечества, которому более 2 000 лет. А учителя математики продолжают его игнорировать.
Гораздо проще преобразовать ряд чисел, начинающийся с 1, в ряд, начинающийся с 0. Сумма ведь не изменится, не правда ли? Нужно перестать "думать учебниками" и начать смотреть... И увидеть, что пары с суммой 101 вполне можно заменить парами с суммой 100 !
0 + 100, 1 + 99, 2 + 98 ... 49 + 51
Как упразднить "правило плюс 1"?
Если честно, то я о таком правиле впервые услышал от того ютубовского репетитора...
Как я до сих пор поступаю, когда требуется определить количество членов какого-нибудь ряда?
Смотрю на последовательность:
1, 2, 3, .. 8, 9, 10
а когда совсем устал, то на более простой ряд:
1, 2, 3, 4, 5
и прикидываю: если вычесть из 5 единицу, то получится 4, но я совершенно ясно вижу 5 чисел! Следовательно, нужно прибавить единицу! Чувство числа, развитое в начальной школе, подсказывает: даже если членов ряда будет целый гугл (10 в сотой степени), закономерность останется той же.
На фиг правила?..
Чтобы через пару - тройку лет заполнить все пространство между лбом и затылком и перестать соображать? А зарабатывать на хлеб с маслом как? Ведь мы ровными шеренгами движемся в эпоху цифровой экономики!
Еще о школьном методе Гаусса: "зачем науку-то из этого делать?.."
Я не зря разместил скриншот из тетрадки сына...
"Что там было, на уроке?"
"Ну, я сосчитал сразу, поднял руку, но она не спросила. Поэтому, пока остальные считали я стал делать ДЗ по русскому языку, чтобы не тратить время. Потом, когда остальные дописали (???), она вызвала меня к доске. Я сказал ответ."
"Правильно, покажи, как ты решал", - сказала учительница. Я показал. Она сказала: "Неправильно, нужно считать так, как я показала!"
"Хорошо, что двойку не поставила. И заставила написать в тетради "ход решения" по-ихнему. Зачем науку-то большую из этого делать?.."
Главное преступление учителя математики
Вряд ли после того случая Карл Гаусс испытал высокое чувство уважения по отношению к школьному учителю математики. Но если бы он знал, как последователи того учителя извратят самую суть метода ... он взревел бы от негодования и через Всемирную организацию интеллектуальной собственности ВОИС добился запрета на использование своего честного имени в школьных учебниках!..
В чем главная ошибка школьного подхода ? Или, как я выразился - преступление школьных учителей математики против детей?
Алгоритм непонимания
Что делают школьные методисты, абсолютное большинство которых думать не умеет ни фига?
Создают методики и алгоритмы (см. ). Это защитная реакция, предохраняющая учителей от критики ("Все делается согласно..."), а детей - от понимания. И таким образом - от желания критиковать учителей! (Вторая производная чиновничьей "мудрости", научный подход к проблеме ). Человек не улавливая смысл скорее будет пенять на собственное непонимание, а не на тупость школьной системы.
Что и происходит: родители пеняют на детей, а учителя... то же на детей, "не понимающих математику!..
Смекаете?
Что сделал маленький Карл?
Абсолютно нешаблонно подошел к шаблонной задаче . Это квинтэссенция Его подхода. Это главное, чему следует учить в школе: думать не учебниками, а головой . Конечно, есть и инструментальная составляющая, которую вполне можно использовать... в поисках более простых и эффективных методов счета .
Метод Гаусса по-Виленкину
В школе учат, что метод Гаусса состоит в том, чтобы
что, если число элементов ряда окажется нечетным , как в задаче, которую задали сыну?..
"Подвох" состоит в том, что в этом случае следует обнаружить "лишнее" число ряда и прибавить его к сумме пар. В нашем примере это число 260 .
Как обнаружить? Переписывая все пары чисел в тетрадь! (Именно почему учительница заставила детей делать эту тупую работу, пытаясь научить "творчеству" методом Гаусса... И именно поэтому такой "метод" практически неприменим к большим рядам данных, И именно поэтому он не является методом Гаусса).
Немного творчества в школьной рутине...
Сын же поступил иначе.
(20 + 500, 40 + 480 ...).
0+500, 20+480, 40+460 ...
Несложно, правда?
А практически делается еще легче, что и позволяет выкроить 2-3 минуты на ДЗ по русскому, пока остальные "считают". К тому же сохраняет количество шагов методики: 5, что не позволяет критиковать подход за антинаучность.
Явно этот подход проще, быстрее и универсальнее, в стиле Метода. Но... учительница не то, что не похвалила, но и заставила переписать "правильным образом" (см. скриншот). То есть предприняла отчаянную попытку задушить творческий импульс и способность понимать математику на корню! Видимо, чтобы потом наняться репетитором... Не на того напала...
Все, что я так долго и нудно описал можно объяснить нормальному ребенку максимум за полчаса. Вместе с примерами.
Причем так, что он это никогда не забудет.
И это будет шаг к пониманию ... не только математики.
Признайтесь: сколько раз в жизни вы складывали методом Гаусса? И я ни разу!
Но инстинкт понимания , который развивается (или гасится) в процессе изучения математических методов в школе... О!.. Это поистине незаменимая вещь!
Особенно в век всеобщей цифровизации, в который мы незаметно вошли под чутким руководством Партии и Правительства.
Несколько слов в защиту учителей...
Несправедливо и неправильно всю ответственность за такой стиль обучения сваливать исключительно на школьных учителей. Действует система.
Некоторые учителя понимают абсурдность происходящего, но что делать? Закон об образовании, ФГОСы, методики, технологические карты уроков... Все должно делаться "в соответствии и на основании" и все должно быть задокументировано. Шаг в сторону - встал в очередь на увольнение. Не будем ханжами: зарплата московских учителей ну очень неплохая... Уволят - куда идти?..
Поэтому сайт этот не об образовании . Он об индивидуальном образовании , единственно возможном способе выбраться из толпы поколения Z ...
Определение и описание метода Гаусса
Метод преобразований Гаусса (также известный как преобразование методом последовательного исключения неизвестных переменных из уравнения или матрицы) для решения систем линейных уравнений представляет собой классический методом решения системы алгебраических уравнений (СЛАУ). Также этот классический метод используют для решения таких задач как получение обратных матриц и определения ранговости матрицы.
Преобразование с помощью метода Гаусса заключается в совершении небольших (элементарных) последовательных изменениях системы линейных алгебраических уравнений, приводящих к исключению переменных из неё сверху вниз с образованием новой треугольной системы уравнений, являющейся равносильной исходной.
Определение 1
Эта часть решения носит название прямого хода решения Гаусса, так как весь процесс осуществляется сверху вниз.
После приведения исходной системы уравнений к треугольной осуществляется нахождение всех переменных системы снизу вверх (то есть первые найденные переменные занимают находятся именно на последних строчках системы или матрицы). Эта часть решения известна также как обратный ход решения методом Гаусса. Заключается его алгоритм в следующем: сначала вычисляется переменные, находящиеся ближе всего к низу системы уравнений или матрицы, затем полученные значения подставляются выше и таким образом находится ещё одна переменная и так далее.
Описание алгоритма метода Гаусса
Последовательность действий для общего решения системы уравнения методом Гаусса заключается в поочередном применении прямого и обратного хода к матрице на основе СЛАУ. Пусть исходная система уравнений имеет следующий вид:
$\begin{cases} a_{11} \cdot x_1 +...+ a_{1n} \cdot x_n = b_1 \\ ... \\ a_{m1} \cdot x_1 + a_{mn} \cdot x_n = b_m \end{cases}$
Чтобы решить СЛАУ методом Гаусса, необходимо записать исходную систему уравнений в виде матрицы:
$A = \begin{pmatrix} a_{11} & … & a_{1n} \\ \vdots & … & \vdots \\ a_{m1} & … & a_{mn} \end{pmatrix}$, $b=\begin{pmatrix} b_1 \\ \vdots \\ b_m \end{pmatrix}$
Матрица $A$ называется основной матрицей и представляет собой записанные по порядку коэффициенты при переменных, а $b$ называется столбцом её свободных членов. Матрица $A$, записанная через черту со столбцом свободных членов называется расширенной матрицей:
$A = \begin{array}{ccc|c} a_{11} & … & a_{1n} & b_1 \\ \vdots & … & \vdots & ...\\ a_{m1} & … & a_{mn} & b_m \end{array}$
Теперь необходимо с помощью элементарных преобразований над системой уравнений (или над матрицей, так как это удобнее) привести её к следующему виду:
$\begin{cases} α_{1j_{1}} \cdot x_{j_{1}} + α_{1j_{2}} \cdot x_{j_{2}}...+ α_{1j_{r}} \cdot x_{j_{r}} +... α_{1j_{n}} \cdot x_{j_{n}} = β_1 \\ α_{2j_{2}} \cdot x_{j_{2}}...+ α_{2j_{r}} \cdot x_{j_{r}} +... α_{2j_{n}} \cdot x_{j_{n}} = β_2 \\ ...\\ α_{rj_{r}} \cdot x_{j_{r}} +... α_{rj_{n}} \cdot x_{j_{n}} = β_r \\ 0 = β_(r+1) \\ … \\ 0 = β_m \end{cases}$ (1)
Матрица, полученная из коэффициентов преобразованной системы уравнения (1) называется ступенчатой, вот так обычно выглядят ступенчатые матрицы:
$A = \begin{array}{ccc|c} a_{11} & a_{12} & a_{13} & b_1 \\ 0 & a_{22} & a_{23} & b_2\\ 0 & 0 & a_{33} & b_3 \end{array}$
Для этих матриц характерен следующий набор свойств:
- Все её нулевые строки стоят после ненулевых
- Если некоторая строка матрицы с номером $k$ ненулевая, то в предыдущей строчке этой же матрицы нулей меньше, чем в этой, обладающей номером $k$.
После получения ступенчатой матрицы необходимо подставить полученные переменные в оставшиеся уравнения (начиная с конца) и получить оставшиеся значения переменных.
Основные правила и разрешаемые преобразования при использовании метода Гаусса
При упрощении матрицы или системы уравнений этим методом нужно использовать только элементарные преобразования.
Таким преобразованиями считаются операции, которые возможно применять к матрице или системе уравнений без изменения её смысла:
- перестановка нескольких строк местами,
- прибавление или вычитание из одной строчки матрицы другой строчки из неё же,
- умножение или деление строчки на константу, не равную нулю,
- строчку, состоящую из одних нулей, полученную в процессе вычисления и упрощения системы, нужно удалить,
- Также нужно удалить лишние пропорциональные строчки, выбрав для системы единственную из них с более подходящими и удобными для дальнейших вычислений коэффициентами.
Все элементарные преобразования являются обратимыми.
Разбор трёх основных случаев, возникающих при решении линейных уравнений используя метод простых преобразований Гаусса
Различают три возникающих случая при использовании метода Гаусса для решения систем:
- Когда система несовместная, то есть у неё нет каких-либо решений
- У системы уравнений есть решение, причём единственное, а количество ненулевых строк и столбцов в матрице равно между собой.
- Система имеет некое количество или множество возможных решений, а количество строк в ней меньше чем количество столбцов.
Исход решения с несовместной системой
Для этого варианта при решении матричного уравнения методом Гаусса характерно получение какой-то строчки с невозможностью выполнения равенства. Поэтому при возникновении хотя бы одного неправильного равенства полученная и исходная системы не имеют решений вне зависимости от остальных уравнений, которые они содержат. Пример несовместной матрицы:
$\begin{array}{ccc|c} 2 & -1 & 3 & 0 \\ 1 & 0 & 2 & 0\\ 0 & 0 & 0 & 1 \end{array}$
В последней строчке возникло невыполняемое равенство: $0 \cdot x_{31} + 0 \cdot x_{32} + 0 \cdot x_{33} = 1$.
Система уравнений, у которой есть только одно решение
Данные системы после приведения к ступенчатой матрице и удаления строчек с нулями имеют одинаковое количество строк и столбцов в основной матрице. Вот простейший пример такой системы:
$\begin{cases} x_1 - x_2 = -5 \\ 2 \cdot x_1 + x_2 = -7 \end{cases}$
Запишем её в виде матрицы:
$\begin{array}{cc|c} 1 & -1 & -5 \\ 2 & 1 & -7 \end{array}$
Чтобы привести первую ячейку второй строчки к нулю, домножим верхнюю строку на $-2$ и вычтем её из нижней строчки матрицы, а верхнюю строчку оставим в исходном виде, в итоге имеем следующее:
$\begin{array}{cc|c} 1 & -1 & -5 \\ 0 & 3 & 10 \end{array}$
Этот пример можно записать в виде системы:
$\begin{cases} x_1 - x_2 = -5 \\ 3 \cdot x_2 = 10 \end{cases}$
Из нижнего уравнения выходит следующее значение $x$: $x_2 = 3 \frac{1}{3}$. Подставим это значение в верхнее уравнение: $x_1 – 3 \frac{1}{3}$, получаем $x_1 = 1 \frac{2}{3}$.
Система, обладающая множеством возможных вариантов решений
Для этой системы характерно меньшее количество значащих строк, чем количество столбцов в ней (учитываются строки основной матрицы).
Переменные в такой системе делятся на два вида: базисные и свободные. При преобразовании такой системы содержащиеся в ней основные переменные необходимо оставить в левой области до знака “=”, а остальные переменные перенести в правую часть равенства.
У такой системы есть только некое общее решение.
Разберём следующую систему уравнений:
$\begin{cases} 2y_1 + 3y_2 + x_4 = 1 \\ 5y_3 - 4y_4 = 1 \end{cases}$
Запишем её в виде матрицы:
$\begin{array}{cccc|c} 2 & 3 & 0 & 1 & 1 \\ 0 & 0 & 5 & 4 & 1 \\ \end{array}$
Наша задача найти общее решение системы. Для этой матрицы базисными переменными будут $y_1$ и $y_3$ (для $y_1$ - так как он стоит на первом месте, а в случае $y_3$ - располагается после нулей).
В качестве базисных переменных выбираем именно те, которые первые в строке не равны нулю.
Оставшиеся переменные называются свободными, через них нам необходимо выразить базисные.
Используя так называемый обратный ход, разбираем систему снизу вверх, для этого сначала выражаем $y_3$ из нижней строчки системы:
$5y_3 – 4y_4 = 1$
$5y_3 = 4y_4 + 1$
$y_3 = \frac{4/5}y_4 + \frac{1}{5}$.
Теперь в верхнее уравнение системы $2y_1 + 3y_2 + y_4 = 1$ подставляем выраженное $y_3$: $2y_1 + 3y_2 - (\frac{4}{5}y_4 + \frac{1}{5}) + y_4 = 1$
Выражаем $y_1$ через свободные переменные $y_2$ и $y_4$:
$2y_1 + 3y_2 - \frac{4}{5}y_4 - \frac{1}{5} + y_4 = 1$
$2y_1 = 1 – 3y_2 + \frac{4}{5}y_4 + \frac{1}{5} – y_4$
$2y_1 = -3y_2 - \frac{1}{5}y_4 + \frac{6}{5}$
$y_1 = -1.5x_2 – 0.1y_4 + 0.6$
Решение готово.
Пример 1
Решить слау методом Гаусса. Примеры. Пример решения системы линейных уравнений заданных матрицей 3 на 3 используя метод Гаусса
$\begin{cases} 4x_1 + 2x_2 – x_3 = 1 \\ 5x_1 + 3x_2 - 2x^3 = 2\\ 3x_1 + 2x_2 – 3x_3 = 0 \end{cases}$
Запишем нашу систему в виде расширенной матрицы:
$\begin{array}{ccc|c} 4 & 2 & -1 & 1 \\ 5 & 3 & -2 & 2 \\ 3 & 2 & -3 & 0\\ \end{array}$
Теперь для удобства и практичности нужно преобразовать матрицу так, чтобы в верхнем углу крайнего столбца была $1$.
Для этого к 1-ой строчке нужно прибавляем строчку из середины, умноженную на $-1$, а саму среднюю строчку записываем как есть, выходит:
$\begin{array}{ccc|c} -1 & -1 & 1 & -1 \\ 5 & 3 & -2 & 2 \\ 3 & 2 & -3 & 0\\ \end{array}$
$\begin{array}{ccc|c} -1 & -1 & 1 & -1 \\ 0 & -2 & 3 & -3 \\ 0 & -1 & 0 & -3\\ \end{array}$
Домножим верхнюю и последнюю строчки на $-1$, а также поменяем местами последнюю и среднюю строки:
$\begin{array}{ccc|c} 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & -2 & 3 & -3\\ \end{array}$
$\begin{array}{ccc|c} 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 3 & 3\\ \end{array}$
И разделим последнюю строчку на $3$:
$\begin{array}{ccc|c} 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 1\\ \end{array}$
Получаем следующую систему уравнений, равносильную исходной:
$\begin{cases} x_1 + x_2 – x_3 = 1\\ x_2 = 3 \\ x_3 = 1 \end{cases}$
Из верхнего уравнения выражаем $x_1$:
$x1 = 1 + x_3 – x_2 = 1 + 1 – 3 = -1$.
Пример 2
Пример решения системы, заданной с помощью матрицы 4 на 4 методом Гаусса
$\begin{array}{cccc|c} 2 & 5 & 4 & 1 & 20 \\ 1 & 3 & 2 & 1 & 11 \\ 2 & 10 & 9 & 7 & 40\\ 3 & 8 & 9 & 2 & 37 \\ \end{array}$.
В начале меняем местами верхнюю исследующую за ней строчки, чтобы получить в левом верхнем углу $1$:
$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 2 & 5 & 4 & 1 & 20 \\ 2 & 10 & 9 & 7 & 40\\ 3 & 8 & 9 & 2 & 37 \\ \end{array}$.
Теперь умножим верхнюю строчку на $-2$ и прибавим ко 2-ой и к 3-ьей. К 4-ой прибавляем 1-ую строку, домноженную на $-3$:
$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & -1 & 0 & -1 & -2 \\ 0 & 4 & 5 & 5 & 18\\ 0 & -1 & 3 & -1 & 4 \\ \end{array}$
Теперь к строке с номером 3 прибавляем строку 2, умноженную на $4$, а к строке 4 прибавляем строку 2, умноженную на $-1$.
$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & -1 & 0 & -1 & -2 \\ 0 & 0 & 5 & 1 & 10\\ 0 & 0 & 3 & 0 & 6 \\ \end{array}$
Домножаем строку 2 на $-1$, а строку 4 делим на $3$ и ставим на место строки 3.
$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & 1 & 0 & 1 & 2 \\ 0 & 0 & 1 & 0 & 2\\ 0 & 0 & 5 & 1 & 10 \\ \end{array}$
Теперь прибавляем к последней строке предпоследнюю, домноженную на $-5$.
$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & 1 & 0 & 1 & 2 \\ 0 & 0 & 1 & 0 & 2\\ 0 & 0 & 0 & 1 & 0 \\ \end{array}$
Решаем полученную систему уравнений:
$\begin{cases} m = 0 \\ g = 2\\ y + m = 2\ \ x + 3y + 2g + m = 11\end{cases}$