МУНИЦИПАЛЬНОЕ АВТОНОМНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 2
Подготовил
Легкоконец Владислав, ученик 10А класса
Практическое применение Теории Графов
Руководитель
Л.И. Носкова, учитель математики
ст.Брюховецкая
2011 г.
1.Введение………………………………………………………………………….………….3
2.История возникновения теории графов………………………………………….………..4
3.Основные определения и теоремы теории графов……………………………….………6
4.Задачи,решаемые при помощи графов……………………………..……………………..8
4.1 Знаменитые задачи………………………………….………………………...8
4.2 Несколько интересных задач………………………………….……………..9
5.Применение графов в различных областях жизни людей……………………………...11
6.Решение задач……………………………………………………………………………...12
7. Заключение………………….…………………………………………………………….13
8. Список литературы………….……………………………………………………………14
9.Приложение…………………………………………………………………….…………15
Введение
Родившись при решении головоломок и занимательных игр, теория графов стала в настоящее время простым, доступным и мощным средством решения вопросов, относящихся к широкому кругу проблем. Графы буквально вездесущи. В виде графов можно, например, интерпретировать схемы дорог и электрические цепи, географические карты и молекулы химических соединений, связи между людьми и группами людей. За последние четыре десятилетия теория графов превратилась в один из наиболее бурно развивающихся разделов математики. Это вызвано запросами стремительно расширяющейся области приложений. Применяется при проектировании интегральных схем и схем управления, при исследовании автоматов, логических цепей, блок- схем программ, в экономике и статистике, химии и биологии, в теории расписаний. Поэтому актуальность темы обусловлена с одной стороны популярностью графов и связанных с ними методов исследований, а с другой, не разработанная, целостная система ее реализации.
Решение многих жизненных задач требует длинных вычислений, а иногда и эти вычисления не приносят успеха. В этом и состоит проблема исследования . Возникает вопрос: нельзя ли для их решения найти простое, рациональное, короткое и изящное решение. Упрощается ли решение задач, если использовать графы? Это определило тему моего исследования : «Практическое применение теории графов»
Целью исследования было с помощью графов научиться быстро решать практические задачи.
Гипотеза исследования. Метод графов очень важен и широко применяется в различных областях науки и жизнедеятельности человека.
Задачи исследования:
1.Изучить литературу и ресурсы сети Интернет по данной проблеме.
2.Проверить эффективность метода графов при решении практических задач.
3. Сделать вывод.
Практическая значимость исследования заключается в том, что результаты несомненно вызовут интерес у многих людей. Разве не пытался кто-то из вас построить генеалогическое дерево своей семьи? А как это сделать грамотно? Руководителю транспортного предприятия наверняка приходится решать проблему более выгодного использования транспорта при перевозке грузов с места назначения в несколько населенных пунктов. Каждый школьник сталкивался с логическими задачами на переливание. Оказывается они решаются при помощи графов легко.
В работе используются следующие методы: наблюдение, поиск, отбор, анализ.
История возникновения теории графов
Родоначальником теории графов принято считать математика Леонарда Эйлера (1707-1783). Историю возникновения этой теории можно проследить по переписке великого ученого. Вот перевод латинского текста, который взят из письма Эйлера к итальянскому математику и инженеру Маринони, отправленного из Петербурга 13 марта 1736 года.
"Некогда мне была предложена задача об острове, расположенном в городе Кенигсберге и окруженном рекой, через которую перекинуто семь мостов.
[Приложение рис.1] Спрашивается, может ли кто-нибудь непрерывно обойти их, проходя только однажды через каждый мост. И тут же мне было сообщено, что никто еще до сих пор не мог это проделать, но никто и не доказал, что это невозможно. Вопрос этот, хотя и банальный, показался мне, однако, достойным внимания тем, что для его решения недостаточны ни геометрия, ни алгебра, ни комбинаторное искусство. После долгих размышлений я нашел легкое правило, основанное на вполне убедительном доказательстве, с помощью которого можно во всех задачах такого рода тотчас же определить, может ли быть совершен такой обход через какое угодно число и как угодно расположенных мостов или не может. Кенигсбергские же мосты расположены так, что их можно представить на следующем рисунке [Приложение рис.2] , на котором A обозначает остров, а B ,C иD – части континента, отделенные друг от друга рукавами реки
По поводу обнаруженного им способа решать задачи подобного рода Эйлер писал:
"Это решение по своему характеру, по-видимому, имеет мало отношения к математике, и мне непонятно, почему следует скорее от математика ожидать этого решения, нежели от какого-нибудь другого человека, ибо это решение подкрепляется одним только рассуждением, и нет необходимости привлекать для нахождения этого решения какие-либо законы, свойственные математике. Итак, я не знаю, каким образом получается, что вопросы, имеющие совсем мало отношения к математике, скорее разрешается математиками, чем другими".
Так можно ли обойти Кенигсбергские мосты, проходя только один раз через каждый из этих мостов? Чтобы найти ответ, продолжим письмо Эйлера к Маринони:
"Вопрос состоит в том, чтобы определить, можно ли обойти все эти семь мостов, проходя через каждый только однажды, или нельзя. Мое правило приводит к следующему решению этого вопроса. Прежде всего, нужно смотреть, сколько есть участков, разделенных водой, – таких, у которых нет другого перехода с одного на другой, кроме как через мост. В данном примере таких участков четыре – A , B , C , D . Далее нужно различать, является ли число мостов, ведущих к этим отдельным участкам, четным или нечетным. Так, в нашем случае к участку A ведут пять мостов, а к остальным – по три моста, т. е. Число мостов, ведущих к отдельным участкам, нечетно, а этого одного уже достаточно для решения задачи. Когда это определено, применяем следующее правило: если бы число мостов, ведущих к каждому отдельному участку, было четным, то тогда обход, о котором идет речь, был бы возможен, и в то же время можно было бы начать этот обход с любого участка. Если же из этих чисел два были бы нечетные, ибо только одно быть нечетным не может, то и тогда мог бы совершиться переход, как это предписано, но только начало обхода непременно должно быть взято от одного из тех двух участков, к которым ведет нечетное число мостов. Если бы, наконец, было больше двух участков, к которым ведет нечетное число мостов, то тогда такое движение вообще невозможно… если можно было привести здесь другие, более серьезные задачи, этот метод мог бы принести еще большую пользу и им не следовало бы пренебрегать".
Основные определения и теоремы теории графов
Теория графов – дисциплина математическая, созданная усилиями математиков, поэтому ее изложение включает в себя и необходимые строгие определения. Итак, приступим к организованному введению основных понятий этой теории.
Определение 1. Графомназывается совокупность конечного числа точек, называемых вершинами графа, и попарно соединяющих некоторые из этих вершин линий, называемых ребрамиили дугами графа.
Это определение можно сформулировать иначе: графомназывается непустое множество точек (вершин) и отрезков (ребер), оба конца которых принадлежат заданному множеству точек
В дальнейшем вершины графа мы будем обозначать латинскими буквами A , B , C , D . Иногда граф в целом будем обозначать одной заглавной буквой.
Определение 2. Вершины графа, которые не принадлежат ни одному ребру, называются изолированными.
Определение 3. Граф, состоящий только из изолированных вершин, называется нуль- графом.
Обозначение: O "– граф с вершинами, не имеющий ребер
Определение 4. Граф, в котором каждая пара вершин соединена ребром, называется полным.
Обозначение: U " – граф, состоящий из n вершин и ребер, соединяющих всевозможные пары этих вершин. Такой граф можно представить как n –угольник, в котором проведены все диагонали
Определение 5. Степеньювершиныназывается число ребер, которым принадлежит вершина.
Определение 6. Граф, степени всех k вершин которого одинаковы, называется однороднымграфомстепениk .
Определение 7. Дополнениемданногографаназывается граф, состоящий из всех ребер и их концов, которые необходимо добавить к исходному графу, чтобы получить полный граф.
Определение 8. Граф, который можно представить на плоскости в таком виде, когда его ребра пересекаются только в вершинах, называется плоским.
Определение 9. Многоугольник плоского графа, не содержащий внутри себя никаких вершин или ребер графа, называют его гранью.
Понятия плоского графа и грани графа применяется при решении задач на "правильное" раскрашивание различных карт.
Определение 10. Путемот A доX называется последовательность ребер, ведущая от A к X , такая, что каждые два соседних ребра имеют общую вершину, и никакое ребро не встречается более одного раза.
Определение 11. Цикломназывается путь, в котором совпадают начальная и конечная точка.
Определение 12. Простым цикломназывается цикл, не проходящий ни через одну из вершин графа более одного раза.
Определение 13. Длиной пути, проложенного на цикле, называется число ребер этого пути.
Определение 14. Две вершины A и B в графе называются связными(несвязными), если в нем существует (не существует) путь, ведущий из A в B .
Определение 15. Граф называется связным, если каждые две его вершины связны; если же в графе найдется хотя бы одна пара несвязных вершин, то граф называется несвязным.
Определение 16. Деревомназывается связный граф, не содержащий циклов.
Трехмерной моделью графа-дерева служит, например, настоящее дерево с его замысловато разветвленной кроной; река и ее притоки также образуют дерево, но уже плоское – на поверхности земли.
Определение 17. Несвязный граф, состоящий исключительно из деревьев, называется лесом.
Определение 18. Дерево, все n вершин которого имеют номера от 1 до n , называют деревом с перенумерованными вершинами.
Итак, мы рассмотрели основные определения теории графов, без которых было бы невозможно доказательство теорем, а, следовательно и решение задач.
Задачи решаемые при помощи графов
Знаменитые задачи
Задача коммивояжера
Задача коммивояжера является одной из знаменитых задач теории комбинаторики. Она была поставлена в 1934 году, и об неё обламывали зубы лучшие математики.
Постановка задачи следующая.
Коммивояжер (бродячий торговец) должен выйти из первого города, посетить по разу в неизвестном порядке города 2,1,3..n и вернуться в первый город. Расстояния между городами известны. В каком порядке следует обходить города, чтобы замкнутый путь (тур) коммивояжера был кратчайшим?
Метод решения задачи коммивояжера
Жадный алгоритм
“иди в ближайший (в который еще не входил) город”.
“Жадным” этот алгоритм назван потому, что на последних шагах приходится жестоко расплачиваться за жадность.
Рассмотрим для примера сеть на рисунке [приложение рис.3]
, представляющую узкий ромб. Пусть коммивояжер стартует из города 1. Алгоритм “иди в ближайший город” выведет его в город 2, затем 3, затем 4; на последнем шаге придется платить за жадность, возвращаясь по длинной диагонали ромба. В результате получится не кратчайший, а длиннейший тур.
Задача о Кенигсбергских мостах.
Задача формулируется следующим образом.
Город Кенигсберг расположен на берегах реки Прегель и двух островах. Различные части города были соединены семью мостами. По воскресеньям горожане совершали прогулки по городу. Вопрос: можно ли совершить прогулку таким образом, чтобы, выйдя из дома, вернуться обратно, пройдя в точности один раз по каждому мосту.
Мосты через реку Прегель расположены как на рисунке
[приложение Рис.1].
Рассмотрим граф, соответствующий схеме мостов [приложение рис.2].
Чтобы ответить на вопрос задачи, достаточно выяснить, является ли граф эйлеровым. (Хотя бы из одной вершины должно выходить четное число мостов). Нельзя, прогуливаясь по городу, пройти по одному разу все мосты и вернуться обратно.
Несколько интересных задач
1. "Маршруты".
Задача 1
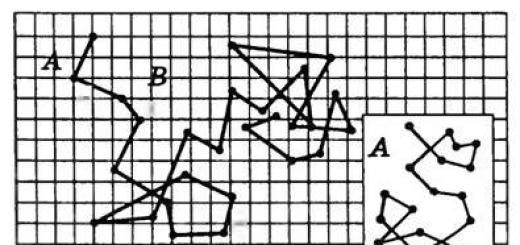
Как вы помните, охотник за мертвыми душами Чичиков побывал у известных помещиков по одному разу у каждого. Он посещал их в следующем порядке: Манилова, Коробочку, Ноздрева, Собакевича, Плюшкина, Тентетникова, генерала Бетрищева, Петуха, Констанжолго, полковника Кошкарева. Найдена схема, на которой Чичиков набросал взаимное расположение имений и проселочных дорог, соединяющих их. Установите, какое имение кому принадлежит, если ни одной из дорог Чичиков не проезжал более одного раза [приложение рис.4].
Решение :
По схеме дорог видно, что путешествие Чичиков начал с имения Е, а окончил имением О. Замечаем, что в имения В и С ведут только две дороги, поэтому по этим дорогам Чичиков должен был проехать. Отметим их жирной линией. Определены участки маршрута, проходящие через А: АС и АВ. По дорогам АЕ, АК и АМ Чичиков не ездил. Перечеркнем их. Отметим жирной линией ЕD ; перечеркнем DK . Перечеркнем МО и МН; отметим жирной линией MF ; перечеркнем FO ; отметим жирной линией FH , НК и КО. Найдем единственно возможный при данном условии маршрут. И получаем: имение Е – принадлежит Манилову, D - Коробочке, С – Ноздреву, А – Собакевичу, В – Плюшкину, М – Тентетникову, F - Бетрищеву, Н – Петуху, К – Констанжолго, О – Кошкареву [приложение рис.5] .
Задача 2
На рисунке изображена схема местности [приложение рис.6].
Передвигаться можно только в направлении стрелок. В каждом пункте можно бывать не более одного раза. Сколькими способами можно попасть из пункта 1 в пункт 9? Какой маршрут самый короткий и какой - самый длинный.
Решение :
Последовательно "расслаиваем" схему в дерево, начиная с вершины 1[приложение рис.7] . Получим дерево. Число возможных способов попадания из 1 в 9 равно числу "висячих" вершин дерева (их 14). Очевидно, кратчайший путь-1-5-9; самый длинный - 1-2-3-6-5-7-8-9.
2 "Группы, знакомства"
Задача 1
Участники музыкального фестиваля, познакомившись, обменялись конвертами с адресами. Докажите, что:
а) всего было передано четное число конвертов;
б) число участников, обменявшихся конвертами нечетное число раз, четно.
Решение: Пусть участники фестиваля А 1 , А 2 , А 3 . . . , А n – вершины графа, а ребра соединяют пары вершин, изображающих ребят, обменявшихся конвертами [Приложение рис.8]
Решение:
а) степень каждой вершины А i показывает число конвертов, которое передал участник А i своим знакомым. Общее число переданных конвертов N равно сумме степеней всех вершин графа N = степ. А 1 + степ. А 2 + + . . . + степ. А n -1 + степ. А n , N =2p , где p – число ребер графа, т.е. N – четное. Следовательно, было передано четное число конвертов;
б) в равенстве N = степ. А 1 + степ. А 2 + + . . . + степ. А n -1 + степ. А n сумма нечетных слагаемых должна быть четной, а это может быть только в том случае, если число нечетных слагаемых четно. А это означает, что число участников, обменявшихся конвертами нечетное число раз, четное.
Задача 2
Однажды Андрей, Борис, Володя, Даша и Галя договорились вечером пойти в кино. Выбор кинотеатра и сеанса они решили согласовать по телефону. Было также решено, что если с кем-то созвониться не удастся, то поход в кино отменяется. Вечером у кинотеатра собрались не все, и поэтому посещение кино сорвалось. На следующий день стали выяснять, кто кому звонил. Оказалось, что Андрей звонил Борису и Володе, Володя звонил Борису и Даше, Борис звонил Андрею и Даше, Даша звонила Андрею и Володе, а Галя звонила Андрею, Володе и Борису. Кто не сумел созвониться и поэтому не пришёл на встречу?
Решение:
Нарисуем пять точек и обозначим их буквами А, Б, В, Г, Д. Это первые буквы имён. Соединим те точки, которые соответствуют именам созвонившихся ребят.
[ приложение рис.9]
Из рисунка видно, что каждый из ребят – Андрей, Борис и Володя - созвонились со всеми остальными. Поэтому эти ребята и пришли к кинотеатру. А Галя и Даша не сумели созвониться между собой (точки Г и Д не соединены отрезком) и поэтому в соответствии с договорённостью в кино не пришли.
Применение графов в различных областях жизни людей
Кроме приведенных примеров, графы широко используются в строительстве, электротехнике, менеджменте, логистике, географии, машиностроении, социологии, программировании, автоматизации технологических процессов и производств, психологии, рекламе. Итак, из всего вышесказанного неопровержимо следует практическая ценность теории графов, доказательство которой и являлось целью данного исследования.
В любой области науки и техники встречаешься с графами. Графы - это замечательные математические объекты, с помощью которых можно решать математические, экономические и логические задачи, различные головоломки и упрощать условия задач по физике, химии, электронике, автоматике. Многие математические факты удобно формулировать на языке графов. Теория графов является частью многих наук. Теория графов - одна из самых красивых и наглядных математических теорий. В последнее время теория графов находит всё больше применений и в прикладных вопросах. Возникла даже компьютерная химия - сравнительно молодая область химии, основанная на применении теории графов.
Молекулярные графы , применяемые в стереохимии и структурной топологии, химии кластеров, полимеров и др., представляют собой неориентированные графы, отображающие строение молекул [приложение рис.10] . Вершины и ребра этих графов отвечают соответственным атомам и химическим связям между ними.
Молекулярные графы и деревья: [приложение рис.10] а, б - мультиграфы соотв. этилена и формальдегида; в-мол. изомеров пентана (деревья 4, 5 изоморфны дереву 2).
В стереохимии организмов наиболее. часто используют молекулярные деревья -основные деревья молекулярных графов, которые содержат только все вершины, соответствующие атомам С. Составление наборов мол. деревьев и установление их изоморфизма позволяют определять мол. структуры и находить полное число изомеров алканов, алкенов и алкинов
Белковые сети
Белковые сети - группы физически взаимодействующих белков, которые функционируют в клетке совместно и скоординированно, контролируя взаимосвязанные процессы, происходящие в организме [приложение рис. 11].
Граф иерархической системы называется деревом. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь. Дерево не содержит циклов и петель.
Обычно у дерева, представляющего иерархическую систему, выделяется одна главная вершина, которая называется корнем дерева. Каждая вершина дерева (кроме корня) имеет только одного предка – обозначенный ею объект входит в один класс верхнего уровня. Любая вершина дерева может порождать несколько потомков – вершин, соответствующих классам нижнего уровня.
Для каждой пары вершин дерева существует единственный путь, их соединяющий. Этим свойством пользуются при нахождении всех предков, например, по мужской линии, любого человека, чья родословная представлена в виде генеалогического дерева, которое является «деревом» и в смысле теории графов.
Пример генеалогического дерева моей семьи [приложение рис.12].
Еще один пример. На рисунке показано библейское генеалогическое дерево [приложение рис.13].
Решение задач
1.Транспортная задача . Пусть в городе Краснодаре находится база с сырьём, которое нужно развести по городам Крымск, Темрюк, Славянск-на-Кубани и Тимашевск одним заездом, затратив при этом как можно меньше времени и топлива и вернувшись обратно в Краснодар.
Решение:
Для начала составим граф всех возможных путей проезда [приложение рис.14] , учитывая реальные дороги между данными населенными пунктами и расстояние между ними. Для решения этой задачи нам потребуется составить еще один граф, древовидный [приложение рис.15] .
Для удобства решения обозначаем города цифрами: Краснодар – 1, Крымск – 2, Темрюк – 3, Славянск – 4, Тимашевск – 5.
В результате вышло 24 решения, но нам нужны только кратчайшие пути. Из всех решений удовлетворяют только два, это 350 км.
Подобно этому можно и, я думаю, нужно рассчитывать реальные перевозки из одного населенного пункта в другие.
Логическая задача на переливание. В ведре 8 л воды, и имеется две кастрюли емкостью 5 и 3 л. требуется отлить в пятилитровую кастрюлю 4 л воды и оставить в ведре 4 л, т. е. разлить воду поровну в ведро и большую кастрюлю.
Решение:
Ситуацию в каждый момент можно описать тремя числами [приложение рис.16].
В результате получаем два решения: одно в 7 ходов, другое в 8 ходов.
Заключение
Итак, для того чтобы научиться решать задачи, надо разобраться в том, что собой они представляют, как они устроены, из каких составных частей они состоят, каковы инструменты, с помощью которых производится решение задач.
Решая практические задачи с помощью теории графов стало ясно видно, что в каждом шаге, в каждом этапе их решения необходимо применить творчество.
С самого начала, на первом этапе, оно заключается в том, что нужно суметь проанализировать и закодировать условие задачи. Второй этап – схематическая запись, которая состоит в геометрическом представлении графов, и на этом этапе элемент творчества очень важен потому, что далеко не просто найти соответствия между элементами условия и соответствующими элементами графа.
Решая транспортную задачу или задачу на составление генеалогического дерева я сделал вывод, что безусловно метод графов интересен, красив и нагляден.
Я убедился, что графы достаточно широко применяются в экономике, управлении, технике. Также теория графов применяется в программировании.Об этом в данной работе не шла речь, но думаю, что это только вопрос времени.
В настоящей научной работе рассмотрены математические графы, области их применения, решено несколько задач с помощью графов. Знание основ теории графов необходимо в различных областях, связанных с управлением производством, бизнесом (например, сетевой график строительства, графики доставки почты). Кроме того, работая над научной работой, я освоил работу на компьютере в текстовом редакторе WORD . Таким образом, задачи научной работы выполнены.
Итак, из всего вышесказанного неопровержимо следует практическая ценность теории графов, доказательство которой и являлось целью данной работы.
Литература
Берж К. Теория графов и ее применения. -M.: ИИЛ, 1962.
Кемени Дж., Снелл Дж., Томпсон Дж. Введение в конечную математику. -M.: ИИЛ, 1963.
Оре О. Графы и их применение. -M.: Мир, 1965.
Харари Ф. Теория графов. -M.: Мир, 1973.
Зыков А.А. Теория конечных графов. -Новосибирск: Наука, 1969.
Березина Л.Ю. Графы и их применение. -M.: Просвещение, 1979. -144 c.
"Соросовский образовательный журнал" №11 1996 (ст. "Плоские графы");
Гарднер М. "Математические досуги", М. "Мир", 1972(глава 35);
Олехник С. Н., Нестеренко Ю. В., Потапов М. К. "Старинные занимательные задачи", М. "Наука", 1988(часть 2, раздел 8; приложение 4);
Приложение

Приложение



П
Рис. 6


Рис. 7
Рис. 8
риложениеПриложение


Приложение

Приложение


П

Рис. 14
риложениеПриложение

Теория графов находит применение, например, в геоинформационных системах (ГИС). Существующие или вновь проектируемые дома, сооружения, кварталы и т. п. рассматриваются как вершины, а соединяющие их дороги, инженерные сети, линии электропередачи и т. п. - как рёбра. Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут.
Теория графов содержит большое количество нерешённых проблем и пока не доказанных гипотез.
Основные сферы применения теории графов:
В химии (для описания структур, путей сложных реакций, правило фаз также может быть интерпретировано как задача теории графов); компьютерная химия - сравнительно молодая область химии, основанная на применении теории графов. Теория графов представляет собой математическую основу хемоинформатики. Теория графов позволяет точно определить число теоретически возможных изомеров у углеводородов и других органических соединений;
В информатике и программировании (граф-схема алгоритма);
В коммуникационных и транспортных системах. В частности, для маршрутизации данных в Интернете;
В экономике;
В логистике;
В схемотехнике (топология межсоединений элементов на печатной плате или микросхеме представляет собой граф или гиперграф).
Выделяют особый вид графа, дерево. Дерево - это связный ациклический граф. Связность означает наличие путей между любой парой вершин, ацикличность - отсутствие циклов и то, что между парами вершин имеется только по одному пути. На Рис 1.3 представлено двоичное дерево .
Двоичное дерево - древовидная структура данных, в которой каждый узел имеет не более двух потомков (детей). Как правило, первый называется родительским узлом , а дети называются левым и правым наследниками .
Матричное представление графов. Матрица инциденций.
Развитие алгоритмических подходов к анализу свойств графов требует определенных способов описания графов, более пригодных для практических вычислений, в том числе с использованием ЭВМ. Рассмотрим три наиболее распространенных способа представления графов.
Предположим, что все вершины и все ребра неориентированного графа или все вершины и все дуги (включая петли) ориентированного графа пронумерованы начиная с единицы. Граф (неориентированный или ориентированный) может быть представлен в виде матрицы типа , где- число вершин, а- число ребер (или дуг). Для неориентированного графа элементы этой матрицы задаются следующим образом:
Для ориентированного графа элементы матрицы задаются так:

Матрицу типа, определенную указанным образом, называютматрицей инциденций.
Пример получения матрицы инциденций. Для изображенного ниже графа (Рис. 2.1 а Рис 2.1 б).


Рис 2.1 а Рис. 2.1 б
Матрица смежности.
Несмотря на то, что представление графа в виде матрицы инциденций играет весьма большую роль в теоретических исследованиях, практически этот способ весьма неэффективен. Прежде всего, в матрице в каждом столбце только два ненулевых элемента, что делает этот способ представления графа неэкономным при большом количестве вершин. Кроме того, решение практических задач с помощью матрицы инциденций весьма трудоемко.
Оценим, например, временные затраты на решение с помощью матрицы инциденций такой простой задачи в ориентированном графе: для данной вершины найти ее "окружение" - множество преемников и множество предшественников вершины, т.е. множество всех вершин, непосредственно достижимых из, и множество всех вершин, из которых она непосредственно достижима.
Для решения этой задачи на матрице инциденций ориентированного графа нужно идти по строке с номером до появления ненулевого элемента (+1 или –1). В случае если обнаружена +1, в соответствующем столбце надо найти строку, в которой записано число –1. Номер строки, в которой стоит это число, дает номер вершины, непосредственно достижимой из данной вершины. Если обнаружена –1, в столбце надо найти строку, в которой записана 1, и получить номер вершины, из которой непосредственно достижима данная вершина. Для получения всего "окружения" надо проделать указанный поиск для всех ненулевых элементов k-й строки. Наиболее трудоемкой процедурой является поиск ненулевого элемента в столбце. Число таких процедур поиска равно степени вершины. Будем в этом случае говорить, что сложность алгоритма анализа окружения вершинысоставляет(порядка).
Можно увидеть, что поиск "окружения" всех вершин займет время порядка произведения числа вершин ориентированного графа на сумму степеней всех вершин, которая, как можно показать, пропорциональна числу дуг ориентированного графа. Таким образом, сложность алгоритма поиска "окружения" составляет , т.е. поиск занимает время порядка произведения числа вершин на число дуг.
Более эффективной матричной структурой, представляющей граф, служит матрица смежности вершин , или булева матрица графа. Это квадратная матрица В порядка n , элементы которой определяют следующим образом:
для
неориентированного графа:
![]()
для
ориентированного графа:
![]()
Для изображенного ниже графа (Рис. 2.2 а ) матрицей инциденций будет матрица, представленная на (Рис 2.2 б).
Начало теории графов все единодушно относят к 1736 г. , когда Л. Эйлер решил популярную в то время задачу о кенигсберских мостах. Однако этот результат более ста лет оставался единственным результатом теории графов. Лишь в середине XIX века инженер- электрик Г. Кирхгоф разработал теорию деревьев для исследования электрических цепей, а математик А. Кэли в связи с описанием строения углеводородов решил перечислительные задачи для трех типов деревьев.
Родившись при решении головоломок и занимательных игр (задачи о шахматном коне, о ферзях, « кругосветное путешествие », задачи о свадьбах и гаремах и т. п.), теория графов стала в настоящее время простым, доступным и мощным средством решения вопросов, относящихся к широкому кругу проблем. Графы буквально вездесущи. В виде графов можно, например, интерпретировать схемы дорог и электрические цепи, географические карты и молекулы химических соединений, связи между людьми и группами людей. За последние четыре десятилетия теория графов превратилась в один из наиболее бурно развивающихся разделов математики. Это вызвано запросами стремительно расширяющейся области приложений. Применяется при проектировании интегральных схем и схем управления, при исследовании автоматов, логических цепей, блок- схем программ, в экономике и статистике, химии и биологии, в теории расписаний. В значительной степени через теорию графов происходит ныне проникновение математических методов в науку и технику.
В настоящей работе рассматривается не собственные задачи теории графов, а то, каким образом используется она в школьном курсе геометрии.
Поэтому актуальность темы исследования обусловлена с одной стороны популярностью графов и связанных с ними методов исследований, которые органически пронизывают на разных уровнях едва ли не всю современную математику, а с другой, не разработана целостная система ее реализации в курсе геометрии.
Цель исследования - изучить применение графов в школьном курсе геометрии.
Объект – процесс обучения геометрии.
Предмет –классная и внеклассная работа
Задачи: 1) определить сущность и содержание применения графов в школьном курсе геометрии;
2) разработать ПМК для проведения уроков геометрии в 7-9 классах.
Ведущая тема – построение графовой модели для доказательства геометрических теорем.
Теоретическая основа:
1. Теория графов возникшая в 1736 году (Леонард Эйлер (1708-1783) получила бурное развитие, остаётся актуальной и сейчас, т. к. в повседневной жизни всё большее применение находят графические иллюстрации, геометрические представления и другие приёмы и методы наглядности.
1. Теория графов находит применение в различных областях современной математики и её многочисленных приложений (Липатов Е. П.)
2. Теория графов применяется в таких областях математики, как математическая логика, комбинаторика и др.
Теоретическая значимость работы заключается в:
Выявление областей применения теории графов;
Использование теории графов к изучению геометрических теорем и задач;
Практическая значимость работы состоит в применении графов в доказательствах геометрических теорем и решении задач.
В результате выполнения данной работы создан:
Программно-методический комплекс для проведения уроков геометрии в 7-9 классах.
Самое трудное в поиске решения задачи - это установление цепочки логических следований, которая приводит к доказываемому утверждению. Чтобы логически грамотно рассуждать, надо развивать навыки такого мышления, которое помогало бы выстраивать разрозненные геометрические факты в логические взаимосвязи.
Для выработки навыков культуры мышления особую роль играют формы письменной речи учащихся. Письменные формы работы являются важнейшим видом деятельности, формирующим устойчивые навыки в логических рассуждениях при доказательствах теорем и решении задач. Форма записи условия задачи, разумные сокращения и обозначения при вычислениях и доказательствах задач дисциплинирует мышление и способствует геометрическому видению. Как известно, видение рождает мышление. Возникает проблема: как установить логические связи между разрозненными геометрическими фактами и как оформить в виде единой целой. Видеть ход доказательства теорем и решения задач позволяет метод граф- схем, который делает доказательство более наглядным и позволяет кратко и точно изложить доказательства теорем и решения задач.
Для этого используется граф-дерево.
Вершины « дерева » (условие теоремы или задачи и последовательность логических связок) изображены прямоугольниками с помещенной в них информацией, которые затем соединены стрелками. Конец граф-схемы содержит доказываемое утверждение. Описанная форма доказательства теорем и решения задач полезна и удобна учащимся, т. к. дает возможность легко выделить основные этапы доказательства теоремы, решения задачи.
Исследовательская часть.
Раздел 1. Изучение истории возникновения теории графов.
Родоначальником теории графов принято считать математика Леонарда Эйлера (1707-1783). Историю возникновения этой теории можно проследить по переписке великого ученого. Вот перевод латинского текста, который взят из письма Эйлера к итальянскому математику и инженеру Маринони, отправленного из Петербурга 13 марта 1736 года.
"Некогда мне была предложена задача об острове, расположенном в городе Кенигсберге и окруженном рекой, через которую перекинуто семь мостов. Спрашивается, может ли кто-нибудь непрерывно обойти их, проходя только однажды через каждый мост. И тут же мне было сообщено, что никто еще до сих пор не мог это проделать, но никто и не доказал, что это невозможно. Вопрос этот, хотя и банальный, показался мне, однако, достойным внимания тем, что для его решения недостаточны ни геометрия, ни алгебра, ни комбинаторное искусство. После долгих размышлений я нашел легкое правило, основанное на вполне убедительном доказательстве, с помощью которого можно во всех задачах такого рода тотчас же определить, может ли быть совершен такой обход через какое угодно число и как угодно расположенных мостов или не может. Кенигсбергские же мосты расположены так, что их можно представить на следующем рисунке, на котором A обозначает остров, а B, C и D – части континента, отделенные друг от друга рукавами реки. Семь мостов обозначены буквами a, b, c, d, e, f, g ".
По поводу обнаруженного им способа решать задачи подобного рода Эйлер писал
"Это решение по своему характеру, по-видимому, имеет мало отношения к математике, и мне непонятно, почему следует скорее от математика ожидать этого решения, нежели от какого-нибудь другого человека, ибо это решение подкрепляется одним только рассуждением, и нет необходимости привлекать для нахождения этого решения какие-либо законы, свойственные математике. Итак, я не знаю, каким образом получается, что вопросы, имеющие совсем мало отношения к математике, скорее разрешается математиками, чем другими".
Так можно ли обойти Кенигсбергские мосты, проходя только один раз через каждый из этих мостов? Чтобы найти ответ, продолжим письмо Эйлера к Маринони:
"Вопрос состоит в том, чтобы определить, можно ли обойти все эти семь мостов, проходя через каждый только однажды, или нельзя. Мое правило приводит к следующему решению этого вопроса. Прежде всего, нужно смотреть, сколько есть участков, разделенных водой, – таких, у которых нет другого перехода с одного на другой, кроме как через мост. В данном примере таких участков четыре – A, B, C, D. Далее нужно различать, является ли число мостов, ведущих к этим отдельным участкам, четным или нечетным. Так, в нашем случае к участку A ведут пять мостов, а к остальным – по три моста, т. е. Число мостов, ведущих к отдельным участкам, нечетно, а этого одного уже достаточно для решения задачи. Когда это определено, применяем следующее правило: если бы число мостов, ведущих к каждому отдельному участку, было четным, то тогда обход, о котором идет речь, был бы возможен, и в то же время можно было бы начать этот обход с любого участка. Если же из этих чисел два были бы нечетные, ибо только одно быть нечетным не может, то и тогда мог бы совершиться переход, как это предписано, но только начало обхода непременно должно быть взято от одного из тех двух участков, к которым ведет нечетное число мостов. Если бы, наконец, было больше двух участков, к которым ведет нечетное число мостов, то тогда такое движение вообще невозможно если можно было привести здесь другие, более серьезные задачи, этот метод мог бы принести еще большую пользу и им не следовало бы пренебрегать".
Обоснование вышеприведенного правила можно найти в письме Л. Эйлера к своему другу Элеру от 3 апреля того же года. Мы перескажем ниже отрывок из этого письма.
Математик писал, что переход возможен, если на участке разветвления реки имеется не более двух областей, в которые ведет нечетное число мостов. Для того, чтобы проще представить себе это, будем стирать на рисунке уже пройденные мосты. Легко проверить, что если мы начнем двигаться в соответствии с правилами Эйлера, пересечем один мост и сотрем его, то на рисунке будет изображен участок, где опять имеется не более двух областей, в которые ведет нечетное число мостов, а при наличии областей с нечетным числом мостов мы будем располагаться в одной из них. Продолжая двигаться так далее, пройдем через все мосты по одному разу.
История с мостами города Кенигсберга имеет современное продолжение.
Задача На озере находится семь островов, которые соединены между собой так, как показано на рисунке 2. На какой остров должен доставить путешественников катер, чтобы они могли пройти по каждому мосту и только один раз? Почему нельзя доставить путешественников на остров A?
Решение. Поскольку эта задача подобна задаче о Кенигсбергских мостах, то при ее решении мы также воспользуемся правилом Эйлера. В результате получим следующий ответ: катер должен доставить путешественников на остров E или F, чтобы они смогли пройти по каждому мосту один раз. Из того же правила Эйлера следует невозможность требуемого обхода, если он начнется с острова A.
В дальнейшем над графами работали Кениг (1774-1833), Гамильтон (1805-1865), из современных математиков – К. Берж, О. Оре, А. Зыков.
Исторически сложилось так, что теория графов зародилась двести с лишним лет назад именно в ходе решения головоломок. Очень долго она находилась в стороне от главных направлений исследований ученых, была в царстве математики на положении Золушки, чьи дарования раскрылись в полной мере лишь тогда, когда она оказалась в центре общего внимания.
Первая работа по теории графов, принадлежащая известному швейцарскому математику Л. Эйлеру, появилась в 1736 г. Толчок к развитию теория графов получила на рубеже ХIX и ХХ столетий, когда резко возросло число работ в области топологии и комбинаторики, с которыми ее связывают самые тесные узы родства. Графы стали использоваться при построении схем электрических цепей и молекулярных схем. Как отдельная математическая дисциплина теория графов была впервые представлена в работе венгерского математика Кенига в 30-е годы ХХ столетия.
В последнее время графы и связанные с ними методы исследований органически пронизывают на разных уровнях едва ли не всю современную математику. Теория графов рассматривается как одна из ветвей топологии; непосредственное отношение она имеет также к алгебре и к теории чисел. Графы эффективно используются в теории планирования и управления, теории расписаний, социологии, математической лингвистике, экономике, биологии, медицине, географии. Широкое применение находят графы в таких областях, как программирование, теория конечных автоматов, электроника, в решении вероятностных и комбинаторных задач, кратчайшего расстояния, и др. Математические развлечения и головоломки тоже являются частью теории графов. Теория графов быстро развивается, находит все новые приложения.
Раздел 2. Основные виды, понятия и структура графов.
Теория графов – дисциплина математическая, созданная усилиями математиков, поэтому ее изложение включает в себя и необходимые строгие определения.
Графом называется совокупность конечного числа точек, называемых вершинами графа, и попарно соединяющих некоторые из этих вершин линий, называемых ребрами или дугами графа.
№ Название графа Определение Рисунок Пример применения этого вида графов
1 Нулевой граф Вершины графа, которые не принадлежат Задача: Аркадий, Борис. Владимир, Григорий и Дмитрий при встрече обменялись ни одному рукопожатиями, каждый пожал руку каждому по одному разу. Сколько всего ребру, называются изолированными. рукопожатий было сделано? Ситуация, соответствующая моменту, когда рукопожатия еще не совершались, представляет собой точечную схему, изображенную на рисунке.
Граф, состоящий только из изолированных вершин, называется нуль-графом.
Обозначение: O" – граф с вершинами, не имеющий ребер
2 Полные графы Граф, в котором каждая пара вершин Заметим, что если полный граф имеет n вершин, то количество ребер будет Совершены все рукопожатия.
Обозначение: U" – граф, состоящий из n 10.
вершин и ребер, соединяющих всевозможные пары этих вершин. Такой граф можно представить как n–угольник, в котором проведены все диагонали
3 Неполные графы Графы, в которых не построены все Ситуация, когда совершены еще не все рукопожатия,пожали руки А и Б, А и Г, Д и возможные ребра, называются неполными Г, В и Д.
4 Путь в графе. Цикл. Путем в графе от одной вершины к другой В точке А расположен гараж для снегоочистительной машины. Водителю машины было называется поручено убрать снег с улиц части города, изображенной на рисунке. Может ли он такая последовательность ребер,по которой закончить свою работу на том перекрестке, где находится гараж, если по каждой можно проложить маршрут между этими улице своего участка города водитель будет проезжать только один раз?
вершинами.
При этом никакое ребро маршрута не должно встречаться более одного раза. Вершина, от Нельзя, так как замкнутый путь, проходящий по всем ребрам графа,причем по которой проложен маршрут, называется каждому ребру только один раз существует,если степени всех вершин графа четные.
началом пути, вершина в конце маршрута -
конец пути. Циклом называется путь, в На рисунке с помощью графа изображена схема дорог между населенными котором совпадают начало с концом. Простымпунктами.
циклом называется цикл, не проходящий Например, из пункта A (вершина графа) в пункт H можно добраться различными ни маршрутами: ADGH, AEH, AEFCEH, ABCEH.
через одну из вершин графа более одного Чем отличается маршрут AEH от маршрута AEFCEH?
раза. Тем, что во втором маршруте на «перекрестке» в точке E мы побывали дважды.
Этот маршрут длиннее, чем AEH. Маршрут AEH можно получить из маршрута
Если же цикл включает в себя все ребра AEFCEH «вычеркнув» из последнего маршрут FCE.
графа по одному разу, то такой цикл Маршрут AEH является путем в графе, а маршрут AEFCEH путем не является.
называется Эйлеровой линией.
Связные и несвязные графы. Определение 1: Можно ли из проволоки длиной 12 дм изготовить каркас куба с ребром длины
Две вершины графа называются связными, 1 дм, не ломая проволоку на части?
если в графе существует путь с концами в этих вершинах. Если такого пути не существует, вершины называются не связными.
Так как путь,проходящий по всем ребрам графа, причем по каждому ребру только один раз, существует лишь в следующих случаях:
1) когда степень каждой вершины четная(путь замкнут)
2)когда только две вершины с нечетной степенью.
Определение 2:
Граф называется связным, если любая пара его вершин - связная.
Граф называется несвязным, если в нем есть хотя бы одна несвязная пара вершин.
6 Деревья Деревом называется любой связный граф, Приложение №1. Генеалогическое древо Жолмурзаевой Томирис.
вершины. Несвязный граф, состоящий исключительно из деревьев, называется лесом.
7 Изоморфные графы. Графы, изображенные на рисунке, дают одну и ту же информацию. Такие графы называют изоморфными (одинаковыми).
8 Понятие плоского графа Граф, который можно представить на Задача. В трех различных домах живут три плоскости в поссорившиеся между собой соседа. Недалеко таком виде, когда его ребра пересекаются от их домов имеются три колодца. Можно ли от только в вершинах, называется каждого дома проложить к каждому из колодцев плоским. тропинку так, чтобы никакие две из них не пересекались?
Решение: После проведения восьми тропинок можно убедиться, что провести девятую, не пересекающуюся ни с какой из ранее проведенных тропинок, не удается.
Построим граф, вершины которого
А, Б, В, 1, 2, 3
соответствуют домам и колодцам условия задачи, и попробуем доказать, что девятую тропинку - ребро графа, не пересекающее остальные ребра, провести нельзя.
Проведенные в графе на рисунке ребра
А1, А2, A3 и В1,В2, ВЗ (соответствующие тропинкам от домов А и В ко всем колодцам).
Построенный граф разбил плоскость на три области: X, У, Z. Вершина Б, в зависимости от ее расположения на плоскости, попадает в одну из этих трех областей. Если вы рассмотрите каждый из трех случаев «попадания» вершины
Б в одну из областей X, Y или Z, то убедитесь, что всякий раз одна из вершин графа 1, 2 или 3
(один из колодцев) будет «недоступной» для вершины Б (т. е. нельзя будет провести одно из ребер Б1, Б2 или Б3. которое не пересекло бы уже имеющихся в графе ребер).
Ответ на вопрос задачи будет: «Нельзя!»
Ориентированные графы Ребро графа называется ориентированным ребром, если одну из его вершин считать началом, а другую - концом этого ребра.
Граф, у которого все ребра ориентированные, называется ориентированным графом.
Итак, я рассмотрела основные понятия теории графов, без которых было бы невозможно доказательство теорем, а, следовательно, и решение задач.
Вывод по проделанной работе:
Я научилась структурировать в таблицу весь информационный материал;
Скомпонованность теоретического материала способствуют наглядному представлению о видах графов и их применению;
Отработала примеры применения теории графов в составлении своего генеалогического древа.
Приложение №1.
ГЕНЕОЛОГИЧЕСКОЕ ДРЕВО
Построить генеалогическое дерево Жолмурзаевой Томирис.
Метод решения.
Графический способ решения задачи.
Графический способ решения задачи заключается в вычерчивании «дерева логических условий». «Дерево» выражает в виде простого чертежа логическую взаимосвязь между родственниками. Каждому поколению на дереве соответствует одна ветвь.
В качестве примера я взяла свое генеалогическое древо.
Раздел 3. Применение теории графов.
С графами мы встречаемся чаще, чем это возможно, кажется на первый взгляд. Примерами графов могут служить любая карта дорог, электросхема, чертеж многоугольников и т. д. Долгое время считалось, что теория графов применяется главным образом при решении логических задач. При решении логических задач часто бывает трудно запомнить многочисленные условия, данные в задаче, и установить связь между ними Решать такие задачи помогают графы, дающие возможность наглядно представить отношения между данными задачи. Сама теория графов рассматривалась как часть геометрии. Однако в двадцатом веке были найдены широкие приложения теории графов в экономике, биологии, химии, электронике, сетевом планировании, комбинаторике и других областях науки и техники. В результате она стала бурно развиваться и превратилась в самостоятельную разветвленную теорию.Решение многих математических задач упрощается, если удается использовать графы. Представление данных в виде графа придает им наглядность. Многие доказательства также упрощаются, приобретают убедительность, если воспользоваться графами.
3. 1. Применение графов в геометрических задачах и теоремах.
С помощью графов можно легко установить цепочки логических следований, которые приводят к доказываемому утверждению. Кратко и точно изложить доказательство теоремы и решение задачи.
Докажите, что у равнобедренного треугольника биссектрисы, проведенные из вершин при основании, равны.
Методы решений.
Доказательство задачи с помощью рассуждений.
Пусть АВС – равнобедренный треугольник с
В1 А1 основанием АВ и биссектрисами АА1 и ВВ1.
Рассмотрим ∆АВВ1 и ∆ВАА1. У них ∟В1АВ=
∟А1ВА как углы при основании равнобедрен – ного треугольника ∆АВС. ∟АВВ1= ∟А1АВ
А В так как АА1 и ВВ1 – биссектрисы углов при основании равнобедренного треугольника. АВ- общая сторона. Значит
∆АВВ1 = ∆ВАВ1 по стороне и двум прилежащим к ней углам. Из равенства треугольников следует равенство их сторон АА1 и ВВ1.
Доказательство задачи с помощью графа.
Доказать: АА=ВВ
Используем для рассуждений граф. Вершины графа- условия теоремы или задачи и этапы доказательства.
Ребра графа – логические следования. Конец граф-схемы – доказываемое утверждение.
Дя выделения составных частей использован цвет. Условие теоремы и задачи – синий. Доказываемое утверждение – красный. Этапы доказательства – черный.
Описанная форма доказательства теорем и решения задач полезна и удобна учащимся, т. к. дает возможность выделить основные этапы доказательства теоремы, решения задачи.
3. 2. Программно- методический комплекс.
а) Пособие для учителя.
Предлагаемое пособие составлено в соответствии с учебником геометрии 7-9 классов А. В. Погорелова. Основное ее назначение обеспечить процесс изучения геометрии необходимыми средствами наглядностей, оказать помощь учителю в преподавании геометрии: облегчить процесс доказательства теорем, усвоение теоретического материала в процессе решения задач. Граф-схемы носят многоплановый характер и в зависимости от целей и форм занятий можно использовать по-разному: как иллюстративные, направленные на усиление наглядности при объяснении нового теоретического материала, при обобщении и систематизации нового материала (граф-схемы с теоремами); как карточки, используемые при проведении индивидуальных и фронтальных опросов (граф-схемы с задачами). К этому пособию предлагается рабочая тетрадь для учащихся. Рабочую тетрадь можно использовать для организации самостоятельной работы учащихся в урочное и внеурочное время.
б) Рабочая тетрадь для учащихся.
Пособие выполнено в виде рабочей тетради. Пособие включает 28 граф-схем с теоремами и 28 граф-схем с задачами. Граф-схемы содержат основной программный материал, который представлен с необходимой наглядностью и представляет собой каркас решения. Учащиеся последовательно заполняют пустые клетки информацией, составляющих решение задачи.
Для выделения составных частей использован цвет. Условие теоремы и задачи – синий, доказываемое утверждение – красный, этапы доказательства – черный.
Пособие полезно для учащихся 7-9 классов.
в) Электронное пособие.
Результаты работы и их обсуждение. Проект представляет собой итог двухлетнего изучения применения графов в школьном курсе математики.
Создание программно – методического комплекса и ее внедрение осуществлялись в ходе:
Проведения занятий клуба «Аристотель» по теме «Решение логических задач с помощью графов».
Применения графов в доказательствах геометрических теорем и задач
На уроках геометрии в 8,9 классе.
Выступления с проектом на школьной научно- практической конференций.
ЗАКЛЮЧЕНИЕ.
Подводя итоги исследования применения графов в школьном курсе геометрии, я пришла к следующему заключению:
1. Преимуществом графового доказательства теорем и решения задач перед традиционным является иллюстрация динамики доказательства теорем и задач.
2. Введение в процесс доказательства геометрических теорем и задач метода граф-схем способствует укреплению у учащихся навыков построения доказательства.
3. Разработанный программно-методический комплекс для изучения геометрии в 7-9 классах: а) пособие для учителя; б) рабочая тетрадь для учащихся; в) электронное пособие полезен учащимся 7-9 классов.
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Подобные документы
Восстановление графов по заданным матрицам смежности вершин. Построение для каждого графа матрицы смежности ребер, инцидентности, достижимости, контрдостижимости. Поиск композиции графов. Определение локальных степеней вершин графа. Поиск базы графов.
лабораторная работа , добавлен 09.01.2009
Теория графов как раздел дискретной математики, исследующий свойства конечных множеств с заданными отношениями между их элементами. Основные понятия теории графов. Матрицы смежности и инцидентности и их практическое применение при анализе решений.
реферат , добавлен 13.06.2011
Основные понятия теории графов. Степень вершины. Маршруты, цепи, циклы. Связность и свойства ориентированных и плоских графов, алгоритм их распознавания, изоморфизм. Операции над ними. Обзор способов задания графов. Эйлеровый и гамильтоновый циклы.
презентация , добавлен 19.11.2013
Описание заданного графа множествами вершин V и дуг X, списками смежности, матрицей инцидентности и смежности. Матрица весов соответствующего неориентированного графа. Определение дерева кратчайших путей по алгоритму Дейкстры. Поиск деревьев на графе.
курсовая работа , добавлен 30.09.2014
Основные понятия теории графов. Расстояния в графах, диаметр, радиус и центр. Применение графов в практической деятельности человека. Определение кратчайших маршрутов. Эйлеровы и гамильтоновы графы. Элементы теории графов на факультативных занятиях.
дипломная работа , добавлен 19.07.2011
Понятие и матричное представление графов. Ориентированные и неориентированные графы. Опеределение матрицы смежности. Маршруты, цепи, циклы и их свойства. Метрические характеристики графа. Применение теории графов в различных областях науки и техники.
курсовая работа , добавлен 21.02.2009
Математическое описание системы автоматического управления с помощью графов. Составление графа и его преобразование, избавление от дифференциалов. Оптимизации ориентированных и неориентированных графов, составления матриц смежности и инцидентности.
лабораторная работа , добавлен 11.03.2012
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF
Наш мир полон не только букв и цифр, но и самых разнообразных изображений. Это и картины, и всевозможные фотографии, а также многочисленные схемы. Схемы встречаются на логотипах компаний и автомобилей, дорожных знаках и картах. Если посмотреть на схему метро или автобусного маршрута, это всего лишь линии с точками. Подобные схемы из линий (ребер) и точек (вершин) называются графами.
Теория графов появилась благодаря одной занимательной задаче, которую решил Леонард Эйлер. История гласит, что в 1736 году этот блестящий математик остановился в Кенигсберге. Город был разделен рекой на 4 части, соединенные семью мостами. Нужно было определить, можно ли обойти все мосты, пройдя по каждому ровно один раз. Эйлер определил, что решить задачу невозможно . Кенигсбергские мосты были разрушены во время Второй мировой войны, но эта история дала начало красивой математической теории - теории графов.
В XX веке теория графов получила невероятное развитие, она нашла многочисленные применения в задачах планирования, архитектуры, инженерии , а особенно в информатике и телекоммуникациях. Графы связаны с комбинаторикой, дискретной математикой, топологией, теорией алгоритмов и другими разделами математики.
Какие же возможности получает ученик, владеющий этой теорией? Сможет ли он достичь каких-то успехов в своей учебе или обычной жизни? Такому исследованию и посвящен данный проект.
Цель проекта: Показать, что методы теории графов дают школьнику инструмент, позволяющий решать сложные олимпиадные задачи, а в жизни - организовывать передачу срочной информации между людьми.
Гипотезы:
С помощью графов можно легко решать многие олимпиадные задачи
Теория графов помогает создать систему срочного оповещения коллектива
Задачи:
Разобраться с методами решения задач при помощи графов
Разработать сайт для тестирования олимпиадных задач
Спроектировать систему Срочного Оповещения Класса при помощи графа
Объекты исследования: олимпиадные задачи, системы оповещения
Предмет исследования: теория графов, web-программирование.
Методы исследований:
методы теории графов
методы web-программирования
План исследований:
Ознакомиться с историей возникновения теории графов
Изучить правила решения олимпиадных задач при помощи графов
Пройти курс «Web-программирование» Школы Информационных Технологий «REAL-IT»
Разработать сайт для тестирования олимпиадных задач по теории графов и опробовать его на друзьях
Спроектировать систему Срочного Оповещения Класса (СОК)
Провести эксперимент с целью тестирования системы СОК
Глава 1. Теория графов в нашей жизни
1.1. Применение теории графов в разных областях
Графы применяются в самых разных областях: при проектировании электрических цепей, телефонных сетей, при поиске маршрутов между населенными пунктами, в экономике .
В химии графы используются для представления различных соединений. С помощью графов можно изобразить как простые молекулы, так и довольно сложные органические соединения.
Теория графов играет ключевую роль в различных этапах архитектурных проектов. После того как определены части проекта и перед тем как перейти от эскизов к чертежам, будет полезно построить граф взаимосвязей элементов проекта. Анализ графов в общественных зданиях поможет определить степень доступности различных отделов, расположение помещений (буфета, библиотеки и др.), а также пожарных лестниц. Графы позволяют существенно упростить анализ сложных ситуаций .
В наше время благодаря интернету - «сети сетей», связывающей компьютеры по всему миру, стала возможной цифровая революция. Мощность компьютеров неуклонно возрастала, но совершить гигантский скачок к цифровому миру удалось именно благодаря сетям. Графы и телекоммуникации всегда шли рука об руку.
На рисунке 1.1 изображены различные схемы соединения компьютеров между собой. Чаще всего встречаются три способа объединения компьютеров в локальную сеть: "общая шина", "звезда", и "кольцо". Каждой схеме соответствует граф, поэтому применяется термин «Сетевая топология». Сетевая топология - это конфигурация графа, вершины которого: компьютеры и маршрутизаторы, а рёбра - линии связи (кабель) между ними . На рисунке 1.2 все топологии изображены в виде графов.
Дерево - это очень простой граф, в котором между любыми двумя вершинами существует единственный путь. Деревья используются в генетике для иллюстрации родственных связей (генеалогические деревья), а также при анализе вероятностей различных событий.
Рисунок.1.1. Варианты построения локальных компьютерных сетей
Рисунок 1.2. Варианты построения локальных компьютерных сетей
а - общая шина, б - звезда, в - кольцо
Существует множество игр, в которых нужно построить определенный граф (игры-лабиринты ) или с помощью графа определить, существует ли выигрышная стратегия.
GPS, карты и автомобильные маршруты, представленные в интернете, - еще один прекрасный пример использования графов. Ребрами в них являются улицы и автодороги, а вершинами - населенные пункты. Вершины таких графов имеют названия, а ребрам соответствуют числа, обозначающие расстояние в километрах. Таким образом, такой граф является помеченным и взвешенным. Графы помогают наглядно представить себе схемы общественного транспорта, что облегчает планирование поездки.
Графы также применяются в нефтегазовой отрасли в системах транспортировки нефти и газа. С помощью графоаналитических методов газотранспортных систем возможно выбрать из всех возможных путей обхода трубопровода наикратчайший вариант .
Развитие информатики привело к тому, что многие математические модели стали использоваться в автоматических процессах. Машина легко справляется с вычислениями, но выбрать наилучший вариант из множества в условиях неопределенности - задача намного более сложная. Появились новые алгоритмы, в которых используются механизмы, напоминающие биологическую революцию. Графы в них используют как способ визуализации процессов. Моделирование нейронов человеческого мозга и принципа их действия легло в основу новой теории - теории нейронных сетей.
1.2. Выводы по главе.
Теория графов нашла свое применение во многих областях науки, техники и повседневной жизни. Однако, несмотря на ее широкое применение в разных областях, в школьном курсе математики ей уделяется лишь поверхностное внимание. В то же время различные эксперименты в сфере образования показывают, что элементы теории графов имеют высокую образовательную ценность, поэтому должны быть включены в школьную программу.
Действительно, школьникам среднего звена весьма полезно будет изучить основы теории графов, поскольку они помогут им в освоении базового курса математики, и особенно - в решении олимпиадных задач по комбинаторике и теории вероятностей .
Глава 2. Теория графов в помощь школьнику
2.1. Теория графов в олимпиадных задачах
Различные математические олимпиады, такие как «Кенгуру», «Дино-олимпиада Учи.ру», Международная эвристическая олимпиада «Совёнок», также часто включают задачи по теории графов в разных формулировках .
Как известно, дети очень любят все, что связано с компьютерами и интернетом, и их не так просто усадить за стол с книжкой по математике. Для того, чтобы вызвать интерес у школьников к теории графов, авторами статьи на основе пройденных курсов по Web-программированию в Школе информационных технологий «REAL-IT» разработан онлайн-тренажер, включающий тестирование по теории графов, расположенный на странице Тюменской частной школы «Эвольвента»: evolventa-tmn.github.io . Школьникам предлагается решить шесть задач различного уровня сложности, он вводит ответы в окошки, а затем по нажатию кнопки «Готово» выдается результат: количество правильно решенных им задач (Рисунок 2.1).
Рисунок 2.1. Фрагмент экрана сайта с вариантами тестирования
Естественно, хитрый ребенок немедленно начнет искать ответы на поисковых серверах, но точно таких формулировок он не найдет, только подобные, например, на сайте научно-методического электронного журнала «Концепт» . Поэтому для получения вожделенного результата: 6 из 6 задач ученику придется разобраться в общих принципах решения задач с помощью теории графов. А в дальнейшем полученные знания помогут ему успешно решать как школьные, так и олимпиадные задачи.
Когда сайт был полностью готов, протестирован и выложен в Интернет, наши одноклассники получили ссылку на него. Интерес к сайту был велик: судя по счетчику посещений, за первую неделю его посетили больше 150 раз! Многие ребята пытались решить задачи, но они показались им сложными. Даже некоторых родителей, имеющих высшее техническое образование, ряд задач поставил в тупик, это говорит о том, что теория графов изучается даже не во всех высших учебных заведениях. Значит, подготовленное нами тестирование будет полезно не только школьникам, но и взрослым!
2.2. Теория графов при проектировании системы оповещения класса
В настоящее время сфере системы срочного управления персоналом в организациях уделяется большое внимание, в связи с тем, что такие системы играют существенную роль в организации всей деятельности сотрудников .
Первоначально системы оповещения и управления эвакуацией были задуманы для срочного информирования работников, персонала и гостей о возгорании в здании, предоставления информации и трансляции важных сведений для быстрой и успешной эвакуации людей . На сегодняшний день такие системы можно наблюдать не только в рамках одной организации или предприятия, но в масштабах всей нашей страны, применяемые в целях повышения безопасности людей.
Необходимо отметить, что большинство используемых систем оповещения ориентировано на взрослых людей. Но самый опасный возраст - это детский. Детям тоже нужны свои системы, позволяющие в кратчайшие сроки оповещать большую часть своих сверстников о надвигающейся опасности или об изменении обстановки.
В школе каждый ребенок проводит значительную часть своего времени: пять - шесть дней в неделю по несколько часов. Поэтому создание системы оповещения детей позволило бы организовать каждого ребенка на быструю и грамотную реакцию на изменившуюся обстановку.
Например, данная система была бы очень полезна при передаче сообщения об опасности, информации о срочном сборе или об изменении обстановки, когда они находятся в разных частях школы или вообще в лесу на отдыхе (Рисунок 2.2)
Рисунок 2.2. Наш класс на экскурсии в ГАУ ДО ТО "Региональный центр допризывной подготовки и патриотического воспитания "Аванпост"
В данной работе предпринята попытка создания Системы Оповещения Коллектива на примере одного класса образовательного учреждения: МАОУ СОШ № 89.
Поскольку дети должны сами распространять информацию, им следует пользоваться только доступными им всем видами связи - мобильной связью. Должен быть оповещен весь списочный состав класса, поэтому для анализа, кто из детей кого из своих друзей готов оповестить, было проведено анкетирование класса. В анкетах изначально было задано ограничение: каждый ребенок успевает позвонить максимум четырем друзьям, а если останется время - еще двоим.
Анкетирование показало довольно высокую активность ребят: в целом по классу будет сделано около 118 звонков. Проанализировать такой объем информации в уме практически невозможно, поэтому было решено воспользоваться информационными технологиями. Модель оповещения коллектива лучше всего представить в виде графа . Ребрами в нем являются звонки (или смс), а вершинами - дети. Поскольку вершины графа имеют названия, а ребрам соответствуют числа, обозначающие вероятность звонка (1 или 0,5), то такой граф является помеченным и взвешенным . Граф помогает наглядно представить себе схему оповещения коллектива, что облегчает моделирование.
Визуализацию графа было решено осуществлять с помощью CASE-средства RAMUS, поскольку он позволяет работать с цветом вершин и ребер, а также позволяет перемещать вершины графа с привязанными к ней ребрами для наглядности. На рисунке 2.3 показан граф системы СОК.
19 ноября 2017 года было проведено тестирование спроектированной системы СОК. Изначально мы планировали, что оповещение пройдет за три круга. Для первого круга (начала оповещения) мы выбрали двух детей, которым никто не хочет звонить, но они звонить готовы, а также самих авторов Проекта (Рис. 2.3, розовые блоки). Дальше информация передается ко второму кругу оповещения (Рис. 2.4, желтые блоки). И на третьем круге оповещения (Рис. 2.4, зеленые блоки) весь класс будет проинформирован. Но в ходе эксперимента мы увидели, что некоторые дети по 1,5-2 часа на тренировке и не смотрят на телефон, другие с отрицательным балансом, поэтому не могут звонить.
Рисунок 2.3. Граф системы оповещения класса
Рисунок 2.4. Круги оповещения системы СОК
Поэтому в реальности наш класс оказался оповещен только за 490 минут - это 8 часов 10 минут. Но зато это были все 100%. Здесь важно то, что наша система имеет структуру не дерева, а графа. А в нем из одной вершины в другую ведут несколько путей, поэтому в любом случае, оповещены будут все!
На рисунке 2.6 показан график оповещенности класса (количество оповещенных человек) в зависимости от времени (в минутах).
Рисунок 2.6. График оповещенности класса
Чтобы было легче следить за оповещенностью, в процессе тестирования дети должны были сообщить авторам Проекта свой любимый предмет, а они вели протокол, когда и кто сообщает информацию.
Еще один результат тестирования - опрос любимых предметов (Рисунок 2.7), показал, что дети нашего класса больше всего любят математику, информатику и подвижные игры! А это значит, что теория графов может им полюбиться так же, как и нам.
Рисунок 2.7. Круговая диаграмма любимых предметов класса
2.3. Выводы по главе.
Нами были проверены обе гипотезы. Разработанный нами сайт для тестирования олимпиадных задач по теории графов помог установить, что ряд олимпиадных задач просто невозможно решить без знаний теории графов, причем, даже взрослым-инженерам. Первая гипотеза получила подтверждение.
Вторая гипотеза также оказалась верной. Спроектированная и протестированная система оповещения коллектива на примере одного класса позволила за 8 часов 10 минут оповестить целый детский коллектив. Путем оптимизации графа можно добиться и более быстрых результатов.
Заключение.
Надеемся, что после знакомства с теорий графов и ее многочисленными применениями в разных областях, в школьниках пробудится интерес к теории графов, и они продолжат изучать этот раздел математики самостоятельно. Результатом изучения будут более высокие результаты на олимпиадах.
Что касается применения теории графов в реальной жизни, актуальность рассматриваемой темы подчеркивает то, что создание системы оповещения детей позволит увеличить скорость передачи срочной информации, охватить большую часть детского коллектива, для которого будет использоваться эта система, сократить время отклика детей, а также обеспечить максимальную безопасность для детского коллектива. Все это указывает на очевидные плюсы внедрения спроектированной системы.
Список литературы
Белобородова А.А. Развитие пространственного мышления при помощи игр-лабиринтов / А.А. Белобородова // «Студенческий научный форум»: материалы VIII Международной студенческой электронной научной конференции.- 2017. https://www.сайт/2017/7/26746
Белобородова, А.А. Разработка web-тренажера для изучения теории графов / А.А. Белобородова, С.В. Пахотин, А.А. Фролов // Новые информационные технологии в нефтегазовой отрасли и образовании: материалы VII Международной научно-технической конференции; отв. ред. О.Н. Кузяков. - Тюмень: ТИУ, 2017. - С. 156-159.
Белобородова А.А. С математикой не заблудишься! / А.А. Белобородова // XVIII Всероссийский детский конкурс научн.-иссл. и творческих работ «Первые шаги в науке»: сборник тезисов.- М.: НС Интеграция, Государственная Дума ФС РФ, Минобрнауки России.- 2016.- С. 110-111.
Генденштейн, Л.Э. Алиса в стране математики. Повесть-сказка / Для младш. и сред. школьного возраста.- Харьков: Изд.- коммер. предприятие "Паритет" ЛТД, 1994.-288 с., илл.
Давлетшин, М.И. Исследование эффективности методов удаления шумов на изображении / М. И. Давлетшин, К.В. Сызранцева // Энергосбережение и инновационные технологии в топливно-энергетическом комплексе: материалы Межд. науч.-практ. конф. студ., аспир., молодых ученых и спец. Т.1 / отв. редактор А.Н. Халин. - Тюмень: ТИУ, 2016. - С. 25- 29.
Карнаухова, А.А. Использование теории графов при решении задач в экономике / А.А. Карнаухова, А.Ф. Долгополова // Материалы VII Международной студенческой электронной научной конференции «Студенческий научный форум». http://www.scienceforum.ru/2015/991 .
Керн, Г. Лабиринты мира. СПб.: Изд-во "Азбука-классика", 2007, 448с.
Краузе, М.В. Применение информационных технологий для проектирования системы оповещения коллектива / М.В. Краузе, А.А. Белобородова, Е.И. Арбузова // Новые информационные технологии в нефтегазовой отрасли и образовании: материалы VII Международной научно-технической конференции; отв. ред. О.Н. Кузяков. - Тюмень: ТИУ, 2017. - С. 153-156.
Курс «Создание сайтов» Школы Информационных Технологий «REAL-IT» http://it-schools.org/faculties/web/
Мир математики: в 40 т. Т.11: Клауди Альсина. Карты метро и тейронные сети. Теория графов./ Пер. с исп.- М.: Де Агостини, 2014.- 144 с.
Москевич Л. В. Обучающая олимпиада - одна из форм внеурочных занятий математикой / Л.В. Москевич // Научно-методический электронный журнал «Концепт». - 2015. - Т. 6. - С. 166-170. - URL: http://e-koncept.ru/2015/65234.htm .
Памятка населению "Оповещение населения в случае угрозы и возникновении чрезвычайной ситуации" http://47.mchs.gov.ru/document/1306125
Румянцев, В.О. Математическое моделирование газотранспортной системы с помощью теории графов / В. О. Румянцев // Проблемы геологии и освоения недр: сб. науч. тр. / ТПУ. - Томск, 2017. - С. 340 - 342.
Сайт МЧС Российской Федерацииhttp://www.mchs.gov.ru/dop/Kompleksnaja_sistema_jekstrennogo_opoves