Lesson and presentation on the topic: "Trigonometric function of a numerical argument, definition, identities"
Additional materials
Dear users, do not forget to leave your comments, feedback, suggestions. All materials are checked by an antivirus program.
Teaching aids and simulators in the online store "Integral" for grade 10
Algebraic problems with parameters, grades 9–11
Software environment "1C: Mathematical constructor 6.1"
What will we study:
1. Definition of a numeric argument.
2. Basic formulas.
3. Trigonometric identities.
4. Examples and tasks for independent solution.
Definition of the trigonometric function of a numeric argument
Guys, we know what sine, cosine, tangent and cotangent are.Let's see if it is possible to find the values of other trigonometric functions through the values of some trigonometric functions?
Let's define the trigonometric function of a numerical element as: $y= sin(t)$, $y= cos(t)$, $y= tg(t)$, $y= ctg(t)$.
Let's remember the basic formulas:
$sin^2(t)+cos^2(t)=1$. By the way, what is the name of this formula?
$tg(t)=\frac(sin(t))(cos(t))$, for $t≠\frac(π)(2)+πk$.
$ctg(t)=\frac(cos(t))(sin(t))$, for $t≠πk$.
Let's derive new formulas.
Trigonometric identities
We know the basic trigonometric identity: $sin^2(t)+cos^2(t)=1$.Guys, let's divide both sides of the identity by $cos^2(t)$.
We get: $\frac(sin^2(t))(cos^2(t))+\frac(cos^2(t))(cos^2(t))=\frac(1)(cos^2 (t))$.
Let's transform: $(\frac(sin(t))(cos(t)))^2+1=\frac(1)(cos^2(t)).$
We get the identity: $tg^2(t)+1=\frac(1)(cos^2(t))$, with $t≠\frac(π)(2)+πk$.
Now we divide both sides of the identity by $sin^2(t)$.
We get: $\frac(sin^2(t))(sin^2(t))+\frac(cos^2(t))(sin^2(t))=\frac(1)(sin^2 (t))$.
Let's transform: $1+(\frac(cos(t))(sin(t)))^2=\frac(1)(sin^2(t)).$
We get a new identity that is worth remembering:
$ctg^2(t)+1=\frac(1)(sin^2(t))$, for $t≠πk$.
We managed to get two new formulas. Remember them.
These formulas are used if, by some known value of a trigonometric function, it is required to calculate the value of another function.
Solving examples for trigonometric functions of a numerical argument
Example 1$cos(t) =\frac(5)(7)$, find $sin(t)$; $tg(t)$; $ctg(t)$ for all t.
Solution:
$sin^2(t)+cos^2(t)=1$.
Then $sin^2(t)=1-cos^2(t)$.
$sin^2(t)=1-(\frac(5)(7))^2=1-\frac(25)(49)=\frac(49-25)(49)=\frac(24) (49)$.
$sin(t)=±\frac(\sqrt(24))(7)=±\frac(2\sqrt(6))(7)$.
$tg(t)=±\sqrt(\frac(1)(cos^2(t))-1)=±\sqrt(\frac(1)(\frac(25)(49))-1)= ±\sqrt(\frac(49)(25)-1)=±\sqrt(\frac(24)(25))=±\frac(\sqrt(24))(5)$.
$ctg(t)=±\sqrt(\frac(1)(sin^2(t))-1)=±\sqrt(\frac(1)(\frac(24)(49))-1)= ±\sqrt(\frac(49)(24)-1)=±\sqrt(\frac(25)(24))=±\frac(5)(\sqrt(24))$.
Example 2
$tg(t) = \frac(5)(12)$, find $sin(t)$; $cos(t)$; $ctg(t)$, for all $0 Solution: We have considered the most basic trigonometric functions (do not be fooled, in addition to sine, cosine, tangent and cotangent, there are a whole lot of other functions, but more on them later), but for now we will consider some of the basic properties of the functions already studied. Whatever real number t is taken, it can be assigned a uniquely defined number sin(t) . True, the correspondence rule is rather complicated and consists in the following. To find the value of sin(t) by the number t, you need: In fact, we are talking about the function s = sin(t) , where t is any real number. We can calculate some values of this function (for example, sin(0) = 0 , \(sin \frac (\pi)(6) = \frac(1)(2) \) etc.), we know some of its properties. In the same way, we can assume that we have already received some ideas about three more functions: s = cos(t) s = tg(t) s = ctg(t) All these functions are called trigonometric functions of the numerical argument t . As you, I hope, guess all trigonometric functions are interconnected and even without knowing the value of one, it can be found through the other. For example, the most important formula of all trigonometry is basic trigonometric identity: \[ sin^(2) t + cos^(2) t = 1 \] As you can see, knowing the value of the sine, you can find the value of the cosine, and vice versa. Also very common formulas relating sine and cosine with tangent and cotangent: \[ \boxed (\tan\; t=\frac(\sin\; t)(\cos\; t), \qquad t \neq \frac(\pi)(2)+ \pi k) \] \[ \boxed (\cot\; t=\frac(\cos\; )(\sin\; ), \qquad t \neq \pi k) \] From the last two formulas, one more trigometric identity can be deduced, connecting this time the tangent and cotangent: \[ \boxed (\tan \; t \cdot \cot \; t = 1, \qquad t \neq \frac(\pi k)(2)) \] Now let's see how these formulas work in practice. EXAMPLE 1. Simplify the expression: a) \(1+ \tan^2 \; t \), b) \(1+ \cot^2 \; t \) a) First of all, we write the tangent, keeping the square: \[ 1+ \tan^2 \; t = 1 + \frac(\sin^2 \; t)(\cos^2 \; t) \] \[ 1 + \frac(\sin^2 \; t)(\cos^2 \; t)= \sin^2\; t + \cos^2 \; t + \frac(\sin^2 \; t)(\cos^2 \; t) \] Now we introduce everything under a common denominator, and we get: \[ \sin^2\; t + \cos^2 \; t + \frac(\sin^2 \; t)(\cos^2 \; t) = \frac(\cos^2 \; t + \sin^2 \; t)(\cos^2 \; t )\] And finally, as we see, the numerator can be reduced to one according to the basic trigonometric identity, as a result we get: \[ 1+ \tan^2 \; = \frac(1)(\cos^2 \; t) \] b) With the cotangent, we perform all the same actions, only the denominator will no longer have a cosine, but a sine, and the answer will turn out like this: \[ 1+ \cot^2 \; = \frac(1)(\sin^2 \; t) \] Having completed this task, we have derived two more very important formulas that connect our functions, which you also need to know like the back of your hand: \[ \boxed (1+ \tan^2 \; = \frac(1)(\cos^2 \; t), \qquad t \neq \frac(\pi)(2)+ \pi k) \] \[ \boxed (1+ \cot^2 \; = \frac(1)(\sin^2 \; t), \qquad t \neq \pi k) \] You must know by heart all the formulas presented within the framework, otherwise further study of trigonometry without them is simply impossible. In the future there will be more formulas and there will be a lot of them, and I assure you that you will definitely remember all of them for a long time, or maybe you won’t remember them, but EVERYONE should know these six pieces! Definition1: The numerical function given by the formula y=sin x is called the sine. This curve is called sinusoid. Function properties y=sin x 2. Function range: E(y)=[-1; one] 3. Parity function: y=sin x – odd,. 4. Periodicity: sin(x+2πn)=sin x, where n is an integer. This function takes the same values after a certain interval. This property of a function is called periodicity. The interval is the period of the function. For the function y=sin x, the period is 2π. The function y=sin x is periodic, with period T=2πn, n is an integer. The smallest positive period T=2π. Mathematically, this can be written as: sin(x+2πn)=sin x, where n is an integer. Definition2: The numerical function given by the formula y=cosx is called the cosine. Function properties y=cos x 1. Function scope: D(y)=R 2. Function scope: E(y)=[-1;1] 3. Parity function: y=cos x is even. 4. Periodicity: cos(x+2πn)=cos x, where n is an integer. The function y=cos x is periodic, with period Т=2π. Definition 3: The numerical function given by the formula y=tg x is called the tangent. Function properties y=tg x 1. Domain of the function: D(y) - all real numbers except π/2+πk, k is an integer. Because at these points the tangent is not defined. 3. Parity function: y=tg x is odd. 4. Periodicity: tg(x+πk)=tg x, where k is an integer. The function y=tg x is periodic with period π. Definition 4: The numerical function given by the formula y=ctg x is called the cotangent. Function properties y=ctg x 1. Function domain: D(y) - all real numbers, except for πk, k is an integer. Because at these points the cotangent is not defined. 2. The scope of the function: E(y)=R. The video lesson "Trigonometric functions of a numerical argument" is a visual material to ensure clarity when explaining the topic in the lesson. During the demonstration, the principle of forming the value of trigonometric functions from a number is considered, a number of examples are described that teach how to calculate the values of trigonometric functions from a number. With the help of this manual, it is easier to form skills in solving relevant problems, to achieve memorization of the material. Using the manual increases the effectiveness of the lesson, contributes to the rapid achievement of learning goals. The title of the topic is shown at the beginning of the lesson. Then the task is to find the corresponding cosine to some numerical argument. It is noted that this problem is solved simply and this can be clearly demonstrated. The screen displays a unit circle centered at the origin. At the same time, it was noticed that the point of intersection of the circle with the positive semi-axis of the abscissa axis is located at the point A (1; 0). An example of a point M is given, which represents the argument t=π/3. This point is marked on the unit circle, and a perpendicular to the abscissa axis descends from it. The found abscissa of the point is the cosine cos t. In this case, the abscissa of the point will be x=1/2. Therefore cos t=1/2. Summarizing the considered facts, it is noted that it makes sense to talk about the function s=cos t. It is noted that students already have some knowledge about this function. Some values of cosine cos 0=1, cos π/2=0, cos π/3=1/2 are calculated. Also related to this function are the functions s=sin t, s=tg t, s=ctg t. It is noted that they have a common name for all - trigonometric functions. Important relationships are demonstrated that are used in solving problems with trigonometric functions: the basic identity sin 2 t+ cos 2 t=1, the expression of tangent and cotangent in terms of sine and cosine tg t=sin t/cos t, where t≠π/2+πk for kϵZ, ctg t= cos t/sin t, where t≠πk for kϵZ, as well as the ratio of tangent to cotangent tg t ctg t=1 where t≠πk/2 for kϵZ. Further, it is proposed to consider the proof of the relation 1+ tan 2 t=1/ cos 2 t, with t≠π/2+πk for kϵZ. To prove the identity, it is necessary to represent tg 2 t as a ratio of sine and cosine, and then bring the terms on the left side to a common denominator 1+ tg 2 t=1+sin 2 t/cos 2 t = (sin 2 t+cos 2 t )/ cos 2 t. Using the basic trigonometric identity, we obtain 1 in the numerator, that is, the final expression 1/ cos 2 t. Q.E.D. The identity 1+ ctg 2 t=1/ sin 2 t is proved similarly, with t≠πk for kϵZ. Just as in the previous proof, the cotangent is replaced by the corresponding ratio of cosine and sine, and both terms on the left side are reduced to a common denominator 1+ ctg 2 t=1+ cos 2 t/sin 2 t= (sin 2 t+cos 2 t)/sin2t. After applying the basic trigonometric identity to the numerator, we get 1/ sin 2 t. This is the desired expression. The solution of examples is considered, in which the acquired knowledge is applied. In the first task, you need to find the values of cost, tgt, ctgt, if the sine of the number sint=4/5 is known, and t belongs to the interval π/2< t<π. Для нахождения косинуса в данном примере рекомендуется использовать тождество sin 2 t+ cos 2 t=1, из которого следует cos 2 t=1-sin 2 t. Зная значение синуса, можно найти косинус cos 2 t=1-(4/5) 2 =9/25. То есть значение косинуса cost=3/5 и cost=-3/5. В условии указано, что аргумент принадлежит второй четверти координатной плоскости. В этой четверти значение косинуса отрицательное. С учетом данного ограничения находим cost=-3/5. Для нахождения тангенса числа пользуемся его определением tgt= sint/cost. Подставив известные значения синуса и косинуса, получаем tgt=4/5:(-3/5)=-4/3. Чтобы найти значение котангенса, также используется определение котангенса ctgt= cost/sint. Подставив известные значения синуса и косинуса в отношение, получаем ctgt=(-3/5):4/5=-3/4. Next, we consider the solution of a similar problem in which the tangent tgt=-8/15 is known, and the argument is limited to the values 3π/2 To find the value of the sine, we use the definition of the tangent tgt = sint / cost. From it we find sint= tgt cost=(-8/15)(15/17)=-8/17. Knowing that the cotangent is the inverse function of the tangent, we find ctgt=1/(-8/15)=-15/8. The video lesson "Trigonometric functions of a numerical argument" is used to increase the effectiveness of a math lesson at school. In the course of distance learning, this material can be used as a visual aid for the formation of problem solving skills, where there are trigonometric functions of a number. To acquire these skills, the student may be recommended to independently consider visual material. TEXT INTERPRETATION: The topic of the lesson is "Trigonometric functions of a numerical argument." Any real number t can be associated with a uniquely defined number cos t. To do this, you must perform the following steps: 1) on the coordinate plane, arrange the number circle so that the center of the circle coincides with the origin, and the starting point A of the circle hits the point (1; 0); 2) find a point on the circle that corresponds to the number t; 3) find the abscissa of this point. This is cos t. Therefore, we will talk about the function s \u003d cos t (es is equal to the cosine of te), where t is any real number. We have already got some idea about this function: All these functions are called trigonometric functions of the numerical argument t. From the definitions of sine, cosine, tangent and cotangent, some relationships follow: 1)sin 2 t + cos 2 t = 1 (sine squared te plus cosine squared te equals one) 2) tgt = at t ≠ + πk, kϵZ 3) ctgt = at t ≠ πk, kϵZ (the cotangent of te is equal to the ratio of the cosine of te to the sine of te when te is not equal to the peak of ka, which belongs to z). 4)tgt ∙ ctgt = 1 for t ≠ , kϵZ We prove two more important formulas: One plus the tangent square of te is equal to the ratio of one to the cosine square of te when te is not equal to pi by two plus pi. Proof. The expression unit plus tangent square te, we will reduce to a common denominator cosine square te. We get in the numerator the sum of the squares of the cosine of te and the sine of te, which is equal to one. And the denominator remains the square of the cosine te. The sum of unity and the square of the cotangent te is equal to the ratio of unity to the square of the sine of te when te is not equal to the peak. Proof. The expression unity plus the cotangent squared te, similarly, we reduce to a common denominator and apply the first relation. Consider examples. EXAMPLE 1. Find cost, tgt, ctgt if sint = and< t < π.(если синус тэ равен четырем пятым и тэ из промежутка от пи на два до пи) Solution. From the first relation, we find the cosine square te equal to one minus the sine square te: cos 2 t \u003d 1 - sin 2 t. So, cos 2 t = 1 -() 2 = (the cosine of the square of te is equal to nine twenty-fifths), that is, cost = (the cosine of te is equal to three fifths) or cost = - (the cosine of te is equal to minus three fifths). By condition, the argument t belongs to the second quarter, and in it cos t< 0 (косинус тэ отрицательный). So cosine te is equal to minus three-fifths, cost = - . Calculate the tangent te: tgt = = ׃ (-)= - ;(the tangent of te is equal to the ratio of the sine of te to the cosine of te, which means four fifths to minus three fifths and equals minus four thirds) Accordingly, we calculate (the cotangent of the number te, since the cotangent of te is equal to the ratio of the cosine of te to the sine of te,) ctgt = = - . (the cotangent of te is minus three fourths). Answer: cost = - , tgt= - ; ctgt = - . (Answer will be filled in as you decide) EXAMPLE 2. It is known that tgt = - and< t < 2π(тангенс тэ равен минус восемь пятнадцатых и тэ принадлежит промежутку от трех пи на два до двух пи). Найти значения cost, sint, ctgt. Solution. We use this ratio, substituting the value in this formula, we get: 1 + (-) 2 \u003d (one per cosine square of te is equal to the sum of one and the square minus eight fifteenths). From here we find cos 2 t = (the cosine square of te is two hundred and twenty-five two hundred and eighty-ninths). So cost = (cosine te equals fifteen seventeenths) or cost = . By condition, the argument t belongs to the fourth quarter, where cost>0. Therefore, cost = .(cosenus te is fifteen seventeenths) Find the value of the argument sinus te. Since from the ratio (show the ratio tgt = at t ≠ + πk, kϵZ) the sine of te is equal to the product of the tangent of te by the cosine of te, then substituting the value of the argument te..the tangent of te is equal to minus eight fifteenths .. by condition, and the cosine of te is equal to solved earlier, we get sint = tgt ∙ cost = (-) ∙ = - , (the sine of te is equal to minus eight seventeenths) ctgt == - . (since the cotangent of te is the reciprocal of the tangent, it means that the cotangent of te is minus fifteen eighteenths) Definition. Trigonometric functions of a numerical argument are the trigonometric functions of the same name of an angle equal to radians. Let us clarify this definition with concrete examples. Example 1. Calculate the value of . Here by we mean an abstract irrational number. By definition. So, . Example 2. Calculate the value of . Here by 1.5 we mean an abstract number. As defined (see annex II). Example 3. Calculate the value Similarly to the previous one, we obtain (see Appendix II). So, in the future, under the argument of trigonometric functions, we will understand the angle (arc) or just a number, depending on the problem that we are solving. And in some cases, the argument can be a value that has another dimension, such as time, etc. Calling the argument an angle (arc), we can mean by it the number with which it is measured in radians.
$tg^2(t)+1=\frac(1)(cos^2(t))$.
Then $\frac(1)(cos^2(t))=1+\frac(25)(144)=\frac(169)(144)$.
We get that $cos^2(t)=\frac(144)(169)$.
Then $cos^2(t)=±\frac(12)(13)$, but $0
We get: $sin(t)=tg(t)*cos(t)=\frac(5)(12)*\frac(12)(13)=\frac(5)(13)$.
$ctg(t)=\frac(1)(tg(t))=\frac(12)(5)$.Tasks for independent solution
1. $tg(t) = -\frac(3)(4)$, find $sin(t)$; $cos(t)$; $ctg(t)$, for all $\frac(π)(2)
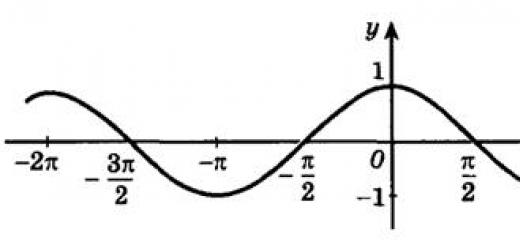
4. $cos(t) = \frac(12)(13)$, find $sin(t)$; $tg(t)$; $ctg(t)$ for all $t$. Trigonometric functions of a numeric argument
Connection of trigonometric functions
ActiveX controls must be enabled in order to make calculations!