\[(\Large(\text(Basic facts about area)))\]

We can say that the area of ​​a polygon is a value that indicates the part of the plane that a given polygon occupies. The area unit is taken as the area of ​​a square with a side of \(1\) cm, \(1\) mm, etc. (single square). Then the area will be measured in cm\(^2\) , mm\(^2\) respectively.

In other words, we can say that the area of ​​​​a figure is a value whose numerical value shows how many times a unit square fits in a given figure.

Area Properties

1. The area of ​​any polygon is a positive value.

2. Equal polygons have equal areas.

3. If a polygon is composed of several polygons, then its area is equal to the sum of the areas of these polygons.

4. The area of ​​a square with side \(a\) is \(a^2\) .

\[(\Large(\text(Area of ​​rectangle and parallelogram)))\]

Theorem: area of ​​a rectangle

The area of ​​a rectangle with sides \(a\) and \(b\) is \(S=ab\) .

Proof

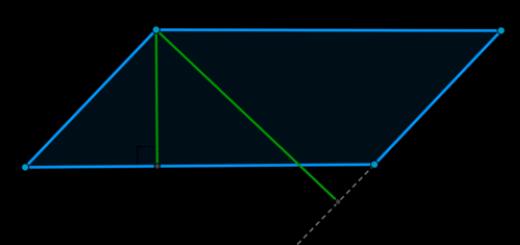
Let's build the rectangle \(ABCD\) to a square with side \(a+b\) , as shown in the figure:

This square consists of a rectangle \(ABCD\) , another rectangle equal to it, and two squares with sides \(a\) and \(b\) . In this way,

\(\begin(multline*) S_(a+b)=2S_(\text(pr-k))+S_a+S_b \Leftrightarrow (a+b)^2=2S_(\text(pr-k))+ a^2+b^2 \Leftrightarrow\\ a^2+2ab+b^2=2S_(\text(pr-k))+a^2+b^2 \Rightarrow S_(\text(pr-k) )=ab \end(multline*)\)

Definition

The height of a parallelogram is the perpendicular drawn from the vertex of the parallelogram to the side (or extension of the side) that does not contain that vertex.
For example, the height \(BK\) falls on the side \(AD\) , and the height \(BH\) falls on the extension of the side \(CD\) :

Theorem: area of ​​a parallelogram

The area of ​​a parallelogram is equal to the product of the height and the side to which this height is drawn.

Proof

Draw perpendiculars \(AB"\) and \(DC"\) as shown in the figure. Note that these perpendiculars are equal to the height of the parallelogram \(ABCD\) .

Then \(AB"C"D\) is a rectangle, hence \(S_(AB"C"D)=AB"\cdot AD\) .

Note that right triangles \(ABB"\) and \(DCC"\) are equal. In this way,

\(S_(ABCD)=S_(ABC"D)+S_(DCC")=S_(ABC"D)+S_(ABB")=S_(AB"C"D)=AB"\cdot AD.\)

\[(\Large(\text(Area of ​​triangle)))\]

Definition

We will call the side to which the altitude is drawn in the triangle the base of the triangle.

Theorem

The area of ​​a triangle is half the product of its base and the height drawn to that base.

Proof

Let \(S\) be the area of ​​the triangle \(ABC\) . Let's take the side \(AB\) as the base of the triangle and draw the height \(CH\) . Let's prove that \ We complete the triangle \(ABC\) to the parallelogram \(ABDC\) as shown in the figure:

Triangles \(ABC\) and \(DCB\) are equal in three sides (\(BC\) is their common side, \(AB = CD\) and \(AC = BD\) as opposite sides of the parallelogram \(ABDC\ ) ), so their areas are equal. Therefore, the area \(S\) of the triangle \(ABC\) is equal to half the area of ​​the parallelogram \(ABDC\) , i.e. \(S = \dfrac(1)(2)AB\cdotCH\).

Theorem

If two triangles \(\triangle ABC\) and \(\triangle A_1B_1C_1\) have equal heights, then their areas are related as the bases to which these heights are drawn.

Consequence

The median of a triangle divides it into two triangles of equal area.

Theorem

If two triangles \(\triangle ABC\) and \(\triangle A_2B_2C_2\) each have the same angle, then their areas are related as the products of the sides forming this angle.

Proof

Let \(\angle A=\angle A_2\) . Let's combine these corners as shown in the figure (the point \(A\) is aligned with the point \(A_2\) ):

Draw heights \(BH\) and \(C_2K\) .

Triangles \(AB_2C_2\) and \(ABC_2\) have the same height \(C_2K\) , therefore: \[\dfrac(S_(AB_2C_2))(S_(ABC_2))=\dfrac(AB_2)(AB)\]

The triangles \(ABC_2\) and \(ABC\) have the same height \(BH\) , therefore: \[\dfrac(S_(ABC_2))(S_(ABC))=\dfrac(AC_2)(AC)\]

Multiplying the last two equalities, we get: \[\dfrac(S_(AB_2C_2))(S_(ABC))=\dfrac(AB_2\cdot AC_2)(AB\cdot AC) \qquad \text( or ) \qquad \dfrac(S_(A_2B_2C_2))(S_ (ABC))=\dfrac(A_2B_2\cdot A_2C_2)(AB\cdot AC)\]

Pythagorean theorem

In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs:

The converse is also true: if in a triangle the square of the length of one side is equal to the sum of the squares of the lengths of the other two sides, then such a triangle is right-angled.

Theorem

The area of ​​a right triangle is half the product of the legs.

Theorem: Heron's formula

Let \(p\) be the semiperimeter of a triangle, \(a\) , \(b\) , \(c\) be the lengths of its sides, then its area is equal to \

\[(\Large(\text(Area of ​​a rhombus and a trapezoid)))\]

Comment

Because rhombus is a parallelogram, then the same formula is true for it, i.e. The area of ​​a rhombus is equal to the product of the height and the side to which this height is drawn.

Theorem

The area of ​​a convex quadrilateral whose diagonals are perpendicular is half the product of the diagonals.

Proof

Consider the quadrilateral \(ABCD\) . Denote \(AO=a, CO=b, BO=x, DO=y\) :

Note that this quadrilateral is made up of four right triangles, therefore, its area is equal to the sum of the areas of these triangles:

\(\begin(multline*) S_(ABCD)=\frac12ax+\frac12xb+\frac12by+\frac12ay=\frac12(ax+xb+by+ay)=\\ \frac12((a+b)x+(a+b) y)=\frac12(a+b)(x+y)\end(multline*)\)

Corollary: area of ​​a rhombus

The area of ​​a rhombus is half the product of its diagonals: \

Definition

The height of a trapezoid is a perpendicular drawn from the top of one base to the other base.

Theorem: area of ​​a trapezoid

The area of ​​a trapezoid is half the sum of the bases times the height.

Proof

Consider a trapezoid \(ABCD\) with bases \(BC\) and \(AD\) . Draw \(CD"\parallel AB\) as shown in the figure:

Then \(ABCD"\) is a parallelogram.

We also draw \(BH"\perp AD, CH\perp AD\) (\(BH"=CH\) are the heights of the trapezoid).

Then \(S_(ABCD")=BH"\cdot AD"=BH"\cdot BC, \quad S_(CDD")=\dfrac12CH\cdot D"D\)

Because a trapezoid consists of a parallelogram \(ABCD"\) and a triangle \(CDD"\) , then its area is equal to the sum of the areas of the parallelogram and the triangle, that is:

\ \[=\dfrac12 CH\left(BC+AD"+D"D\right)=\dfrac12 CH\left(BC+AD\right)\]

Everyone who studied mathematics and geometry at school knows these sciences at least superficially. But over time, if they are not practiced, knowledge is forgotten. Many even believe that they just wasted their time studying geometric calculations. However, they are wrong. Technical workers perform daily work related to geometric calculations. As for the calculation of the area of ​​a polygon, this knowledge also finds its application in life. They will be needed at least in order to calculate the area of ​​\u200b\u200bthe land. So let's learn how to find the area of ​​a polygon.

Polygon definition

First, let's define what a polygon is. This is a flat geometric figure, which was formed as a result of the intersection of three or more lines. Another simple definition: a polygon is a closed polyline. Naturally, at the intersection of lines, intersection points are formed, their number is equal to the number of lines that form a polygon. The points of intersection are called the vertices, and the segments formed from the straight lines are called the sides of the polygon. Adjacent segments of a polygon are not on the same straight line. Line segments that are nonadjacent are those that do not pass through common points.

The sum of the areas of triangles

How to find the area of ​​a polygon? The area of ​​a polygon is the inner part of the plane, which was formed at the intersection of the segments or sides of the polygon. Since a polygon is a combination of shapes such as a triangle, rhombus, square, trapezoid, there is simply no universal formula for calculating its area. In practice, the most universal method is the division of a polygon into simpler figures, the area of ​​which is not difficult to find. By adding the sums of the areas of these simple figures, we get the area of ​​the polygon.

Through the area of ​​the circle

In most cases, the polygon has a regular shape and forms a figure with equal sides and angles between them. Calculating the area in this case is very simple using the inscribed or circumscribed circle. If the area of ​​the circle is known, then it must be multiplied by the perimeter of the polygon, and then the resulting product divided by 2. As a result, the formula for calculating the area of ​​such a polygon is obtained: S = ½∙P∙r., Where P is the area of ​​the circle, and r is the perimeter of the polygon .

The method of splitting a polygon into “convenient” shapes is the most popular in geometry, it allows you to quickly and correctly find the area of ​​a polygon. The 4th grade of high school usually learns such methods.

Lesson from the series " Geometric Algorithms»

Hello dear reader.

The solution of many computational geometry problems is based on finding polygon area. In this lesson, we will derive a formula for calculating the area of ​​a polygon using the coordinates of its vertices, and write a function to calculate this area.

A task. Calculate the area of ​​a polygon, given by the coordinates of its vertices, in clockwise order.

Information from computational geometry

To derive the formula for the area of ​​a polygon, we need information from computational geometry, namely, the concept of an oriented area of ​​a triangle.

The oriented area of ​​a triangle is the usual area provided with a sign. Oriented Area Sign of a Triangle ABC the same as the oriented angle between the vectors and . That is, its sign depends on the order in which the vertices are enumerated.

On the rice. 1 triangle ABC is a right triangle. Its oriented area is equal to (it is greater than zero, since the pair , is positively oriented). The same value can be calculated in another way.

Let O is an arbitrary point of the plane. In our figure, the area of ​​triangle ABC is obtained by subtracting the areas of OAB and OCA from the area of ​​triangle OBC. Thus, you just need add oriented areas triangles OAB, OBC and OCA. This rule works for any choice of point O.

Similarly, to calculate the area of ​​any polygon, you need to add the oriented areas of the triangles

The sum will be the area of ​​the polygon, taken with a plus sign if the polygon is on the left when going around the polygon (bypassing the boundary counterclockwise), and with a minus sign if it is on the right (bypassing clockwise).

So, the calculation of the area of ​​a polygon was reduced to finding the area of ​​a triangle. Let's see how to express it in coordinates.

The cross product of two vectors on a plane is the area of ​​the parallelogram built on these vectors.

The vector product expressed in terms of the coordinates of the vectors:

The area of ​​the triangle will be equal to half of this area:

It is convenient to take the origin of coordinates as the point O, then the coordinates of the vectors on the basis of which the oriented areas are calculated will coincide with the coordinates of the points.

Let (x 1, y 1), (x 2, y 2), ..., (x N, y N) - the coordinates of the vertices of the given polygon in clockwise or counterclockwise order. Then its oriented area S will be equal to:

This is our working formula, it is used in our program.

If the coordinates of the vertices were given in counterclockwise order, then the number S, calculated by this formula will be positive. Otherwise, it will be negative, and in order to obtain the usual geometric area, we need to take its absolute value.

So, consider a program for finding the area of ​​a polygon given by the coordinates of the vertices.

Program geom6; Const n_max=200; (max points+1) type b=record x,y:real; end; myArray= array of b; var input:text; A:myArray; s:real; i,n:integer; procedure ZapMas(var n:integer; var A:myArray); (Filling array) begin assign(input,"input.pas"); reset(input); readln(input, n); for i:=1 to n do read(input, a[i].x,a[i].y); close(input); end; function Square(A:myarray): real; (Polygon area calculation) var i:integer; S: real begin a.x:=a.x; a.y:=a.y; s:=0; for i:=1 to n do s:= s + (a[i].x*a.y - a[i].y*a.x); s:=abs(s/2); Square:= S end; (Square) begin (main) Zapmas(n, a); PrintMas(a); S:=Square(a); writeln("S= ",s:6:2); end.

The vertex coordinates are read from the input.pas. file, stored in an array BUT as records with two fields. For the convenience of bypassing the polygon, n + 1 elements are introduced in the array, the value of which is equal to the value of the first element of the array.

Input data:
5
0.6 2.1 1.8 3.6 2.2 2.3 3.6 2.4 3.1 0.5

Output:
S= 3.91

We have solved the problem of finding the area of ​​a polygon by the coordinates of its vertices. The tasks are getting harder. If you have comments on this article, or wishes, write in the comments. I will be very grateful to you for your cooperation.

See you at the next lesson.

1.1 Calculation of areas in antiquity

1.2 Different approaches to the study of the concepts of "area", "polygon", "area of ​​a polygon"

1.2.1 The concept of area. Area Properties

1.2.2 The concept of a polygon

1.2.3 The concept of the area of ​​a polygon. Descriptive definition

1.3 Various formulas for the areas of polygons

1.4 Derivation of polygon area formulas

1.4.1 Area of ​​a triangle. Heron's formula

1.4.2 Area of ​​a rectangle

1.4.3 Area of ​​a trapezoid

1.4.4 Area of ​​a quadrilateral

1.4.5 Universal formula

1.4.6 Area of ​​an n-gon

1.4.7 Calculating the area of ​​a polygon from the coordinates of its vertices

1.4.8 Pick Formula

1.5 The Pythagorean theorem on the sum of the areas of squares built on the legs of a right triangle

1.6 Equivalence of triangles. Bogliai-Gervin theorem

1.7 Ratio of areas of similar triangles

1.8 Figures with the largest area

1.8.1 Trapezoid or rectangle

1.8.2 A remarkable property of a square

1.8.3 Plots of different shape

1.8.4 Triangle with largest area

Chapter 2. Methodological features of studying the areas of polygons in mathematical classes

2.1 Thematic planning and features of teaching in classes with in-depth study of mathematics

2.2 Lesson methodology

2.3 Results of experimental work

Conclusion

Literature

Introduction

The topic "Area of ​​polygons" is an integral part of the school mathematics course, which is quite natural. Indeed, historically, the very emergence of geometry is associated with the need to compare land plots of one form or another. At the same time, it should be noted that the educational opportunities for the disclosure of this topic in secondary school are far from being fully used.

The main task of teaching mathematics at school is to ensure a strong and conscious mastery of the system of mathematical knowledge and skills necessary for every member of modern society in everyday life and work, sufficient to study related disciplines and continue education.

Along with the solution of the main task, an in-depth study of mathematics provides for the formation of a steady interest in the subject in students, the identification and development of their mathematical abilities, an orientation towards professions that are significantly related to mathematics, and preparation for studying at a university.

Qualification work includes the content of the mathematics course of a general education school and a number of additional questions that are directly adjacent to this course and deepen it along the main ideological lines.

The inclusion of additional questions serves two interrelated purposes. On the one hand, this is the creation, in conjunction with the main sections of the course, of a base to meet the interests and develop the abilities of students with a penchant for mathematics, on the other hand, the fulfillment of meaningful gaps in the main course, giving the content of in-depth study the necessary integrity.

The qualifying work consists of an introduction, two chapters, a conclusion and cited literature. The first chapter discusses the theoretical foundations of the study of the areas of polygons, and the second chapter deals directly with the methodological features of the study of areas.

Chapter 1

1.1Calculation of areas in antiquity

The rudiments of geometric knowledge related to the measurement of areas are lost in the depths of millennia.

Back in 4 - 5 thousand years ago, the Babylonians were able to determine the area of ​​a rectangle and a trapezoid in square units. The square has long served as a standard for measuring areas due to many of its remarkable properties: equal sides, equal and right angles, symmetry and general perfection of form. Squares are easy to build, or you can fill a plane without gaps.

In ancient China, the measure of area was a rectangle. When masons determined the area of ​​a rectangular house wall, they multiplied the height and width of the wall. This is the accepted definition in geometry: the area of ​​a rectangle is equal to the product of its adjacent sides. Both of these sides must be expressed in the same linear units. Their product will be the area of ​​the rectangle, expressed in the corresponding square units. Let's say if the height and width of the wall are measured in decimeters, then the product of both measurements will be expressed in square decimeters. And if the area of ​​each facing Plot is a square decimeter, then the resulting product will indicate the number of tiles needed for facing. This follows from the statement underlying the measurement of areas: the area of ​​a figure made up of non-intersecting figures is equal to the sum of their areas.

The ancient Egyptians 4,000 years ago used almost the same techniques as we do to measure the area of ​​a rectangle, triangle, and trapezoid: the base of the triangle was divided in half, and multiplied by the height; for a trapezoid, the sum of the parallel sides was divided in half and multiplied by the height, and so on. To calculate the area

quadrilateral with sides (Fig. 1.1), the formula (1.1) was applied

those. half-sums of opposite sides were multiplied.

This formula is obviously incorrect for any quadrilateral; it follows from it, in particular, that the areas of all rhombuses are the same. Meanwhile, it is obvious that the areas of such rhombuses depend on the magnitude of the angles at the vertices. This formula is only valid for a rectangle. With its help, you can approximately calculate the area of ​​quadrilaterals, in which the angles are close to right.

To determine the area

an isosceles triangle (Fig. 1.2), in which the Egyptians used the approximate formula:
(1.2) Fig. 1.2 The error made in this case is the smaller, the smaller the difference between the side and the height of the triangle, in other words, the closer the top (and) to the base of the height from. That is why the approximate formula (1.2) is applicable only for triangles with a relatively small vertex angle.

But already the ancient Greeks knew how to correctly find the areas of polygons. In his Elements, Euclid does not use the word "area", since by the very word "figure" he understands a part of a plane bounded by one or another closed line. Euclid does not express the result of measuring the area as a number, but compares the areas of different figures with each other.

Like other scientists of antiquity, Euclid deals with the transformation of some figures into others, they are equal in size. The area of ​​a compound figure will not change if its parts are arranged differently, but without crossing. Therefore, for example, it is possible, based on the formulas for the area of ​​a rectangle, to find the formulas for the areas of other figures. So, the triangle is divided into such parts, from which you can then make a rectangle of equal area to it. From this construction it follows that the area of ​​a triangle is equal to half the product of its base and height. Resorting to such a redrawing, they find that the area of ​​the parallelogram is equal to the product of the base and the height, the area of ​​the trapezoid is the product of half the sum of the bases and the height.

When masons have to tile a wall of complex configuration, they can determine the area of ​​the wall by counting the number of tiles that went into tiling. Some tiles, of course, will have to be chipped so that the edges of the cladding coincide with the edge of the wall. The number of all tiles that went into work evaluates the wall area with an excess, the number of unbroken tiles - with a disadvantage. As the size of the cells decreases, the amount of waste decreases, and the area of ​​the wall, determined by the number of tiles, is calculated more and more accurately.

One of the late Greek mathematicians - encyclopedists, whose works were mainly applied in nature, was Heron of Alexandria, who lived in the 1st century. n. e. Being an outstanding engineer, he was also called "Heron the Mechanic". In his work Dioptrics, Heron describes various machines and practical measuring instruments.

One of Heron's books was named by him "Geometrics" and is a kind of collection of formulas and corresponding problems. It contains examples for calculating the areas of squares, rectangles and triangles. Heron writes about finding the area of ​​a triangle along its sides: “Let, for example, one side of a triangle have a length of 13 measured cords, the second 14 and the third 15. To find the area, do the following. Add 13, 14 and 15; you get 42. Half of that is 21. Subtract from this three sides one by one; first subtract 13 - it remains 8, then 14 - it remains 7, and finally 15 - it remains 6. Now multiply them: 21 times 8 will give 168, take this 7 times - you get 1176, and this 6 more times - you get 7056. From here the square root will be 84. This is how many measuring cords will be in the area of ​​the triangle.

• educational: teach students to find the area of ​​a polygon using the methods they have chosen, form initial representations
• polygon, graphic and measuring skills;
• developing: development of methods of mental activity of students when performing tasks from observation, calculations to clarifying the patterns of calculating the area of ​​a polygon;
• educating: revealing the subjective experience of students, encouraging actions, aspirations of students as the basis for educating positive personality traits;
• methodical: creating conditions for the manifestation of cognitive activity of students.

Lesson equipment:

1. Whiteboard design: on the left - polygon shapes, on the right - a blank canvas of the board for writing in the lesson, in the center - a polygon-rectangle.
2. Leaflet "For research".
3. Tools of the teacher and students (chalk, pointer, ruler, research sheet, figures, drawing paper, marker).

Lesson method:

• On the interaction of the teacher and students - dialogue-communication;
• According to the method of solving problems - partial-search;
• According to the way of mental activity - (SUD) developmental training.

The form of the lesson is frontal, in pairs, individual.

The type of lesson is a lesson in mastering new knowledge, skills and abilities.

The structure of the lesson is a gradual deepening into the topic, flexible, dialogic.

During the classes

Greetings.

The lesson is beautiful and brings joy when we think and work together. Today we will consider the figures, determine their names, think, search and find solutions. We wish each other successful work.

Knowledge update.

Consider the figures (polygons on the board).

They are all together. Why? What is their common feature? (Polygons).

Name this polygon (5-gon, 6-gon…)

Do you know what the area of ​​a polygon is?

Then show on one of the figures.

(Generalization by the teacher: area is part of a plane inside a closed geometric figure.)

In Russian, this word has several meanings.

(The student in the dictionary introduces the meanings.)

1. Part of a plane inside a closed geometric figure.
2. Large undeveloped and flat area.
3. A place for any purpose.

Which value is used in mathematics?

In mathematics, the first value is used.

(There is a figure on the board).

Is it a polygon? Yes.

Name the shape differently. Rectangle.

Show length, width.

How to find the area of ​​a polygon?

Write the formula using letters and symbols.

If the length of our rectangle is 20 cm, the width is 10 cm. What is the area?

The area is 200 cm 2

Think about how to attach a ruler so that the figure is divided into:

Did you see what parts the figure consists of? And now, on the contrary, we will assemble the whole in parts.

(Parts of the figure lie on the desks. Children assemble a rectangle from them).

Draw conclusions from your observations.

The whole figure can be divided into parts and from parts to make a whole.

Houses based on triangles and quadrangles were figures, silhouettes. Here's what they turned out to be.

(Demonstration of drawings made by students at home. One of the works is analyzed).

What figures did you use? You have a complex polygon.

Statement of the educational task.

In the lesson, we must answer the question: how to find the area of ​​​​a complex polygon?

Why does a person need to find the area?

(Answers of children and generalization by the teacher).

The task of determining the area arose from practice.

(The plan of the school site is shown.)

In order to build a school, they first created a plan. Then the territory was divided into sections of a certain area, buildings, flower beds, a stadium were placed. In this case, the site has a certain shape - the shape of a polygon.

The solution of the educational problem.

(Patterns are handed out for research.)

There is a figure in front of you. Name her.

Polygon, hexagon.

Find the area of ​​the polygon. What should be done for this?

Divide into rectangles.

(In case of difficulty, there will be another question: “What shapes does the polygon consist of?”).

From two rectangles.

Divide the shape into rectangles using a ruler and pencil. Designate the numbers 1 and 2 received parts.

Let's take measurements.

Find the area of ​​the first figure.

(Students suggest the following solutions and write them on the board.)

• S 1 \u003d 5? 2 \u003d 10 cm 2
• S 2 \u003d 5? 1 \u003d 5 cm 2

Knowing the area of ​​​​the parts, how to find the area of ​​\u200b\u200bthe whole figure?

S \u003d 10 + 5 \u003d 15 cm 2

• S 1 \u003d 6? 2 \u003d 12 cm 2
• S 2 \u003d 3? 1 \u003d 3 cm 2
• S \u003d 12 + 3 \u003d 15 cm 2.

Compare the results and draw a conclusion.

Let's follow our steps

How is the area of ​​a polygon found?

An algorithm is compiled and written on the poster:?

1. Divide the figure into parts

2. Find the areas of the parts of these polygons (S 1, S 2).

3. Find the area of ​​the whole polygon (S 1 + S 2).

Speak the algorithm.

(Several students pronounce the algorithm).

We found two ways, and maybe there are more?

And you can finish the figure.

How many rectangles did you get?

Let's designate parts 1 and 2. Let's make measurements.

Find the area of ​​each part of the polygon.

• S1=6? 5=30cm 2
• S 2 \u003d 5? 3 \u003d 15 cm 2

How to find the area of ​​our hexagon?

S \u003d 30 - 15 \u003d 15 cm 2

Let's create an algorithm:

Finished the figure to a rectangle

Found S 1 and S 2 .

We found the difference S 1 - S 2.

Compare two algorithms. Make a conclusion. What actions are the same? Where did our actions differ?

Close your eyes, lower your heads. Mentally repeat the algorithm.

We have done research work, considered different methods and now we can find the area of ​​any polygon.

Performance check.

Test yourself.

Here are the polygons.

Find the area of ​​one figure of choice, while you can use different methods.

The work is done independently. Children choose a figure. Find the area in one of the ways. Verification is the key on the board.

What can be said about the form? (Form different)

What is the area of ​​these polygons? (The areas of these polygons are equal)

Evaluate the results.

Who has it right - put "+".

Who has doubts, difficulties - “?”

Consultants provide assistance to the guys, look for mistakes, help correct them.

Homework:

Compose your research sheets, calculate the area of ​​a polygon in different ways.

Summary of the lesson.

So, guys, what do you tell your parents about how to find the area of ​​​​a geometric figure - a polygon.

Lesson from the series " Geometric Algorithms»

Hello dear reader.

The solution of many computational geometry problems is based on finding polygon area. In this lesson, we will derive a formula for calculating the area of ​​a polygon using the coordinates of its vertices, and write a function to calculate this area.

A task. Calculate the area of ​​a polygon, given by the coordinates of its vertices, in clockwise order.

Information from computational geometry

To derive the formula for the area of ​​a polygon, we need information from computational geometry, namely, the concept of an oriented area of ​​a triangle.

The oriented area of ​​a triangle is the usual area provided with a sign. Oriented Area Sign of a Triangle ABC the same as the oriented angle between the vectors and. That is, its sign depends on the order in which the vertices are enumerated.

On the rice. 1 triangle ABC is a right triangle. Its oriented area is (it is greater than zero, since the pair is positively oriented). The same value can be calculated in another way.

Let O is an arbitrary point of the plane. In our figure, the area of ​​triangle ABC is obtained by subtracting the areas of OAB and OCA from the area of ​​triangle OBC. Thus, you just need add oriented areas triangles OAB, OBC and OCA. This rule works for any choice of point O.

Similarly, to calculate the area of ​​any polygon, you need to add the oriented areas of the triangles

The sum will be the area of ​​the polygon, taken with a plus sign if the polygon is on the left when going around the polygon (bypassing the boundary counterclockwise), and with a minus sign if it is on the right (bypassing clockwise).

So, the calculation of the area of ​​a polygon was reduced to finding the area of ​​a triangle. Let's see how to express it in coordinates.

The cross product of two vectors on a plane is the area of ​​the parallelogram built on these vectors.

The vector product expressed in terms of the coordinates of the vectors:

If the coordinates of the vertices were given in counterclockwise order, then the number S, calculated by this formula will be positive. Otherwise, it will be negative, and in order to obtain the usual geometric area, we need to take its absolute value.

So, consider a program for finding the area of ​​a polygon given by the coordinates of the vertices.

3. If a polygon is composed of several polygons, then its area is equal to the sum of the areas of these polygons.

4. The area of ​​a square with side \(a\) is \(a^2\) .

\[(\Large(\text(Area of ​​rectangle and parallelogram)))\]

Theorem: area of ​​a rectangle

The area of ​​a rectangle with sides \(a\) and \(b\) is \(S=ab\) .

Proof

Let's build the rectangle \(ABCD\) to a square with side \(a+b\) , as shown in the figure:

This square consists of a rectangle \(ABCD\) , another rectangle equal to it, and two squares with sides \(a\) and \(b\) . In this way,

\(\begin(multline*) S_(a+b)=2S_(\text(pr-k))+S_a+S_b \Leftrightarrow (a+b)^2=2S_(\text(pr-k))+ a^2+b^2 \Leftrightarrow\\ a^2+2ab+b^2=2S_(\text(pr-k))+a^2+b^2 \Rightarrow S_(\text(pr-k) )=ab \end(multline*)\)

Definition

The height of a parallelogram is the perpendicular drawn from the vertex of the parallelogram to the side (or extension of the side) that does not contain that vertex.
For example, the height \(BK\) falls on the side \(AD\) , and the height \(BH\) falls on the extension of the side \(CD\) :

Theorem: area of ​​a parallelogram

The area of ​​a parallelogram is equal to the product of the height and the side to which this height is drawn.

Proof

Draw perpendiculars \(AB"\) and \(DC"\) as shown in the figure. Note that these perpendiculars are equal to the height of the parallelogram \(ABCD\) .

Then \(AB"C"D\) is a rectangle, hence \(S_(AB"C"D)=AB"\cdot AD\) .

Note that right triangles \(ABB"\) and \(DCC"\) are equal. In this way,

\(S_(ABCD)=S_(ABC"D)+S_(DCC")=S_(ABC"D)+S_(ABB")=S_(AB"C"D)=AB"\cdot AD.\)

\[(\Large(\text(Area of ​​triangle)))\]

Definition

We will call the side to which the altitude is drawn in the triangle the base of the triangle.

Theorem

The area of ​​a triangle is half the product of its base and the height drawn to that base.

Proof

Let \(S\) be the area of ​​the triangle \(ABC\) . Let's take the side \(AB\) as the base of the triangle and draw the height \(CH\) . Let's prove that \ Let's build the triangle \(ABC\) to the parallelogram \(ABDC\) as shown in the figure:

Triangles \(ABC\) and \(DCB\) are equal in three sides (\(BC\) is their common side, \(AB = CD\) and \(AC = BD\) as opposite sides of the parallelogram \(ABDC\ )), so their areas are equal. Therefore, the area \(S\) of the triangle \(ABC\) is equal to half the area of ​​the parallelogram \(ABDC\) , i.e. \(S = \dfrac(1)(2)AB\cdotCH\).

Theorem

If two triangles \(\triangle ABC\) and \(\triangle A_1B_1C_1\) have equal heights, then their areas are related as the bases to which these heights are drawn.

Consequence

The median of a triangle divides it into two triangles of equal area.

Theorem

If two triangles \(\triangle ABC\) and \(\triangle A_2B_2C_2\) each have the same angle, then their areas are related as the products of the sides forming this angle.

Proof

Let \(\angle A=\angle A_2\) . Let's combine these corners as shown in the figure (the point \(A\) is aligned with the point \(A_2\)):

Draw heights \(BH\) and \(C_2K\) .

Triangles \(AB_2C_2\) and \(ABC_2\) have the same height \(C_2K\) , therefore: \[\dfrac(S_(AB_2C_2))(S_(ABC_2))=\dfrac(AB_2)(AB)\]

The triangles \(ABC_2\) and \(ABC\) have the same height \(BH\) , therefore: \[\dfrac(S_(ABC_2))(S_(ABC))=\dfrac(AC_2)(AC)\]

Multiplying the last two equalities, we get: \[\dfrac(S_(AB_2C_2))(S_(ABC))=\dfrac(AB_2\cdot AC_2)(AB\cdot AC) \qquad \text( or ) \qquad \dfrac(S_(A_2B_2C_2))(S_ (ABC))=\dfrac(A_2B_2\cdot A_2C_2)(AB\cdot AC)\]

Pythagorean theorem

In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs:

The converse is also true: if in a triangle the square of the length of one side is equal to the sum of the squares of the lengths of the other two sides, then such a triangle is right-angled.

Theorem

The area of ​​a right triangle is half the product of the legs.

Theorem: Heron's formula

Let \(p\) be the semiperimeter of a triangle, \(a\) , \(b\) , \(c\) be the lengths of its sides, then its area is equal to \

\[(\Large(\text(Area of ​​a rhombus and a trapezoid)))\]

Comment

Because rhombus is a parallelogram, then the same formula is true for it, i.e. The area of ​​a rhombus is equal to the product of the height and the side to which this height is drawn.

Theorem

The area of ​​a convex quadrilateral whose diagonals are perpendicular is half the product of the diagonals.

Proof

Consider the quadrilateral \(ABCD\) . Denote \(AO=a, CO=b, BO=x, DO=y\) :

Note that this quadrangle is made up of four right triangles, therefore, its area is equal to the sum of the areas of these triangles:

\(\begin(multline*) S_(ABCD)=\frac12ax+\frac12xb+\frac12by+\frac12ay=\frac12(ax+xb+by+ay)=\\ \frac12((a+b)x+(a+b) y)=\frac12(a+b)(x+y)\end(multline*)\)

Corollary: area of ​​a rhombus

The area of ​​a rhombus is half the product of its diagonals:

Definition

The height of a trapezoid is a perpendicular drawn from the top of one base to the other base.

Theorem: area of ​​a trapezoid

The area of ​​a trapezoid is half the sum of the bases times the height.

Proof

Consider a trapezoid \(ABCD\) with bases \(BC\) and \(AD\) . Draw \(CD"\parallel AB\) as shown in the figure:

Then \(ABCD"\) is a parallelogram.

We also draw \(BH"\perp AD, CH\perp AD\) (\(BH"=CH\) are the heights of the trapezoid).

Then \(S_(ABCD")=BH"\cdot AD"=BH"\cdot BC, \quad S_(CDD")=\dfrac12CH\cdot D"D\)

Because a trapezoid consists of a parallelogram \(ABCD"\) and a triangle \(CDD"\) , then its area is equal to the sum of the areas of the parallelogram and the triangle, that is:

\ \[=\dfrac12 CH\left(BC+AD"+D"D\right)=\dfrac12 CH\left(BC+AD\right)\]

Everyone who studied mathematics and geometry at school knows these sciences at least superficially. But over time, if they are not practiced, knowledge is forgotten. Many even believe that they just wasted their time studying geometric calculations. However, they are wrong. Technical workers perform daily work related to geometric calculations. As for the calculation of the area of ​​a polygon, this knowledge also finds its application in life. They will be needed at least in order to calculate the area of ​​\u200b\u200bthe land. So let's learn how to find the area of ​​a polygon.

Polygon definition

First, let's define what a polygon is. This is a flat geometric figure, which was formed as a result of the intersection of three or more lines. Another simple definition: a polygon is a closed polyline. Naturally, at the intersection of lines, intersection points are formed, their number is equal to the number of lines that form a polygon. The points of intersection are called the vertices, and the segments formed from the straight lines are called the sides of the polygon. Adjacent segments of a polygon are not on the same straight line. Line segments that are nonadjacent are those that do not pass through common points.

The sum of the areas of triangles

How to find the area of ​​a polygon? The area of ​​a polygon is the inner part of the plane, which was formed at the intersection of the segments or sides of the polygon. Since a polygon is a combination of shapes such as a triangle, rhombus, square, trapezoid, there is simply no universal formula for calculating its area. In practice, the most universal method is the division of a polygon into simpler figures, the area of ​​which is not difficult to find. By adding the sums of the areas of these simple figures, we get the area of ​​​​the polygon.

Through the area of ​​the circle

In most cases, the polygon has a regular shape and forms a figure with equal sides and angles between them. Calculating the area in this case is very simple using the inscribed or circumscribed circle. If the area of ​​the circle is known, then it must be multiplied by the perimeter of the polygon, and then the resulting product divided by 2. As a result, the formula for calculating the area of ​​such a polygon is obtained: S = ½∙P∙r., Where P is the area of ​​the circle, and r is the perimeter of the polygon .

The method of splitting a polygon into “convenient” shapes is the most popular in geometry, it allows you to quickly and correctly find the area of ​​a polygon. The 4th grade of high school usually learns such methods.

Area, one of the basic quantities associated with geometric shapes. In the simplest cases, it is measured by the number of unit squares filling a flat figure, that is, squares with a side equal to one length. The calculation of P. was already in antiquity ... ...

This term has other meanings, see Area (meanings). The area of ​​a flat figure is an additive numerical characteristic of a figure that belongs entirely to one plane. In the simplest case, when the figure can be divided into finite ... ... Wikipedia

I Area is one of the basic quantities associated with geometric shapes. In the simplest cases, it is measured by the number of unit squares filling a flat figure, that is, squares with a side equal to one length. Calculation P. ... ... Great Soviet Encyclopedia

This term has other meanings, see Area (meanings). Area Unit L² SI units m² ... Wikipedia

G. 1. Part of the earth's surface, a space naturally limited or specially allocated for some purpose. ott. Water space. ott. Big, flat place, space. 2. Flat undeveloped public space ... ... Modern explanatory dictionary of the Russian language Efremova

This article is proposed for deletion. An explanation of the reasons and a corresponding discussion can be found on the Wikipedia page: To be deleted / September 2, 2012. While the discussion process is not completed, the article can be improved, but should be ... ... Wikipedia

Two figures in R2 having equal areas and, respectively, two polygons M1 and M 2 such that they can be cut into polygons so that the parts that make up M 1 are respectively congruent to the parts that make up M 2. For, equal area ... ... Mathematical Encyclopedia

B=7, G=8, B + G/2 − 1= 10 Pick's theorem is a classical result of combinatorial geometry and geometry of numbers. Area of ​​a polygon with an integer ... Wikipedia

This term has other meanings, see Pick's Theorem. V = 7, Г = 8, В + Г/2 − 1 = 10 Pick's formula (or Pick's theorem) is a classical result of combinatorial geometry and geometry of numbers. Square ... Wikipedia

A domain (connected open set) on the boundary of a convex body in Euclidean space E 3. The entire boundary of a convex body is called. complete V. p. If the body is finite, then complete V. p. closed. If the body is infinite, then the complete V. p. endless... ... Mathematical Encyclopedia