Solution do it with a calculator. We write out the extended and main matrices: 
The main matrix A is separated by a dotted line. From above, we write the unknown systems, bearing in mind the possible permutation of the terms in the equations of the system. Determining the rank of the extended matrix, we simultaneously find the rank of the main one. In matrix B, the first and second columns are proportional. Of the two proportional columns, only one can fall into the basic minor, so let's move, for example, the first column beyond the dashed line with the opposite sign. For the system, this means the transfer of terms from x 1 to the right side of the equations. 
We bring the matrix to a triangular form. We will work only with rows, since multiplying a matrix row by a number other than zero and adding to another row for the system means multiplying the equation by the same number and adding it to another equation, which does not change the solution of the system. Working with the first row: multiply the first row of the matrix by (-3) and add to the second and third rows in turn. Then we multiply the first row by (-2) and add it to the fourth one. 
The second and third lines are proportional, therefore, one of them, for example the second, can be crossed out. This is equivalent to deleting the second equation of the system, since it is a consequence of the third one. 
Now we work with the second line: multiply it by (-1) and add it to the third. 
The dashed minor has the highest order (of all possible minors) and is non-zero (it is equal to the product of the elements on the main diagonal), and this minor belongs to both the main matrix and the extended one, hence rangA = rangB = 3 .
Minor 
is basic. It includes coefficients for unknown x 2, x 3, x 4, which means that the unknown x 2, x 3, x 4 are dependent, and x 1, x 5 are free.
We transform the matrix, leaving only the basic minor on the left (which corresponds to point 4 of the above solution algorithm). 
The system with coefficients of this matrix is equivalent to the original system and has the form
x 4 =3-4x 5 , x 3 =3-4x 5 -2x 4 =3-4x 5 -6+8x 5 =-3+4x 5
x 2 =x 3 +2x 4 -2+2x 1 +3x 5 = -3+4x 5 +6-8x 5 -2+2x 1 +3x 5 = 1+2x 1 -x 5
We got relations expressing dependent variables x 2, x 3, x 4 through free x 1 and x 5, that is, we found a general solution:
Giving arbitrary values to the free unknowns, we obtain any number of particular solutions. Let's find two particular solutions:
1) let x 1 = x 5 = 0, then x 2 = 1, x 3 = -3, x 4 = 3;
2) put x 1 = 1, x 5 = -1, then x 2 = 4, x 3 = -7, x 4 = 7.
Thus, we found two solutions: (0.1, -3,3,0) - one solution, (1.4, -7.7, -1) - another solution.
Example 2. Investigate compatibility, find a general and one particular solution of the system 
Solution. Let's rearrange the first and second equations to have a unit in the first equation and write the matrix B. 
We get zeros in the fourth column, operating on the first row: 
Now get the zeros in the third column using the second row: 
The third and fourth rows are proportional, so one of them can be crossed out without changing the rank:
Multiply the third row by (-2) and add to the fourth: 
We see that the ranks of the main and extended matrices are 4, and the rank coincides with the number of unknowns, therefore, the system has a unique solution:
-x 1 \u003d -3 → x 1 \u003d 3; x 2 \u003d 3-x 1 → x 2 \u003d 0; x 3 \u003d 1-2x 1 → x 3 \u003d 5.
x 4 \u003d 10- 3x 1 - 3x 2 - 2x 3 \u003d 11.
Example 3. Examine the system for compatibility and find a solution if it exists. 
Solution. We compose the extended matrix of the system. 
Rearrange the first two equations so that there is a 1 in the upper left corner:
Multiplying the first row by (-1), we add it to the third: 
Multiply the second line by (-2) and add to the third: 
The system is inconsistent, since the main matrix received a row consisting of zeros, which is crossed out when the rank is found, and the last row remains in the extended matrix, that is, r B > r A .
Exercise. Investigate this system of equations for compatibility and solve it by means of matrix calculus.
Solution
Example. Prove the compatibility of a system of linear equations and solve it in two ways: 1) by the Gauss method; 2) Cramer's method. (enter the answer in the form: x1,x2,x3)
Solution :doc :doc :xls
Answer: 2,-1,3.
Example. A system of linear equations is given. Prove its compatibility. Find a general solution of the system and one particular solution.
Solution
Answer: x 3 \u003d - 1 + x 4 + x 5; x 2 \u003d 1 - x 4; x 1 = 2 + x 4 - 3x 5
Exercise. Find general and particular solutions for each system.
Solution. We study this system using the Kronecker-Capelli theorem.
We write out the extended and main matrices:
| 1 | 1 | 14 | 0 | 2 | 0 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
| x 1 | x2 | x 3 | x4 | x5 |
Here matrix A is in bold type.
We bring the matrix to a triangular form. We will work only with rows, since multiplying a matrix row by a number other than zero and adding to another row for the system means multiplying the equation by the same number and adding it to another equation, which does not change the solution of the system.
Multiply the 1st row by (3). Multiply the 2nd row by (-1). Let's add the 2nd line to the 1st:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Multiply the 2nd row by (2). Multiply the 3rd row by (-3). Let's add the 3rd line to the 2nd:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Multiply the 2nd row by (-1). Let's add the 2nd line to the 1st:
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
The selected minor has the highest order (among possible minors) and is different from zero (it is equal to the product of the elements on the reciprocal diagonal), and this minor belongs to both the main matrix and the extended one, therefore rang(A) = rang(B) = 3 Since the rank of the main matrix is equal to the rank of the extended one, then the system is collaborative.
This minor is basic. It includes coefficients for unknown x 1, x 2, x 3, which means that the unknown x 1, x 2, x 3 are dependent (basic), and x 4, x 5 are free.
We transform the matrix, leaving only the basic minor on the left.
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -1 | 3 | -6 |
| 2 | 3 | -3 | 1 | -3 | 2 |
| x 1 | x2 | x 3 | x4 | x5 |
27x3=
- x 2 + 13x 3 = - 1 + 3x 4 - 6x 5
2x 1 + 3x 2 - 3x 3 = 1 - 3x 4 + 2x 5
By the method of elimination of unknowns we find:
We got relations expressing dependent variables x 1, x 2, x 3 through free x 4, x 5, that is, we found common decision:
x 3 = 0
x2 = 1 - 3x4 + 6x5
x 1 = - 1 + 3x 4 - 8x 5
uncertain, because has more than one solution.
Exercise. Solve the system of equations.
Answer:x 2 = 2 - 1.67x 3 + 0.67x 4
x 1 = 5 - 3.67x 3 + 0.67x 4
Giving arbitrary values to the free unknowns, we obtain any number of particular solutions. The system is uncertain
System of m linear equations with n unknowns called a system of the form
where aij and b i (i=1,…,m; b=1,…,n) are some known numbers, and x 1 ,…,x n- unknown. In the notation of the coefficients aij first index i denotes the number of the equation, and the second j is the number of the unknown at which this coefficient stands.
The coefficients for the unknowns will be written in the form of a matrix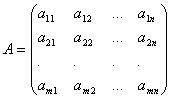 
, which we will call system matrix.
The numbers on the right sides of the equations b 1 ,…,b m called free members.
Aggregate n numbers c 1 ,…,c n called decision of this system, if each equation of the system becomes an equality after substituting numbers into it c 1 ,…,c n instead of the corresponding unknowns x 1 ,…,x n.
Our task will be to find solutions to the system. In this case, three situations may arise:
A system of linear equations that has at least one solution is called joint. Otherwise, i.e. if the system has no solutions, then it is called incompatible.
Consider ways to find solutions to the system.
MATRIX METHOD FOR SOLVING SYSTEMS OF LINEAR EQUATIONS
Matrices make it possible to briefly write down a system of linear equations. Let a system of 3 equations with three unknowns be given:
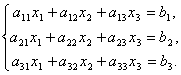
Consider the matrix of the system 
and matrix columns of unknown and free members 
Let's find the product
those. as a result of the product, we obtain the left-hand sides of the equations of this system. Then, using the definition of matrix equality, this system can be written as
or shorter A∙X=B.
Here matrices A and B are known, and the matrix X unknown. She needs to be found, because. its elements are the solution of this system. This equation is called matrix equation.
Let the matrix determinant be different from zero | A| ≠ 0. Then the matrix equation is solved as follows. Multiply both sides of the equation on the left by the matrix A-1, the inverse of the matrix A: . Because the A -1 A = E and E∙X=X, then we obtain the solution of the matrix equation in the form X = A -1 B .
Note that since the inverse matrix can only be found for square matrices, the matrix method can only solve those systems in which the number of equations is the same as the number of unknowns. However, the matrix notation of the system is also possible in the case when the number of equations is not equal to the number of unknowns, then the matrix A is not square and therefore it is impossible to find a solution to the system in the form X = A -1 B.
Examples. Solve systems of equations.
CRAMER'S RULE
Consider a system of 3 linear equations with three unknowns:
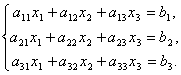
Third-order determinant corresponding to the matrix of the system, i.e. composed of coefficients at unknowns,
called system determinant.
We compose three more determinants as follows: we replace successively 1, 2 and 3 columns in the determinant D with a column of free terms
Then we can prove the following result.
Theorem (Cramer's rule). If the determinant of the system is Δ ≠ 0, then the system under consideration has one and only one solution, and
Proof. So, consider a system of 3 equations with three unknowns. Multiply the 1st equation of the system by the algebraic complement A 11 element a 11, 2nd equation - on A21 and 3rd - on A 31:
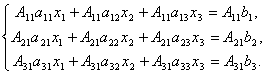
Let's add these equations:
Consider each of the brackets and the right side of this equation. By the theorem on the expansion of the determinant in terms of the elements of the 1st column
Similarly, it can be shown that and .
Finally, it is easy to see that 
Thus, we get the equality: .
Consequently, .
The equalities and are derived similarly, whence the assertion of the theorem follows.
Thus, we note that if the determinant of the system is Δ ≠ 0, then the system has a unique solution and vice versa. If the determinant of the system is equal to zero, then the system either has an infinite set of solutions or has no solutions, i.e. incompatible.
Examples. Solve a system of equations
GAUSS METHOD
The previously considered methods can be used to solve only those systems in which the number of equations coincides with the number of unknowns, and the determinant of the system must be different from zero. The Gaussian method is more universal and is suitable for systems with any number of equations. It consists in the successive elimination of unknowns from the equations of the system.
Consider again a system of three equations with three unknowns:
.
We leave the first equation unchanged, and from the 2nd and 3rd we exclude the terms containing x 1. To do this, we divide the second equation by a 21 and multiply by - a 11 and then add with the 1st equation. Similarly, we divide the third equation into a 31 and multiply by - a 11 and then add it to the first one. As a result, the original system will take the form:
Now, from the last equation, we eliminate the term containing x2. To do this, divide the third equation by , multiply by and add it to the second. Then we will have a system of equations:
Hence from the last equation it is easy to find x 3, then from the 2nd equation x2 and finally from the 1st - x 1.
When using the Gaussian method, the equations can be interchanged if necessary.
Often, instead of writing a new system of equations, they limit themselves to writing out the extended matrix of the system:
and then bring it to a triangular or diagonal form using elementary transformations.
To elementary transformations matrices include the following transformations:
- permutation of rows or columns;
- multiplying a string by a non-zero number;
- adding to one line other lines.
Examples: Solve systems of equations using the Gauss method.
Thus, the system has an infinite number of solutions.
Systems of equations are widely used in the economic industry in the mathematical modeling of various processes. For example, when solving problems of production management and planning, logistics routes (transport problem) or equipment placement.
Equation systems are used not only in the field of mathematics, but also in physics, chemistry and biology, when solving problems of finding the population size.
A system of linear equations is a term for two or more equations with several variables for which it is necessary to find a common solution. Such a sequence of numbers for which all equations become true equalities or prove that the sequence does not exist.
Linear Equation
Equations of the form ax+by=c are called linear. The designations x, y are the unknowns, the value of which must be found, b, a are the coefficients of the variables, c is the free term of the equation.
Solving the equation by plotting its graph will look like a straight line, all points of which are the solution of the polynomial.
Types of systems of linear equations
The simplest are examples of systems of linear equations with two variables X and Y.
F1(x, y) = 0 and F2(x, y) = 0, where F1,2 are functions and (x, y) are function variables.
Solve a system of equations - it means to find such values (x, y) for which the system becomes a true equality, or to establish that there are no suitable values of x and y.
A pair of values (x, y), written as point coordinates, is called a solution to a system of linear equations.
If the systems have one common solution or there is no solution, they are called equivalent.
Homogeneous systems of linear equations are systems whose right side is equal to zero. If the right part after the "equal" sign has a value or is expressed by a function, such a system is not homogeneous.
The number of variables can be much more than two, then we should talk about an example of a system of linear equations with three variables or more.
Faced with systems, schoolchildren assume that the number of equations must necessarily coincide with the number of unknowns, but this is not so. The number of equations in the system does not depend on the variables, there can be an arbitrarily large number of them.
Simple and complex methods for solving systems of equations
There is no general analytical way to solve such systems, all methods are based on numerical solutions. The school course of mathematics describes in detail such methods as permutation, algebraic addition, substitution, as well as the graphical and matrix method, the solution by the Gauss method.
The main task in teaching methods of solving is to teach how to correctly analyze the system and find the optimal solution algorithm for each example. The main thing is not to memorize a system of rules and actions for each method, but to understand the principles of applying a particular method.
The solution of examples of systems of linear equations of the 7th grade of the general education school program is quite simple and is explained in great detail. In any textbook on mathematics, this section is given enough attention. The solution of examples of systems of linear equations by the method of Gauss and Cramer is studied in more detail in the first courses of higher educational institutions.
Solution of systems by the substitution method
The actions of the substitution method are aimed at expressing the value of one variable through the second. The expression is substituted into the remaining equation, then it is reduced to a single variable form. The action is repeated depending on the number of unknowns in the system
Let's give an example of a system of linear equations of the 7th class by the substitution method:
As can be seen from the example, the variable x was expressed through F(X) = 7 + Y. The resulting expression, substituted into the 2nd equation of the system in place of X, helped to obtain one variable Y in the 2nd equation. The solution of this example does not cause difficulties and allows you to get the Y value. The last step is to check the obtained values.
It is not always possible to solve an example of a system of linear equations by substitution. The equations can be complex and the expression of the variable in terms of the second unknown will be too cumbersome for further calculations. When there are more than 3 unknowns in the system, the substitution solution is also impractical.
Solution of an example of a system of linear inhomogeneous equations:
Solution using algebraic addition
When searching for a solution to systems by the addition method, term-by-term addition and multiplication of equations by various numbers are performed. The ultimate goal of mathematical operations is an equation with one variable.
Applications of this method require practice and observation. It is not easy to solve a system of linear equations using the addition method with the number of variables 3 or more. Algebraic addition is useful when the equations contain fractions and decimal numbers.
Solution action algorithm:
- Multiply both sides of the equation by some number. As a result of the arithmetic operation, one of the coefficients of the variable must become equal to 1.
- Add the resulting expression term by term and find one of the unknowns.
- Substitute the resulting value into the 2nd equation of the system to find the remaining variable.
Solution method by introducing a new variable
A new variable can be introduced if the system needs to find a solution for no more than two equations, the number of unknowns should also be no more than two.
The method is used to simplify one of the equations by introducing a new variable. The new equation is solved with respect to the entered unknown, and the resulting value is used to determine the original variable.
It can be seen from the example that by introducing a new variable t, it was possible to reduce the 1st equation of the system to a standard square trinomial. You can solve a polynomial by finding the discriminant.
It is necessary to find the value of the discriminant using the well-known formula: D = b2 - 4*a*c, where D is the desired discriminant, b, a, c are the multipliers of the polynomial. In the given example, a=1, b=16, c=39, hence D=100. If the discriminant is greater than zero, then there are two solutions: t = -b±√D / 2*a, if the discriminant is less than zero, then there is only one solution: x= -b / 2*a.
The solution for the resulting systems is found by the addition method.
A visual method for solving systems
Suitable for systems with 3 equations. The method consists in plotting graphs of each equation included in the system on the coordinate axis. The coordinates of the points of intersection of the curves will be the general solution of the system.
The graphic method has a number of nuances. Consider several examples of solving systems of linear equations in a visual way.
As can be seen from the example, two points were constructed for each line, the values of the variable x were chosen arbitrarily: 0 and 3. Based on the values of x, the values for y were found: 3 and 0. Points with coordinates (0, 3) and (3, 0) were marked on the graph and connected by a line.
The steps must be repeated for the second equation. The point of intersection of the lines is the solution of the system.
In the following example, it is required to find a graphical solution to the system of linear equations: 0.5x-y+2=0 and 0.5x-y-1=0.
As can be seen from the example, the system has no solution, because the graphs are parallel and do not intersect along their entire length.
The systems from Examples 2 and 3 are similar, but when constructed, it becomes obvious that their solutions are different. It should be remembered that it is not always possible to say whether the system has a solution or not, it is always necessary to build a graph.
Matrix and its varieties
Matrices are used to briefly write down a system of linear equations. A matrix is a special type of table filled with numbers. n*m has n - rows and m - columns.
A matrix is square when the number of columns and rows is equal. A matrix-vector is a single-column matrix with an infinitely possible number of rows. A matrix with units along one of the diagonals and other zero elements is called identity.
An inverse matrix is such a matrix, when multiplied by which the original one turns into a unit one, such a matrix exists only for the original square one.
Rules for transforming a system of equations into a matrix
With regard to systems of equations, the coefficients and free members of the equations are written as numbers of the matrix, one equation is one row of the matrix.
A matrix row is called non-zero if at least one element of the row is not equal to zero. Therefore, if in any of the equations the number of variables differs, then it is necessary to enter zero in place of the missing unknown.
The columns of the matrix must strictly correspond to the variables. This means that the coefficients of the variable x can only be written in one column, for example the first, the coefficient of the unknown y - only in the second.
When multiplying a matrix, all matrix elements are successively multiplied by a number.
Options for finding the inverse matrix
The formula for finding the inverse matrix is quite simple: K -1 = 1 / |K|, where K -1 is the inverse matrix and |K| - matrix determinant. |K| must not be equal to zero, then the system has a solution.
The determinant is easily calculated for a two-by-two matrix, it is only necessary to multiply the elements diagonally by each other. For the "three by three" option, there is a formula |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + a 3 b 2 c 1 . You can use the formula, or you can remember that you need to take one element from each row and each column so that the column and row numbers of the elements do not repeat in the product.
Solution of examples of systems of linear equations by the matrix method
The matrix method of finding a solution makes it possible to reduce cumbersome entries when solving systems with a large number of variables and equations.
In the example, a nm are the coefficients of the equations, the matrix is a vector x n are the variables, and b n are the free terms.
Solution of systems by the Gauss method
In higher mathematics, the Gauss method is studied together with the Cramer method, and the process of finding a solution to systems is called the Gauss-Cramer method of solving. These methods are used to find the variables of systems with a large number of linear equations.
The Gaussian method is very similar to substitution and algebraic addition solutions, but is more systematic. In the school course, the Gaussian solution is used for systems of 3 and 4 equations. The purpose of the method is to bring the system to the form of an inverted trapezoid. By algebraic transformations and substitutions, the value of one variable is found in one of the equations of the system. The second equation is an expression with 2 unknowns, and 3 and 4 - with 3 and 4 variables, respectively.
After bringing the system to the described form, the further solution is reduced to the sequential substitution of known variables into the equations of the system.
In school textbooks for grade 7, an example of a Gaussian solution is described as follows:
As can be seen from the example, at step (3) two equations were obtained 3x 3 -2x 4 =11 and 3x 3 +2x 4 =7. The solution of any of the equations will allow you to find out one of the variables x n.
Theorem 5, which is mentioned in the text, states that if one of the equations of the system is replaced by an equivalent one, then the resulting system will also be equivalent to the original one.
The Gaussian method is difficult for middle school students to understand, but is one of the most interesting ways to develop the ingenuity of children studying in the advanced study program in math and physics classes.
For ease of recording calculations, it is customary to do the following:
Equation coefficients and free terms are written in the form of a matrix, where each row of the matrix corresponds to one of the equations of the system. separates the left side of the equation from the right side. Roman numerals denote the numbers of equations in the system.
First, they write down the matrix with which to work, then all the actions carried out with one of the rows. The resulting matrix is written after the "arrow" sign and continue to perform the necessary algebraic operations until the result is achieved.
As a result, a matrix should be obtained in which one of the diagonals is 1, and all other coefficients are equal to zero, that is, the matrix is reduced to a single form. We must not forget to make calculations with the numbers of both sides of the equation.
This notation is less cumbersome and allows you not to be distracted by listing numerous unknowns.
The free application of any method of solution will require care and a certain amount of experience. Not all methods are applied. Some ways of finding solutions are more preferable in a particular area of human activity, while others exist for the purpose of learning.
We continue to deal with systems of linear equations. So far, we have considered systems that have a unique solution. Such systems can be solved in any way: substitution method("school") by Cramer's formulas, matrix method, Gauss method. However, two more cases are widespread in practice when:
1) the system is inconsistent (has no solutions);
2) the system has infinitely many solutions.
For these systems, the most universal of all solution methods is used - Gauss method. In fact, the "school" method will also lead to the answer, but in higher mathematics it is customary to use the Gaussian method of successive elimination of unknowns. Those who are not familiar with the Gauss method algorithm, please study the lesson first Gauss method
The elementary matrix transformations themselves are exactly the same, the difference will be in the end of the solution. First, consider a couple of examples where the system has no solutions (inconsistent).
Example 1
What immediately catches your eye in this system? The number of equations is less than the number of variables. There is a theorem that says: “If the number of equations in the system is less than the number of variables, then the system is either inconsistent or has infinitely many solutions. And it remains only to find out.
The beginning of the solution is quite ordinary - we write the extended matrix of the system and, using elementary transformations, we bring it to a stepwise form:
(one). On the upper left step, we need to get (+1) or (-1). There are no such numbers in the first column, so rearranging the rows will not work. The unit will have to be organized independently, and this can be done in several ways. We did so. To the first line we add the third line, multiplied by (-1).
(2). Now we get two zeros in the first column. To the second line, add the first line, multiplied by 3. To the third line, add the first, multiplied by 5.
(3). After the transformation is done, it is always advisable to see if it is possible to simplify the resulting strings? Can. We divide the second line by 2, at the same time getting the desired one (-1) on the second step. Divide the third line by (-3).
(four). Add the second line to the third line. Probably, everyone paid attention to the bad line, which turned out as a result of elementary transformations:
. It is clear that this cannot be so.
Indeed, we rewrite the resulting matrix
back to the system of linear equations:
If as a result of elementary transformations a string of the form , whereλ is a non-zero number, then the system is inconsistent (has no solutions).
How to record the end of a task? You need to write down the phrase:
“As a result of elementary transformations, a string of the form is obtained, where λ ≠ 0 ". Answer: "The system has no solutions (inconsistent)."
Please note that in this case there is no reverse move of the Gaussian algorithm, there are no solutions and there is simply nothing to find.
Example 2
Solve a system of linear equations 
This is a do-it-yourself example. Full solution and answer at the end of the lesson.
Again, we remind you that your solution process may differ from our solution process, the Gauss method does not set an unambiguous algorithm, you need to guess the procedure and the actions themselves in each case yourself.
One more technical feature of the solution: elementary transformations can be stopped At once, as soon as a line like , where λ ≠ 0 . Consider a conditional example: suppose that after the first transformation we get a matrix
.
This matrix has not yet been reduced to a stepped form, but there is no need for further elementary transformations, since a line of the form has appeared, where λ ≠ 0 . It should be immediately answered that the system is incompatible.
When a system of linear equations has no solutions, this is almost a gift to the student, because a short solution is obtained, sometimes literally in 2-3 steps. But everything in this world is balanced, and the problem in which the system has infinitely many solutions is just longer.
Example 3:
Solve a system of linear equations
There are 4 equations and 4 unknowns, so the system can either have a single solution, or have no solutions, or have infinitely many solutions. Whatever it was, but the Gauss method in any case will lead us to the answer. This is its versatility.
The beginning is again standard. We write the extended matrix of the system and, using elementary transformations, bring it to a step form:
That's all, and you were afraid.
(one). Please note that all the numbers in the first column are divisible by 2, so on the upper left step we are also satisfied with a deuce. To the second line we add the first line, multiplied by (-4). To the third line we add the first line, multiplied by (-2). To the fourth line we add the first line, multiplied by (-1).
Attention! Many may be tempted from the fourth line subtract first line. This can be done, but it is not necessary, experience shows that the probability of an error in calculations increases several times. We just add: to the fourth line we add the first line, multiplied by (-1) - exactly!
(2). The last three lines are proportional, two of them can be deleted. Here again it is necessary to show increased attention, but are the lines really proportional? For reinsurance, it will not be superfluous to multiply the second row by (-1), and divide the fourth row by 2, resulting in three identical rows. And only after that remove two of them. As a result of elementary transformations, the extended matrix of the system is reduced to a stepped form:
When completing a task in a notebook, it is advisable to make the same notes in pencil for clarity.
We rewrite the corresponding system of equations: 
The “usual” only solution of the system does not smell here. Bad line where λ ≠ 0, also no. Hence, this is the third remaining case - the system has infinitely many solutions.
The infinite set of solutions of the system is briefly written in the form of the so-called general system solution.
We will find the general solution of the system using the reverse motion of the Gauss method. For systems of equations with an infinite set of solutions, new concepts appear: "basic variables" and "free variables". First, let's define what variables we have basic, and what variables - free. It is not necessary to explain in detail the terms of linear algebra, it is enough to remember that there are such basis variables and free variables.
Basic variables always "sit" strictly on the steps of the matrix. In this example, the base variables are x 1 and x 3 .
Free variables are everything remaining variables that did not get a step. In our case, there are two: x 2 and x 4 - free variables.
Now you need allbasis variables express only throughfree variables. The reverse move of the Gaussian algorithm traditionally works from the bottom up. From the second equation of the system, we express the basic variable x 3:
Now look at the first equation: 
. First, we substitute the found expression into it:
It remains to express the basic variable x 1 through free variables x 2 and x 4:
The result is what you need - all basis variables ( x 1 and x 3) expressed only through free variables ( x 2 and x 4):
Actually, the general solution is ready:
.
How to write down the general solution? First of all, free variables are written into the general solution “on their own” and strictly in their places. In this case, the free variables x 2 and x 4 should be written in the second and fourth positions:
.
The resulting expressions for the basic variables and obviously needs to be written in the first and third positions:
From the general solution of the system, one can find infinitely many private decisions. It's very simple. free variables x 2 and x 4 are called so because they can be given any final values. The most popular values are zero values, since this is the easiest way to obtain a particular solution.
Substituting ( x 2 = 0; x 4 = 0) into the general solution, we get one of the particular solutions:
, or is a particular solution corresponding to free variables with values ( x 2 = 0; x 4 = 0).
Ones are another sweet couple, let's substitute ( x 2 = 1 and x 4 = 1) into the general solution:
, i.e. (-1; 1; 1; 1) is another particular solution.
It is easy to see that the system of equations has infinitely many solutions since we can give free variables any values.
Each a particular solution must satisfy to each system equation. This is the basis for a “quick” check of the correctness of the solution. Take, for example, a particular solution (-1; 1; 1; 1) and substitute it into the left side of each equation in the original system:
Everything has to come together. And with any particular solution you get, everything should also converge.
Strictly speaking, the verification of a particular solution sometimes deceives, i.e. some particular solution can satisfy each equation of the system, and the general solution itself is actually found incorrectly. Therefore, first of all, the verification of the general solution is more thorough and reliable.
How to check the resulting general solution 
?
It's not difficult, but it requires quite a long transformation. We need to take expressions basic variables, in this case 
and , and substitute them into the left side of each equation of the system.
To the left side of the first equation of the system:
The right side of the original first equation of the system is obtained.
To the left side of the second equation of the system:
The right side of the original second equation of the system is obtained.
And further - to the left parts of the third and fourth equations of the system. This check is longer, but it guarantees the 100% correctness of the overall solution. In addition, in some tasks it is required to check the general solution.
Example 4:
Solve the system using the Gauss method. Find a general solution and two private ones. Check the overall solution.
This is a do-it-yourself example. Here, by the way, again the number of equations is less than the number of unknowns, which means that it is immediately clear that the system will be either inconsistent or with an infinite number of solutions.
Example 5:
Solve a system of linear equations. If the system has infinitely many solutions, find two particular solutions and check the general solution
Solution: Let us write down the extended matrix of the system and, with the help of elementary transformations, bring it to a stepped form:
(one). Add the first line to the second line. To the third line we add the first line multiplied by 2. To the fourth line we add the first line multiplied by 3.
(2). To the third line we add the second line, multiplied by (-5). To the fourth line we add the second line, multiplied by (-7).
(3). The third and fourth lines are the same, we delete one of them. Here is such a beauty:
Basis variables sit on steps, so they are base variables.
There is only one free variable, which did not get a step: .
(four). Reverse move. We express the basic variables in terms of the free variable:
From the third equation:
Consider the second equation and substitute the found expression into it:
, 
, ,
Consider the first equation and substitute the found expressions and into it:
Thus, the general solution with one free variable x 4:
Once again, how did it happen? free variable x 4 sits alone in its rightful fourth place. The resulting expressions for the basic variables , , are also in their places.
Let us immediately check the general solution.
We substitute the basic variables , , into the left side of each equation of the system:
The corresponding right-hand sides of the equations are obtained, thus, the correct general solution is found.
Now from the found general solution 
we get two particular solutions. All variables are expressed here through a single free variable x four . You don't need to break your head.
Let x 4 = 0, then 
is the first particular solution.
Let x 4 = 1, then 
is another particular solution.
Answer: Common decision: . Private Solutions:
and .
Example 6:
Find the general solution of the system of linear equations.
We have already checked the general solution, the answer can be trusted. Your course of action may differ from our course of action. The main thing is that the general solutions coincide. Probably, many have noticed an unpleasant moment in the solutions: very often, during the reverse course of the Gauss method, we had to fiddle with ordinary fractions. In practice, this is true, cases where there are no fractions are much less common. Be prepared mentally, and most importantly, technically.
Let us dwell on the features of the solution that were not found in the solved examples. The general solution of the system may sometimes include a constant (or constants).
For example, the general solution: . Here one of the basic variables is equal to a constant number: . There is nothing exotic in this, it happens. Obviously, in this case, any particular solution will contain a five in the first position.
Rarely, but there are systems in which the number of equations is greater than the number of variables. However, the Gauss method works under the most severe conditions. You should calmly bring the extended matrix of the system to a stepped form according to the standard algorithm. Such a system may be inconsistent, may have infinitely many solutions, and, oddly enough, may have a unique solution.
We repeat in our advice - in order to feel comfortable when solving a system using the Gauss method, you should fill your hand and solve at least a dozen systems.
Solutions and answers:
Example 2:
Solution:Let us write down the extended matrix of the system and, using elementary transformations, bring it to a stepped form.
Performed elementary transformations:
(1) The first and third lines have been swapped.
(2) The first line was added to the second line, multiplied by (-6). The first line was added to the third line, multiplied by (-7).
(3) The second line was added to the third line, multiplied by (-1).
As a result of elementary transformations, a string of the form, where λ ≠ 0 .So the system is inconsistent.Answer: there are no solutions.
Example 4:
Solution:We write the extended matrix of the system and, using elementary transformations, bring it to a step form:
Conversions performed:
(one). The first line multiplied by 2 was added to the second line. The first line multiplied by 3 was added to the third line.
There is no unit for the second step , and transformation (2) is aimed at obtaining it.
(2). The second line was added to the third line, multiplied by -3.
(3). The second and third rows were swapped (the resulting -1 was moved to the second step)
(four). The second line was added to the third line, multiplied by 3.
(5). The sign of the first two lines was changed (multiplied by -1), the third line was divided by 14.
Reverse move:
(one). Here are the basic variables (which are on steps), and are free variables (who did not get the step).
(2). We express the basic variables in terms of free variables:
From the third equation: .
(3). Consider the second equation:, particular solutions:
Answer: Common decision: 
Complex numbers
In this section, we will introduce the concept complex number, consider algebraic, trigonometric and show form complex number. We will also learn how to perform operations with complex numbers: addition, subtraction, multiplication, division, exponentiation and root extraction.
To master complex numbers, you do not need any special knowledge from the course of higher mathematics, and the material is available even to a schoolboy. It is enough to be able to perform algebraic operations with "ordinary" numbers, and remember trigonometry.
First, let's remember the "ordinary" Numbers. In mathematics they are called set of real numbers and are marked with the letter R, or R (thick). All real numbers sit on the familiar number line:
The company of real numbers is very colorful - here are integers, and fractions, and irrational numbers. In this case, each point of the numerical axis necessarily corresponds to some real number.
As appears from Cramer's theorems, when solving a system of linear equations, three cases may occur:
First case: the system of linear equations has a unique solution
(the system is consistent and definite)
Second case: the system of linear equations has an infinite number of solutions
(the system is consistent and indeterminate)
** 
,
those. the coefficients of the unknowns and the free terms are proportional.
Third case: the system of linear equations has no solutions
(system inconsistent)
So the system m linear equations with n variables is called incompatible if it has no solutions, and joint if it has at least one solution. A joint system of equations that has only one solution is called certain, and more than one uncertain.
Examples of solving systems of linear equations by the Cramer method
Let the system
.
Based on Cramer's theorem
………….
,
where 
-
system identifier. The remaining determinants are obtained by replacing the column with the coefficients of the corresponding variable (unknown) with free members:
Example 2
.
Therefore, the system is definite. To find its solution, we calculate the determinants
By Cramer's formulas we find:
So, (1; 0; -1) is the only solution to the system.
To check the solutions of the systems of equations 3 X 3 and 4 X 4, you can use the online calculator, the Cramer solving method.
If there are no variables in the system of linear equations in one or more equations, then in the determinant the elements corresponding to them are equal to zero! This is the next example.
Example 3 Solve the system of linear equations by Cramer's method:
.
Solution. We find the determinant of the system:
Look carefully at the system of equations and at the determinant of the system and repeat the answer to the question in which cases one or more elements of the determinant are equal to zero. So, the determinant is not equal to zero, therefore, the system is definite. To find its solution, we calculate the determinants for the unknowns
By Cramer's formulas we find:
So, the solution of the system is (2; -1; 1).
6. General system of linear algebraic equations. Gauss method.
As we remember, Cramer's rule and the matrix method are unsuitable in cases where the system has infinitely many solutions or is inconsistent. Gauss method – the most powerful and versatile tool for finding solutions to any system of linear equations, which the in every case lead us to the answer! The algorithm of the method in all three cases works the same way. If the Cramer and matrix methods require knowledge of determinants, then the application of the Gauss method requires knowledge of only arithmetic operations, which makes it accessible even to primary school students.
First, we systematize the knowledge about systems of linear equations a little. A system of linear equations can:
1) Have a unique solution.
2) Have infinitely many solutions.
3) Have no solutions (be incompatible).
The Gauss method is the most powerful and versatile tool for finding a solution any systems of linear equations. As we remember Cramer's rule and matrix method are unsuitable in cases where the system has infinitely many solutions or is inconsistent. A method of successive elimination of unknowns anyway lead us to the answer! In this lesson, we will again consider the Gauss method for case No. 1 (the only solution to the system), the article is reserved for the situations of points No. 2-3. I note that the method algorithm itself works in the same way in all three cases.
Let's return to the simplest system from the lesson How to solve a system of linear equations?
and solve it using the Gaussian method.
The first step is to write extended matrix system:
. By what principle the coefficients are recorded, I think everyone can see. The vertical line inside the matrix does not carry any mathematical meaning - it's just a strikethrough for ease of design.
Reference:I recommend to remember terms linear algebra. System Matrix is a matrix composed only of coefficients for unknowns, in this example, the matrix of the system: . Extended System Matrix is the same matrix of the system plus a column of free terms, in this case: . Any of the matrices can be called simply a matrix for brevity.
After the extended matrix of the system is written, it is necessary to perform some actions with it, which are also called elementary transformations.
There are the following elementary transformations:
1) Strings matrices can be rearranged places. For example, in the matrix under consideration, you can safely rearrange the first and second rows: 
2) If there are (or appeared) proportional (as a special case - identical) rows in the matrix, then it follows delete from the matrix, all these rows except one. Consider, for example, the matrix 
. In this matrix, the last three rows are proportional, so it is enough to leave only one of them: 
.
3) If a zero row appeared in the matrix during the transformations, then it also follows delete. I will not draw, of course, the zero line is the line in which only zeros.
4) The row of the matrix can be multiply (divide) for any number non-zero. Consider, for example, the matrix . Here it is advisable to divide the first line by -3, and multiply the second line by 2: 
. This action is very useful, as it simplifies further transformations of the matrix.
5) This transformation causes the most difficulties, but in fact there is nothing complicated either. To the row of the matrix, you can add another string multiplied by a number, different from zero. Consider our matrix from a practical example: . First, I will describe the transformation in great detail. Multiply the first row by -2: 
, and to the second line we add the first line multiplied by -2: 
. Now the first line can be divided "back" by -2: . As you can see, the line that is ADDED LI – hasn't changed. Is always the line is changed, TO WHICH ADDED UT.
In practice, of course, they don’t paint in such detail, but write shorter: 
Once again: to the second line added the first row multiplied by -2. The line is usually multiplied orally or on a draft, while the mental course of calculations is something like this:
“I rewrite the matrix and rewrite the first row: 
»
First column first. Below I need to get zero. Therefore, I multiply the unit above by -2:, and add the first to the second line: 2 + (-2) = 0. I write the result in the second line: 
»
“Now the second column. Above -1 times -2: . I add the first to the second line: 1 + 2 = 3. I write the result to the second line: 
»
“And the third column. Above -5 times -2: . I add the first line to the second line: -7 + 10 = 3. I write the result in the second line: »
Please think carefully about this example and understand the sequential calculation algorithm, if you understand this, then the Gauss method is practically "in your pocket". But, of course, we are still working on this transformation.
Elementary transformations do not change the solution of the system of equations
! ATTENTION: considered manipulations can not use, if you are offered a task where the matrices are given "by themselves". For example, with "classic" matrices in no case should you rearrange something inside the matrices!
Let's return to our system. She's practically broken into pieces.
Let us write the augmented matrix of the system and, using elementary transformations, reduce it to stepped view:
(1) The first row was added to the second row, multiplied by -2. And again: why do we multiply the first row by -2? In order to get zero at the bottom, which means getting rid of one variable in the second line.
(2) Divide the second row by 3.
The purpose of elementary transformations –
convert the matrix to step form: 
. In the design of the task, they directly draw out the “ladder” with a simple pencil, and also circle the numbers that are located on the “steps”. The term "stepped view" itself is not entirely theoretical; in the scientific and educational literature, it is often called trapezoidal view or triangular view.
As a result of elementary transformations, we have obtained equivalent original system of equations:
Now the system needs to be "untwisted" in the opposite direction - from the bottom up, this process is called reverse Gauss method.
In the lower equation, we already have the finished result: .
Consider the first equation of the system and substitute the already known value of “y” into it:
Let us consider the most common situation, when the Gaussian method is required to solve a system of three linear equations with three unknowns.
Example 1
Solve the system of equations using the Gauss method: 
Let's write the augmented matrix of the system: 
Now I will immediately draw the result that we will come to in the course of the solution: 
And I repeat, our goal is to bring the matrix to a stepped form using elementary transformations. Where to start taking action?
First, look at the top left number: 
Should almost always be here unit. Generally speaking, -1 (and sometimes other numbers) will also suit, but somehow it has traditionally happened that a unit is usually placed there. How to organize a unit? We look at the first column - we have a finished unit! Transformation one: swap the first and third lines: 
Now the first line will remain unchanged until the end of the solution. Now fine.
The unit in the top left is organized. Now you need to get zeros in these places: 
Zeros are obtained just with the help of a "difficult" transformation. First, we deal with the second line (2, -1, 3, 13). What needs to be done to get zero in the first position? Need to the second line add the first line multiplied by -2. Mentally or on a draft, we multiply the first line by -2: (-2, -4, 2, -18). And we consistently carry out (again mentally or on a draft) addition, to the second line we add the first line, already multiplied by -2:
The result is written in the second line: 
Similarly, we deal with the third line (3, 2, -5, -1). To get zero in the first position, you need to the third line add the first line multiplied by -3. Mentally or on a draft, we multiply the first line by -3: (-3, -6, 3, -27). And to the third line we add the first line multiplied by -3:
The result is written in the third line:
In practice, these actions are usually performed verbally and written down in one step: 
No need to count everything at once and at the same time. The order of calculations and "insertion" of results consistent and usually like this: first we rewrite the first line, and puff ourselves quietly - CONSISTENTLY and CAREFULLY:
And I have already considered the mental course of the calculations themselves above.
In this example, this is easy to do, we divide the second line by -5 (since all numbers there are divisible by 5 without a remainder). At the same time, we divide the third line by -2, because the smaller the number, the simpler the solution:
At the final stage of elementary transformations, one more zero must be obtained here: 
For this to the third line we add the second line, multiplied by -2:
Try to parse this action yourself - mentally multiply the second line by -2 and carry out the addition.
The last action performed is the hairstyle of the result, divide the third line by 3.
As a result of elementary transformations, an equivalent initial system of linear equations was obtained: 
Cool.
Now the reverse course of the Gaussian method comes into play. The equations "unwind" from the bottom up.
In the third equation, we already have the finished result:
Let's look at the second equation: . The meaning of "z" is already known, thus:
And finally, the first equation: . "Y" and "Z" are known, the matter is small:
Answer: 
As has been repeatedly noted, for any system of equations, it is possible and necessary to check the found solution, fortunately, this is not difficult and fast.
Example 2
This is an example for self-solving, a sample of finishing and an answer at the end of the lesson.
It should be noted that your course of action may not coincide with my course of action, and this is a feature of the Gauss method. But the answers must be the same!
Example 3
Solve a system of linear equations using the Gauss method 
We write the extended matrix of the system and, using elementary transformations, bring it to a step form:
We look at the upper left "step". There we should have a unit. The problem is that there are no ones in the first column at all, so nothing can be solved by rearranging the rows. In such cases, the unit must be organized using an elementary transformation. This can usually be done in several ways. I did this:
(1) To the first line we add the second line, multiplied by -1. That is, we mentally multiplied the second line by -1 and performed the addition of the first and second lines, while the second line did not change.
Now at the top left "minus one", which suits us perfectly. Who wants to get +1 can perform an additional gesture: multiply the first line by -1 (change its sign).
(2) The first row multiplied by 5 was added to the second row. The first row multiplied by 3 was added to the third row.
(3) The first line was multiplied by -1, in principle, this is for beauty. The sign of the third line was also changed and moved to the second place, thus, on the second “step, we had the desired unit.
(4) The second line multiplied by 2 was added to the third line.
(5) The third row was divided by 3.
A bad sign that indicates a calculation error (less often a typo) is a “bad” bottom line. That is, if we got something like below, and, accordingly, 
, then with a high degree of probability it can be argued that an error was made in the course of elementary transformations.
We charge the reverse move, in the design of examples, the system itself is often not rewritten, and the equations are “taken directly from the given matrix”. The reverse move, I remind you, works from the bottom up. Yes, here is a gift:
Answer: 
.
Example 4
Solve a system of linear equations using the Gauss method 
This is an example for an independent solution, it is somewhat more complicated. It's okay if someone gets confused. Full solution and design sample at the end of the lesson. Your solution may differ from mine.
In the last part, we consider some features of the Gauss algorithm.
The first feature is that sometimes some variables are missing in the equations of the system, for example: 
How to correctly write the augmented matrix of the system? I already talked about this moment in the lesson. Cramer's rule. Matrix method. In the expanded matrix of the system, we put zeros in place of the missing variables: 
By the way, this is a fairly easy example, since there is already one zero in the first column, and there are fewer elementary transformations to perform.
The second feature is this. In all the examples considered, we placed either –1 or +1 on the “steps”. Could there be other numbers? In some cases they can. Consider the system: 
.
Here on the upper left "step" we have a deuce. But we notice the fact that all the numbers in the first column are divisible by 2 without a remainder - and another two and six. And the deuce at the top left will suit us! At the first step, you need to perform the following transformations: add the first line multiplied by -1 to the second line; to the third line add the first line multiplied by -3. Thus, we will get the desired zeros in the first column.
Or another hypothetical example: 
. Here, the triple on the second “rung” also suits us, since 12 (the place where we need to get zero) is divisible by 3 without a remainder. It is necessary to carry out the following transformation: to the third line, add the second line, multiplied by -4, as a result of which the zero we need will be obtained.
The Gauss method is universal, but there is one peculiarity. You can confidently learn how to solve systems by other methods (Cramer's method, matrix method) literally from the first time - there is a very rigid algorithm. But in order to feel confident in the Gauss method, you should “fill your hand” and solve at least 5-10 systems. Therefore, at first there may be confusion, errors in calculations, and there is nothing unusual or tragic in this.
Rainy autumn weather outside the window .... Therefore, for everyone, a more complex example for an independent solution:
Example 5
Solve a system of four linear equations with four unknowns using the Gauss method. 
Such a task in practice is not so rare. I think that even a teapot who has studied this page in detail understands the algorithm for solving such a system intuitively. Basically the same - just more action.
The cases when the system has no solutions (inconsistent) or has infinitely many solutions are considered in the lesson. Incompatible systems and systems with a common solution. There you can fix the considered algorithm of the Gauss method.
Wish you success!
Solutions and answers:
Example 2: Solution: Let's write the augmented matrix of the system and with the help of elementary transformations we will bring it to a stepped form.
Performed elementary transformations:
(1) The first row was added to the second row, multiplied by -2. The first line was added to the third line, multiplied by -1. Attention! Here it may be tempting to subtract the first from the third line, I strongly do not recommend subtracting - the risk of error greatly increases. We just fold!
(2) The sign of the second line was changed (multiplied by -1). The second and third lines have been swapped. note that on the “steps” we are satisfied not only with one, but also with -1, which is even more convenient.
(3) To the third line, add the second line, multiplied by 5.
(4) The sign of the second line was changed (multiplied by -1). The third line was divided by 14.
Reverse move:
Answer: 
.
Example 4: Solution: Let's write the augmented matrix of the system and with the help of elementary transformations we bring it to the step form:
Conversions performed:
(1) The second line was added to the first line. Thus, the desired unit is organized on the upper left “step”.
(2) The first row multiplied by 7 was added to the second row. The first row multiplied by 6 was added to the third row.
With the second "step" everything is worse, the "candidates" for it are the numbers 17 and 23, and we need either one or -1. Transformations (3) and (4) will be aimed at obtaining the desired unit
(3) The second line was added to the third line, multiplied by -1.
(4) The third line, multiplied by -3, was added to the second line.
The necessary thing on the second step is received
.
(5) To the third line added the second, multiplied by 6.
Within the lessons Gauss method and Incompatible systems/systems with a common solution we considered inhomogeneous systems of linear equations, where free member(which is usually on the right) at least one of the equations was different from zero.
And now, after a good warm-up with matrix rank, we will continue to polish the technique elementary transformations on the homogeneous system of linear equations.
According to the first paragraphs, the material may seem boring and ordinary, but this impression is deceptive. In addition to further developing techniques, there will be a lot of new information, so please try not to neglect the examples in this article.
