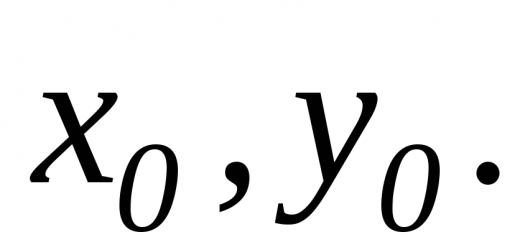1 von 22
Beschreibung der Präsentation anhand einzelner Folien:
Folie Nr. 1
Wissenschaftliches Handbuch zur Algebra Thema: „Logarithmische und Exponentialgleichungen und Ungleichheiten“ Vervollständigt von: Manuilova L.N. – Mathematiklehrerin, MBOU-Sekundarschule Nr. 76, Ischewsk, Udmurtien
Folie Nr. 2
Inhalt: Kapitel 1. 1.1. Das Konzept des Logarithmus 1.2. Eigenschaften des Logarithmus 1.3. Logarithmische Gleichungen A. Theoretischer Teil B. Beispiele 1.4. Logarithmische Ungleichungen A. Theoretischer Teil B. Beispiele Kapitel 2. 2.1. Die Potenz einer positiven Zahl beträgt 2,2. Exponentialfunktion 2.3. Exponentialgleichungen A. Theoretischer Teil B. Beispiele 2.4. Exponentielle Ungleichungen A. Theoretischer Teil B. Beispiele Kapitel 3. 3.1. Test zum Thema „Logarithmische Gleichungen und Ungleichungen“ I Komplexitätsgrad II Komplexitätsgrad III Komplexitätsgrad 3.2. Test zum Thema „Exponentialgleichungen und Ungleichungen“ I Komplexitätsgrad II Komplexitätsgrad III Komplexitätsgrad
Folie Nr. 3
1.1 Das Konzept des Logarithmus y x y = b b M 1 0 n y = ax (a > 1) x y = ax (0< a < 1) y= b M 1 0 b у Для любого положительного числа b существует, и притом только одно, число n, такое, что b = an . Это число называют логарифмом числа b по основанию a. n Логарифмом положительного числа b по основанию a (a >0, a ≠ 0) ist eine Zahl n mit b = an. Der Logarithmus einer positiven Zahl b zur Basis a (a > 0,a ≠ 1) wird wie folgt bezeichnet: n = loga b Aus der Definition von Logarithmus ist es offensichtlich Daraus folgt für a > 0 , a ≠ 1, b > 0: a loga b = b
Folie Nr. 4
Logarithmische Funktion y y x x 1 2 2 1 1 1 -1 -1 2 2 -2 -2 3 0 0 y = log2 x y = log3 x y = log⅓x y = log½x Die Funktion y = loga x wird logarithmische Funktion genannt. Eigenschaften der Funktion y = loga x, für a > 0: Stetig und ansteigend im Intervall (0;+∞); Wenn x→+∞, dann y→+∞; wenn x→0, dann y→ -∞. Da loga1=0, folgt aus Eigenschaft 1: wenn x > 1, dann y > 0; wenn 0< х < 1 ,то у < 0. Свойства функции y = loga x, при 0 < a < 1: Непрерывна и убывает на промежутке (0;+∞); Если х→ +∞, то у→ -∞; если х→0, то у→+∞. Так как loga1=0, то из свойства 1 следует: если х >1, dann y< 0; если 0 < х < 1 ,то у >0.
Folie Nr. 5
Seien a, M und N positive Zahlen mit a ≠ 1 und k ist eine reelle Zahl. Dann gelten die Gleichungen: 1. loga (M N) = loga M + loga N – Logarithmus des Produkts positiver Zahlen gleich der Summe Logarithmen dieser Zahlen. 2. loga M = loga M – loga N – Der Logarithmus des Quotienten positiver Zahlen N ist gleich der Differenz zwischen den Logarithmen des Dividenden und des Divisors. 3. loga Mk = k · loga M – Der Logarithmus der Potenz einer positiven Zahl ist gleich dem Produkt aus dem Exponenten und dem Logarithmus dieser Zahl. 4. loga M = logb M → loga b = 1 – Formel zum Umrechnen von Logarithmen von einer logb a logb a-Basis in eine andere. Einzelfälle: 1. log10 b = log b – Man nennt den Logarithmus einer positiven Zahl b zur Basis 10 dezimaler Logarithmus Zahlen b. 2. loge b = ln b – Der Logarithmus einer positiven Zahl b zur Basis e heißt natürlicher Logarithmus Zahlen b 1.2 Eigenschaften von Logarithmen
Folie Nr. 6
1. Sei a eine gegebene positive Zahl ungleich 1, b eine gegebene reelle Zahl. Dann heißt die Gleichung loga x = b die einfachste logarithmische Gleichung. Zum Beispiel Gleichungen a) log3 x = 3 ; (1) b) log⅓ x = -2 ; (2) c) log25 x + 5·log4 x·log3 x + 7·log22 x = 0 ; (3) sind die einfachsten logarithmischen Gleichungen. Wenn eine Zahl x0 nach der Definition eines Logarithmus die numerische Gleichheit loga x = b erfüllt, dann ist die Zahl x0 ab, und diese Zahl x0 = ab ist die einzige. Somit hat die Gleichung loga x = b für jede reelle Zahl b eine eindeutige Wurzel x0 = ab. 2. Gleichungen, die sich nach dem Ersetzen der Unbekannten in die einfachsten logarithmischen Gleichungen verwandeln: a) log5 (4x – 3) = 2; (4) b) 2 + 1 = -1 ; (5) log(3x + 1) + log0,01 log(3x + 1) 1.3 Gleichungen (Theoretischer Teil)
Folie Nr. 7
1.3 Beispiele log3 x = 3 Schreiben wir die Gleichung in der Form um: log3 x = log3 27 Dann ist es offensichtlich, dass diese Gleichung eine einzige Wurzel x0 = 27 hat. Antwort: 27. b) log1/3 x = -2 Diese Gleichung hat eine einzelne Wurzel x0 = ( ⅓)-2 =9 Antwort: 9. c) log25 x + 5 · log4 x · log3 x + 7 · log22 x = 0 (1) Indem wir alle Logarithmen auf die gleiche Basis reduzieren, schreiben wir die um Gleichung als: 1 + 5 + 7 = 0 (2) log25 x · log5 4 · log5 3 log25 2 Da jeder Term der in Klammern eingeschlossenen Summe positiv ist, ist die Summe nicht gleich Null. Daher sind Gleichung (1) und damit Gleichung (2) äquivalent zur Gleichung log25 x = 0, die eine einzige Wurzel x0 = 1 hat. Daher hat Gleichung (1) eine einzige Wurzel x0 = 1. Antwort: 1 . a, b – die einfachsten Gleichungen; c ist eine Gleichung, die sich nach Transformationen in den einfachsten Logarithmus verwandelt. Die gleichung
Folie Nr. 8
1.3 Beispiele a) log5 (4x – 3) = 2 (1) Indem wir das neue bekannte t = 4x – 3 einführen, schreiben wir die Gleichung in der Form um: log5 t = 2. Diese Gleichung hat eine einzige Wurzel t1 = 52 =25. Um die Wurzel der Gleichung (1) zu finden, müssen Sie die Gleichung lösen: 4x – 3 = 25. (2) Sie hat eine einzige Wurzel x1 =7. Daher hat Gleichung (1) auch eine einzige Wurzel x1=7. Antwort: 7. b) 2 + 1 = -1 (1) log(3x + 1) + log0,01 log(3x + 1) Einführung einer neuen Unbekannten t = log (3x + 1) und Berücksichtigung von log 0,01 = -2, schreiben wir Gleichung (1) in der Form um: 2 + 1 = -1 (2) t - 2 t Nachdem wir die rationale Gleichung (2) gelöst haben, stellen wir fest, dass sie zwei Wurzeln t1 = -2 und t2 = hat 1. Um alle Wurzeln der Gleichung (1) zu finden, müssen die Wurzeln der beiden Gleichungen log(3x + 1) = -2 und log(3x + 1) = 1 kombiniert werden. Die erste Gleichung ist äquivalent zur Gleichung 3x + 1 = 10-2, was eine einzelne Wurzel x1 = -0,33 hat. Die zweite Gleichung entspricht der Gleichung 3x + 1 = 10, die ebenfalls eine einzige Wurzel x2 = 3 hat. Antwort: -0,33 ; 3. a, b – Gleichungen, die durch Ersetzen des Unbekannten auf das Einfachste reduziert werden
Folie Nr. 9
1.4 Ungleichungen (Theoretischer Teil) Sei a eine gegebene positive Zahl ungleich 1, b eine gegebene reelle Zahl. Dann sind die Ungleichungen: logà x > b (1) logà x< b (2) являются простейшими logarithmische Ungleichungen. Die Ungleichungen (1) und (2) können wie folgt umgeschrieben werden: loga x > loga x0 (3) loga x< loga x0 (4) , где x0 = ab . Если a >1, dann wächst die Funktion y = loga x über ihren gesamten Definitionsbereich, d.h. auf dem Intervall (0;+∞). Daher ist es für jede Zahl x > x0 wahr numerische Ungleichheit loga x > loga x0 und für jede Zahl x aus dem Intervall 0< x < x0 справедливо числовое неравенство logа x < logа x0 . Кроме того, равенство logа x = logа x0 справедливо лишь при х = х0 . Таким образом, при а >1 und einer beliebigen reellen Zahl b ist die Menge aller Lösungen der Ungleichung (3) das Intervall (x0 ;+ ∞) und die Menge aller Lösungen der Ungleichung (4) ist das Intervall (0; x0). Wenn 0< a < 1, то функция y = loga х убывает. Поэтому для любого числа x >x0 die numerische Ungleichung loga x ist wahr< loga x0 , а для любого числа х из промежутка 0 < x < x0 справедливо числовое неравенство loga x >loga x0 . Außerdem gilt die Gleichung loga x = loga x0 nur für x = x0. Also bei 0< a < 1 и любом действительном числе b множество всех решений неравенства (3) есть интервал (0; х0) , а множество всех решений неравенства (4) есть интервал (х0 ;+∞).
Folie Nr. 10
1.4 Ungleichungen (Theoretischer Teil) On Koordinatenebene xOy Betrachten Sie die Graphen der Funktion y = loga x und y = b. Die Gerade y = b schneidet den Graphen der Funktion y = loga x in einem einzigen Punkt x0 = ab. Wenn a > 1, dann liegt für jedes x > x0 der entsprechende Punkt im Graphen der Funktion y = loga x über der Geraden y = b, d.h. für jedes x > x0 ist die entsprechende Ordinate y = ax größer als die Ordinate ax0, und für jedes x aus dem Intervall 0< x < x0 соответствующая точка графика функции y = loga x находится ниже прямой y = b. Если же 0 < a <1, то, наоборот, для каждого x >x0 der entsprechende Punkt im Graphen der Funktion y = loga x liegt unterhalb der Geraden y = b, und für jedes x der Intervalle 0< x < x0 соответствующая точка графика функции y = loga x находится выше прямой y = b. у у х х 1 1 1 1 х0 0 0 y = b y = loga x (a >1) y = b y = loga x (0< a < 1) х0
Folie Nr. 11
1.4 Beispiele Lösen wir die Ungleichung log1/3 x > -2. (1) Da -2 = log⅓ 9, dann kann Ungleichung (1) umgeschrieben werden als log ⅓x > log ⅓ 9 (2) Da ⅓< 1, то функция y = log⅓ x убывающая. Поэтому множество всех решений неравенства (2), а значит и неравенства (1), есть интервал 0 < x <9. Ответ: (0;9). 2. Решим неравенство log4 x >½. (3) Da ½ = log4 2, dann kann Ungleichung (3) umgeschrieben werden als log4 x > log4 2 (4) Da 4 > 1, dann nimmt die Funktion y = log4 x zu. Daher ist die Menge aller Lösungen der Ungleichung (4) und damit der Ungleichung (3) das Intervall (2;+∞). Antwort: (2;+∞). (siehe Abb. 1) x y 1 2 3 4 1 -1 0 Abb. 1 y = ½ y = log4 x
Folie Nr. 12
1.4 Beispiele Lösen wir die Ungleichung log3 x – 3log9 x – log81 x > 1,5. (5) Da log9 x = (log3 x) / (log3 9) = (log3 x) / 2 = ½ (log3 x), log81 x = (log3 x) / (log3 81) = (log3 x) / 4 = ¼ (log3 x), dann kann Ungleichung (5) umgeschrieben werden als: (1 – 1,5 – ¼) log3 x > 1,5 oder als log3 x< log3 1/9. (6) Так как 3 >1, dann nimmt die Funktion y = log3 x zu. Daher ist die Menge aller Lösungen der Ungleichung (6) und damit der Ungleichung (5) das Intervall 0< x < 1/9 (рис.2) Ответ: (0 ; 1/9). y x 1 2 0 -1 y = log3 x y = -2 (рис.2) 1/9
Folie Nr. 13
2.1 Potenz einer positiven Zahl Potenz von c rationaler Indikator Sei a eine positive Zahl und p/q Rationale Zahl(q ≥ 2). Per Definition ist die Zahl a hoch p/q die arithmetische Wurzel der Potenz q von a hoch p, d. h. a p/q = q√ap . SATZ. Sei a eine positive Zahl, p eine ganze Zahl, k und q ganze Zahlen, q ≥ 2, k ≥ 2. Dann gelten folgende Gleichungen: a) ap/q = (a1/p)p ; b) ap/q = a pk /qk ; c) ap = a pq /q ; Eigenschaften eines Grades mit einem rationalen Exponenten THEOREM 1. Eine positive Zahl a zu einem Grad mit einem beliebigen rationalen Exponenten r ist positiv: ar > 0 THEOREM 2. Sei a eine positive Zahl und r1, r2 und r sind rationale Zahlen. Dann gelten die folgenden Eigenschaften: 1. Bei der Multiplikation von Potenzen mit rationalen Exponenten derselben positiven Zahl addieren die Exponenten: ar1 ∙ ar2 = ar1 + r2. 2. Bei der Division von Potenzen mit rationalen Exponenten derselben positiven Zahl werden die Exponenten subtrahiert: ar1: ar2 = ar1 – r2. 3. Beim Erhöhen einer Potenz mit einem rationalen Exponenten einer positiven Zahl in rationaler Grad Exponenten werden multipliziert: (a r1) r2 = a r1∙ r2. SATZ 3. Seien a und b positive Zahlen und r eine rationale Zahl. Dann gelten folgende Eigenschaften eines Grades mit rationalem Exponenten: Ein Grad mit rationalem Exponenten des Produkts positiver Zahlen ist gleich dem Produkt gleicher Potenzen der Faktoren: (ab)r = ar ∙ br . Die Potenz mit rationalem Exponenten des Quotienten positiver Zahlen ist gleich dem Quotienten gleicher Potenzen von Dividend und Divisor: (a / b)r = ar / br. THEOREM 4. Sei die Zahl a > 1 und r eine rationale Zahl. Dann ist ar > 1 für r > 0 0< ar < 1 при r < 0 ТЕОРЕМА 5. Пусть число a >1 und die rationalen Zahlen r1 und r2 erfüllen die Ungleichung r1< r2 . Тогда a r1 < a r2 . ТЕОРЕМА 6. Пусть число a принадлежит интервалу (0;1), а рациональные числа r1 и r2 удовлетворяют неравенству r1< r2 . Тогда a r1 < a r2 .
Folie Nr. 14
2.2 Exponentialfunktion Betrachten Sie die Funktion y = a (1) mit a > 0 und a ≠ 0 auf der Menge der rationalen Zahlen. Für jede rationale Zahl r ist eine Zahl ar definiert. So ist Funktion (1) zunächst auf der Menge der rationalen Zahlen definiert. Der Graph dieser Funktion im Koordinatensystem x0y ist eine Sammlung von Punkten (x; ax), wobei x eine beliebige rationale Zahl ist. Für a > 1 ist dieser Graph schematisch in Abbildung (1) dargestellt, für 0< a < 1 – на рисунке (2). у у x x 1 2 1 2 3 -2 -1 -2 -1 0 1 1 2 2 Рис. 1 Рис. 2 Её называют Exponentialfunktion mit Sockel a.
Folie Nr. 15
2.3 Exponentialgleichungen (Theoretischer Teil) 1. Sei a eine gegebene positive Zahl ungleich 1, b eine gegebene reelle Zahl. Dann heißt die Gleichung ax = b (1) die einfachste Exponentialgleichung. Beispielsweise sind die Gleichungen 2x = 8, (1/3)x = 9, 25x = -25 die einfachsten Exponentialgleichungen. Die Wurzel (oder Lösung) einer Gleichung mit einem unbekannten x ist die Zahl x0. Wenn man sie anstelle von x in die Gleichung einsetzt, erhält man die korrekte numerische Gleichheit. Eine Gleichung zu lösen bedeutet, alle ihre Wurzeln zu finden oder zu zeigen, dass es keine gibt. Da ax0 > 0 für jede reelle Zahl x0 gilt, für die die numerische Gleichheit ax0 = b wahr wäre, erfüllt Singular x0 = loga b. Somit gilt Gleichung (1): Für b ≤ 0 hat keine Wurzeln; Für b > 0 hat es eine einzige Wurzel x0 = loga b. 2. Gleichungen, die nach dem Ersetzen der Unbekannten zu den einfachsten Exponentialgleichungen werden.
Folie Nr. 16
2.3 Beispiele Lösen wir die Gleichung (1/2)x = 2 (2) Da 2 > 1, hat diese Gleichung eine einzige Wurzel x0 = log½ 2 = -1. Antwort 1. Lösen wir die Gleichung 3x = 5 (3) Da 5 > 0, hat diese Gleichung eine einzige Wurzel x0 = log3 5. Antwort: log3 5. Lösen Sie die Gleichung 25x = -25 Da -25< 0, то это уравнение не имеет корней. Ответ: нет корней. Для отыскания корня уравнения ax = b (1) при b >0 wird diese Gleichung oft als ax = aα geschrieben, wobei α = loga b. Dann ist es offensichtlich, dass die einzige Wurzel dieser Gleichung und damit der Gleichung (1) die Zahl α ist. Da Gleichung (2) in der Form (1/2)x = (1/2)-1 geschrieben werden kann, ist ihre einzige Wurzel x0 = -1. Da Gleichung (3) als 3x = 3log 35 geschrieben werden kann, ist ihre einzige Wurzel x0 = log3 5.
Folie Nr. 17
2.3 Beispiele Schauen wir uns nun Gleichungen an, die sich nach einfachen Transformationen in einfache Exponentialgleichungen verwandeln. Lösen wir die Gleichung 5x+2 - 2 5x - 3 5x+1 = 200 (4) Da 5x+2 = 25 5x, 5x+1 = 5 5x, kann Gleichung (4) als 5x ( 25 - 2 – 15) = 200 oder in der Form 5x = 52 (5) Es ist offensichtlich, dass Gleichung (5) und damit Gleichung (4) eine einzige Wurzel x0 = 2 haben. Antwort: 2. Lösen Sie die Gleichung 4 3x - 9 2x = 0 (6) Da 2x ≠ 0 für jede reelle Zahl ist, erhalten wir durch Division von Gleichung (6) durch 2x die Gleichung 4 (3/2)x - 9 = 0, (7), die Gleichung (6) entspricht. Gleichung (7) kann als (3/2)x = (3/2)2 umgeschrieben werden. (8) Da Gleichung (8) eine einzige Wurzel x0 = 2 hat, hat die äquivalente Gleichung (6) eine einzige Wurzel x0 = 2. Antwort: 2.
Folie Nr. 18
2.3 Beispiele Lösen wir die Gleichung 9 2x2-4x + 2 - 2 · 34x2 – 8x + 3 -1 = 0. (9) Nachdem wir Gleichung (9) in der Form 34x2 – 8x + 3 = 1 umgeschrieben haben, führen wir eine neue Unbekannte t = 4x2 – 8x + 3 ein. Dann kann Gleichung (9) in der Form 3t = 1 umgeschrieben werden. (10 ) Da Gleichung (10) eine einzige Wurzel t1 = 0 hat, ist es zum Finden der Wurzeln von Gleichung (9) notwendig, die Gleichung 4x2 – 8x + 3 = 0 zu lösen. Diese Gleichung hat zwei Wurzeln x1 = 1 /2, x2 = 3/2, also hat die Gleichung (9) die gleichen Wurzeln. Antwort: 1/2 ; 3/2. Betrachten Sie nun die Lösung von Gleichungen, die sich nach Einführung einer neuen Unbekannten t in quadratische oder rationale Gleichungen mit Unbekanntem t verwandeln. Lösen wir die Gleichung 4x - 3 2x + 2 = 0. (11) Da 4x = (2x)2 ist, kann Gleichung (11) als (2x)2 - 3 2x + 2 = 0 umgeschrieben werden. Durch Einführung einer neuen Unbekannten t = 2x, erhalten wir eine quadratische Gleichung t2 - 3t + 2 = 0, die zwei Wurzeln t1 = 1, t2 = 2 hat. Um alle Wurzeln von Gleichung (11) zu finden, müssen wir daher alle Wurzeln von kombinieren die beiden Gleichungen 2x = 1 und 2x = 2 Nachdem wir diese einfachsten Exponentialgleichungen gelöst haben, stellen wir fest, dass alle Wurzeln der Gleichung (11) x1 = 0 sind; x2 = 1. Antwort: 0; 1 .
Folie Nr. 19
2.4 Exponentielle Ungleichungen (Theoretischer Teil) Sei a eine gegebene positive Zahl ungleich 1, b eine gegebene reelle Zahl. Dann sind die Ungleichungen ax > b (1) und ax< b (2) называют простейшими показательными неравенствами. Например, неравенства: 2x < 3 , (1/3)x >4√3, 25x< -25 являются простейшими показательными неравенствами. Решением неравенства с неизвестным х называют число х0 , при подстановке которого в неравенство вместо х получается верное числовое неравенство. Решить неравенство - значит найти все его решения или показать, что их нет. Поскольку a x0 >0 für jede reelle Zahl x0, dann gilt für b ≤ 0 die Ungleichung a x0 > b für jede reelle Zahl x0, aber es gibt keine einzige reelle Zahl x0, für die die numerische Ungleichung a x0 wahr wäre< b . Таким образом, если b ≤ 0 , то множество всех решений неравенства (1) есть интервал (-∞;+∞), а неравенство (2) решений не имеет. Если же b >0, dann können die Ungleichungen (1) und (2) als ax > ax0 (1) und ax umgeschrieben werden< ax0 , (2) , где х0 = loga b. Рассмотрим решение неравенств (3) и (4) сначала при а >1. Da für eine solche die Funktion y = ax zunimmt, gilt für jede Zahl x > > ax0 und für jede Zahl x > x0 die numerische Ungleichung ax< ax0 . Кроме того, равенство ax = ax0 справедливо лишь при х = x0 .
Folie Nr. 20
2.4 Exponentielle Ungleichungen (Theoretischer Teil) Somit ist für b > 0 und a > 1 die Menge aller Lösungen der Ungleichung (3) das Intervall (x0 ;+∞) und die Menge aller Lösungen der Ungleichung (4). das Intervall (-∞; x0) , wobei x0 = loga b. Sei nun 0< a < 1. Так как для такого а функция y = aх является убывающей, то для любого числа х >x0 die numerische Ungleichheit ax ist wahr< ax0 . Кроме того, равенство ax = ax0 справедливо лишь при х = x0 . Таким образом, при b >0 und 0< a < 1 множество всех решений неравенства (3) есть интервал (-∞; x0), а множество всех решений неравенства (4) есть интервал (x0 ;+∞), где x0 = loga b. Приведенное выше решение простейших показательных неравенств можно дополнить графической иллюстрацией. Рассмотрим графики функций y = aх и y = b. Ясно, что при b ≤ 0 прямая y = b не пересекает график функции y = aх, так как расположена под кривой y = aх (а, б). Поэтому для любых х выполняется неравенство ax >b und es gibt kein x, für das die Ungleichung ax gilt< b . При b >0 Gerade y = b schneidet den Graphen der Funktion y = aх in einem einzigen Punkt x0 = loga b. 1 y y x x y = 0 y = 0 y = ax (a > 1) 0 1 y = b (b< 0) y = b (b < 0) 1 0 1 y = ax (0 < a < 1) a) б)
Folie Nr. 22
2.4 Beispiele Lösen Sie die Ungleichung 2x< 8 . (1) Так как 8 >0, dann kann Ungleichung (1) als 2x umgeschrieben werden< 23. (2) Так как 2 >1, dann steigt die Funktion y = 2x. Daher sind alle Lösungen der Ungleichung (2) und damit der Ungleichung (1) x< 3. Ответ: (-∞; 3). Решим неравенство (1/3)х < 5 . (3) Так как 5 >0, dann kann diese Ungleichung (3) als (1/3) x umgeschrieben werden< (1/3) log⅓ 5 . (4) Так как 0 < 1/3 < 1, то функция y = (1/3)x убывающая. Поэтому решениями неравенства (4), а значит и неравенства (3), являются все х >log⅓5. Antwort: (log⅓ 5; +∞). Betrachten wir eine Ungleichung, die nach dem Ersetzen des Unbekannten zur einfachsten wird exponentielle Ungleichheit. Lösen wir die Ungleichung 5 3x2 - 2x – 6< 1/5 . (5) Введя новое неизвестное t = 3x2 - 2x – 6, перепишем неравенство (5) в виде 5t < 5-1 . Так как 5 >1, dann sind alle Lösungen dieser Ungleichung alle t< -1. следовательно, все решения неравенства (5) есть решения неравенства 3x2 - 2x – 6 < -1. (6) Решив quadratische Ungleichung(6) finden wir alle seine Lösungen: -1< x < 5/3 . Они являются решениями неравенства (5). Ответ: (-1 ; 5/3).
Logarithmische Gleichungen, ihre Arten und Lösungsmethoden Konzentration der Aufmerksamkeit: Konzentration der Aufmerksamkeit ist gleich N. N = (Anzahl der richtigen Antworten) x 0,125 x 100 %. Schreib es auf besonderer Fall Formeln für den Übergang zum Logarithmus einer anderen Basis Schreiben Sie die Formel für den Übergang zum Logarithmus einer anderen Basis. Was ist der Logarithmus einer Potenz einer Zahl und einer Basis gleich? Was ist der Logarithmus der Basis? Was ist der Logarithmus einer Potenz einer Zahl? Was ist der Logarithmus des Quotienten? Wie groß ist der Logarithmus des Produkts? Formulieren Sie die Definition des Logarithmus. Beantworten Sie die Frage
Lassen Sie uns überlegen gegenseitige Übereinkunft Graph der Funktion y = log a x (a > 0, a ≠ 1) und der Geraden y = b. y = log a x (a>1) y x 0 y = log a x (0
Logarithmische Gleichungen, ihre Typen und Methoden zur Lösung. SCHLUSSFOLGERUNG: Der Graph der Funktion y = log a x (a > 0, a ≠ 1) und die Gerade y = b schneiden sich in einem einzigen Punkt, d. h. Die Gleichung log a x = b, a > 0, a ≠ 1, x > 0 hat eine eindeutige Lösung x 0 = a b.
DEFINITION: Die Gleichung log a x = b, a > 0, a ≠ 1, x > 0 heißt die einfachste logarithmische Gleichung. Logarithmische Gleichungen, ihre Arten und Lösungsmethoden Beispiel:
Arten und Methoden zur Lösung logarithmischer Gleichungen. DEFINITION: Logarithmische Gleichungen sind solche, die eine Unbekannte unter dem Logarithmuszeichen oder an der Basis des Logarithmus (oder beiden) enthalten. Logarithmische Gleichungen, ihre Arten und Lösungsmethoden
Arten und Methoden zur Lösung logarithmischer Gleichungen. NACHTRAG: Bei der Lösung logarithmischer Gleichungen ist Folgendes zu berücksichtigen: Fläche akzeptable Werte Logarithmus: Unter dem Logarithmuszeichen können nur positive Größen stehen; an der Basis von Logarithmen gibt es nur positive Größen, die von Eins verschieden sind; Eigenschaften von Logarithmen; Potenzierungswirkung. Logarithmische Gleichungen, ihre Arten und Lösungsmethoden
Logarithmische Gleichungen, ihre Typen und Methoden zur Lösung Typen und Methoden zur Lösung logarithmischer Gleichungen. 1) Die einfachsten logarithmischen Gleichungen. Beispiel Nr. 1 Antwort: Lösung:
Logarithmische Gleichungen, ihre Typen und Methoden zur Lösung Typen und Methoden zur Lösung logarithmischer Gleichungen. 2) Logarithmische Gleichungen, reduziert auf die einfachsten logarithmischen Gleichungen. Beispiel Nr. 1 Antwort: Lösung:
Logarithmische Gleichungen, ihre Typen und Methoden zur Lösung Typen und Methoden zur Lösung logarithmischer Gleichungen. 2) Logarithmische Gleichungen, reduziert auf die einfachsten logarithmischen Gleichungen. Beispiel Nr. 2 Antwort: Lösung:
Logarithmische Gleichungen, ihre Typen und Methoden zur Lösung Typen und Methoden zur Lösung logarithmischer Gleichungen. 2) Logarithmische Gleichungen, reduziert auf die einfachsten logarithmischen Gleichungen. Beispiel Nr. 3 Antwort: Lösung:
Logarithmische Gleichungen, ihre Typen und Methoden zur Lösung Typen und Methoden zur Lösung logarithmischer Gleichungen. 2) Logarithmische Gleichungen, reduziert auf die einfachsten logarithmischen Gleichungen. Beispiel Nr. 4 Antwort: Lösung:
Logarithmische Gleichungen, ihre Typen und Methoden zur Lösung Typen und Methoden zur Lösung logarithmischer Gleichungen. 3) Logarithmische Gleichungen, reduziert auf quadratische Gleichungen. Beispiel Nr. 1 Antwort: Lösung:
Logarithmische Gleichungen, ihre Typen und Methoden zur Lösung Typen und Methoden zur Lösung logarithmischer Gleichungen. 3) Logarithmische Gleichungen reduzieren sich auf quadratische Gleichungen. Beispiel Nr. 2 Antwort: Lösung: Im gefundenen Bereich zulässiger Werte der Variablen x transformieren wir die Gleichung mit den Eigenschaften von Logarithmen. Unter Berücksichtigung des Bereichs akzeptabler Werte erhalten wir: 10; 100
Logarithmische Gleichungen, ihre Typen und Methoden zur Lösung Typen und Methoden zur Lösung logarithmischer Gleichungen. 4) Logarithmische Gleichungen, reduziert auf rationale Gleichungen. Beispiel Nr. 1 Antwort: Lösung: Kehren wir zur Variablen x zurück
Logarithmische Gleichungen, ihre Typen und Methoden zur Lösung Typen und Methoden zur Lösung logarithmischer Gleichungen. 4) Logarithmische Gleichungen, Reduzierung auf rationale Gleichungen. Beispiel Nr. 2 Antwort: Lösung: Im gefundenen Bereich zulässiger Werte der Variablen x transformieren wir gegebene Gleichung und wir erhalten: Kehren wir zur Variablen x zurück:
Logarithmische Gleichungen, ihre Typen und Methoden zur Lösung Typen und Methoden zur Lösung logarithmischer Gleichungen. 5) Logarithmische Gleichungen mit einer Variablen in der Basis und unter dem Logarithmuszeichen. Beispiel Nr. 1 Antwort: Lösung: Im gefundenen Bereich zulässiger Werte der Variablen x transformieren wir die Gleichung und erhalten: Unter Berücksichtigung des Bereichs zulässiger Werte der Variablen x erhalten wir:
Logarithmische Gleichungen, ihre Typen und Methoden zur Lösung Typen und Methoden zur Lösung logarithmischer Gleichungen. 5) Logarithmische Gleichungen mit einer Variablen in der Basis und unter dem Logarithmuszeichen. Beispiel Nr. 2 Antwort: Lösung: Im gefundenen Bereich zulässiger Werte der Variablen x entspricht die Gleichung der Menge: Unter Berücksichtigung des Bereichs zulässiger Werte der Variablen x erhalten wir: 5; 6.
Logarithmische Gleichungen, ihre Arten und Lösungsmethoden
- Gewährleistung der Wiederholung, Verallgemeinerung und Systematisierung des Materials zum Thema;
- Bedingungen für die Kontrolle und Selbstkontrolle der erworbenen Kenntnisse und Fähigkeiten schaffen;
- Förderung der Bildung von Fähigkeiten zur Anwendung von Techniken: Vergleich, Verallgemeinerung, Hervorhebung des Wesentlichen, Übertragung von Wissen auf eine neue Situation, Entwicklung einer mathematischen Sichtweise;
- Bedingungen für die Entwicklung des kognitiven Interesses der Schüler schaffen;
- die Verantwortung für die Qualität und das Ergebnis der im Unterricht geleisteten Arbeit, die mathematische Tätigkeit, die Fähigkeit zur Gruppenarbeit und die allgemeine Kultur zu kultivieren.
- Überprüfen Sie das theoretische Material. Achten Sie besonders auf die ODZ der logarithmischen Funktion.
- Systematisieren Sie Methoden zur Lösung logarithmischer Gleichungen.
- Wissensdiagnostik durchführen.
Unterrichtsart: Unterricht zur Verallgemeinerung und Systematisierung von Wissen.
Unterrichtsformat: Workshop
Ausstattung: Lehrbuch, Unterrichtsmaterialien, einzelne Karten für selbständiges Arbeiten, Wissensaufzeichnungsbögen, Medienprojektor.
Während des Unterrichts
1. Organisatorischer Moment
Die Studierenden werden über das Unterrichtsthema und die Ziele informiert und die Relevanz der Wiederholung dieses Themas zur Vorbereitung auf das Einheitliche Staatsexamen hervorgehoben.
2. Hausaufgaben überprüfen
3. Vorkenntnisse aktualisieren
Die Studierenden erarbeiten mündlich Übungen, die auf der Leinwand mithilfe eines Projektors präsentiert werden.
Berechnung
1 Option 2)
Option 2 2)
3)
5)
4. Bildung von Fähigkeiten und Fertigkeiten.
Arbeiten Sie in Gruppen, gefolgt von Tests.
1) Lösen logarithmischer Gleichungen durch Definition des Logarithmus.
Antwort:Antwort: 256
2) Durch Potenzierung gelöste Gleichungen.
Zuerst müssen Sie die Gleichung des Systems lösen und basierend auf der Ungleichung des Systems werden die Wurzeln ausgewählt.
Antwort: 3
Antwort: 3,5Durch Substitution gelöste Gleichungen.
Antwort:
Diese Gleichung ist äquivalent zur Gleichung
Dann lass es sein
Antwort:
Durch Logarithmus gelöste Gleichungen.
=Also Antwort: 0,1; 10..
.
ODZ: x. Nehmen wir den Logarithmus beider Seiten zur Basis 10.
Wo
Antwort 1; 4.
Gleichungen der Form
Diese Gleichung entspricht der Gleichung für
.
DZ wird vom System bestimmt
DZ wird vom System bestimmt
Antwort: ( (0;)

Gleichungen werden mithilfe verschiedener Eigenschaften von Logarithmen gelöst.
Wenn wir die Formel anwenden, erhalten wir
Wenn wir diese x-Werte in die ursprüngliche Gleichung einsetzen, sehen wir, dass dies die Wurzel der Gleichung ist und 0,1 nicht die Wurzel der Gleichung ist.
Antwort:
Die Gleichungen, die den Schülern Schwierigkeiten bereiteten, werden von den Schülern, die sie gelöst haben, an der Tafel gelöst.
5. Minute des Sportunterrichts
Sie verschränkten ihre Hände zu einem „Schloss“, streckten sie vor sich aus, hoben sie hoch und streckten sich gut. Ärzte sagen, dass in diesem Moment das „Enzym des Glücks“ freigesetzt wird.
6. Selbstständiges Arbeiten
(Schieben Sie den Bildschirm und die Karten für jeden Schüler auf.) Die Schüler werden gebeten, ihre Fähigkeiten zu bewerten und die Aufgabenstufe A, B oder C zu wählen.
Nach Abschluss der Arbeit reichen die Studierenden diese zur Prüfung ein. Die Antworten und eine kurze Lösung werden auf dem Bildschirm angezeigt. Die Studierenden werden ermutigt, ihre Arbeit zu überprüfen und zu bewerten, indem sie eine Note für die selbstständige Arbeit vergeben.
6. Hausaufgaben
Wiederholen Sie P.6.2, 6.3. DM. C – 21 Nr. 2 (b, c), Nr. 3 (d, e) Optionen 3 und 4.
7. Zusammenfassung der Lektion
Heute haben wir also logarithmische Gleichungen gelöst. Fassen wir nun zusammen, welche Methoden wir zum Lösen von Gleichungen verwendet haben:
- unter Verwendung der Definition des Logarithmus,
- unter Verwendung der grundlegenden logarithmischen Identität,
- mit der Potenzierungsmethode,
- Einführung einer neuen Variable,
- Übergang von einer Gleichung mit unterschiedlichen Basen zu einer Gleichung,
- unter Verwendung der Eigenschaften des Logarithmus.
Vergabe von Noten anhand der Anzahl „+“ im Heft, für die Lösung auf der Tafel und auf den Karten. Ermittlung der Schülerleistung.
Unsere Lektion ist zu Ende. Haben wir unsere Ziele erreicht?
Die Zeit vergeht wie im Flug, heute sind Sie Zehntklässler und morgen schon Absolventen. Denken Sie bei der Prüfungsvorbereitung niemals daran, dass Sie die Aufgabe nicht bewältigen werden, sondern malen Sie sich im Gegenteil gedanklich ein Erfolgsbild aus, dann werden Sie auf jeden Fall Erfolg haben!
Literatur:
- Nikolsky S.M., Potapov M.K., Reshetnikov N.N., Shevkin A.V.. Algebra und Beginn der mathematischen Analyse. 10. Klasse. Anleitung für Bildungsinstitutionen: Grund- und Profilebene. – M., 2009
- Potapov M.K., Shevkin A.V.. Algebra und Beginn der mathematischen Analyse. Didaktische Materialien für die 10. Klasse. – M., 2009.
- Shepeleva Yu.V.. Algebra und Beginn der mathematischen Analyse. Thematische und Abschlusstests für die 10. Klasse. – M., 2009.
- Lysenko F.F.. Einheitliches Staatsexamen Mathematik-2009. Legion. – M., 2009.
- Klovo A.G.. Einheitliches Staatsexamen Mathematik-2010 - M., 2010.
- Erina T.M. Algebra. Logarithmische Gleichungen und Ungleichungen – M, 2004.
Verwenden Sie beim Lösen logarithmischer Gleichungen und Ungleichungen die Eigenschaften von Logarithmen sowie die Eigenschaften der logarithmischen Funktion
y=log a x, a > 0, a 1:
1) Definitionsbereich: x > 0;
2) Bereich: y R ;
3) log a x 1 =log a x 2 x 1 =x 2 ;
4) Für a>1 erhöht sich die Funktion y=log a x, für 0< a < 1 функция y=log a x убывает при всех x >0, d.h.
a >1 und log a x 1 >log a x 2 x 1 >x 2 ,
0 log a x 2 x 1< x 2 ;
Beim Übergang von logarithmischen Gleichungen (Ungleichungen) zu Gleichungen (Ungleichungen), die kein Logarithmuszeichen enthalten, sollte man den Bereich zulässiger Werte (APV) der ursprünglichen Gleichung (Ungleichung) berücksichtigen.
Aufgaben und Tests zum Thema „Logarithmische Gleichungen“
- Logarithmische Gleichungen
Lektionen: 4 Aufgaben: 25 Tests: 1
- Systeme exponentieller und logarithmischer Gleichungen - Demonstrativ und logarithmische Funktionen Klasse 11
Lektionen: 1 Aufgaben: 15 Tests: 1
- §5.1. Logarithmische Gleichungen lösen
Lektionen: 1 Aufgaben: 38
- §7 Exponentielle und logarithmische Gleichungen und Ungleichungen - Abschnitt 5. Exponentielle und logarithmische Funktionen, Klasse 10
Lektionen: 1 Aufgaben: 17
- Äquivalenz von Gleichungen - Gleichungen und Ungleichungen 11. Klasse
Lektionen: 2 Aufgaben: 9 Tests: 1
Bei der Lösung logarithmischer Gleichungen ist es in vielen Fällen notwendig, die Eigenschaften des Logarithmus eines Produkts, eines Quotienten oder eines Grades zu nutzen. In Fällen, in denen in einer logarithmischen Gleichung Logarithmen mit unterschiedlichen Basen vorhanden sind, wird die Verwendung verwendet angegebenen Eigenschaften erst nach dem Übergang zu Logarithmen mit gleichen Basen möglich.
Darüber hinaus sollte die Lösung der logarithmischen Gleichung mit der Ermittlung des Bereichs zulässiger Werte (O.D.Z.) beginnen. gegebene Gleichung, Weil Während des Lösungsprozesses können Fremdwurzeln auftreten. Vergessen Sie beim Ausfüllen der Lösung nicht, die gefundenen Wurzeln auf Zugehörigkeit zu O.D.Z. zu überprüfen.
Sie können logarithmische Gleichungen lösen, ohne O.D.Z. zu verwenden. In diesem Fall ist die Verifizierung ein zwingender Bestandteil der Lösung.
Beispiele.
Gleichungen lösen:
a) log 3 (5x – 1) = 2.
Lösung:
ODZ: 5x – 1 > 0; x > 1/5.
log 3 (5x– 1) = 2,
log 3 (5x – 1) = log 3 3 2,
5x - 1 =9,
x = 2.
1 Option
- 1. Finden Sie das Produkt der Wurzeln der Gleichung: log π (x 2 + 0,1) = 0
1) - 1,21; 2) - 0,9; 3) 0,81; 4) 1,21.
- 2. Geben Sie das Intervall an, zu dem die Wurzeln der Gleichung gehören: log 0,5 (x - 9) = 1 + log 0,5 5
1) (11; 13); 2) (9; 11); 3) (-12; -10); 4) [ -10; -9 ].
- 3. Geben Sie das Intervall an, zu dem die Wurzel der Gleichung log 4 (4 - x) + log 4 x = 1 gehört
1) (-3; -1); 2) (0; 2); 3) [ 2; 3 ]; 4) [ 4; 8 ].
- 4. Finden Sie die Summe der Wurzeln der Gleichung log √3 x 2 = log √3 (9x - 20)
1) - 13; 2) - 5; 3) 5; 4) 9.
- 5. Geben Sie das Intervall an, zu dem die Wurzel der Gleichung log 1/3 (2x - 3) 5 = 15 gehört
1) [ -3; 2); 2) [ 2; 5); 3) [ 5; 8); 4) [ 8; 11).
- 6. . Geben Sie das Intervall an, zu dem die Wurzel der Gleichung lg (x + 7) - log (x + 5) = 1 gehört
1) (-∞; -7); 2) (-7; -5); 3) (-5; -3); 4) (0; +∞).
- 7. Lösen Sie die Ungleichung log 3 (4 - 2x) >= 1
1) (-∞; 0,5 ]; 2) (-∞; 2 ]; 3) [ 2; + ∞); 4) [ 0,5; + ∞).
- 8. Lösen Sie den Ungleichungslog π (3x + 2)<= log π (х - 1)
1) (-2/3; + ∞); 2) (-∞; - 2/3 ]; 3) [ -1,5; - 2/3 ]; 4) Es gibt keine Lösungen.
- 9. Lösen Sie die Ungleichung log 1/9 (6 - 0,3x) > -1
1) (-10; +∞); 2) (-∞; -10); 3) (-10; 20); 4) (-0,1; 20).
- 10. Finden Sie die Anzahl der ganzzahligen negativen Lösungen der Ungleichung lg (x + 5)<= 2 - lg 2
15; 2) 4; 3) 10; 4) keine
Option 2
- 1. Finden Sie das Produkt der Wurzeln der Gleichung: lg (x 2 + 1) = 1
1) - 99; 2) - 9; 3) 33; 4) -33.
- 2. Geben Sie das Intervall an, zu dem die Wurzel der Gleichung log 4 (x - 5) = log 25 5 gehört
1) (-4; -2); 2) (6; 8); 3) (3; 6); 4) [ -8; -6 ].
- 3. Geben Sie das Intervall an, zu dem die Wurzel der Gleichung log 0,4 (5 - 2x) - log 0,4 2 = 1 gehört
1) (-∞; -2); 2) [ -2; 1 ]; 3) [ 1; 2 ]; 4) (2; +∞).
- 4. Ermitteln Sie die Summe der Wurzeln der Gleichung log (4x - 3) = 2 log x
1) - 2; 2) 4; 3) -4; 4) 2.
- 5. Geben Sie das Intervall an, zu dem die Wurzel der Gleichung log 2 (64x²) = 6 gehört
1) [ 5; 7]; 2) [ 9; 11 ]; 3) (3; 5); 4) [ 1; 3 ].
- 6. . Geben Sie das Intervall an, zu dem die Wurzel der Gleichung gehört log 2 (x - 1)³ = 6 log 2 3
1) [ 0; 5); 2) [ 5; 8); 3) [ 8; 11); 4) [ 11; 14).
- 7. Lösen Sie das Ungleichungsprotokoll 0,8 (0,25 - 0,1x) > -1
1) (-∞; 2,5); 2) (-10; 2,5); 3) (2,5; + ∞); 4) (-10; + ∞).
- 8. Lösen Sie das Ungleichungsprotokoll 1,25 (0,8x + 0,4)<= - l
1) (-0,5; + ∞); 2) (-∞; - 0,5 ]; 3) (-0,5; 0,5 ]; 4) (-2; 2 ] .
- 9. Lösen Sie das Ungleichungsprotokoll 10/3 (1 - 1,4x)< -1
1) (0,5; +∞); 2) (-∞; 0,5); 3) (1,4; 2); 4) (0,5; 5/7).
- 10. Finden Sie die Anzahl der ganzzahligen Lösungen für die Ungleichung log 0,5 (x - 2) >= - 2
15; 2) 4; 3) unendlich viele; 4) keine.
Schlüssel
| A1 | A2 | A3 | A4 | A5 | A6 | A7 | B1 | B2 | C1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 Option | 2 | 1 | 3 | 4 | 1 | 3 | 1 | 4 | 3 | 2 |
| Option 2 | 2 | 2 | 4 | 2 | 4 | 3 | 2 | 3 | 4 | 2 |