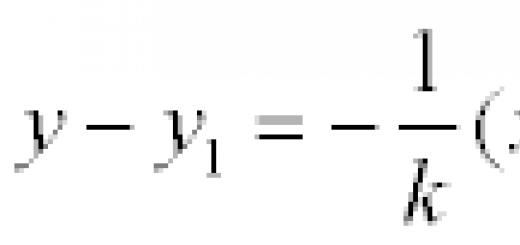The simplest problems with a straight line on a plane. The relative position of the lines. Angle between straight lines. Angle between two intersecting planes: definition, examples of finding Find the angle between straight lines online calculator

Definition. If two lines are given y = k 1 x + b 1, y = k 2 x + b 2, then the acute angle between these lines will be defined as

Two lines are parallel if k 1 = k 2. Two lines are perpendicular if k 1 = -1/ k 2.

Theorem. The lines Ax + Bу + C = 0 and A 1 x + B 1 y + C 1 = 0 are parallel when the coefficients A 1 = λA, B 1 = λB are proportional. If also C 1 = λC, then the lines coincide. The coordinates of the point of intersection of two lines are found as a solution to the system of equations of these lines.

Equation of a line passing through a given point

Perpendicular to a given line

Definition. A straight line passing through the point M 1 (x 1, y 1) and perpendicular to the straight line y = kx + b is represented by the equation:

Distance from point to line

Theorem. If a point M(x 0, y 0) is given, then the distance to the line Ax + Bу + C = 0 is determined as

Proof. Let point M 1 (x 1, y 1) be the base of the perpendicular dropped from point M to a given straight line. Then the distance between points M and M 1:

(1)

The coordinates x 1 and y 1 can be found by solving the system of equations:

The second equation of the system is the equation of a line passing through a given point M 0 perpendicular to a given line. If we transform the first equation of the system to the form:

A(x – x 0) + B(y – y 0) + Ax 0 + By 0 + C = 0,

then, solving, we get:

Substituting these expressions into equation (1), we find:

The theorem has been proven.

Example. Determine the angle between the lines: y = -3 x + 7; y = 2 x + 1.

k 1 = -3; k 2 = 2; tgφ = ; φ= p /4.

Example. Show that the lines 3x – 5y + 7 = 0 and 10x + 6y – 3 = 0 are perpendicular.

Solution. We find: k 1 = 3/5, k 2 = -5/3, k 1* k 2 = -1, therefore, the lines are perpendicular.

Example. Given are the vertices of the triangle A(0; 1), B (6; 5), C (12; -1). Find the equation of the height drawn from vertex C.

Solution. We find the equation of side AB: ; 4 x = 6 y – 6;

2 x – 3 y + 3 = 0;

The required height equation has the form: Ax + By + C = 0 or y = kx + b. k = . Then y = . Because the height passes through point C, then its coordinates satisfy this equation: from where b = 17. Total: .

Answer: 3 x + 2 y – 34 = 0.

The equation of a line passing through a given point in a given direction. Equation of a line passing through two given points. The angle between two straight lines. The condition of parallelism and perpendicularity of two straight lines. Determining the point of intersection of two lines

1. Equation of a line passing through a given point A(x 1 , y 1) in a given direction, determined by the slope k,

y - y 1 = k(x - x 1). (1)

This equation defines a pencil of lines passing through a point A(x 1 , y 1), which is called the beam center.

2. Equation of a line passing through two points: A(x 1 , y 1) and B(x 2 , y 2), written like this:

The angular coefficient of a straight line passing through two given points is determined by the formula

3. Angle between straight lines A And B is the angle by which the first straight line must be rotated A around the point of intersection of these lines counterclockwise until it coincides with the second line B. If two straight lines are given by equations with a slope

y = k 1 x + B 1 ,

y = k 2 x + B 2 , (4)

then the angle between them is determined by the formula

It should be noted that in the numerator of the fraction, the slope of the first line is subtracted from the slope of the second line.

If the equations of a line are given in general form

A 1 x + B 1 y + C 1 = 0,

A 2 x + B 2 y + C 2 = 0, (6)

the angle between them is determined by the formula

4. Conditions for parallelism of two lines:

a) If the lines are given by equations (4) with an angular coefficient, then the necessary and sufficient condition for their parallelism is the equality of their angular coefficients:

k 1 = k 2 . (8)

b) For the case when the lines are given by equations in general form (6), a necessary and sufficient condition for their parallelism is that the coefficients for the corresponding current coordinates in their equations are proportional, i.e.

5. Conditions for perpendicularity of two straight lines:

a) In the case when the lines are given by equations (4) with an angular coefficient, a necessary and sufficient condition for their perpendicularity is that their angular coefficients are inverse in magnitude and opposite in sign, i.e.

This condition can also be written in the form

k 1 k 2 = -1. (11)

b) If the equations of lines are given in general form (6), then the condition for their perpendicularity (necessary and sufficient) is to satisfy the equality

A 1 A 2 + B 1 B 2 = 0. (12)

6. The coordinates of the point of intersection of two lines are found by solving the system of equations (6). Lines (6) intersect if and only if

1. Write the equations of lines passing through the point M, one of which is parallel and the other perpendicular to the given line l.

Corner φ general equations A 1 x + B 1 y + C 1 = 0 and A 2 x + B 2 y + C 2 = 0, calculated by the formula:

Corner φ between two lines given canonical equations(x-x 1)/m 1 = (y-y 1)/n 1 and (x-x 2)/m 2 = (y-y 2)/n 2, calculated by the formula:

Distance from point to line

Each plane in space can be represented as a linear equation called general equation plane

Special cases.

o If in equation (8) , then the plane passes through the origin.

o When (,) the plane is parallel to the axis (axis, axis), respectively.

o When (,) the plane is parallel to the plane (plane, plane).

Solution: use (7)

Answer: general plane equation.

Example.

A plane in the rectangular coordinate system Oxyz is given by the general equation of the plane . Write down the coordinates of all normal vectors of this plane.

We know that the coefficients of the variables x, y and z in the general equation of a plane are the corresponding coordinates of the normal vector of this plane. Therefore, the normal vector of a given plane has coordinates. The set of all normal vectors can be defined as:

Write the equation of the plane if in the rectangular coordinate system Oxyz in space it passes through the point , A is the normal vector of this plane.

We present two solutions to this problem.

From the condition we have . We substitute this data into the general equation of the plane passing through the point:

Write the general equation of a plane parallel to the coordinate plane Oyz and passing through the point .

A plane that is parallel to the coordinate plane Oyz can be given by a general incomplete plane equation of the form . Since the point belongs to the plane by condition, then the coordinates of this point must satisfy the equation of the plane, that is, the equality must be true. From here we find. Thus, the required equation has the form.

Solution. The cross product, by definition 10.26, is orthogonal to the vectors p and q. Consequently, it is orthogonal to the desired plane and the vector can be taken as its normal vector. Let's find the coordinates of vector n:

that is . Using formula (11.1), we obtain

By opening the brackets in this equation, we arrive at the final answer.

Answer: .

Let's rewrite the normal vector in the form and find its length:

According to the above:

Answer:

Parallel planes have the same normal vector. 1) From the equation we find the normal vector of the plane:.

2) Let’s compose the equation of the plane using the point and normal vector:

Answer:

Vector equation of a plane in space

Parametric equation of a plane in space

Equation of a plane passing through a given point perpendicular to a given vector

Let a rectangular Cartesian coordinate system be given in three-dimensional space. Let us formulate the following problem:

Write an equation for a plane passing through a given point M(x 0, y 0, z 0) perpendicular to the given vector n = ( A, B, C} .

Solution. Let P(x, y, z) is an arbitrary point in space. Dot P belongs to the plane if and only if the vector MP = {x − x 0, y − y 0, z − z 0) orthogonal to the vector n = {A, B, C) (Fig. 1).

Having written the condition for the orthogonality of these vectors (n, MP) = 0 in coordinate form, we get:

A(x − x 0) + B(y − y 0) + C(z − z 0) = 0

Equation of a plane using three points

In vector form

In coordinates

Mutual arrangement of planes in space

– general equations of two planes. Then:

1) if , then the planes coincide;

2) if , then the planes are parallel;

3) if or , then the planes intersect and the system of equations

(6)

are the equations of the straight line of intersection of these planes.

Solution: We compose the canonical equations of the line using the formula:

Answer:

We take the resulting equations and mentally “pinch off”, for example, the left piece: . Now let's equate this piece to any number(remember that there was already a zero), for example, to one: . Since , then the other two “pieces” should also be equal to one. Essentially, you need to solve the system:

Compose parametric equations of the following straight lines:

Solution: Lines are given by canonical equations and at the first stage you should find some point belonging to the line and its direction vector.

a) From the equations remove the point and the direction vector: . You can choose another point (how to do this is described above), but it is better to take the most obvious one. By the way, to avoid mistakes, always substitute its coordinates into the equations.

Let's create parametric equations for this line:

The convenience of parametric equations is that they make it very easy to find other points on a line. For example, let's find a point whose coordinates, say, correspond to the value of the parameter:

Thus: b) Consider the canonical equations . Choosing a point here is not difficult, but treacherous: (be careful not to confuse the coordinates!!!). How to remove the guide vector? You can speculate about what this line is parallel to, or you can use a simple formal technique: the proportion contains “Y” and “Z”, so we write down the direction vector , and put a zero in the remaining space: .

Let's compose the parametric equations of the straight line:

c) Let’s rewrite the equations in the form , that is, “zet” can be anything. And if by any, then let, for example, . Thus, the point belongs to this line. To find the direction vector, we use the following formal technique: in the original equations there are “x” and “y”, and in the direction vector at these places we write zeros: . In the remaining space we put unit: . Instead of one, any number except zero will do.

Let's write down the parametric equations of the straight line:

$\blacktriangleright$ Dihedral angle is an angle formed by two half-planes and a straight line $a$, which is their common boundary.

$\blacktriangleright$ To find the angle between the planes $\xi$ and $\pi$ , you need to find the linear angle (and spicy or straight) dihedral angle formed by the planes $\xi$ and $\pi$ :

Step 1: let $\xi\cap\pi=a$ (the line of intersection of the planes). In the plane $\xi$ we mark an arbitrary point $F$ and draw $FA\perp a$ ;

Step 2: carry out $FG\perp \pi$ ;

Step 3: according to TTP ($FG$ – perpendicular, $FA$ – oblique, $AG$ – projection) we have: $AG\perp a$ ;

Step 4: The angle $\angle FAG$ is called the linear angle of the dihedral angle formed by the planes $\xi$ and $\pi$ .

Note that the triangle $AG$ is right-angled.
Note also that the plane $AFG$ constructed in this way is perpendicular to both planes $\xi$ and $\pi$ . Therefore, we can say it differently: angle between planes$\xi$ and $\pi$ is the angle between two intersecting lines $c\in \xi$ and $b\in\pi$ forming a plane perpendicular to and $\xi\ ) , and \(\pi$ .

Task 1 #2875

Task level: More difficult than the Unified State Exam

Given a quadrangular pyramid, all edges of which are equal, and the base is a square. Find $6\cos \alpha$ , where $\alpha$ is the angle between its adjacent side faces.

Let $SABCD$ be a given pyramid ($S$ is a vertex) whose edges are equal to $a$ . Consequently, all side faces are equal equilateral triangles. Let's find the angle between the faces $SAD$ and $SCD$ .

Let's do $CH\perp SD$ . Because $\triangle SAD=\triangle SCD$, then $AH$ will also be the height of $\triangle SAD$ . Therefore, by definition, $\angle AHC=\alpha$ is the linear angle of the dihedral angle between the faces $SAD$ and $SCD$ .
Since the base is a square, then $AC=a\sqrt2$ . Note also that $CH=AH$ is the height of an equilateral triangle with side $a$, therefore, $CH=AH=\frac(\sqrt3)2a$ .
Then, by the cosine theorem from $\triangle AHC$ : \[\cos \alpha=\dfrac(CH^2+AH^2-AC^2)(2CH\cdot AH)=-\dfrac13 \quad\Rightarrow\quad 6\cos\alpha=-2.\]

Answer: -2

Task 2 #2876

Task level: More difficult than the Unified State Exam

The planes $\pi_1$ and $\pi_2$ intersect at an angle whose cosine is equal to $0.2$. The planes $\pi_2$ and $\pi_3$ intersect at right angles, and the line of intersection of the planes $\pi_1$ and $\pi_2$ is parallel to the line of intersection of the planes $\pi_2$ and $\ pi_3$ . Find the sine of the angle between the planes $\pi_1$ and $\pi_3$ .

Let the line of intersection of $\pi_1$ and $\pi_2$ be a straight line $a$, the line of intersection of $\pi_2$ and $\pi_3$ be a straight line $b$, and the line of intersection $\pi_3$ and $\pi_1$ – straight line $c$ . Since $a\parallel b$ , then $c\parallel a\parallel b$ (according to the theorem from the section of the theoretical reference “Geometry in space” $\rightarrow$ “Introduction to stereometry, parallelism”).

Let's mark the points $A\in a, B\in b$ so that $AB\perp a, AB\perp b$ (this is possible since $a\parallel b$ ). Let us mark $C\in c$ so that $BC\perp c$ , therefore, $BC\perp b$ . Then $AC\perp c$ and $AC\perp a$ .
Indeed, since $AB\perp b, BC\perp b$ , then $b$ is perpendicular to the plane $ABC$ . Since $c\parallel a\parallel b$, then the lines $a$ and $c$ are also perpendicular to the plane $ABC$, and therefore to any line from this plane, in particular, the line \ (AC\) .

It follows that $\angle BAC=\angle (\pi_1, \pi_2)$, $\angle ABC=\angle (\pi_2, \pi_3)=90^\circ$, $\angle BCA=\angle (\pi_3, \pi_1)$. It turns out that $\triangle ABC$ is rectangular, which means \[\sin \angle BCA=\cos \angle BAC=0.2.\]

Answer: 0.2

Task 3 #2877

Task level: More difficult than the Unified State Exam

Given straight lines $a, b, c$ intersecting at one point, and the angle between any two of them is equal to $60^\circ$ . Find $\cos^(-1)\alpha$ , where $\alpha$ is the angle between the plane formed by lines $a$ and $c$ and the plane formed by lines $b\ ) and \(c$ . Give your answer in degrees.

Let the lines intersect at the point $O$ . Since the angle between any two of them is equal to $60^\circ$, then all three straight lines cannot lie in the same plane. Let us mark the point $A$ on the line $a$ and draw $AB\perp b$ and $AC\perp c$ . Then $\triangle AOB=\triangle AOC$ as rectangular along the hypotenuse and acute angle. Therefore, $OB=OC$ and $AB=AC$ .
Let's do $AH\perp (BOC)$ . Then by the theorem about three perpendiculars $HC\perp c$ , $HB\perp b$ . Since $AB=AC$ , then $\triangle AHB=\triangle AHC$ as rectangular along the hypotenuse and leg. Therefore, $HB=HC$ . This means that $OH$ is the bisector of the angle $BOC$ (since the point $H$ is equidistant from the sides of the angle).

Note that in this way we also constructed the linear angle of the dihedral angle formed by the plane formed by the lines $a$ and $c$ and the plane formed by the lines $b$ and $c$ . This is the angle $ACH$ .

Let's find this angle. Since we chose the point $A$ arbitrarily, let us choose it so that $OA=2$ . Then in rectangular $\triangle AOC$ : \[\sin 60^\circ=\dfrac(AC)(OA) \quad\Rightarrow\quad AC=\sqrt3 \quad\Rightarrow\quad OC=\sqrt(OA^2-AC^2)=1.\ ] Since $OH$ is a bisector, then $\angle HOC=30^\circ$ , therefore, in a rectangular $\triangle HOC$ : \[\mathrm(tg)\,30^\circ=\dfrac(HC)(OC)\quad\Rightarrow\quad HC=\dfrac1(\sqrt3).\] Then from the rectangular $\triangle ACH$ : \[\cos\angle \alpha=\cos\angle ACH=\dfrac(HC)(AC)=\dfrac13 \quad\Rightarrow\quad \cos^(-1)\alpha=3.\]

Answer: 3

Task 4 #2910

Task level: More difficult than the Unified State Exam

The planes $\pi_1$ and $\pi_2$ intersect along the straight line $l$ on which the points $M$ and $N$ lie. The segments $MA$ and $MB$ are perpendicular to the straight line $l$ and lie in the planes $\pi_1$ and $\pi_2$ respectively, and $MN = 15$ , $AN = 39$ , $BN = 17$ , $AB = 40$ . Find $3\cos\alpha$ , where $\alpha$ is the angle between the planes $\pi_1$ and $\pi_2$ .

The triangle $AMN$ is right-angled, $AN^2 = AM^2 + MN^2$, whence \ The triangle $BMN$ is right-angled, $BN^2 = BM^2 + MN^2$, from which \We write the cosine theorem for the triangle $AMB$: \ Then \ Since the angle $\alpha$ between the planes is an acute angle, and $\angle AMB$ turned out to be obtuse, then $\cos\alpha=\dfrac5(12)$ . Then \

Answer: 1.25

Task 5 #2911

Task level: More difficult than the Unified State Exam

$ABCDA_1B_1C_1D_1$ is a parallelepiped, $ABCD$ is a square with side $a$, point $M$ is the base of the perpendicular dropped from the point $A_1$ to the plane $(ABCD)$ , in addition, $M$ is the point of intersection of the diagonals of the square $ABCD$ . It is known that $A_1M = \dfrac(\sqrt(3))(2)a$. Find the angle between the planes $(ABCD)$ and $(AA_1B_1B)$ . Give your answer in degrees.

Let's construct $MN$ perpendicular to $AB$ as shown in the figure.

Since $ABCD$ is a square with side $a$ and $MN\perp AB$ and $BC\perp AB$ , then $MN\parallel BC$ . Since $M$ is the point of intersection of the diagonals of the square, then $M$ is the middle of $AC$, therefore, $MN$ is the middle line and $MN =\frac12BC= \frac(1)(2)a$.
$MN$ is the projection of $A_1N$ onto the plane $(ABCD)$, and $MN$ is perpendicular to $AB$, then, by the theorem of three perpendiculars, $A_1N$ is perpendicular to $AB $ and the angle between the planes $(ABCD)$ and $(AA_1B_1B)$ is $\angle A_1NM$ .
\[\mathrm(tg)\, \angle A_1NM = \dfrac(A_1M)(NM) = \dfrac(\frac(\sqrt(3))(2)a)(\frac(1)(2)a) = \sqrt(3)\qquad\Rightarrow\qquad\angle A_1NM = 60^(\circ)\]

Answer: 60

Task 6 #1854

Task level: More difficult than the Unified State Exam

In a square $ABCD$ : $O$ – the point of intersection of the diagonals; $S$ – does not lie in the plane of the square, $SO \perp ABC$ . Find the angle between the planes $ASD$ and $ABC$ if $SO = 5$ and $AB = 10$ .

Right triangles $\triangle SAO$ and $\triangle SDO$ are equal in two sides and the angle between them ($SO \perp ABC$ $\Rightarrow$ $\angle SOA = \angle SOD = 90^\circ$; $AO = DO$ , because $O$ – point of intersection of the diagonals of the square, $SO$ – common side) $\Rightarrow$ $AS = SD$ $\Rightarrow$ $\triangle ASD$ – isosceles. Point $K$ is the middle of $AD$, then $SK$ is the height in the triangle $\triangle ASD$, and $OK$ is the height in the triangle $AOD$ $\ Rightarrow$ plane $SOK$ is perpendicular to planes $ASD$ and $ABC$ $\Rightarrow$ $\angle SKO$ – linear angle equal to the desired dihedral angle.

In $\triangle SKO$ : $OK = \frac(1)(2)\cdot AB = \frac(1)(2)\cdot 10 = 5 = SO$$\Rightarrow$ $\triangle SOK$ – isosceles right triangle $\Rightarrow$ $\angle SKO = 45^\circ$ .

Answer: 45

Task 7 #1855

Task level: More difficult than the Unified State Exam

Right triangles $\triangle SAO$ , $\triangle SDO$ , $\triangle SOB$ and $\triangle SOC$ are equal in two sides and the angle between them ($SO \perp ABC$ $\Rightarrow$ $\angle SOA = \angle SOD = \angle SOB = \angle SOC = 90^\circ$; $AO = OD = OB = OC$, because $O$ – point of intersection of the diagonals of the square, $SO$ – common side) $\Rightarrow$ $AS = DS = BS = CS$ $\Rightarrow$ $\triangle ASD$ and $\triangle BSC$ are isosceles. Point $K$ is the middle of $AD$, then $SK$ is the height in the triangle $\triangle ASD$, and $OK$ is the height in the triangle $AOD$ $\ Rightarrow$ plane $SOK$ is perpendicular to plane $ASD$ . Point $L$ is the middle of $BC$, then $SL$ is the height in the triangle $\triangle BSC$, and $OL$ is the height in the triangle $BOC$ $\ Rightarrow$ plane $SOL$ (aka plane $SOK$) is perpendicular to the plane $BSC$ . Thus, we obtain that $\angle KSL$ is a linear angle equal to the desired dihedral angle.

$KL = KO + OL = 2\cdot OL = AB = 10$$\Rightarrow$ $OL = 5$ ; $SK = SL$ – heights in equal isosceles triangles, which can be found using the Pythagorean theorem: $SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50$. It can be noticed that $SK^2 + SL^2 = 50 + 50 = 100 = KL^2$$\Rightarrow$ for a triangle $\triangle KSL$ the inverse Pythagorean theorem holds $\Rightarrow$ $\triangle KSL$ – right triangle $\Rightarrow$ $\angle KSL = 90^\ circ$ .

Answer: 90

Preparing students to take the Unified State Exam in mathematics, as a rule, begins with repeating basic formulas, including those that allow you to determine the angle between planes. Despite the fact that this section of geometry is covered in sufficient detail within the school curriculum, many graduates need to repeat the basic material. Understanding how to find the angle between planes, high school students will be able to quickly calculate the correct answer when solving a problem and count on receiving decent scores on the results of passing the unified state exam.

Main nuances

To ensure that the question of how to find a dihedral angle does not cause difficulties, we recommend following a solution algorithm that will help you cope with Unified State Examination tasks.

First you need to determine the straight line along which the planes intersect.

Then you need to select a point on this line and draw two perpendiculars to it.

The next step is to find the trigonometric function of the dihedral angle formed by the perpendiculars. The most convenient way to do this is with the help of the resulting triangle, of which the angle is a part.

The answer will be the value of the angle or its trigonometric function.

Preparing for the exam test with Shkolkovo is the key to your success

During classes on the eve of passing the Unified State Exam, many schoolchildren are faced with the problem of finding definitions and formulas that allow them to calculate the angle between 2 planes. A school textbook is not always at hand exactly when needed. And in order to find the necessary formulas and examples of their correct application, including for finding the angle between planes on the Internet online, sometimes you need to spend a lot of time.

The Shkolkovo mathematical portal offers a new approach to preparing for the state exam. Classes on our website will help students identify the most difficult sections for themselves and fill gaps in knowledge.

We have prepared and clearly presented all the necessary material. Basic definitions and formulas are presented in the “Theoretical Information” section.

In order to better understand the material, we also suggest practicing the appropriate exercises. A large selection of tasks of varying degrees of complexity, for example, on, is presented in the “Catalog” section. All tasks contain a detailed algorithm for finding the correct answer. The list of exercises on the website is constantly supplemented and updated.

While practicing solving problems that require finding the angle between two planes, students have the opportunity to save any task online as “Favorites.” Thanks to this, they will be able to return to it the required number of times and discuss the progress of its solution with a school teacher or tutor.

Angle between straight lines in space we will call any of the adjacent angles formed by two straight lines drawn through an arbitrary point parallel to the data.

Let two lines be given in space:

Obviously, the angle φ between straight lines can be taken as the angle between their direction vectors and . Since , then using the formula for the cosine of the angle between vectors we get

The conditions of parallelism and perpendicularity of two straight lines are equivalent to the conditions of parallelism and perpendicularity of their direction vectors and:

Two straight parallel if and only if their corresponding coefficients are proportional, i.e. l 1 parallel l 2 if and only if parallel .

Two straight perpendicular if and only if the sum of the products of the corresponding coefficients is equal to zero: .

U goal between line and plane

Let it be straight d- not perpendicular to the θ plane;
d′− projection of a line d to the θ plane;
The smallest angle between straight lines d And d′ we will call angle between a straight line and a plane.
Let us denote it as φ=( d,θ)
If d⊥θ, then ( d,θ)=π/2

Oi→j→k→− rectangular coordinate system.
Plane equation:

θ: Ax+By+Cz+D=0

We assume that the straight line is defined by a point and a direction vector: d[M 0,p→]
Vector n→(A,B,C)⊥θ
Then it remains to find out the angle between the vectors n→ and p→, let us denote it as γ=( n→,p→).

If the angle γ<π/2 , то искомый угол φ=π/2−γ .

If the angle is γ>π/2, then the desired angle is φ=γ−π/2

sinφ=sin(2π−γ)=cosγ

sinφ=sin(γ−2π)=−cosγ

Then, angle between straight line and plane can be calculated using the formula:

sinφ=∣cosγ∣=∣ ∣ Ap 1+Bp 2+Cp 3∣ ∣ √A 2+B 2+C 2√p 21+p 22+p 23

Question29. The concept of quadratic form. Sign definiteness of quadratic forms.

Quadratic form j (x 1, x 2, …, x n) n real variables x 1, x 2, …, x n is called a sum of the form
, (1)

Where a ij – some numbers called coefficients. Without loss of generality, we can assume that a ij = a ji.

The quadratic form is called valid, If a ij Î GR. Matrix of quadratic form is called a matrix made up of its coefficients. The quadratic form (1) corresponds to the only symmetric matrix
That is A T = A. Consequently, quadratic form (1) can be written in matrix form j ( X) = x T Ah, Where x T = (X 1 X 2 … x n). (2)

And, conversely, every symmetric matrix (2) corresponds to a unique quadratic form up to the notation of variables.

Rank of quadratic form is called the rank of its matrix. The quadratic form is called non-degenerate, if its matrix is non-singular A. (recall that the matrix A is called non-degenerate if its determinant is not equal to zero). Otherwise, the quadratic form is degenerate.

positive definite(or strictly positive) if

j ( X) > 0 , for anyone X = (X 1 , X 2 , …, x n), except X = (0, 0, …, 0).

Matrix A positive definite quadratic form j ( X) is also called positive definite. Therefore, a positive definite quadratic form corresponds to a unique positive definite matrix and vice versa.

The quadratic form (1) is called negatively defined(or strictly negative) if

j ( X) < 0, для любого X = (X 1 , X 2 , …, x n), except X = (0, 0, …, 0).

Similarly as above, a matrix of negative definite quadratic form is also called negative definite.

Consequently, the positive (negative) definite quadratic form j ( X) reaches the minimum (maximum) value j ( X*) = 0 at X* = (0, 0, …, 0).

Note that most quadratic forms are not sign-definite, that is, they are neither positive nor negative. Such quadratic forms vanish not only at the origin of the coordinate system, but also at other points.

When n> 2, special criteria are required to check the sign of a quadratic form. Let's look at them.

Major minors quadratic form are called minors:

that is, these are minors of the order of 1, 2, ..., n matrices A, located in the upper left corner, the last of them coincides with the determinant of the matrix A.

Positive Definiteness Criterion (Sylvester criterion)

X) = x T Ah was positive definite, it is necessary and sufficient that all major minors of the matrix A were positive, that is: M 1 > 0, M 2 > 0, …, Mn > 0. Negative certainty criterion In order for the quadratic form j ( X) = x T Ah was negative definite, it is necessary and sufficient that its principal minors of even order be positive, and of odd order - negative, i.e.: M 1 < 0, M 2 > 0, M 3 < 0, …, (–1)n

Problem 1

Find the cosine of the angle between the lines $\frac(x+3)(5) =\frac(y-2)(-3) =\frac(z-1)(4) $ and $\left\(\begin(array )(c) (x=2\cdot t-3) \\ (y=-t+1) \\ (z=3\cdot t+5) \end(array)\right. $.

Let two lines be given in space: $\frac(x-x_(1) )(m_(1) ) =\frac(y-y_(1) )(n_(1) ) =\frac(z-z_(1 ) )(p_(1) ) $ and $\frac(x-x_(2) )(m_(2) ) =\frac(y-y_(2) )(n_(2) ) =\frac(z- z_(2) )(p_(2) ) $. Let's choose an arbitrary point in space and draw through it two auxiliary lines parallel to the data. The angle between these lines is any of the two adjacent angles formed by the auxiliary lines. The cosine of one of the angles between straight lines can be found using the well-known formula $\cos \phi =\frac(m_(1) \cdot m_(2) +n_(1) \cdot n_(2) +p_(1) \cdot p_( 2) )(\sqrt(m_(1)^(2) +n_(1)^(2) +p_(1)^(2) ) \cdot \sqrt(m_(2)^(2) +n_( 2)^(2) +p_(2)^(2) ) ) $. If the value $\cos \phi >0$, then an acute angle between the lines is obtained, if $\cos \phi

Canonical equations of the first line: $\frac(x+3)(5) =\frac(y-2)(-3) =\frac(z-1)(4) $.

The canonical equations of the second line can be obtained from the parametric ones:

\ \ \

Thus, the canonical equations of this line are: $\frac(x+3)(2) =\frac(y-1)(-1) =\frac(z-5)(3) $.

We calculate:

\[\cos \phi =\frac(5\cdot 2+\left(-3\right)\cdot \left(-1\right)+4\cdot 3)(\sqrt(5^(2) +\ left(-3\right)^(2) +4^(2) ) \cdot \sqrt(2^(2) +\left(-1\right)^(2) +3^(2) ) = \frac(25)(\sqrt(50) \cdot \sqrt(14) ) \approx 0.9449.\]

Problem 2

The first line passes through the given points $A\left(2,-4,-1\right)$ and $B\left(-3,5,6\right)$, the second line passes through the given points $C\left (1,-2,8\right)$ and $D\left(6,7,-2\right)$. Find the distance between these lines.

Let a certain line be perpendicular to the lines $AB$ and $CD$ and intersect them at points $M$ and $N$, respectively. Under these conditions, the length of the segment $MN$ is equal to the distance between the lines $AB$ and $CD$.

We construct the vector $\overline(AB)$:

\[\overline(AB)=\left(-3-2\right)\cdot \bar(i)+\left(5-\left(-4\right)\right)\cdot \bar(j)+ \left(6-\left(-1\right)\right)\cdot \bar(k)=-5\cdot \bar(i)+9\cdot \bar(j)+7\cdot \bar(k ).\]

Let the segment depicting the distance between the lines pass through the point $M\left(x_(M) ,y_(M) ,z_(M) \right)$ on the line $AB$.

We construct the vector $\overline(AM)$:

\[\overline(AM)=\left(x_(M) -2\right)\cdot \bar(i)+\left(y_(M) -\left(-4\right)\right)\cdot \ bar(j)+\left(z_(M) -\left(-1\right)\right)\cdot \bar(k)=\] \[=\left(x_(M) -2\right)\ cdot \bar(i)+\left(y_(M) +4\right)\cdot \bar(j)+\left(z_(M) +1\right)\cdot \bar(k).\]

The vectors $\overline(AB)$ and $\overline(AM)$ are the same, therefore they are collinear.

It is known that if the vectors $\overline(a)=x_(1) \cdot \overline(i)+y_(1) \cdot \overline(j)+z_(1) \cdot \overline(k)$ and $ \overline(b)=x_(2) \cdot \overline(i)+y_(2) \cdot \overline(j)+z_(2) \cdot \overline(k)$ are collinear, then their coordinates are proportional, then there is $\frac(x_((\it 2)) )((\it x)_((\it 1)) ) =\frac(y_((\it 2)) )((\it y)_( (\it 1)) ) =\frac(z_((\it 2)) )((\it z)_((\it 1)) ) $.

$\frac(x_(M) -2)(-5) =\frac(y_(M) +4)(9) =\frac(z_(M) +1)(7) =m$, where $m $ is the result of division.

From here we get: $x_(M) -2=-5\cdot m$; $y_(M) +4=9\cdot m$; $z_(M) +1=7\cdot m$.

We finally obtain expressions for the coordinates of point $M$:

We construct the vector $\overline(CD)$:

\[\overline(CD)=\left(6-1\right)\cdot \bar(i)+\left(7-\left(-2\right)\right)\cdot \bar(j)+\ left(-2-8\right)\cdot \bar(k)=5\cdot \bar(i)+9\cdot \bar(j)-10\cdot \bar(k).\]

Let the segment representing the distance between the lines pass through the point $N\left(x_(N) ,y_(N) ,z_(N) \right)$ on the line $CD$.

We construct the vector $\overline(CN)$:

\[\overline(CN)=\left(x_(N) -1\right)\cdot \bar(i)+\left(y_(N) -\left(-2\right)\right)\cdot \ bar(j)+\left(z_(N) -8\right)\cdot \bar(k)=\] \[=\left(x_(N) -1\right)\cdot \bar(i)+ \left(y_(N) +2\right)\cdot \bar(j)+\left(z_(N) -8\right)\cdot \bar(k).\]

The vectors $\overline(CD)$ and $\overline(CN)$ coincide, therefore, they are collinear. We apply the condition of collinearity of vectors:

$\frac(x_(N) -1)(5) =\frac(y_(N) +2)(9) =\frac(z_(N) -8)(-10) =n$, where $n $ is the result of division.

From here we get: $x_(N) -1=5\cdot n$; $y_(N) +2=9\cdot n$; $z_(N) -8=-10\cdot n$.

We finally obtain expressions for the coordinates of point $N$:

We construct the vector $\overline(MN)$:

\[\overline(MN)=\left(x_(N) -x_(M) \right)\cdot \bar(i)+\left(y_(N) -y_(M) \right)\cdot \bar (j)+\left(z_(N) -z_(M) \right)\cdot \bar(k).\]

We substitute expressions for the coordinates of points $M$ and $N$:

\[\overline(MN)=\left(1+5\cdot n-\left(2-5\cdot m\right)\right)\cdot \bar(i)+\] \[+\left(- 2+9\cdot n-\left(-4+9\cdot m\right)\right)\cdot \bar(j)+\left(8-10\cdot n-\left(-1+7\cdot m\right)\right)\cdot \bar(k).\]

Having completed the steps, we get:

\[\overline(MN)=\left(-1+5\cdot n+5\cdot m\right)\cdot \bar(i)+\left(2+9\cdot n-9\cdot m\right )\cdot \bar(j)+\left(9-10\cdot n-7\cdot m\right)\cdot \bar(k).\]

Since the lines $AB$ and $MN$ are perpendicular, the scalar product of the corresponding vectors is equal to zero, that is, $\overline(AB)\cdot \overline(MN)=0$:

\[-5\cdot \left(-1+5\cdot n+5\cdot m\right)+9\cdot \left(2+9\cdot n-9\cdot m\right)+7\cdot \ left(9-10\cdot n-7\cdot m\right)=0;\] \

Having completed the steps, we obtain the first equation for determining $m$ and $n$: $155\cdot m+14\cdot n=86$.

Since the lines $CD$ and $MN$ are perpendicular, the scalar product of the corresponding vectors is equal to zero, that is, $\overline(CD)\cdot \overline(MN)=0$:

\ \[-5+25\cdot n+25\cdot m+18+81\cdot n-81\cdot m-90+100\cdot n+70\cdot m=0.\]

Having completed the steps, we obtain the second equation for determining $m$ and $n$: $14\cdot m+206\cdot n=77$.

We find $m$ and $n$ by solving the system of equations $\left\(\begin(array)(c) (155\cdot m+14\cdot n=86) \\ (14\cdot m+206\cdot n =77)\end(array)\right.$.

We apply the Cramer method:

Find the coordinates of points $M$ and $N$:

\ \

Finally:

Finally, we write the vector $\overline(MN)$:

$\overline(MN)=\left(2.691-\left(-0.6215\right)\right)\cdot \bar(i)+\left(1.0438-0.7187\right)\cdot \bar (j)+\left(4.618-2.6701\right)\cdot \bar(k)$ or $\overline(MN)=3.3125\cdot \bar(i)+0.3251\cdot \bar( j)+1.9479\cdot \bar(k)$.

The distance between lines $AB$ and $CD$ is the length of the vector $\overline(MN)$:$d=\sqrt(3.3125^(2) +0.3251^(2) +1.9479^( 2) ) \approx 3.8565$ lin. units