Trigonometry formulas: multiplication. Trigonometric equations - formulas, solutions, examples. Formulas for sine and cosine from sum and difference

On this page you will find all the main trigonometric formulas, which will help you solve many exercises, greatly simplifying the expression itself.

Trigonometric formulas - mathematical equalities for trigonometric functions that hold for all acceptable values argument.

Formulas specify the relationships between the basic trigonometric functions - sine, cosine, tangent, cotangent.

The sine of an angle is the y coordinate of a point (ordinate) on unit circle. The cosine of an angle is the x coordinate of a point (abscissa).

Tangent and cotangent are, respectively, the ratios of sine to cosine and vice versa.
`sin\\alpha,\cos\\alpha`
`tg \ \alpha=\frac(sin\ \alpha)(cos \ \alpha),` ` \alpha\ne\frac\pi2+\pi n, \ n \in Z`
`ctg \ \alpha=\frac(cos\ \alpha)(sin\ \alpha),` ` \alpha\ne\pi+\pi n, \n \in Z`

And two that are used less often - secant, cosecant. They represent the ratios of 1 to cosine and sine.

`sec \ \alpha=\frac(1)(cos\ \alpha),` ` \alpha\ne\frac\pi2+\pi n,\ n \in Z`
`cosec \ \alpha=\frac(1)(sin \ \alpha),` ` \alpha\ne\pi+\pi n,\ n \in Z`

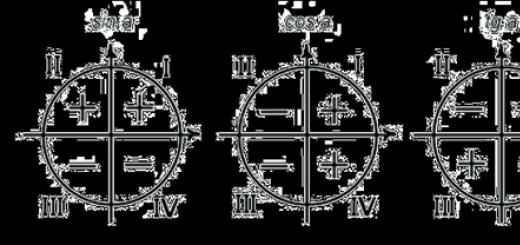
From the definitions of trigonometric functions it is clear what signs they have in each quadrant. The sign of the function depends only on which quadrant the argument is located in.

When changing the sign of the argument from “+” to “-”, only the cosine function does not change its value. It's called even. Its graph is symmetrical about the y-axis.

The remaining functions (sine, tangent, cotangent) are odd. When changing the sign of the argument from “+” to “-”, their value also changes to negative. Their graphs are symmetrical about the origin.

`sin(-\alpha)=-sin \ \alpha`
`cos(-\alpha)=cos \ \alpha`
`tg(-\alpha)=-tg \ \alpha`
`ctg(-\alpha)=-ctg \ \alpha`

Basic trigonometric identities

Basic trigonometric identities- these are formulas that establish a connection between trigonometric functions of one angle (`sin\\alpha,\cos\\alpha,\tg\\alpha,\ctg\\alpha`) and which allow you to find the value of each of these functions through any known other .
`sin^2 \alpha+cos^2 \alpha=1`
`tg \ \alpha \cdot ctg \ \alpha=1, \ \alpha\ne\frac(\pi n) 2, \n \in Z`
`1+tg^2 \alpha=\frac 1(cos^2 \alpha)=sec^2 \alpha,` ` \alpha\ne\frac\pi2+\pi n,\n \in Z`
`1+ctg^2 \alpha=\frac 1(sin^2 \alpha)=cosec^2 \alpha,` ` \alpha\ne\pi n, \n \in Z`

Formulas for the sum and difference of angles of trigonometric functions

Formulas for adding and subtracting arguments express trigonometric functions of the sum or difference of two angles in terms of trigonometric functions of these angles.
`sin(\alpha+\beta)=` `sin \ \alpha\ cos \ \beta+cos \ \alpha\ sin \ \beta`
`sin(\alpha-\beta)=` `sin \ \alpha\ cos \ \beta-cos \ \alpha\ sin \ \beta`
`cos(\alpha+\beta)=` `cos \ \alpha\ cos \ \beta-sin \ \alpha\ sin \ \beta`
`cos(\alpha-\beta)=` `cos \ \alpha\ cos \ \beta+sin \ \alpha\ sin \ \beta`
`tg(\alpha+\beta)=\frac(tg \ \alpha+tg \ \beta)(1-tg \ \alpha\ tg \ \beta)`
`tg(\alpha-\beta)=\frac(tg \ \alpha-tg \ \beta)(1+tg \ \alpha \ tg \ \beta)`
`ctg(\alpha+\beta)=\frac(ctg \ \alpha \ ctg \ \beta-1)(ctg \ \beta+ctg \ \alpha)`
`ctg(\alpha-\beta)=\frac(ctg \ \alpha\ ctg \ \beta+1)(ctg \ \beta-ctg \ \alpha)`

Double angle formulas

`sin \ 2\alpha=2 \ sin \ \alpha \cos \ \alpha=` `\frac (2 \ tg \ \alpha)(1+tg^2 \alpha)=\frac (2 \ ctg \ \alpha )(1+ctg^2 \alpha)=` `\frac 2(tg \ \alpha+ctg \ \alpha)`
`cos\2\alpha=cos^2 \alpha-sin^2 \alpha=` `1-2 \sin^2 \alpha=2 \cos^2 \alpha-1=` `\frac(1-tg^ 2\alpha)(1+tg^2\alpha)=\frac(ctg^2\alpha-1)(ctg^2\alpha+1)=` `\frac(ctg \ \alpha-tg \ \alpha) (ctg \ \alpha+tg \ \alpha)`
`tg \ 2\alpha=\frac(2 \ tg \ \alpha)(1-tg^2 \alpha)=` `\frac(2 \ ctg \ \alpha)(ctg^2 \alpha-1)=` `\frac 2(\ctg \ \alpha-tg \ \alpha)`
`ctg \ 2\alpha=\frac(ctg^2 \alpha-1)(2 \ctg \ \alpha)=` `\frac (\ctg \ \alpha-tg \ \alpha)2`

Triple angle formulas

`sin \ 3\alpha=3 \ sin \ \alpha-4sin^3 \alpha`
`cos \ 3\alpha=4cos^3 \alpha-3 \ cos \ \alpha`
`tg \ 3\alpha=\frac(3 \ tg \ \alpha-tg^3 \alpha)(1-3 \ tg^2 \alpha)`
`ctg \ 3\alpha=\frac(ctg^3 \alpha-3 \ ctg \ \alpha)(3 \ ctg^2 \alpha-1)`

Half angle formulas

`sin \ \frac \alpha 2=\pm \sqrt(\frac (1-cos \ \alpha)2)`
`cos \ \frac \alpha 2=\pm \sqrt(\frac (1+cos \ \alpha)2)`
`tg \ \frac \alpha 2=\pm \sqrt(\frac (1-cos \ \alpha)(1+cos \ \alpha))=` `\frac (sin \ \alpha)(1+cos \ \ alpha)=\frac (1-cos \ \alpha)(sin \ \alpha)`
`ctg \ \frac \alpha 2=\pm \sqrt(\frac (1+cos \ \alpha)(1-cos \ \alpha))=` `\frac (sin \ \alpha)(1-cos \ \ alpha)=\frac (1+cos \ \alpha)(sin \ \alpha)`

Formulas for half, double and triple arguments express the functions `sin, \cos, \tg, \ctg` of these arguments (`\frac(\alpha)2, \2\alpha, \3\alpha,... `) through these functions argument `\alpha`.

Their conclusion can be obtained from the previous group (addition and subtraction of arguments). For example, identities double angle easy to obtain by replacing `\beta` with `\alpha`.

Degree reduction formulas

Formulas of squares (cubes, etc.) of trigonometric functions allow you to move from 2,3,... degrees to trigonometric functions of the first degree, but multiple angles (`\alpha, \3\alpha, \...` or `2\alpha, \ 4\alpha, \...`).
`sin^2 \alpha=\frac(1-cos \ 2\alpha)2,` ` (sin^2 \frac \alpha 2=\frac(1-cos \ \alpha)2)`
`cos^2 \alpha=\frac(1+cos \ 2\alpha)2,` ` (cos^2 \frac \alpha 2=\frac(1+cos \ \alpha)2)`
`sin^3 \alpha=\frac(3sin \ \alpha-sin \ 3\alpha)4`
`cos^3 \alpha=\frac(3cos \ \alpha+cos \ 3\alpha)4`
`sin^4 \alpha=\frac(3-4cos \ 2\alpha+cos \ 4\alpha)8`
`cos^4 \alpha=\frac(3+4cos \ 2\alpha+cos \ 4\alpha)8`

Formulas for the sum and difference of trigonometric functions

The formulas are transformations of the sum and difference of trigonometric functions of different arguments into a product.

`sin \ \alpha+sin \ \beta=` `2 \ sin \frac(\alpha+\beta)2 \ cos \frac(\alpha-\beta)2`
`sin \ \alpha-sin \ \beta=` `2 \cos \frac(\alpha+\beta)2 \sin \frac(\alpha-\beta)2`
`cos \ \alpha+cos \ \beta=` `2 \cos \frac(\alpha+\beta)2 \cos \frac(\alpha-\beta)2`
`cos \ \alpha-cos \ \beta=` `-2 \ sin \frac(\alpha+\beta)2 \ sin \frac(\alpha-\beta)2=` `2 \ sin \frac(\alpha+\ beta)2\sin\frac(\beta-\alpha)2`
`tg \ \alpha \pm tg \ \beta=\frac(sin(\alpha \pm \beta))(cos \ \alpha \ cos \ \beta)`
`ctg \ \alpha \pm ctg \ \beta=\frac(sin(\beta \pm \alpha))(sin \ \alpha \ sin \ \beta)`
`tg \ \alpha \pm ctg \ \beta=` `\pm \frac(cos(\alpha \mp \beta))(cos \ \alpha \ sin \ \beta)`

Here the transformation of addition and subtraction of functions of one argument into a product occurs.

`cos \ \alpha+sin \ \alpha=\sqrt(2) \cos (\frac(\pi)4-\alpha)`
`cos \ \alpha-sin \ \alpha=\sqrt(2) \ sin (\frac(\pi)4-\alpha)`
`tg \ \alpha+ctg \ \alpha=2 \cosec \2\alpha;` `tg \ \alpha-ctg \ \alpha=-2 \ctg \2\alpha`

The following formulas convert the sum and difference of one and a trigonometric function into a product.

`1+cos \ \alpha=2 \cos^2 \frac(\alpha)2`
`1-cos \ \alpha=2 \ sin^2 \frac(\alpha)2`
`1+sin \ \alpha=2 \ cos^2 (\frac (\pi) 4-\frac(\alpha)2)`
`1-sin \ \alpha=2 \ sin^2 (\frac (\pi) 4-\frac(\alpha)2)`
`1 \pm tg \ \alpha=\frac(sin(\frac(\pi)4 \pm \alpha))(cos \frac(\pi)4 \cos \ \alpha)=` `\frac(\sqrt (2) sin(\frac(\pi)4 \pm \alpha))(cos \ \alpha)`
`1 \pm tg \ \alpha \ tg \ \beta=\frac(cos(\alpha \mp \beta))(cos \ \alpha \ cos \ \beta);` ` \ctg \ \alpha \ctg \ \ beta \pm 1=\frac(cos(\alpha \mp \beta))(sin \ \alpha \ sin \ \beta)`

Formulas for converting products of functions

Formulas for converting the product of trigonometric functions with arguments `\alpha` and `\beta` into the sum (difference) of these arguments.
`sin \ \alpha \ sin \ \beta =` `\frac(cos(\alpha - \beta)-cos(\alpha + \beta))(2)`
`sin\alpha \cos\beta =` `\frac(sin(\alpha - \beta)+sin(\alpha + \beta))(2)`
`cos \ \alpha \cos \ \beta =` `\frac(cos(\alpha - \beta)+cos(\alpha + \beta))(2)`
`tg \ \alpha \ tg \ \beta =` `\frac(cos(\alpha - \beta)-cos(\alpha + \beta))(cos(\alpha - \beta)+cos(\alpha + \ beta)) =` `\frac(tg \ \alpha + tg \ \beta)(ctg \ \alpha + ctg \ \beta)`
`ctg \ \alpha \ ctg \ \beta =` `\frac(cos(\alpha - \beta)+cos(\alpha + \beta))(cos(\alpha - \beta)-cos(\alpha + \ beta)) =` `\frac(ctg \ \alpha + ctg \ \beta)(tg \ \alpha + tg \ \beta)`
`tg \ \alpha \ ctg \ \beta =` `\frac(sin(\alpha - \beta)+sin(\alpha + \beta))(sin(\alpha + \beta)-sin(\alpha - \ beta))`

Universal trigonometric substitution

These formulas express trigonometric functions in terms of the tangent of a half angle.
`sin \ \alpha= \frac(2tg\frac(\alpha)(2))(1 + tg^(2)\frac(\alpha)(2)),` ` \alpha\ne \pi +2\ pi n, n \in Z`
`cos \ \alpha= \frac(1 - tg^(2)\frac(\alpha)(2))(1 + tg^(2)\frac(\alpha)(2)),` ` \alpha \ ne \pi +2\pi n, n \in Z`
`tg \ \alpha= \frac(2tg\frac(\alpha)(2))(1 - tg^(2)\frac(\alpha)(2)),` ` \alpha \ne \pi +2\ pi n, n \in Z,` ` \alpha \ne \frac(\pi)(2)+ \pi n, n \in Z`
`ctg \ \alpha = \frac(1 - tg^(2)\frac(\alpha)(2))(2tg\frac(\alpha)(2)),` ` \alpha \ne \pi n, n \in Z,` `\alpha \ne \pi + 2\pi n, n \in Z`

Reduction formulas

Reduction formulas can be obtained using such properties of trigonometric functions as periodicity, symmetry, and the property of shifting by a given angle. They allow functions of an arbitrary angle to be converted into functions whose angle is between 0 and 90 degrees.

For angle (`\frac (\pi)2 \pm \alpha`) or (`90^\circ \pm \alpha`):
`sin(\frac (\pi)2 - \alpha)=cos \ \alpha;` ` sin(\frac (\pi)2 + \alpha)=cos \ \alpha`
`cos(\frac (\pi)2 - \alpha)=sin \ \alpha;` ` cos(\frac (\pi)2 + \alpha)=-sin \ \alpha`
`tg(\frac (\pi)2 — \alpha)=ctg \ \alpha;` ` tg(\frac (\pi)2 + \alpha)=-ctg \ \alpha`
`ctg(\frac (\pi)2 — \alpha)=tg \ \alpha;` ` ctg(\frac (\pi)2 + \alpha)=-tg \ \alpha`
For angle (`\pi \pm \alpha`) or (`180^\circ \pm \alpha`):
`sin(\pi - \alpha)=sin \ \alpha;` ` sin(\pi + \alpha)=-sin \ \alpha`
`cos(\pi - \alpha)=-cos \ \alpha;` ` cos(\pi + \alpha)=-cos \ \alpha`
`tg(\pi - \alpha)=-tg \ \alpha;` ` tg(\pi + \alpha)=tg \ \alpha`
`ctg(\pi - \alpha)=-ctg \ \alpha;` ` ctg(\pi + \alpha)=ctg \ \alpha`
For angle (`\frac (3\pi)2 \pm \alpha`) or (`270^\circ \pm \alpha`):
`sin(\frac (3\pi)2 — \alpha)=-cos \ \alpha;` ` sin(\frac (3\pi)2 + \alpha)=-cos \ \alpha`
`cos(\frac (3\pi)2 — \alpha)=-sin \ \alpha;` ` cos(\frac (3\pi)2 + \alpha)=sin \ \alpha`
`tg(\frac (3\pi)2 — \alpha)=ctg \ \alpha;` ` tg(\frac (3\pi)2 + \alpha)=-ctg \ \alpha`
`ctg(\frac (3\pi)2 — \alpha)=tg \ \alpha;` ` ctg(\frac (3\pi)2 + \alpha)=-tg \ \alpha`
For angle (`2\pi \pm \alpha`) or (`360^\circ \pm \alpha`):
`sin(2\pi - \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi - \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi - \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi - \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`

Expressing some trigonometric functions in terms of others

`sin \ \alpha=\pm \sqrt(1-cos^2 \alpha)=` `\frac(tg \ \alpha)(\pm \sqrt(1+tg^2 \alpha))=\frac 1( \pm \sqrt(1+ctg^2 \alpha))`
`cos \ \alpha=\pm \sqrt(1-sin^2 \alpha)=` `\frac 1(\pm \sqrt(1+tg^2 \alpha))=\frac (ctg \ \alpha)( \pm \sqrt(1+ctg^2 \alpha))`
`tg \ \alpha=\frac (sin \ \alpha)(\pm \sqrt(1-sin^2 \alpha))=` `\frac (\pm \sqrt(1-cos^2 \alpha))( cos\\alpha)=\frac 1(ctg\\alpha)`
`ctg \ \alpha=\frac (\pm \sqrt(1-sin^2 \alpha))(sin \ \alpha)=` `\frac (cos \ \alpha)(\pm \sqrt(1-cos^ 2 \alpha))=\frac 1(tg \ \alpha)`

Trigonometry literally translates to “measuring triangles.” It begins to be studied at school, and continues in more detail at universities. Therefore, basic formulas in trigonometry are needed starting from grade 10, as well as for passing the Unified State Exam. They denote connections between functions, and since there are many of these connections, there are also a lot of formulas themselves. It is not easy to remember them all, and it is not necessary - if necessary, they can all be displayed.

Trigonometric formulas are used in integral calculus, as well as in trigonometric simplifications, calculations, and transformations.

Trigonometry, trigonometric formulas

The relationships between the basic trigonometric functions - sine, cosine, tangent and cotangent - are specified trigonometric formulas. And since there are quite a lot of connections between trigonometric functions, this explains the abundance of trigonometric formulas. Some formulas connect trigonometric functions of the same angle, others - functions of a multiple angle, others - allow you to reduce the degree, fourth - express all functions through the tangent of a half angle, etc.

In this article we will list in order all the basic trigonometric formulas, which are sufficient to solve the vast majority of trigonometry problems. For ease of memorization and use, we will group them by purpose and enter them into tables.

Basic trigonometric identities define the relationship between sine, cosine, tangent and cotangent of one angle. They follow from the definition of sine, cosine, tangent and cotangent, as well as the concept of the unit circle. They allow you to express one trigonometric function in terms of any other.

For a detailed description of these trigonometry formulas, their derivation and examples of application, see the article basic trigonometric identities.

Top of page

Reduction formulas

Reduction formulas follow from the properties of sine, cosine, tangent and cotangent, that is, they reflect the property of periodicity of trigonometric functions, the property of symmetry, as well as the property of shift by a given angle. These trigonometric formulas allow you to move from working with arbitrary angles to working with angles ranging from zero to 90 degrees.

The rationale for these formulas, a mnemonic rule for remembering them, and examples of their application can be studied in the article reduction formulas.

Top of page

Addition formulas

Trigonometric addition formulas show how trigonometric functions of the sum or difference of two angles are expressed in terms of trigonometric functions of those angles. These formulas serve as the basis for deriving the following trigonometric formulas.

For more information, see the article Addition formulas.

Top of page

Formulas for double, triple, etc. angle

Formulas for double, triple, etc. angle (they are also called multiple angle formulas) show how trigonometric functions of double, triple, etc. angles () are expressed in terms of trigonometric functions of a single angle. Their derivation is based on addition formulas.

More detailed information is collected in the article formulas for double, triple, etc. corner.

Top of page

Half angle formulas

Half angle formulas show how trigonometric functions of a half angle are expressed in terms of the cosine of a whole angle. These trigonometric formulas follow from the double angle formulas.

Their conclusion and examples of application can be found in the article on half-angle formulas.

Top of page

Degree reduction formulas

Trigonometric formulas for reducing degrees are intended to facilitate the transition from natural degrees trigonometric functions to sines and cosines to the first degree, but multiple angles. In other words, they allow you to reduce the powers of trigonometric functions to the first.

Top of page

Formulas for the sum and difference of trigonometric functions

Main purpose formulas for the sum and difference of trigonometric functions is to go to the product of functions, which is very useful when simplifying trigonometric expressions. These formulas are also widely used in solving trigonometric equations, as they allow you to factor the sum and difference of sines and cosines.

For the derivation of formulas, as well as examples of their application, see the article formulas for the sum and difference of sine and cosine.

Top of page

Formulas for the product of sines, cosines and sine by cosine

The transition from the product of trigonometric functions to a sum or difference is carried out using the formulas for the product of sines, cosines and sine by cosine.

Top of page

Universal trigonometric substitution

We complete our review of the basic formulas of trigonometry with formulas expressing trigonometric functions in terms of the tangent of a half angle. This replacement was called universal trigonometric substitution. Its convenience lies in the fact that all trigonometric functions are expressed in terms of the tangent of a half angle rationally without roots.

For more complete information, see the article universal trigonometric substitution.

Top of page

Algebra: Textbook for 9th grade. avg. school/Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Ed. S. A. Telyakovsky. - M.: Education, 1990. - 272 pp.: ill. - ISBN 5-09-002727-7
Bashmakov M. I. Algebra and the beginnings of analysis: Textbook. for 10-11 grades. avg. school — 3rd ed. - M.: Education, 1993. - 351 p.: ill. — ISBN 5-09-004617-4.
Algebra and the beginning of analysis: Proc. for 10-11 grades. general education institutions / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn and others; Ed. A. N. Kolmogorov. - 14th ed. - M.: Education, 2004. - 384 pp.: ill. - ISBN 5-09-013651-3.
Gusev V. A., Mordkovich A. G. Mathematics (a manual for those entering technical schools): Proc. allowance.- M.; Higher school, 1984.-351 p., ill.

Trigonometric formulas- these are the most necessary formulas in trigonometry, necessary to express trigonometric functions that are performed for any value of the argument.

Addition formulas.

sin (α + β) = sin α cos β + sin β cos α

sin (α - β) = sin α cos β - sin β cos α

cos (α + β) = cos α · cos β — sin α · sin β

cos (α - β) = cos α cos β + sin α sin β

tg (α + β) = (tg α + tg β) ÷ (1 - tg α tg β)

tg (α - β) = (tg α - tg β) ÷ (1 + tg α · tg β)

ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β - ctg α)

ctg (α - β) = (ctg α · ctg β - 1) ÷ (ctg β + ctg α)

Double angle formulas.

cos 2α = cos²α -sin²α

cos 2α = 2cos²α — 1

cos 2α = 1 - 2sin²α

sin 2α = 2sinα cosα

tg 2α = (2tg α) ÷ (1 - tg² α)

ctg 2α = (ctg²α — 1) ÷ (2ctgα )

Triple angle formulas.

sin 3α = 3sin α – 4sin³ α

cos 3α = 4cos³α - 3cosα

tg 3α = (3tgα — tg³α ) ÷ (1 — 3tg²α )

ctg 3α = (3ctg α - ctg³ α) ÷ (1 - 3ctg² α)

Half angle formulas.

Reduction formulas.

Function/angle in rad.	π/2 - α	π/2 + α			3π/2 - α	3π/2 + α	2π - α	2π + α




Function/angle in °	90° - α	90° + α	180° - α	180° + α	270° - α	270° + α	360° - α	360° + α

Detailed description of reduction formulas.

Basic trigonometric formulas.

Basic trigonometric identity:

sin 2 α+cos 2 α=1

This identity is the result of applying the Pythagorean theorem to a triangle in the unit trigonometric circle.

The relationship between cosine and tangent is:

1/cos 2 α−tan 2 α=1 or sec 2 α−tan 2 α=1.

This formula is a consequence of the basic trigonometric identity and is obtained from it by dividing the left and right sides by cos2α. It is assumed that α≠π/2+πn,n∈Z.

Relation between sine and cotangent:

1/sin 2 α−cot 2 α=1 or csc 2 α−cot 2 α=1.

This formula also follows from the basic trigonometric identity (obtained from it by dividing the left and right sides by sin2α. Here it is assumed that α≠πn,n∈Z.

Tangent definition:

tanα=sinα/cosα,

Where α≠π/2+πn,n∈Z.

Definition of cotangent:

cotα=cosα/sinα,

Where α≠πn,n∈Z.

Corollary from the definitions of tangent and cotangent:

tanα⋅ cotα=1,

Where α≠πn/2,n∈Z.

Definition of secant:

secα=1/cosα,α≠π/2+πn,n∈ Z

Definition of cosecant:

cscα=1/sinα,α≠πn,n∈ Z

Trigonometric inequalities.

The simplest trigonometric inequalities:

sinx > a, sinx ≥ a, sinx< a, sinx ≤ a,

cosx > a, cosx ≥ a, cosx< a, cosx ≤ a,

tanx > a, tanx ≥ a, tanx< a, tanx ≤ a,

cotx > a, cotx ≥ a, cotx< a, cotx ≤ a.

Squares of trigonometric functions.

Formulas for cubes of trigonometric functions.

TrigonometryMathematics. Trigonometry. Formulas. Geometry. Theory

We have looked at the most basic trigonometric functions (don’t be fooled, in addition to sine, cosine, tangent and cotangent, there are many other functions, but more on them later), but for now let’s look at some basic properties of the functions already studied.

Trigonometric functions of numeric argument

Whatever real number t is taken, it can be associated with a uniquely defined number sin(t).

True, the matching rule is quite complex and consists of the following.

To find the value of sin(t) from the number t, you need:

arrange number circle on coordinate plane so that the center of the circle coincides with the origin of coordinates, and the starting point A of the circle falls at point (1; 0);
find a point on the circle corresponding to the number t;
find the ordinate of this point.
this ordinate is the desired sin(t).

Actually we're talking about about the function s = sin(t), where t is any real number. We know how to calculate some values of this function (for example, sin(0) = 0, \(sin \frac (\pi)(6) = \frac(1)(2) \), etc.), we know some of its properties.

Relationship between trigonometric functions

As you, I hope, can guess, all trigonometric functions are interconnected and even without knowing the meaning of one, it can be found through another.

For example, the most important formula in all trigonometry is basic trigonometric identity:

\[ sin^(2) t + cos^(2) t = 1 \]

As you can see, knowing the value of the sine, you can find the value of the cosine, and also vice versa.

Trigonometry formulas

Also very common formulas connecting sine and cosine with tangent and cotangent:

\[ \boxed (\tan\; t=\frac(\sin\; t)(\cos\; t), \qquad t \neq \frac(\pi)(2)+ \pi k) \]

\[ \boxed (\cot\; t=\frac(\cos\; )(\sin\; ), \qquad t \neq \pi k) \]

From the last two formulas one can derive another trigometric identity, this time connecting tangent and cotangent:

\[ \boxed (\tan \; t \cdot \cot \; t = 1, \qquad t \neq \frac(\pi k)(2)) \]

Now let's see how these formulas work in practice.

EXAMPLE 1. Simplify the expression: a) \(1+ \tan^2 \; t \), b) \(1+ \cot^2 \; t \)

a) First of all, let’s write the tangent, keeping the square:

\[ 1+ \tan^2 \; t = 1 + \frac(\sin^2 \; t)(\cos^2 \; t) \]

\[ 1 + \frac(\sin^2 \; t)(\cos^2 \; t)= \sin^2\; t + \cos^2\; t + \frac(\sin^2 \; t)(\cos^2 \; t) \]

Now let's enter everything under common denominator, and we get:

\[ \sin^2\; t + \cos^2\; t + \frac(\sin^2 \; t)(\cos^2 \; t) = \frac(\cos^2 \; t + \sin^2 \; t)(\cos^2 \; t ) \]

And finally, as we see, the numerator can be reduced to one by the main trigonometric identity, as a result we get: \[ 1+ \tan^2 \; = \frac(1)(\cos^2 \; t) \]

b) With the cotangent we perform all the same actions, only the denominator will no longer be a cosine, but a sine, and the answer will be like this:

\[ 1+ \cot^2 \; = \frac(1)(\sin^2 \; t) \]

Having completed this task, we derived two more very important formulas that connect our functions, which we also need to know like the back of our hands:

\[ \boxed (1+ \tan^2 \; = \frac(1)(\cos^2 \; t), \qquad t \neq \frac(\pi)(2)+ \pi k) \]

\[ \boxed (1+ \cot^2 \; = \frac(1)(\sin^2 \; t), \qquad t \neq \pi k) \]

You must know all the formulas presented by heart, otherwise further study of trigonometry without them is simply impossible. In the future there will be more formulas and there will be a lot of them and I assure you that you will definitely remember all of them for a long time, or maybe you won’t remember them, but EVERYONE should know these six things!

A complete table of all basic and rare trigonometric reduction formulas.

Here you can find trigonometric formulas in a convenient form. And trigonometric reduction formulas can be found on another page.

Basic trigonometric identities

— mathematical expressions for trigonometric functions, executed for each argument value.

sin² α + cos² α = 1
tg α cot α = 1
tg α = sin α ÷ cos α
cot α = cos α ÷ sin α
1 + tg² α = 1 ÷ cos² α
1 + cotg² α = 1 ÷ sin² α

Addition formulas

sin (α + β) = sin α cos β + sin β cos α
sin (α - β) = sin α cos β - sin β cos α
cos (α + β) = cos α · cos β — sin α · sin β
cos (α - β) = cos α cos β + sin α sin β
tg (α + β) = (tg α + tg β) ÷ (1 - tg α · tg β)
tg (α - β) = (tg α - tg β) ÷ (1 + tg α · tg β)
ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β - ctg α)
ctg (α - β) = (ctg α · ctg β - 1) ÷ (ctg β + ctg α)

https://uchim.org/matematika/trigonometricheskie-formuly - uchim.org

Double angle formulas

cos 2α = cos² α - sin² α
cos 2α = 2cos² α - 1
cos 2α = 1 - 2sin² α
sin 2α = 2sin α cos α
tg 2α = (2tg α) ÷ (1 - tg² α)
ctg 2α = (ctg² α - 1) ÷ (2ctg α)

Triple angle formulas

sin 3α = 3sin α – 4sin³ α
cos 3α = 4cos³ α – 3cos α
tg 3α = (3tg α - tg³ α) ÷ (1 - 3tg² α)
ctg 3α = (3ctg α - ctg³ α) ÷ (1 - 3ctg² α)

Degree reduction formulas

sin² α = (1 - cos 2α) ÷ 2
sin³ α = (3sin α – sin 3α) ÷ 4
cos² α = (1 + cos 2α) ÷ 2
cos³ α = (3cos α + cos 3α) ÷ 4
sin² α · cos² α = (1 – cos 4α) ÷ 8
sin³ α · cos³ α = (3sin 2α – sin 6α) ÷ 32

Transition from product to sum

sin α cos β = ½ (sin (α + β) + sin (α - β))
sin α sin β = ½ (cos (α - β) - cos (α + β))
cos α cos β = ½ (cos (α - β) + cos (α + β))

We have listed quite a lot of trigonometric formulas, but if something is missing, please write.

Everything for studying » Mathematics at school » Trigonometric formulas - cheat sheet

To bookmark a page, press Ctrl+D.

Group with a bunch useful information(Subscribe if you have an Unified State Exam or Unified State Exam):

The entire database of abstracts, coursework, theses and others educational materials is provided free of charge. By using the site materials, you confirm that you have read the user agreement and agree with all its points in full.

transformation of groups is considered in detail general solutions trigonometric equations. The third section examines non-standard trigonometric equations, the solutions of which are based on the functional approach.

All formulas (equations) of trigonometry: sin(x) cos(x) tan(x) ctg(x)

The fourth section discusses trigonometric inequalities. Methods for solving elementary problems are discussed in detail. trigonometric inequalities, both on the unit circle and...

... angle 1800-α= along the hypotenuse and acute angle: => OB1=OB; A1B1=AB => x = -x1,y = y1=> So, in school course In geometry, the concept of a trigonometric function is introduced by geometric means due to their greater accessibility. The traditional methodological scheme for studying trigonometric functions is as follows: 1) first, trigonometric functions are determined for acute angle rectangular...

… Homework 19(3.6), 20(2.4) Setting a goal Updating basic knowledge Properties of trigonometric functions Reduction formulas New material Values of trigonometric functions Solving the simplest trigonometric equations Reinforcement Solving problems Objective of the lesson: today we will calculate the values of trigonometric functions and solve ...

... the formulated hypothesis needed to solve the following problems: 1. Identify the role of trigonometric equations and inequalities in teaching mathematics; 2. Develop a methodology for developing the ability to solve trigonometric equations and inequalities, aimed at developing trigonometric concepts; 3. Experimentally test the effectiveness of the developed method. To solve...

Trigonometric formulas

We present to your attention various formulas related to trigonometry.

(8) Cotangent of double angle

cotg(2α) =

ctg 2 (α) - 1 2ctg(α)

(9) Sine of a triple angle sin(3α) = 3sin(α)cos 2 (α) - sin 3 (α) (10) Cosine of triple angle cos(3α) = cos 3 (α) - 3cos(α)sin 2 (α) (11) Cosine of the sum/difference cos(α±β) = cos(α)cos(β) ∓ sin(α)sin(β) (12) Sine of the sum/difference sin(α±β) = sin(α)cos(β) ± cos(α)sin(β) (13) Tangent of the sum/difference (14) Cotangent of the sum/difference (15) Product of sines sin(α)sin(β) = ½(cos(α-β) - cos(α+β)) (16) Product of cosines cos(α)cos(β) = ½(cos(α+β) + cos(α-β)) (17) Product of sine and cosine sin(α)cos(β) = ½(sin(α+β) + sin(α-β)) (18) Sum/difference of sines sin(α) ± sin(β) = 2sin(½(α±β))cos(½(α∓β)) (19) Sum of cosines cos(α) + cos(β) = 2cos(½(α+β))cos(½(α-β)) (20) Difference of cosines cos(α) - cos(β) = -2sin(½(α+β))sin(½(α-β)) (21) Sum/difference of tangents (22) Formula for reducing the degree of sine sin 2 (α) = ½(1 - cos(2α)) (23) Formula for reducing the degree of cosine cos 2 (α) = ½(1 + cos(2α)) (24) Sum/difference of sine and cosine (25) Sum/difference of sine and cosine with coefficients (26) Basic relation of arcsine and arccosine arcsin(x) + arccos(x) = π/2 (27) Basic relationship between arctangent and arccotangent arctan(x) + arcctg(x) = π/2

General formulas

— printable version

Definitions Sine of angle α (designation sin(α)) is the ratio of the leg opposite to angle α to the hypotenuse. Cosine of angle α (designation cos(α)) is the ratio of the leg adjacent to the angle α to the hypotenuse. Angle tangent α (designation tan(α)) is the ratio of the side opposite to angle α to the adjacent side. An equivalent definition is the ratio of the sine of an angle α to the cosine of the same angle - sin(α)/cos(α). Cotangent of angle α (designation cotg(α)) is the ratio of the leg adjacent to the angle α to the opposite one. An equivalent definition is the ratio of the cosine of an angle α to the sine of the same angle - cos(α)/sin(α). Other trigonometric functions: secant — sec(α) = 1/cos(α); cosecant - cosec(α) = 1/sin(α). Note We do not specifically write the sign * (multiply) - where two functions are written in a row, without a space, it is implied. Clue To derive formulas for cosine, sine, tangent or cotangent of multiple (4+) angles, it is enough to write them according to the formulas respectively. cosine, sine, tangent or cotangent of the sum, or reduce to the previous cases, reducing to the formulas of triple and double angles. Addition Derivatives table

Page navigation.

Basic trigonometric identities

For a detailed description of these trigonometry formulas, their derivation and examples of application, see the article.

Reduction formulas

The rationale for these formulas, a mnemonic rule for memorizing them and examples of their application can be studied in the article.

Addition formulas

Formulas for double, triple, etc. angle

More detailed information is collected in the article formulas for double, triple, etc. angle

Half angle formulas

Half angle formulas show how trigonometric functions of a half angle are expressed in terms of the cosine of a whole angle. These trigonometric formulas follow from the double angle formulas.

Their conclusion and examples of application can be found in the article.

Degree reduction formulas

Trigonometric formulas for reducing degrees are designed to facilitate the transition from natural powers of trigonometric functions to sines and cosines in the first degree, but multiple angles. In other words, they allow you to reduce the powers of trigonometric functions to the first.

Formulas for the sum and difference of trigonometric functions

Formulas for the product of sines, cosines and sine by cosine

The transition from the product of trigonometric functions to a sum or difference is carried out using the formulas for the product of sines, cosines and sine by cosine.

Universal trigonometric substitution

References.

Algebra: Textbook for 9th grade. avg. school/Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Ed. S. A. Telyakovsky. - M.: Education, 1990. - 272 pp.: ill. - ISBN 5-09-002727-7
Bashmakov M. I. Algebra and the beginnings of analysis: Textbook. for 10-11 grades. avg. school - 3rd ed. - M.: Education, 1993. - 351 p.: ill. - ISBN 5-09-004617-4.
Algebra and the beginning of analysis: Proc. for 10-11 grades. general education institutions / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn and others; Ed. A. N. Kolmogorov. - 14th ed. - M.: Education, 2004. - 384 pp.: ill. - ISBN 5-09-013651-3.
Gusev V. A., Mordkovich A. G. Mathematics (a manual for those entering technical schools): Proc. allowance.- M.; Higher school, 1984.-351 p., ill.

All rights reserved.
Protected by copyright law. No part of the site, including internal materials and appearance, may be reproduced in any form or used without the prior written permission of the copyright holder.

Centered at a point A.
α - angle expressed in radians.

Definition
Sine (sin α)- This trigonometric function, depending on the angle α between the hypotenuse and the leg right triangle, equal to the ratio length of the opposite side |BC| to the length of the hypotenuse |AC|.

Cosine (cos α) is a trigonometric function depending on the angle α between the hypotenuse and the leg of a right triangle, equal to the ratio of the length of the adjacent leg |AB| to the length of the hypotenuse |AC|.

Accepted notations

;
;
.

Graph of the sine function, y = sin x

Graph of the cosine function, y = cos x

Properties of sine and cosine

Periodicity

Functions y = sin x and y = cos x periodic with period 2π.

Parity

The sine function is odd. The cosine function is even.

Domain of definition and values, extrema, increase, decrease

The sine and cosine functions are continuous in their domain of definition, that is, for all x (see proof of continuity). Their main properties are presented in the table (n - integer).

	y= sin x	y= cos x
Scope and continuity	- ∞ < x < + ∞	- ∞ < x < + ∞
Range of values	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Increasing
Descending
Maxima, y = 1
Minima, y = - 1
Zeros, y = 0
Intercept points with the ordinate axis, x = 0	y= 0	y= 1