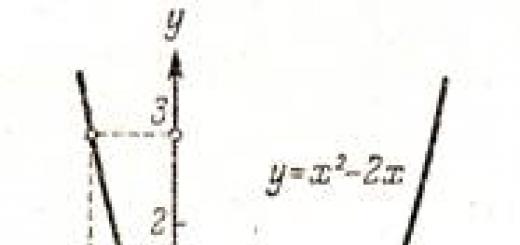Die Abhängigkeit einer Variablen y von einer Variablen x, bei der jeder Wert von x einem einzelnen Wert von y entspricht, wird als Funktion bezeichnet. Zur Bezeichnung verwenden Sie die Notation y=f(x). Jede Funktion hat eine Reihe grundlegender Eigenschaften, wie etwa Monotonie, Parität, Periodizität und andere.
Schauen Sie sich die Paritätseigenschaft genauer an.
Eine Funktion y=f(x) wird auch dann aufgerufen, wenn sie die folgenden zwei Bedingungen erfüllt:
2. Der Wert der Funktion am Punkt x, der zum Definitionsbereich der Funktion gehört, muss gleich dem Wert der Funktion am Punkt -x sein. Das heißt, für jeden Punkt x muss die folgende Gleichheit aus dem Definitionsbereich der Funktion erfüllt sein: f(x) = f(-x).
Graph einer geraden FunktionWenn Sie einen Graphen einer geraden Funktion zeichnen, ist dieser symmetrisch zur Oy-Achse.
Beispielsweise ist die Funktion y=x^2 gerade. Schauen wir es uns an. Der Definitionsbereich ist die gesamte numerische Achse, was bedeutet, dass sie symmetrisch zum Punkt O ist.
Nehmen wir ein beliebiges x=3. f(x)=3^2=9.
f(-x)=(-3)^2=9. Daher ist f(x) = f(-x). Somit sind beide Bedingungen erfüllt, was bedeutet, dass die Funktion gerade ist. Unten ist ein Diagramm der Funktion y=x^2.
Die Abbildung zeigt, dass der Graph symmetrisch zur Oy-Achse ist.
Graph einer ungeraden FunktionEine Funktion y=f(x) heißt ungerade, wenn sie die folgenden zwei Bedingungen erfüllt:
1. Der Definitionsbereich einer bestimmten Funktion muss in Bezug auf Punkt O symmetrisch sein. Das heißt, wenn ein Punkt a zum Definitionsbereich der Funktion gehört, muss der entsprechende Punkt -a auch zum Definitionsbereich gehören der gegebenen Funktion.
2. Für jeden Punkt x muss die folgende Gleichheit aus dem Definitionsbereich der Funktion erfüllt sein: f(x) = -f(x).
Der Graph einer ungeraden Funktion ist symmetrisch in Bezug auf Punkt O – den Koordinatenursprung. Beispielsweise ist die Funktion y=x^3 ungerade. Schauen wir es uns an. Der Definitionsbereich ist die gesamte numerische Achse, was bedeutet, dass sie symmetrisch zum Punkt O ist.
Nehmen wir ein beliebiges x=2. f(x)=2^3=8.
f(-x)=(-2)^3=-8. Daher ist f(x) = -f(x). Somit sind beide Bedingungen erfüllt, was bedeutet, dass die Funktion ungerade ist. Unten ist ein Diagramm der Funktion y=x^3.
Die Abbildung zeigt das deutlich komische Funktion y=x^3 ist symmetrisch zum Ursprung.
Eine Funktion heißt gerade (ungerade), wenn irgendetwas und die Gleichheit vorliegen 
.
Der Graph einer geraden Funktion ist symmetrisch zur Achse 
.
Der Graph einer ungeraden Funktion ist symmetrisch zum Ursprung.
Beispiel 6.2. Untersuchen Sie, ob eine Funktion gerade oder ungerade ist
1)
;
2)
;
3)
.
Lösung.
1) Die Funktion wird definiert, wenn 
. Wir werden finden 
.
Diese. 
. Dies bedeutet, dass diese Funktion gerade ist.
2) Die Funktion wird definiert, wenn 
Diese. 
. Daher ist diese Funktion ungerade.
3) Die Funktion ist für definiert, d.h. Für
,
. Daher ist die Funktion weder gerade noch ungerade. Nennen wir es eine Funktion allgemeiner Form.
Funktion 
heißt in einem bestimmten Intervall steigend (fallend), wenn in diesem Intervall jedem größeren Wert des Arguments ein größerer (kleinerer) Wert der Funktion entspricht.
Funktionen, die über ein bestimmtes Intervall ansteigen (abfallen), werden als monoton bezeichnet.
Wenn die Funktion 
differenzierbar auf dem Intervall 
und hat eine positive (negative) Ableitung 
, dann die Funktion 
nimmt in diesem Intervall zu (ab).
Beispiel 6.3. Finden Sie Intervalle der Monotonie von Funktionen
1)
;
3)
.
Lösung.
1) Diese Funktion ist auf dem gesamten Zahlenstrahl definiert. Finden wir die Ableitung.
Die Ableitung ist gleich Null, wenn 
Und 
. Der Definitionsbereich ist die Zahlenachse, geteilt durch Punkte 
,
in Intervallen. Bestimmen wir das Vorzeichen der Ableitung in jedem Intervall.
In der Pause 
Ist die Ableitung negativ, nimmt die Funktion in diesem Intervall ab.
In der Pause 
Die Ableitung ist positiv, daher nimmt die Funktion über dieses Intervall zu.
2) Diese Funktion ist definiert, wenn 
oder
.
Wir bestimmen das Vorzeichen des quadratischen Trinoms in jedem Intervall.
Somit ist der Definitionsbereich der Funktion
Finden wir die Ableitung 
,
, Wenn 
, d.h. 
, Aber 
. Bestimmen wir das Vorzeichen der Ableitung in den Intervallen 
.
In der Pause 
Die Ableitung ist negativ, daher nimmt die Funktion im Intervall ab 
. In der Pause 
Die Ableitung ist positiv, die Funktion nimmt über das Intervall zu 
.
Punkt 
wird als maximaler (minimaler) Punkt der Funktion bezeichnet 
, wenn es eine solche Umgebung des Punktes gibt 
das ist für jeden etwas 
Von dieser Umgebung aus gilt die Ungleichung 
.
Die Maximal- und Minimalpunkte einer Funktion werden als Extrempunkte bezeichnet.
Wenn die Funktion 
am Punkt 
ein Extremum hat, dann ist die Ableitung der Funktion an diesem Punkt gleich Null oder existiert nicht (eine notwendige Bedingung für die Existenz eines Extremums).
Die Punkte, an denen die Ableitung Null ist oder nicht existiert, werden als kritisch bezeichnet.
5. Ausreichende Bedingungen Existenz eines Extremums.Regel 1. Wenn während des Übergangs (von links nach rechts) durch den kritischen Punkt 
Derivat 
ändert das Vorzeichen von „+“ zu „–“, dann am Punkt 
Funktion 
hat ein Maximum; wenn von „–“ bis „+“, dann das Minimum; Wenn 
ändert das Vorzeichen nicht, dann gibt es kein Extremum.
Regel 2. Lassen Sie es auf den Punkt kommen 
erste Ableitung einer Funktion 
gleich Null 
, und die zweite Ableitung existiert und ist von Null verschieden. Wenn 
, Das 
– Höchstpunktzahl, wenn 
, Das 
– Minimalpunkt der Funktion.
Beispiel 6.4. Entdecken Sie die Maximal- und Minimalfunktionen:
1)
;
2)
;
3)
;
4)
.
Lösung.
1) Die Funktion ist im Intervall definiert und stetig 
.
Finden wir die Ableitung 
und löse die Gleichung 
, d.h. 
.Von hier 
- kritische Punkte.
Bestimmen wir das Vorzeichen der Ableitung in den Intervallen, 
.
Beim Durchfahren von Punkten 
Und 
Die Ableitung ändert das Vorzeichen von „–“ zu „+“, also gemäß Regel 1 
– Mindestpunktzahl.
Beim Passieren eines Punktes 
Die Ableitung ändert das Vorzeichen von „+“ zu „–“, also 
– Höchstpunktzahl.
,
.
2) Die Funktion ist im Intervall definiert und stetig 
. Finden wir die Ableitung 
.
Nachdem ich die Gleichung gelöst habe 
, wir werden finden 
Und 
- kritische Punkte. Wenn der Nenner 
, d.h. 
, dann existiert die Ableitung nicht. Also, 
– dritter kritischer Punkt. Bestimmen wir das Vorzeichen der Ableitung in Intervallen.
Daher hat die Funktion an diesem Punkt ein Minimum 
, Maximum in Punkten 
Und 
.
3) Eine Funktion ist definiert und stetig, wenn 
, d.h. bei 
.
Finden wir die Ableitung 
.
Lassen Sie uns kritische Punkte finden: 
Nachbarschaften von Punkten 
gehören nicht zum Definitionsbereich und sind daher keine Extrema. Schauen wir uns also die kritischen Punkte an 
Und 
.
4) Die Funktion ist im Intervall definiert und stetig 
. Verwenden wir Regel 2. Finden Sie die Ableitung 
.
Lassen Sie uns kritische Punkte finden:
Finden wir die zweite Ableitung 
und bestimmen Sie sein Vorzeichen an den Punkten 
An Punkten 
Funktion hat ein Minimum.
An Punkten 
Die Funktion hat ein Maximum.
Im Juli 2020 startet die NASA eine Expedition zum Mars. Raumfahrzeug wird dem Mars ein elektronisches Medium mit den Namen aller registrierten Expeditionsteilnehmer liefern.
Die Anmeldung der Teilnehmer ist offen. Holen Sie sich Ihr Ticket zum Mars über diesen Link.
Wenn dieser Beitrag Ihr Problem gelöst hat oder er Ihnen einfach gefallen hat, teilen Sie den Link dazu mit Ihren Freunden in sozialen Netzwerken.
Eine dieser Codeoptionen muss kopiert und in den Code Ihrer Webseite eingefügt werden, vorzugsweise zwischen Tags und oder unmittelbar nach dem Tag. Gemäß der ersten Option lädt MathJax schneller und verlangsamt die Seite weniger. Aber die zweite Option überwacht und lädt automatisch die neuesten Versionen von MathJax. Wenn Sie den ersten Code eingeben, muss dieser regelmäßig aktualisiert werden. Wenn Sie den zweiten Code einfügen, werden die Seiten langsamer geladen, aber Sie müssen die MathJax-Updates nicht ständig überwachen.
Der einfachste Weg, MathJax zu verbinden, ist in Blogger oder WordPress: Fügen Sie im Site-Kontrollfeld ein Widget hinzu, das zum Einfügen von JavaScript-Code von Drittanbietern entwickelt wurde, kopieren Sie die erste oder zweite Version des oben dargestellten Download-Codes hinein und platzieren Sie das Widget näher an den Anfang der Vorlage (übrigens ist dies überhaupt nicht notwendig, da das MathJax-Skript asynchron geladen wird). Das ist alles. Lernen Sie nun die Markup-Syntax von MathML, LaTeX und ASCIIMathML und Sie können mit der Einbettung beginnen mathematische Formeln zu den Webseiten Ihrer Website.
Ein weiterer Silvesterabend ... frostiges Wetter und Schneeflocken auf der Fensterscheibe ... All dies veranlasste mich, erneut über ... Fraktale zu schreiben und was Wolfram Alpha darüber weiß. Bei dieser Gelegenheit gibt es interessanter Artikel, das Beispiele zweidimensionaler fraktaler Strukturen enthält. Hier werden wir uns mehr ansehen komplexe Beispiele dreidimensionale Fraktale.
Ein Fraktal kann visuell als geometrische Figur oder Körper dargestellt (beschrieben) werden (was bedeutet, dass beide eine Menge, in diesem Fall eine Menge von Punkten) sind, deren Details dieselbe Form wie die ursprüngliche Figur selbst haben. Das heißt, es handelt sich um eine selbstähnliche Struktur, deren Details wir bei Vergrößerung genauso sehen wie ohne Vergrößerung. Im Falle von gewöhnlichen geometrische Figur(kein Fraktal), beim Vergrößern sehen wir Details, die mehr enthalten einfache Form als die Originalfigur selbst. Bei einer ausreichend hohen Vergrößerung sieht beispielsweise ein Teil einer Ellipse wie ein gerades Liniensegment aus. Dies ist bei Fraktalen nicht der Fall: Bei jeder Vergrößerung werden wir wieder dieselbe komplexe Form sehen, die sich bei jeder Vergrößerung immer wieder wiederholt.
Benoit Mandelbrot, der Begründer der Fraktalwissenschaft, schrieb in seinem Artikel Fraktale und Kunst im Namen der Wissenschaft: „Fraktale sind geometrische Formen, die in ihren Details ebenso komplex sind wie in ihrer allgemeinen Form. Das heißt, wenn ein Teil eines Fraktals auf die Größe des Ganzen vergrößert wird, erscheint es als Ganzes, entweder exakt oder vielleicht mit einer leichten Verformung.“
Verstecken anzeigen
Methoden zur Angabe einer FunktionDie Funktion sei durch die Formel gegeben: y=2x^(2)-3. Indem Sie der unabhängigen Variablen x beliebige Werte zuweisen, können Sie mit dieser Formel die entsprechenden Werte der abhängigen Variablen y berechnen. Wenn beispielsweise x=-0,5 ist, finden wir mithilfe der Formel, dass der entsprechende Wert von y y=2 \cdot (-0,5)^(2)-3=-2,5 ist.
Wenn Sie einen beliebigen Wert des Arguments x in der Formel y=2x^(2)-3 nehmen, können Sie nur einen Wert der entsprechenden Funktion berechnen. Die Funktion kann als Tabelle dargestellt werden:
| X | −2 | −1 | 0 | 1 | 2 | 3 |
| j | −4 | −3 | −2 | −1 | 0 | 1 |
Anhand dieser Tabelle können Sie sehen, dass für den Argumentwert −1 der Funktionswert −3 entspricht; und der Wert x=2 entspricht y=0 usw. Es ist auch wichtig zu wissen, dass jeder Argumentwert in der Tabelle nur einem Funktionswert entspricht.
Mithilfe von Diagrammen können weitere Funktionen spezifiziert werden. Anhand eines Diagramms wird ermittelt, welcher Wert der Funktion mit einem bestimmten Wert x korreliert. In den meisten Fällen handelt es sich dabei um einen Näherungswert der Funktion.
Gerade und ungerade FunktionEine Funktion ist eine gerade Funktion, wenn f(-x)=f(x) für jedes x im Definitionsbereich gilt. Eine solche Funktion ist symmetrisch zur Oy-Achse.
Eine Funktion ist eine ungerade Funktion, wenn f(-x)=-f(x) für jedes x im Definitionsbereich gilt. Eine solche Funktion ist symmetrisch zum Ursprung O (0;0) .
Die Funktion ist weder gerade noch ungerade und wird Funktion genannt Gesamtansicht, wenn es keine Symmetrie um die Achse oder den Ursprung aufweist.
Untersuchen wir die folgende Funktion auf Parität:
f(x)=3x^(3)-7x^(7)
D(f)=(-\infty ; +\infty) mit einem symmetrischen Definitionsbereich relativ zum Ursprung. f(-x)= 3 \cdot (-x)^(3)-7 \cdot (-x)^(7)= -3x^(3)+7x^(7)= -(3x^(3) -7x^(7))= -f(x) .
Das bedeutet, dass die Funktion f(x)=3x^(3)-7x^(7) ungerade ist.
Periodische FunktionEs wird die Funktion y=f(x) aufgerufen, in deren Definitionsbereich für jedes x die Gleichheit f(x+T)=f(x-T)=f(x) gilt periodische Funktion mit Periode T \neq 0 .
Wiederholen des Graphen einer Funktion auf einem beliebigen Segment der x-Achse mit der Länge T.
Die Intervalle, in denen die Funktion positiv ist, also f(x) > 0, sind Segmente der Abszissenachse, die den Punkten des Funktionsgraphen entsprechen, die über der Abszissenachse liegen.
f(x) > 0 auf (x_(1); x_(2)) \cup (x_(3); +\infty)
Intervalle, in denen die Funktion negativ ist, d. h. f(x)< 0 - отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих ниже оси абсцисс.
f(x)< 0 на (-\infty; x_{1}) \cup (x_{2}; x_{3})
Eine Funktion y=f(x), x \in
Ein Beispiel für eine von unten begrenzte Funktion: y=\sqrt(1+x^(2)) da y=\sqrt(1+x^(2)) \geq 1 für jedes x .
Eine Funktion y=f(x), x \in X heißt oben beschränkt, wenn es eine Zahl B gibt, für die für jedes x \in X die Ungleichung f(x) \neq B gilt.
Ein Beispiel für eine von unten begrenzte Funktion: y=\sqrt(1-x^(2)), x \in [-1;1] da y=\sqrt(1+x^(2)) \neq 1 für jedes x \ in [-1;1] .
Eine Funktion y=f(x), x \in X heißt normalerweise beschränkt, wenn es eine Zahl K > 0 gibt, für die die Ungleichung \left | gilt f(x)\right | \neq K für jedes x \in X .
Ein Beispiel für eine beschränkte Funktion: y=\sin x ist auf dem gesamten Zahlenstrahl beschränkt, da \left | \sin x \right | \neq 1 .
Zunehmende und abnehmende FunktionEs ist üblich, von einer Funktion zu sprechen, die über das betrachtete Intervall zunimmt, wenn ein größerer Wert von x einem größeren Wert der Funktion y=f(x) entspricht. Daraus folgt, dass bei zwei beliebigen Werten des Arguments x_(1) und x_(2) aus dem betrachteten Intervall mit x_(1) > x_(2) das Ergebnis y(x_(1)) > ist y(x_(2)).
Eine Funktion, die im betrachteten Intervall abnimmt, wird als abnehmende Funktion bezeichnet, wenn ein größerer Wert von x einem kleineren Wert der Funktion y(x) entspricht. Daraus folgt, dass, wenn man aus dem betrachteten Intervall zwei beliebige Werte des Arguments x_(1) und x_(2) und x_(1) > x_(2) nimmt, das Ergebnis y(x_(1)) sein wird.< y(x_{2}) .
Die Wurzeln einer Funktion werden üblicherweise als die Punkte bezeichnet, an denen die Funktion F=y(x) die Abszissenachse schneidet (sie werden durch Lösen der Gleichung y(x)=0 erhalten).
a) Wenn für x > 0 eine gerade Funktion zunimmt, dann nimmt sie für x ab< 0
b) Wenn eine gerade Funktion bei x > 0 abnimmt, nimmt sie bei x zu< 0
.png)
c) Wenn eine ungerade Funktion bei x > 0 zunimmt, dann nimmt sie auch bei x zu< 0
d) Wenn eine ungerade Funktion für x > 0 abnimmt, dann nimmt sie auch für x ab< 0
.png)
Der minimale Punkt der Funktion y=f(x) wird normalerweise als Punkt x=x_(0) bezeichnet, in dessen Umgebung es andere Punkte gibt (außer dem Punkt x=x_(0)), und für diese gilt dann die Ungleichung f( x ) > f(x_(0)) . y_(min) – Bezeichnung der Funktion am Min-Punkt.
Der Maximalpunkt der Funktion y=f(x) wird normalerweise als Punkt x=x_(0) bezeichnet, in dessen Umgebung es andere Punkte gibt (außer dem Punkt x=x_(0)), und für diese gilt dann die Ungleichung f( X )< f(x^{0}) . y_{max} - обозначение функции в точке max.
VoraussetzungNach dem Satz von Fermat gilt: f"(x)=0, wenn die Funktion f(x), die am Punkt x_(0) differenzierbar ist, an diesem Punkt ein Extremum hat.
Ausreichender ZustandBerechnungsschritte:
Die Ihnen bis zu einem gewissen Grad bekannt waren. Dort wurde auch darauf hingewiesen, dass der Bestand an Funktionsimmobilien sukzessive wieder aufgefüllt wird. In diesem Abschnitt werden zwei neue Eigenschaften besprochen.
Definition 1.
Die Funktion y = f(x), x є X, wird auch dann aufgerufen, wenn für jeden Wert x aus der Menge X die Gleichheit f (-x) = f (x) gilt.
Definition 2.
Die Funktion y = f(x), x є X, heißt ungerade, wenn für jeden Wert x aus der Menge X die Gleichheit f (-x) = -f (x) gilt.
Beweisen Sie, dass y = x 4 eine gerade Funktion ist.
Lösung. Wir haben: f(x) = x 4, f(-x) = (-x) 4. Aber(-x) 4 = x 4. Das bedeutet, dass für jedes x die Gleichheit f(-x) = f(x) gilt, d.h. Die Funktion ist gerade.
Ebenso lässt sich beweisen, dass die Funktionen y - x 2, y = x 6, y - x 8 gerade sind.
Beweisen Sie, dass y = x 3 ~ eine ungerade Funktion ist.
Lösung. Wir haben: f(x) = x 3, f(-x) = (-x) 3. Aber (-x) 3 = -x 3. Das bedeutet, dass für jedes x die Gleichheit f (-x) = -f (x) gilt, d.h. Die Funktion ist seltsam.
Ebenso lässt sich beweisen, dass die Funktionen y = x, y = x 5, y = x 7 ungerade sind.
Sie und ich waren bereits mehr als einmal davon überzeugt, dass neue Begriffe in der Mathematik meist einen „irdischen“ Ursprung haben, d.h. Sie können irgendwie erklärt werden. Dies ist sowohl bei geraden als auch bei ungeraden Funktionen der Fall. Siehe: y - x 3, y = x 5, y = x 7 sind ungerade Funktionen, während y = x 2, y = x 4, y = x 6 gerade Funktionen sind. Und im Allgemeinen können wir für jede Funktion der Form y = x" (im Folgenden werden wir diese Funktionen speziell untersuchen), bei der n eine natürliche Zahl ist, schließen: Wenn n nicht ist gerade Zahl, dann ist die Funktion y = x" ungerade; wenn n eine gerade Zahl ist, dann ist die Funktion y = xn gerade.
Es gibt auch Funktionen, die weder gerade noch ungerade sind. Dies ist zum Beispiel die Funktion y = 2x + 3. Tatsächlich ist f(1) = 5 und f (-1) = 1. Wie Sie sehen können, ist hier also weder die Identität f(-x) = f ( x), noch die Identität f(-x) = -f(x).
Eine Funktion kann also gerade, ungerade oder keines von beidem sein.
Untersuchung der Frage, ob gegebene Funktion gerade oder ungerade wird üblicherweise als Untersuchung einer Funktion auf Parität bezeichnet.
In den Definitionen 1 und 2 wir reden überüber die Werte der Funktion an den Punkten x und -x. Dies setzt voraus, dass die Funktion sowohl am Punkt x als auch am Punkt -x definiert ist. Dies bedeutet, dass Punkt -x gleichzeitig mit Punkt x zum Definitionsbereich der Funktion gehört. Wenn eine Zahlenmenge X zusammen mit jedem ihrer Elemente x auch das Gegenelement -x enthält, dann heißt X eine symmetrische Menge. Nehmen wir an, (-2, 2), [-5, 5], (-oo, +oo) sind symmetrische Mengen, während )
