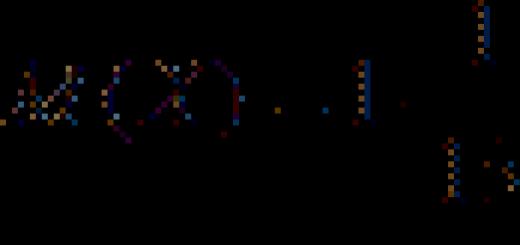Centered at a point A.
α - angle expressed in radians.

Definition
Sine (sin α) is a trigonometric function depending on the angle α between the hypotenuse and the leg right triangle, equal to the ratio length of the opposite side |BC| to the length of the hypotenuse |AC|.

Cosine (cos α) is a trigonometric function depending on the angle α between the hypotenuse and the leg of a right triangle, equal to the ratio of the length of the adjacent leg |AB| to the length of the hypotenuse |AC|.

Accepted notations

;
;
.

;
;
.

Graph of the sine function, y = sin x

Graph of the cosine function, y = cos x

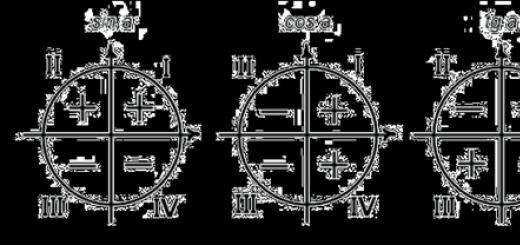
Properties of sine and cosine

Periodicity

Functions y = sin x and y = cos x periodic with period 2π.

Parity

The sine function is odd. The cosine function is even.

Domain of definition and values, extrema, increase, decrease

The sine and cosine functions are continuous in their domain of definition, that is, for all x (see proof of continuity). Their main properties are presented in the table (n - integer).

	y= sin x	y= cos x
Scope and continuity	- ∞ < x < + ∞	- ∞ < x < + ∞
Range of values	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Increasing
Descending
Maxima, y ​​= 1
Minima, y ​​= - 1
Zeros, y = 0
Intercept points with the ordinate axis, x = 0	y= 0	y= 1

Basic formulas

Sum of squares of sine and cosine

Formulas for sine and cosine from sum and difference

;
;

Formulas for the product of sines and cosines

Sum and difference formulas

Expressing sine through cosine

;
;
;
.

Expressing cosine through sine

;
;
;
.

Expression through tangent

; .

When , we have:
; .

At :
; .

Table of sines and cosines, tangents and cotangents

This table shows the values ​​of sines and cosines for certain values ​​of the argument.

Expressions through complex variables

;

Euler's formula

Expressions through hyperbolic functions

;
;

Derivatives

; . Deriving formulas > > >

Derivatives of nth order:
{ -∞ < x < +∞ }

Secant, cosecant

Inverse functions

The inverse functions of sine and cosine are arcsine and arccosine, respectively.

Arcsine, arcsin

Arccosine, arccos

Used literature:
I.N. Bronstein, K.A. Semendyaev, Handbook of mathematics for engineers and college students, “Lan”, 2009.

Basic Concepts

Let us first recall the definition even, odd and periodic functions.

Definition 2

An even function is a function that does not change its value when the sign of the independent variable changes:

Definition 3

A function that repeats its values ​​at some regular interval:

T -- period of the function.

Even and odd trigonometric functions

Consider the following figure (Fig. 1):

Figure 1.

Here $\overrightarrow(OA_1)=(x_1,y_1)$ and $\overrightarrow(OA_2)=(x_2,y_2)$ are vectors of unit length, symmetric about the $Ox$ axis.

It is obvious that the coordinates of these vectors are related by the following relations:

Since the trigonometric functions of sine and cosine can be determined using the unit trigonometric circle, then we find that the sine function will be odd, and the cosine function will be an even function, that is:

Periodicity of trigonometric functions

Consider the following figure (Fig. 2).

Figure 2.

Here $\overrightarrow(OA)=(x,y)$ is a vector of unit length.

Let's make a complete revolution with the vector $\overrightarrow(OA)$. That is, let's turn given vector by $2\pi $ radians. After this, the vector will completely return to its original position.

Since the trigonometric functions of sine and cosine can be determined using the unit trigonometric circle, we obtain that

That is, the sine and cosine functions are periodic functions with the smallest period $T=2\pi $.

Let us now consider the functions of tangent and cotangent. Since $tgx=\frac(sinx)(cosx)$, then

Since $сtgx=\frac(cosx)(sinx)$, then

Examples of problems using parity, oddness and periodicity of trigonometric functions

Example 1

Prove the following statements:

a) $tg(385)^0=tg(25)^0$

c) $sin((-721)^0)=-sin1^0$

a) $tg(385)^0=tg(25)^0$

Since tangent is a periodic function with a minimum period $(360)^0$, we get

b) $(cos \left(-13\pi \right)\ )=-1$

Since cosine is an even and periodic function with a minimum period of $2\pi $, we get

\[(cos \left(-13\pi \right)\ )=(cos 13\pi \ )=(cos \left(\pi +6\cdot 2\pi \right)=cos\pi \ )=- 1\]

c) $sin((-721)^0)=-sin1^0$

Since sine is an odd and periodic function with a minimum period of $(360)^0$, we get

The dependence of a variable y on a variable x, in which each value of x corresponds to a single value of y, is called a function. For designation use the notation y=f(x). Each function has a number of basic properties, such as monotonicity, parity, periodicity and others.

Properties of parity and periodicity

Let us consider in more detail the properties of parity and periodicity, using the example of the basic trigonometric functions: y=sin(x),y=cos(x), y=tg(x), y=ctg(x).

A function y=f(x) is called even if it satisfies the following two conditions:

2. The value of the function at point x, belonging to the domain of definition of the function, must be equal to the value of the function at point -x. That is, for any point x, the following equality must be satisfied from the domain of definition of the function: f(x) = f(-x).

If you plot a graph of an even function, it will be symmetrical about the Oy axis.

For example, the trigonometric function y=cos(x) is even.

Properties of oddness and periodicity

A function y=f(x) is called odd if it satisfies the following two conditions:

1. The domain of definition of a given function must be symmetrical with respect to point O. That is, if some point a belongs to the domain of definition of the function, then the corresponding point -a must also belong to the domain of definition of the given function.

2. For any point x, the following equality must be satisfied from the domain of definition of the function: f(x) = -f(x).

The graph of an odd function is symmetrical with respect to point O - the origin of coordinates.

For example, the trigonometric functions y=sin(x), y=tg(x), y=ctg(x) are odd.

Periodicity of trigonometric functions

The function y=f (x) is called periodic if there is a certain number T!=0 (called the period of the function y=f (x)), such that for any value of x belonging to the domain of definition of the function, the numbers x + T and x-T also belong to the domain of definition of the function and the equality f(x)=f(x+T)=f(x-T) holds.

It should be understood that if T is the period of the function, then the number k*T, where k is any integer other than zero, will also be the period of the function. Based on the above, we find that any periodic function has infinitely many periods. Most often, the conversation is about the smallest period of a function.

The trigonometric functions sin(x) and cos(x) are periodic, with the smallest period equal to 2*π.

satisfying the system of inequalities:

b) Consider a set of numbers on the number line that satisfy the system of inequalities:

Find the sum of the lengths of the segments that make up this set.

§ 7. The simplest formulas

In § 3 we established for sharp cornersα such a formula:

			sin2 α + cos2 α = 1.
				Same formula			in case
				when α is any			actually
				le, let M be a point on trigonometry
				ical circle corresponding to
				number α (Fig. 7.1). Then		M has co-
				ordinates x = cos α, y
				However, every point (x; y) lying on
				circle of unit radius with center
				trome at the origin, satisfying
				satisfies the equation x2 + y2		1, where from
				cos2 α + sin2 α = 1, as required.

So, the formula cos2 α + sin2 α = 1 follows from the equation of the circle. It may seem that we have thereby given a new proof of this formula for acute angles (in comparison with that indicated in § 3, where we used the Pythagorean theorem). The difference, however, is purely external: when deriving the equation of a circle x2 + y2 = 1, the same Pythagorean theorem is used.

For acute angles we also obtained other formulas, for example

According to the symbol, the right side is always non-negative, while the left side may well be negative. For the formula to be true for all α, it must be squared. The resulting equality is: cos2 α = 1/(1 + tan2 α). Let us prove that this formula is true for all α:1

1/(1 + tan2			sin2 α			cos2 α	Cos2 α.
			cos2 α			sin2 α + cos2 α

Problem 7.1. Derive all the formulas below from the definitions and the formula sin2 α + cos2 α = 1 (we have already proven some of them):

sin2 α + cos2 α = 1;

tg2 α =

tg2 α

sin2 α =

tg α · ctg α = 1;

cos2 α

1 + tan2 α

ctg2 α

Ctg2

cos2 α =

1 + cotg2 α

sin2

These formulas allow, knowing the value of one of the trigonometric functions given number, almost find everything else-

new Let, for example, we know that sin x = 1/2. Then cos2 x =

1−sin2 x = 3/4, so cos x is either 3/2 or − 3/2. To find out which of these two numbers cos x is equal to, additional information is needed.

Problem 7.2. Show with examples that both of the above cases are possible.

Problem 7.3. a) Let tan x = −1. Find sin x. How many answers does this problem have?

b) Let, in addition to the conditions of point a) we know that sin x< 0. Сколько теперь ответов у задачи?

1 For which tan α is defined, i.e. cos α 6= 0.

Problem 7.4. Let sin x = 3/5, x [π/2; 3π/2]. Find tg x.

Problem 7.5. Let tan x = 3, cos x > sin x. Find cos x, sin x.

Problem 7.6. Let tg x = 3/5. Find sin x + 2 cos x. cos x − 3 sin x

Problem 7.7. Prove the identities:

tan α − sin α

c) sin α + cos α cot α + sin α tan α + cos α =

Problem 7.8. Simplify the expressions:

a) (sin α + cos α)2 + (sin α − cos α)2 ; b) (tg α + ctg α)2 + (tg α − ctg α)2 ;

c) sin α(2 + cot α)(2 cot α + 1) − 5 cos α.

§ 8. Periods of trigonometric functions

The numbers x, x+2π, x−2π correspond to the same point on the trigonometric circle (if you walk an extra circle along the trigonometric circle, you will come back to where you were). This implies the following identities, which were already discussed in § 5:

sin(x + 2π) = sin(x − 2π) = sin x; cos(x + 2π) = cos(x − 2π) = cos x.

In connection with these identities we have already used the term “period”. Let us now give precise definitions.

Definition. The number T 6= 0 is called the period of the function f if for all x the equalities f(x − T) = f(x + T) = f(x) are true (it is assumed that x + T and x − T are included in the domain of definition of the function , if it includes x). A function is called periodic if it has a period (at least one).

Periodic functions naturally arise when describing oscillatory processes. One of such processes has already been discussed in § 5. Here are more examples:

1) Let ϕ = ϕ(t) be the angle of deviation of the swinging pendulum of the clock from the vertical at the moment t. Then ϕ is a periodic function of t.

2) The voltage (“potential difference,” as a physicist would say) between two sockets of an AC outlet, es-

whether it is considered as a function of time, is a periodic function1.

3) Let us hear the musical sound. Then the air pressure at a given point is a periodic function of time.

If a function has a period T, then the periods of this function will also be the numbers −T, 2T, −2T. . . - in a word, all numbers nT, where n is an integer that is not equal to zero. Indeed, let us check, for example, that f(x + 2T) = f(x):

f(x + 2T) = f((x + T) + T) = f(x + T) = f(x).

Definition. The smallest positive period of a function f is - in accordance with the literal meaning of the words - a positive number T such that T is a period of f and no positive number less than T is a period of f.

A periodic function is not required to have the smallest positive period (for example, a function that is constant has a period of any number at all and, therefore, it does not have the smallest positive period). We can also give examples of non-constant periodic functions that do not have the smallest positive period. Nevertheless, in most interesting cases, the smallest positive period of periodic functions exists.

1 When they say “the voltage in the network is 220 volts,” they mean its “rms value,” which we will talk about in § 21. The voltage itself changes all the time.

Rice. 8.1. Period of tangent and cotangent.

In particular, the smallest positive period of both sine and cosine is 2π. Let's prove this, for example, for the function y = sin x. Let, contrary to what we claim, sine has a period T such that 0< T < 2π. При x = π/2 имеем sin x = = 1. Будем теперь увеличивать x. В точке x + T значение синуса должно быть также равно 1. Но в следующий раз синус будет равен 1 только при x = (π/2) + 2π. Поэтому период синуса быть меньше 2π не может. Доказательство для косинуса аналогично.

The smallest positive period of the function describing the oscillations (as in our examples 1–3) is simply called the period of these oscillations.

Since 2π is the period of sine and cosine, it will also be the period of tangent and cotangent. However, for these functions, 2π is not the smallest period: the smallest positive period of the tangent and cotangent will be π. In fact, the points corresponding to the numbers x and x + π on the trigonometric circle are diametrically opposed: from point x to point x + 2π one must travel a distance π exactly equal to half the circle. Now, if we use the definition of tangent and cotangent using the axes of tangents and cotangents, the equalities tg(x + π) = tan x and ctg(x + π) = ctg x will become obvious (Fig. 8.1). It is easy to check (we will suggest doing this in the problems) that π is indeed the smallest positive period of the tangent and cotangent.

One note about terminology. The words “period of a function” are often used to mean “smallest positive period.” So if in an exam you are asked: “Is 100π the period of the sine function?”, do not rush to answer, but clarify whether you mean the smallest positive period or just one of the periods.

Trigonometric functions - typical example periodic functions: any “not very bad” periodic function can in some sense be expressed in terms of trigonometric ones.

Problem 8.1. Find the smallest positive periods of the functions:

				c) y = cos πx;

d) y = cos x + cos(1.01x).

Problem 8.2. The dependence of voltage in an alternating current network on time is given by the formula U = U0 sin ωt (here t is time, U is voltage, U0 and ω are constants). The frequency of alternating current is 50 Hertz (this means that the voltage makes 50 oscillations per second).

a) Find ω, assuming that t is measured in seconds;

b) Find the (smallest positive) period of U as a function of t.

Problem 8.3. a) Prove that the smallest positive period of the cosine is 2π;

b) Prove that the smallest positive period of the tangent is equal to π.

Problem 8.4. Let the smallest positive period of the function f be T. Prove that all its other periods are of the form nT for some integers n.

Problem 8.5. Prove that the following functions are not periodic.

Trigonometric functions periodic, that is, they are repeated after a certain period. As a result, it is enough to study the function on this interval and extend the discovered properties to all other periods.

Instructions

1. If you are given a primitive expression in which there is only one trigonometric function (sin, cos, tg, ctg, sec, cosec), and the angle inside the function is not multiplied by any number, and it itself is not raised to any power - use the definition. For expressions containing sin, cos, sec, cosec, boldly set the period to 2P, and if the equation contains tg, ctg, then P. Say, for the function y=2 sinx+5, the period will be equal to 2P.

2. If the angle x under the sign of a trigonometric function is multiplied by some number, then in order to find the period of this function, divide the typical period by this number. Let's say you are given a function y = sin 5x. The typical period for a sine is 2P; dividing it by 5, you get 2P/5 - this is the desired period of this expression.

3. To find the period of a trigonometric function raised to a power, evaluate the parity of the power. For even degree reduce the typical period by half. Let's say, if you are given the function y = 3 cos^2x, then the typical period 2P will decrease by 2 times, so the period will be equal to P. Please note that the functions tg, ctg are periodic to P to every degree.

4. If you are given an equation containing the product or quotient of two trigonometric functions, first find the period for all of them separately. After this, find the minimum number that would contain the integer of both periods. Let's say the function y=tgx*cos5x is given. For tangent the period is P, for cosine 5x the period is 2P/5. The minimum number in which both of these periods can be accommodated is 2P, thus the desired period is 2P.

5. If you find it difficult to do it in the suggested way or doubt the result, try to do it by definition. Take T as the period of the function; it is larger than zero. Substitute the expression (x + T) instead of x into the equation and solve the resulting equality as if T were a parameter or a number. As a result, you will discover the value of the trigonometric function and be able to find the smallest period. Let's say, as a result of the relief, you get the identity sin (T/2) = 0. The minimum value of T at which it is performed is 2P, this will be the result of the task.

A periodic function is a function that repeats its values ​​after some non-zero period. The period of a function is a number that, when added to the argument of a function, does not change the value of the function.

You will need

• Knowledge of elementary mathematics and basic review.

Instructions

1. Let us denote the period of the function f(x) by the number K. Our task is to discover this value of K. To do this, imagine that the function f(x), using the definition of a periodic function, we equate f(x+K)=f(x).

2. We solve the resulting equation regarding the unknown K, as if x were a constant. Depending on the value of K, there will be several options.

3. If K>0 – then this is the period of your function. If K=0 – then the function f(x) is not periodic. If the solution to the equation f(x+K)=f(x) does not exist for any K not equal zero, then such a function is called aperiodic and it also has no period.

Video on the topic

Pay attention!
All trigonometric functions are periodic, and all polynomial functions with a degree greater than 2 are aperiodic.

Useful advice
The period of a function consisting of 2 periodic functions, is the least universal multiple of the periods of these functions.

Trigonometric equations are equations that contain trigonometric functions of an unknown argument (for example: 5sinx-3cosx =7). In order to learn how to solve them, you need to know some ways to do this.

Instructions

1. Solving such equations consists of 2 stages. The first is reforming the equation to acquire its simplest form. The simplest trigonometric equations are: Sinx=a; Cosx=a, etc.

2. The second is the solution to the resulting simplest trigonometric equation. There are basic ways to solve equations of this type: Solving algebraically. This method is famously known from school, from an algebra course. Otherwise called the method of variable replacement and substitution. Using reduction formulas, we transform, make a substitution, and then find the roots.

3. Factoring an equation. First, we move all the terms to the left and factor them.

4. Reducing the equation to a homogeneous one. Equations are called homogeneous equations if all terms are of the same degree and the sine and cosine of the same angle. In order to solve it, you should: first transfer all its terms from the right side to the left side; move all universal factors out of brackets; equate factors and brackets to zero; equated brackets give a homogeneous equation of a lower degree, which should be divided by cos (or sin) to the highest degree; solve the result algebraic equation regarding tan.

5. The next way is to move to a half angle. Say, solve the equation: 3 sin x – 5 cos x = 7. Let’s move on to the half angle: 6 sin (x / 2) · cos (x / 2) – 5 cos? (x / 2) + 5 sin ? (x / 2) = 7 sin ? (x / 2) + 7 cos ? (x/ 2) , after which we reduce all terms into one part (preferably the right side) and solve the equation.

6. Entry of auxiliary angle. When we replace the integer value cos(a) or sin(a). The sign “a” is an auxiliary angle.

7. A method of reforming a product into a sum. Here you need to apply the appropriate formulas. Let's say given: 2 sin x · sin 3x = cos 4x. Solve it by transforming the left side into a sum, that is: cos 4x – cos 8x = cos 4x ,cos 8x = 0 ,8x = p / 2 + pk ,x = p / 16 + pk / 8.

8. The final method is called multi-function substitution. We transform the expression and make a change, say Cos(x/2)=u, and then solve the equation with the parameter u. When purchasing the total, we convert the value to the opposite.

Video on the topic

If we consider points on a circle, then points x, x + 2π, x + 4π, etc. coincide with each other. Thus, trigonometric functions on a straight line periodically repeat their meaning. If the period is famous functions, it is possible to construct a function on this period and repeat it on others.

Instructions

1. The period is a number T such that f(x) = f(x+T). In order to find the period, solve the corresponding equation, substituting x and x+T as an argument. In this case, they use the already well-known periods for functions. For the sine and cosine functions the period is 2π, and for the tangent and cotangent functions it is π.

2. Let the function f(x) = sin^2(10x) be given. Consider the expression sin^2(10x) = sin^2(10(x+T)). Use the formula to reduce the degree: sin^2(x) = (1 – cos 2x)/2. Then you get 1 – cos 20x = 1 – cos 20(x+T) or cos 20x = cos (20x+20T). Knowing that the period of the cosine is 2π, 20T = 2π. This means T = π/10. T is the minimum correct period, and the function will be repeated after 2T, and after 3T, and in the other direction along the axis: -T, -2T, etc.

Useful advice
Use formulas to reduce the degree of a function. If you already know the periods of some functions, try to reduce the existing function to known ones.

Examining a function for evenness and oddness helps to build a graph of the function and understand the nature of its behavior. For this research, you need to compare this function written for the argument “x” and for the argument “-x”.

Instructions

1. Write down the function you want to investigate in the form y=y(x).

2. Replace the argument of the function with “-x”. Substitute this argument into a functional expression.

3. Simplify the expression.

4. Thus, you have the same function written for arguments “x” and “-x”. Look at these two entries. If y(-x)=y(x), then this is even function.If y(-x)=-y(x), then this odd function.If it is impossible to say about a function that y(-x)=y(x) or y(-x)=-y(x), then by the property of parity it is a function of universal form. That is, it is neither even nor odd.

5. Write down your findings. Now you can use them in constructing a graph of a function or in a future analytical study of the properties of a function.

6. It is also possible to talk about the evenness and oddness of a function in the case when the graph of the function is already given. Let's say the graph served as the result of a physical experiment. If the graph of a function is symmetrical about the ordinate axis, then y(x) is an even function. If the graph of a function is symmetrical about the abscissa axis, then x(y) is an even function. x(y) is a function inverse to the function y(x). If the graph of a function is symmetrical about the origin (0,0), then y(x) is an odd function. It will also be odd inverse function x(y).

7. It is important to remember that the idea of ​​evenness and oddness of a function has a direct connection with the domain of definition of the function. If, say, an even or odd function does not exist at x=5, then it does not exist at x=-5, which cannot be said about a function of a universal form. When establishing even and odd parity, pay attention to the domain of the function.

8. Finding a function for evenness and oddness correlates with finding a set of function values. To find the set of values ​​of an even function, it is enough to look at half of the function, to the right or to the left of zero. If at x>0 the even function y(x) takes values ​​from A to B, then it will take the same values ​​at x<0.Для нахождения множества значений, принимаемых нечетной функцией, тоже довольно разглядеть только одну часть функции. Если при x>0 odd function y(x) takes a range of values ​​from A to B, then at x<0 она будет принимать симметричный диапазон значений от (-В) до (-А).

“Trigonometric” once began to be called functions that are determined by the dependence of the acute angles in a right triangle on the lengths of its sides. Such functions include, first of all, sine and cosine, secondly, the inverse of these functions, secant and cosecant, their derivatives tangent and cotangent, as well as the inverse functions arcsine, arccosine, etc. It is more positive to speak not about the “solution” of such functions, but about their “calculation”, that is, about finding a numerical value.

Instructions

1. If the argument of the trigonometric function is unknown, then its value can be calculated by an indirect method based on the definitions of these functions. To do this, you need to know the lengths of the sides of the triangle, the trigonometric function for one of the angles of which needs to be calculated. Let's say, by definition, the sine of an acute angle in a right triangle is the ratio of the length of the leg opposite this angle to the length of the hypotenuse. It follows from this that to find the sine of an angle it is enough to know the lengths of these 2 sides. A similar definition states that the sine of an acute angle is the ratio of the length of the leg adjacent to this angle to the length of the hypotenuse. The tangent of an acute angle can be calculated by dividing the length of the opposite leg by the length of the adjacent one, and the cotangent requires dividing the length of the adjacent leg by the length of the opposite one. To calculate the secant of an acute angle, you need to find the ratio of the length of the hypotenuse to the length of the leg adjacent to the required angle, and the cosecant is determined by the ratio of the length of the hypotenuse to the length of the opposite leg.

2. If the argument of the trigonometric function is correct, then you do not need to know the lengths of the sides of the triangle - you can use tables of values ​​or calculators of trigonometric functions. Such a calculator is included in the standard programs of the Windows operating system. To launch it, you can press the Win + R key combination, enter the calc command and click the “OK” button. In the program interface, expand the “View” section and select the “Engineer” or “Scientist” item. After this, it is possible to introduce the argument of the trigonometric function. To calculate the functions sine, cosine and tangent, rather after entering the value, click on the corresponding interface button (sin, cos, tg), and to find their inverse arcsine, arccosine and arctangent, you should check the Inv checkbox in advance.

3. There are also alternative methods. One of them is to go to the website of the search engine Nigma or Google and enter the desired function and its argument as a search query (say, sin 0.47). These search engines have built-in calculators, so after sending such a request you will receive the value of the trigonometric function you entered.

Video on the topic

Tip 7: How to discover the value of trigonometric functions

Trigonometric functions first appeared as tools for abstract mathematical calculations of the dependences of the values ​​of acute angles in a right triangle on the lengths of its sides. Now they are widely used in both scientific and technical fields of human activity. For utilitarian calculations of trigonometric functions from given arguments, you can use various tools - several of them that are especially accessible are described below.

Instructions

1. Use, say, the calculator program installed by default with the operating system. It opens by selecting the “Calculator” item in the “Service” folder from the “Typical” subsection, located in the “All programs” section. This section can be found by opening the main menu of the operating system by clicking on the “Start” button. If you are using the Windows 7 version, then you are likely to simply enter the word “Calculator” in the “Discover programs and files” field of the main menu, and then click on the corresponding link in the search results.

2. Enter the angle value for which you want to calculate the trigonometric function, and then click on the button corresponding to this function - sin, cos or tan. If you are concerned about inverse trigonometric functions (arc sine, arc cosine or arc tangent), then first click the button labeled Inv - it reverses the functions assigned to the calculator's guide buttons.

3. In earlier versions of the OS (say, Windows XP), to access trigonometric functions, you need to open the “View” section in the calculator menu and select the “Engineering” line. In addition, instead of the Inv button, the interface of older versions of the program has a checkbox with the same inscription.

4. You can do without a calculator if you have Internet access. There are many services on the Internet that offer trigonometric function calculators organized in different ways. One of the particularly convenient options is built into the Nigma search engine. Going to its main page, simply enter the value that worries you in the search query field - say, “arc tangent 30 degrees”. After clicking the “Detect!” button The search engine will calculate and show the result of the calculation - 0.482347907101025.

Video on the topic

Trigonometry is a branch of mathematics for understanding functions that express different dependences of the sides of a right triangle on the values ​​of the acute angles at the hypotenuse. Such functions were called trigonometric, and to facilitate working with them, trigonometric functions were derived identities .

Performance identities in mathematics it denotes an equality that is satisfied for all values ​​of the arguments of the functions included in it. Trigonometric identities are equalities of trigonometric functions, confirmed and accepted to simplify work with trigonometric formulas. A trigonometric function is an elementary function of the dependence of one of the legs of a right triangle on the value of the acute angle at the hypotenuse. The six basic trigonometric functions that are most often used are sin (sine), cos (cosine), tg (tangent), ctg (cotangent), sec (secant) and cosec (cosecant). These functions are called direct functions, there are also inverse functions, say, sine - arcsine, cosine - arccosine, etc. Initially, trigonometric functions were reflected in geometry, after which they spread to other areas of science: physics, chemistry, geography, optics, probability theory , as well as acoustics, music theory, phonetics, computer graphics and many others. Nowadays it is difficult to imagine mathematical calculations without these functions, although in the distant past they were used only in astronomy and architecture. Trigonometric identities are used to simplify work with long trigonometric formulas and reduce them to a digestible form. There are six main trigonometric identities; they are related to direct trigonometric functions: tg ? = sin?/cos?; sin^2? +cos^2? = 1; 1 + tg^2? = 1/cos^2?; 1 + 1/tg^2? = 1/sin^2?; sin (?/2 – ?) = cos ?; cos (?/2 – ?) = sin ?. These identities easy to confirm from the properties of the ratio of sides and angles in a right triangle: sin ? = BC/AC = b/c; cos? = AB/AC = a/c; tg? = b/a. The first identity tg ? = sin ?/cos ? follows from the ratio of the sides in the triangle and the exclusion of side c (hypotenuse) when dividing sin by cos. The identity ctg ? is defined in the same way. = cos ?/sin ?, because ctg ? = 1/tg ?.By the Pythagorean theorem a^2 + b^2 = c^2. Let's divide this equality by c^2, we get the second identity: a^2/c^2 + b^2/c^2 = 1 => sin^2 ? + cos^2 ? = 1.Third and fourth identities obtained by dividing, respectively, by b^2 and a^2: a^2/b^2 + 1 = c^2/b^2 => tg^2 ? + 1 = 1/cos^2 ?;1 + b^2/a^2 = c^2/a^2 => 1 + 1/tg^2 ? = 1/sin^ ? or 1 + ctg^2 ? = 1/sin^2 ?. Fifth and sixth basic identities are proven by determining the sum of the acute angles of a right triangle, which is equal to 90° or?/2.More difficult trigonometric identities: formulas for adding arguments, double and triple angles, reducing degrees, reforming the sum or product of functions, as well as formulas for trigonometric substitution, namely expressions of basic trigonometric functions through tg of a half angle: sin ?= (2*tg ?/2)/(1 + tan^2 ?/2);cos ? = (1 – tg^2 ?/2)/(1 = tg^2 ?/2);tg ? = (2*tg ?/2)/(1 – tg^2 ?/2).

The need to find the minimum meaning mathematical functions is of actual interest in solving applied problems, say, in economics. Huge meaning minimizing losses is essential for business activities.

Instructions

1. In order to discover the minimum meaning functions, it is necessary to determine at what value of the argument x0 the inequality y(x0) will be satisfied? y(x), where x? x0. As usual, this problem is solved over a certain interval or in each range of values functions, if one is not specified. One aspect of the solution is finding fixed points.

2. A stationary point is called meaning argument in which the derivative functions goes to zero. According to Fermat's theorem, if a differentiable function takes an extremal meaning at some point (in this case, a local minimum), then this point is stationary.

3. Minimum meaning the function often takes on exactly this point, but it cannot be determined invariably. Moreover, it is not always possible to say with precision what the minimum is functions or he accepts the infinitely small meaning. Then, as usual, they find the limit to which it tends as it decreases.

4. In order to determine the minimum meaning functions, you need to perform a sequence of actions consisting of four stages: finding the domain of definition functions, acquisition of fixed points, overview of values functions at these points and at the ends of the gap, detecting the minimum.

5. It turns out that some function y(x) is given on an interval with boundaries at points A and B. Find the domain of its definition and find out whether the interval is its subset.

6. Calculate Derivative functions. Equate the resulting expression to zero and find the roots of the equation. Check whether these stationary points fall within the gap. If not, then they are not taken into account at the next stage.

7. Examine the gap for the type of boundaries: open, closed, compound or immeasurable. This determines how you search for the minimum meaning. Let's say the segment [A, B] is a closed interval. Plug them into the function and calculate the values. Do the same with a stationary point. Select the lowest total.

8. With open and immeasurable intervals the situation is somewhat more difficult. Here you will have to look for one-sided limits that do not invariably give an unambiguous result. Say, for an interval with one closed and one punctured boundary [A, B), one should find a function at x = A and a one-sided limit lim y at x? B-0.