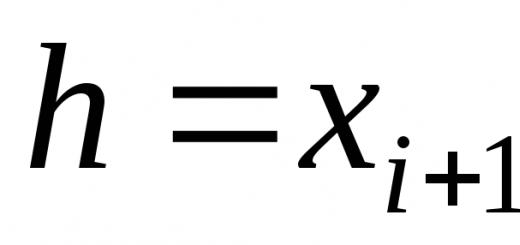This method proposes to approximate the integrand on a partial segment by a parabola passing through the points
(x j , f(x j)), Where j = i-1; i-0.5; i, that is, we approximate the integrand function by a Lagrange interpolation polynomial of the second degree:

After carrying out the integration, we get:

That's what it is Simpson's formula or the parabolic formula. On the segment
[a, b] Simpson's formula takes the form

A graphical representation of the Simpson method is shown in Fig. 2.4.

Rice. 10.4. Simpson method

Let’s get rid of fractional indices in expression (2.16) by redesignating the variables:

Then Simpson's formula takes the form

The error of formula (2.18) is estimated by the following expression:

Where h·n = b-a, . Thus, the error of Simpson's formula is proportional to O(h 4).

Comment. It should be noted that in Simpson’s formula the integration segment is necessarily divided into even number of intervals.

10.5. Calculation of definite integrals by methods
Monte Carlo

The methods discussed earlier are called deterministic , that is, devoid of the element of chance.

Monte Carlo methods(MMK) are numerical methods for solving mathematical problems using the modeling of random variables. MMCs allow one to successfully solve mathematical problems caused by probabilistic processes. Moreover, when solving problems that are not associated with any probabilities, you can artificially come up with a probabilistic model (and even more than one) that allows you to solve these problems. Consider the calculation of the definite integral

When calculating this integral using the rectangle formula, the interval [ a, b] split into N identical intervals, in the middle of which the values ​​of the integrand were calculated. By calculating the function values ​​at random nodes, you can get a more accurate result:

Here γ i is a random number uniformly distributed over the interval
. The error in calculating the MMC integral is ~ , which is significantly greater than that of previously studied deterministic methods.

In Fig. Figure 2.5 presents a graphical implementation of the Monte Carlo method for calculating a single integral with random nodes (2.21) and (2.22).

(2.23)

Rice. 10.6. Integration by Monte Carlo method (2nd case)

As can be seen in Fig. 2.6, the integral curve lies in the unit square, and if we are able to obtain pairs of random numbers uniformly distributed over the interval, then the resulting values ​​(γ 1, γ 2) can be interpreted as the coordinates of a point in the unit square. Then, if quite a lot of these pairs of numbers are obtained, we can approximately assume that
. Here S is the number of pairs of points falling under the curve, and N– the total number of pairs of numbers.

Example 2.1. Calculate the following integral:

The problem was solved using various methods. The results obtained are summarized in table. 2.1.

Table 2.1

Comment. The choice of a table integral allowed us to compare the error of each method and find out the effect of the number of partitions on the accuracy of the calculations.

11 APPROXIMATE SOLUTION OF NONLINEAR
AND TRANSCENDENT EQUATIONS

Formula

Simpson's formula is the integral of an interpolation polynomial of the second degree on the segment:

where , and are the values ​​of the function at the corresponding points (at the ends of the segment and in its middle).

Error

Provided that the function on the segment has a fourth derivative, the error, according to the formula found by Giuseppe Peano, is equal to:

Due to the fact that the value is often unknown, the following inequality is used to estimate the error:

Representation in the form of the Runge-Kutta method

Simpson's formula can be represented as a table of the Runge-Kutta method as follows:

Compound formula (Cotes formula)

To more accurately calculate the integral, the interval is divided into segments of equal length and Simpson's formula is applied to each of them. The value of the original integral is the sum of the integration results on all segments.

where is the step size, and are the integration nodes, the boundaries of elementary segments on which Simpson’s formula is applied. Usually, for a uniform mesh, this formula is written in other notation (the segment is divided into nodes) in the form

The formula can also be written using only the known values ​​of the function, that is, the values ​​in the nodes:

where means that the index changes from one in increments of two. You should pay attention to the doubling of the coefficient before the amount. This is due to the fact that in this case the role of intermediate nodes is played by the original integration nodes.

The total error when integrating over a segment with a step (in this case, in particular, , ) is determined by the formula:

.

If it is impossible to estimate the error using the maximum of the fourth derivative (for example, it does not exist on a given interval or tends to infinity), a rougher estimate can be used:

.

Notes

Literature

• Kostomarov D. P., Favorsky A. P. “Introductory lectures on numerical methods”
• Petrov I. B., Lobanov A. I. Lectures on computational mathematics

Wikimedia Foundation. 2010.

• Western Union
• Patagonian parrot

See what the “Simpson Formula” is in other dictionaries:

SIMPSON FORMULA- (parabola formula) formula for the approximate calculation of definite integrals (quadrature formula), Named after T. Simpson (1743) ... Big Encyclopedic Dictionary

SIMPSON FORMULA- (formula of parabolas), formula for approximate calculation of definition. integrals (quadrature formula), having the form where A = (b a)/2n, fk = f(a + kh), k = 0, 1, 2, ..., 2n. Named after T. Simpson (1743) ...

Simpson formula- formula for the approximate calculation of definite integrals, having the form: , where h = (b a)/2n; fi, = f (a + ih), i = 0, 1, 2,..., 2n. S. f. sometimes called the parabola formula, because the derivation of this formula is based on... ... Great Soviet Encyclopedia

Simpson formula- parabola formula, a formula for the approximate calculation of definite integrals (quadrature formula), having the form where h = (b–a)/2n, fk = f(a + kh), k = 0, 1, 2, ..., 2n. Named after T. Simpson (1743). * * * SIMPSON SIMPSON FORMULA... ... encyclopedic Dictionary

Rectangle formula

Trapezoid formula- Definite integral as the area of ​​a figure Numerical integration (historical name: quadrature) calculation of the value of a definite integral (usually approximate), based on the fact that the value of the integral is numerically equal to the area... ... Wikipedia

SIMPSON FORMULA- a special case of the Newton Cotes quadrature formula, in which three nodes are taken: Let the interval [a, b] be divided into partial intervals, i=0, 1, 2, ..., n 1, length h=(b a)/ n, while n is considered an even number, and to calculate the integral ... Mathematical Encyclopedia

Simpson formula- ... Wikipedia

Simpson method- Simpson's formula refers to methods of numerical integration. It was named after the British mathematician Thomas Simpson (1710-1761). Let's consider the segment. Let the values ​​of the real function f(x) at points a, (a+b)/2, b be known.... ... Wikipedia

QUADRATURE FORMULA- formula used for approximate calculation of the definition. integrals over the values ​​of the integrand at a finite number of points. Examples of K. f. rectangle formula, trapezoid formula, Simpson formula... Natural science. encyclopedic Dictionary

We divide the integration segment into an even number of elementary segments of equal length by points with a step
(
). On every segment
We approximate the integrand by a polynomial of the second degree, which on this segment has the form
. notice, that i here only accepts odd values ​​from 1 to
. Thus, the integrand function is approximated by a set of quadratic polynomials or a spline of the second degree.

Let's calculate an arbitrary integral from the right side.

Odds ,And can be found from the interpolation condition, that is, from the equations

,

Note that the point is the midpoint of the segment
, hence
. Let's substitute this expression into the second interpolation equation:

.

Let's multiply this equation by 4 and add it to the others:

The last expression coincides exactly with the expression in square brackets of formula (5.1). Hence,

Which means

Thus, Simpson's formula looks like:

Estimation of the error of quadrature formulas.

Let us estimate the error when using the average rectangle method under the assumption that the function
infinitely differentiable.

Let us expand the integrand function
in a Taylor series in the vicinity of a point ,
.

The last row contains only odd powers x. Then

With a small step size h main contribution to the error R will contribute the value
, called the leading error term R.

Let's apply the method of average rectangles to the function
on the segment
in increments h. Then

.

So,
, Where
– constant value. Error in approximate equality
is an infinitesimal quantity of higher order compared to at
.

Step degree h, to which the remainder is proportional R, is called the order of accuracy of the integration method. The average rectangle method has second order accuracy.

Let us estimate the error when using the trapezoidal method also under the assumption that the function
infinitely differentiable.

Let us expand the integrand into a Taylor series in the vicinity of the point (
).

Leading error term R:

.

Applying the left rectangle method to a function
on the segment
in increments h, we get

.

So, the trapezoidal method also has second order accuracy.

Similarly, it can be shown that the left and right rectangle methods have the first, and the Simpson method, the fourth order of accuracy.

Lecture 17.

“Runge's rule for practical error assessment.

The concept of adaptive algorithms.

Special cases of numerical integration.

Cell method. Calculation of multiple integrals."

Runge's rule for practical error assessment.

Let some integration method have the order of accuracy k, that is
, Where – error, A– coefficient depending on the method of integration and the integrand function, h– partition step. Then

and when you step

,

The derived formula is called Runge's first formula. It is of great practical importance. If you need to calculate the integral with accuracy  , then we must calculate approximate values ​​of the integral, doubling the number of elementary segments until we achieve the inequality

Then, neglecting infinitesimal quantities, we can assume that

If we want to obtain a more accurate value of the desired integral, then for the refined value J we can accept instead
amount

.

This is Runge's second formula. Unfortunately, the uncertainty of this refined value remains uncertain, but is usually an order of magnitude greater than the accuracy of the original method (when the value is J we accept
).

For example, consider the trapezoid method. As shown above, the order of accuracy k of this method is equal to 2.

Where
. According to Runge's second formula

Where
is the approximate value of the integral found by the Simpson method with a step. Since the order of this method is 4, in this example the use of the second Runge formula increased the order of accuracy by 2.

Let us split the integration segment [ A, b] to an even number n equal parts in increments h. On each segment [ X 0, X 2], [X 2, X 4],..., [x i-1, x i+1],..., [ x n-2, x n] integrand function f(X) we replace with an interpolation polynomial of the second degree:

The coefficients of these quadratic trinomials can be found from the conditions for the equality of the polynomial at the points of the corresponding tabular data. We can take as a Lagrange interpolation polynomial of the second degree passing through the points :

The sum of elementary areas and (Fig. 3.3) can be calculated using a definite integral. Taking into account the equalities we get

-

Rice. 3.3. Illustration for Simpson's method

Having carried out such calculations for each elementary segment, we summarize the resulting expressions:

This expression for S is taken as the value of the definite integral:

(3.35)

The resulting relationship is called Simpson's formula or parabola formula.

This formula can be obtained in other ways, for example, by using the trapezoidal method twice when partitioning the segment [ A, b] into parts with steps h and 2 h or by combining the formulas of rectangles and trapezoids (see Section 3.2.6).

Sometimes Simpson's formula is written using half-integer indices. In this case, the number of segments of the partition P arbitrary (not necessarily even), and Simpson's formula has the form

(3.36)

It is easy to see that formula (3.36) coincides with (3.35) if formula (3.35) is applied for the number of segments of the partition 2 n and step h/2.

Example. Calculate the integral using Simpson's method

Function values ​​at n = 10, h = 0.1 are given in table. 3.3. Applying formula (3.35), we find

The result of numerical integration using Simpson's method was found to coincide with the exact value (six significant figures).

One of the possible algorithms for calculating a definite integral using Simpson's method is shown in Fig. 3.4. The boundaries of the integration segment [ A, b],error ε, as well as a formula for calculating the values ​​of the integrand y =f(x) .

Rice. 3.4. Simpson method algorithm

Initially, the segment is divided into two parts with a step h =(b- a)/2. The value of the integral is calculated I 1. Then the number of steps is doubled, the value is calculated I 2 in increments h/2. The condition for the end of the account is taken in the form . If this condition is not met, a new step is divided in half, etc.

Note that shown in Fig. 3.4 the algorithm is not optimal: when calculating each approximation I 2 function values ​​are not used f(x), already found at the previous stage. More economical algorithms will be discussed in Section. 3.2.7.

To construct the Simpson formula, we first consider the following problem: calculate the area S of a curvilinear trapezoid bounded above by the graph of the parabola y = Ax 2 + Bx + C, on the left by the line x = - h, on the right by the straight line x = h and below by the segment [-h; h]. Let the parabola pass through three points (Fig. 8): D(-h; y 0) E(0; y 1) and F(h; y 2), and x 2 - x 1 = x 1 - x 0 = h . Hence,

x 1 = x 0 + h = 0; x 2 = x 0 + 2h.

Then the area S is equal to the integral:

Let's express this area through h, y 0, y 1 and y 2. To do this, we calculate the coefficients of the parabola A, B, C. From the condition that the parabola passes through points D, E and F, we have:

Solving this system, we get: C = y 1 ; A=

Substituting these values ​​of A and C into (3), we obtain the required area

Let us now move on to the derivation of Simpson's formula for calculating the integral

To do this, we divide the integration segment into 2n equal parts of length

At the division points (Fig. 4). a = x 0, x 1, x 2, ..., x 2n-2, x 2n-1, x 2n = b,

We add the values ​​of the integrand function f: y 0, y 1, y 2, ...,y 2n-2, y 2n-1, y 2n, where y i = f(x i), x i = a + ih (i = 0, 1, 2,...,2n).

On the segment, we replace the integrand with a parabola passing through the points (x 0 ; y 0), (x 1 ; y 1) and (x 2 ; y 2), and to calculate the approximate value of the integral from x 0 to x 2 we use the formula (4 ). Then (shaded area in Fig. 4):

Similarly we find:

................................................

Adding the resulting equalities, we have:

Formula (5) is called generalized Simpson formula or parabola formula, since when it is derived, the graph of the integrand on a partial segment of length 2h is replaced by the arc of a parabola.

Job assignment:

1. As directed by the teacher or in accordance with an option from Tables 4 tasks (see Appendix) take conditions - integrand function, limits of integration.

2. Create a block diagram of the program and a program that should:

Request the accuracy of the calculation of a certain integral, the lower and upper limits of integration;

Calculate the given integral using the following methods: for options 1,4,7, 10... - right, for options 2,5,8,... - middle; for options 2,5,8,... - left rectangles. Print the number of partitions of the integration range at which the specified calculation accuracy is achieved;

Calculate the given integral by the trapezoidal method (for even options) and the Simpson method (for odd options).

Print the number of partitions of the integration range at which the specified calculation accuracy is achieved;

Output the values ​​of the control function for the given value of the argument and compare with the calculated values ​​of the integral. Draw conclusions.

Control questions

1. What is a definite integral?

2. Why, along with analytical methods, numerical methods for calculating definite integrals are used.

3. What is the essence of the basic numerical methods for calculating definite integrals.

4. The influence of the number of partitions on the accuracy of calculating a certain integral using numerical methods.

5. How to calculate the integral by any method with a given accuracy?