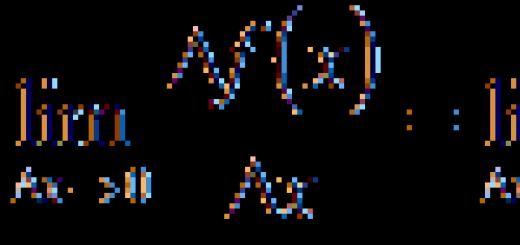Arithmetische Folge: Was ist das? Arithmetische Folge. Lehrbuch zum Einheitlichen Staatsexamen und zur Staatsexamensformel zur Ermittlung der a1-Rechenfolge

Ja, ja: Zahlenfolge ist kein Spielzeug für dich :)

Nun, Freunde, wenn Sie diesen Text lesen, dann sagt mir der interne Cap-Beweis, dass Sie noch nicht wissen, was eine arithmetische Folge ist, Sie es aber wirklich (nein, so: SOOOOO!) wissen wollen. Deshalb werde ich Sie nicht mit langen Einleitungen quälen und direkt zur Sache kommen.

Zunächst ein paar Beispiele. Schauen wir uns mehrere Zahlenreihen an:

1; 2; 3; 4; ...
15; 20; 25; 30; ...
$\sqrt(2);\ 2\sqrt(2);\ 3\sqrt(2);...$

Was haben alle diese Sets gemeinsam? Auf den ersten Blick nichts. Aber tatsächlich gibt es etwas. Nämlich: jedes nächste Element unterscheidet sich vom vorherigen durch die gleiche Nummer.

Urteile selbst. Der erste Satz besteht einfach aus aufeinanderfolgenden Zahlen, wobei jede nächste um eins höher ist als die vorherige. Im zweiten Fall beträgt der Unterschied zwischen benachbarten Zahlen bereits fünf, dieser Unterschied ist jedoch immer noch konstant. Im dritten Fall gibt es überhaupt Wurzeln. Allerdings gilt $2\sqrt(2)=\sqrt(2)+\sqrt(2)$ und $3\sqrt(2)=2\sqrt(2)+\sqrt(2)$, d.h. und in diesem Fall erhöht sich jedes nächste Element einfach um $\sqrt(2)$ (und haben Sie keine Angst, dass diese Zahl irrational ist).

Also: Alle solchen Folgen werden arithmetische Folgen genannt. Lassen Sie uns eine strenge Definition geben:

Definition. Eine Folge von Zahlen, bei der sich jede nächste Zahl um genau den gleichen Betrag von der vorherigen unterscheidet, wird als arithmetische Folge bezeichnet. Der genaue Betrag, um den sich die Zahlen unterscheiden, wird als Progressionsdifferenz bezeichnet und am häufigsten mit dem Buchstaben $d$ bezeichnet.

Notation: $\left(((a)_(n)) \right)$ ist die Progression selbst, $d$ ist ihre Differenz.

Und nur ein paar wichtige Hinweise. Erstens wird nur der Fortschritt berücksichtigt bestellt Zahlenfolge: Sie dürfen streng in der Reihenfolge gelesen werden, in der sie geschrieben sind – und sonst nichts. Zahlen können nicht neu angeordnet oder vertauscht werden.

Zweitens kann die Folge selbst entweder endlich oder unendlich sein. Beispielsweise ist die Menge (1; 2; 3) offensichtlich eine endliche arithmetische Folge. Wenn Sie jedoch etwas im Geiste schreiben (1; 2; 3; 4; ...), ist dies bereits eine unendliche Entwicklung. Die Auslassungspunkte nach der Vier scheinen darauf hinzudeuten, dass noch einige weitere Zahlen folgen werden. Unendlich viele zum Beispiel. :)

Ich möchte auch darauf hinweisen, dass die Fortschritte zunehmend oder abnehmend sein können. Wir haben bereits steigende Einsen gesehen – die gleiche Menge (1; 2; 3; 4; ...). Hier sind Beispiele für abnehmende Verläufe:

49; 41; 33; 25; 17; ...
17,5; 12; 6,5; 1; −4,5; −10; ...
$\sqrt(5);\ \sqrt(5)-1;\ \sqrt(5)-2;\ \sqrt(5)-3;...$

Okay, okay: Das letzte Beispiel mag übermäßig kompliziert erscheinen. Aber den Rest, denke ich, verstehen Sie. Deshalb führen wir neue Definitionen ein:

Definition. Arithmetische Folge angerufen:

zunehmend, wenn jedes nächste Element größer als das vorherige ist;

abnehmend, wenn im Gegenteil jedes nachfolgende Element kleiner ist als das vorherige.

Darüber hinaus gibt es sogenannte „stationäre“ Sequenzen – sie bestehen aus der gleichen sich wiederholenden Zahl. Zum Beispiel (3; 3; 3; ...).

Bleibt nur noch eine Frage: Wie kann man einen zunehmenden Verlauf von einem abnehmenden unterscheiden? Glücklicherweise hängt hier alles nur vom Vorzeichen der Zahl $d$ ab, d.h. Fortschrittsunterschiede:

Wenn $d \gt 0$, dann nimmt die Progression zu;
Wenn $d \lt 0$, dann nimmt die Progression offensichtlich ab;
Schließlich gibt es den Fall $d=0$ – in diesem Fall wird die gesamte Folge auf eine stationäre Folge identischer Zahlen reduziert: (1; 1; 1; 1; ...) usw.

Versuchen wir, die Differenz $d$ für die drei oben angegebenen abnehmenden Verläufe zu berechnen. Dazu reicht es aus, zwei beliebige benachbarte Elemente (z. B. das erste und das zweite) zu nehmen und die Zahl links von der Zahl rechts abzuziehen. Es wird so aussehen:

41−49=−8;
12−17,5=−5,5;
$\sqrt(5)-1-\sqrt(5)=-1$.

Wie wir sehen, war die Differenz in allen drei Fällen tatsächlich negativ. Und nachdem wir nun die Definitionen mehr oder weniger herausgefunden haben, ist es an der Zeit, herauszufinden, wie Progressionen beschrieben werden und welche Eigenschaften sie haben.

Progressionsterme und Wiederholungsformel

Da die Elemente unserer Sequenzen nicht vertauscht werden können, können sie nummeriert werden:

\[\left(((a)_(n)) \right)=\left$ ((a)_(1)),\ ((a)_(2)),((a)_(3 )),... \Rechts$\]

Die einzelnen Elemente dieser Menge werden als Mitglieder einer Progression bezeichnet. Sie sind durch eine Nummer gekennzeichnet: erstes Mitglied, zweites Mitglied usw.

Darüber hinaus sind, wie wir bereits wissen, benachbarte Terme der Progression durch die Formel verknüpft:

\[((a)_(n))-((a)_(n-1))=d\Rightarrow ((a)_(n))=((a)_(n-1))+d \]

Kurz gesagt, um den $n$-ten Term einer Progression zu finden, müssen Sie den $n-1$-ten Term und die Differenz $d$ kennen. Diese Formel wird als rekurrent bezeichnet, da Sie mit ihrer Hilfe eine beliebige Zahl nur finden können, wenn Sie die vorherige (und tatsächlich alle vorherigen) kennen. Das ist sehr umständlich, deshalb gibt es eine raffiniertere Formel, die alle Berechnungen auf den ersten Term und die Differenz reduziert:

\[((a)_(n))=((a)_(1))+\left(n-1 \right)d\]

Diese Formel ist Ihnen bestimmt schon einmal begegnet. Sie geben es gerne in allen möglichen Nachschlagewerken und Lösungsbüchern wieder. Und in jedem vernünftigen Mathematiklehrbuch ist es eines der ersten.

Ich empfehle Ihnen jedoch, ein wenig zu üben.

Aufgabe Nr. 1. Schreiben Sie die ersten drei Terme der arithmetischen Folge $\left(((a)_(n)) \right)$ auf, wenn $((a)_(1))=8,d=-5$.

Lösung. Wir kennen also den ersten Term $((a)_(1))=8$ und die Differenz der Progression $d=-5$. Verwenden wir die gerade angegebene Formel und ersetzen wir $n=1$, $n=2$ und $n=3$:

\[\begin(align) & ((a)_(n))=((a)_(1))+\left(n-1 \right)d; \\ & ((a)_(1))=((a)_(1))+\left(1-1 \right)d=((a)_(1))=8; \\ & ((a)_(2))=((a)_(1))+\left(2-1 \right)d=((a)_(1))+d=8-5= 3; \\ & ((a)_(3))=((a)_(1))+\left(3-1 \right)d=((a)_(1))+2d=8-10= -2. \\ \end(align)\]

Antwort: (8; 3; −2)

Das ist alles! Bitte beachten Sie: Unser Fortschritt nimmt ab.

Natürlich konnte $n=1$ nicht ersetzt werden – der erste Term ist uns bereits bekannt. Durch das Einsetzen der Einheit waren wir jedoch davon überzeugt, dass unsere Formel auch für den ersten Term funktioniert. In anderen Fällen lief alles auf banale Arithmetik hinaus.

Aufgabe Nr. 2. Schreiben Sie die ersten drei Terme einer arithmetischen Folge auf, wenn ihr siebter Term gleich −40 und ihr siebzehnter Term gleich −50 ist.

Lösung. Schreiben wir den Problemzustand in vertrauten Worten:

\[((a)_(7))=-40;\quad ((a)_(17))=-50.\]

\[\left\( \begin(align) & ((a)_(7))=((a)_(1))+6d \\ & ((a)_(17))=((a) _(1))+16d \\ \end(align) \right.\]

\[\left\( \begin(align) & ((a)_(1))+6d=-40 \\ & ((a)_(1))+16d=-50 \\ \end(align) \Rechts.\]

Ich habe das Systemzeichen gesetzt, weil diese Anforderungen gleichzeitig erfüllt sein müssen. Beachten wir nun, dass wir Folgendes erhalten, wenn wir die erste von der zweiten Gleichung subtrahieren (wir haben das Recht dazu, da wir ein System haben):

\[\begin(align) & ((a)_(1))+16d-\left(((a)_(1))+6d \right)=-50-\left(-40 \right); \\ & ((a)_(1))+16d-((a)_(1))-6d=-50+40; \\&10d=-10; \\&d=-1. \\ \end(align)\]

So einfach ist es, den Fortschrittsunterschied zu finden! Es bleibt nur noch, die gefundene Zahl in eine der Gleichungen des Systems einzusetzen. Zum Beispiel im ersten:

\[\begin(matrix) ((a)_(1))+6d=-40;\quad d=-1 \\ \Downarrow \\ ((a)_(1))-6=-40; \\ ((a)_(1))=-40+6=-34. \\ \end(matrix)\]

Da wir nun den ersten Term und den Unterschied kennen, müssen wir noch den zweiten und dritten Term finden:

\[\begin(align) & ((a)_(2))=((a)_(1))+d=-34-1=-35; \\ & ((a)_(3))=((a)_(1))+2d=-34-2=-36. \\ \end(align)\]

Bereit! Das Problem ist behoben.

Antwort: (−34; −35; −36)

Beachten Sie die interessante Eigenschaft der Progression, die wir entdeckt haben: Wenn wir den $n$-ten und den $m$-ten Term nehmen und sie voneinander subtrahieren, erhalten wir die Differenz der Progression multipliziert mit der $n-m$-Zahl:

\[((a)_(n))-((a)_(m))=d\cdot \left(n-m \right)\]

Einfach, aber sehr nützliche Eigenschaft, was Sie unbedingt wissen müssen – mit seiner Hilfe können Sie die Lösung vieler Fortschrittsprobleme deutlich beschleunigen. Hier ist ein klares Beispiel dafür:

Aufgabe Nr. 3. Der fünfte Term einer arithmetischen Folge ist 8,4 und der zehnte Term ist 14,4. Finden Sie den fünfzehnten Term dieser Progression.

Lösung. Da $((a)_(5))=8,4$, $((a)_(10))=14,4$ und wir $((a)_(15))$ finden müssen, stellen wir Folgendes fest:

\[\begin(align) & ((a)_(15))-((a)_(10))=5d; \\ & ((a)_(10))-((a)_(5))=5d. \\ \end(align)\]

Aber nach der Bedingung $((a)_(10))-((a)_(5))=14,4-8,4=6$, also $5d=6$, woraus wir haben:

\[\begin(align) & ((a)_(15))-14,4=6; \\ & ((a)_(15))=6+14,4=20,4. \\ \end(align)\]

Antwort: 20.4

Das ist alles! Wir mussten keine Gleichungssysteme erstellen und den ersten Term und die Differenz berechnen – alles war in nur wenigen Zeilen gelöst.

Schauen wir uns nun eine andere Art von Problem an – die Suche nach negativen und positiven Begriffen einer Progression. Es ist kein Geheimnis, dass, wenn eine Progression zunimmt und ihr erster Term negativ ist, früher oder später positive Terme darin auftauchen. Und umgekehrt: Die Bedingungen einer abnehmenden Progression werden früher oder später negativ.

Gleichzeitig ist es nicht immer möglich, diesen Moment „frontal“ zu finden, indem man die Elemente nacheinander durchgeht. Oft werden Aufgaben so geschrieben, dass die Berechnungen ohne Kenntnis der Formeln mehrere Blätter Papier in Anspruch nehmen würden – wir würden einfach einschlafen, während wir die Antwort finden. Versuchen wir daher, diese Probleme schneller zu lösen.

Aufgabe Nr. 4. Wie viele negative Terme gibt es in der arithmetischen Folge −38,5; −35,8; ...?

Lösung. Also $((a)_(1))=-38,5$, $((a)_(2))=-35,8$, woraus wir sofort den Unterschied finden:

Beachten Sie, dass die Differenz positiv ist, die Progression also zunimmt. Der erste Term ist negativ, also werden wir tatsächlich irgendwann auf positive Zahlen stoßen. Die Frage ist nur, wann dies geschehen wird.

Versuchen wir herauszufinden: bis wann (also bis was natürliche Zahl$n$) bleibt die Negativität der Terme erhalten:

\[\begin(align) & ((a)_(n)) \lt 0\Rightarrow ((a)_(1))+\left(n-1 \right)d \lt 0; \\ & -38,5+\left(n-1 \right)\cdot 2,7 \lt 0;\quad \left| \cdot 10 \right. \\ & -385+27\cdot \left(n-1 \right) \lt 0; \\ & -385+27n-27 \lt 0; \\ & 27n \lt 412; \\ & n \lt 15\frac(7)(27)\Rightarrow ((n)_(\max ))=15. \\ \end(align)\]

Die letzte Zeile bedarf einer Erklärung. Wir wissen also, dass $n \lt 15\frac(7)(27)$. Andererseits begnügen wir uns nur mit ganzzahligen Werten der Zahl (im Übrigen: $n\in \mathbb(N)$), die größte zulässige Zahl ist also genau $n=15$ und auf keinen Fall 16 .

Aufgabe Nr. 5. In der arithmetischen Folge $(()_(5))=-150,(()_(6))=-147$. Finden Sie die Nummer des ersten positiven Termes dieser Folge.

Dies wäre genau das gleiche Problem wie das vorherige, aber wir kennen $((a)_(1))$ nicht. Aber die Nachbarterme sind bekannt: $((a)_(5))$ und $((a)_(6))$, sodass wir den Unterschied der Progression leicht finden können:

Versuchen wir außerdem, den fünften Term durch den ersten und die Differenz mithilfe der Standardformel auszudrücken:

\[\begin(align) & ((a)_(n))=((a)_(1))+\left(n-1 \right)\cdot d; \\ & ((a)_(5))=((a)_(1))+4d; \\ & -150=((a)_(1))+4\cdot 3; \\ & ((a)_(1))=-150-12=-162. \\ \end(align)\]

Nun gehen wir analog zur vorherigen Aufgabe vor. Lassen Sie uns herausfinden, an welcher Stelle in unserer Reihenfolge positive Zahlen erscheinen:

\[\begin(align) & ((a)_(n))=-162+\left(n-1 \right)\cdot 3 \gt 0; \\ & -162+3n-3 \gt 0; \\ & 3n \gt 165; \\ & n \gt 55\Rightarrow ((n)_(\min ))=56. \\ \end(align)\]

Die kleinste ganzzahlige Lösung dieser Ungleichung ist die Zahl 56.

Bitte beachten Sie: In der letzten Aufgabe kam es auf eine strikte Ungleichung an, sodass die Option $n=55$ für uns nicht geeignet ist.

Nachdem wir nun gelernt haben, wie man einfache Probleme löst, gehen wir zu komplexeren Problemen über. Aber lassen Sie uns zunächst eine weitere sehr nützliche Eigenschaft arithmetischer Folgen untersuchen, die uns in Zukunft viel Zeit und ungleiche Zellen ersparen wird. :) :)

Arithmetisches Mittel und gleiche Einrückungen

Betrachten wir mehrere aufeinanderfolgende Terme der steigenden arithmetischen Folge $\left(((a)_(n)) \right)$. Versuchen wir, sie auf dem Zahlenstrahl zu markieren:

Terme einer arithmetischen Folge auf dem Zahlenstrahl

Ich habe ausdrücklich beliebige Begriffe $((a)_(n-3)),...,((a)_(n+3))$ markiert und nicht einige $((a)_(1)) ,\ ((a)_(2)),\ ((a)_(3))$ usw. Denn die Regel, die ich Ihnen jetzt erzähle, funktioniert für alle „Segmente“ gleich.

Und die Regel ist ganz einfach. Merken wir uns die wiederkehrende Formel und schreiben sie für alle markierten Begriffe auf:

\[\begin(align) & ((a)_(n-2))=((a)_(n-3))+d; \\ & ((a)_(n-1))=((a)_(n-2))+d; \\ & ((a)_(n))=((a)_(n-1))+d; \\ & ((a)_(n+1))=((a)_(n))+d; \\ & ((a)_(n+2))=((a)_(n+1))+d; \\ \end(align)\]

Diese Gleichheiten können jedoch anders umgeschrieben werden:

\[\begin(align) & ((a)_(n-1))=((a)_(n))-d; \\ & ((a)_(n-2))=((a)_(n))-2d; \\ & ((a)_(n-3))=((a)_(n))-3d; \\ & ((a)_(n+1))=((a)_(n))+d; \\ & ((a)_(n+2))=((a)_(n))+2d; \\ & ((a)_(n+3))=((a)_(n))+3d; \\ \end(align)\]

Na so was? Und die Tatsache, dass die Terme $((a)_(n-1))$ und $((a)_(n+1))$ im gleichen Abstand von $((a)_(n)) $ liegen . Und dieser Abstand ist gleich $d$. Das Gleiche gilt für die Terme $((a)_(n-2))$ und $((a)_(n+2))$ – sie werden auch aus $((a)_(n) entfernt. )$ im gleichen Abstand gleich $2d$. Wir können bis ins Unendliche fortfahren, aber die Bedeutung wird durch das Bild gut veranschaulicht

Die Terme der Progression liegen im gleichen Abstand vom Mittelpunkt

Was bedeutet das für uns? Das bedeutet, dass $((a)_(n))$ gefunden werden kann, wenn die Nachbarzahlen bekannt sind:

\[((a)_(n))=\frac(((a)_(n-1))+((a)_(n+1)))(2)\]

Wir haben eine hervorragende Aussage abgeleitet: Jeder Term einer arithmetischen Folge ist gleich dem arithmetischen Mittel seiner benachbarten Terme! Außerdem: Wir können von unserem $((a)_(n))$ nach links und rechts nicht um einen Schritt, sondern um $k$ Schritte zurückgehen – und die Formel wird immer noch korrekt sein:

\[((a)_(n))=\frac(((a)_(n-k))+((a)_(n+k)))(2)\]

Diese. wir können leicht einige $((a)_(150))$ finden, wenn wir $((a)_(100))$ und $((a)_(200))$ kennen, weil $(( a)_ (150))=\frac(((a)_(100))+((a)_(200)))(2)$. Auf den ersten Blick mag es scheinen, dass uns diese Tatsache nichts Nützliches bringt. In der Praxis sind jedoch viele Probleme speziell auf die Verwendung des arithmetischen Mittels zugeschnitten. Schau mal:

Aufgabe Nr. 6. Finden Sie alle Werte von $x$, für die die Zahlen $-6((x)^(2))$, $x+1$ und $14+4((x)^(2))$ aufeinanderfolgende Terme von sind eine arithmetische Folge (in der angegebenen Reihenfolge).

Lösung. Da diese Zahlen Mitglieder einer Progression sind, ist die Bedingung des arithmetischen Mittels für sie erfüllt: Das zentrale Element $x+1$ kann durch benachbarte Elemente ausgedrückt werden:

\[\begin(align) & x+1=\frac(-6((x)^(2))+14+4((x)^(2)))(2); \\ & x+1=\frac(14-2((x)^(2)))(2); \\ & x+1=7-((x)^(2)); \\ & ((x)^(2))+x-6=0. \\ \end(align)\]

Es ist klassisch geworden quadratische Gleichung. Seine Wurzeln: $x=2$ und $x=-3$ sind die Antworten.

Antwort: −3; 2.

Aufgabe Nr. 7. Finden Sie die Werte von $$, für die die Zahlen $-1;4-3;(()^(2))+1$ eine arithmetische Folge bilden (in dieser Reihenfolge).

Lösung. Lassen Sie uns den Mittelterm noch einmal durch das arithmetische Mittel benachbarter Terme ausdrücken:

\[\begin(align) & 4x-3=\frac(x-1+((x)^(2))+1)(2); \\ & 4x-3=\frac(((x)^(2))+x)(2);\quad \left| \cdot 2 \right.; \\ & 8x-6=((x)^(2))+x; \\ & ((x)^(2))-7x+6=0. \\ \end(align)\]

Wieder eine quadratische Gleichung. Und wieder gibt es zwei Wurzeln: $x=6$ und $x=1$.

Antwort 1; 6.

Wenn Sie bei der Lösung eines Problems auf brutale Zahlen stoßen oder sich über die Richtigkeit der gefundenen Antworten nicht ganz sicher sind, gibt es eine wunderbare Technik, mit der Sie überprüfen können: Haben wir das Problem richtig gelöst?

Nehmen wir an, wir haben in Aufgabe Nr. 6 die Antworten −3 und 2 erhalten. Wie können wir überprüfen, ob diese Antworten richtig sind? Lassen Sie uns sie einfach in den Originalzustand stecken und sehen, was passiert. Ich möchte Sie daran erinnern, dass wir drei Zahlen haben ($-6(()^(2))$, $+1$ und $14+4(()^(2))$, die eine arithmetische Folge bilden müssen. Ersetzen wir $x=-3$:

\[\begin(align) & x=-3\Rightarrow \\ & -6((x)^(2))=-54; \\ & x+1=-2; \\ & 14+4((x)^(2))=50. \end(align)\]

Wir haben die Zahlen −54; −2; 50, die sich um 52 unterscheiden, sind zweifellos eine arithmetische Folge. Das Gleiche passiert für $x=2$:

\[\begin(align) & x=2\Rightarrow \\ & -6((x)^(2))=-24; \\ & x+1=3; \\ & 14+4((x)^(2))=30. \end(align)\]

Wieder eine Progression, allerdings mit einer Differenz von 27. Somit wurde das Problem richtig gelöst. Wer möchte, kann das zweite Problem selbst überprüfen, aber ich sage gleich: Auch da stimmt alles.

Im Allgemeinen sind wir bei der Lösung der letzten Probleme auf ein anderes gestoßen interessante Tatsache, was auch beachtet werden muss:

Wenn drei Zahlen so sind, dass die zweite das arithmetische Mittel der ersten und letzten ist, dann bilden diese Zahlen eine arithmetische Folge.

Das Verständnis dieser Aussage wird es uns in Zukunft ermöglichen, die notwendigen Fortschritte auf der Grundlage der Bedingungen des Problems buchstäblich zu „konstruieren“. Aber bevor wir uns auf eine solche „Konstruktion“ einlassen, sollten wir noch eine weitere Tatsache beachten, die sich direkt aus dem bereits Besprochenen ergibt.

Elemente gruppieren und summieren

Kehren wir noch einmal zur Zahlenachse zurück. Beachten wir dort mehrere Mitglieder der Progression, zwischen denen vielleicht. ist vielen anderen Mitgliedern wert:

Auf dem Zahlenstrahl sind 6 Elemente markiert

Versuchen wir, den „linken Schwanz“ durch $((a)_(n))$ und $d$ und den „rechten Schwanz“ durch $((a)_(k))$ und $d$ auszudrücken. Es ist sehr einfach:

\[\begin(align) & ((a)_(n+1))=((a)_(n))+d; \\ & ((a)_(n+2))=((a)_(n))+2d; \\ & ((a)_(k-1))=((a)_(k))-d; \\ & ((a)_(k-2))=((a)_(k))-2d. \\ \end(align)\]

Beachten Sie nun, dass die folgenden Beträge gleich sind:

\[\begin(align) & ((a)_(n))+((a)_(k))=S; \\ & ((a)_(n+1))+((a)_(k-1))=((a)_(n))+d+((a)_(k))-d= S; \\ & ((a)_(n+2))+((a)_(k-2))=((a)_(n))+2d+((a)_(k))-2d= S. \end(align)\]

Einfach ausgedrückt, wenn wir zunächst zwei Elemente der Progression betrachten, die in ihrer Summe einer Zahl $S$ entsprechen, und dann beginnen, von diesen Elementen in entgegengesetzte Richtungen zu treten (aufeinander zu oder umgekehrt, um uns zu entfernen), Dann Die Summen der Elemente, auf die wir stoßen, werden ebenfalls gleich sein$S$. Am deutlichsten lässt sich dies grafisch darstellen:

Gleiche Einrückungen ergeben gleiche Beträge

Verständnis dieser Fakt wird es uns ermöglichen, Probleme grundlegend besser zu lösen hohes Level Schwierigkeiten als diejenigen, die wir oben betrachtet haben. Zum Beispiel diese:

Aufgabe Nr. 8. Bestimmen Sie die Differenz einer arithmetischen Folge, bei der der erste Term 66 ist und das Produkt aus dem zweiten und zwölften Term das kleinstmögliche ist.

Lösung. Schreiben wir alles auf, was wir wissen:

\[\begin(align) & ((a)_(1))=66; \\&d=? \\ & ((a)_(2))\cdot ((a)_(12))=\min . \end(align)\]

Wir kennen also den Fortschrittsunterschied $d$ nicht. Tatsächlich wird die gesamte Lösung um die Differenz herum aufgebaut, da das Produkt $((a)_(2))\cdot ((a)_(12))$ wie folgt umgeschrieben werden kann:

\[\begin(align) & ((a)_(2))=((a)_(1))+d=66+d; \\ & ((a)_(12))=((a)_(1))+11d=66+11d; \\ & ((a)_(2))\cdot ((a)_(12))=\left(66+d \right)\cdot \left(66+11d \right)= \\ & =11 \cdot \left(d+66 \right)\cdot \left(d+6 \right). \end(align)\]

Für diejenigen im Tank: Ich habe den Gesamtmultiplikator von 11 aus der zweiten Klammer genommen. Somit ist das gewünschte Produkt eine quadratische Funktion bezüglich der Variablen $d$. Betrachten Sie daher die Funktion $f\left(d \right)=11\left(d+66 \right)\left(d+6 \right)$ – ihr Graph wird eine Parabel mit nach oben gerichteten Zweigen sein, weil Wenn wir die Klammern erweitern, erhalten wir:

\[\begin(align) & f\left(d \right)=11\left(((d)^(2))+66d+6d+66\cdot 6 \right)= \\ & =11(( d)^(2))+11\cdot 72d+11\cdot 66\cdot 6 \end(align)\]

Wie Sie sehen, beträgt der Koeffizient des höchsten Termes 11 – das ist eine positive Zahl, wir haben es also eigentlich mit einer Parabel mit aufsteigenden Ästen zu tun:

Zeitplan quadratische Funktion- Parabel
Bitte beachten Sie: Diese Parabel nimmt ihren Minimalwert an ihrem Scheitelpunkt mit der Abszisse $((d)_(0))$ an. Natürlich können wir diese Abszisse mit dem Standardschema berechnen (es gibt die Formel $((d)_(0))=(-b)/(2a)\;$), aber es wäre viel sinnvoller, sie zu notieren dass der gewünschte Scheitelpunkt auf der Achsensymmetrie der Parabel liegt, daher ist der Punkt $((d)_(0))$ gleich weit von den Wurzeln der Gleichung $f\left(d \right)=0$ entfernt:

\[\begin(align) & f\left(d \right)=0; \\ & 11\cdot \left(d+66 \right)\cdot \left(d+6 \right)=0; \\ & ((d)_(1))=-66;\quad ((d)_(2))=-6. \\ \end(align)\]

Deshalb hatte ich es nicht besonders eilig, die Klammern zu öffnen: In ihrer ursprünglichen Form waren die Wurzeln sehr, sehr leicht zu finden. Daher ist die Abszisse gleich dem Mittelwert Arithmetische Zahlen−66 und −6:

\[((d)_(0))=\frac(-66-6)(2)=-36\]

Was gibt uns die entdeckte Zahl? Damit wird das benötigte Produkt eingenommen kleinster Wert(Übrigens haben wir $((y)_(\min ))$ nie berechnet – das wird von uns nicht verlangt). Gleichzeitig ist diese Zahl die Differenz zum ursprünglichen Verlauf, d.h. Wir haben die Antwort gefunden. :)

Antwort: −36

Aufgabe Nr. 9. Fügen Sie zwischen den Zahlen $-\frac(1)(2)$ und $-\frac(1)(6)$ drei Zahlen ein, sodass sie zusammen mit diesen Zahlen eine arithmetische Folge bilden.

Lösung. Im Wesentlichen müssen wir eine Folge von fünf Zahlen erstellen, mit dem ersten und letzte Nummer ist bereits bekannt. Bezeichnen wir die fehlenden Zahlen durch die Variablen $x$, $y$ und $z$:

\[\left(((a)_(n)) \right)=\left\( -\frac(1)(2);x;y;z;-\frac(1)(6) \right\ )\]

Beachten Sie, dass die Zahl $y$ die „Mitte“ unserer Folge ist – sie hat den gleichen Abstand von den Zahlen $x$ und $z$ sowie von den Zahlen $-\frac(1)(2)$ und $-\frac (1)( 6)$. Und wenn wir von den Zahlen $x$ und $z$ ausgehen, sind wir dabei dieser Moment können wir $y$ nicht bekommen, dann ist die Situation an den Enden der Progression anders. Erinnern wir uns an das arithmetische Mittel:

Wenn wir nun $y$ kennen, werden wir die verbleibenden Zahlen finden. Beachten Sie, dass $x$ zwischen den Zahlen $-\frac(1)(2)$ und $y=-\frac(1)(3)$ liegt, die wir gerade gefunden haben. Deshalb

Mit ähnlichen Überlegungen finden wir die verbleibende Zahl:

Bereit! Wir haben alle drei Zahlen gefunden. Schreiben wir sie in der Antwort in der Reihenfolge auf, in der sie zwischen den ursprünglichen Zahlen eingefügt werden sollen.

Antwort: $-\frac(5)(12);\ -\frac(1)(3);\ -\frac(1)(4)$

Aufgabe Nr. 10. Fügen Sie zwischen den Zahlen 2 und 42 mehrere Zahlen ein, die zusammen mit diesen Zahlen eine arithmetische Folge bilden, wenn Sie wissen, dass die Summe der ersten, zweiten und letzten der eingefügten Zahlen 56 beträgt.

Lösung. Ein noch komplexeres Problem, das jedoch nach dem gleichen Schema wie die vorherigen gelöst wird – durch das arithmetische Mittel. Das Problem ist, dass wir nicht genau wissen, wie viele Zahlen eingefügt werden müssen. Nehmen wir daher zur Sicherheit an, dass es nach dem Einfügen aller Zahlen genau $n$ Zahlen gibt, und die erste davon ist 2 und die letzte ist 42. In diesem Fall kann die erforderliche arithmetische Folge in der Form dargestellt werden:

\[\left(((a)_(n)) \right)=\left$ 2;((a)_(2));((a)_(3));...;(( a)_(n-1));42 \right$\]

\[((a)_(2))+((a)_(3))+((a)_(n-1))=56\]

Beachten Sie jedoch, dass sich die Zahlen $((a)_(2))$ und $((a)_(n-1))$ aus den Zahlen 2 und 42 an den Rändern durch einen Schritt zueinander ergeben, d.h. . in die Mitte der Sequenz. Und das bedeutet das

\[((a)_(2))+((a)_(n-1))=2+42=44\]

Aber dann kann der oben geschriebene Ausdruck wie folgt umgeschrieben werden:

\[\begin(align) & ((a)_(2))+((a)_(3))+((a)_(n-1))=56; \\ & \left(((a)_(2))+((a)_(n-1)) \right)+((a)_(3))=56; \\ & 44+((a)_(3))=56; \\ & ((a)_(3))=56-44=12. \\ \end(align)\]

Wenn wir $((a)_(3))$ und $((a)_(1))$ kennen, können wir den Unterschied der Progression leicht finden:

\[\begin(align) & ((a)_(3))-((a)_(1))=12-2=10; \\ & ((a)_(3))-((a)_(1))=\left(3-1 \right)\cdot d=2d; \\ & 2d=10\Rightarrow d=5. \\ \end(align)\]

Jetzt müssen nur noch die restlichen Begriffe gefunden werden:

\[\begin(align) & ((a)_(1))=2; \\ & ((a)_(2))=2+5=7; \\ & ((a)_(3))=12; \\ & ((a)_(4))=2+3\cdot 5=17; \\ & ((a)_(5))=2+4\cdot 5=22; \\ & ((a)_(6))=2+5\cdot 5=27; \\ & ((a)_(7))=2+6\cdot 5=32; \\ & ((a)_(8))=2+7\cdot 5=37; \\ & ((a)_(9))=2+8\cdot 5=42; \\ \end(align)\]

Somit gelangen wir bereits im 9. Schritt zum linken Ende der Sequenz – der Zahl 42. Insgesamt mussten nur 7 Zahlen eingefügt werden: 7; 12; 17; 22; 27; 32; 37.

Antwort: 7; 12; 17; 22; 27; 32; 37

Textaufgaben mit Progressionen

Abschließend möchte ich ein paar relative Überlegungen anstellen einfache Aufgaben. So einfach ist das: Für die meisten Schüler, die in der Schule Mathematik lernen und das oben Geschriebene nicht gelesen haben, mögen diese Probleme schwierig erscheinen. Dennoch sind dies die Arten von Problemen, die in der OGE und im Einheitlichen Staatsexamen in Mathematik auftauchen, daher empfehle ich Ihnen, sich damit vertraut zu machen.

Aufgabe Nr. 11. Das Team produzierte im Januar 62 Teile und in jedem Folgemonat 14 Teile mehr als im Vormonat. Wie viele Teile hat das Team im November produziert?

Lösung. Offensichtlich stellt die Anzahl der pro Monat aufgelisteten Teile eine zunehmende arithmetische Progression dar. Darüber hinaus:

\[\begin(align) & ((a)_(1))=62;\quad d=14; \\ & ((a)_(n))=62+\left(n-1 \right)\cdot 14. \\ \end(align)\]

November ist der 11. Monat des Jahres, also müssen wir $((a)_(11))$ finden:

\[((a)_(11))=62+10\cdot 14=202\]

Somit werden im November 202 Teile produziert.

Aufgabe Nr. 12. Die Buchbindewerkstatt hat im Januar 216 Bücher gebunden, und in jedem Folgemonat wurden vier Bücher mehr gebunden als im Vormonat. Wie viele Bücher hat der Workshop im Dezember gebunden?

Lösung. Alles das selbe:

$\begin(align) & ((a)_(1))=216;\quad d=4; \\ & ((a)_(n))=216+\left(n-1 \right)\cdot 4. \\ \end(align)$

Dezember ist der letzte, 12. Monat des Jahres, also suchen wir nach $((a)_(12))$:

\[((a)_(12))=216+11\cdot 4=260\]

Das ist die Antwort: Im Dezember werden 260 Bücher gebunden.

Nun, wenn Sie bis hierher gelesen haben, möchte ich Ihnen gratulieren: Sie haben den „Kurs für junge Kämpfer“ in arithmetischen Progressionen erfolgreich abgeschlossen. Sie können sicher mit der nächsten Lektion fortfahren, in der wir die Formel für die Summe der Progressionen sowie wichtige und sehr nützliche Konsequenzen daraus studieren.

Die Matrix $A^(-1)$ heißt die Umkehrung der quadratischen Matrix $A$, wenn die Bedingung $A^(-1)\cdot A=A\cdot A^(-1)=E$ erfüllt ist, wobei $E $ die Identitätsmatrix ist, deren Ordnung gleich der Ordnung der Matrix $A$ ist.

Eine nicht singuläre Matrix ist eine Matrix, deren Determinante ungleich Null ist. Dementsprechend ist eine singuläre Matrix eine Matrix, deren Determinante gleich Null ist.

Die inverse Matrix $A^(-1)$ existiert genau dann, wenn die Matrix $A$ nicht singulär ist. Wenn die inverse Matrix $A^(-1)$ existiert, dann ist sie eindeutig.

Es gibt mehrere Möglichkeiten, die Umkehrung einer Matrix zu finden, und wir werden uns zwei davon ansehen. Auf dieser Seite wird die Adjungierte-Matrix-Methode besprochen, die in den meisten höheren Mathematikkursen als Standard gilt. Die zweite Methode zur Ermittlung der inversen Matrix (die Methode der Elementartransformationen), die die Verwendung der Gauß-Methode oder der Gauß-Jordan-Methode beinhaltet, wird im zweiten Teil besprochen.

Methode der adjungierten Matrix

Gegeben sei die Matrix $A_(n\times n)$. Um die inverse Matrix $A^(-1)$ zu finden, sind drei Schritte erforderlich:

Finden Sie die Determinante der Matrix $A$ und stellen Sie sicher, dass $\Delta A\neq 0$, d.h. dass Matrix A nicht singulär ist.
Bilden Sie algebraische Komplemente $A_(ij)$ jedes Elements der Matrix $A$ und schreiben Sie die Matrix $A_(n\times n)^(*)=\left(A_(ij) \right)$ aus der gefundenen Algebra Ergänzungen.
Schreiben Sie die inverse Matrix unter Berücksichtigung der Formel $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$.

Die Matrix $(A^(*))^T$ wird oft als adjungiert (reziprok, verbündet) zur Matrix $A$ bezeichnet.

Wenn die Lösung manuell erfolgt, ist die erste Methode nur für Matrizen relativ kleiner Ordnung geeignet: zweite (), dritte (), vierte (). Die Umkehrung einer Matrix finden Auftrag von oben, andere Methoden werden verwendet. Zum Beispiel die Gaußsche Methode, die im zweiten Teil besprochen wird.

Beispiel Nr. 1

Finden Sie die Umkehrung der Matrix $A=\left(\begin(array) (cccc) 5 & -4 &1 & 0 \\ 12 &-11 &4 & 0 \\ -5 & 58 &4 & 0 \\ 3 & - 1 & -9 & 0 \end(array) \right)$.

Da alle Elemente der vierten Spalte gleich Null sind, ist $\Delta A=0$ (d. h. die Matrix $A$ ist singulär). Da $\Delta A=0$ ist, gibt es keine inverse Matrix zur Matrix $A$.

Antwort: Matrix $A^(-1)$ existiert nicht.

Beispiel Nr. 2

Finden Sie die Umkehrung der Matrix $A=\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right)$. Prüfung durchführen.

Wir verwenden die Methode der adjungierten Matrix. Finden wir zunächst die Determinante der gegebenen Matrix $A$:

$$ \Delta A=\left| \begin(array) (cc) -5 & 7\\ 9 & 8 \end(array)\right|=-5\cdot 8-7\cdot 9=-103. $$

Da $\Delta A \neq 0$ ist, existiert die inverse Matrix, daher werden wir mit der Lösung fortfahren. Algebraische Komplemente finden

\begin(aligned) & A_(11)=(-1)^2\cdot 8=8; \; A_(12)=(-1)^3\cdot 9=-9;\\ & A_(21)=(-1)^3\cdot 7=-7; \; A_(22)=(-1)^4\cdot (-5)=-5.\\ \end(aligned)

Wir erstellen eine Matrix algebraischer Additionen: $A^(*)=\left(\begin(array) (cc) 8 & -9\\ -7 & -5 \end(array)\right)$.

Wir transponieren die resultierende Matrix: $(A^(*))^T=\left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right)$ (the Die resultierende Matrix wird oft als adjungierte oder mit der Matrix $A$ verbündete Matrix bezeichnet. Mit der Formel $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$ erhalten wir:

$$ A^(-1)=\frac(1)(-103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right) =\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right) $$

Somit wird die inverse Matrix gefunden: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array )\right) $. Um die Wahrheit des Ergebnisses zu überprüfen, reicht es aus, die Wahrheit einer der Gleichungen zu überprüfen: $A^(-1)\cdot A=E$ oder $A\cdot A^(-1)=E$. Überprüfen wir die Gleichheit $A^(-1)\cdot A=E$. Um weniger mit Brüchen arbeiten zu müssen, ersetzen wir die Matrix $A^(-1)$ nicht in der Form $\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \ end(array)\right)$, und in der Form $-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array )\right)$:

$$ A^(-1)\cdot(A) =-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end( array)\right)\cdot\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right) =-\frac(1)(103)\cdot\left( \begin(array) (cc) -103 & 0 \\ 0 & -103 \end(array)\right) =\left(\begin(array) (cc) 1 & 0 \\ 0 & 1 \end(array )\right) =E $$

Antwort: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right)$.

Beispiel Nr. 3

Finden Sie die inverse Matrix für die Matrix $A=\left(\begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right)$ . Prüfung durchführen.

Beginnen wir mit der Berechnung der Determinante der Matrix $A$. Die Determinante der Matrix $A$ ist also:

$$ \Delta A=\left| \begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right| = 18-36+56-12=26. $$

Da $\Delta A\neq 0$ ist, existiert die inverse Matrix, daher werden wir mit der Lösung fortfahren. Wir finden die algebraischen Komplemente jedes Elements einer gegebenen Matrix:

Wir erstellen eine Matrix algebraischer Additionen und transponieren sie:

$$ A^*=\left(\begin(array) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37\end(array) \right); \; (A^*)^T=\left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right) . $$

Mit der Formel $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$ erhalten wir:

$$ A^(-1)=\frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37\end(array) \right)= \left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \end(array) \right) $$

Also $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 & -3/26 & 37/26 \end(array) \right)$. Um die Wahrheit des Ergebnisses zu überprüfen, reicht es aus, die Wahrheit einer der Gleichungen zu überprüfen: $A^(-1)\cdot A=E$ oder $A\cdot A^(-1)=E$. Überprüfen wir die Gleichheit $A\cdot A^(-1)=E$. Um weniger mit Brüchen arbeiten zu müssen, ersetzen wir die Matrix $A^(-1)$ nicht in der Form $\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \ \ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end(array) \right)$ und in der Form $\frac(1)(26 )\cdot \left( \begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right)$:

$$ A\cdot(A^(-1)) =\left(\begin(array)(ccc) 1 & 7 & 3 \\ -4 & 9 & 4\\ 0 & 3 & 2\end(array) \right)\cdot \frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\ end(array) \right) =\frac(1)(26)\cdot\left(\begin(array) (ccc) 26 & 0 & 0 \\ 0 & 26 & 0 \\ 0 & 0 & 26\end (array) \right) =\left(\begin(array) (ccc) 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end(array) \right) =E $$

Die Prüfung war erfolgreich, die inverse Matrix $A^(-1)$ wurde korrekt gefunden.

Antwort: $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 /13 & -3/26 & 37/26 \end(array) \right)$.

Beispiel Nr. 4

Finden Sie die Matrixinverse der Matrix $A=\left(\begin(array) (cccc) 6 & -5 & 8 & 4\\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7\\ -4 & 8 & -8 & -3 \end(array) \right)$.

Für eine Matrix vierter Ordnung ist es etwas schwierig, die inverse Matrix mithilfe algebraischer Additionen zu finden. Allerdings sind solche Beispiele in Tests treffen.

Um die Umkehrung einer Matrix zu finden, müssen Sie zunächst die Determinante der Matrix $A$ berechnen. Der beste Weg, dies in dieser Situation zu tun, besteht darin, die Determinante entlang einer Zeile (Spalte) zu zerlegen. Wir wählen eine beliebige Zeile oder Spalte aus und finden die algebraischen Komplemente jedes Elements der ausgewählten Zeile oder Spalte.

Für die erste Zeile erhalten wir beispielsweise:

$$ A_(11)=\left|\begin(array)(ccc) 7 & 5 & 2\\ 5 & 3 & 7\\ 8 & -8 & -3 \end(array)\right|=556; \; A_(12)=-\left|\begin(array)(ccc) 9 & 5 & 2\\ 7 & 3 & 7 \\ -4 & -8 & -3 \end(array)\right|=-300 ; $$ $$ A_(13)=\left|\begin(array)(ccc) 9 & 7 & 2\\ 7 & 5 & 7\\ -4 & 8 & -3 \end(array)\right|= -536;\; A_(14)=-\left|\begin(array)(ccc) 9 & 7 & 5\\ 7 & 5 & 3\\ -4 & 8 & -8 \end(array)\right|=-112. $$

Die Determinante der Matrix $A$ wird nach folgender Formel berechnet:

$$ \Delta(A)=a_(11)\cdot A_(11)+a_(12)\cdot A_(12)+a_(13)\cdot A_(13)+a_(14)\cdot A_(14 )=6\cdot 556+(-5)\cdot(-300)+8\cdot(-536)+4\cdot(-112)=100. $$

$$ \begin(aligned) & A_(21)=-77;\;A_(22)=50;\;A_(23)=87;\;A_(24)=4;\\ & A_(31) =-93;\;A_(32)=50;\;A_(33)=83;\;A_(34)=36;\\ & A_(41)=473;\;A_(42)=-250 ;\;A_(43)=-463;\;A_(44)=-96. \end(ausgerichtet) $$

Matrix algebraischer Komplemente: $A^*=\left(\begin(array)(cccc) 556 & -300 & -536 & -112\\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36\\ 473 & -250 & -463 & -96\end(array)\right)$.

Adjungierte Matrix: $(A^*)^T=\left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96\end(array)\right)$.

Inverse Matrix:

$$ A^(-1)=\frac(1)(100)\cdot \left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96 \end(array) \right)= \left(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/ 25 & 1/25 & 9/25 & -24/25 \end(array) \right) $$

Die Prüfung kann, falls gewünscht, auf die gleiche Weise wie in den vorherigen Beispielen erfolgen.

Antwort: $A^(-1)=\left(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/25 & 9/25 & -24/25 \end(array) \right) $.

Im zweiten Teil betrachten wir eine andere Möglichkeit, die inverse Matrix zu finden, die die Verwendung von Transformationen der Gaußschen Methode oder der Gauß-Jordan-Methode beinhaltet.

Matrixdeterminante

Das Finden der Determinante einer Matrix ist ein sehr häufiges Problem in der höheren Mathematik und Algebra. Auf den Wert der Matrixdeterminante kann man beim Lösen in der Regel nicht verzichten komplexe Systeme Gleichungen. Die Cramer-Methode zur Lösung von Gleichungssystemen basiert auf der Berechnung der Determinante einer Matrix. Mithilfe der Definition einer Determinante wird das Vorhandensein und die Eindeutigkeit einer Lösung eines Gleichungssystems bestimmt. Daher ist es schwierig, die Bedeutung der Fähigkeit, die Determinante einer Matrix in der Mathematik richtig und genau zu finden, zu überschätzen. Methoden zur Lösung von Determinanten sind theoretisch recht einfach, aber mit zunehmender Größe der Matrix werden die Berechnungen sehr umständlich und erfordern große Sorgfalt und viel Zeit. Es ist sehr leicht, bei solch komplexen mathematischen Berechnungen einen kleinen Fehler oder Tippfehler zu machen, der zu einem Fehler in der endgültigen Antwort führt. Also selbst wenn Sie finden Matrixdeterminante Für sich selbst ist es wichtig, das Ergebnis zu überprüfen. Dies kann mit unserem Service „Determinante einer Matrix online ermitteln“ erfolgen. Unser Service liefert stets absolut genaue Ergebnisse, die keine Fehler oder Schreibfehler enthalten. Sie können unabhängige Berechnungen ablehnen, da sie aus angewandter Sicht keine Ergebnisse liefern Determinante der Matrix Es hat keinen pädagogischen Charakter, sondern erfordert einfach viel Zeit und numerische Berechnungen. Daher, wenn in Ihrer Aufgabe Definition der Matrixdeterminante Sind Hilfs-, Nebenberechnungen, nutzen Sie unseren Service und Finden Sie die Determinante einer Matrix online!

Alle Berechnungen werden automatisch mit höchster Genauigkeit durchgeführt und sind absolut kostenlos. Wir verfügen über eine sehr komfortable Schnittstelle zur Eingabe von Matrixelementen. Der Hauptunterschied zwischen unserem Service und ähnlichen Diensten besteht jedoch in der Empfangsmöglichkeit detaillierte Lösung. Unser Service bei Berechnen Sie die Determinante einer Matrix online verwendet stets die einfachste und kürzeste Methode und beschreibt detailliert jeden Schritt der Transformationen und Vereinfachungen. So erhält man nicht nur den Wert der Determinante der Matrix, das Endergebnis, sondern auch eine ganze Detaillösung.

Eine Zahlenfolge, bei der jedes Mitglied, beginnend mit dem zweiten, gleich dem vorherigen ist, addiert zur gleichen Zahl für eine gegebene Folge, wird als arithmetische Folge bezeichnet. Angerufen wird jeweils die Nummer, die zur vorherigen Nummer addiert wird Unterschied der arithmetischen Progression und wird durch den Buchstaben bezeichnet D.

Die Zahlenfolge ist also eine 1; eine 2; eine 3; eine 4; eine 5; ... und n wird eine arithmetische Folge sein, wenn a 2 = a 1 + d;

a 3 = a 2 + d;

Sie sagen, dass eine arithmetische Folge mit einem gemeinsamen Term gegeben ist und n. Schreiben Sie auf: Es wird eine arithmetische Folge angegeben (ein).

Eine arithmetische Folge gilt als definiert, wenn ihr erster Term bekannt ist eine 1 und Unterschied D.

Beispiele für arithmetische Folge

Beispiel 1. 1; 3; 5; 7; 9;...Hier eine 1 = 1; D = 2.

Beispiel 2. 8; 5; 2; -1; -4; -7; -10;... Hier eine 1 = 8; D =-3.

Beispiel 3.-16; -12; -8; -4;... Hier eine 1 = -16; D = 4.

Beachten Sie, dass jeder Term der Progression, beginnend mit dem zweiten, gleich dem arithmetischen Mittel seiner benachbarten Terme ist.

In 1 Beispiel zweites Semester 3 =(1+5): 2 ; diese. a 2 = (a 1 + a 3) : 2; drittes Mitglied 5 =(3+7): 2;

d.h. a 3 = (a 2 + a 4) : 2.

Es gilt also die Formel:

Tatsächlich ist jedoch jedes Mitglied einer arithmetischen Folge, beginnend mit dem zweiten, nicht nur dem arithmetischen Mittel seiner benachbarten Mitglieder, sondern auch gleich äquidistant von seinen Mitgliedern, d.h.

Lass uns umdrehen Beispiel 2. Nummer -1 ist der vierte Term einer arithmetischen Folge und hat den gleichen Abstand vom ersten und siebten Term (a 1 = 8 und 7 = -10).

Nach Formel (**) gilt:

Lassen Sie uns die Formel herleiten N- Term einer arithmetischen Folge.

Wir erhalten also den zweiten Term der arithmetischen Folge, wenn wir die Differenz zum ersten addieren D; Den dritten Term erhalten wir, wenn wir die Differenz zum zweiten addieren D oder fügen Sie dem ersten Term zwei Unterschiede hinzu D; Den vierten Term erhalten wir, wenn wir die Differenz zum dritten addieren D oder fügen Sie drei Unterschiede zum ersten hinzu D usw.

Sie haben es erraten: a 2 = a 1 + d;

a 3 = a 2 + d = a 1 + 2d;

a 4 = a 3 + d = a 1 + 3d;

…………………….

a n = a n-1 + d = a 1 + (n-1) d.

Die resultierende Formel ein = A 1 + (N-1) D (***)

angerufen FormelNTerm einer arithmetischen Folge.

Lassen Sie uns nun darüber sprechen, wie Sie die Summe der ersten n Terme einer arithmetischen Folge ermitteln. Bezeichnen wir diesen Betrag mit S n.

Durch die Neuanordnung der Terme ändert sich der Wert der Summe nicht, sie kann also auf zwei Arten geschrieben werden.

S n= a 1 + a 2 + a 3 + a 4 + … + a n-3 + a n-2 + a n-1 + a n und

S n = a n + a n-1 + a n-2 + a n-3 + …...+ a 4 + a 3 + a 2 + a 1

Fügen wir diese beiden Gleichheiten Term für Term hinzu:

2S n= (a 1 + a n) + (a 2 + a n-1) + (a 3 + a n-2) + (a 4 + a n-3) + …

Für jede nicht singuläre Matrix A gibt es eine eindeutige Matrix A -1, so dass

A*A -1 =A -1 *A = E,

wobei E die Identitätsmatrix der gleichen Ordnungen wie A ist. Die Matrix A -1 wird als Umkehrung der Matrix A bezeichnet.

Falls jemand es vergessen hat: In der Identitätsmatrix sind bis auf die mit Einsen gefüllte Diagonale alle anderen Positionen mit Nullen gefüllt, ein Beispiel für eine Identitätsmatrix:

Finden der inversen Matrix mit der Methode der adjungierten Matrix

Die inverse Matrix wird durch die Formel definiert:

wo A ij - Elemente a ij.

Diese. Um die inverse Matrix zu berechnen, müssen Sie die Determinante dieser Matrix berechnen. Finden Sie dann die algebraischen Komplemente für alle ihre Elemente und bilden Sie daraus eine neue Matrix. Als nächstes müssen Sie diese Matrix transportieren. Und dividieren Sie jedes Element der neuen Matrix durch die Determinante der ursprünglichen Matrix.

Schauen wir uns ein paar Beispiele an.

Finden Sie A -1 für eine Matrix

Lösung: Finden wir A -1 mithilfe der Methode der adjungierten Matrix. Wir haben det A = 2. Finden wir die algebraischen Komplemente der Elemente der Matrix A. In diesem Fall sind die algebraischen Komplemente der Matrixelemente die entsprechenden Elemente der Matrix selbst, genommen mit einem Vorzeichen gemäß der Formel

Wir haben A 11 = 3, A 12 = -4, A 21 = -1, A 22 = 2. Wir bilden die adjungierte Matrix

Wir transportieren die Matrix A*:

Wir finden die inverse Matrix mit der Formel:

Wir bekommen:

Finden Sie mit der Adjungierten-Matrix-Methode A -1 if

Lösung: Zunächst berechnen wir die Definition dieser Matrix, um die Existenz der inversen Matrix zu überprüfen. Wir haben

Hier haben wir zu den Elementen der zweiten Zeile die zuvor mit (-1) multiplizierten Elemente der dritten Zeile hinzugefügt und dann die Determinante für die zweite Zeile erweitert. Da die Definition dieser Matrix ungleich Null ist, existiert ihre inverse Matrix. Um die adjungierte Matrix zu konstruieren, ermitteln wir die algebraischen Komplemente der Elemente dieser Matrix. Wir haben

Nach der Formel

Transportmatrix A*:

Dann nach der Formel

Finden der inversen Matrix mit der Methode der Elementartransformationen

Zusätzlich zu der Methode zum Ermitteln der inversen Matrix, die sich aus der Formel ergibt (die Methode der adjungierten Matrix), gibt es eine Methode zum Ermitteln der inversen Matrix, die als Methode der Elementartransformationen bezeichnet wird.

Elementare Matrixtransformationen

Die folgenden Transformationen werden als elementare Matrixtransformationen bezeichnet:

1) Neuanordnung von Zeilen (Spalten);

2) Multiplizieren einer Zeile (Spalte) mit einer Zahl ungleich Null;

3) Addieren der entsprechenden Elemente einer anderen Zeile (Spalte) zu den Elementen einer Zeile (Spalte), zuvor multipliziert mit einer bestimmten Zahl.

Um die Matrix A -1 zu finden, erstellen wir eine rechteckige Matrix B = (A|E) der Ordnungen (n; 2n) und weisen der Matrix A rechts die Identitätsmatrix E durch eine Trennlinie zu: