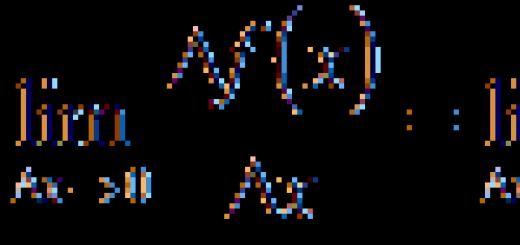Ein Funktionsgraph ist eine visuelle Darstellung des Verhaltens einer Funktion auf einer Koordinatenebene. Diagramme helfen Ihnen, verschiedene Aspekte einer Funktion zu verstehen, die nicht aus der Funktion selbst bestimmt werden können. Sie können Diagramme für viele Funktionen erstellen, denen jeweils eine bestimmte Formel zugewiesen wird. Der Graph einer beliebigen Funktion wird mithilfe eines bestimmten Algorithmus erstellt (falls Sie den genauen Prozess der grafischen Darstellung einer bestimmten Funktion vergessen haben).

Schritte

Eine lineare Funktion grafisch darstellen

Bestimmen Sie, ob die Funktion linear ist. Die lineare Funktion wird durch eine Formel der Form gegeben F (x) = k x + b (\displaystyle F(x)=kx+b) oder y = k x + b (\displaystyle y=kx+b)(zum Beispiel), und sein Graph ist eine gerade Linie. Somit umfasst die Formel eine Variable und eine Konstante (Konstante) ohne Exponenten, Wurzelzeichen oder Ähnliches. Wenn eine Funktion eines ähnlichen Typs gegeben ist, ist es recht einfach, einen Graphen einer solchen Funktion zu zeichnen. Hier sind weitere Beispiele für lineare Funktionen:

Verwenden Sie eine Konstante, um einen Punkt auf der Y-Achse zu markieren. Die Konstante (b) ist die „y“-Koordinate des Punktes, an dem der Graph die Y-Achse schneidet. Das heißt, es ist ein Punkt, dessen „x“-Koordinate gleich 0 ist. Wenn also x = 0 ist, wird es in die Formel eingesetzt , dann y = b (konstant). In unserem Beispiel y = 2 x + 5 (\displaystyle y=2x+5) die Konstante ist gleich 5, d. h. der Schnittpunkt mit der Y-Achse hat die Koordinaten (0,5). Platzieren Sie diesen Punkt auf Koordinatenebene.

Finden Neigung gerade. Er entspricht dem Multiplikator der Variablen. In unserem Beispiel y = 2 x + 5 (\displaystyle y=2x+5) bei der Variablen „x“ gibt es einen Faktor von 2; somit ist der Steigungskoeffizient gleich 2. Der Steigungskoeffizient bestimmt den Neigungswinkel der Geraden zur X-Achse, d. h. je größer der Steigungskoeffizient, desto schneller steigt oder fällt die Funktion.

Schreiben Sie die Steigung als Bruch. Der Winkelkoeffizient ist gleich dem Tangens des Neigungswinkels, also dem Verhältnis des vertikalen Abstands (zwischen zwei Punkten auf einer Geraden) zum horizontalen Abstand (zwischen denselben Punkten). In unserem Beispiel beträgt die Steigung 2, sodass wir sagen können, dass der vertikale Abstand 2 und der horizontale Abstand 1 beträgt. Schreiben Sie dies als Bruch: 2 1 (\displaystyle (\frac (2)(1))).

• Wenn die Steigung negativ ist, nimmt die Funktion ab.

1. Zeichnen Sie von dem Punkt, an dem die gerade Linie die Y-Achse schneidet, einen zweiten Punkt unter Verwendung vertikaler und horizontaler Abstände. Zeitplan lineare Funktion kann aus zwei Punkten konstruiert werden. In unserem Beispiel hat der Schnittpunkt mit der Y-Achse die Koordinaten (0,5); Von diesem Punkt aus bewegt man sich 2 Felder nach oben und dann 1 Feld nach rechts. Markieren Sie einen Punkt; es wird die Koordinaten (1,7) haben. Jetzt können Sie eine gerade Linie zeichnen.

   Zeichnen Sie mit einem Lineal eine gerade Linie durch zwei Punkte. Um Fehler zu vermeiden, suchen Sie den dritten Punkt. In den meisten Fällen kann die Grafik jedoch auch mit zwei Punkten erstellt werden. Sie haben also eine lineare Funktion gezeichnet.

   Punkte auf der Koordinatenebene darstellen

   1. Definieren Sie eine Funktion. Die Funktion wird als f(x) bezeichnet. Alle möglichen Werte der Variablen „y“ werden als Domäne der Funktion bezeichnet, und alle möglichen Werte der Variablen „x“ werden als Domäne der Funktion bezeichnet. Betrachten Sie zum Beispiel die Funktion y = x+2, nämlich f(x) = x+2.

      Zeichnen Sie zwei sich schneidende senkrechte Linien. Die horizontale Linie ist die X-Achse. Die vertikale Linie ist die Y-Achse.

      Beschriften Sie die Koordinatenachsen. Teilen Sie jede Achse in gleiche Segmente und nummerieren Sie sie. Der Schnittpunkt der Achsen ist 0. Für die X-Achse: Positive Zahlen werden rechts (von 0) aufgetragen, negative Zahlen links. Für die Y-Achse werden oben positive Zahlen (ab 0) und unten negative Zahlen aufgetragen.

      Finden Sie die Werte von „y“ aus den Werten von „x“. In unserem Beispiel ist f(x) = x+2. Setzen Sie bestimmte x-Werte in diese Formel ein, um die entsprechenden y-Werte zu berechnen. Wenn Sie eine komplexe Funktion erhalten, vereinfachen Sie diese, indem Sie das „y“ auf einer Seite der Gleichung isolieren.

      • -1: -1 + 2 = 1
      • 0: 0 +2 = 2
      • 1: 1 + 2 = 3

   2. Zeichnen Sie die Punkte auf der Koordinatenebene ein. Gehen Sie für jedes Koordinatenpaar wie folgt vor: Suchen Sie den entsprechenden Wert auf der X-Achse und zeichnen Sie eine vertikale Linie (gepunktet); Suchen Sie den entsprechenden Wert auf der Y-Achse und zeichnen Sie eine horizontale Linie (gestrichelte Linie). Markieren Sie den Schnittpunkt der beiden gepunkteten Linien. Sie haben also einen Punkt im Diagramm eingezeichnet.

      Löschen Sie die gepunkteten Linien. Tun Sie dies, nachdem Sie alle Punkte des Diagramms auf der Koordinatenebene aufgetragen haben. Hinweis: Der Graph der Funktion f(x) = x ist eine gerade Linie, die durch den Koordinatenmittelpunkt [Punkt mit den Koordinaten (0,0)] verläuft; Der Graph f(x) = x + 2 ist eine Gerade parallel zur Geraden f(x) = x, aber um zwei Einheiten nach oben verschoben und verläuft daher durch den Punkt mit den Koordinaten (0,2) (weil die Konstante 2 ist) .

   Eine komplexe Funktion grafisch darstellen

   Finden Sie die Nullstellen der Funktion. Die Nullstellen einer Funktion sind die Werte der x-Variablen mit y = 0, das heißt, das sind die Punkte, an denen der Graph die X-Achse schneidet. Beachten Sie, dass nicht alle Funktionen Nullstellen haben, aber sie sind die ersten Schritt im Prozess der grafischen Darstellung einer Funktion. Um die Nullstellen einer Funktion zu finden, setzen Sie sie mit Null gleich. Zum Beispiel:

   Suchen und markieren Sie die horizontalen Asymptoten. Eine Asymptote ist eine Linie, der sich der Graph einer Funktion annähert, die sie jedoch nie schneidet (d. h. in diesem Bereich ist die Funktion nicht definiert, beispielsweise bei der Division durch 0). Markieren Sie die Asymptote mit einer gepunkteten Linie. Wenn die Variable „x“ im Nenner eines Bruchs steht (z. B. y = 1 4 − x 2 (\displaystyle y=(\frac (1)(4-x^(2))))), setze den Nenner auf Null und finde „x“. In den erhaltenen Werten der Variablen „x“ ist die Funktion nicht definiert (in unserem Beispiel zeichnen Sie gepunktete Linien durch x = 2 und x = -2), da Sie nicht durch 0 dividieren können. Aber Asymptoten existieren nicht nur in Fällen, in denen die Funktion enthält gebrochener Ausdruck. Daher empfiehlt es sich, den gesunden Menschenverstand zu nutzen:

1. Gebrochene lineare Funktion und ihr Graph

Eine Funktion der Form y = P(x) / Q(x), wobei P(x) und Q(x) Polynome sind, wird als gebrochene rationale Funktion bezeichnet.

Sie sind wahrscheinlich bereits mit dem Konzept der rationalen Zahlen vertraut. Ebenfalls rationale Funktionen sind Funktionen, die als Quotient zweier Polynome dargestellt werden können.

Wenn eine gebrochene rationale Funktion der Quotient zweier linearer Funktionen ist – Polynome ersten Grades, d.h. Funktion der Form

y = (ax + b) / (cx + d), dann heißt es gebrochen linear.

Beachten Sie, dass in der Funktion y = (ax + b) / (cx + d) c ≠ 0 ist (sonst wird die Funktion linear y = ax/d + b/d) und dass a/c ≠ b/d (sonst ist). Funktion ist konstant). Die lineare Bruchfunktion ist für alle reellen Zahlen außer x = -d/c definiert. Graphen gebrochener linearer Funktionen unterscheiden sich in ihrer Form nicht von dem Graphen y = 1/x, den Sie kennen. Eine Kurve, die ein Graph der Funktion y = 1/x ist, heißt Hyperbel. Mit unbegrenzter Vergrößerung von x Absolutwert Die Funktion y = 1/x nimmt im Absolutwert unendlich ab und beide Zweige des Diagramms nähern sich der x-Achse: der rechte nähert sich von oben und der linke von unten. Die Linien, denen sich die Zweige einer Hyperbel nähern, werden als ihre bezeichnet Asymptoten.

Beispiel 1.

y = (2x + 1) / (x – 3).

Lösung.

Wählen wir den gesamten Teil aus: (2x + 1) / (x – 3) = 2 + 7/(x – 3).

Nun ist leicht zu erkennen, dass der Graph dieser Funktion aus dem Graphen der Funktion y = 1/x durch die folgenden Transformationen erhalten wird: Verschiebung um 3 Einheitssegmente nach rechts, siebenfache Streckung entlang der Oy-Achse und Verschiebung um 2 Gerätesegmente nach oben.

Jeder Bruch y = (ax + b) / (cx + d) kann auf ähnliche Weise geschrieben werden, wobei der „ganzzahlige Teil“ hervorgehoben wird. Folglich sind die Graphen aller gebrochenen linearen Funktionen Hyperbeln, die auf unterschiedliche Weise entlang der Koordinatenachsen verschoben und entlang der Oy-Achse gestreckt sind.

Um einen beliebigen Graphen zu erstellen gebrochene lineare Funktion Es ist überhaupt nicht notwendig, den Bruch, der diese Funktion definiert, umzuwandeln. Da wir wissen, dass der Graph eine Hyperbel ist, reicht es aus, die Geraden zu finden, denen sich seine Zweige nähern – die Asymptoten der Hyperbel x = -d/c und y = a/c.

Beispiel 2.

Finden Sie die Asymptoten des Graphen der Funktion y = (3x + 5)/(2x + 2).

Lösung.

Die Funktion ist bei x = -1 nicht definiert. Das bedeutet, dass die Gerade x = -1 als vertikale Asymptote dient. Um die horizontale Asymptote zu finden, wollen wir herausfinden, wie sich die Werte der Funktion y(x) nähern, wenn der Absolutwert des Arguments x zunimmt.

Teilen Sie dazu Zähler und Nenner des Bruchs durch x:

y = (3 + 5/x) / (2 + 2/x).

Da x → ∞, tendiert der Bruch zu 3/2. Das bedeutet, dass die horizontale Asymptote die Gerade y = 3/2 ist.

Beispiel 3.

Zeichnen Sie die Funktion y = (2x + 1)/(x + 1).

Lösung.

Wählen wir den „ganzen Teil“ des Bruchs aus:

(2x + 1) / (x + 1) = (2x + 2 – 1) / (x + 1) = 2(x + 1) / (x + 1) – 1/(x + 1) =

2 – 1/(x + 1).

Nun ist leicht zu erkennen, dass der Graph dieser Funktion aus dem Graphen der Funktion y = 1/x durch die folgenden Transformationen erhalten wird: eine Verschiebung um 1 Einheit nach links, eine symmetrische Darstellung bezüglich Ox und eine Verschiebung um 2 Einheitensegmente nach oben entlang der Oy-Achse.

Domäne D(y) = (-∞; -1)ᴗ(-1; +∞).

Wertebereich E(y) = (-∞; 2)ᴗ(2; +∞).

Schnittpunkte mit Achsen: c Oy: (0; 1); c Ox: (-1/2; 0). Die Funktion nimmt in jedem Intervall des Definitionsbereichs zu.

Antwort: Abbildung 1.

2. Bruchrationale Funktion

Betrachten Sie eine gebrochene rationale Funktion der Form y = P(x) / Q(x), wobei P(x) und Q(x) Polynome mit höherem Grad als dem ersten sind.

Beispiele für solche rationalen Funktionen:

y = (x 3 – 5x + 6) / (x 7 – 6) oder y = (x – 2) 2 (x + 1) / (x 2 + 3).

Wenn die Funktion y = P(x) / Q(x) den Quotienten zweier Polynome mit höherem Grad als dem ersten darstellt, ist ihr Graph in der Regel komplexer und es kann manchmal schwierig sein, ihn genau zu konstruieren , mit allen Details. Allerdings reicht es oft aus, Techniken zu verwenden, die denen ähneln, die wir oben bereits vorgestellt haben.

Der Bruch sei ein echter Bruch (n< m). Известно, что любую несократимую rationaler Bruch kann man sich vorstellen, und noch mehr der einzige Weg, als Summe endliche Zahl elementare Brüche, dessen Form durch Zerlegung des Nenners des Bruchs Q(x) in das Produkt reeller Faktoren bestimmt wird:

P(x)/Q(x) = A 1 /(x – K 1) m1 + A 2 /(x – K 1) m1-1 + … + A m1 /(x – K 1) + …+

L 1 /(x – K s) ms + L 2 /(x – K s) ms-1 + … + L ms /(x – K s) + …+

+ (B 1 x + C 1) / (x 2 +p 1 x + q 1) m1 + … + (B m1 x + C m1) / (x 2 +p 1 x + q 1) + …+

+ (M 1 x + N 1) / (x 2 +p t x + q t) m1 + … + (M m1 x + N m1) / (x 2 +p t x + q t).

Offensichtlich kann der Graph einer gebrochenen rationalen Funktion als Summe der Graphen elementarer Brüche erhalten werden.

Zeichnen von Graphen gebrochener rationaler Funktionen

Betrachten wir verschiedene Möglichkeiten, Graphen einer gebrochenen rationalen Funktion zu erstellen.

Beispiel 4.

Zeichnen Sie einen Graphen der Funktion y = 1/x 2 .

Lösung.

Wir verwenden den Graphen der Funktion y = x 2, um einen Graphen von y = 1/x 2 zu konstruieren, und verwenden die Technik des „Teilens“ der Graphen.

Domäne D(y) = (-∞; 0)ᴗ(0; +∞).

Wertebereich E(y) = (0; +∞).

Es gibt keine Schnittpunkte mit den Achsen. Die Funktion ist gerade. Steigt für alle x ab dem Intervall (-∞; 0), sinkt für x von 0 bis +∞.

Antwort: Abbildung 2.

Beispiel 5.

Zeichnen Sie die Funktion y = (x 2 – 4x + 3) / (9 – 3x).

Lösung.

Domäne D(y) = (-∞; 3)ᴗ(3; +∞).

y = (x 2 – 4x + 3) / (9 – 3x) = (x – 3)(x – 1) / (-3(x – 3)) = -(x – 1)/3 = -x/ 3 + 1/3.

Hier verwendeten wir die Technik der Faktorisierung, Reduktion und Reduktion auf eine lineare Funktion.

Antwort: Abbildung 3.

Beispiel 6.

Zeichnen Sie die Funktion y = (x 2 – 1)/(x 2 + 1) grafisch auf.

Lösung.

Der Definitionsbereich ist D(y) = R. Da die Funktion gerade ist, ist der Graph symmetrisch zur Ordinate. Bevor wir ein Diagramm erstellen, transformieren wir den Ausdruck noch einmal und heben den gesamten Teil hervor:

y = (x 2 – 1)/(x 2 + 1) = 1 – 2/(x 2 + 1).

Beachten Sie, dass die Isolierung des ganzzahligen Teils in der Formel einer gebrochenen rationalen Funktion eine der wichtigsten Aufgaben beim Erstellen von Diagrammen ist.

Wenn x → ±∞, dann ist y → 1, d. h. die Gerade y = 1 ist eine horizontale Asymptote.

Antwort: Abbildung 4.

Beispiel 7.

Betrachten wir die Funktion y = x/(x 2 + 1) und versuchen wir, ihren größten Wert genau zu finden, d. h. am meisten Hochpunkt rechte Hälfte der Grafik. Um dieses Diagramm genau zu erstellen, reicht der heutige Wissensstand nicht aus. Offensichtlich kann unsere Kurve nicht sehr hoch „steigen“, weil Der Nenner beginnt schnell, den Zähler zu „überholen“. Mal sehen, ob der Wert der Funktion gleich 1 sein kann. Dazu müssen wir die Gleichung x 2 + 1 = x, x 2 – x + 1 = 0 lösen. Diese Gleichung hat nicht echte Wurzeln. Das bedeutet, dass unsere Annahme falsch ist. Um das Meiste zu finden sehr wichtig Funktion müssen Sie herausfinden, bei welchem ​​größten A die Gleichung A = x/(x 2 + 1) eine Lösung hat. Ersetzen wir die ursprüngliche Gleichung durch eine quadratische: Аx 2 – x + А = 0. Diese Gleichung hat eine Lösung, wenn 1 – 4А 2 ≥ 0. Von hier aus finden wir Höchster Wert A = 1/2.

Antwort: Abbildung 5, max y(x) = ½.

Sie haben noch Fragen? Sie wissen nicht, wie man Funktionen grafisch darstellt?
Um Hilfe von einem Tutor zu erhalten, registrieren Sie sich.
Die erste Lektion ist kostenlos!

Wenn Sie Material ganz oder teilweise kopieren, ist ein Link zur Quelle erforderlich.

Die Funktion y=x^2 heißt quadratische Funktion. Zeitplan quadratische Funktion ist eine Parabel. Generelle Form Die Parabel ist in der folgenden Abbildung dargestellt.

Quadratische Funktion

Abb. 1. Gesamtansicht der Parabel

Wie aus der Grafik ersichtlich ist, ist es symmetrisch zur Oy-Achse. Die Oy-Achse wird als Symmetrieachse der Parabel bezeichnet. Dies bedeutet, dass Sie im Diagramm eine gerade Linie parallel zur Ox-Achse über dieser Achse zeichnen. Dann schneidet es die Parabel an zwei Punkten. Der Abstand dieser Punkte zur Oy-Achse wird gleich sein.

Die Symmetrieachse teilt den Graphen einer Parabel in zwei Teile. Diese Teile werden Parabeläste genannt. Und der Punkt einer Parabel, der auf der Symmetrieachse liegt, wird als Scheitelpunkt der Parabel bezeichnet. Das heißt, die Symmetrieachse verläuft durch den Scheitelpunkt der Parabel. Die Koordinaten dieses Punktes sind (0;0).

Grundlegende Eigenschaften einer quadratischen Funktion

1. Bei x =0, y=0 und y>0 bei x0

2. Die quadratische Funktion erreicht an ihrem Scheitelpunkt ihren Minimalwert. Ymin bei x=0; Außerdem ist zu beachten, dass die Funktion keinen Maximalwert hat.

3. Die Funktion nimmt im Intervall (-∞;0] ab und nimmt im Intervall zu. Durch Lösen der Gleichung \(x"\left(t \right) = 0,\) bestimmen wir die stationären Punkte der Funktion \(x\ left(t \right):\ ) \[ (x"\left(t \right) = 0,)\;\; (\Rightarrow 3(t^2) + 2t - 1 = 0,)\;\; (\Rightarrow (t_(1, 2)) = \frac(( - 2 \pm \sqrt (16) ))(6) = - 1;\;\frac(1)(3).) \] Für \ (t = 1\) erreicht die Funktion \ (x\left(t \right)\) ein Maximum gleich \and an dem Punkt \(t = \large\frac(1)(3)\normalsize\), den sie hat ein Minimum gleich \[ (x\left(( \frac(1)(3)) \right) ) = ((\left((\frac(1)(3)) \right)^3) + (\ left((\frac(1)(3)) \right)^2) - \left((\frac(1)(3)) \right) ) = (\frac(1)((27)) + \ frac(1)(9) - \frac(1 )(3) = - \frac(5)((27)).) \] Betrachten Sie die Ableitung \(y"\left(t \right):\) \ [ (y"\left(t \right) = ( \left(((t^3) + 2(t^2) - 4t) \right)^\prime ) ) = (3(t^2) + 4t - 4.) \] Finden Sie die stationären Punkte der Funktion \(y \left(t \right):\) \[ (y"\left(t \right) = 0,)\;\; (\Rightarrow 3 (t^2) + 4t - 4 = 0,)\;\ ; (\Rightarrow (t_(1,2)) = \frac(( - 4 \pm \sqrt (64) ))(6) = - 2 ;\;\frac(2)(3).) \] Auch hier erreicht die Funktion \(y\left(t \right)\) ein Maximum am Punkt \(t = -2:\) \ und ein Minimum am Punkt \(t = \large\frac(2)(3)\normalsize :\) \[ (y\left((\frac(2)(3)) \right) ) = ((\left ((\frac(2)(3)) \right)^3) + 2(\ left((\frac(2)(3)) \right)^2) - 4 \cdot \frac(2)(3 ) ) = (\frac(8)((27)) + \frac(8)( 9) - \frac(8)(3) ) = ( - \frac((40))((27)).) \] Graphen der Funktionen \(x\left(t \right)\), \(y\ left(t \right)\) sind schematisch in Abbildung \(15a.\) dargestellt.

Abb.15a		Abb.15b

Abb.15c

Beachten Sie, dass \[ (\lim\limits_(t \to \pm \infty ) x\left(t \right) = \pm \infty ,)\;\;\; (\lim\limits_(t \to \pm \infty ) y\left(t \right) = \pm \infty ,) \] dann hat die Kurve \(y\left(x \right)\) weder eine Vertikale noch keine horizontalen Asymptoten. Da außerdem \[ (k = \lim\limits_(t \to \pm \infty ) \frac((y\left(t \right)))((x\left(t \right))) ) = ( \lim\limits_(t \to \pm \infty ) \frac(((t^3) + 2(t^2) - 4t))(((t^3) + (t^2) - t) ) ) = (\lim\limits_(t \to \pm \infty ) \frac((1 + \frac(2)(t) - \frac(4)(((t^2)))))(( 1 + \frac(1)(t) - \frac(1)(((t^2))))) = 1,) \] \[ (b = \lim\limits_(t \to \pm \infty ) \left[ (y\left(t \right) - kx\left(t \right)) \right] ) = (\lim\limits_(t \to \pm \infty ) \left((\cancel(\ color (blau)(t^3)) + \color(rot)(2(t^2)) - \color(grün)(4t) - \cancel(\color(blau)(t^3)) - \ color (red)(t^2) + \color(green)(t)) \right) ) = (\lim\limits_(t \to \pm \infty ) \left((\color(red)(t^ 2 ) - \color(green)(3t)) \right) = + \infty ,) \] dann hat die Kurve \(y\left(x \right)\) auch keine schrägen Asymptoten.

Bestimmen wir die Schnittpunkte des Graphen \(y\left(x \right)\) mit den Koordinatenachsen. Der Schnittpunkt mit der x-Achse erfolgt an folgenden Punkten: \[ (y\left(t \right) = (t^3) + 2(t^2) - 4t = 0,)\;\; (\Rightarrow t\left(((t^2) + 2t - 4) \right) = 0;) \]

1. \(((t^2) + 2t - 4 = 0,)\;\; (\Rightarrow D = 4 - 4 \cdot \left(( - 4) \right) = 20,)\;\; (\ Rightarrow (t_(2,3)) = \large\frac(( - 2 \pm \sqrt (20) ))(2)\normalsize = - 1 \pm \sqrt 5 .) \)

\ \[ (x\left(((t_2)) \right) = x\left(( - 1 - \sqrt 5 ) \right) ) = ((\left(( - 1 - \sqrt 5 ) \right) ^3) + (\left(( - 1 - \sqrt 5 ) \right)^2) - \left(( - 1 - \sqrt 5 ) \right) ) = ( - \left((1 + 3\sqrt 5 + 15 + 5\sqrt 5 ) \right) + \left((1 + 2\sqrt 5 + 5) \right) + 1 + \sqrt 5 ) = ( - 16 - 8\sqrt 5 + 6 + 2\ sqrt 5 + 1 + \sqrt 5 ) = ( - 9 - 5\sqrt 5 \ approx 20,18;) \] \[ (x\left(((t_3)) \right) = x\left(( - 1 + \ sqrt 5 ) \right) ) = ((\left(( - 1 + \sqrt 5 ) \right)^3) + (\left(( - 1 + \sqrt 5 ) \right)^2) - \ left( ( - 1 + \sqrt 5 ) \right) ) = ( - \left((1 - 3\sqrt 5 + 15 - 5\sqrt 5 ) \right) + \left((1 - 2\sqrt 5 + 5) \right) + 1 - \sqrt 5 ) = ( - 16 + 8\sqrt 5 + 6 - 2\sqrt 5 + 1 - \sqrt 5 ) = ( - 9 + 5\sqrt 5 \ca. 2,18. ) \] In Auf die gleiche Weise finden wir die Schnittpunkte des Graphen mit der Ordinatenachse: \[ (x\left(t \right) = (t^3) + (t^2) - t = 0,)\;\; (\Rightarrow t\left(((t^2) + t - 1) \right) = 0;) \]

1. \(((t^2) + t - 1 = 0,)\;\; (\Rightarrow D = 1 - 4 \cdot \left(( - 1) \right) = 5,)\;\; (\ Rightarrow (t_(2,3)) = \large\frac(( - 1 \pm \sqrt (5) ))(2)\normalsize.) \)

\ \[ (y\left(((t_2)) \right) = y\left((\frac(( - 1 - \sqrt 5 ))(2)) \right) ) = ((\left((\ frac(( - 1 - \sqrt 5 ))(2)) \right)^3) + 2(\left((\frac(( - 1 - \sqrt 5 ))(2)) \right)^2) - 4\left((\frac(( - 1 - \sqrt 5 ))(2)) \right) ) = ( - \frac(1)(8)\left((1 + 3\sqrt 5 + 15 + 5\sqrt 5 ) \right) + \frac(1)(2)\left((1 + 2\sqrt 5 + 5) \right) + 2\left((1 + \sqrt 5 ) \right) ) = ( - \cancel(2) - \cancel(\sqrt 5) + 3 + \cancel(\sqrt 5) + \cancel(2) + 2\sqrt 5 ) = (3 + 2\sqrt 5 \ca. 7,47 ;) \] \[ (y\left(((t_3)) \right) = y\left((\frac(( - 1 + \sqrt 5 ))(2)) \right) ) = ((\left (( \frac(( - 1 + \sqrt 5 ))(2)) \right)^3) + 2(\left((\frac(( - 1 + \sqrt 5 ))(2)) \right) ^2 ) - 4\left((\frac(( - 1 + \sqrt 5 ))(2)) \right) ) = ( - \frac(1)(8)\left((1 - 3\sqrt 5 + 15 - 5\sqrt 5 ) \right) + \frac(1)(2)\left((1 - 2\sqrt 5 + 5) \right) + 2\left((1 - \sqrt 5 ) \right ) ) = ( - \cancel(2) + \cancel(\sqrt 5) + 3 - \cancel(\sqrt 5) + \cancel(2) - 2\sqrt 5 ) = (3 - 2\sqrt 5 \ approx - 1,47 .) \] Teilen Sie die Achse \(t\) in \(5\) Intervalle: \[ (\left(( - \infty , - 2) \right),)\;\; (\left(( - 2, - 1) \right),)\;\; (\left(( - 1,\frac(1)(3)) \right),)\;\; (\left((\frac(1)(3),\frac(2)(3)) \right),)\;\; (\left((\frac(2)(3), + \infty ) \right).) \] Auf dem ersten Intervall \(\left(( - \infty , - 2) \right)\) Werte \(x \) und \(y\) steigen von \(-\infty\) auf \(x\left(( - 2) \right) = - 2\) und \(y\left(( - 2) \right) = 8.\) Dies ist schematisch in Abbildung \(15b.\) dargestellt.

Im zweiten Intervall \(\left(( - 2, - 1) \right)\) steigt die Variable \(x\) von \(x\left(( - 2) \right) = - 2\) auf \ (x \left(( - 1) \right) = 1,\) und die Variable \(y\) nimmt von \(y\left(( - 2) \right) = 8\) auf \(y\left (( - 1) \right) = 5.\) Hier haben wir einen Abschnitt einer abnehmenden Kurve \(y\left(x \right).\) Sie schneidet die Ordinatenachse im Punkt \(\left((0,3 + 2\sqrt 5 ) \right).\)

Im dritten Intervall \(\left(( - 1,\large\frac(1)(3)\normalsize) \right)\) nehmen beide Variablen ab. Der Wert von \(x\) ändert sich von \(x\left(( - 1) \right) = 1\) zu \(x\left((\large\frac(1)(3)\normalsize) \right ) = - \large\frac(5)((27))\normalsize.\) Dementsprechend nimmt der Wert von \(y\) von \(y\left(( - 1) \right) = 5\) auf ab \(y\ left((\large\frac(1)(3)\normalsize) \right) = - \large\frac(29)((27))\normalsize.\) Kurve \(y\left(x \right)\ ) schneidet den Koordinatenursprung.

Im vierten Intervall \(\left((\large\frac(1)(3)\normalsize,\large\frac(2)(3)\normalsize) \right)\) nimmt die Variable \(x\) ab \( x\left((\large\frac(1)(3)\normalsize) \right) = - \large\frac(5)((27))\normalsize\) zu \(x\left((\ large\ frac(2)(3)\normalsize) \right) = \large\frac(2)((27))\normalsize,\) und die Variable \(y\) nimmt von \(y\left(( \large\ frac(1)(3)\normalsize) \right) = - \large\frac(29)((27))\normalsize\) zu \(y\left((\large\frac(2)( 3)\ normalsize) \right) = - \large\frac(40)((27))\normalsize.\) In diesem Abschnitt schneidet die Kurve \(y\left(x \right)\) die Ordinatenachse bei Punkt \(\left( (0,3 - 2\sqrt 5 ) \right).\)

Schließlich sind im letzten Intervall \(\left((\large\frac(2)(3)\normalsize, + \infty ) \right)\) beide Funktionen \(x\left(t \right)\), \ ( y\left(t \right)\) erhöhen. Die Kurve \(y\left(x \right)\) schneidet die x-Achse im Punkt \(x = - 9 + 5\sqrt 5 \ungefähr 2,18.\)

Um die Form der Kurve \(y\left(x \right)\) zu verdeutlichen, berechnen wir die Maximal- und Minimalpunkte. Die Ableitung \(y"\left(x \right)\) wird ausgedrückt als \[ (y"\left(x \right) = (y"_x) ) = (\frac(((y"_t))) ( ((x"_t))) ) = (\frac((((\left(((t^3) + 2(t^2) - 4t) \right))^\prime )))((( ( \left(((t^3) + (t^2) - t) \right))^\prime ))) ) = (\frac((3(t^2) + 4t - 4))(( 3 (t^2) + 2t - 1)) ) = (\frac((\cancel(3)\left((t + 2) \right)\left((t - \frac(2)(3)) \right)))((\cancel(3)\left((t + 1) \right)\left((t - \frac(1)(3)) \right))) ) = (\frac(( \ left((t + 2) \right)\left((t - \frac(2)(3)) \right)))(\left((t + 1) \right)\left((t - \ frac(1)(3)) \right))).) \] Die Änderung des Vorzeichens der Ableitung \(y"\left(x \right)\) ist in Abbildung \(15c.\) dargestellt. Es kann man sieht, dass am Punkt \(t = - 2,\), d.h. an der Grenze des \(I\)-ten und \(II\)-ten Intervalls hat die Kurve ein Maximum und bei \(t = \large\frac(2)(3)\normalsize\) (am Grenze des \(IV\)-ten und \(V\)-ten Intervalls) gibt es ein Minimum. Beim Durchgang durch den Punkt \(t = \large\frac(1)(3)\normalsize\) ändert die Ableitung ebenfalls das Vorzeichen von Plus nach Minus, aber in diesem Bereich ist die Kurve \(y\left(x \right) \) ist keine eindeutige Funktion. Daher ist der angegebene Punkt kein Extremum.

Wir untersuchen auch die Konvexität dieser Kurve. Zweite Ableitung\(y""\left(x \right)\) hat die Form: \[ y""\left(x \right) = (y""_(xx)) = \frac((((\left( ( (y"_x)) \right))"_t)))(((x"_t))) = \frac((((\left((\frac((3(t^2) + 4t - 4 ) )((3(t^2) + 2t - 1))) \right))^\prime )))((((\left(((t^3) + (t^2) - t) \ right ))^\prime ))) = \frac((\left((6t + 4) \right)\left((3(t^2) + 2t - 1) \right) - \left((3( t ^2) + 4t - 4) \right)\left((6t + 2) \right)))((((\left((3(t^2) + 2t - 1) \right))^3 ) )) = \frac((18(t^3) + 12(t^2) + 12(t^2) + 8t - 6t - 4 - \left((18(t^3) + 24(t^ 2 ) - 24t + 6(t^2) + 8t - 8) \right)))((((\left((3(t^2) + 2t - 1) \right))^3))) = \ frac((\cancel(\color(blue)(18(t^3))) + \color(red)(24(t^2)) + \color(green)(2t) - \color(maroon) ( 4) - \cancel(\color(blue)(18(t^3))) - \color(red)(30(t^2)) + \color(green)(16t) + \color(maroon) ( 8)))((((\left((3(t^2) + 2t - 1) \right))^3))) = \frac(( - \color(red)(6(t^2 ) ) + \color(grün)(18t) + \color(kastanienbraun)(4)))((((\left((3(t^2) + 2t - 1) \right))^3))) = \frac(( - 6\left((t - \frac((9 - \sqrt (105) ))(6)) \right)\left((t - \frac((9 + \sqrt (105) ) )(6)) \right)))((((\left((t + 1) \right))^3)((\left((3t - 1) \right))^3))). \] Folglich ändert die zweite Ableitung ihr Vorzeichen beim Durchgang durch die folgenden Punkte (Abb.\(15с\)): \[ ((t_1) = - 1:\;\;x\left(( - 1 ) \right ) = 1,)\;\; (y\left(( - 1) \right) = 5;) \] \[ ((t_2) = \frac((9 - \sqrt (105) ))(6):)\;\; (x\left((\frac((9 - \sqrt (105) ))(6)) \right) \ca. 0,24;)\;\; (y\left((\frac((9 - \sqrt (105) ))(6)) \right) \ approx 0,91;) \] \[ ((t_3) = \frac(1)(3) :) \;\; (x\left((\frac(1)(3)) \right) = - \frac(5)((27)),)\;\; (y\left((\frac(1)(3)) \right) = - \frac((29))((27));) \] \[ ((t_4) = \frac((9 + \ sqrt (105) ))(6):)\;\; (x\left((\frac((9 + \sqrt (105) ))(6)) \right) \ca. 40,1;)\;\; (y\left((\frac((9 + \sqrt (105) ))(6)) \right) \ approx 40,8.) \] Daher stellen die angegebenen Punkte Wendepunkte der Kurve \(y\left( x \right).\)

Eine schematische Darstellung der Kurve \(y\left(x \right)\) ist oben in Abbildung \(15b.\) dargestellt.